The Effect of Fractional Orders on the Transmission Power and Efficiency of Fractional-Order Wireless Power Transmission System

Abstract

To avoid the problems of integer-order magnetic resonant wireless power transmission (WPT) systems, such as low output power and transmission efficiency, high resonant frequency, frequency splitting, and parameter coupling, a novel WPT system based on the fractional-order calculus theory is proposed; the resonant frequency and coupling coefficient can be regulated by the fractional order, so that this system has completely different transmission characteristics from the integer-order WPT system. Therefore, in this paper, the circuit model based on the phasor method of fractional-order WPT system is established, and the output power and transmission efficiency of the system are analyzed. In addition, the comparative analysis of output power and transmission efficiency under different fractional orders are performed to estimate the optimal combination of fractional orders, which is beneficial to produce better characteristics of output power and transmission efficiency and provides a theoretical basis for the design and implementation of an experimental system.

1. Introduction

Fractional calculus appeared at the same time as traditional integer-order calculus: its history can be traced back to the letter Leibniz wrote to L’Hospital in 1695 [1]. In the letter, Leibniz proposed the question of extending the differential order from integer to non-integer, which is regarded as the birth of fractional calculus. However, fractional calculus did not developed as quickly as traditional calculus due to its complex analysis and lack of application. In the 19th century, the logic definitions of fractional calculus were proposed by Liouville in 1834, Riemann in 1847, Grünwald in 1867, and Caputo in 1967 [2,3,4,5], and the theoretical system of fractional calculus was gradually perfected. In recent years, fractional calculus has been widely investigated and applied to the modeling of many real phenomenon or actual systems, such as super capacitor [6], skin effect of the inductor [7], and fractal structures [8]. Besides, the concept of fractional order has been used in many areas such as physics, environmental hydraulics, biomedical applications, automatic control theory, electromagnetics, electrical circuits, and chaotic systems, etc. In the analysis of the fractional-order electrical circuits, Radwan generalized the fundamentals of the conventional RL, RC, and RLC (R is the circuit symbol for resistor, L is the circuit symbol for inductor, C is the circuit symbol for capacitor) circuits in a fractional-order sense [9,10], and introduced the generalized concept of the mutual inductance in the fractional-order domain [11].

Recently, Caputo’s definition has been widely used. The detailed Caputo’s definition of the fractional-order derivative of order α can be written as [3,4].

$${}_{c}D_t^{\alpha }f\left(t\right)=\{\begin{array}{cc}\frac{1}{\mathrm{\Gamma }\left(n-\alpha \right)}{\displaystyle {\int }_c^t\frac{f^{\left(n\right)}\left(\tau \right)}{{\left(t-\tau \right)}^{\alpha +1-n}}d\tau }& n-1<\alpha <n\\ \frac{d^n}{d{t}^n}f\left(t\right)& \alpha =n\end{array}$$

(1)

where c and t are the initial time and required time of calculation, n is an integer, Γ(z) is a gamma function, which is defined as $\mathrm{\Gamma }\left(z\right)={\displaystyle {\int }_0^{\infty }{e}^{-t}{t}^{z-1}}dt$.

The Laplace transform of Equation (1) with zero initial conditions is

$$L\left\{{}_{0}D_t^{\alpha }f\left(t\right)\right\}=s^{\alpha }F\left(s\right)$$

(2)

The concept of wireless power transmission (WPT) was proposed by Nikola Tesla more than a hundred years ago, but the breakthrough in this technology occurred in 2007 when Marin Soljačić proposed the concept of WPT via strongly coupled magnetic resonances, which transfers 60 watts with 40% efficiency over distances in excess of 2 m [12]. Since then, this technology has been widely studied by more scholars.

While the existing theoretical analysis of the WPT system is based on the integral-order calculus theory, many practical problems such as the skin effect of inductance and the distribution of capacitance potential cannot be explained by the integral-order circuit theory. In addition, the integral-order magnetic resonant WPT system has some problems, including low output power, low efficiency, high resonant frequency, coupling of parameters, frequency splitting, and electromagnetic radiation. In order to avoid these problems effectively, a novel WPT system based on the fractional-order calculus theory was proposed, whose resonant frequency and coupling coefficient can be adjusted by the fractional order to improve the transmission performance of the system. Therefore, in this paper, the effect of the fractional orders on the output power and transmission efficiency of the WPT system is analyzed. Firstly, the circuit model of the fractional-order WPT system is established, then, the modified expressions of output power and transmission efficiency are derived. Finally, the influence of the fractional orders (α₁, α₂, β) on output power and transmission efficiency are analyzed in detail.

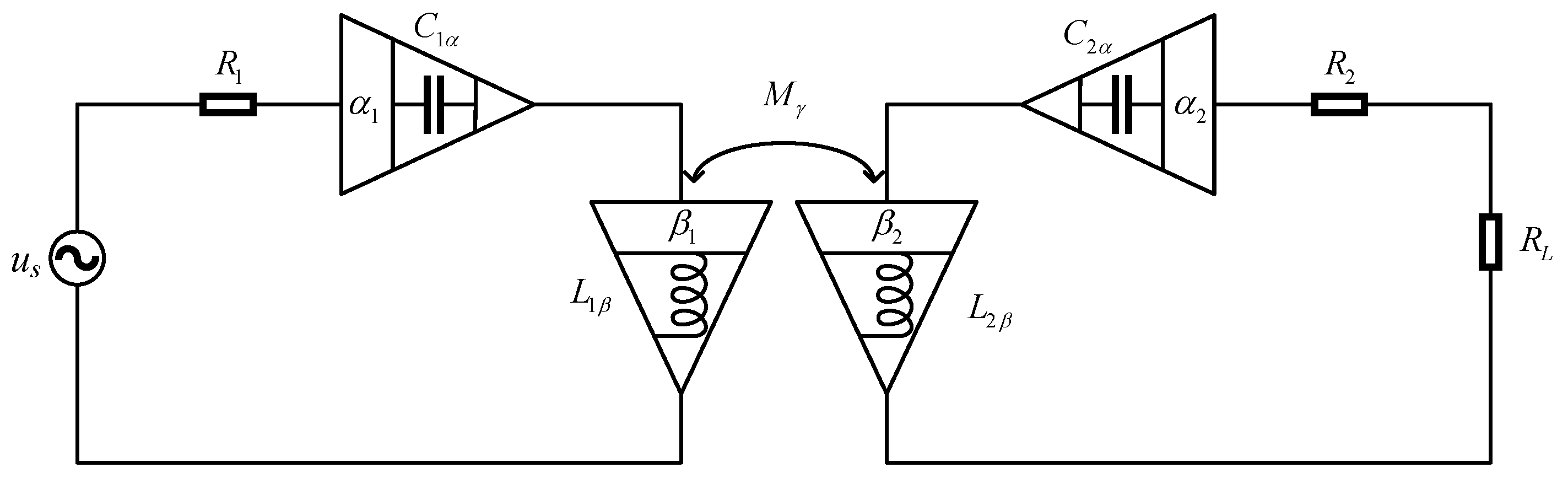
2. System Structure and Modeling

Generally, a fractional-order WPT system consists mainly of a source, transmitter, receiver, and load. The source u_s is usually achieved by an inverter, such as half-bridge, full-bridge, and others, which serves as power supply for the whole system. The transmitter contains an inductance L_1β with fractional-order characteristics, a capacitance C_1α with fractional-order characteristics, and an internal resistance R₁ of the transmitting circuit. The receiver also comprises a fractional-order inductance L_2β, a fractional-order capacitance C_2α, an internal resistance R₂ of the receiving circuit, and a load R_L. The circuit coupling is realized through the mutual inductance M_γ between the transmitting and receiving coil. The simplified schematic diagram is shown in Figure 1, in which L_1β and L_2β are pseudo-inductance values of the fractional-order inductance of the transmitter and receiver, respectively, C_1α and C_2α are pseudo-capacitance values of the fractional-order capacitance of the transmitter and receiver, respectively, β₁ and β₂ are the fractional orders of the fractional-order inductance of the transmitter and receiver, respectively, α₁ and α₂ are the fractional orders of the fractional-order capacitance of the transmitter and receiver, respectively, and M_γ and γ are pseudo-inductance value and the fractional order of fractional-order mutual inductance, respectively.

The dynamics of this fractional-order WPT system can be fully described by the differential equations as follows

$$\{\begin{array}{l}{u}_s=i_1{R}_1+u_{C_1}+L_{1\beta }\frac{d^{{\beta }_1}{i}_1}{d{t}^{{\beta }_1}}+M_{\gamma }\frac{d^{\gamma }{i}_2}{d{t}^{\gamma }}\\ 0=i_2\left(R_2+R_L\right)+u_{C_2}+L_{2\beta }\frac{d^{{\beta }_2}{i}_2}{d{t}^{{\beta }_2}}+M_{\gamma }\frac{d^{\gamma }{i}_1}{d{t}^{\gamma }}\\ i_1=C_{1\alpha }\frac{d^{{\alpha }_1}{u}_{C_1}}{d{t}^{{\alpha }_1}}\\ i_2=C_{2\alpha }\frac{d^{{\alpha }_2}{u}_{C_2}}{d{t}^{{\alpha }_2}}\end{array}$$

(3)

where i₁ and i₂ are currents flowing through the fractional-order inductances, u_C1 and u_C2 are voltages across the fractional-order capacitances, and u_s is the output voltage of power supply.

To simplify the analysis, give the phasor forms of Equation (3) and simplify it as

$$\{\begin{array}{l}{\dot{U}}_s\left(j\omega \right)=Z_1{\dot{I}}_1\left(j\omega \right)+Z_M{\dot{I}}_2\left(j\omega \right)\\ 0=Z_M{\dot{I}}_1\left(j\omega \right)+Z_2{\dot{I}}_2\left(j\omega \right)\end{array}$$

(4)

Here, Z₁ is the equivalent impedance of the transmitter, Z₂ is the equivalent impedance of the receiver, and Z_M is the equivalent mutual impedance, which are defined as follows

$$\{\begin{array}{l}{Z}_1=\left(R_1+R_{L1}+R_{C1}\right)+j\left(X_{L1}-X_{C1}\right)\\ Z_2=\left(R_2+R_L+R_{L2}+R_{C2}\right)+j\left(X_{L2}-X_{C2}\right)\\ Z_M=R_M+j{X}_M\end{array}$$

(5)

where R_L1 and R_C1 are equivalent resistances of fractional-order inductance and fractional-order capacitance of the transmitter, respectively, X_L1 and X_C1 are equivalent reactances of fractional-order inductance and fractional-order capacitance of the transmitter, respectively, R_L2 and R_C2 are equivalent resistances of fractional-order inductance and fractional-order capacitance of the receiver, respectively, X_L2 and X_C2 are equivalent reactances of fractional-order inductance and fractional-order capacitance of the receiver, respectively, and R_M and X_M are equivalent resistance and equivalent reactance of fractional-order mutual inductance, respectively, which are described as follows

$$\{\begin{array}{l}{R}_{L1}={\omega }^{{\beta }_1}{L}_{1\beta }\cos \frac{{\beta }_1\pi }{2},R_{C1}=\frac{1}{{\omega }^{{\alpha }_1}{C}_{1\alpha }}\cos \frac{{\alpha }_1\pi }{2},X_{L1}={\omega }^{{\beta }_1}{L}_{1\beta }\sin \frac{{\beta }_1\pi }{2},X_{C1}=\frac{1}{{\omega }^{{\alpha }_1}{C}_{1\alpha }}\sin \frac{{\alpha }_1\pi }{2}\\ R_{L2}={\omega }^{{\beta }_2}{L}_{2\beta }\cos \frac{{\beta }_2\pi }{2},R_{C2}=\frac{1}{{\omega }^{{\alpha }_2}{C}_{2\alpha }}\cos \frac{{\alpha }_2\pi }{2},X_{L2}={\omega }^{{\beta }_2}{L}_{2\beta }\sin \frac{{\beta }_2\pi }{2},X_{C2}=\frac{1}{{\omega }^{{\alpha }_2}{C}_{2\alpha }}\sin \frac{{\alpha }_2\pi }{2}\\ R_M={\omega }^{\gamma }{M}_{\gamma }\cos \frac{\gamma \pi }{2},X_M={\omega }^{\gamma }{M}_{\gamma }\sin \frac{\gamma \pi }{2}\end{array}$$

(6)

From Equations (4) and (5), the currents flowing through the fractional-order inductances of the transmitter and receiver can be derived as

$$\{\begin{array}{l}{\dot{I}}_1\left(j\omega \right)=\frac{Z_2{\dot{U}}_s\left(j\omega \right)}{Z_1{Z}_2-Z_M^2}\\ {\dot{I}}_2\left(j\omega \right)=-\frac{Z_M{\dot{U}}_s\left(j\omega \right)}{Z_1{Z}_2-Z_M^2}\end{array}$$

(7)

Considering that the fractional-order elements have a negative resistance property, the input power P_in of the system is modified as

$$\begin{array}{l}{P}_{in}={\left|I_1\right|}^2\left[R_1+\frac{1-\mathrm{sgn}({\beta }_1-1)}{2}{R}_{L_1}+\frac{1-\mathrm{sgn}({\alpha }_1-1)}{2}{R}_{C_1}\right]+{\left|I_2\right|}^2\left[R_2+R_L+\frac{1-\mathrm{sgn}({\beta }_2-1)}{2}{R}_{L_2}+\frac{1-\mathrm{sgn}({\alpha }_2-1)}{2}{R}_{C_2}\right]+2\frac{1-\mathrm{sgn}(\gamma -1)}{2}{R}_M\mathrm{Re}\left(I_1^{\ast }{I}_2\right)\\ =\frac{\left\{\begin{array}{l}\left[{\left(R_2+R_L+R_{L2}+R_{C2}\right)}^2+{\left(X_{L2}-X_{C2}\right)}^2\right]\left[R_1+\frac{1-\mathrm{sgn}({\beta }_1-1)}{2}{R}_{L_1}+\frac{1-\mathrm{sgn}({\alpha }_1-1)}{2}{R}_{C_1}\right]\\ +\left(R_M^2+X_M^2\right)\left[R_2+R_L+\frac{1-\mathrm{sgn}({\beta }_2-1)}{2}{R}_{L_2}+\frac{1-\mathrm{sgn}({\alpha }_2-1)}{2}{R}_{C_2}\right]\\ -R_M\left[1-\mathrm{sgn}(\gamma -1)\right]\left[\left(R_2+R_L+R_{L2}+R_{C2}\right)R_M+\left(X_{L2}-X_{C2}\right)X_M\right]\end{array}\right\}}{\left\{\begin{array}{l}{\left[\left(R_1+R_{L1}+R_{C1}\right)\left(R_2+R_L+R_{L2}+R_{C2}\right)-R_M^2+X_M^2-\left(X_{L1}-X_{C1}\right)\left(X_{L2}-X_{C2}\right)\right]}^2\\ +{\left[\left(X_{L1}-X_{C1}\right)\left(R_2+R_L+R_{L2}+R_{C2}\right)+\left(X_{L2}-X_{C2}\right)\left(R_1+R_{L1}+R_{C1}\right)-2R_M{X}_M\right]}^2\end{array}\right\}}{U}_s^2\end{array}$$

(8)

where sgn(x) is defined as $\mathrm{sgn}(x)=\{\begin{array}{cc}1& x>0\\ -1& x\le 0\end{array}$.

The power delivered to the load P_o can be expressed as

$$P_o={\left|I_2\right|}^2{R}_L=\frac{\left(R_M^2+X_M^2\right)R_L}{\left\{\begin{array}{l}{\left[\left(R_1+R_{L1}+R_{C1}\right)\left(R_2+R_L+R_{L2}+R_{C2}\right)-R_M^2+X_M^2-\left(X_{L1}-X_{C1}\right)\left(X_{L2}-X_{C2}\right)\right]}^2\\ +{\left[\left(X_{L1}-X_{C1}\right)\left(R_2+R_L+R_{L2}+R_{C2}\right)+\left(X_{L2}-X_{C2}\right)\left(R_1+R_{L1}+R_{C1}\right)-2R_M{X}_M\right]}^2\end{array}\right\}}{U}_s^2$$

(9)

Therefore, the transmission efficiency η can be described as

$$\begin{array}{l}\eta =\frac{R_L}{\left\{\begin{array}{l}\frac{{\left|I_1\right|}^2}{{\left|I_2\right|}^2}\left[R_1+\frac{1-\mathrm{sgn}({\beta }_1-1)}{2}{R}_{L_1}+\frac{1-\mathrm{sgn}({\alpha }_1-1)}{2}{R}_{C_1}\right]+\left[R_2+R_L+\frac{1-\mathrm{sgn}({\beta }_2-1)}{2}{R}_{L_2}+\frac{1-\mathrm{sgn}({\alpha }_2-1)}{2}{R}_{C_2}\right]\\ -\frac{\left[1-\mathrm{sgn}(\gamma -1)\right]\left[\left(R_2+R_L+R_{L2}+R_2\right)R_M+\left(X_{L2}-X_{C2}\right)X_M\right]}{R_M^2+X_M^2}{R}_M\end{array}\right\}}\\ =\frac{R_L}{\left\{\begin{array}{l}\frac{{\left(R_2+R_L+R_{L2}+R_{C2}\right)}^2+{\left(X_{L2}-X_{C2}\right)}^2}{R_M^2+X_M^2}\left[R_1+\frac{1-\mathrm{sgn}({\beta }_1-1)}{2}{R}_{L_1}+\frac{1-\mathrm{sgn}({\alpha }_1-1)}{2}{R}_{C_1}\right]+\left[R_2+R_L+\frac{1-\mathrm{sgn}({\beta }_2-1)}{2}{R}_{L_2}+\frac{1-\mathrm{sgn}({\alpha }_2-1)}{2}{R}_{C_2}\right]\\ -\frac{\left[1-\mathrm{sgn}(\gamma -1)\right]\left[\left(R_2+R_L+R_{L2}+R_2\right)R_M+\left(X_{L2}-X_{C2}\right)X_M\right]}{R_M^2+X_M^2}{R}_M\end{array}\right\}}\end{array}$$

(10)

When the whole system meets the condition of resonance, the angular frequencies of transmitter and receiver are equal to the angular frequency of power supply, as shown in the following

$${\omega }_0=\sqrt[{\alpha }_1+{\beta }_1]{\frac{\sin \frac{{\alpha }_1\pi }{2}}{L_1{C}_1\sin \frac{{\beta }_1\pi }{2}}}=\sqrt[{\alpha }_2+{\beta }_2]{\frac{\sin \frac{{\alpha }_2\pi }{2}}{L_2{C}_2\sin \frac{{\beta }_2\pi }{2}}}$$

(11)

Substituting Equations (6) and (11) into Equations (8)–(10), the input power, output power, and transmission efficiency at the resonance of system are

$$P_{in}=\frac{\left\{\begin{array}{l}{\left(R_2+R_L+R_{L2}+R_{C2}\right)}^2\left[R_1+\frac{1-\mathrm{sgn}({\beta }_1-1)}{2}{R}_{L_1}+\frac{1-\mathrm{sgn}({\alpha }_1-1)}{2}{R}_{C_1}\right]\\ +\left(R_M^2+X_M^2\right)\left[R_2+R_L+\frac{1-\mathrm{sgn}({\beta }_2-1)}{2}{R}_{L_2}+\frac{1-\mathrm{sgn}({\alpha }_2-1)}{2}{R}_{C_2}\right]-\left[1-\mathrm{sgn}(\gamma -1)\right]\left(R_2+R_L+R_{L2}+R_{C2}\right)R_M^2\end{array}\right\}}{{\left[\left(R_1+R_{L1}+R_{C1}\right)\left(R_2+R_L+R_{L2}+R_{C2}\right)-R_M^2+X_M^2\right]}^2+4R_M^2{X}_M^2}{U}_s^2$$

(12)

$$P_o=\frac{\left(R_M^2+X_M^2\right)R_L}{{\left[\left(R_1+R_{L1}+R_{C1}\right)\left(R_2+R_L+R_{L2}+R_{C2}\right)-R_M^2+X_M^2\right]}^2+4R_M^2{X}_M^2}{U}_s^2$$

(13)

$$\eta =\frac{\left(R_M^2+X_M^2\right)R_L}{\left\{\begin{array}{l}{\left(R_2+R_L+R_{L2}+R_{C2}\right)}^2\left[R_1+\frac{1-\mathrm{sgn}({\beta }_1-1)}{2}{R}_{L_1}+\frac{1-\mathrm{sgn}({\alpha }_1-1)}{2}{R}_{C_1}\right]+\left(R_M^2+X_M^2\right)\left[R_2+R_L+\frac{1-\mathrm{sgn}({\beta }_2-1)}{2}{R}_{L_2}+\frac{1-\mathrm{sgn}({\alpha }_2-1)}{2}{R}_{C_2}\right]\\ -\left[1-\mathrm{sgn}(\gamma -1)\right]\left(R_2+R_L+R_{L2}+R_2\right)R_M^2\end{array}\right\}}$$

(14)

Obviously, when the values of all fractional orders are unity, the expressions of input power, output power, and transmission efficiency are the same as those of the integer-order WPT system.

3. Analysis of Transmission Power and Efficiency

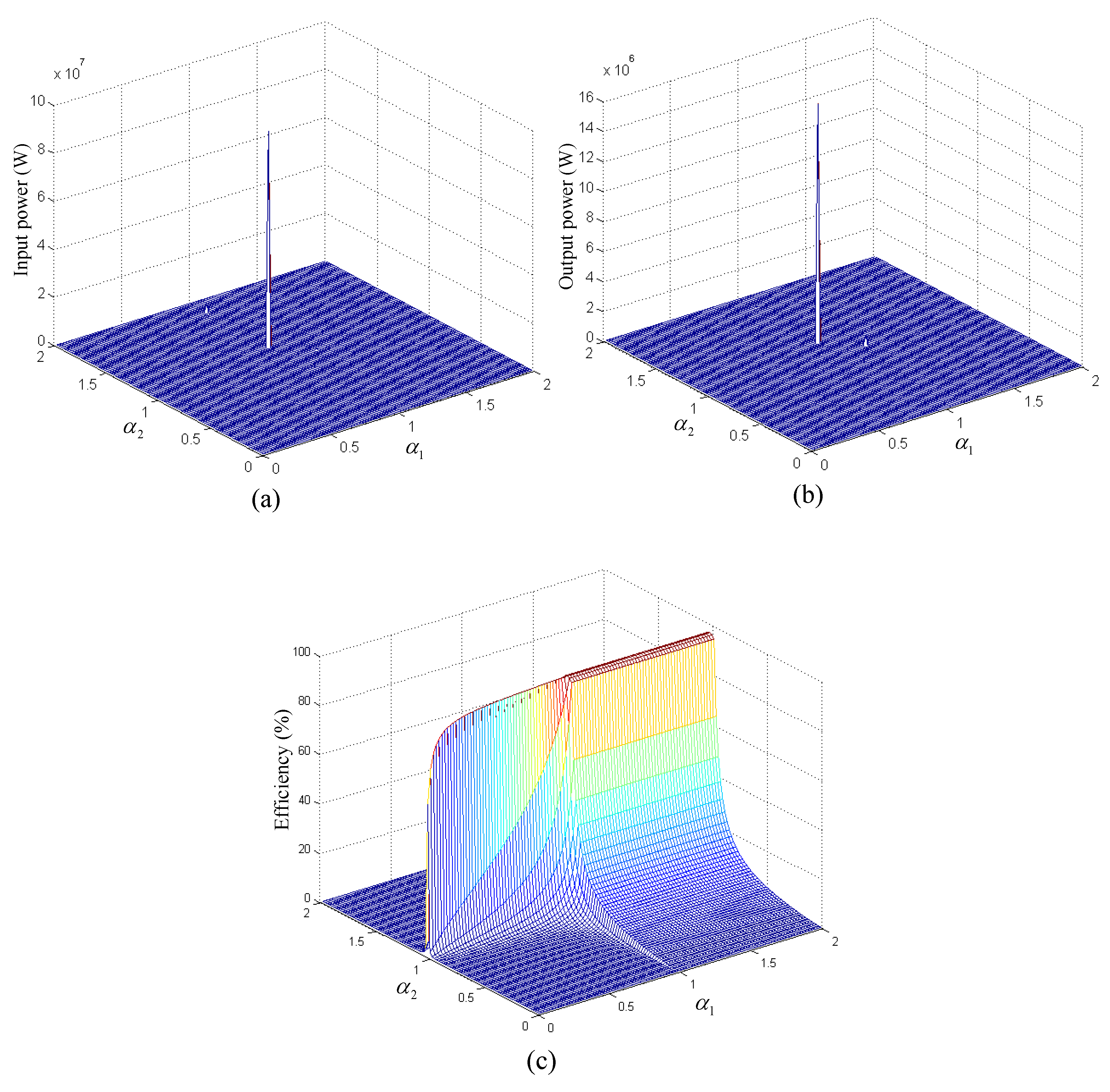
For a fractional-order element, it has a negative-resistance component when its fractional order is greater than 1. Without loss of generality, assuming the fractional order of mutual inductance is unity, that is γ = 1, for a WPT system with four fractional-order elements, there are 16 kinds of combinations of fractional orders as shown in Figure 2.

Combining the analysis of Figure 2 and Equations (8) and (10), it can be seen that the system’s input power and transmission efficiency have different expressions under different fractional orders. At present, the mechanism and manufacturing schemes of fractional-order inductors with 1 < β < 2 are still in the research stage, which is a valuable but difficult research topic; there are no articles of relevant studies. However, the fractional-order capacitors with 1 < α < 2 have been implemented in the electric power electronic devices [13]. Thus, this paper will only discuss the output power and transmission efficiency of the system with 0 < β_1,2 ≤ 1 and 0 < α_1,2 < 2. To intuitively show the transmission characteristics of the fractional-order WPT system, the parameters used for analysis are: the effective value of power supply U_s = 20 V, internal resistances of the transmitting and receiving circuit are R₁ = R₂ = 0.5 Ω, pseudo-inductances values of the transmitting and receiving circuit are L_1β = L_2β = 100 µH, the load resistance is R_L = 12 Ω, the pseudo-inductances value of mutual inductance is M_γ = 10 µH, and the resonant frequency is f₀ = 300 kHz. Here, to simplify the analysis, it is assumed that the fractional-order inductances of the transmitter and receiver are identical, that is β₁ = β₂ = β (0 < β ≤ 1).

Substituting the above parameters into Equations (12)–(14), and considering the fractional order of inductance is an integer (β = 1), the curves of output power and transmission efficiency at the resonance state as a function of fractional orders (α₁, α₂) are very complicated, as shown in Figure 3 and Figure 4.

From Figure 3 and Figure 4, it can be seen that the variation of transmission efficiency with α₁ is completely different from that with α₂, but the variation of output power with α₁ is very similar to that with α₂. When the system is in resonance, the fractional order of the inductances is β = 1, and when the fractional order of the receiver’s resonant capacitor α₂ is a fixed value, the transmission efficiency increases with the increase of α₁ in the case of 0 < α₁ ≤ 1, and the transmission efficiency remains constant in the case of 1 < α₁ < 2. The output power has a maximum as α₁ increases in the range of 0 < α₁ < 2, the corresponding values of α₁ are different under different fixed values of α₂, but they are all close to 1 when β = 1. However, when the fractional order of the transmitter’s resonant capacitor α₁ is a fixed value, the transmission efficiency increases first and then decreases with the increase of α₂, which has a maximum value, and the corresponding value of α₂ is close to 1. The output power also has a maximum value as α₂ increases in the range of 0 < α₂ < 2, the corresponding values of α₂ are different under different fixed values of α₁. From the above analysis, it can be seen that the system with β = 1 has better characteristics of output power and transmission efficiency when the fractional orders of transmitter’s and receiver’s resonant capacitor satisfy the conditions that 1 ≤ α₁ < 2 and 0.8 < α₂ < 1.2.

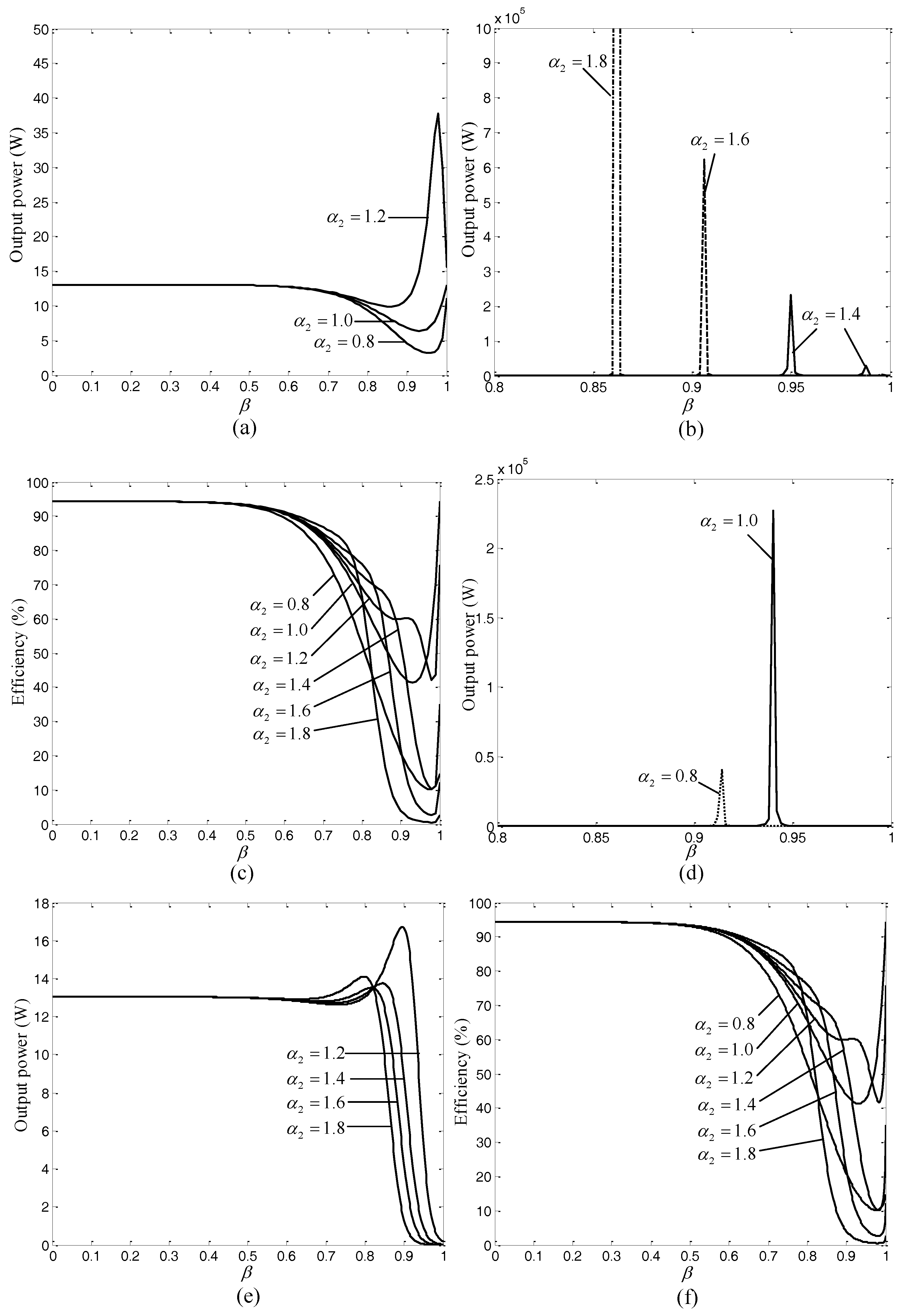
To understand the change law of output power and transmission efficiency with β, the variation of output power and transmission efficiency with β under different α₁ and α₂ is shown in Figure 5. As illustrated in Figure 5, the output power decreases first, then increases and then decreases with the increase of β. Whereas, the transmission efficiency decreases first and then increases with the increase of β. In addition, the law of output power varying with β is similar when α₁ ≥ 1.0, and the law of transmission efficiency varying with β is not affected by the variation of α₁ (1 ≤ α₁ < 2), thus, only two sets of curves are given here.

4. Conclusions

This paper establishes the circuit model of the fractional-order WPT system via the phasor method, derives the modified expressions of output power and transmission efficiency, and analyzes the influence of the fractional order (α₁, α₂, β) on output power and transmission efficiency in detail by numerical simulation. From the theoretical analysis, it can be seen that each fractional order (α₁, α₂ or β) has different effects on the transmission efficiency, the transmission efficiency increases as α₁ increases in the case of 0 < α₁ ≤ 1, but it remains constant in the case of 1 < α₁ < 2, the transmission efficiency has a maximum value with the increase of α₂, and the transmission efficiency decreases first and then increases with the increase of β. Nevertheless, the effect of fractional orders (α₁, α₂, β) on output power is similar and the output power has a maximum value as the fractional orders (α₁, α₂ or β) increase. Therefore, the optimal range of fractional orders (α₁, α₂, β) can be determined by the above theoretical analysis, which is beneficial to obtain better characteristics of output power and transmission efficiency.