Novel Method for Identifying Fault Location of Mixed Lines
Abstract
:1. Introduction
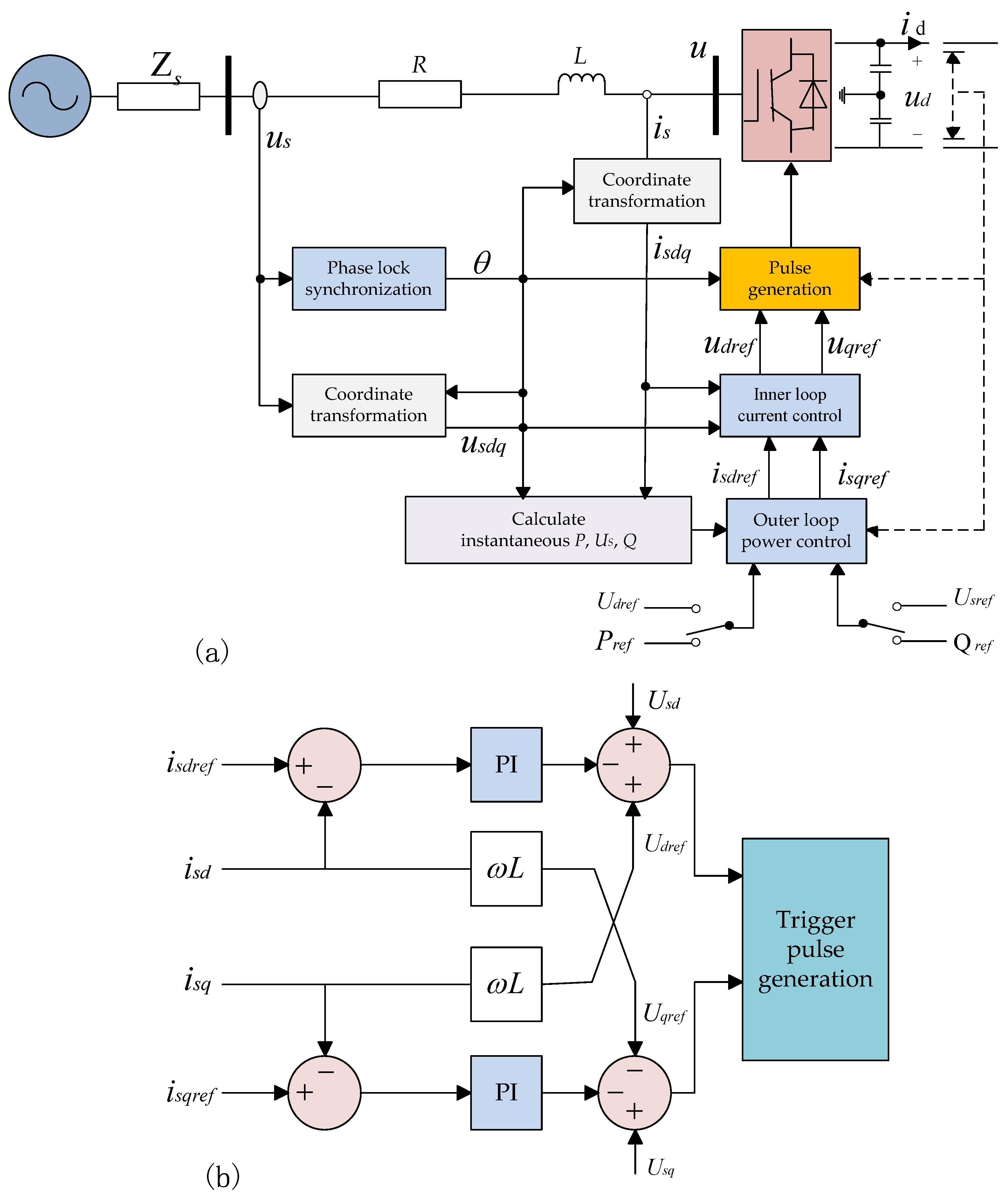
2. VSC-HVDC Transmission System Structure and Characteristics
3. Mothod Analysis and Application
3.1. Theoretical Background
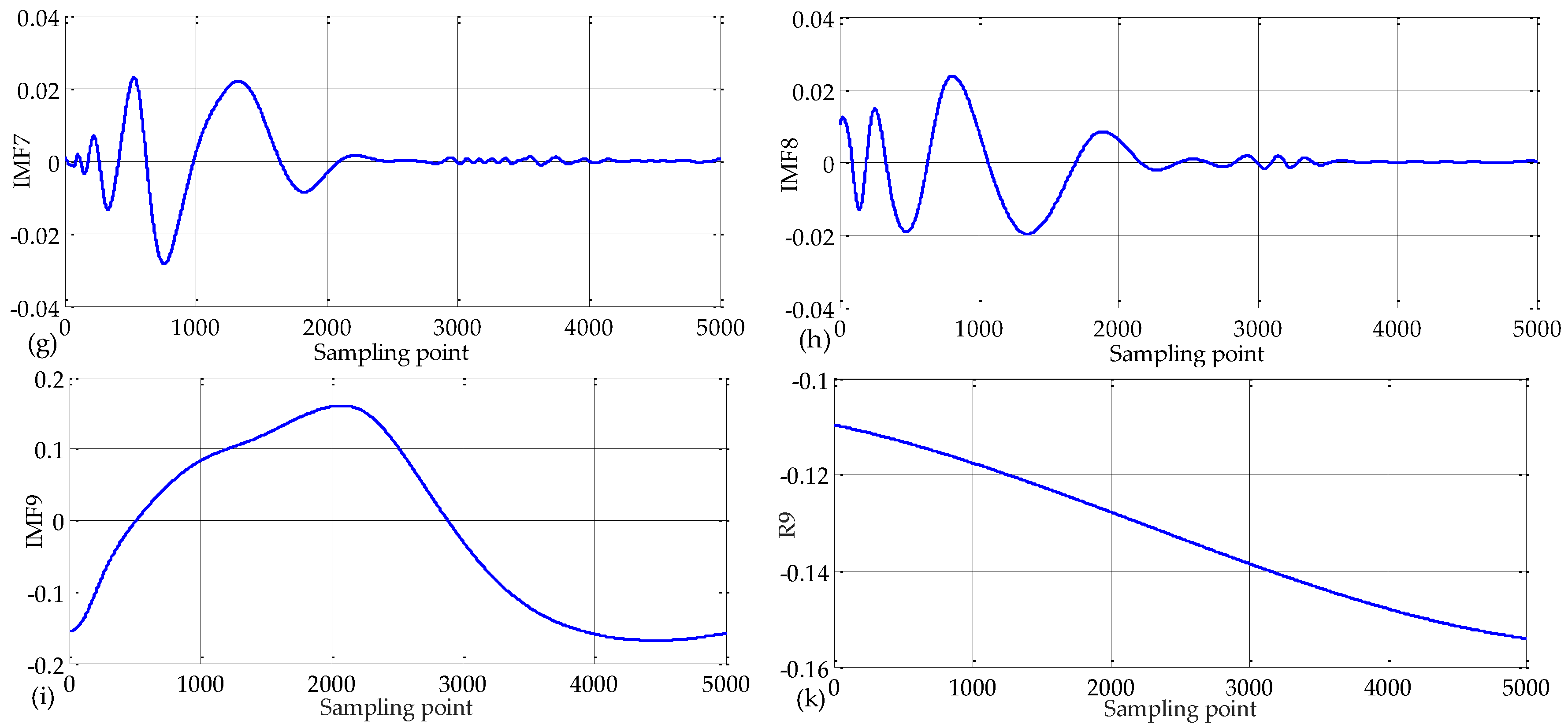
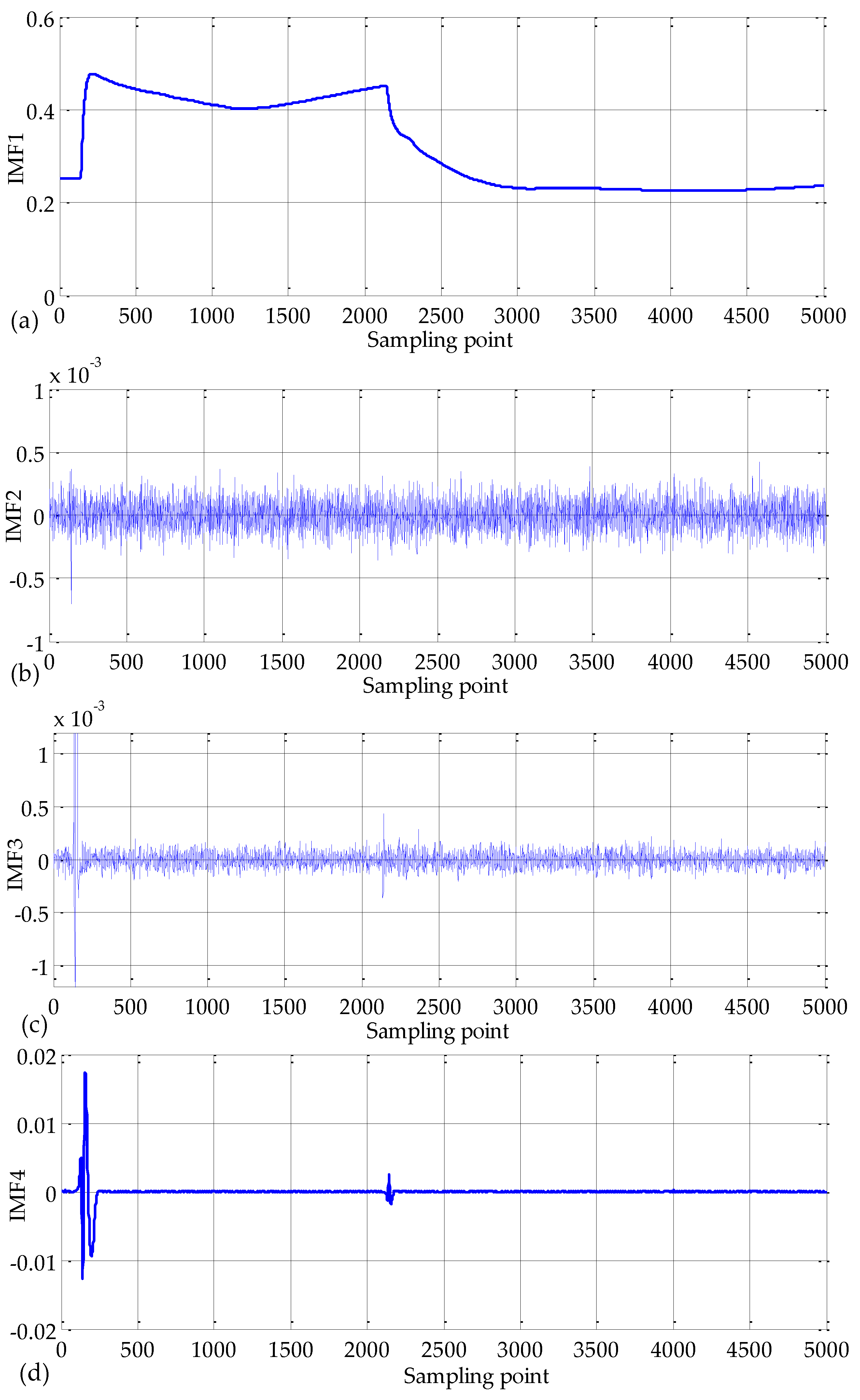
3.1.1. Variational Mode Decomposition (VMD)
Construction of Variational Problems
Solution of the Variational Problem
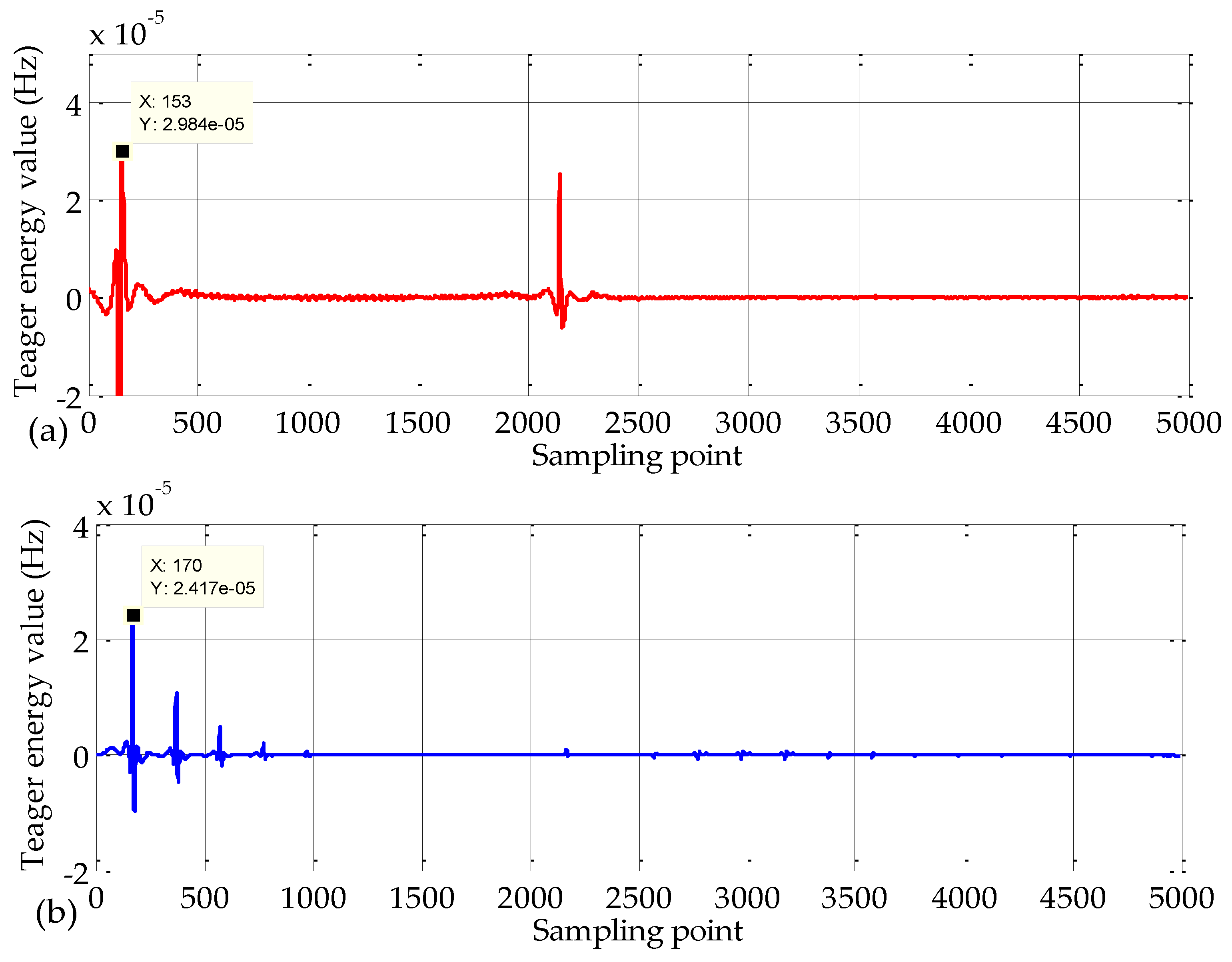
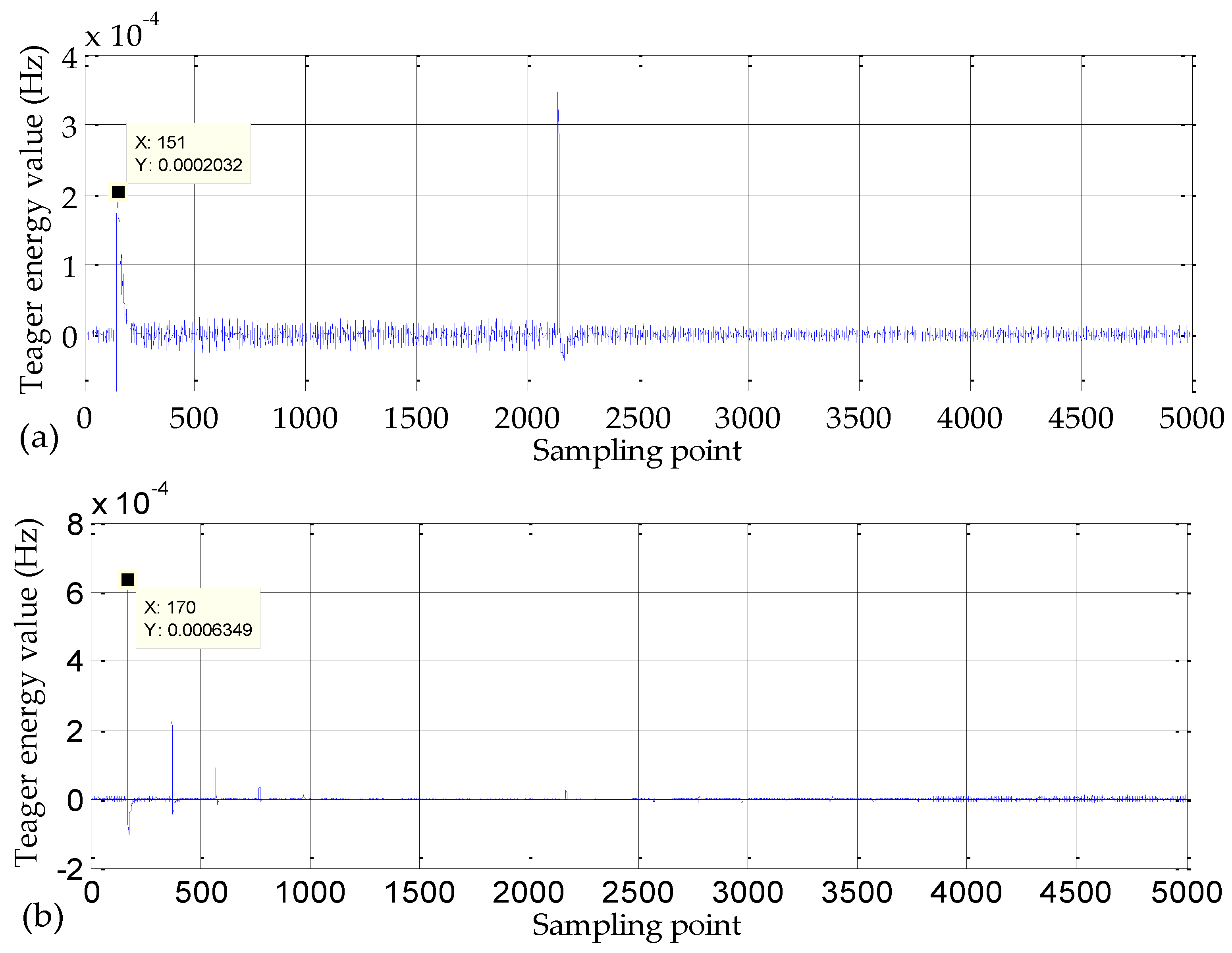
3.1.2. Teager Energy Operator (TEO)
3.2. VMD and TEO for Fault Location
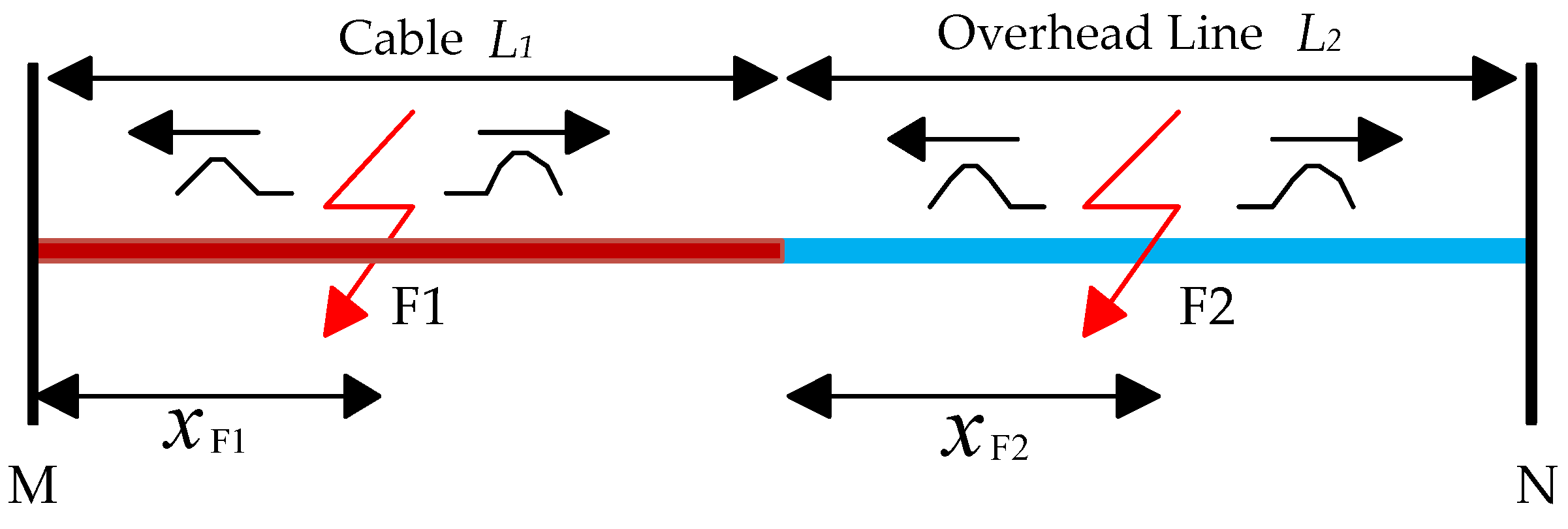
3.2.1. Fault Location Based on Traveling Wave Theory
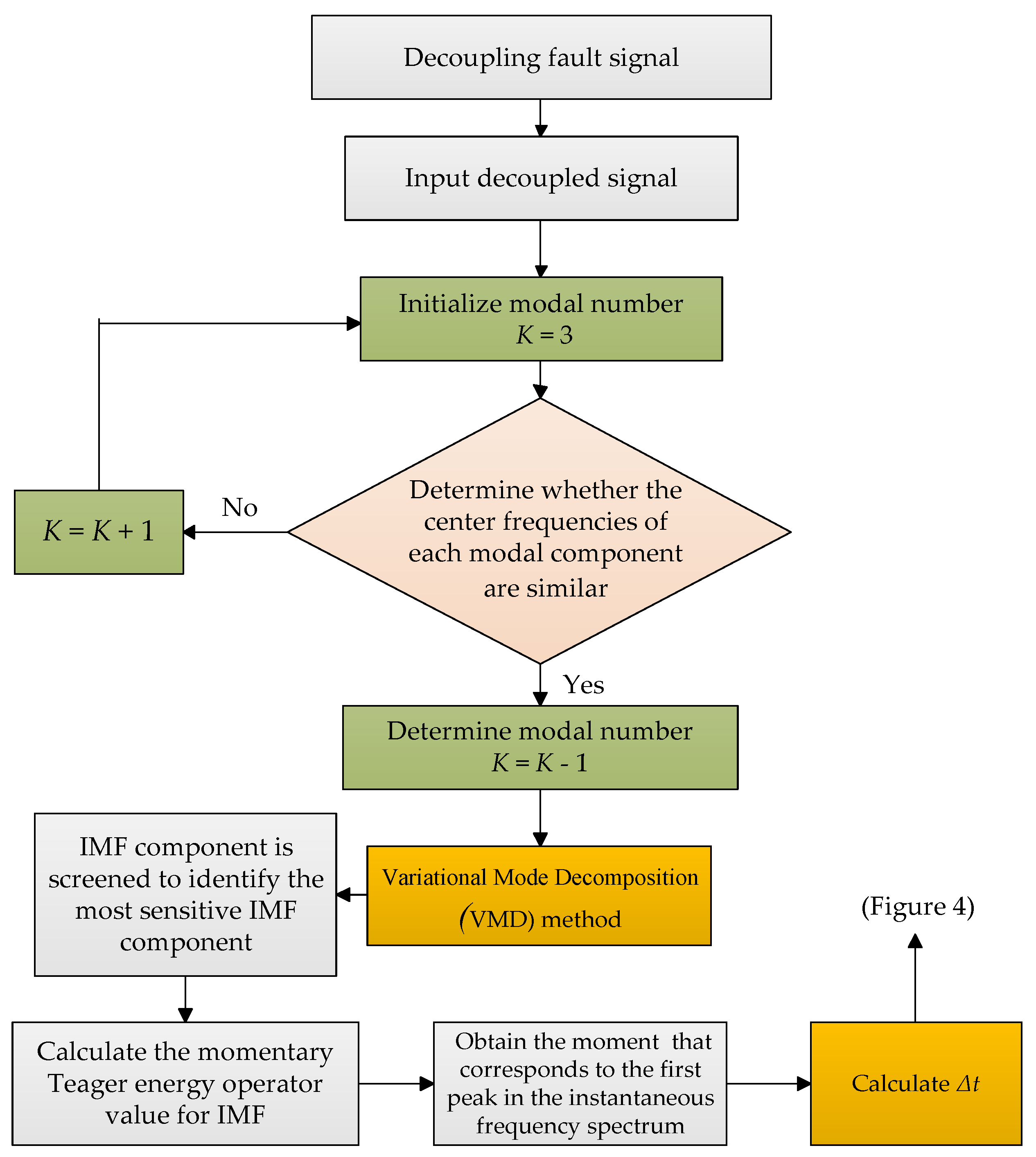
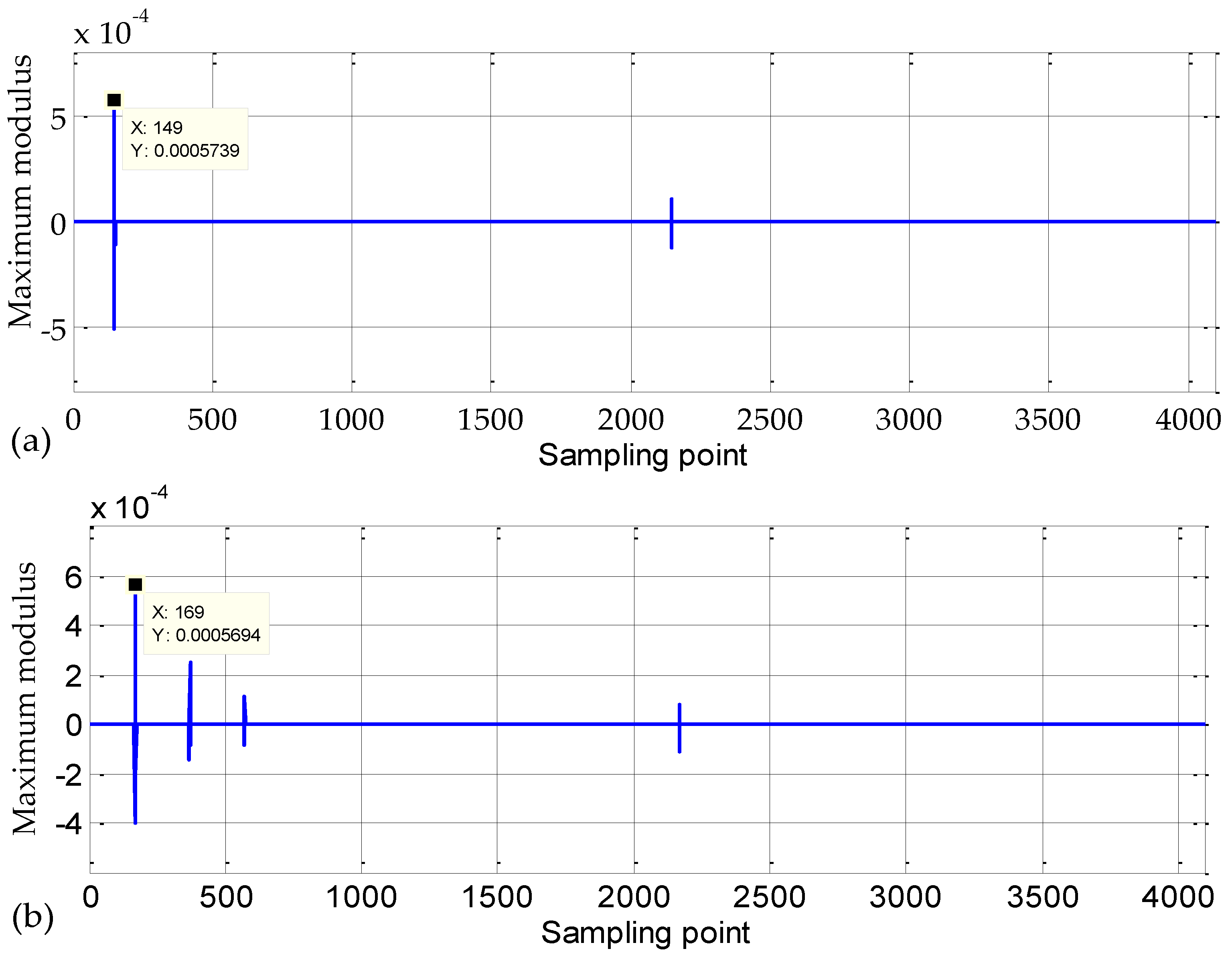
3.2.2. Process of Fault Location
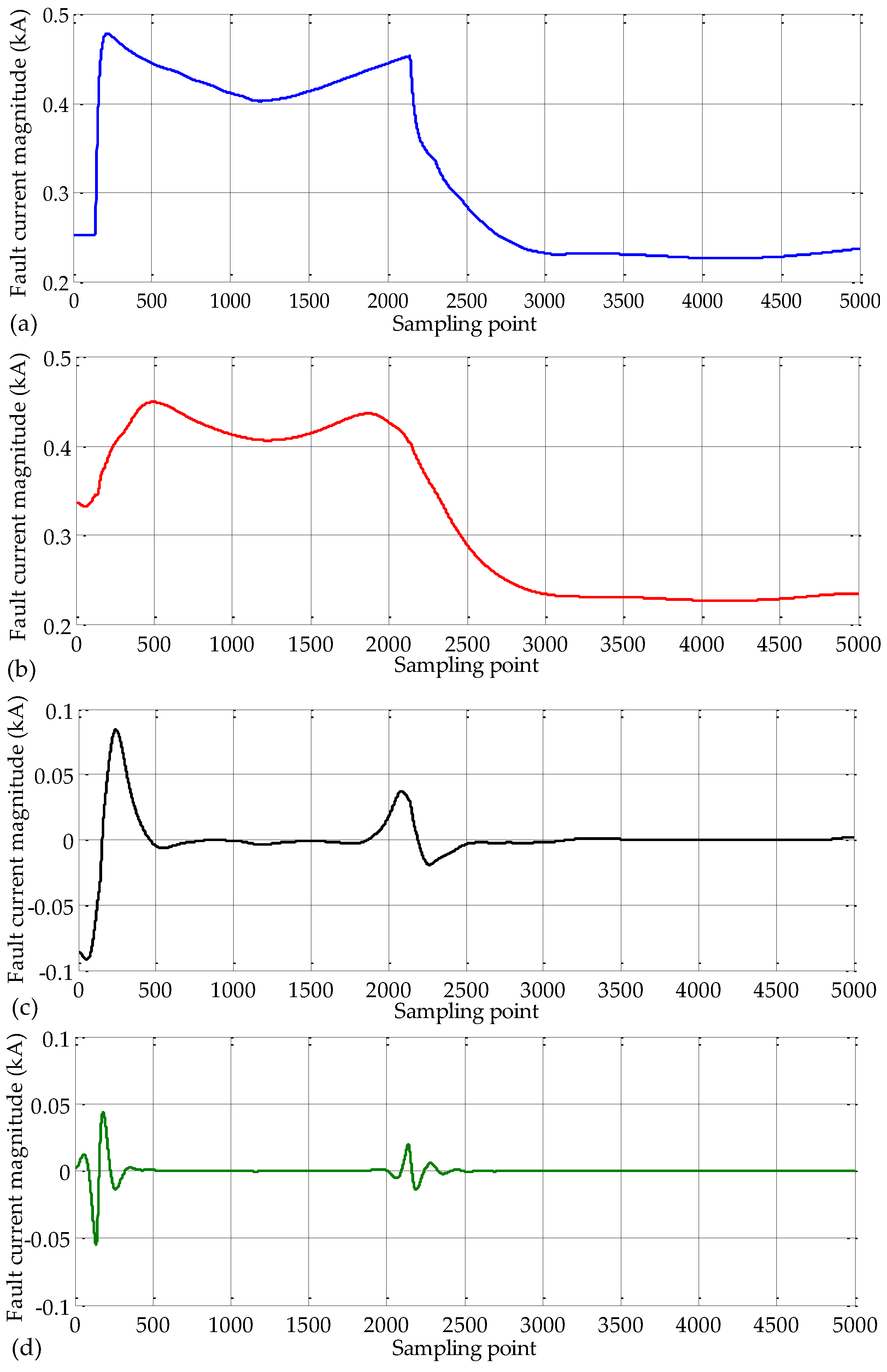
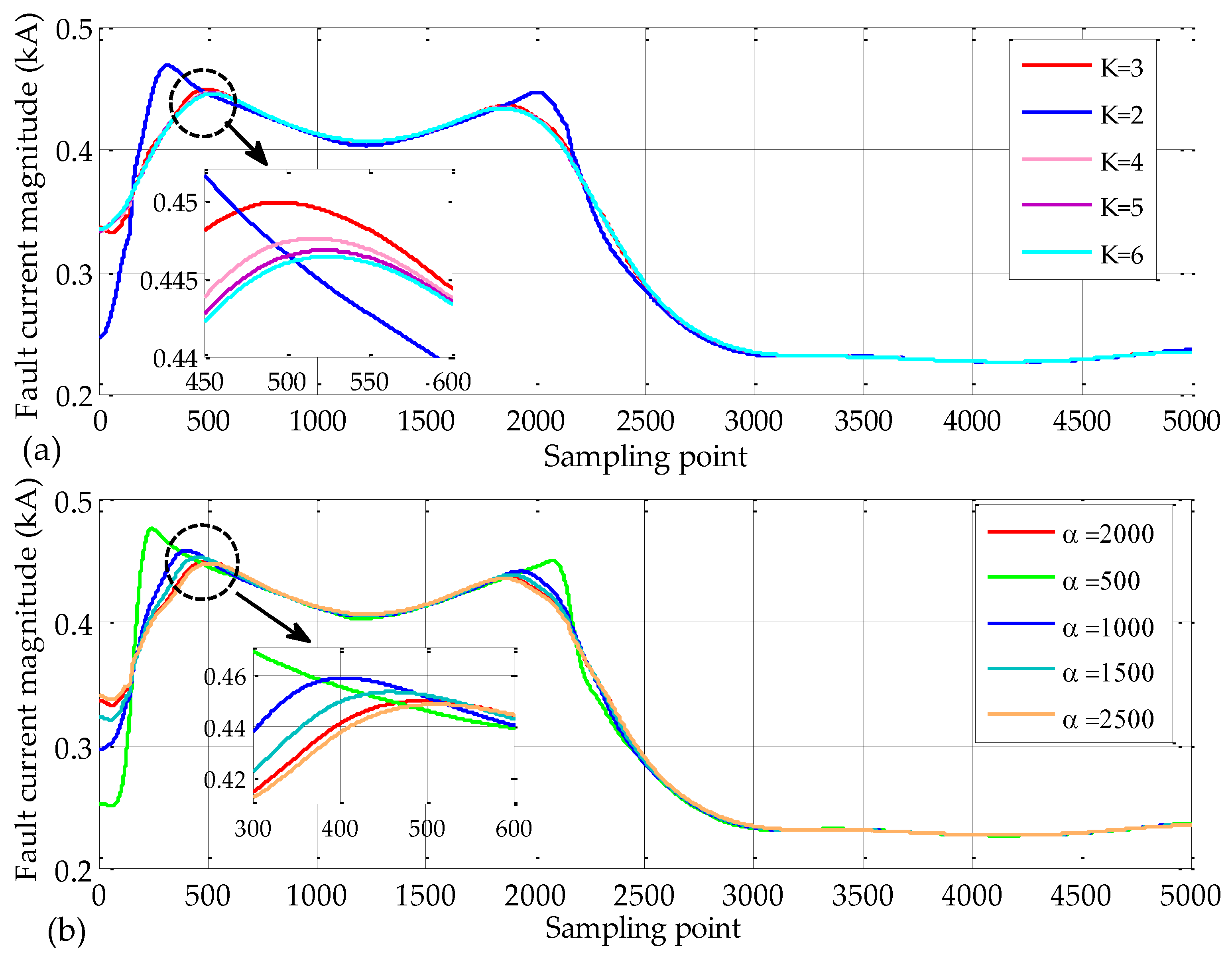
4. Results and Analysis
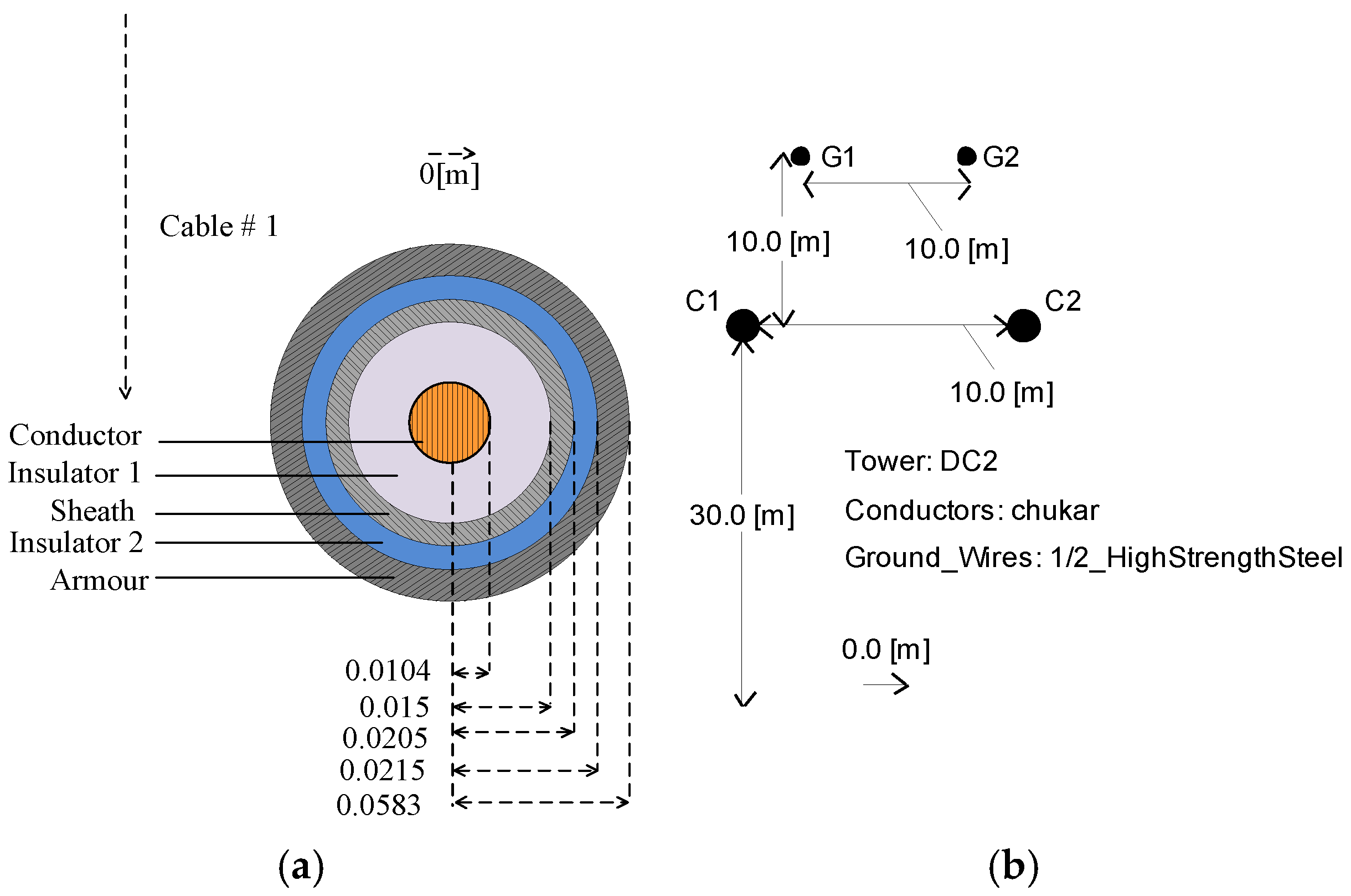
4.1. Tested Model and Related Parameters
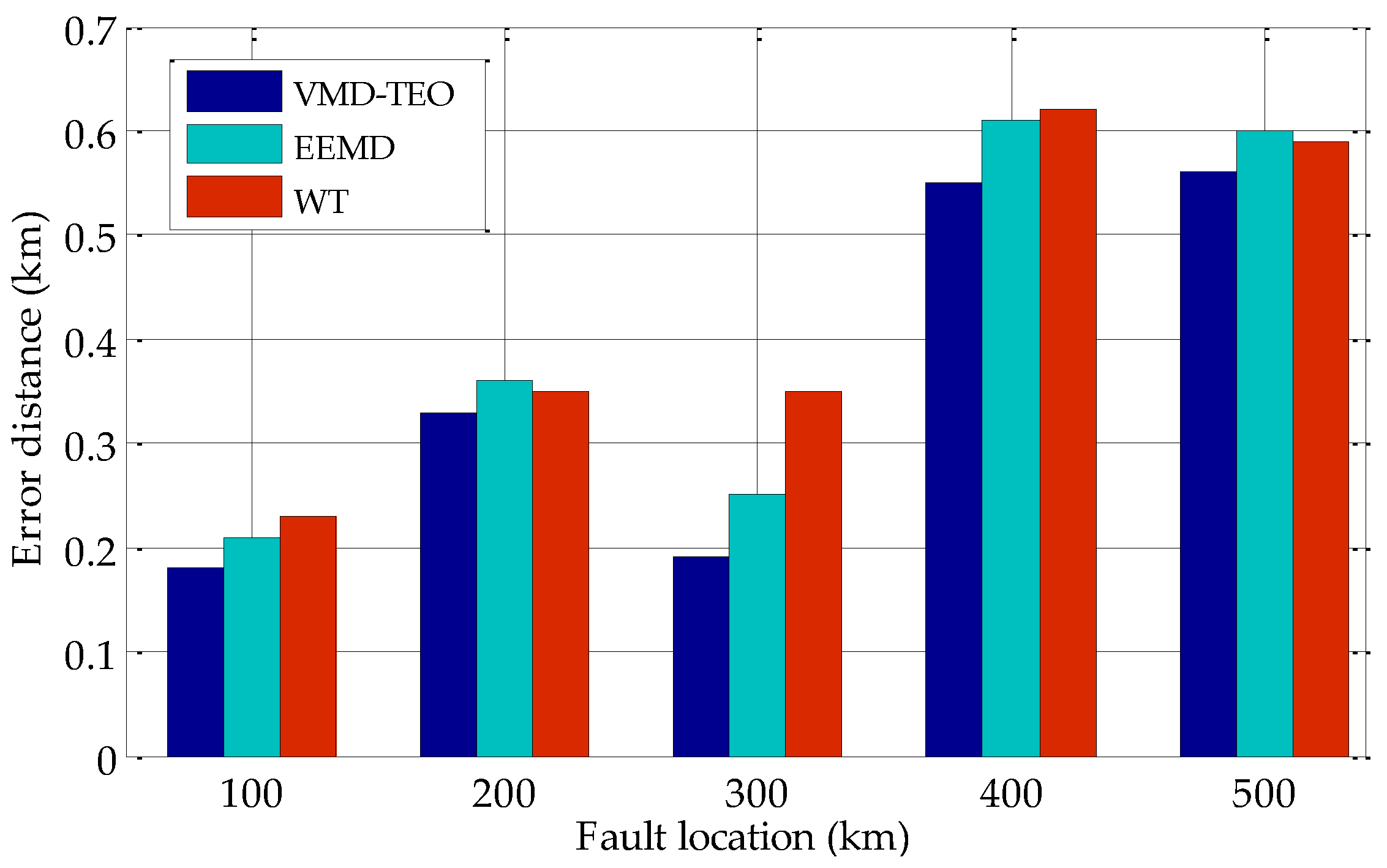
4.2. Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| uk(t) | The original signal f into the Intrinsic Mode Function, which is expressed as K modal function |
| δ(t) | The reciprocal of the instantaneous frequency of uk(t) |
| ωk | The frequency center of K modal function |
| ∂t | Find the partial derivative of function with respect to t |
| A | The quadratic penalty factor |
| L | The augmented Lagrangian expression for solution of variational problem |
| λ(t) | Lagrange multiplication operator |
| argmin | Find all arguments that make the function a minimum value |
| Update the modes uk by solving the equivalent minimization problem | |
| The equivalent minimization problem is solved in a spectral domain | |
| A Wiener filtering of the current residual | |
| The barycenter of the power spectrum of the current modal function | |
| {uk(t)} | The real part after the inverse Fourier transform of |
| The energy operator of the continuous signal f (t) | |
| The energy operator of the discrete signal f (n) | |
| v1 | The traveling wave velocity on the cable |
| v2 | The traveling wave velocity on the overhead line |
| xF1 | The fault distance |
| xF2 | The distance from F2 to the junction of the hybrid line |
| Δt | The difference between the time when the traveling wave reaches terminals M and N |
| L1 | The length of the cable |
| L2 | The length of the overhead line |
| im0 | The currents of the zero-mode traveling wave after decoupling |
| im1 | The currents of the one-mode traveling wave after decoupling |
| iP | The currents of the positive electrode |
| iN | The currents of the negative electrode |
| S | The decoupling matrix |
| K | The modal number |
| τ | The bandwidth |
References
- Reed, G.F.; Al Hassan, H.A.; Korytowski, M.J.; Lewis, P.T.; Grainger, B.M. Comparison of HVAC and HVDC solutions for offshore wind farms with a procedure for system economic evaluation. In Proceedings of the IEEE Energytech, Cleveland, OH, USA, 21–23 May 2013. [Google Scholar]
- Song, G.; Cai, X.; Gao, S. Survey of fault location research for HVDC transmission lines. Power Syst. Prot. Control 2012, 40, 133–137. (In Chinese) [Google Scholar]
- Hamidi, R.J.; Livani, H.; Rezaiesarlak, R. Traveling-wave detection technique using short-time matrix pencil method. IEEE Trans. Power Deliv. 2017, 32, 2565–2574. [Google Scholar]
- Lopes, F.; Dantas, K.; Silva, K.; Costa, F.B. Accurate two-terminal transmission line fault location using traveling waves. IEEE Trans. Power Deliv. 2017, 33, 873–880. [Google Scholar] [CrossRef]
- Hamidi, R.J.; Livani, H. Traveling-wave-based fault-location algorithm for hybrid multiterminal circuits. IEEE Trans. Power Deliv. 2017, 32, 135–144. [Google Scholar] [CrossRef]
- Wu, J.; Li, H.; Wang, G.; Liang, Y. An improved traveling-wave protection scheme for LCC-HVDC transmission lines. IEEE Trans. Power Deliv. 2017, 32, 106–116. [Google Scholar] [CrossRef]
- Pathirana, A.N. Travelling Wave Based DC Line Fault Location in VSC HVDC Systems. Master’s Thesis, University of Manitoba, Winnipeg, MB, Canada, 2013. [Google Scholar]
- Magnago, F.H.; Abur, A. Fault location using wavelets. IEEE Trans. Power Deliv. 1998, 13, 1475–1480. [Google Scholar] [CrossRef]
- Borghetti, A.; Bosetti, M.; Di Silvestro, M.; Nucci, C.A.; Paolone, M. Continuous-wavelet transform for fault location in distribution power networks: Definition of mother wavelets inferred from fault originated transients. IEEE Trans. Power Syst. 2008, 23, 380–388. [Google Scholar] [CrossRef]
- Bernadic, A.; Leonowicz, Z. Fault location in power networks with mixed feeders using the complex space-phasor and Hilbert–Huang transform. Electr. Power Energy. Syst. 2012, 42, 208–219. [Google Scholar] [CrossRef] [Green Version]
- Moravej, Z.; Movahhedneya, M.; Radman, G.; Pazoki, M. Effective fault location technique in three-terminal transmission line using Hilbert and discrete wavelet transform. In Proceedings of the 2015 IEEE International Conference on Electro/Information Technology (EIT), Dekalb, IL, USA, 21–23 May 2015. [Google Scholar]
- Huang, N.E. Introduction to the Hilbert Huang Transform and Its Related Mathematical Problems. In Hilbert-Huang Transform and Its Applications; World Scientific: Singapore, 2005; Volume 5, pp. 1–26. [Google Scholar]
- Liu, J.; Duan, J.; Lu, H.; Sun, Y. Fault location method based on EEMD and traveling-wave speed characteristics for HVDC transmission lines. J. Eng. Appl. Sci. 2015, 3, 106–113. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Aneesh, C.; Kumar, S.; Hisham, P.M. Performance comparison of Variational Mode Decomposition over empirical Wavelet Transform for the classification of power quality disturbances using Support Vector Machine. Procedia Comput. Sci. 2015, 46, 372–380. [Google Scholar] [CrossRef]
- Rockafellar, R.T. A dual approach to solving nonlinear programming problems by unconstrained optimization. Math. Program. 1973, 5, 354–373. [Google Scholar] [CrossRef] [Green Version]
- Bertsekas, D.P. Constrained Optimization and Lagrange Multiplier Methods. Computer Science and Applied Mathematics; Academic Press: Boston, MA, USA, 1982. [Google Scholar]
- Teager, H. Some observations on oral air flow duringphonation. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 599–601. [Google Scholar] [CrossRef]
- Maragos, P.; Kaiser, J.F.; Quatieri, T.F. Energy separation in signal modulations with application to speech analysis. IEEE Trans. Signal Process. 1993, 41, 3024–3051. [Google Scholar] [CrossRef]
- Hassan, H.A.A.; Grainger, B.M.; McDermott, T.E.; Reed, G.F. Fault location identification of a hybrid HVDC-VSC system containing cable and overhead line segments using transient data. In Proceedings of the IEEE PES T&D 2016, Dallas, TX, USA, 3–5 May 2016. [Google Scholar]
- Guo, H.; Crossley, P. Design of a time synchronization system based on GPS and IEEE 1588 for transmission substations. IEEE Trans. Power Deliv. 2017, 32, 2091–2100. [Google Scholar] [CrossRef]
- Livani, H.; Evrenosoglu, C.Y. A machine learning and wavelet-based fault location method for hybrid transmission lines. IEEE Trans. Smart Grid 2014, 5, 51–59. [Google Scholar] [CrossRef]
- Song, G.; Li, D.; Chu, X. One-terminal fault location for VSC-HVDC transmission lines based on principles of parameter identification. Power Syst. Technol. 2012, 36, 94–99. (In Chinese) [Google Scholar]
- Xu, M.; Cai, Z.; Liu, Y. A novel fault location method for HVDC transmission line based on the broadband travelling wave information. Trans. China Electrotech. Soc. 2013, 28, 259–265. (In Chinese) [Google Scholar]
- Gao, S.; Suonan, J.; Song, G. Fault location method for HVDC transmission lines on the basis of the distributed parameter model. Proc. CSEE 2010, 30, 75–80. (In Chinese) [Google Scholar]
- Zhao, H.; Li, L. Fault diagnosis of wind turbine bearing based on Variational Mode Decomposition and Teager energy operator. IET Renew. Power Gener. 2017, 11, 453–460. [Google Scholar] [CrossRef]
- Nanayakkara, O.M.K.K.; Rajapakse, A.D.; Wachal, R. Location of DC line faults in conventional HVDC systems with segments of cables and overhead lines using terminal measurements. IEEE Trans. Power Deliv. 2012, 27, 279–288. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A comparative study of Empirical Mode Decomposition-based short-term wind speed forecasting methods. IEEE Trans. Sustain. Energy 2015, 6, 236–244. [Google Scholar] [CrossRef]




| Fault Location/km | Transition Resistance/Ω | Ranging Position/km | Error Distance/km | Error Percentage/% |
|---|---|---|---|---|
| 100 | 0/100/200 | 100.19 | 0.19 | 0.19 |
| 150 | 0/100/200 | 149.77 | 0.23 | 0.153 |
| 200 | 0/100/200 | 200.33 | 0.33 | 0.165 |
| 250 | 0/100/200 | 249.68 | 0.32 | 0.128 |
| 300 | 0/100/200 | 300.195 | 0.195 | 0.065 |
| 400 | 0/100/200 | 400.54 | 0.54 | 0.135 |
| 450 | 0/100/200 | 449.72 | 0.28 | 0.062 |
| 500 | 0/100/200 | 500.56 | 0.56 | 0.112 |
| 600 | 0/100/200 | 599.49 | 0.51 | 0.085 |
| 700 | 0/100/200 | 700.58 | 0.58 | 0.083 |
| Fault Location/km | Fault Type | Ranging Position/km | Error Distance | Fault Location/km |
|---|---|---|---|---|
| 150 | PG | 149.77 | 0.23 | 0.153 |
| NG | 149.77 | 0.23 | 0.153 | |
| PN | 149.76 | 0.24 | 0.16 | |
| 250 | PG | 249.68 | 0.32 | 0.128 |
| NG | 249.69 | 0.31 | 0.124 | |
| PN | 249.68 | 0.32 | 0.128 | |
| 400 | PG | 400.54 | 0.54 | 0.135 |
| NG | 400.54 | 0.54 | 0.135 | |
| PN | 400.54 | 0.54 | 0.135 | |
| 450 | PG | 449.72 | 0.28 | 0.062 |
| NG | 449.72 | 0.28 | 0.062 | |
| PN | 449.72 | 0.28 | 0.062 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, L.; Liu, H.; Dai, L.V.; Liu, Y. Novel Method for Identifying Fault Location of Mixed Lines. Energies 2018, 11, 1529. https://doi.org/10.3390/en11061529
Wang L, Liu H, Dai LV, Liu Y. Novel Method for Identifying Fault Location of Mixed Lines. Energies. 2018; 11(6):1529. https://doi.org/10.3390/en11061529
Chicago/Turabian StyleWang, Lei, Hui Liu, Le Van Dai, and Yuwei Liu. 2018. "Novel Method for Identifying Fault Location of Mixed Lines" Energies 11, no. 6: 1529. https://doi.org/10.3390/en11061529






