Bayesian Energy Measurement and Verification Analysis

Abstract

Energy Measurement and Verification (M&V) aims to make inferences about the savings achieved in energy projects, given the data and other information at hand. Traditionally, a frequentist approach has been used to quantify these savings and their associated uncertainties. We demonstrate that the Bayesian paradigm is an intuitive, coherent, and powerful alternative framework within which M&V can be done. Its advantages and limitations are discussed, and two examples from the industry-standard International Performance Measurement and Verification Protocol (IPMVP) are solved using the framework. Bayesian analysis is shown to describe the problem more thoroughly and yield richer information and uncertainty quantification results than the standard methods while not sacrificing model simplicity. We also show that Bayesian methods can be more robust to outliers. Bayesian alternatives to standard M&V methods are listed, and examples from literature are cited.

1. Introduction

This study argues for the adoption of the Bayesian paradigm in energy Measurement and Verification (M&V) analysis. As such, no new Bayesian methods will be developed. Instead, the advantages, limitations, and application of the Bayesian approach to M&V will be explored. Since the focus is on application, a full explanation of the underlying theory of the Bayesian paradigm will not be given. Readers are referred to Sivia and Skilling [1] or Kruschke [2] for a basic introduction, or von der Linden et al. [3] or Gelman et al. [4] for more complete treatments.

The argument made below is not that current methods are completely wrong or that the Bayesian paradigm is the only viable option, but that the field can benefit from a increased adoption of Bayesian thinking because of its ease of implementation and accuracy of the results.

This paper is arranged as follows. After discussing the background of current M&V analysis methods and the opportunities for improvement in Section 1.1, the Bayesian paradigm is introduced and its practical benefits and some caveats are discussed in Section 2. Section 3 offers two well-known examples and their Bayesian solutions. We also discuss robustness and hierarchical modelling. Section 4 gives a reference list of Bayesian solutions to common M&V cases.

1.1. Background

M&V is the discipline in which the savings from energy efficiency, demand response, and demand-side management projects are quantified [5], based on measurements and energy models. A large proportion of such M&V studies quantify savings for building projects, both residential and commercial. The process usually involves taking measurements or sampling a population to create a baseline, after which an intervention is done. The results are also measured, and the savings are inferred as the difference between the actual post-intervention energy use, and what it would have been, had no intervention taken place. These savings are expressed in probabilistic terms following the International Standards Organization (ISO) Guide to the Expression of Uncertainty in Measurement (GUM) [6]. M&V study results often form the basis of payment decisions in energy performance contracts, and the risk-implications of such studies are therefore of interest to decision makers.

The Bayesian option will not affect the foundational M&V methodologies such as retrofit isolation or whole facility measurement, but only the way the data are analysed once one of these methods has been decided upon.

M&V guidelines such as the International Performance Measurement and Verification Protocol (IPMVP) [5], the American Society of Heating, Refrigeration, and Air Conditioning Engineers (ASHRAE)’s Guideline 14 on Measurement of Energy, Demand, and Water Savings [7], or the United States Department of Energy’s Uniform Methods Project (UMP) [8], as well as most practitioners, use frequentist (or classical) statistics for analysis. Because of its popularity in the twentieth century, most practitioners are unaware that this is only one statistical paradigm and that its assumptions can be limiting. The term ‘frequentist’ derives from the method that equates probability with long-run frequency. For coin flips or samples from a production line, this assumption may be valid. However, for many events, equating probability with frequency seems strained because a large, hypothetical long-run population needs to be imagined for the probability-as-frequency-view to hold. Kruschke [2] gives an example where a coin is flipped twenty times and seven heads are observed. The question is then: what is the probability of the coin being fair? The frequentist answer will depend on the imagined population from which the data were obtained. This population could be obtained by “stopping after 20 flips”, but it could also be “stopping after seven heads” or “stopping after two minutes of flipping” or “to compare it to another coin that was flipped twenty times”. In each case, the probability that it is a fair coin changes, even though the data did not—termed incoherence [9]. In fact, the probabilities are dependent on the analyst’s intention. By changing his intention, he can alter the probabilities. This problem becomes even more severe in real-world energy savings inference problems with many more factors. The hypothetical larger population from which the energy use at a specific time on a specific day for a specific facility was sampled is difficult to imagine. That is not to say that a frequentist statistical analysis cannot be done, or be useful. However, it often does not answer the question that the analyst is asking, committing an “error of the third kind”. Analysts have become used to these ‘statistical’ answers (e.g., “not able to reject the null hypothesis”), and have accepted such confusion as part of statistics. For example, consider two mainstays of frequentist M&V: confidence intervals (CIs) and p-values. CIs are widely used in M&V to quantify uncertainty. According to Neyman, who devised these intervals, they do not convey a degree of belief, or confidence, as is often thought. Frequentist confidence intervals are produced by a method that yields an interval that contains the true value only in a specified percentage (say 90%) of cases [10]. This may seem like practically the same thing, but an explanation from most frequentist statistics textbooks will then seem very confusing. Consider Montgomery and Runger’s Applied Statistics and Probability for Engineers [11], under “Interpreting a Confidence Interval” (CI). They explain that, with frequentist CIs, one cannot say that the interval contains the true number with a probability of e.g., 90%. The interval either contains the value, or it does not. Therefore, the probability is either zero or one, but the analyst does not know which. Therefore, the interval cannot be associated with a probability. Furthermore, it is a random interval (emphasis theirs) because the upper and lower bounds of the interval are random variables.

Consider now the p-value. Because of the confusion surrounding this statistic, the American Statistical Association issued a statement regarding its use [12], in which they state that p-values neither signify probabilities of the hypothesis being true or false, nor are they probabilities that the result arose by chance. They go on to say that business (or policy) decisions should not be based on p-value thresholds. p-values do not measure effect sizes or result importances, and by themselves are not adequate measures of evidence.

Such statements by professional statisticians leave most M&V practitioners justifiably confused. It is not that these methods are invalid, but that they have been co-opted to answer different kinds of questions to what they actually answer. The reason for their popularity in the 20th century has more to do with their computational ease, compared to the more formal and mathematical Bayesian methods, than with their appropriateness. The Bayesian conditional-probability paradigm is much older than the frequentist one but used to be impractical for computational reasons. However, with the rise in computing power and new numeric methods for solving Bayesian models, this is no longer a consideration.

2. The Bayesian Paradigm

Instead of approaching uncertainty in terms of long-run frequency, the Bayesian paradigm views uncertainty as a state of knowledge or a degree of belief, the sense most often meant by people when thinking about uncertainty. These uncertainties are calculated using conditional-probability logic and calculus, proceeding from first principles. For example, consider two conditions M and S. Let $Pr\left(\right)$ denote a probability and | “conditional on” or “given”. Furthermore, let I be the background information about the problem. Bayes’ theorem states that:

$$Pr\left(S\right|M,I)=\frac{Pr\left(M\right|S,I)Pr(S\left|I\right)}{Pr\left(M\right|I)}.$$

(1)

Now, as stated previously, M&V is about verifying the savings achieved, based on some measurements and an energy model, and quantifying the uncertainty in this figure. If we let S be the savings, and M the measurements, Bayes’ theorem as stated above answers that question exactly: it supplies a probability of the savings given the measurements and any background information that might be available; $Pr\left(S\right|M)$. Bayes’ theorem is, therefore, the natural expression of the M&V aim:

$$\mathrm{Verification}|\mathrm{Measurement}\equiv Pr(S\left|M\right).$$

Whereas the frequentist paradigm views the data as random realisations of a process with fixed parameters, the Bayesian paradigm views the data (measurements) as fixed, and the underlying parameters as uncertain (thereby avoid the incoherence of the coin flip example [9]). This seems like a trivial distinction at first but is significant: the frequentist only solves for $Pr\left(M\right|S)$: the probability of observing that data, given the underlying savings value. However, that is not the question M&V seeks to answer. In the frequentist paradigm, the analyst does not invert this as Bayes’ theorem does to find the probability distribution on the savings, given the data. Therefore, in the frequentist case, the wrong question is being answered, as alluded to above (Technical note: to be fair, we note that, for constant priors, the likelihood may be equivalent to the posterior. When it is the case, the frequentist likelihood may borrow from Bayesian theory and be interpreted as a probability).

It is this inversion process that has often been intractable in higher dimensions until the advent of Markov Chain Monte Carlo (MCMC) techniques and increased computing power (Technical note: other Monte Carlo-based inversion techniques such as rejection or importance sampling are only efficient enough to be practical in low-dimensional settings. Note that we use Monte Carlo here in the sense of a straightforward sense of generating random numbers according to standard distributions [13]). MCMC software has allowed users to specify a model (e.g., a linear regression model), supply the observations or data (measurements), and infer the values on the model parameters probabilistically. This is called probabilistic programming. Probabilistic programming is compelling because, instead of working with point estimates on all unknown parameters (e.g., slope and intercept in a straight-line regression model), one describes the system in terms of probability distributions. Working with probability distributions rather than point estimates is preferable, since it is well known that doing calculations with point estimates can lead to erroneous conclusions [14]. When doing forward-calculations as illustrated in Figure 1, it is therefore desirable to use distributions on unknown variables and then apply a Monte Carlo simulation or Mellin Transform Moment Calculation method [15,16] to obtain a probability distribution on the result. MCMC allows one to do the inverse: inferring parameter distributions from given data and a model. Therefore, MCMC is to regression what Monte Carlo simulation is to deterministic computation. The adoption of the Bayesian paradigm therefore allows the analyst to move from deterministic to probabilistic M&V, as shown in Figure 1.

For the inversion described above to work, the $Pr\left(S\right|I)$ term, called the prior, needs to be specified. Although the prior can be used to incorporate information into the model, which is not available through the data alone, it is, in essence, merely a mathematical device allowing inversion. The prior is often specified as “non-informative”—a flat probability distribution over the region of interest, allowing the data to “speak for itself” through the likelihood term. This will be discussed in more detail below. The other term, $Pr\left(M\right|I)$, need not be specified in numeric MCMC models—it is a normalising factor ensuring that the right-hand side of the equation can integrate to unity, making it a proper probability density function (Technical note: this term becomes important in more sophisticated Bayesian analyses where model selection or experimental design is done [1]). The left-hand side of the equation is called the posterior distribution and is proportional, therefore, to the product of the prior and the likelihood.

Advanced Bayesian models may be nuanced, but the fundamental mechanics as described above stay the same for all Bayesian analyses: specify priors, describe the likelihood, and solve to find the posterior on the parameters of interest.

2.1. Practical Benefits

Besides the theoretical attractiveness discussed above, the Bayesian paradigm also offers many practical benefits for energy M&V:

• Because Bayesian models are probabilistic, uncertainty is automatically and exactly quantified.
• Uncertainty calculations in the Bayesian approach can be much less conservative than standard approaches. Shonder and Im [17] show a 40% reduction in uncertainty in one case. Since project payment is often dependent on savings uncertainties being within certain bounds, using the Bayesian approach can increase project feasibility.
• By making the priors and energy model explicit, the Bayesian approach ensures greater transparency—one of the five key principles of M&V [5].
• The Bayesian approach is widely used and is rapidly gaining popularity in other scientific fields. Lira [18] relates that even the GUM (adopted by many societies of physics, chemistry, electrotechnics, etc.) is being rewritten to be more consistent with this approach. Since M&V reports uncertainty according to the GUM, Bayesian calculations would be useful.
• Bayesian models are more universal and flexible than standard methods. Bayesian modelling can be highly sophisticated, but the core of probabilistic thinking is consistent throughout. This is different to frequentist statistics where knowledge of one or even many tests will not necessarily aid the analyst in understanding a new metric, or approach to a problem not seen before. Many frequentist tests are ad hoc and apply only to specific situations. For example, t-tests have little to do with regression in frequentism, but, in Bayesian thinking, they are expressions of the same idea.
• Being modular, Bayesian modelling is more flexible. Ordinary least squares (OLS) linear regression assumes residuals are normally distributed and that the variance is constant for all points. In a probabilistic Bayesian model, the parameters can be distributed according to any distribution, but the posterior for each will be determined by the data (if the prior is appropriately chosen). Models are also modular and can be designed to suit the problem. For example, it is no different to create terms for serial correlation, or heteroscedasticity (non-constant variance) than it is to specify an ordinary linear model. This also allows for easy specification of non-routine adjustments, the handling of missing values, and the incorporation of unmeasured yet important quantities such as measurement error, often problematic for energy models. For the retrofit isolation with a key parameter measurement approach, the unmeasured parameters (the estimates) can also be incorporated in this way.
• Bayesian models can account for model-selection uncertainty. There are often multiple reasonable energy models which could describe a specific case—for example: time and dry-bulb temperature; occupancy and dry-bulb temperature; temperature, humidity, and occupancy, etc. The analyst usually chooses one model, discards the rest, and reports the uncertainty produced in that specific model. However, this uncertainty does not account for model selection. In other words, there is an uncertainty associated with choosing that specific model above another reasonable one. Bayesian model averaging allows many models to be specified simultaneously, and averages their results by automatically weighting each model’s influence on the final result by that model’s explanatory power. This gives a far more realistic uncertainty value [4].
• Because uncertainty is automatically quantified, CIs can be interpreted in the way most people understand them: degrees of belief about the value of the parameter.
• The Bayesian approach is well-suited to “small data” problems. This seems like a minor point in developed countries where questions surrounding big data are more pressing. However, big (energy) data is a decidedly “first-world problem”. In developing countries, a lack of meters makes M&V expensive, and it is useful to have a method that is consistent on smaller data sets as well.
• Bayesian approaches allow real-time or online updating of estimates [19,20,21]. For many other machine learning techniques, the data need to be split into testing and training sets, the model trained on the training set, and then used to predict the testing set period. As new data becomes available, the model needs to be retrained in many cases (Technical note: Artificial Neural Networks (ANNs), stochastic gradient descent and passive-aggressive algorithms, as well as Dynamic Linear Models can also be updated online), making it computationally expensive to keep a model updated. In a Bayesian paradigm, previous data can be summarised by the prior so that the model need not be retrained.
• The Bayesian approach allows for the incorporation of prior information where appropriate. The danger in this will be discussed in Section 2.2. However, in cases where it is warranted, known values or ranges for certain coefficients can be specified in the prior. This has been done successfully for energy projects [22,23,24,25]. Prior information is also useful in longitudinal studies, where measurements or samples from previous years can be taken into account [20,21].
• When the savings need to be calculated for “normalised conditions”, for example, a ‘typical meteorological year’, rather than the conditions during the post-retrofit monitoring period, it is not possible to quantify uncertainty using current methods. However, Shonder and Im [17] have shown that it can be naturally and easily quantified using the Bayesian approach.

2.2. Caveats

The Bayesian approach also comes with certain caveats that M&V practitioners and policy makers should bear in mind.

• Modelling is non-generic. In point 5 above, it was stated that the Bayesian approach is more universal. This is true in the sense that the same basic approach is used for many different kinds of problems. However, the inherent modularity of the method as described in point 6 means that there is not a one-size-fits-all generic template in Bayesian modelling, the way there usually is in frequentist modelling. This necessitates more thinking from the analyst. However, we believe this to be an advantage: frequentist approaches make it easier to think less, but as a consequence, also to build poor models, which has led to the current replication crisis seen in research [26] and a general mistrust of statistical results [27]. High quality models require some thought and care, in any paradigm.
• As with any method, it is not immune to abuse. The most popular criticism is that, by having a prior distribution on the savings, the posterior may be biased in a way not warranted by the data, making the result subjective. This is certainly possible. However, having a prior in an M&V analysis is actually an advantage.

  (a)

  As stated above, it allows for greater modelling transparency. The Bayesian form forces the analyst to be explicit about his or her modelling assumptions, and to defend them. Such assumptions cannot be imported by (accidentally or purposefully) choosing one test over another, as in the frequentist case.

  (b)

  It is sometimes necessary to include priors to avoid bias. Ioannidis [28] and Button [29] have shown that many medical studies contain false conclusions due to biased results. The bias that was introduced was to consider positive and negative outcomes from a clinical trial equally likely. However, the prior odds of an experimental treatment working is much lower than the odds of that treatment not working. Ignoring these prior odds leads to a high false-positive rate, since many of the positive results are actually false and due to noise. In M&V, the situation is reversed: the prior odds of energy projects saving energy are high. Having a neutral prior would therefore bias a result towards conservatism (Technical note: conservatism is one of the key principles of M&V [5], but we do not hereby advocate for neutral priors in all cases). Nevertheless, Button’s study is an excellent illustration of why priors are an important part of probability calculus.

  (c)

  Because the assumptions and distributions used are clearly stated, it precludes hedging the M&V result with phrases such as “however, from previous studies/experience, we know that this is a conservative figure ⋯”. Because the prior was stated and defended at the outset, the final result should already incorporate it and should not be hedged.

  (d)

  The thorough analyst will test the effect of different priors on the posterior, demonstrating the bias introduced through his modelling assumptions, and justifying its use.

• Bayesian methods can be computationally expensive for large datasets and complex models. It is true that numerical solvers are becoming more efficient and computational power is increasing. However, in comparison with matrix inversion techniques used for linear regression, for example, Bayesian methods are much slower and may be inappropriate for real-time applications [30].
• The forecasting accuracy of other machine learning (ML) methods can be higher than regression in some cases [31,32], although regression-based approaches such as time-of-week-and-temperature [33] still perform very well [32,34] and may be preferred for simplicity. Note that this is a limitation of regression, not the overall Bayesian paradigm, although regression is the way most M&V analysts would use Bayesian methods. Many ML techniques also have Bayesian approaches, for example Bayesian tree-based ensemble methods [35] or Bayesian Artificial Neural Networks [36,37]. It also depends on the problem: it is not possible to know beforehand which model will work the best [38]. ML algorithms without Bayesian implementations also still only produce point estimates. Therefore, they cannot be compared to the full probabilistic approach, which provides much richer information and is not just a forecasting technique, but a full inference paradigm.
• The parametric from of the model needs to be specified. Parametric Bayesian models as described in most of this study can only be correct in so far as their functional form describes the underlying physical process. Functional form misspecification is a real possibility. This is different to the machine learning methods described in the previous paragraph, which do not rely on a functional form being specified. Non-parametric models have their own benefits and limitations: for cases where the underlying physical process is well-understood, a parametric model can be more accurate. However, non-parametric methods such as Gaussian Processes (GPs) [22,39] or Gaussian Mixture Models [40] still require some model specification at a higher level (hyperparameters). GP models, for example, rely on an appropriate covariance function for valid inference. For more information on GPs for machine learning, see Rasmussen and Williams [41].

3. Bayesian M&V Examples

To demystify the Bayesian approach, two basic M&V calculations will be demonstrated. The reader will notice the recurring theme of expressing all variables as (conditional) probability distributions.

3.1. Sampling Estimation

Consider the following example from the IPMVP 2012 [5] (Appendix B-1). Twelve readings are taken by a meter. These are reported as monthly readings, but are assumed to be uncorrelated with any independent variables or other readings, and are therefore construed to be random samples. The values are:

$$\mathbf{D}=[950,1090,850,920,1120,820,760,1210,1040,930,1110,1200].$$

(2)

The units are not reported and the results below are therefore left dimensionless, although kWh would be a reasonable assumption. These data were carefully chosen, and have a mean $\mu =1000$, sample standard deviation $s_s=150$.

3.1.1. IPMVP Solution

The standard error is $SE=43$. The confidence interval on the mean is calculated as:

$$CI=\mu \pm t\times SE.$$

(3)

Since $t_{90\%,11}=1.80$, the 90% confidence interval on the mean was calculated as $1000\pm 1.80\times 43=(933,1077)$, or a 7.7% precision. Metering uncertainty is not considered in this calculation.

3.1.2. Bayesian Solution

The Bayesian estimate of the mean is calculated as follows. First, prior distributions on the data need to be specified. Vague priors will be used:

$$Pr\left(\mu \right)\sim Uniform[0,2000],$$

(4)

$$Pr\left(\sigma \right)\sim Uniform[0,1000].$$

(5)

A t-distribution will be used for the likelihood below, and the degrees of freedom parameter ($\nu$) of this distribution will, therefore, need to be specified. One could fix $\nu$ for the t-distribution at 12, since there are twelve data points and traditionally $\nu$ has been taken to signify this number. However, if outliers are present or if the data has more or less dispersion than the standard t-distribution with as many data points, this would not be realistic. It is therefore warranted to indicate the uncertainty in the data by specifying a prior distribution on $\nu$ also: a hyperprior. Kruschke [42] recommends an exponential distribution with the mean equal to the number of data points. This allows equal probability of $\nu$ being higher or lower than the default value:

$$Pr\left(\nu \right)\sim Exponential[1/12].$$

(6)

If the vector of the parameters is $\mathit{\theta }=(\mu ,\sigma ,\nu )$, then the likelihood can be written as:

$$Pr\left(\mathbf{D}\right|\mathit{\theta })\sim StudentT\left[Pr\left(\mu \right),Pr\left(\sigma \right),Pr\left(\nu \right)\right].$$

(7)

Note that the t-distribution is not used because of the t-test, but because its heavier tails are more accommodating of outliers. Any distribution could have been specified if there was good reason to do so. The posterior on $\mu$ is plotted in Figure 2. It was simulated in PyMC3 using the Automatic Differentiation Variational Inference (ADVI) algorithm with 100,000 draws, which is stable and converges on the posterior distribution in 10.76 s on a middle-range laptop computer. Although the mathematical notation may seem intimidating to practitioners who are not used to it, writing this in the probabilistic Python programming package PyMC3 [43] demonstrates the intuitive nature of such a model:

import pymc3 as pm

with pm.Model() as bayesian_sampling_model:

# Hyperpriors and priors:

mean = pm.Uniform(’mean’, 0, 2000)

std = pm.Uniform(’std’, 0, 1000)

nu = pm.Exponential(’nu’, 1/len(data))

# Likelihood

likelihood = pm.StudentT(’likelihood’, mu=mean, sd=std, nu=nu, observed=data)

# ADVI calculation

trace = pm.variational.sample_vp(vparams=pm.variational.advi(n=100000))

It is important to note that no probability statements about the values inside the frequentist interval can be made, nor can one fit a distribution to the interval. The distribution indicated is strictly a Bayesian one. The Bayesian (highest density) interval is slightly wider than the frequentist confidence interval, at a precision of 8.5%. If $\nu$ were fixed at 12 (indicating that we are certain that the data does indeed reflect a t-distribution with 12 degrees of freedom exactly), Bayesian and frequentist intervals correspond exactly. However, the Bayesian alternative allows for a more realistic value. With comparisons between two groups (two-sample t-tests), the effect of uncertainty in the priors becomes even more pronounced [42].

The posterior distribution can now be used to answer many interesting questions. For instance, what is the probability, given the data at hand, that the true mean is below 900? Or, is it safe to assume that the standard value of 950 is reflected by this sample, or should the null hypothesis be rejected? (If previous data to this effect is available, it could be included in the prior, maybe using the equivalent prior sample size method [44]). The frequentist may say that there is not enough evidence to reject the null, but cannot accept it either. In the Bayesian paradigm, 950 falls comfortably within the 90% confidence range, and can therefore be accepted at that level. As a further question, if this is an energy performance contracting project, and we assume that the data points are different facilities rather than different months, would it be worthwhile taking a larger sample to increase profits, if we believe that the true mean is 1100 (on which see Lindley [45], Bernardo [46] and Goldberg [47]).

It is therefore evident that the Bayesian result yields richer and more useful information using intuitive mathematics.

3.2. Regression

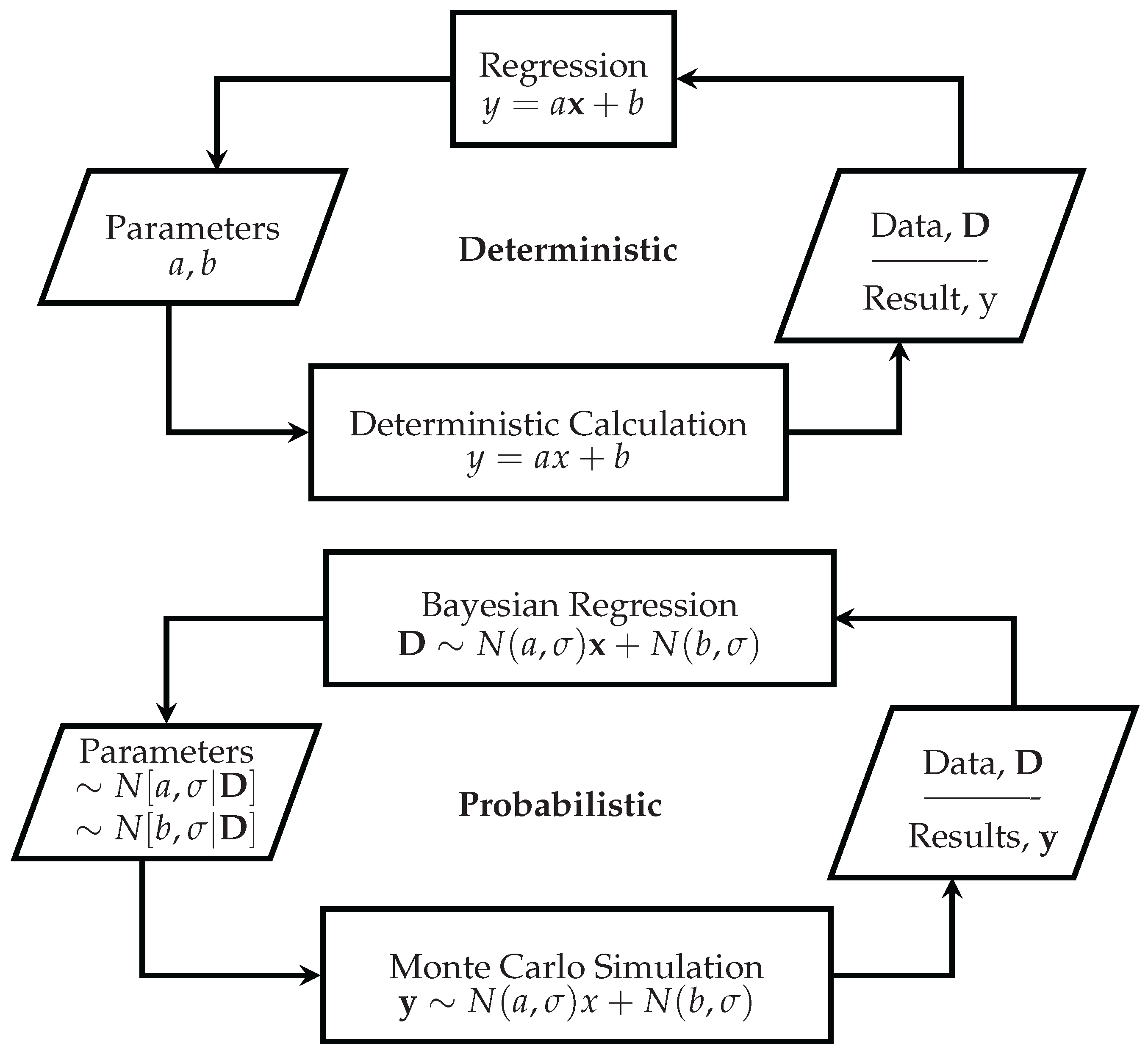
In M&V, one often uses the baseline data (${\mathbf{D}}_b$) to infer the baseline (pre-retrofit) model parameters $\mathit{\theta }$ through an inverse method:

$$\mathit{\theta }=f^{-1}({\mathbf{D}}_b,\tau ),$$

(8)

where $f(·)$ is a function relating the independent variables (energy governing factors) to the energy use of the facility, and $\tau$ is time. The model parameters describe the sensitivity of the energy model to the independent variables such as occupancy, outside air temperature, or production volume.

As an aside, this section will discuss an elementary parametric energy model using Bayesian regression, similar to standard linear regression. In practice, a two-parameter linear regression model seldom captures the different states of a facility’s energy use, for example, heating at low temperatures, a comfortable range, and cooling at high temperatures. Piecewise linear regression techniques are often used [48,49,50,51,52], and they tend to work reasonably well if their assumptions are satisfied, but they are not stable in all cases, are approximate, and the assumptions are often restrictive. Shonder and Im [17] provide a Bayesian alternative. A non-parametric model using a Gaussian Process could also be used, and since one does not need to specify a parametric model, it allows very flexible models to be fit while still quantifying uncertainty. This is especially useful for models where energy use is a nonlinear function of the energy governing factors. However, to keep the example simple and focussed, only a simple parametric model will be considered below.

3.2.1. Example

Suppose one has a simple regression model where the energy use of a building $\mathbf{E}$ is correlated with the outside air temperature through the number of Cooling Degree Days (CDD). One cooling degree day is defined as an instance where the average daily temperature is one degree above the thermostat set point for one day, and the building therefore requires one degree of cooling (Technical note: a more accurate description would be the “building balance point”, where the building’s mass and insulation balance external forcings [53]). Let the intercept coefficient be ${\theta }_0$, the slope coefficient ${\theta }_1$, and the Gaussian error term $\mathit{ϵ}$. One could then write:

$$\mathbf{E}={\theta }_0+{\theta }_1\mathbf{CDD}+\mathit{ϵ}.$$

(9)

In standard linear regression, one would write $\widehat{\mathit{\theta }}$ as the vector of two coefficients and do some linear algebra to obtain their estimates. There would be a standard error on each, which would indicate their uncertainties, and if the assumptions of linear regression, such as normality of residuals, independence of data, homoscedasticity, etc. hold, then it would be accurate. In Bayesian regression, one would describe the distributions on the parameters:

$$Pr\left(\mathit{\theta }\right|\mathbf{D})\propto Pr\left(\mathbf{D}\right|\mathit{\theta })Pr\left(\mathit{\theta }\right)\sim N[\widehat{\mathit{\theta }},\mathbf{\sigma }],$$

(10)

where $\mathbf{\sigma }$ is the vector of the standard deviations on the estimates. Generating random pairs of values from the posterior, at a given value of CDD, according to the appropriate distributions, will yield the posterior predictive distribution. This is the distribution of energy use at a given temperature, or over the range of temperatures. Overlaying such realisations onto the actual data is called the posterior predictive check (PPC).

Now, consider a concrete example. The IPMVP 2012 [5] (Appendix B-6) contains a simple regression example of creating a baseline of a building’s cooling load. The twelve data points themselves were not given, but a very similar data set yielding almost identical regression characteristics has been engineered and is shown in 

Table 1. Cooling Degree Day (CDD) Data for International Performance Measurement and Verification Protocol (IPMVP) Example B-6. Note that these data were reverse-engineered to yield the same regression results as reported in the IPMVP. The original data were not reported in the IPMVP.

Month	Jan	Feb	Mar	Apr	May	Jun	Jul	Aug	Sep	Oct	Nov	Dec
CDD	312	292	222	112	92	22	12	32	157	207	182	302
Energy Use	7823	7585	7486	6646	6185	5933	5381	5917	7158	7064	7231	8250

.

A linear regression model was fit to the data, and yielded the result shown in 

Table 2. Linear regression fit characteristics for data in Table 1. The coefficient of determination is $R^2=0.93$, which is identical to the IPMVP case. These results may be compared to Bayesian summary statistics in Table 3.

Parameter	Value	Standard Error	95% Interval
Slope coefficient	7.75	0.67	[6.26, 9.23]
Intercept coefficient	5634	129	[5347, 5921]

.

3.2.2. IPMVP Solution

The IPMVP then proceeds to calculate the uncertainty in the annual energy figure by multiplying the standard error on the estimate (the average standard error) by $t_{95\%}$ and the average consumption in the average month, and assumes that this value is constant for all months. As discussed in this study, this approach is problematic, and can at best be seen as approximate. Since it is treated in some detail in the IPMVP, the analysis will not be repeated here.

3.2.3. Bayesian Solution

The key to the Bayesian method is to approach the problem probabilistically, and therefore view all parameters in Equation (9) as probability distributions, and specify them as such. In this regression model, there are three parameters of interest: the intercept (${\theta }_0$), slope (${\theta }_1$), and the response ($\mathbf{E}$). This response is the likelihood function, familiar to most readers as the frequentist approach. These distributions need to be specified in the Bayesian model. First, consider the priors on the slope and intercept. These can be vague. Technical note: the uniform prior on ${\theta }_0$ in Equation (11) is actually technically incorrect: it may seem uniform in terms of gradient but is not uniform when the angle of the slope is considered. It is therefore not “rotationally invariant” and biases the estimate towards higher angles [54]. The correct prior is $Pr\left(\theta \right|I)\sim {(1+{\theta }^2)}^{-\frac{3}{2}}$; this is uniform on the slope angle. The reason that Equation (11) works in this case is that the exponential weight of the likelihood masks the effect. However, this is not always the case, and analysts should be careful of such priors in regression analysis:

$$Pr\left({\theta }_0\right)\sim Uniform[0,10000],$$

(11)

and

$$Pr\left({\theta }_1\right)\sim Uniform[0,20].$$

(12)

Now, consider the likelihood. In frequentist statistics, one needs to assume that $\mathbf{E}$ in Equation (9) is normally distributed. In the Bayesian paradigm, one may do so, but it is not necessary. A Student’s t-distribution is often used instead of a Normal distribution in other statistical calculations (e.g., t-tests) due to its additional (“degrees of freedom”) parameter, which accommodates the variance arising from small sample sizes more successfully. As in Section 3.1.2, an exponential distribution on the degrees of freedom (${\nu }_p$) is specified. It has also been found that specifying a Half-Cauchy distribution on the standard deviation (${\sigma }_p$) works well [55]. Therefore, the hyperpriors are specified as:

$$Pr\left({\nu }_p\right)\sim Exponential\left[{12}^{-1}\right]$$

(13)

and:

$$Pr\left({\sigma }_p\right)\sim HalfCauchy\left[1\right].$$

(14)

The mean of the likelihood is the final hyperparameter that needs to be specified. This is simply Equation (9), written with the priors:

$${\mu }_p=Pr\left({\theta }_0\right)+Pr\left({\theta }_1\right)\mathbf{CDD}.$$

(15)

The full likelihood can thus be written as:

$$Pr\left(\mathbf{CDD}\right|\mathbf{E})\sim StudentT\left(\mu ={\mu }_p,\nu =Pr\left({\nu }_p\right),\sigma =Pr\left({\sigma }_p\right)\right).$$

(16)

The PyMC3 code is shown below:

import pymc3 as pm

with pm.Model() as bayesian_regression_model:

# Hyperpriors and priors:

nu = pm.Exponential(’nu’, lam=1/len(CDD))

sigma = pm.HalfCauchy(’sigma’, beta=1)

slope = pm.Uniform(’slope’, lower=0, upper=20)

intercept = pm.Uniform(’intercept’, lower=0, upper=10000)

# Energy model:

regression_eq = intercept + slope*CDD

# Likelihood:

y = pm.StudentT(’y’, mu=regression_eq, nu=nu, sd=sigma, observed=E)

# MCMC calculation:

trace = pm.sample(draws=10000, step=pm.NUTS(), njobs=4)

The last line of the code above invokes the MCMC sampler algorithm to solve the model. In this case, the No U-Turn Sampler (NUTS) [56] was used, running four traces of 10,000 samples each, simultaneously on a four-core laptop computer, in 3.5 min fewer samples, could also have been used.

A discussion of the inner workings and tests for adequate convergence of the MCMC is beyond the scope of the study and has been done in detail elsewhere in literature [4]. The key idea for M&V practitioners is that the MCMC, like MC simulation, must converge, and must have done enough iterations after convergence to approximate the posterior distribution numerically. For most simple models such as the ones used in most M&V applications, a few thousand iterations are usually adequate for inference. Two popular checks for posterior validity are the Gelman–Rubin statistic $\widehat{R}$ [57,58] and the effective sample size (ESS). The Gelman–Rubin statistic compares the four chains specified in the program above, started at random places, to see if they all converged on the same posterior values. If they did, their ratios should be close to unity. This is easily done in PyMC3 with the pm.gelman_rubin(trace) command, which indicates $\widehat{R}$ equal to one to beyond the third decimal place. However, even if the MCMC has converged, it does not mean that the chain is long enough to approximate the posterior distribution adequately because the MCMC mechanism produces a serially correlated (autocorrelated) chain. It is therefore necessary to calculate the effective sample size: the sample size taking autocorrelation into account. In PyMC3, one can invoke the pm.effective_n(trace) command, which shows that the ESSs for the parameters of interest are well over 1000 each for the current case study. As a first-order approximation, we can therefore be satisfied that the MCMC has yielded satisfactory estimates.

The MCMC results can be inspected in various ways. The posteriors on the parameters of interest are shown in Figure 3. If a normal distribution is specified on the likelihood in Equation (16) rather than the Student’s t, the posterior means are identical to the linear regression point estimates—an expected result, since OLS regression is a special case of the more general Bayesian approach. Using a t-distributed likelihood yields slightly different, but practically equivalent, results. The mean or mode of a given posterior is not of as much interest as the full distribution, since this full distribution will be used for any subsequent calculation. However, the mean of the posterior distribution(s) is given in 

Table 3. Summary statistics for Bayesian posterior distributions shown in Figure 3 when a Student’s t-distribution is used on the likelihood. Compare to linear regression results in Table 2. HDI: Highest Density Intervals.

Parameter	Value	95% HDI
Slope coefficient	7.69	[6.21, 9.24]
Intercept coefficient	5634	[5351, 5937]

for the curious reader.

Two brief notes on Bayesian intervals are necessary. As discussed in Section 1.1, the frequentist ‘confidence’ interval is a misnomer. To distinguish Bayesian from frequentist intervals, Bayesian intervals are often called ‘credible’ intervals, although they are much closer to what most people think of when referring to a frequentist confidence interval. The second note is that Bayesians often use HDIs, also known as highest posterior density intervals. These are related to the area under the probability density curve, rather than points on the x-axis. In frequentist statistics, we are used to equal-tailed confidence intervals since we compute them by taking the mean, and then adding or subtracting a fixed number—the standard error multiplied by the t-value, for example. This works well for symmetrical distributions such as the Normal, as is assumed in many frequentist methods. However, real data distributions are often asymmetrical, and forcing an equal-tailed confidence interval onto an asymmetric distribution leads to including an unlikely range of values on the one side, while excluding more likely values on the other. An HDI solves this problem. It does not have equal tails but has equally-likely upper and lower bounds.

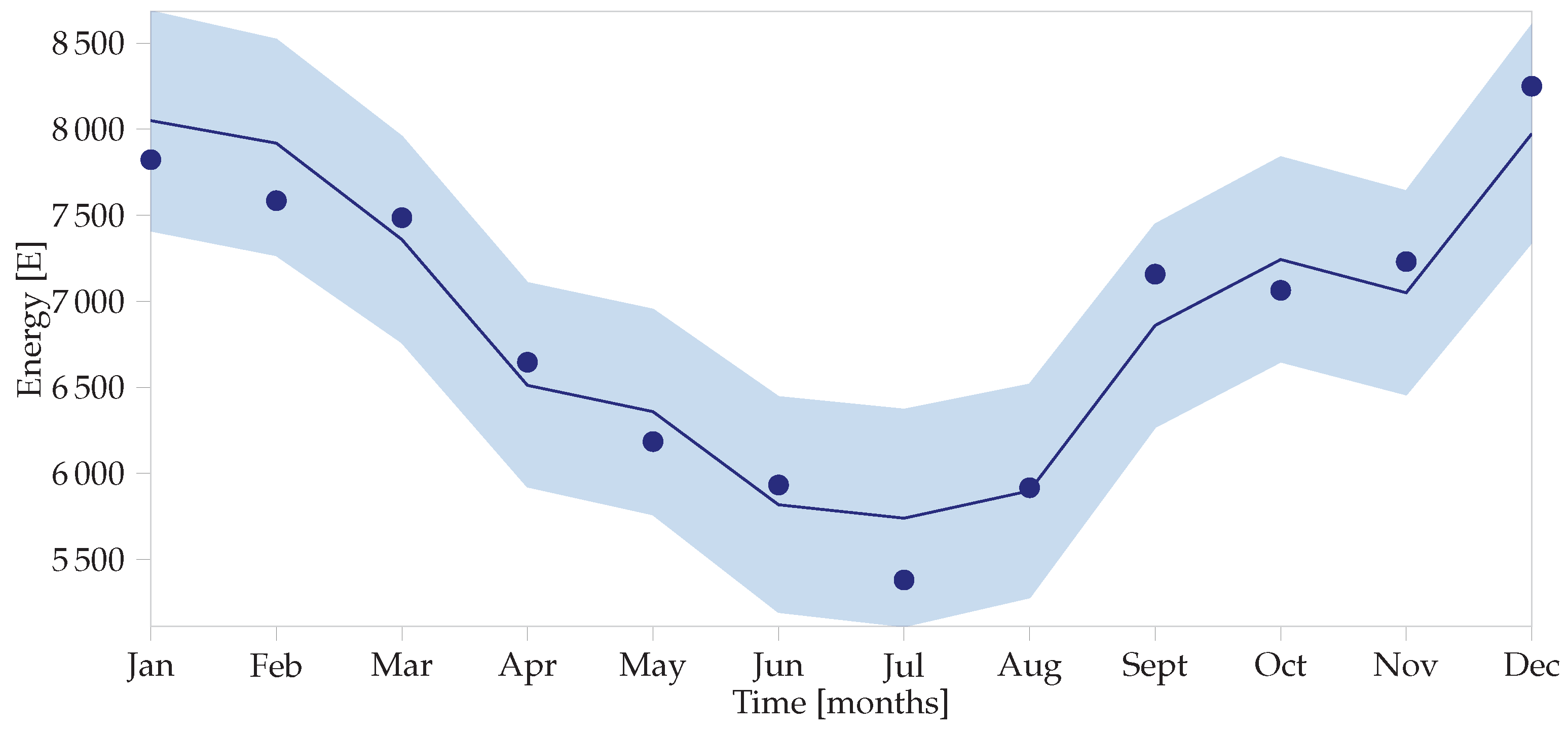
The posterior distributions shown in Figure 3 are seldom of use in themselves and are more interesting when combined in a calculation to determine the uncertainties in the baseline as shown in Figure 4, also known as the adjusted baseline. To do so, the posterior predictive distribution needs to be calculated using the pm.sample_ppc() command, which resamples from the posterior distributions, much like the MC simulation forward-step of Figure 1.

The Bayesian model can also be used to calculate the adjusted baseline, or what the post-implementation period energy use would have been, had no intervention been made. The difference between this value and the actual energy use during the reporting period is the energy saved. For the example under consideration, the IPMVP assumes that an average month in the post-implementation period: one with 162 CDDs. It also assumes that the actual reporting period energy use is 4300 kWh, measured with negligible metering error.

To calculate the savings distribution using the Bayesian method, one would do an MC simulation of:

$$Savings\sim {\mathit{\theta }}_0+162{\mathit{\theta }}_1-4300,$$

(17)

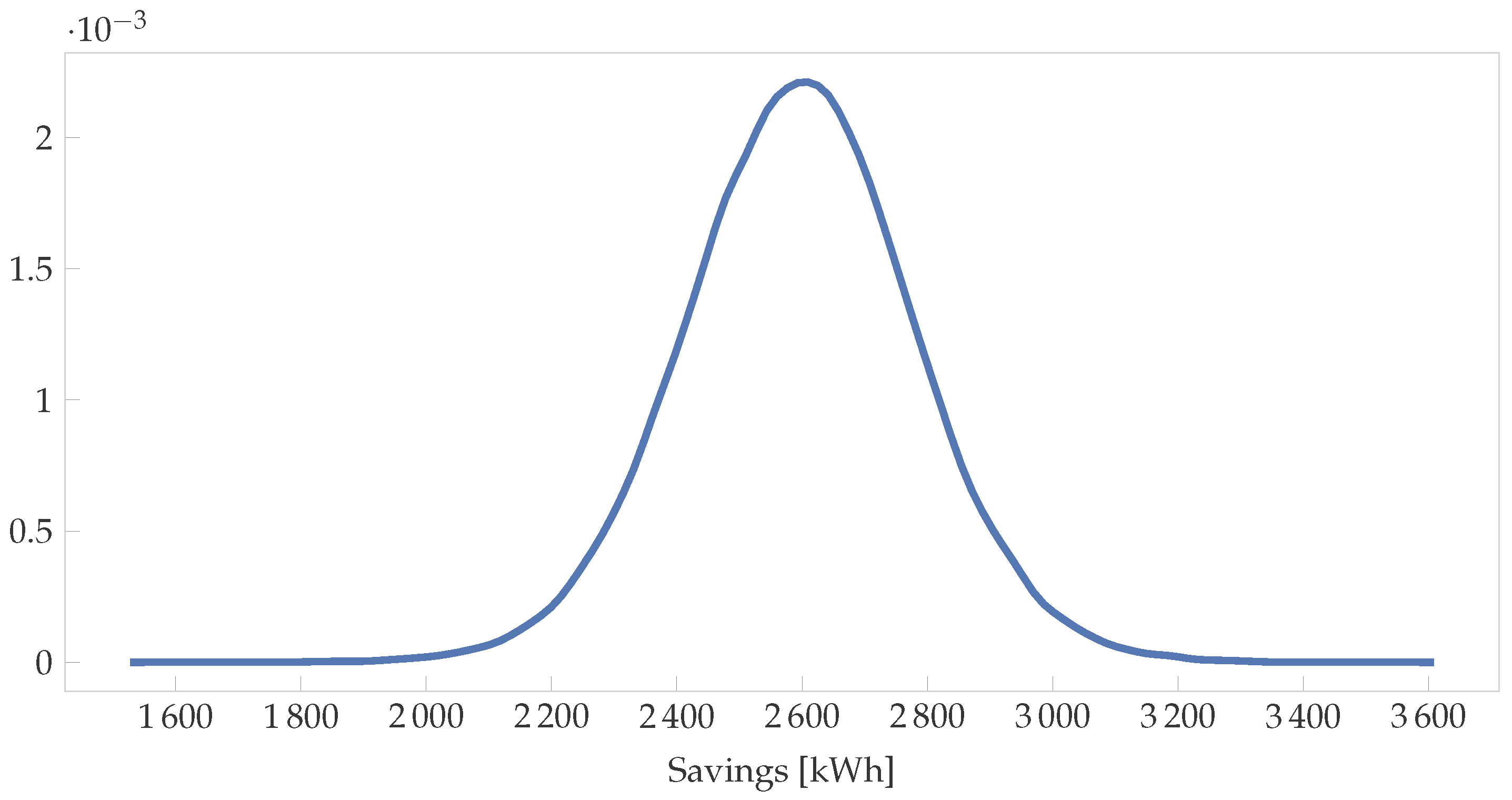
where ${\mathit{\theta }}_0$ and ${\mathit{\theta }}_1$ are the distributions shown in Figure 3. Note that they are correlated and so using the PPC method described above would be the correct approach. Running this simulation with 10,000 samples yields the distribution shown in Figure 5. The 95% HDI is [2229, 2959], while the frequentist interval is [1810, 3430] for the same data—a much wider interval. Furthermore, the IPMVP then assumes averages and multiplies these figures to get annual savings and uncertainties. In the Bayesian paradigm, the HDIs can be different for every month (or time step) as shown in Figure 4, yielding more accurate overall savings uncertainty values.

3.2.4. Robustness to Outliers

As alluded to above, using the Student’s t-distribution rather than the normal distribution allows for Bayesian regression to be robust to outliers [59]. The heavier tails more easily accommodate an outlying data point by automatically altering the degrees-of-freedom hyperparameter to adapt to the non-normally distributed data. Uncertainty in the estimates is increased, but this reflects the true state of knowledge about the system more realistically than alternative assumptions of light tails, and is therefore warranted. The robustness of such regression does not give the M&V practitioner carte blanche to ignore outliers. One should always seek to understand the reason for an outlier; if the operating conditions of the facility were significantly different, the analyst should consider neglecting (or ‘condoning’) the data point. However, it is not always possible to trace the reasons for all outliers, and inherently robust models are useful (Technical note: the treatment here is very basic, and for illustration. More advanced Bayesian approaches are also available. For example, if there are only a few outliers, a mixture model may be used [60]. If there is a systematic problem such an unknown error variable, one can “marginalise” the offending variable out. The right-hand and top distributions of Figure 3 are marginal distributions: e.g., the distribution on the slope, with the intercept marginalised out, and vice versa. For an M&V example of marginalisation where an unknown measurement error is marginalised out, see Carstens [61] (Section 3.5.3). von der Linden et al. provides a thorough treatment of all the options for dealing with outliers [3] (Ch. 22)).

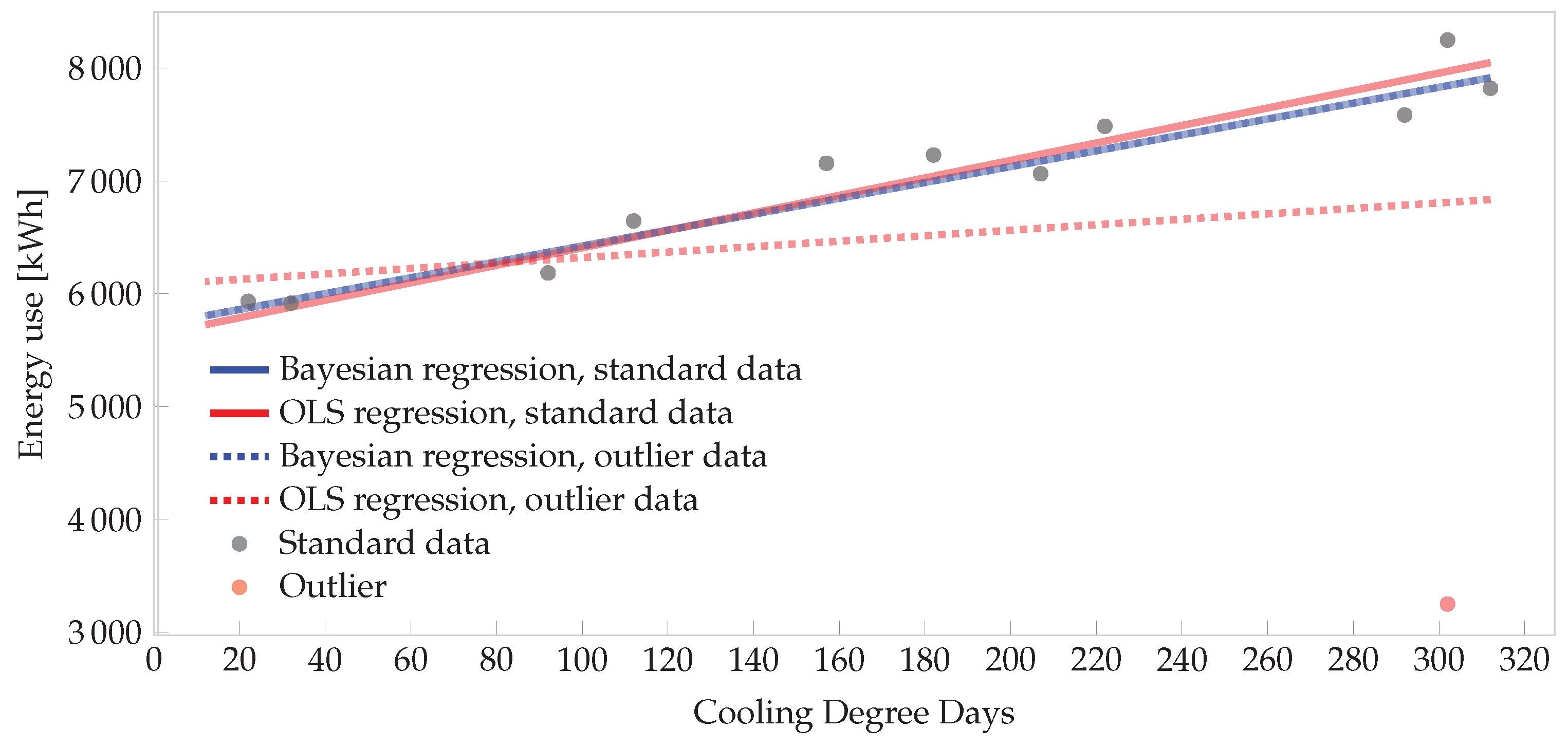
To demonstrate the robustness of such a Bayesian model, consider the regression case above. Suppose that for some reason the December cooling load was 3250 kWh and not 8250 kWh, indicated by the red point in the lower right-hand corner of Figure 6. If OLS regression were used, and this point is not removed, it would skew the whole model. However, the t-distributed likelihood in the Bayesian model is robust to the outlier. The effect is demonstrated in Figure 6. Four lines are plotted: the solid lines are for the data set without the outlier. The dashed lines are for the data set with the outlier. In the Bayesian model, the two regression lines are almost identical and close to the OLS regression line for the standard set. However, the OLS regression on the outlier set is dramatically biased and would underestimate the energy use for hot months due to the outlier.

3.2.5. Hierarchical Models

A further advantage in the Bayesian paradigm is the use of hierarchical, or multilevel models. This is a feature of the model structure rather than the Bayesian calculation itself (it also works for MLE) [2], but it is nevertheless useful in M&V. Suppose that multiple measures are installed at multiple sites so that the IPMVP Option C: Whole Building Retrofit is used for M&V. The UMP Chapter 8 [62] reports that there are two ways to analyse such data. The two-stage approach involves first analysing each facility separately and then using these results for the overall analysis in stage two. The fixed effects approach analyses all buildings simultaneously but assumes that the effect sizes are constant across facilities, using an average effect for all buildings. Hierarchical modelling considers both the individual facility’s energy saving and the overall effect simultaneously. It does this by assuming that the group effects are different realisations of an overarching distribution with a mean and variance, which is used as a prior. This can lead to ‘shrinkage’ in the parameter uncertainty estimates because the group effects are mutually informative. For groups with little data, the overarching effect distribution plays a larger role, and for groups with more data, a smaller role. In addition, the overall variance is reduced because the sources of inter-facility variance are isolated from that of inter-measure variance. The result for a hierarchical model is that the effect estimation for an individual facility is influenced by the overall estimate of the measured effect, as well as by the data for the facility. As another example, consider a program that retrofits air conditioning units in different provinces in South Africa. One could fix the savings effect across all facilities, but this will underestimate some and overestimate others. Otherwise, one could analyse by facility, then by province, and then overall. The hierarchical model provides a better alternative in these cases, and comprises the bulk of many Bayesian data analysis texts [2,4]. Booth, Choudhary, and Spiegelhalter have provided an excellent example of using hierarchical Bayesian models in energy M&V [63].

4. Bayesian Alternatives for Standard M&V Analyses

At this point, an M&V analyst may want to try the Bayesian method for an M&V problem, but where to start? In

Table 4. Common M&V (Measurement and Verification) cases and their Bayesian alternatives.

Problem Type	Variant	Bayesian Alternative	Example Reference
Sampling	Single Sample		Section 3.1, [2]
	Randomised Control Trial	Bayesian Estimation	[42]
	ANOVA	Hierarchical modelling	[64]
Regression	Standard	Bayesian regression	Section 3.2, [19]
	With change points	Bayesian regression	[17]
	Pooled fixed effects	Hierarchical modelling	[63]
	Non-parametric	Gaussian Process	[39,65,66]
Longitudinal	Persistence	Dynamic Generalised	[20]
		Linear Model
Meter calibration		Simulation Extrapolation	[67]
		with Bayesian refinement

, some Bayesian alternatives to standard M&V analyses are given. The references cited are mostly from M&V studies, although some general statistical sources are also listed where applicable.

5. Conclusions

The Bayesian paradigm provides a coherent and intuitive approach to energy measurement and verification. It does so by defining the basic M&V question—the savings inference given measurements—using conditional probabilities. It also provides a simpler and more intuitive understanding of probability and uncertainty because it allows the analyst to answer real questions in a straightforward manner, unlike traditional statistics. Due to recent technological and mathematical advances being incorporated into software, analysts need not be expert statisticians to harness the power and flexibility of this method.

The probabilistic nature of Bayesian analysis allows for automatic and accurate uncertainty quantification in savings models. The richer nature of the Bayesian result is shown in a sampling and a regression problem, where it is found that the Bayesian method allows for more realistic modelling and a greater variety of questions that can be answered. Its flexibility is also demonstrated by constructing a robust regression model, which is much less sensitive to outliers that standard ordinary least squares regression traditionally used in M&V.