Experimental Investigation of Flow Domain Division in Beds Packed with Different Sized Particles
Abstract
:1. Introduction
2. Materials and Methods
2.1. Equipment Set-Up and Method
2.2. Experiment Materials and Scheme
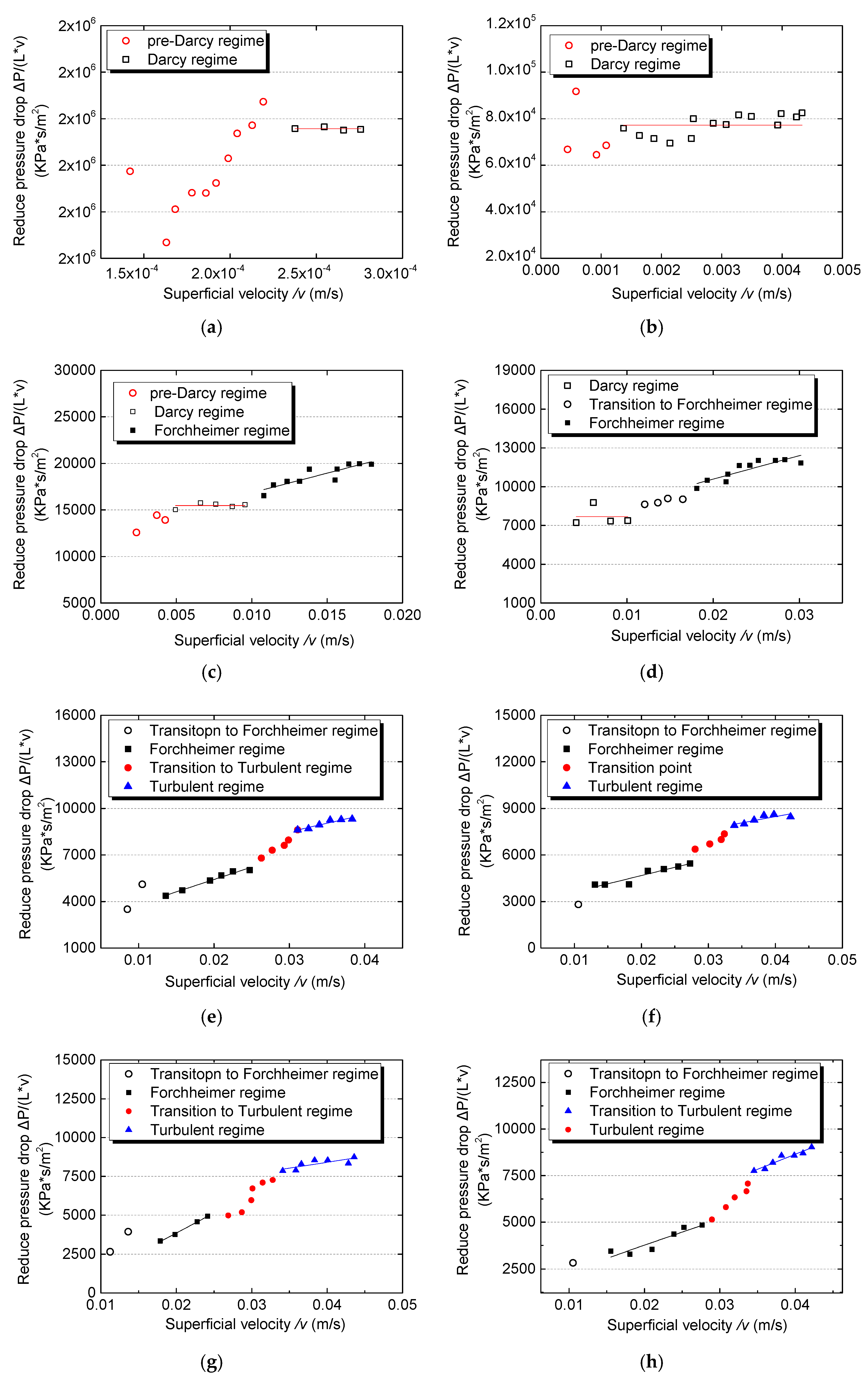
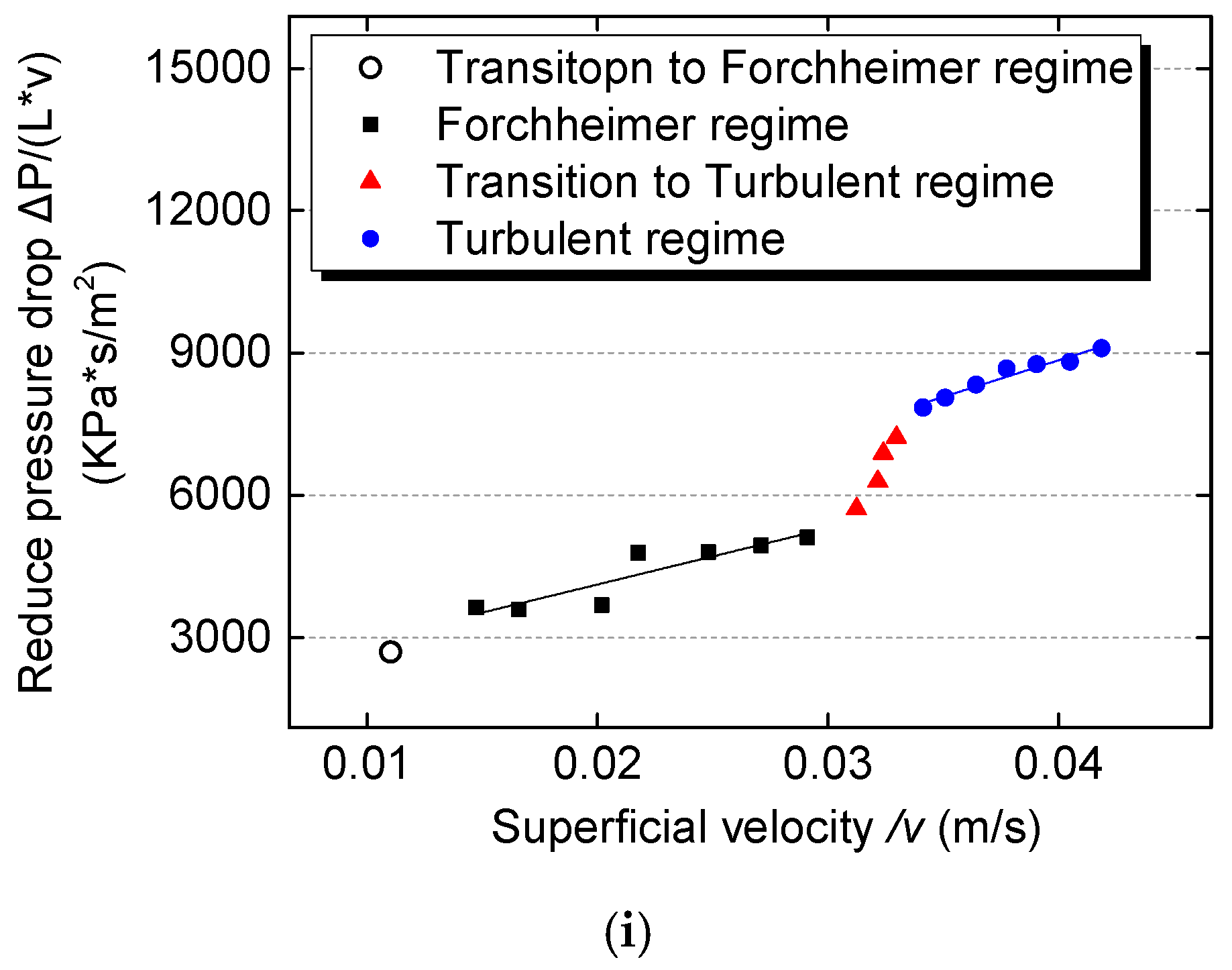
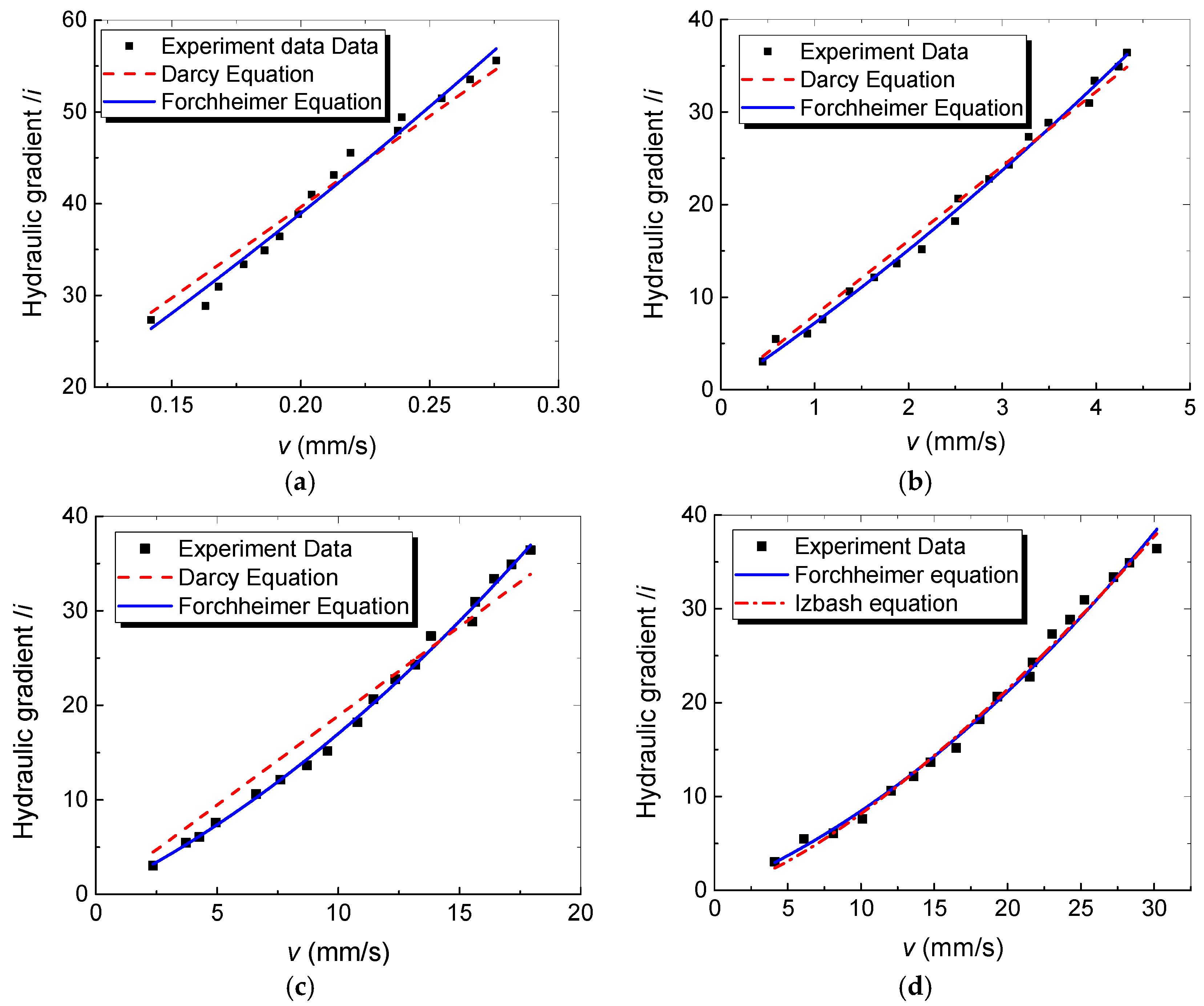
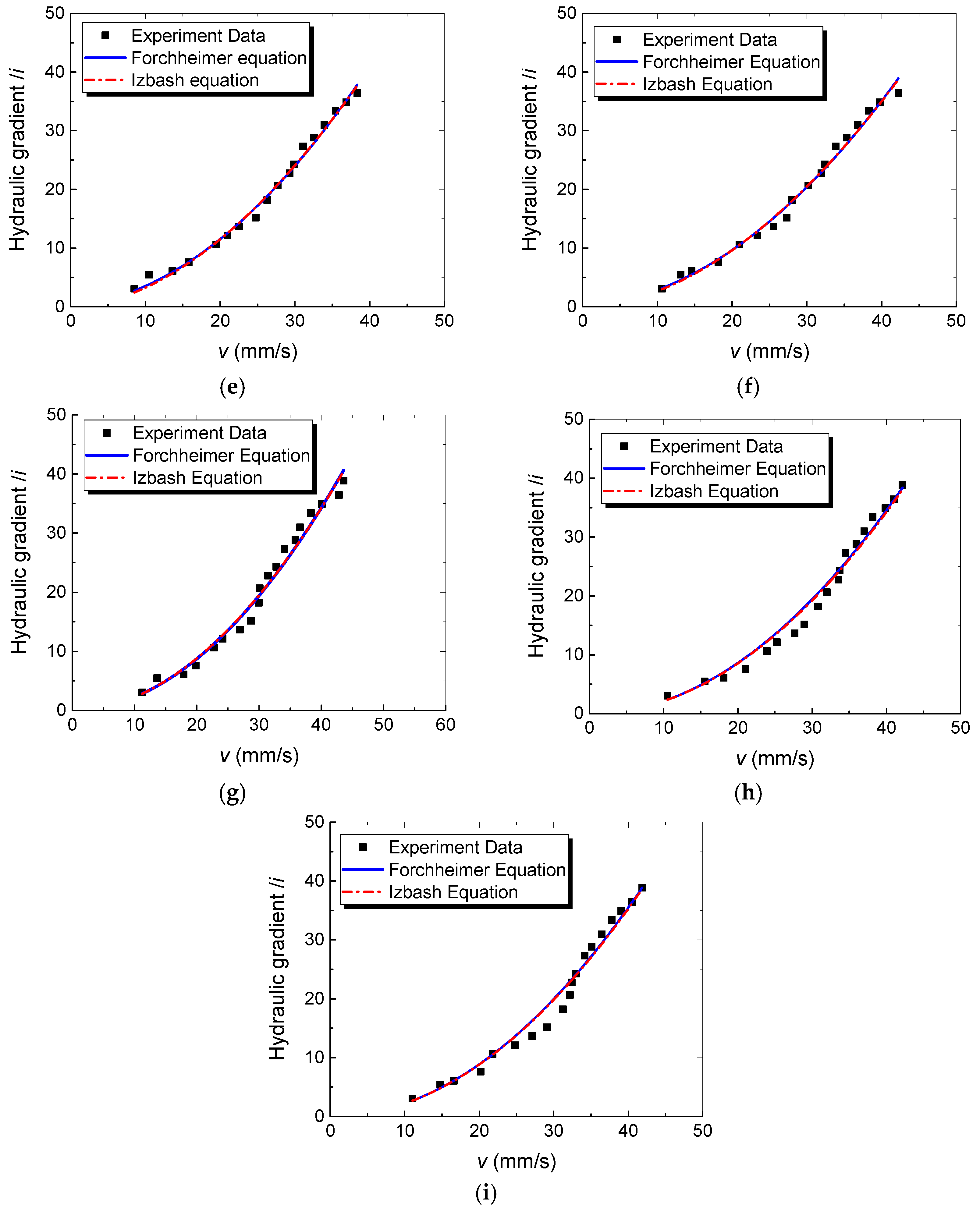
3. Flow Regime Identification
- Transition from pre-Darcy flow to Darcy flow;
- Transition from Darcy flow to Forchheimer flow;
- Transition from Forchheimer flow to turbulent flow.
4. Influence of Particle Diameter on Key Parameters
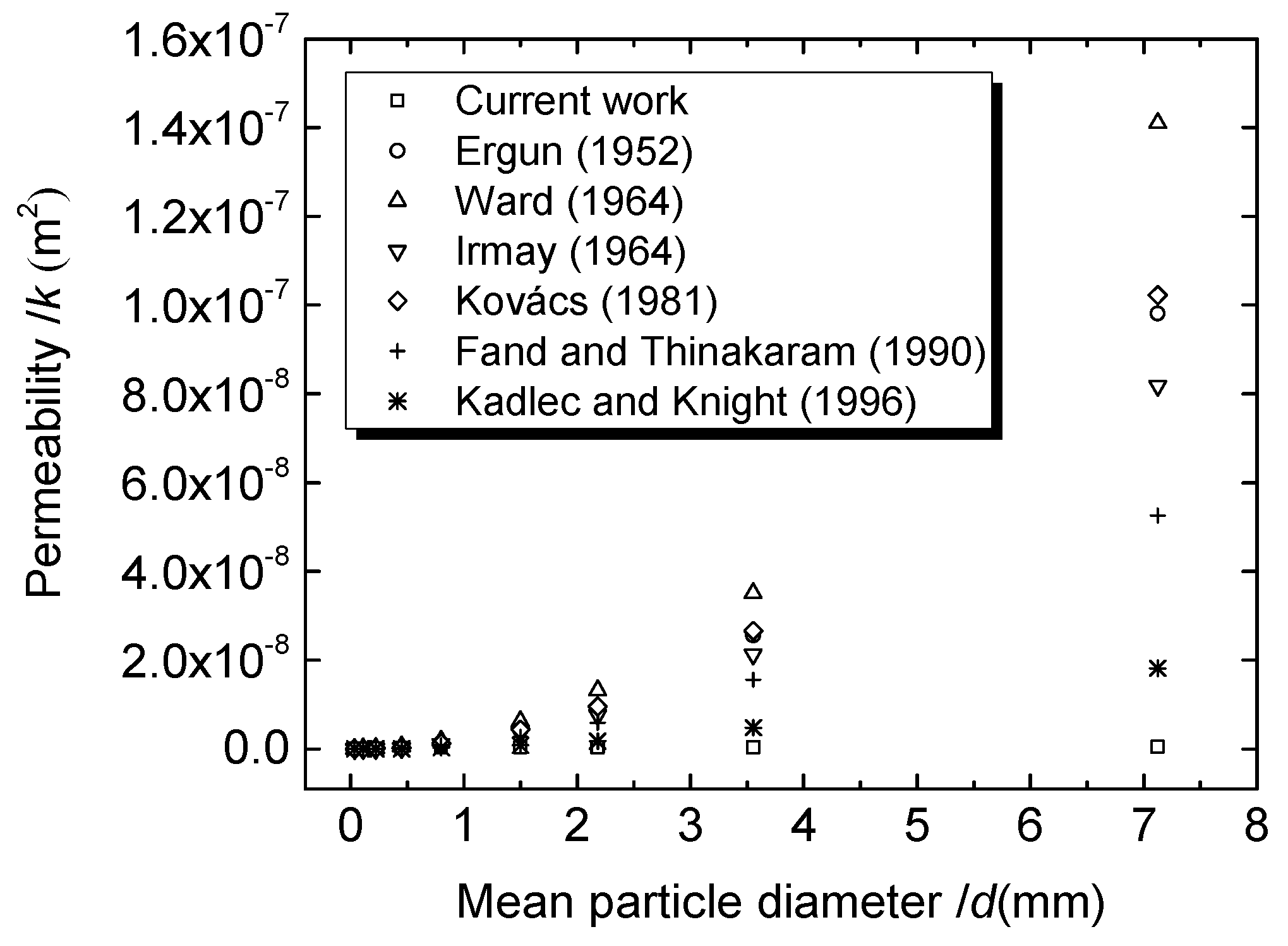
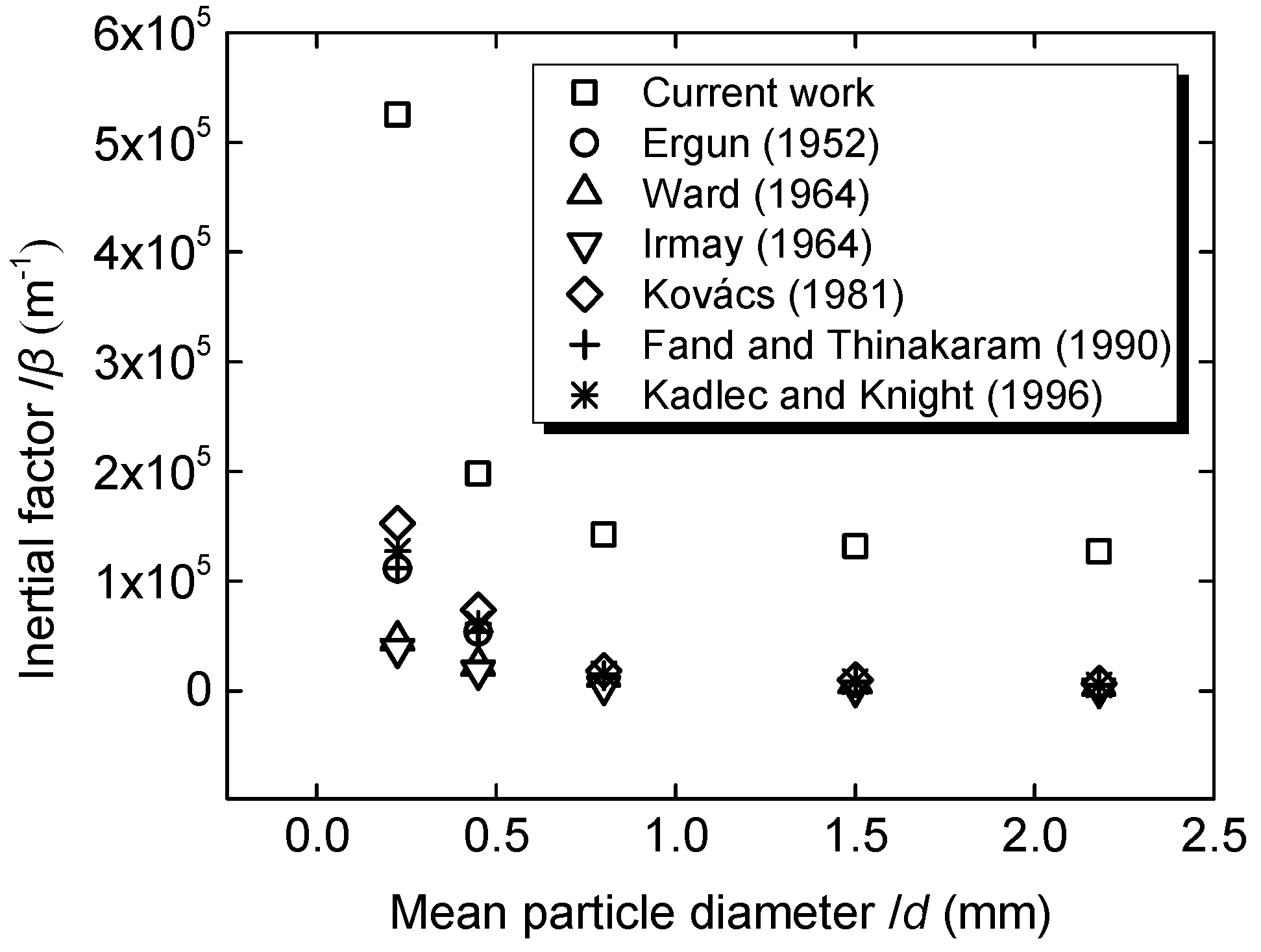
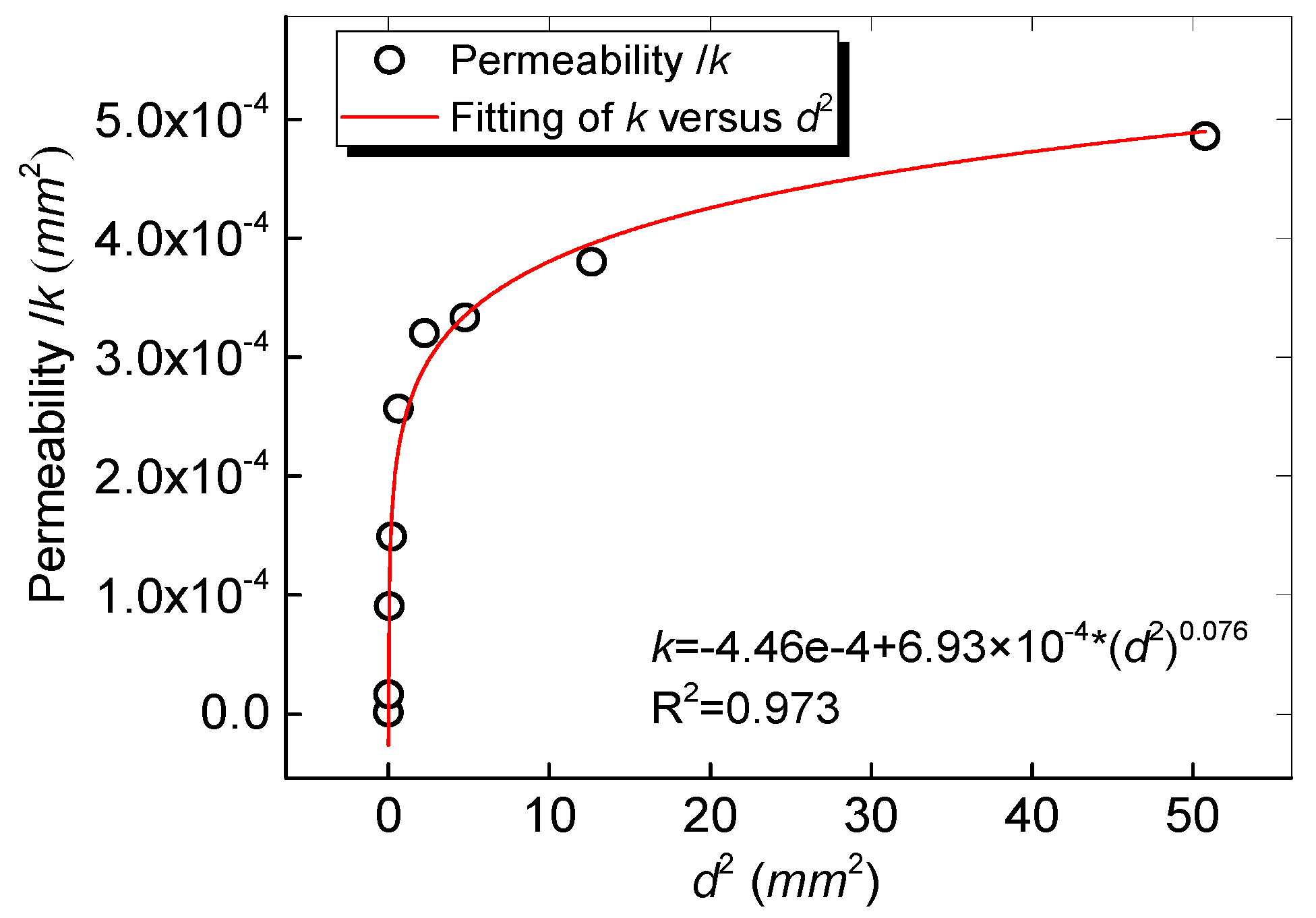
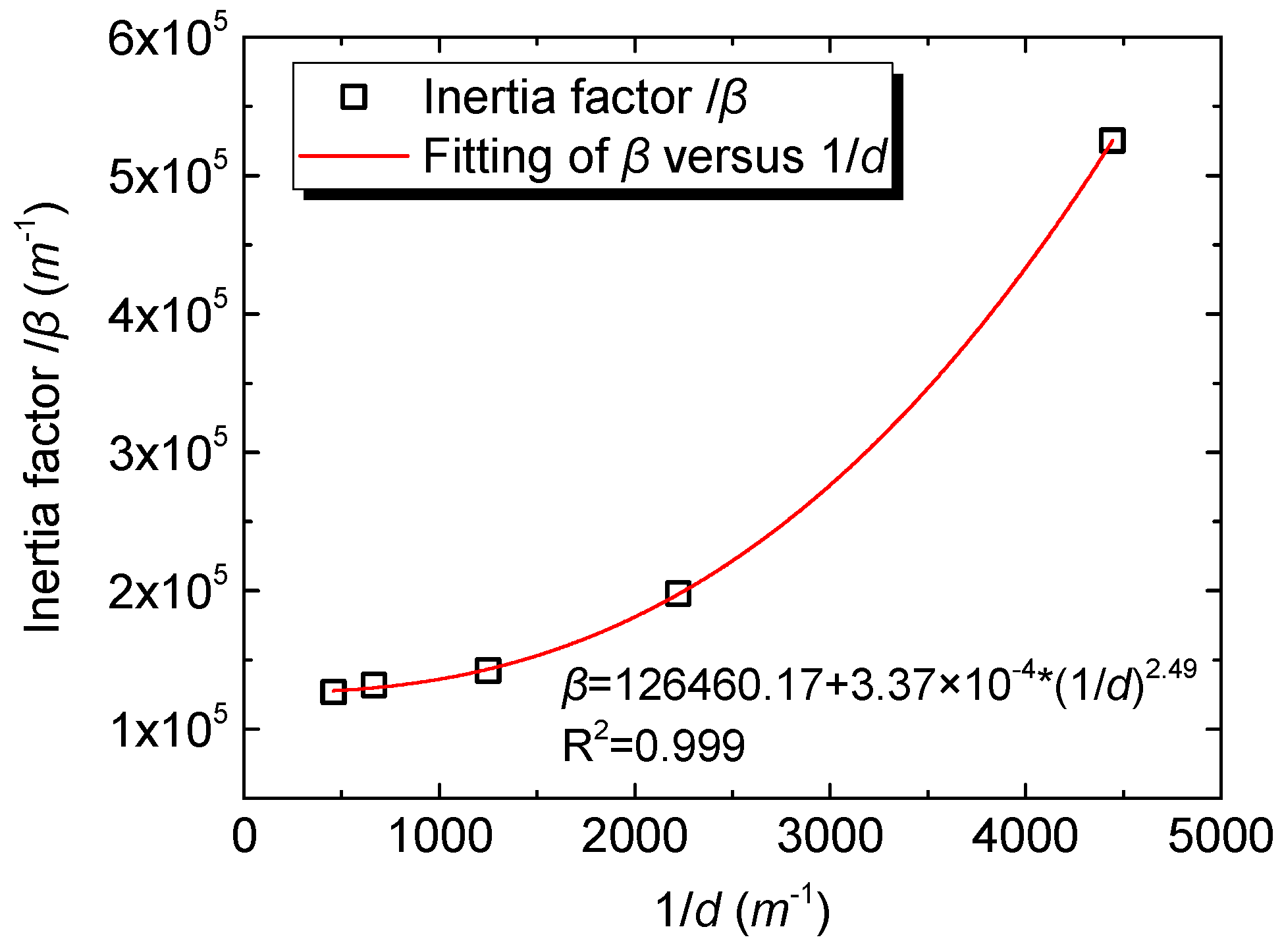
4.1. Influence of Particle Diameter, Shape and Roughness on Permeability k and Inertia Factor β
- Fluid adherence, no-slip resistance between fluid and solid surface; as well as
- Form force, responsible for the quadratic term of Forchheimer equation.
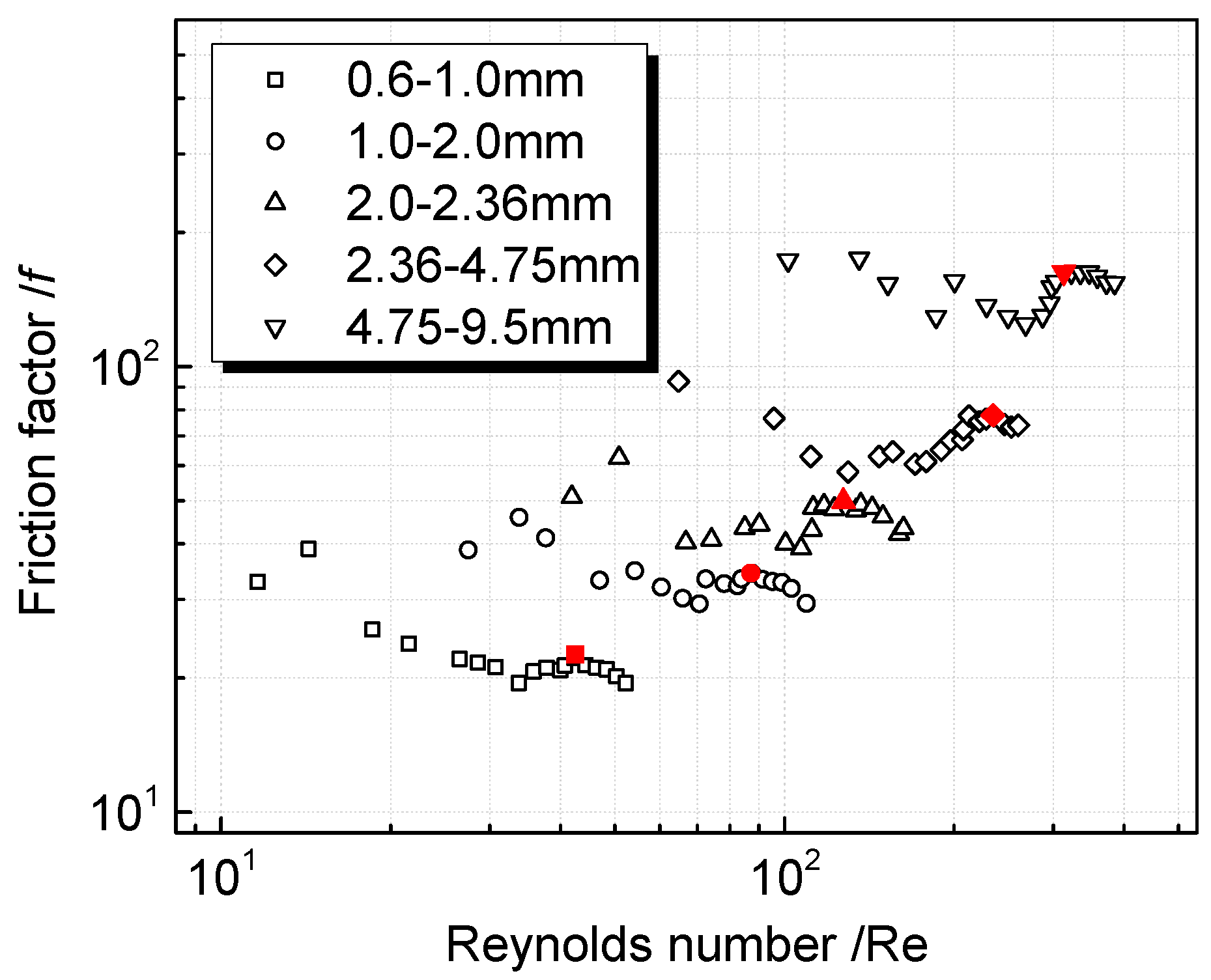
4.2. Influence of Particle Diameter on Friction Factor
4.3. Influence of Particle Diameter on Critical Re and Fo
5. Determination of Various Flow Domain Equations
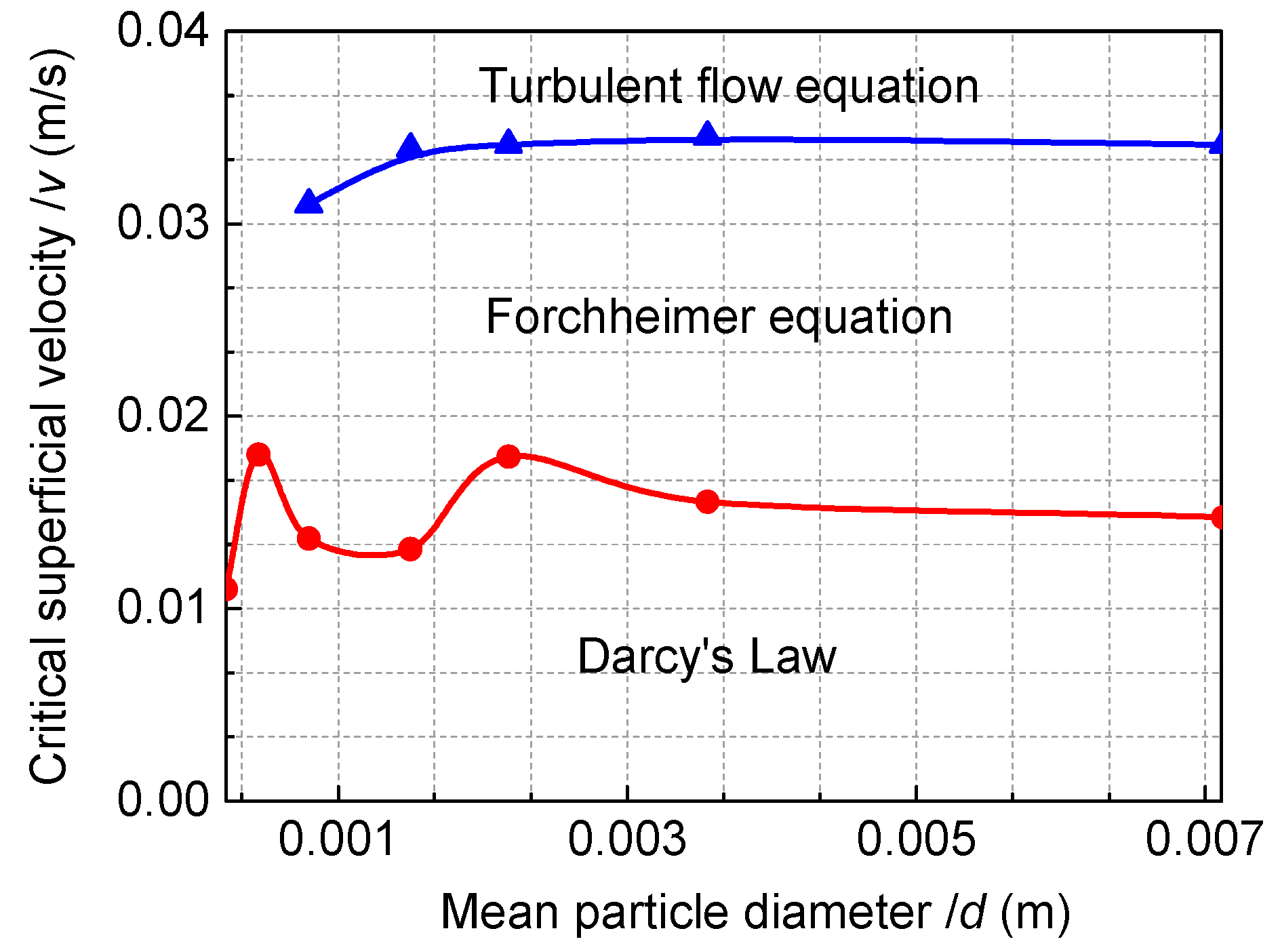
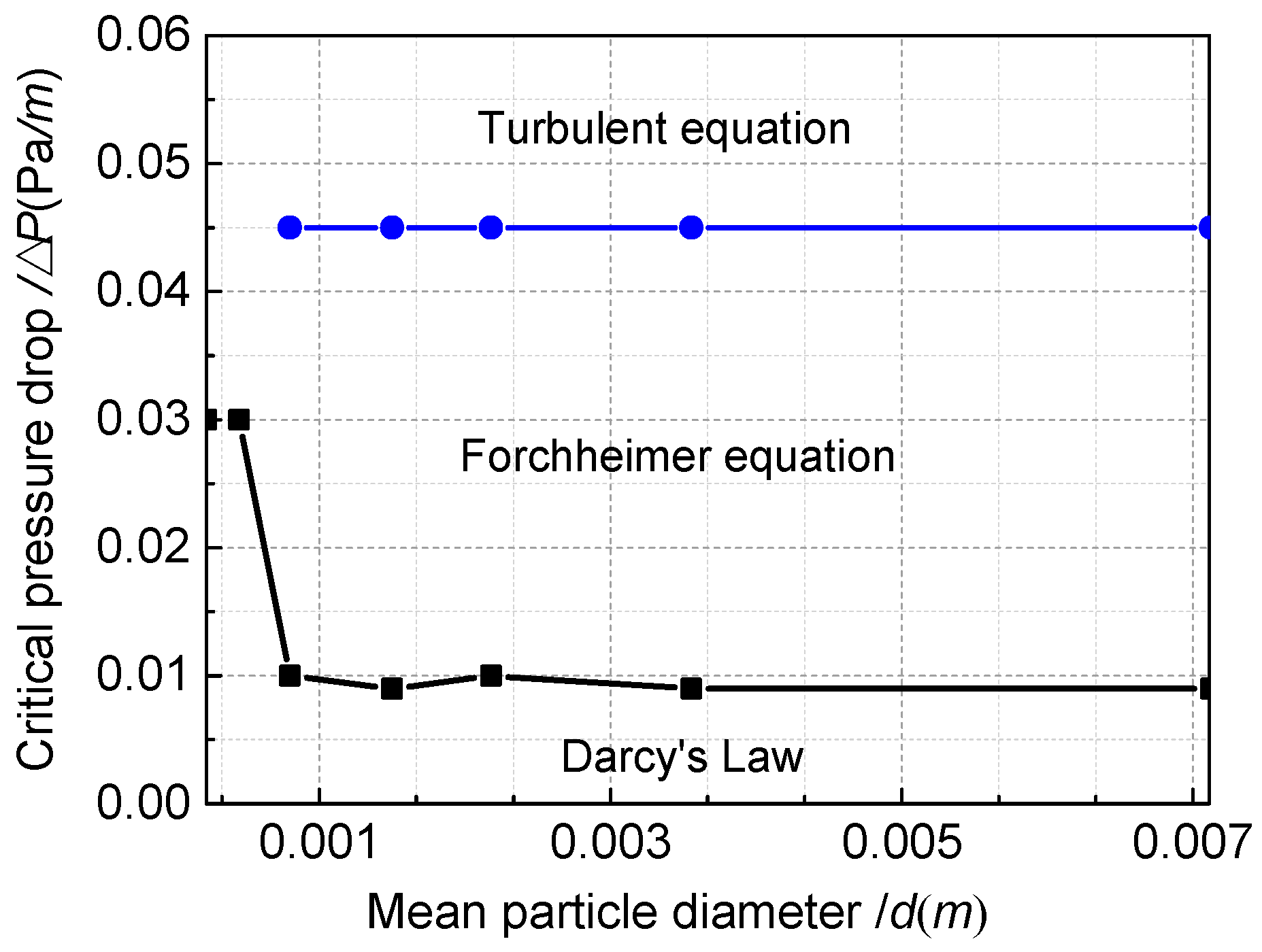
6. Flow Region Division and Seepage Equation Selection
7. Conclusions
- The permeability increases exponentially with particle diameter for the case of fluid flow through a particle-packed medium. A ‘discount effect’ for permeability should be caused by the non-spherical shape and roughness of the particle. A suitable equation of permeability was obtained experimentally:
- In contrast with permeability, the inertia factor reduces exponentially with an increase in particle diameter. An ‘additive effect’ should be caused by the non-spherical shape and roughness of particles for the inertia factor. The relationship between inertia factor and mean particle diameter was obtained:
- Three different flow regions have been divided. The availability range of seepage equation was verified based on the division results, which is shown in the graph of superficial velocity against mean particle diameter. The Darcy region is located at the creeping velocity in the range of 0 < v < 0.011 m/s with Darcy’s law being more suitable (Equation (5)). The Forchheimer region is found at 0.018 < v < 0.0345 m/s with the quadratic law suitable in this case (Equation (6)). The turbulent flow domain occurred at v > 0.0345 m/s with the power law being applied in this case with an exponential value of 2 (Equation (8)).
- According to the results of flow region–division, the availability range for seepage equation was obtained, which is shown in the curve of pressure drop (ΔP) plot against mean grain diameter. The Darcy domain should be found at ΔP < 0.03 MPa for a granular size of 0–0.6 mm and at ΔP < 0.009–0.01 MPa for a granular size of 0.6–9.5 mm. The Forchheimer domain is located in 0.01 < ΔP <0.045 MPa for a granular size of 0.6–9.5 mm. Turbulent flow occurred at ΔP ≥ 0.045 MPa for a granular size of 0.6–9.5 mm.
- The inertia effect becomes more pronounced with an increase in the particle diameter when the flow transition occurs. Furthermore, the particle-packed medium with smaller granules had a greater energy loss during this process.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, Y.; Neuman, S.P. Flow to a well in a five-layer system with application to the Oxnard Basin. Ground Water 2007, 45, 672–682. [Google Scholar] [CrossRef] [PubMed]
- Wen, Z.; Huang, G.; Zhan, H. An analytical solution for non-darcian flow in a confined aquifer using the power law function. Adv. Water Resour. 2008, 31, 44–55. [Google Scholar] [CrossRef]
- Wen, Z.; Huang, G.; Zhan, H. Non-darcian flow to a well in an aquifer-aquitard system. Adv. Water Resour. 2008, 31, 1754–1763. [Google Scholar] [CrossRef]
- Wang, J.; Liu, X.; Xiang, J.; Jiang, Y.; Feng, B. Laboratory model tests on water inrush in foundation pit bottom. Environ. Earth Sci. 2016, 75, 1072. [Google Scholar] [CrossRef]
- Sen, Z. Nonlinear flow toward wells. J. Hydraul. Eng. 1989, 115, 193–209. [Google Scholar] [CrossRef]
- Wen, Z.; Huang, G.; Zhan, H. Non-darcian flow in a single confined vertical fracture toward a well. J. Hydrol. 2006, 330, 698–708. [Google Scholar] [CrossRef]
- Ma, D.; Bai, H.; Miao, X.; Pu, H.; Jiang, B.; Chen, Z. Compaction and seepage properties of crushed limestone particle mixture: An experimental investigation for Ordovician karst collapse pillar groundwater inrush. Environ. Earth Sci. 2016, 75, 11. [Google Scholar] [CrossRef]
- Yin, S.X.; Zhang, J.C. Impacts of karst paleo-sinkholes on mining and environment in Northern China. Environ. Geol. 2005, 48, 1077–1083. [Google Scholar] [CrossRef]
- Miao, X.; Li, S.; Chen, Z.; Liu, W. Experimental study of seepage properties of broken sandstone under different porosities. Transp. Porous Media 2011, 86, 805–814. [Google Scholar] [CrossRef]
- Wang, Q.; Zhan, H.; Tang, Z. Forchheimer flow to a well-considering time-dependent critical radius. Hydrol. Earth Syst. Sci. 2014, 18, 2437–2448. [Google Scholar] [CrossRef]
- Li, Y.; Li, X.; Teng, S.; Xu, D. Effect of the non-darcy flow boundary in low permeability reservoirs. Environ. Prog. Sustain. Energy 2015, 34, 1822–1831. [Google Scholar] [CrossRef]
- Huyakorn, P.; Dudgeon, C.R. Investigation of two-regime well flow. J. Hydrauli. Div. 1976, 102, 1149–1165. [Google Scholar]
- Basak, P. Analytical solutions for two-regime well flow problems. J. Hydrol. 1978, 38, 147–159. [Google Scholar] [CrossRef]
- Mackie, C. Determination of nonlinear formation losses in pumping wells. In Proceedings of the International Conference on Groundwater and Man, Sydney, Australia, 5–9 December 1983; Volume 1, pp. 199–209. [Google Scholar]
- Wen, Z.; Huang, G.; Zhan, H.; Li, J. Two-region non-darcian flow toward a well in a confined aquifer. Adv. Water Resour. 2008, 31, 818–827. [Google Scholar] [CrossRef]
- Wenhao, S.; Tianhong, Y.; Honglei, L. Non-darcy flow model and numerical simulation for water-inrush in fractured rock mass. Chin. J. Rock Mech. Eng. 2016, 35, 446–455. [Google Scholar] [CrossRef]
- Ma, D.; Zhou, Z.; Wu, J.; Li, Q.; Bai, H. Grain size distribution effect on the hydraulic properties of disintegrated coal mixtures. Energies 2017, 10, 612. [Google Scholar] [CrossRef]
- Macdonald, I.; El-Sayed, M.; Mow, K.; Dullien, F. Flow through porous media-the Ergun equation revisited. Ind. Eng. Chem. Fundam. 1979, 18, 199–208. [Google Scholar] [CrossRef]
- Burcharth, H.F.; Andersen, O.H. On the one-dimensional steady and unsteady porous flow equations. Coast. Eng. 1995, 24, 233–257. [Google Scholar] [CrossRef]
- Allen, K.G.; von Backstroem, T.W.; Kroeger, D.G. Packed bed pressure drop dependence on particle shape, size distribution, packing arrangement and roughness. Powder Technol. 2013, 246, 590–600. [Google Scholar] [CrossRef]
- Carman, P.C. Fluid flow through granular beds. Trans. Inst. Chem. Eng. 1937, 15, 150–166. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
- Ward, J. Turbulent flow in porous media. J. Hydraul. Div. 1964, 90, 1–12. [Google Scholar]
- Irmay, S. Theoretical models of flow through porous media. In Proceedings of the International Symposium on Transport of Water in Porous Media, Paris, France, 1964; Volume 29, pp. 37–43. [Google Scholar]
- Kovacs, G. Seepage Hydraulics; Elsevier Scientific Publishing Company: Amsterdam, The Netherlands, 1981; ISBN 0-444-99755-5. [Google Scholar]
- Fand, R.M.; Thinakaran, R. The influence of the wall on flow through pipes packed with spheres. J. Fluids Eng. 1990, 112, 84–88. [Google Scholar] [CrossRef]
- Kadlec, R.H.; Wallace, S. Treatment Wetlands, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2008; pp. 43–44. ISBN 978-1-56670-526-4. [Google Scholar]
- Sidiropoulou, M.G.; Moutsopoulos, K.N.; Tsihrintzis, V.A. Determination of forchheimer equation coefficients a and b. Hydrol. Process. 2007, 21, 534–554. [Google Scholar] [CrossRef]
- Hayes, R.E.; Afacan, A.; Boulanger, B. An equation-of-motion for an incompressible newtonian fluid in a packed-bed. Transp. Porous Media 1995, 18, 185–198. [Google Scholar] [CrossRef]
- Dias, R.P.; Fernandes, C.S.; Teixeira, J.A.; Mota, M.; Yelshin, A. Permeability analysis in bisized porous media: Wall effect between particles of different size. J. Hydrol. 2008, 349, 470–474. [Google Scholar] [CrossRef] [Green Version]
- Tian, F.-Y.; Huang, L.-F.; Fan, L.-W.; Qian, H.-L.; Yu, Z.-T. Wall effects on the pressure drop in packed beds of irregularly shaped sintered ore particles. Powder Technol. 2016, 301, 1284–1293. [Google Scholar] [CrossRef]
- Soni, J.; Islam, N.; Basak, P. An experimental evaluation of non-darcian flow in porous media. J. Hydrol. 1978, 38, 231–241. [Google Scholar] [CrossRef]
- Huang, K.; Wan, J.W.; Chen, C.X.; He, L.Q.; Mei, W.B.; Zhang, M.Y. Experimental investigation on water flow in cubic arrays of spheres. J. Hydrol. 2013, 492, 61–68. [Google Scholar] [CrossRef]
- Sedghi-Asl, M.; Rahimi, H.; Salehi, R. Non-darcy flow of water through a packed column test. Transp. Porous Media 2014, 101, 215–227. [Google Scholar] [CrossRef]
- Benenati, R.F.; Brosilow, C.B. Void fraction distribution in beds of spheres. Am. Inst. Chem. Eng. 1962, 8, 359–361. [Google Scholar] [CrossRef]
- Beavers, G.S.; Sparrow, E.M.; Rodenz, D.E. Influence of bed size on the flow characteristics and porosity of randomly packed beds of spheres. J. Appl. Mech. 1973, 40, 655–660. [Google Scholar] [CrossRef]
- Li, Z.; Wan, J.; Huang, K.; Chang, W.; He, Y. Effects of particle diameter on flow characteristics in sand columns. Int. J. Heat Mass Transf. 2017, 104, 533–536. [Google Scholar] [CrossRef]
- Ma, D.; Bai, H.; Chen, Z.; Pu, H. Effect of particle mixture on seepage properties of crushed mudstones. Transp. Porous Media 2015, 108, 257–277. [Google Scholar] [CrossRef]
- Roblee, L.; Baird, R.; Tierney, J. Radial porosity variations in packed beds. AIChE J. 1958, 4, 460–464. [Google Scholar] [CrossRef]
- Basak, P. Non-darcy flow and its implications to seepage problems. J. Irrig. Drain. Div. 1977, 103, 459–473. [Google Scholar]
- Macini, P.; Mesini, E.; Viola, R. Laboratory measurements of non-darcy flow coefficients in natural and artificial unconsolidated porous media. J. Pet. Sci. Eng. 2011, 77, 365–374. [Google Scholar] [CrossRef]
- Zeng, Z.W.; Grigg, R. A criterion for non-darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; American Elsevier Pub. Co., Inc.: San Diego, CA, USA, 1972; pp. 125–127. [Google Scholar]
- Venkataraman, P.; Rao, P.R.M. Darcian, transitional, and turbulent flow through porous media. J. Hydraul. Eng. 1998, 124, 840–846. [Google Scholar] [CrossRef]
- Legrand, J. Revisited analysis of pressure drop in flow through crushed rocks. J. Hydraul. Eng. 2002, 128, 1027–1031. [Google Scholar] [CrossRef]
- Chen, Z.; Qian, J.-Z.; Luo, S.-H.; Zhan, H.-B. Experimental study of friction factor for groundwater flow in a single rough fracture. J. Hydrodyn. 2009, 21, 820–825. [Google Scholar] [CrossRef]
- Fand, R.M.; Kim, B.Y.K.; Lam, A.C.C.; Phan, R.T. Resistance to the flow of fluids through simple and complex porous media whose matrices are composed of randomly packed spheres. J. Fluids Eng 1987, 109, 268–273. [Google Scholar] [CrossRef]
- Kececioglu, I.; Jiang, Y. Flow through porous media of packed spheres saturated with water. J. Fluids Eng. 1994, 116, 164–170. [Google Scholar] [CrossRef]
- Dukhan, N.; Minjeur, C.A., II. A two-permeability approach for assessing flow properties in metal foam. J. Porous Mater. 2011, 18, 417–424. [Google Scholar] [CrossRef]
- Bagci, O.; Dukhan, N.; Ozdemir, M. Flow regimes in packed beds of spheres from pre-darcy to turbulent. Transp. Porous Media 2014, 104, 501–520. [Google Scholar] [CrossRef]
- Kundu, P.; Kumar, V.; Mishra, I.M. Experimental and numerical investigation of fluid flow hydrodynamics in porous media: Characterization of pre-darcy, darcy and non-darcy flow regimes. Powder Technol. 2016, 303, 278–291. [Google Scholar] [CrossRef]
- Zhu, T.; Ye, W. Origin of knudsen forces on heated microbeams. Phys. Rev. E 2010, 82, 036308. [Google Scholar] [CrossRef] [PubMed]
- Zhu, T.; Ye, W. Theoretical and numerical studies of noncontinuum gas-phase heat conduction in micro/nano devices. Numer. Heat Trans. Part B 2010, 57, 203–226. [Google Scholar] [CrossRef]
- Wang, S.; Feng, Q.; Han, X. A hybrid analytical/numerical model for the characterization of preferential flow path with non-darcy flow. PLoS ONE 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Fourar, M.; Radilla, G.; Lenormand, R.; Moyne, C. On the non-linear behavior of a laminar single-phase flow through two and three-dimensional porous media. Adv. Water Resour. 2004, 27, 669–677. [Google Scholar] [CrossRef]
- Skjetne, E.; Auriault, J.L. High-velocity laminar and turbulent flow in porous media. Transp. Porous Media 1999, 36, 131–147. [Google Scholar] [CrossRef]
- Tzelepis, V.; Moutsopoulos, K.N.; Papaspyros, J.N.E.; Tsihrintzis, V.A. Experimental investigation of flow behavior in smooth and rough artificial fractures. J. Hydrol. 2015, 521, 108–118. [Google Scholar] [CrossRef]
- Lage, J. The fundamental theory of flow through permeable niedia from darcy to turbulence. In Transport Phenomena in Porous Media; Elsevier Science: Amsterdam, The Netherlands, 1998; p. 1. [Google Scholar]
- Cherubini, C.; Giasi, C.I.; Pastore, N. Bench scale laboratory tests to analyze non-linear flow in fractured media. Hydrol. Earth Syst. Sci. 2012, 16, 2511–2522. [Google Scholar] [CrossRef]
- Sedghi-Asl, M.; Rahimi, H. Adoption of manning's equation to 1d non-darcy flow problems. J. Hydraul. Res. 2011, 49, 814–817. [Google Scholar] [CrossRef]
- Chaudhary, K.; Cardenas, M.B.; Deng, W.; Bennett, P.C. The role of eddies inside pores in the transition from darcy to forchheimer flows. Geophys. Res. Lett. 2011, 38. [Google Scholar] [CrossRef]
- Tsihrintzis, V.A.; Madiedo, E.E. Hydraulic resistance determination in marsh wetlands. Water Resour. Manag. 2000, 14, 285–309. [Google Scholar] [CrossRef]
- Brackbill, T.P.; Kandlikar, S.G. Application of lubrication theory and study of roughness pitch during laminar, transition, and low reynolds number turbulent flow at microscale. Heat Trans. Eng. 2010, 31, 635–645. [Google Scholar] [CrossRef]
- Falkovich, G.; Sreenivasan, K.R. Lessons from hydrodynamic turbulence. Phys. Today 2006, 59, 43. [Google Scholar] [CrossRef]
- Ruth, D.; Ma, H. On the derivation of the forchheimer equation by means of the averaging theorem. Transp. Porous Media 1992, 7, 255–264. [Google Scholar] [CrossRef]
- Irmay, S. On the theoretical derivation of darcy and forchheimer formulas. Eos Trans. Am. Geophys. Union 1958, 39, 702–707. [Google Scholar] [CrossRef]
- Chen, Z.X.; Lyons, S.L.; Qin, G. Derivation of the forchheimer law via homogenization. Trans. Porous Media 2001, 44, 325–335. [Google Scholar] [CrossRef]
- Bordier, C.; Zimmer, D. Drainage equations and non-darcian modelling in coarse porous media or geosynthetic materials. J. Hydrol. 2000, 228, 174–187. [Google Scholar] [CrossRef]
- Moutsopoulos, K.N.; Papaspyros, I.N.E.; Tsihrintzis, V.A. Experimental investigation of inertial flow processes in porous media. J. Hydrol. 2009, 374, 242–254. [Google Scholar] [CrossRef]
- Yamada, H.; Nakamura, F.; Watanabe, Y.; Murakami, M.; Nogami, T. Measuring hydraulic permeability in a streambed using the packer test. Hydrol. Process. 2005, 19, 2507–2524. [Google Scholar] [CrossRef]
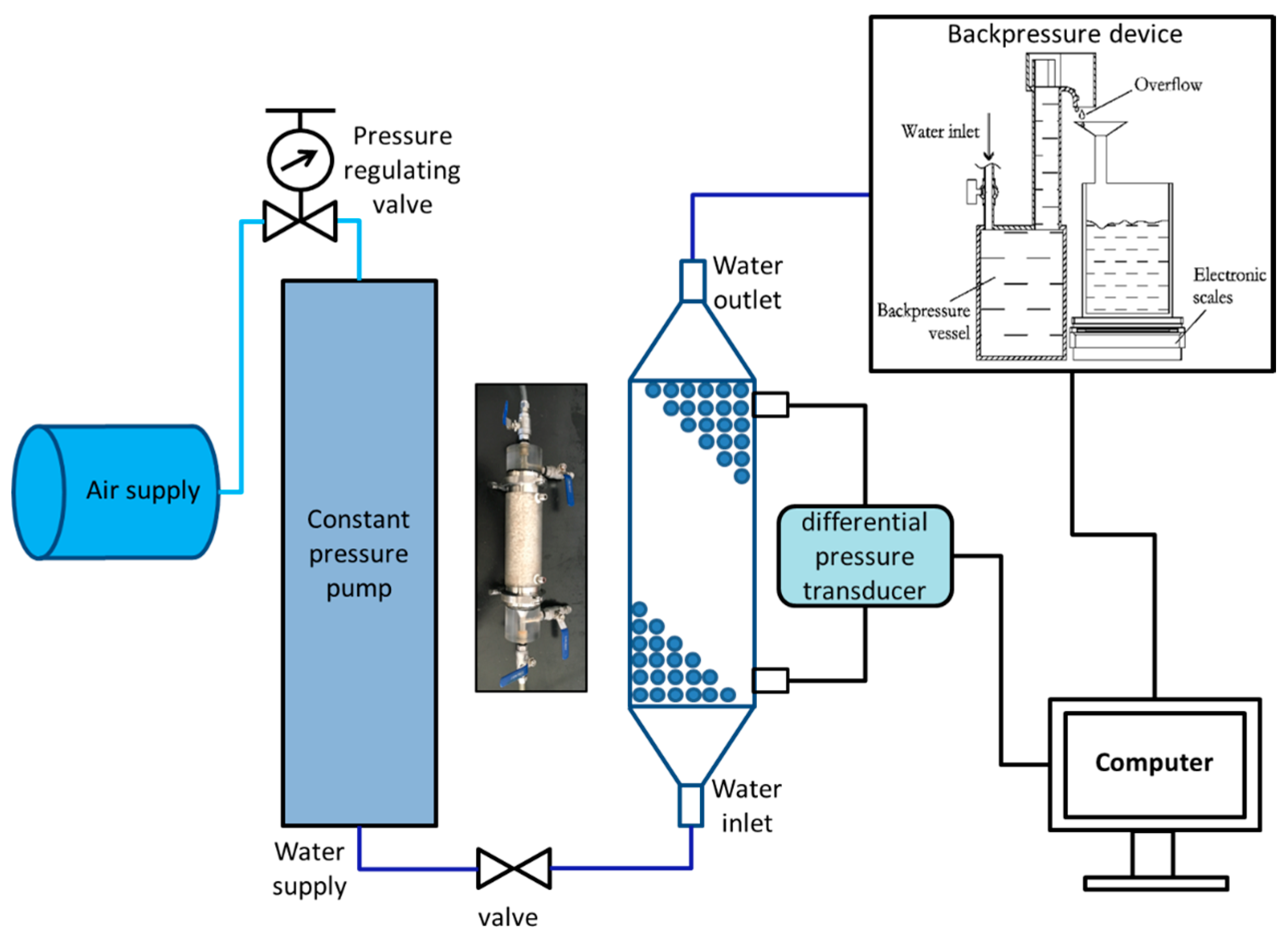


| Material | Particle Packed Column | Particle Diameter Range (d/mm) | Mean Particle Diameter (mm) | Density (kg/m3) | Fractional Void Volume of Packing Column (%) |
|---|---|---|---|---|---|
| Wind-blown sand | a | 0–0.075 | 0.0375 | 2620 | 35.19 |
| b | 0.075–0.15 | 0.1125 | 2620 | 35.33 | |
| c | 0.15–0.3 | 0.225 | 2620 | 35.56 | |
| d | 0.3–0.6 | 0.45 | 2620 | 35.94 | |
| River sand | e | 0.6–1.0 | 0.8 | 2650 | 44.78 |
| f | 1.0–2.0 | 1.5 | 2650 | 44.28 | |
| g | 2.0–2.36 | 2.18 | 2650 | 44.58 | |
| Crushed quartz | h | 2.36–4.75 | 3.555 | 2820 | 45.06 |
| i | 4.75–9.5 | 7.125 | 2820 | 44.63 |
| Particle Packed Column | Onset of Darcy Flow | Onset of Forchheimer Flow | Onset of Turbulent Flow | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Pressure Drop/ΔP (MPa) | Superficial Velocity/v (m/s) | Reynolds Number/Re | Forchheimer Number/Fo | Friction Factor/f | Pressure Drop/ΔP (MPa) | Superficial Velocity/v (m/s) | Reynolds Number/Re | Forchheimer Number/Fo | Friction Factor/f | Pressure Drop/ΔP (MPa) | Superficial Velocity/v (m/s) | Reynolds Number/Re | Forchheimer Number/Fo | Friction Factor/f | |
| a | 0.0814 | 2.39 × 10−4 | 0.019 | 0 | 196,653.2 | - | - | - | - | - | - | - | - | - | |
| b | 0.0175 | 0.00137 | 0.33 | 0.092 | 387.89 | - | - | - | - | - | - | - | - | - | |
| c | 0.0125 | 0.00495 | 2.39 | 0.18 | 43.22 | 0.03 | 0.011 | 5.22 | 0.39 | 21.78 | - | - | - | - | |
| d | - | - | - | - | - | 0.03 | 0.018 | 17.31 | 0.41 | 15.83 | - | - | - | - | |
| e | - | - | - | - | - | 0.01 | 0.0136 | 18.58 | 0.38 | 19.50 | 0.045 | 0.0310 | 42.39 | 0.87 | 22.23 |
| f | - | - | - | - | - | 0.009 | 0.0131 | 33.86 | 0.42 | 29.36 | 0.045 | 0.0339 | 87.59 | 1.09 | 34.33 |
| g | - | - | - | - | - | 0.01 | 0.0179 | 66.73 | 0.58 | 44.19 | 0.045 | 0.0341 | 127.32 | 1.10 | 49.87 |
| h | - | - | - | - | - | 0.009 | 0.0155 | 95.72 | 0.61 | 60.41 | 0.045 | 0.0345 | 212.64 | 1.36 | 77.54 |
| i | - | - | - | - | - | 0.009 | 0.0147 | 179.68 | 0.92 | 124.57 | 0.045 | 0.0341 | 322.55 | 2.13 | 163.12 |
| Permeability k (m2) | Inertial Factory β (m−1) | |
|---|---|---|
| Ergun (1952) | ||
| Ward (1964) | ||
| Irmay (1964) | ||
| Kovács (1981) | ||
| Fand and Thinakaram (1990) | ||
| Kadlec and Knight (1996) |
| Data Source | Medium Character | m | n |
|---|---|---|---|
| Huang et al. (2013) | Cubic arrays of smooth sphere | 1 | 1 |
| Sedghi-Asl et al. (2014) | Random arrays rounded aggregates | 0.631 | 1.02 |
| Our research | Random arrays sand and crushed stone | 0.076 | 2.49 |
| Sample Number | Darcy’s Law i = Kv (Equation (5)) | Forchheimer Equation i = Av + Bv2 (Equation (6)) | Power law i = λvm (Equation (7)) | |||
|---|---|---|---|---|---|---|
| a | i = 198.152v | R2 = 0.999 | i = 164.182v+152.506v2 | R2 = 0.983 | — | — |
| b | i = 8.05v | R2 = 0.998 | i = 6.86v+0.346v2 | R2 = 0.995 | — | — |
| c | i = 1.889v | R2 = 0.993 | i = 1.246v+0.045v2 | R2 = 0.996 | — | — |
| d | — | — | i = 0.5694v+0.0247v2 | R2 = 0.988 | i = 0.27v1.462 | R2 = 0.987 |
| e | — | — | i = 0.0966v+0.0236v2 | R2 = 0.993 | i = 0.040v1.884 | R2 = 0.992 |
| f | — | — | i = 0.0703v+0.0204v2 | R2 = 0.991 | i = 0.0321v1.899 | R2 = 0.991 |
| g | — | — | i = 0.0182v+0.0210v2 | R2 = 0.980 | i = 0.0253v1.955 | R2 = 0.980 |
| h | — | — | i = 1 × 10−5v+0.0216v2 | R2 = 0.980 | i = 0.0214v2 | R2 = 0.981 |
| i | — | — | i = 1 × 10−5v+0.0222v2 | R2 = 0.977 | i = 0.0221v2 | R2 = 0.978 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Yang, T.; Xu, Z.; Yang, B. Experimental Investigation of Flow Domain Division in Beds Packed with Different Sized Particles. Energies 2017, 10, 1401. https://doi.org/10.3390/en10091401
Yang X, Yang T, Xu Z, Yang B. Experimental Investigation of Flow Domain Division in Beds Packed with Different Sized Particles. Energies. 2017; 10(9):1401. https://doi.org/10.3390/en10091401
Chicago/Turabian StyleYang, Xin, Tianhong Yang, Zenghe Xu, and Bin Yang. 2017. "Experimental Investigation of Flow Domain Division in Beds Packed with Different Sized Particles" Energies 10, no. 9: 1401. https://doi.org/10.3390/en10091401






