Heat Conduction in Porous Media Characterized by Fractal Geometry

Abstract

Fractal geometry (fractional Brownian motion—FBM) is introduced to characterize the pore distribution of porous material. Based on this fractal characterization, a mathematical model of heat conduction is presented to study heat conduction behaviors in porous material with a focus on effective thermal conductivity. The role of pore structure on temperature distribution and heat flux is examined and investigated for fractal porous material. In addition, the effects of fractal dimension, porosity, and the ratio of solid-matrix-to-fluid-phase thermal conductivity (k_s/k_f) on effective thermal conductivity are evaluated. The results indicate that pore structure has an important effect on heat conduction inside porous material. Increasing porosity lowers thermal conductivity. Even when porosity remains constant, effective thermal conductivity is affected by the fractal dimensions of the porous material. For porous material, the heat conduction capability weakens with increased fractal dimension. Additionally, fluid-phase thermal conduction across pores is effective in porous material only when k_s/k_f < 50. Otherwise, effective thermal conductivity for porous material with a given pore structure depends primarily on the thermal conductivity of the solid matrix.

1. Introduction

The heat conduction of porous media has drawn particular attention owing to their extensive applications [1,2], such as the thermal insulation material [3], geothermal soil medium [4,5], ceramics, clothing chemical engineering, geophysical exploration and human biomedical engineering. The porous media is a material containing interconnected pores with non-uniform size and shape. In complex structures, the thermal conductivity of a porous material depends not only on porosity and thermal property but also on pore structures. To study soil thermal conduction, it is crucial to understand how pore structure affects the heat conduction behaviors of porous material.

During recent decades, both theoretical and data-driven research has been used to study thermal conductivity for several types of porous material, typically calculated by network combinations of series and parallel models [6,7,8,9]. Constrained by their sole dependence on porosity, these models have limitations in exploring the role of pore structure on the effective thermal conductivity of the porous material, which makes these theoretical predictions only valid in some circumstances. The effective thermal conductivity (k_eff) mentioned here is the property to conduct heat through the multi-compositions within the porous media, which can be calculated based on Fourier’s law. Along with theoretical solutions, numerical simulations—by taking into account pore distribution by using computational heat transfer methods—have also been employed to study the heat transfer characteristics of porous material, such as lattice Boltzmann method [10], mean-square displacement method [11], finite volume method [12,13], the volume averaging theory [14], and the shooting method [15]. The determination of effective thermal conductivity is crucial as input data for a number of approaches employed in numerical simulation of heat and fluid flow in porous media, as for instance when the generalized model is employed. In the model of packed bed thermal storage system, the effective thermal conductivity of the porous media is desirable to estimate the time required to heat up the solid particles [16]. In the model of a chemical reactor, the thermal transport behaviors of the porous media are the premise to accurately predict the reaction rate induced by the inlet temperature disturbances [17]. The effective thermal conductivity is also the basic parameter to model the free surface fluid flow and heat transfer through porous media [18] for engineering applications such as oil recovery techniques, metal processing, and injection molding.

The accurate characterization of interconnected pore networks is a prerequisite for the determination of effective thermal conductivity of the porous material. Accordingly, several methods have been introduced to generate pore structures of multi-phase porous materials, including the discrete reduced distance method [19], the grain sedimentation algorithm [20], and statistical correlation functions [21,22]. It has been demonstrated that pore distribution inside porous material is statistically self-similar and performs multi-scale features. This implies that the above reconstruction methods cannot reflect the detailed nature of porous material [23]. In complicated pore networks, a proper scale-invariant characterization is needed for studying porous material.

Fractal geometry, a more reasonable reconstruction method, has emerged as a powerful tool to characterize complex structures, one that possesses the features of statistical self-similarity and multi-scale. With these features, the fractal dimension, D, determines the heterogeneity of the resulting pore structure of the porous medium. A larger fractal dimension indicates the more irregular pore distribution. Fortunately, fractal geometry has been successfully utilized to explore mass transfer phenomena in porous media, such as soil [24,25] and dry building materials [26,27]. In light of this successful utilization, fractal geometry is herein introduced to describe pore distribution for the investigation of heat conduction in the porous material. While there have been a number of studies of heat conduction behaviors for several types of porous material, especially in the determination of effective thermal conductivity, there is still insufficient work on porous material that uses fractal analysis. Feng et al. [28], Xu et al. [29], and Yu et al. [30] developed fractal models for predicting effective thermal conductivity for porous materials using electrical analogy and fractal geometry and pointed out that the fractal dimension is an important parameter for determining thermal conductivity. Pitchumani and Yao [31] developed a unified approach using local fractals to describe a fibrous composite, and Pitchumani [32] also evaluated the thermal conductivity of disordered composite material using a fractal model. Additionally, transport in three-dimensional porous material considering fractal behavior has also been reported [33,34,35]. However, it remains unclear how the detailed nature of porous structures affects heat conduction and thermal conductivity. In addition, temperature and heat-flux distributions, which can intuitively represent the heat conduction behaviors of fractal porous material, have not been studied thoroughly. In particular, the influence of fractal dimension on heat transfer behaviors is still little understood.

In summary, effective thermal conductivity is a crucial parameter in the numerical simulation of heat and fluid flow in porous media and it is of significance for engineering applications. Therefore, in the current study, a mathematical model of heat transfer through a porous material is presented to study heat conduction behaviors inside the porous material, with special attention paid to thermal conductivity. In this model, pore structure is reconstructed using fractal geometry based on fractional Brownian motion (FBM). The role of pore structure on temperature and heat flux distributions is examined and investigated. In addition, the effects of fractal dimension, porosity, and solid matrix/fluid phase thermal conductivity ratios (k_s/k_f) on effective thermal conductivity are evaluated.

2. Fractal Characterization of Porous Media

Porous material, whether natural (for example, rock and soil) or artificial (for example, metal foams), exhibits a certain degree of disorder. It has been proven that the microstructure of porous material shows statistically fractal properties [36,37,38]. Fractional Brownian motion f_H(x), a continuous-time Gaussian process, has demonstrated the ability to reconstruct fractal porous material [36,37,38] and satisfies

$$\langle f_H(x+rh)-f_H(x)\rangle =0$$

(1)

$$\langle {[f_H(x+rh)-f_H(x)]}^2\rangle =r^{2H}\langle {[f_H(x+h)-f_H(x)]}^2\rangle$$

(2)

where < ∙ > indicates the expected value, H represents the Hurst coefficient, and r and h are the positive constants, which range from 0 to 1. It is purely random and exhibits regular Brownian motion when H = 1/2. Equations (1) and (2) describe the statistical characteristics of the mean value and variance of the incremental process of FBM, respectively. According to Equation (2), the variance of the incremental process of FBM presents proportional property, which indicates that the incremental process of fractional Brownian motion is a self-similar Gaussian process providing vital information on the geometric reconstruction of fractal porous media.

In accordance with the statistics of fractional Brownian motion, the random midpoint displacement algorithm has been widely employed to generate stochastic fractal images [36,37,38,39]. In this paper, a random midpoint displacement algorithm is adopted to construct a two-dimensional fractal porous material, as in previous works [36,37]. This algorithm starts with a square grid and then randomly generates the values at each grid point from four adjacent points (see Figure 1a–d). These values represent the relevant square pore size, which is determined by the scalar function f_H(x) mentioned above. As shown in Figure 1, the algorithm is implemented according to the following steps:

(i)

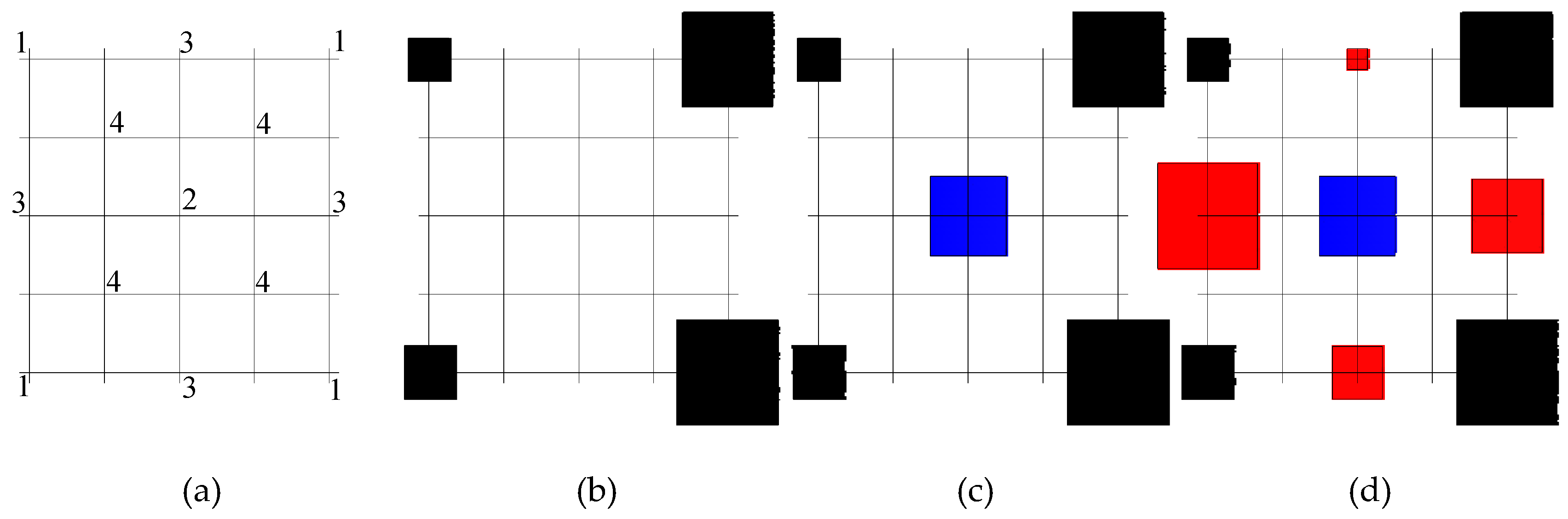
The values of function f_H,1(x) at the four corner points are generated from a Gaussian distribution N(0, σ₀²), where σ₀² is the variance (see Figure 1b).

(ii)

The value of function f_H,2(x) at the center of the square (here, 2) is obtained by linearly interpolating between the four corner values and adding a random number df₁ from N(0, σ₁²), where the quantity σ₁² satisfies the relation (see Figure 1c),

$${{\sigma }_1}^2={(1/\sqrt{2})}^{2H}{{\sigma }_0}^2(1-2^{H-2}).$$

(3)

(iii)

The values of function f_H,3(x) at the midpoints of each side (here, 3) are obtained by linearly interpolating between two adjacent corner values and adding a random number df₂ from N(0, σ₂²), where σ₂² satisfies the relation (see Figure 1d),

$${{\sigma }_2}^2={(1/\sqrt{2})}^{2H}{{\sigma }_1}^2$$

(4)

(iv)

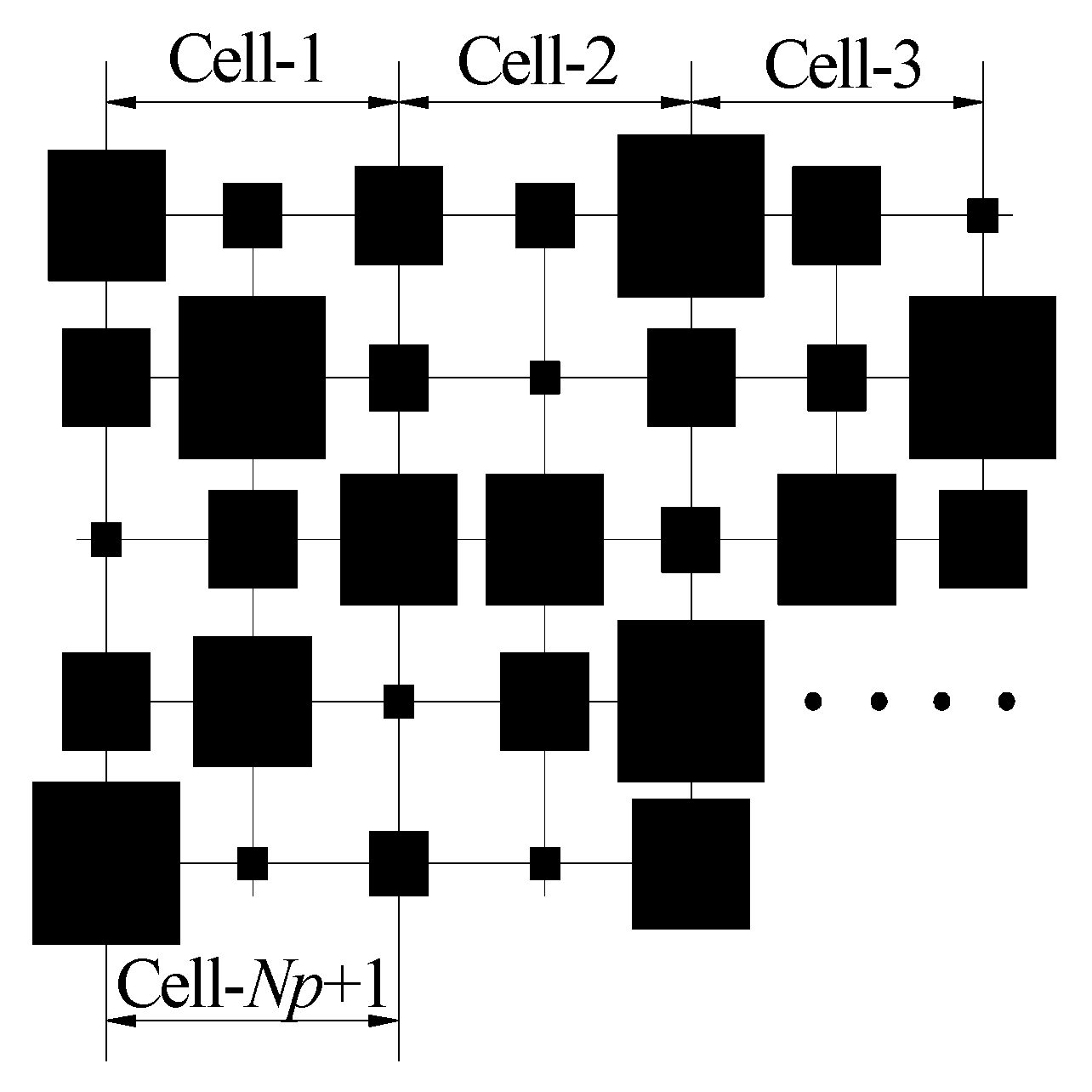
After the first run of the routine, nine sub-squares are obtained, which is characterized by the values of function f_H,j(x) (see Figure 1d). The same procedures are repeated for each sub-square until the nth level. The corresponding variance of space displacement at each level will scale with a factor of ${(1/\sqrt{2})}^{2H}$. Therefore, we will have a 2D lattice array with a total of (2ⁿ + 1) × (2ⁿ + 1) points. In order to obtain the given porosity, we should also rescale the values of function f_H,j(x) by the use of Kikkinides et al.’s method [36].

The procedures described above generate single-cell FBM material with a limited number of pores [36]. To overcome this shortcoming, an improved algorithm is proposed, illustrated in Figure 2. In the new algorithm, the original square lattice is divided into several cells and each one is decorated according to the single-cell FBM procedures. Note that the grid points at the boundaries receive a contribution from both adjacent cells. The modified multiple-cell FBM procedures can generate fractal porous material with any degree of correlation, allowing considerably larger sizes compared with the correlation length.

Once an existing porous material is given, a two-dimensional (2D) matrix of binary pixels is applied to characterize the digitized image of a 2D section of a porous medium, in which the 0 and 1 are to describe the solid and pore phases. As a result, the phase function of the porous medium can be expressed as

$$Z(x)=\{\begin{array}{ll}1& \mathrm{if} x \mathrm{belongs} \mathrm{to} \mathrm{pore} \mathrm{space}\\ 0& \mathrm{otherwise}\end{array}$$

(5)

Based on the phase function, the normalized autocorrelation function R(u) and the porosity ε are determined by the statistical averages

$$R(u)=\frac{\langle (Z(x)-\epsilon )(Z(x+u)-\epsilon )\rangle }{\epsilon -{\epsilon }^2}$$

(6)

$$\epsilon =\langle Z(x)\rangle$$

(7)

In this situation, the FBM procedure is utilized to generate the porous media which is of the same porosity and the same (similar) autocorrelation function as the real-life materials by properly selecting the parameters of Hurst coefficient H, individual cells N_p, and level number of single-cell n.

3. Heat Transfer in Porous Media

3.1. Theoretical Model

Here, we aim to elucidate the role of pore structure on the heat conduction of porous material, especially to explore the role of both fractal dimension and porosity on heat conductivity. Undoubtedly, a three-dimensional (3D) structure of the porous material is more realistic. However, the 2D numerical simulation scheme is highly efficient in computation. In addition, a 2D pore distribution, as characterized by fractional Brownian motion (FBM), has clearly included the qualities of fractal dimension and porosity. Therefore, a numerical simulation of heat conduction for the porous material is carried out in a 2D porous geometry in which the pore distribution is characterized by FBM. In the fractal characterization, the porous material is represented as a square area composed of two parts: the black area represents the continuous solid phase while the white area is the discrete fluid phase. As shown in Figure 3, the computation domain is composed of the auxiliary solid phase and fractal porous material. In order to avoid the distortion of the temperature profile for porous media due to the imposition of thermal boundary condition, an auxiliary solid phase is located before and after the porous media, and the constant heat flux boundary condition is imposed on the left-hand side of the auxiliary solid matrix, rather than porous media. Note that the auxiliary solid phase is solid with the same thermal properties as the solid matrix of fractal porous material, and the auxiliary solid phase is unconsidered in the determination of thermal conductivity for the porous media. For such a configuration, the length of fractal porous material (L) is 9 mm, the number of the individual cells (N_p) is 3, the level of a single-cell (n) is 2, and the length of auxiliary solid phase (L₁) is 0.9 mm. In the simulation, the air is selected as the fluid phase, and its thermal conductivity is assumed to be k_f = 0.02W/(m·K). Note that the thermal conductivity of solid matrix k_s is treated as a variable to analyze the influence of thermal conductivity rate k_s/k_f on the heat transfer performance of the porous material.

This paper focuses on the role of pore structure on the heat transfer performance of the porous material. To simplify the calculation, the following assumptions are applied: (i) Steady heat conduction; (ii) The thermal conductivities of fluid and solid matrix are assumed to be constant; (iii) The convection and radiation in the pore space are neglected.

In accordance with the assumptions detailed above, the energy equation of the steady thermal conduction inside the 2D fractal porous material is simplified as:

$$\frac{\partial }{\partial x}\left(k\frac{\partial T}{\partial x}\right)+\frac{\partial }{\partial y}\left(k\frac{\partial T}{\partial y}\right)=0$$

(8)

where T denotes temperature, k = k(x, y) denotes the local thermal conductivity, as defined by

$$k=\{\begin{array}{l}{k}_f,\begin{array}{c}\begin{array}{c}\mathrm{if} (x,y) \mathrm{belongs} \mathrm{to} \mathrm{pore} \mathrm{space}\end{array}\end{array}\\ k_s,\begin{array}{c}\mathrm{otherwise}\end{array}\end{array}$$

(9)

In the model, the heat conductions in the fluid and solid phases are considered separately, i.e., the thermal tortuosity is evaluated based on the fractal description of the porous matrix.

To close the mathematical formulation of the heat conduction of porous material, it is required to specify the left, right, top, and bottom boundary conditions. The left boundary of the computation domain is set as a heat flux boundary, and written as:

$${-k_s\frac{\partial T}{\partial x}|}_{x=0}=q$$

(10)

where q represents heat flux. The right boundary of the computation domain is set as a temperature boundary, expressed as:

$${T|}_{x=L+2L_1}=\mathrm{constant}$$

(11)

The top and bottom boundaries are assumed as the adiabatic boundary:

$${\frac{\partial T}{\partial y}|}_{y=0}=0,{\frac{\partial T}{\partial y}|}_{y=\mathrm{L}}=0.$$

(12)

In the simulation, the heat flux is assumed to be q = 0.4 W/cm², and the constant temperature at the right boundary is set as T|_x=L+2L1 = 10 °C. The definition of the above boundary conditions is a usual method to calculate the effective thermal conductivity in the investigation of porous media.

When the generalized model is employed, the determination of effective thermal conductivity can be employed as input data for a number of approaches employed in numerical investigations, such as the packed bed thermal storage, the reaction and heat transport, and the free surface fluid flow and heat transfer through porous media.

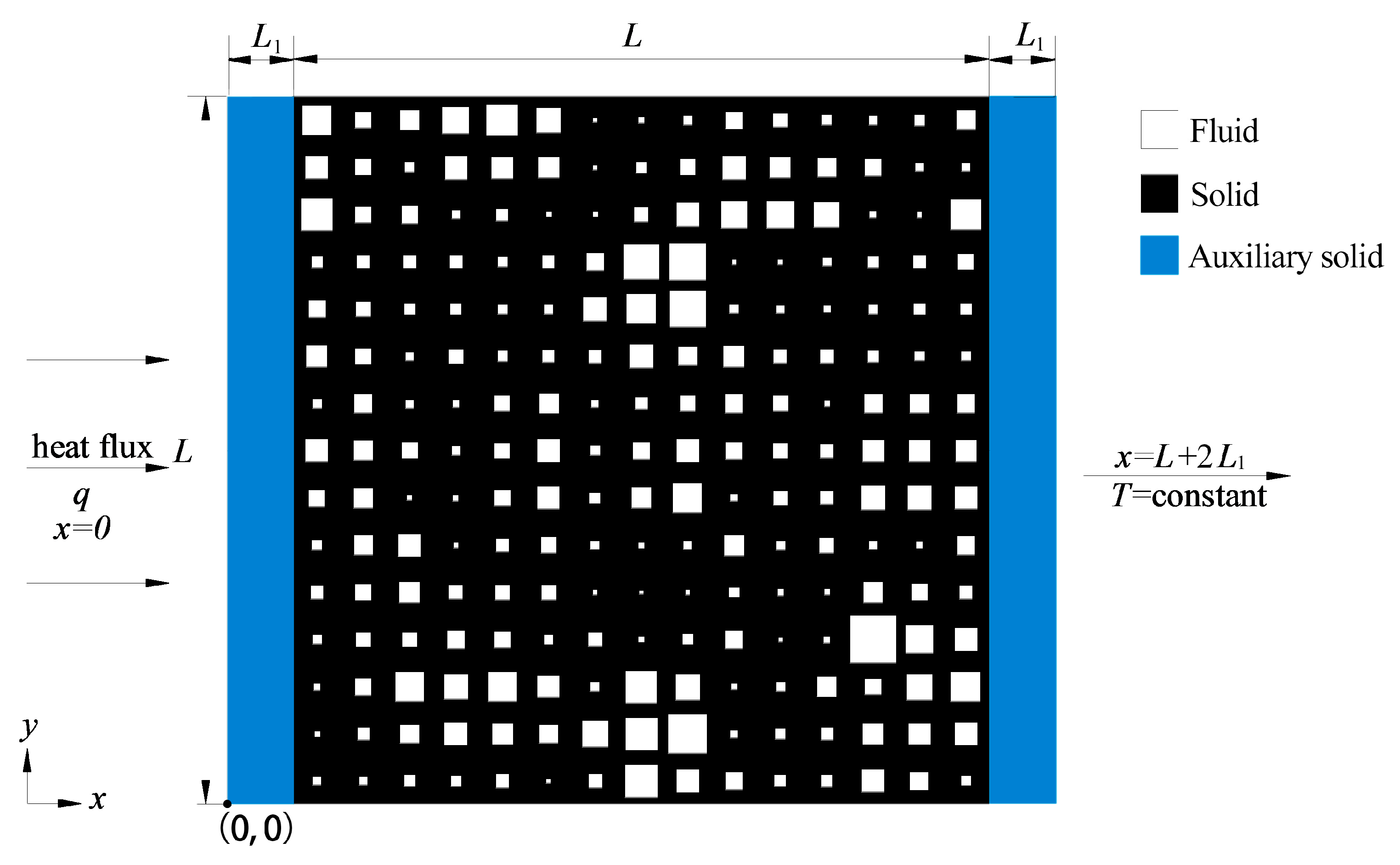
3.2. Numerical Simulation

Since the geometric structure of the fractal porous material shown in Figure 3 is very complex, the unstructured mesh method is used to arrive at a numerical solution. The mesh is mainly composed of quadrilateral grid elements, and a few triangular grid elements are also applied to improve the quality of mesh. The shell surface mesh is generated by selecting the patch dependent method, which satisfactorily describes the geometric features of the complex structure and creates a high-quality mesh, automatically giving priority to quadrilateral grid elements. A grid independence test of heat conduction in the fractal porous material is carried out for several mesh sizes to predict the effective thermal conductivity, so as to validate the numerical analysis in the present study. This test proved that the numerical results obtained in the current investigation are grid independent.

The energy equation for the temperature field in the fractal porous material is numerically solved by the use of a control volume-based finite difference method. After computing the integral of Equation (8) in each control volume, a series of diagonally dominant linear equations of temperature will be achieved. The Gauss–Seidel iterative method is implemented to solve these discrete equations, and the temperature field of the fractal porous material is obtained. During the process of iteration, the convergence time is adjusted by changing the relaxation factor of the energy equation. In addition, the convergence of the numerical solution is judged not only by monitoring the residual temperature levels but also by checking the relevant integrated parameters and examining the energy balances. In this paper, all calculations are based on double precision. The final relaxation factor of the energy equation is 0.8, and the solution is finally regarded as convergent when the residual is less than 10⁻¹² and the heat flow rates on both sides reach equilibrium.

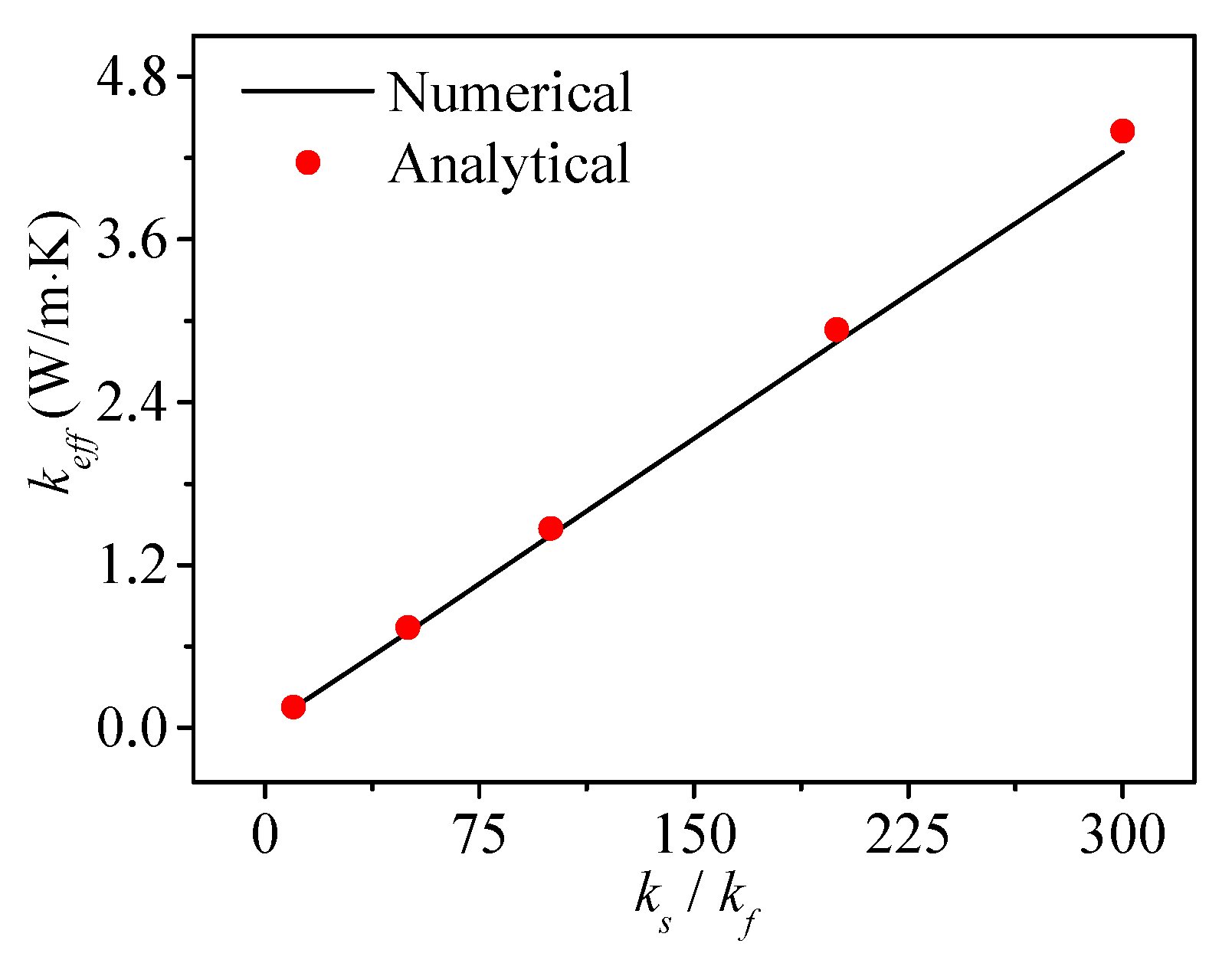
3.3. Case Verification

To validate the present model, a previously published study of the heat conduction process in porous material with periodic pores is simulated in the current study. In 1954, Maxwell presented an exact solution of thermal conductivity in a homogenous continuous material with periodically distributed and non-interacting spheres using potential theory. Then, based on a large number of experiments, Eucken deduced the Maxwell–Eucken Equation [40]:

$$k_{eff}=k_s\left[\frac{k_f+2k_s+2\epsilon \left(k_f-k_s\right)}{k_f+2k_s-\epsilon \left(k_f-k_s\right)}\right]$$

(13)

where ε is porosity. Equation (13) indicates that the thermal conductivity of the fluid and solid phases are two important factors determining the effective thermal conductivity of the porous material. In this paper, for the porous material with periodically distributed and non-interacting pores shown in Figure 4, thermal conduction cases with different k_s/k_f are simulated to verify the mathematical model above. The details of the verification are: model dimensions of 5 mm × 5 mm, pore radius of 0.25 mm, mesh number of 64,194, heat flux q = 2000 W/m², fluid thermal conductivity k_f = 0.02 W/(m∙K). The comparison between the numerical results and the analytical data is shown in Figure 5. As indicated, the numerical results obtained by this paper accord with the analytical data. This accordance proves that the proposed theoretical model is valid for predicting heat transfer in the porous material.

4. Results and Discussion

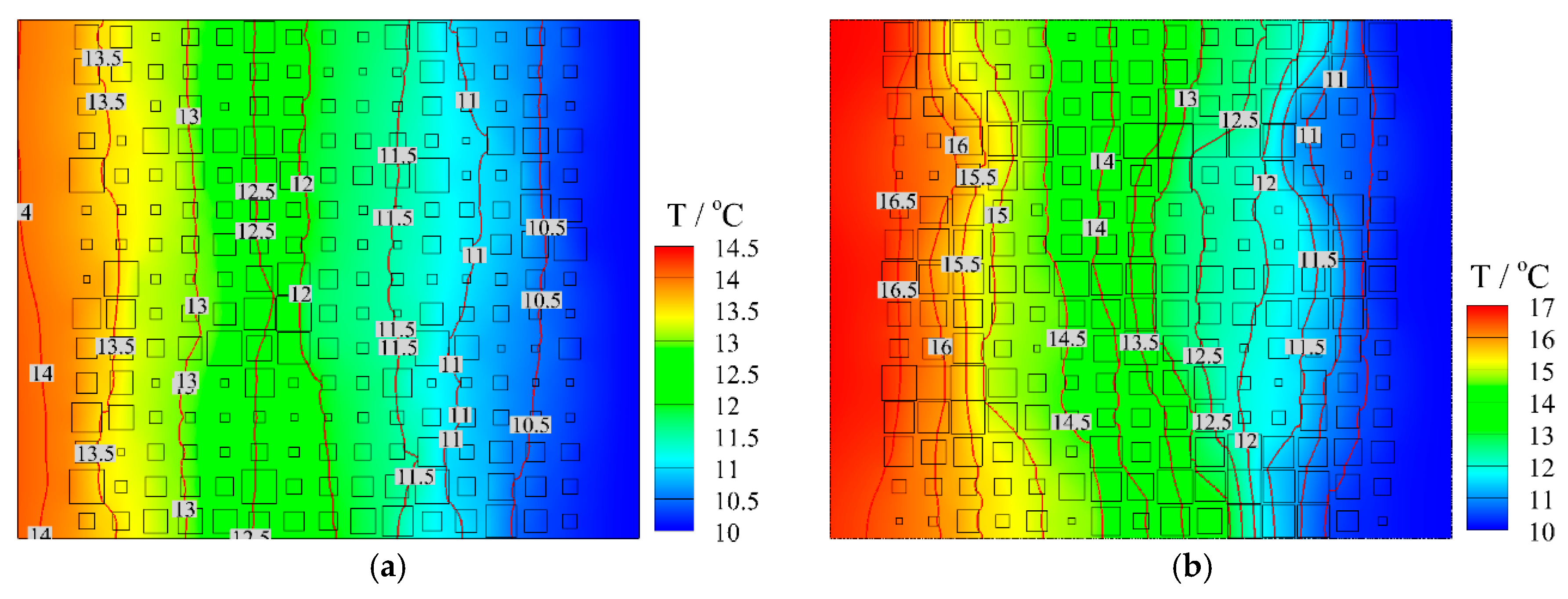
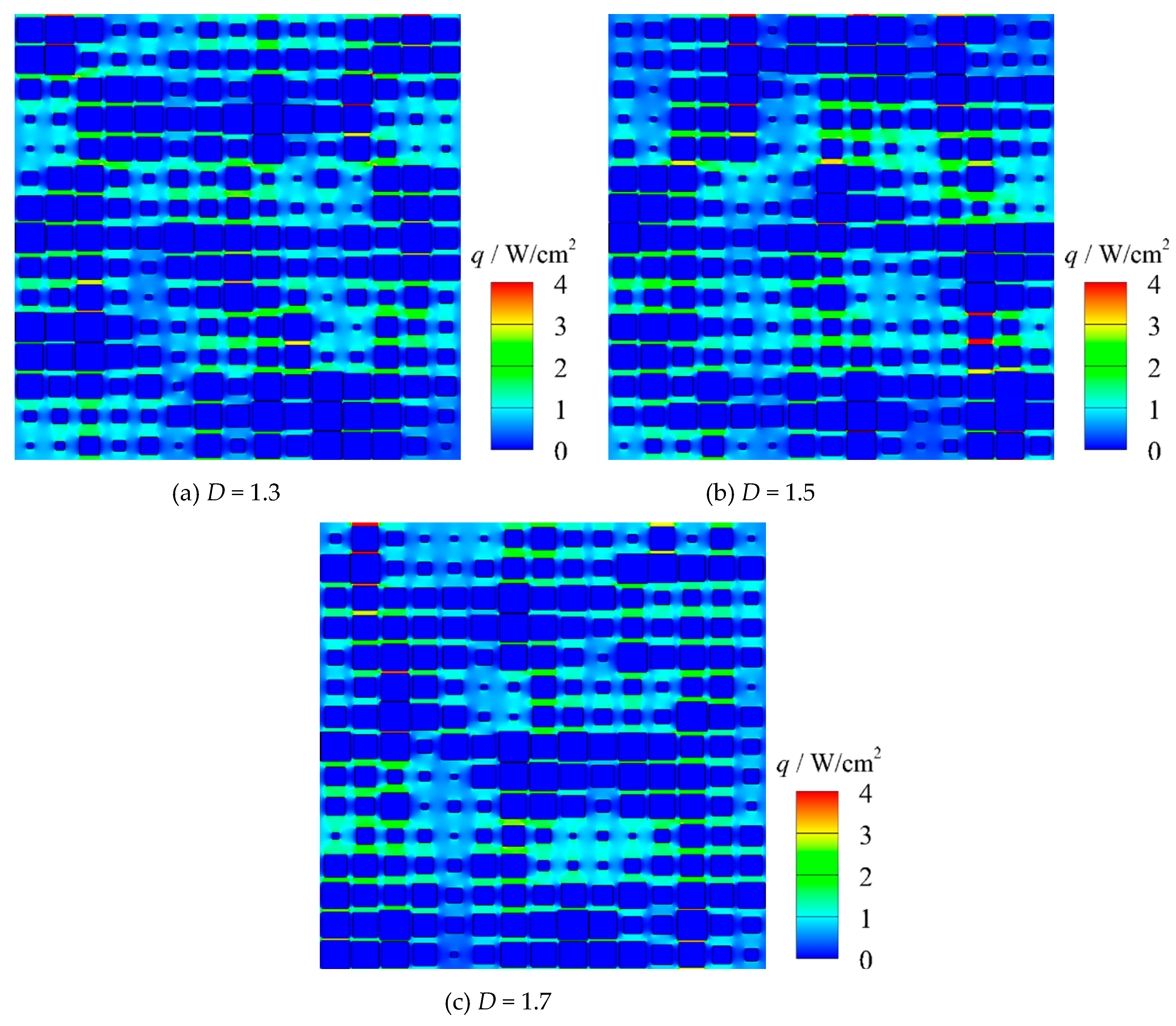
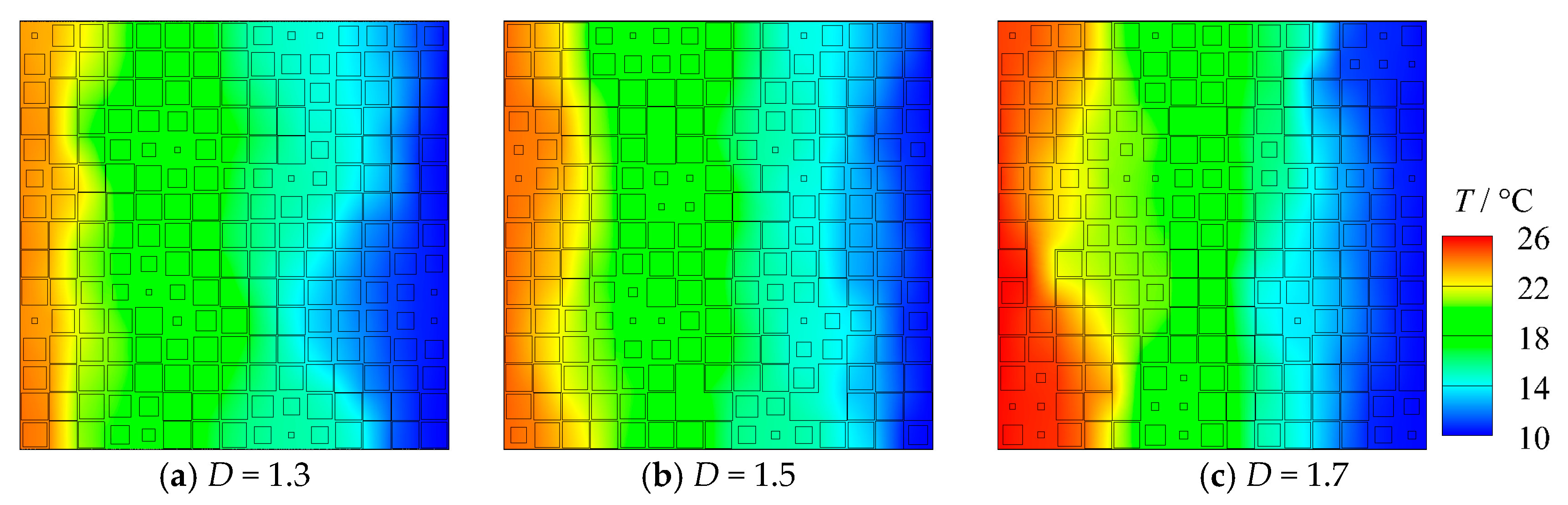
4.1. Heat Conduction Behavior

The pore structure of the porous material is anisotropic and stochastic. For heat flow inside the porous material, the existence of non-uniform pore structures leads to complicated heat conduction, which plays a significant role in the heat transfer performance of the porous material. To analyze heat conduction behaviors, Figure 6 presents the temperature distribution of fractal porous material. As seen in the figure, the temperature field is obviously perturbed for fractal porous material, and the isotherms are no longer straight. The temperature distribution is no longer uniform and shows an irregular distribution along the heat-flow direction owing to the uneven pore structure. This phenomenon can be explained by the fact that non-uniform pore structure triggers different heat flow inside the fractal porous material.

The fractal dimension determines the heterogeneity of the resulting pore structure of the porous medium. The larger the fractal dimension is, the more irregular the pore distribution. Heat flux is dominated by the solid phase, in part because it is continuous and its thermal conductivity is far larger than a fluid phase. To gain a clearer understanding of the role of pore structure on heat conduction behavior, Figure 7 intuitively compares the local heat flux distribution of different fractal porous material at pore scale. For these different porous media, the porosity is identical but the fractal dimension is different. As seen, pore structure significantly affects heat flux distributions in the fractal porous material. Heat flow across the porous material is more easily disturbed for a larger fractal dimension due to more irregular pore distribution, that is, the variation of heat flow is more gentle across porous material with a smaller fractal dimension. As shown, the large heat flux paths are observed in a long straight solid phase. The porous material with smaller fractal dimension provides a longer straight solid phase and hence is beneficial to enhanced heat conductance.

As shown in Figure 7, there is a significant difference in heat flow across the solid matrix and the dispersed pores. Heat flux through the solid matrix is larger than that of the fluid phase, and heat flux is very small in the area with clustered large pores. In the area where large pores are dispersed by small pores, the difference in the heat flux is more obvious, which can be explained by the local average conductivity there being dominated by the low conductivity of the fluid phase area. Interestingly, peak heat flux through the solid matrix is more likely to appear in the narrow gap between large pores. The explanation is that the total heat flux is the same for a cross-section, and the main heat is transferred through the solid matrix; the narrower gap between large pores implies that more heat is required to transfer through this gap.

4.2. Effective Thermal Conductivity

So far as the steady-state heat transfer, total heat flux through each cross-section of the porous material is conserved. Therefore, on the basis of the law of energy conservation and the Fourier law, effective thermal conductivity can be obtained by calculating the temperature field for the porous material:

$$k_{eff}=Q\frac{L}{(T_{x=L_1}-T_{x=L+L_1})A}$$

(14)

where A represents the cross-section area perpendicular to the heat flow direction, Q represents the heat flow rate, and L is the characteristic length of the fractal porous material. In the simulation, the constant heat flux, q, is imposed at the left side boundary condition, so the heat flow rate can be determined by Q = q∙A. In this context, the effects on the effective thermal conductivity of fractal dimension, porosity, and k_s/k_f on the fractal porous material are examined in this paper.

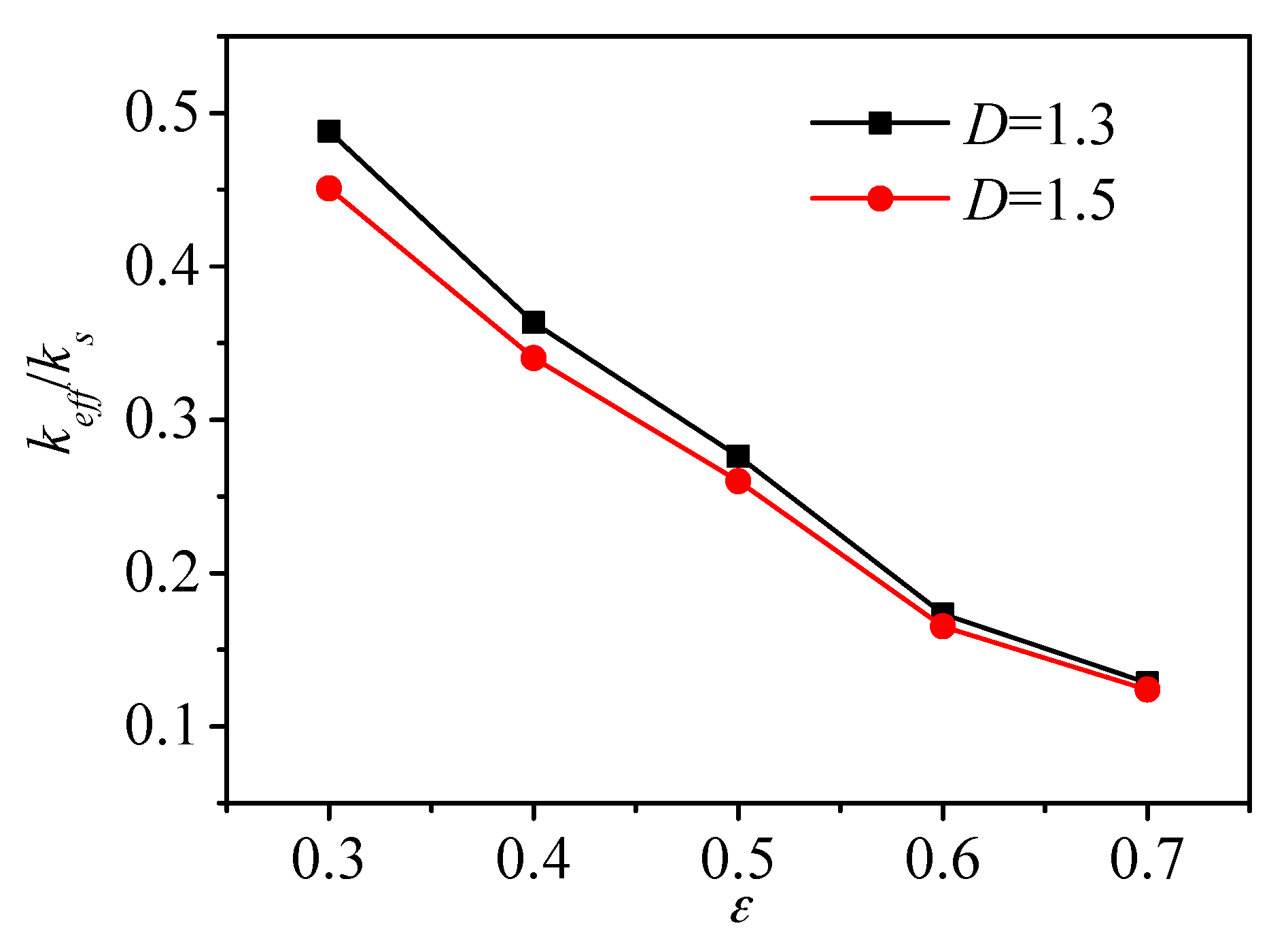
4.2.1. Effect of Porosity

Porosity is an important factor in the determination of effective thermal conductivity. Considering the close pore structures and the greater thermal conductivity of the solid matrix compared to the fluid phase, larger porosity leads to lower thermal conductivity. Figure 8 plots effective thermal conductivity with variable porosity for the porous material with two fractal dimensions. As seen in the figure, no matter what the fractal dimension of porous material is, an increase in porosity lowers thermal conductivity. Note that there is a rapid decrease in thermal conductivity for porosity ε < 0.6, while the decreasing trend slows for larger porosity. That is, at low porosity, the thermal conductivity of the solid matrix is the major factor for heat transfer. Conversely, as porosity increases, the role of fluid-phase thermal conductivity becomes more important. This is also indicated by the demonstration that thermal conductivity is larger for a smaller fractal dimension; that is, heat conduction performance is better for porous material with a smaller fractal dimension.

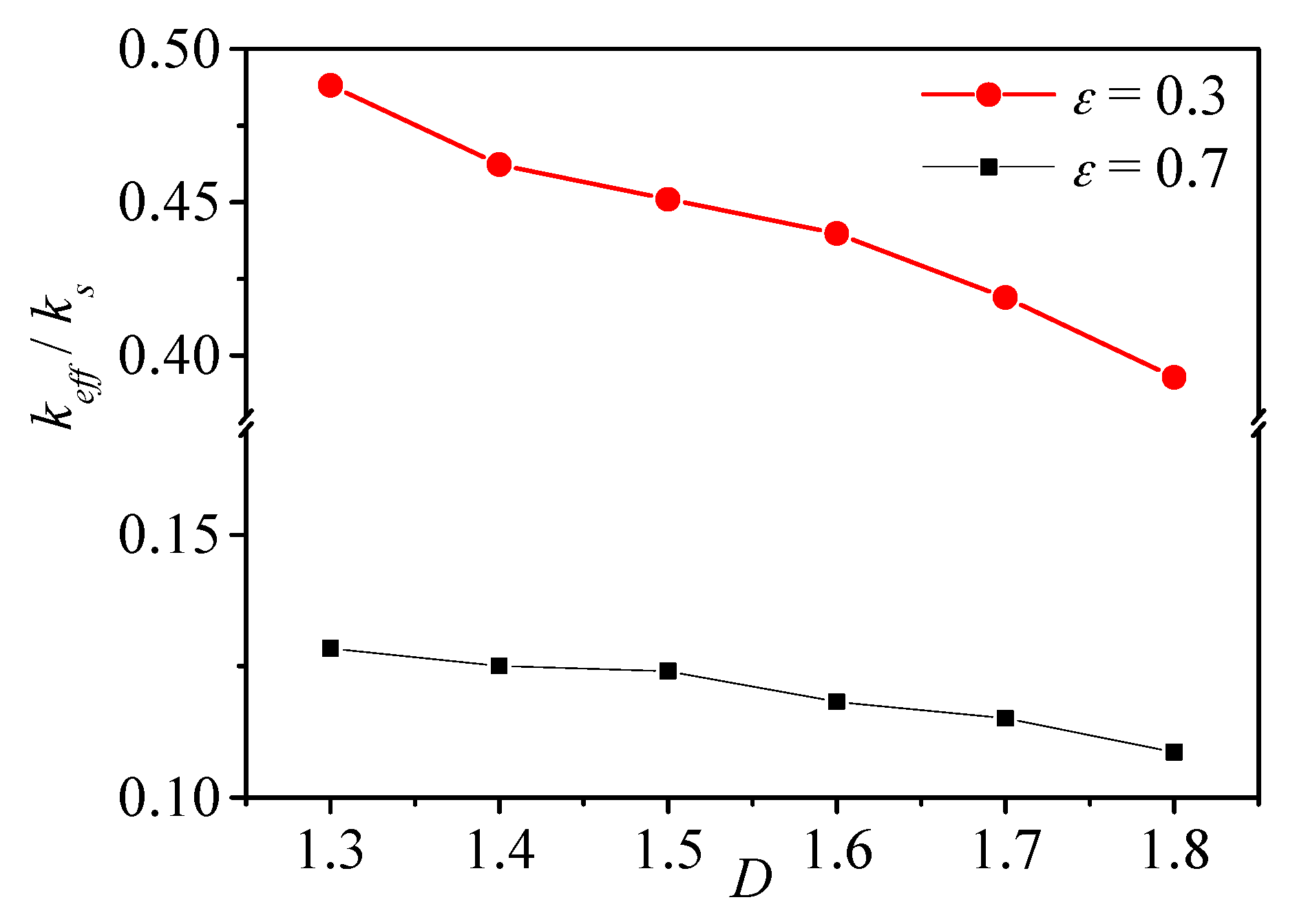
4.2.2. Effect of Fractal Dimension

Fractal dimension is the other significant parameter for the fractal object. For porous material, the fractal dimension is closely related to pore structure distribution, which directly exhibits the compactness of pore structure. In other words, the fractal dimension can describe the correlation of pore sizes in the porous material to the same extent. The larger the fractal dimension of porous material is, the weaker the pore structure correlation. As has been shown, the fractal dimension of FBM is a function of the Hurst exponent, which can be written as:

$$D=d_T+1-H$$

(15)

where d_T is the topological dimension.

The fractal dimension determines the distribution of pore structure, which results in a significant influence on heat flow across the porous material and finally affects thermal conductivity. Figure 9 shows effective thermal conductivity as a function of the fractal dimension of porous material. It can be seen that the fractal dimension negatively correlates with effective thermal conductivity. Effective thermal conductivity k_eff/k_s shows a monotonous decrease as fractal dimension increases. As stated above, the structural correlation of porous material weakens as the fractal dimension increases, which leads to more thermal resistance across the fractal porous material, in this case resulting in a corresponding increase in the temperature gradient, as clearly shown in Figure 10. In other words, the heat conduction capability of porous material weakens as the fractal dimension increases.

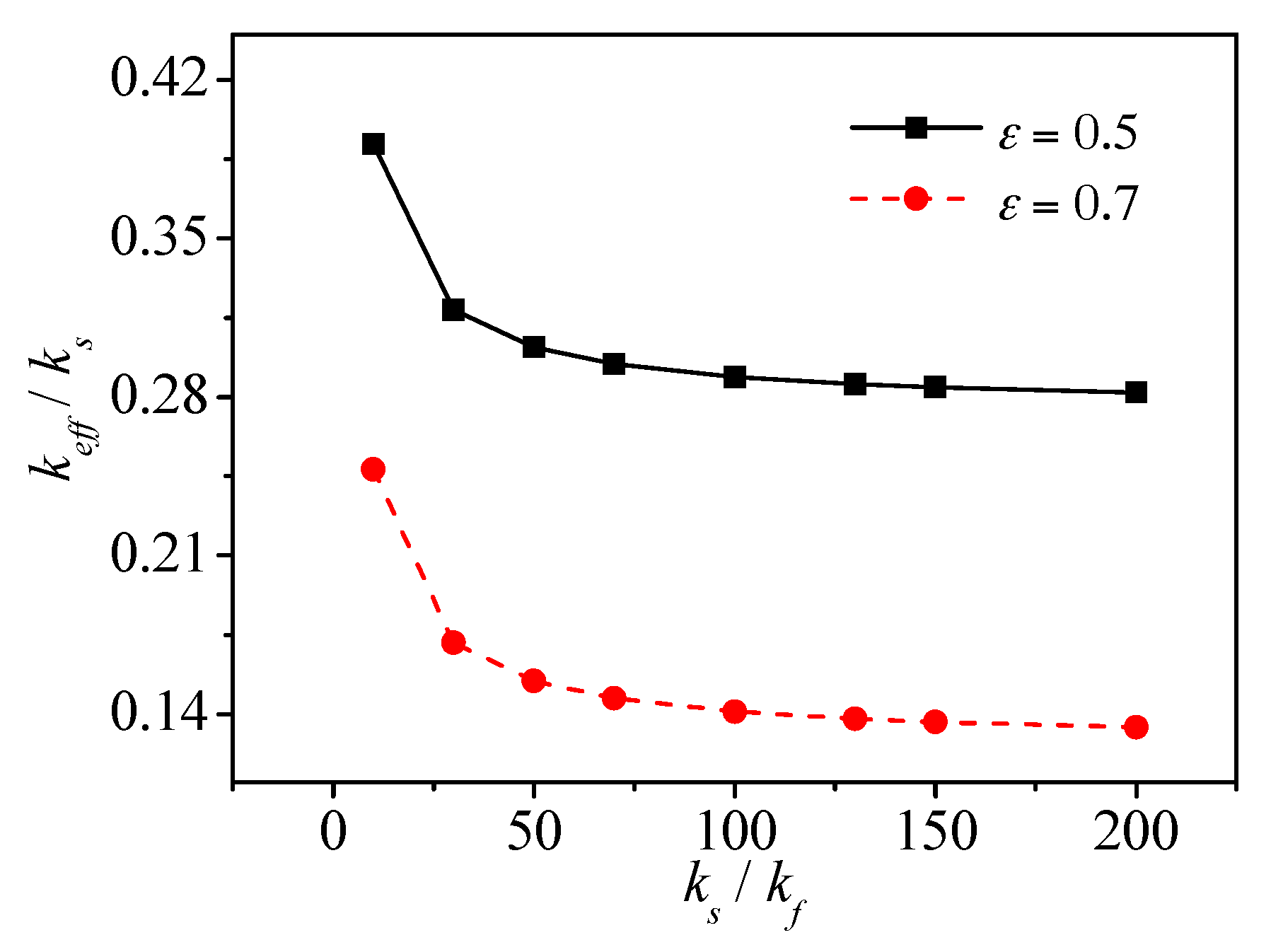
4.2.3. Effect of the Ratio of Thermal Conductivity between Solid Matrix and Fluid Phase

The porous material is composed of a solid matrix and a fluid phase. It is intuitive that effective thermal conductivity is directly related to k_s/k_f. In this case, it is interesting to quantitatively analyze effective thermal conductivity with respect to k_s/k_f. In this paper, a fractal porous material with two porosities is simulated; the thermal conductivity of the fluid phase is fixed while the thermal conductivity of the solid matrix is varied.

Figure 11 describes the effect of k_s/k_f on effective thermal conductivity for fractal porous material with two porosities. As shown in the figure, thermal conduction of the fluid phase in pores is effective in porous material only when k_s/k_f < 50. Otherwise, the effective thermal conductivity of porous material with a given pore structure depends mainly on the thermal conductivity of the solid matrix. This is also indicated by the demonstration that thermal conduction is better for smaller porosity.

5. Conclusions

In this paper, fractal geometry (fractional Brownian motion—FBM) is applied to characterize the pore distribution of porous material. By this fractal characterization, a steady-state model of heat conduction is presented to investigate how pore structure affects the heat transfer properties of the porous material. The role of pore structure on temperature and heat flux distributions has been examined and investigated. The effects of fractal dimension, porosity, and k_s/k_f on effective thermal conductivity have been evaluated. The major conclusions are as follows:

(1)

For the heat conduction process, the temperature field inside porous material is perturbed by the pore distribution. Owing to the uneven distribution of pores, the isotherms inside the porous material are no longer uniform, and temperature distribution is irregular along the heat flow direction. Interestingly, the peak heat flux through the solid matrix is more likely to appear in the narrow gaps between large pores.

(2)

An increase in porosity leads to a smaller effective thermal conductivity. Even when porosity remains constant, effective thermal conductivity is also affected by the fractal dimension. Increases in fractal dimension lead to a weaker pore structure correlation, which introduces greater thermal resistance across the fractal porous material and hence results in an increase of the temperature gradient. Therefore, the capability of heat conduction is weaker for porous material with a larger fractal dimension.

(3)

The ratio of thermal conductivity of the solid matrix to the fluid phase (k_s/k_f) is another important parameter in determining heat conduction. The heat conduction of the fluid phase in pores is effective in porous material only if k_s/k_f < 50; otherwise, the effective thermal conductivity of a given pore structure is mainly dependent on the thermal conductivity of the solid matrix.