Extremely Efficient Design of Organic Thin Film Solar Cells via Learning-Based Optimization

Abstract

Design of efficient thin film photovoltaic (PV) cells require optical power absorption to be computed inside a nano-scale structure of photovoltaics, dielectric and plasmonic materials. Calculating power absorption requires Maxwell’s electromagnetic equations which are solved using numerical methods, such as finite difference time domain (FDTD). The computational cost of thin film PV cell design and optimization is therefore cumbersome, due to successive FDTD simulations. This cost can be reduced using a surrogate-based optimization procedure. In this study, we deploy neural networks (NNs) to model optical absorption in organic PV structures. We use the corresponding surrogate-based optimization procedure to maximize light trapping inside thin film organic cells infused with metallic particles. Metallic particles are known to induce plasmonic effects at the metal–semiconductor interface, thus increasing absorption. However, a rigorous design procedure is required to achieve the best performance within known design guidelines. As a result of using NNs to model thin film solar absorption, the required time to complete optimization is decreased by more than five times. The obtained NN model is found to be very reliable. The optimization procedure results in absorption enhancement greater than 200%. Furthermore, we demonstrate that once a reliable surrogate model such as the developed NN is available, it can be used for alternative analyses on the proposed design, such as uncertainty analysis (e.g., fabrication error).

1. Introduction

Photovoltaic (PV) energy shares in electricity generation have continually grown since the beginning of commercial silicon-based solar cells over 50 years ago [1]. It is also conveniently predicted that PV energy will be the leading renewable energy source due to availability, price decrease, and technology improvement [1,2]. In order to reach the future growth expectations, most of the PV research has been dedicated to increasing the efficiency limits of PV cells and decreasing manufacturing cost per unit of energy.

One of the ways to improve PV conversion efficiency is by modifying material properties. A well-known affect called light trapping, which is mostly achieved by surface patterning of the cell and inducing plasmonic effects, can significantly improve solar light absorption in silicon [3,4]. These techniques increase effective optical thickness without actually increasing the physical thickness of PV material, thus avoiding undesirable carrier recombination [5]. Carrier recombination hinders photocurrent conversion of absorbed photons, thus making the solar cell electrically undesirable.

Gaining physical insight into the dependency of optical performance of a thin film to shapes, dimensions, material choices and other parameters of plasmonic nano-textures or nano-particles is critical in designing efficient cells. This has been the subject of extensive review in the field of nano-technology in the past 15 years. The research has led us to several design guidelines. In general, it is agreed that particle shape, dimension and position in the cell should be taken into account for a rigorous design of a plasmonic photovoltaic device [6]. In addition, precise computational simulators that model electromagnetic equations and material properties at nano-scale and solar optical wavelenghts should be accompanied by powerful optimization algorithms for a feasible and efficient design [7,8,9,10,11,12,13]. Optical modeling of thin film PV cells requires solving Maxwell’s electromagnetic equations because interaction of light with subwavelength structures cannot be explained with simple ray tracing models. On the other hand, solutions of Maxwell’s equations require spatial and temporal discretization of the complex domains, often facilitated by computational solvers such as the Finite Difference Time Domain (FDTD) method. These methods require extensive resources and time. When one searches for the best optical properties in the design and optimization framework, many repeated numerical FDTD simulations must be carried out for an entire wavelength range, which makes the search process extremely burdensome. When more than a handful of parameters are aimed to be optimized, the procedure becomes so time-consuming that even with the state-of-the-art numerical optimization algorithms, a rigorous design is practically infeasible. The only remedy to such a challenge is the use of “surrogate modeling”. This means replacing the black-box (FDTD) simulations with an accurate regression model. Such a model can be used for both optimization and analysis, leading to the concept of Surrogate-Based Optimization (SBO). Neural Networks (NN) are well-studied models in machine learning with the ability to approximate functions of arbitrarily high nonlinearity. NNs have been proven to be useful in many engineering problems [14,15,16,17] as a function approximator. However, NNs—and more broadly any surrogate model—have never been used in optimization of photovoltaic cells, and in particular optics equations at subwavelength scales. This paper aims to demonstrate this capability for learning and optimization for the first time.

In this work, we propose using NN as a surrogate model to design a plasmonic organic photovoltaic (OPV) device. The details of the physical model and advantages of OPV are presented in Section 2. The rest of the paper is organized as follows: a brief explanation of NN-based optimization is given in Section 3 and the results of the optimization are presented in Section 4. Sensitivity analysis is also conducted to predict the dependence of the results on small changes in the inputs.

2. Description of the Physical Model

OPV provides ease of fabrication and inexpensive material choices for the active layer [18,19] even though the power conversion efficiency (PCE) is relatively lower than the inorganic rivals. There has been significant improvement in the PCE of these structures by using bulk heterojunction (BHJ) blend compared to bilayer donor/acceptor design due to the large interfacial area between the donor and acceptor of BHJ [20]. Recently, researchers have made several efforts at optimizing the nanomorphology of OPV [21,22,23,24,25]. In general, the increase in the optical efficiency is accompanied by increase in optical thickness, which increases recombination when the distance of the possible electron–hole creation zone is farther away from the p–n junction than collection length [5]. Therefore, even though the absorption efficiency is improved, increased recombination hinders photocurrent generation. One of the methods to increase absorbed power without increasing absorption thickness is to induce plasmonic effects by using metallic nanoparticles. Plasmonics deal with the behavior of free electrons at the metal–dielectric or metal–semiconductor interface. When light hits a metallic surface, free electrons are excited, and an electrical field is created. This excitation is called surface plasmon polaritons (SPPs) and it enhances the created number of electron–hole pairs [26]. Specifically, the mechanisms of SPPs are creating multiple light scatterings, creating electron–hole pairs by near field effects and coupling light to surface plasmon polaritons [6].

A standard configuration of OPV with silver nanospheres is demonstrated in Figure 1. Ag nanospheres are assumed to have radius $r$ and are placed inside a poly(3-hexylthiophene):(6,6)-phenyl-C61-butyric-acid-methyl ester (P3HT:PCBM) layer of thickness $t_1$ at a vertical distance $s$ from the bottom and are repeated at a period of $P$. The Ag-filled active layer is stacked by poly(3,4-ethylenedioxythiophene): poly(styrenesulfonate) (PEDOT:PSS) with thickness $t_2$ and an aluminum back reflector layer. The 3D view of the proposed OPV and the simplified 2D view are presented in Figure 1a,b. The problem is reduced from 3D to 2D based on the premises of the study by Moreno et al. [27]. In all the simulations of the present study, a plane wave source is propagated from the top to the bottom at a specified wavelength $\lambda$ and at incident angle $\theta =0$. Bloch and perfectly matched layer (PML) boundary conditions are imposed for $x$ and $z$ coordinates, respectively. Real and imaginary parts of the materials used in the simulations are taken from the literature [28,29,30].

The enhancement in the absorbed power can be quantified by the absorption enhancement factor (EF). This quantity is defined as the ratio of the number of photons absorbed by the active layer of the plasmonic photovoltaic cell to the absorbed photons without plasmonic contribution (i.e., bare thin film). One of the design criteria for the cell geometry is to maximize EF. In mathematical terms:

$$EF=\left({\displaystyle \int }\lambda {\alpha }_p\left(\lambda \right)I_{1.5AM}\left(\lambda \right)d\lambda \right){\left({\displaystyle \int }\lambda {\alpha }_b\left(\lambda \right)I_{1.5AM}\left(\lambda \right)d\lambda \right)}^{-1},$$

(1)

where ${\alpha }_p$ and ${\alpha }_b$ are the absorbed optical power by plasmonic (with nanoparticle) and bare (without nanoparticle) photovoltaic cells, $I_{1.5AM}\left(\lambda \right)$ is the AM 1.5 standard terrestrial solar spectrum [31] and integration is done over the wavelength range of interest.

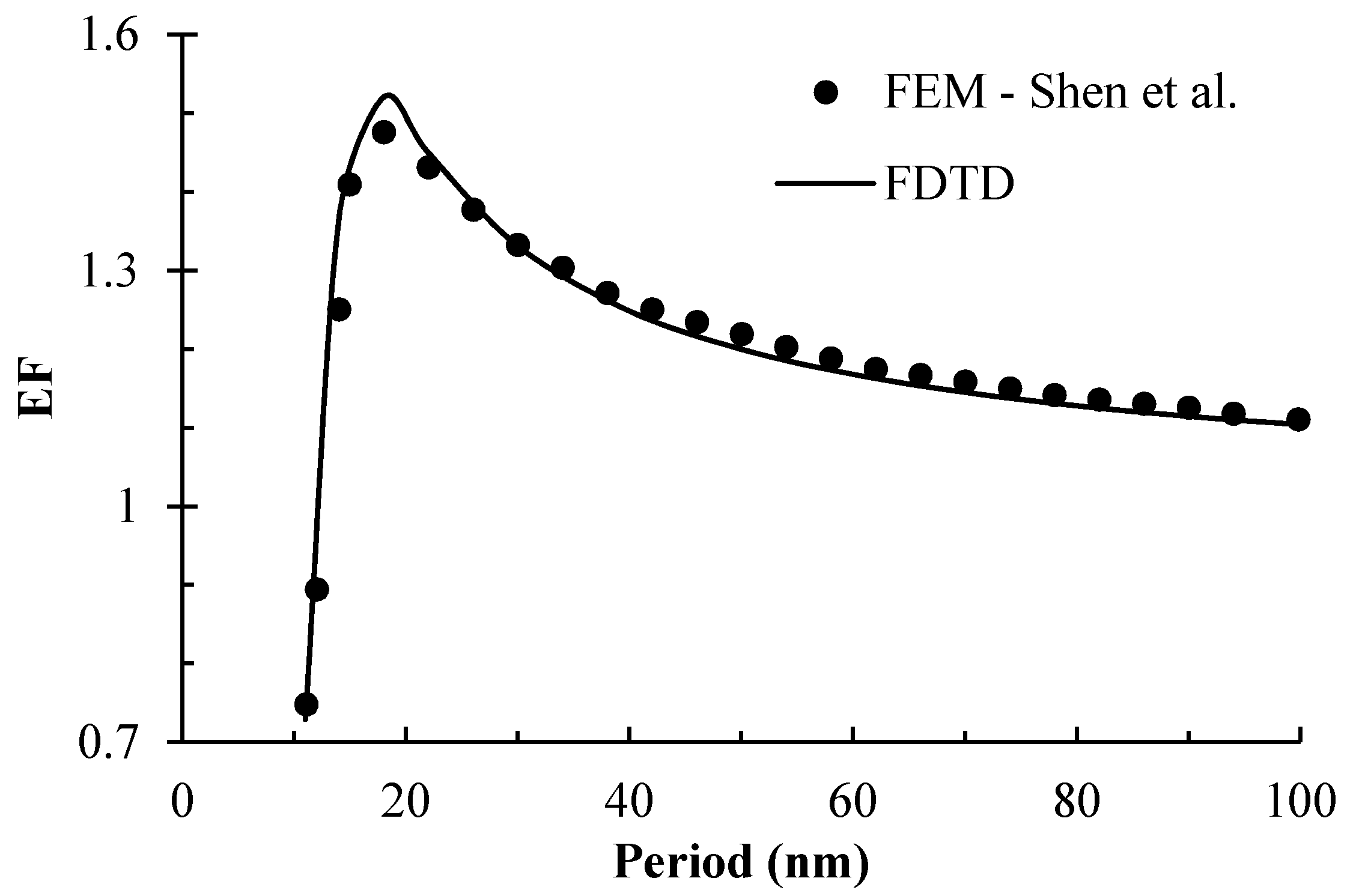
The absorbed fraction of optical power can be obtained by solving underlying physical equations, i.e., Maxwell’s electromagnetic equations. Maxwell’s equations are a set of partial differential equations which describe the relationship between electric and magnetic fields and incident light. Maxwell’s equations are generally solved numerically, except for a few simple cases where analytical solutions exist. One of the most popular methods for solving these equations is the Finite Difference Time Domain (FDTD) method which discretizes the spatial and temporal grid called Yee’s cell. In this study, a commercial software [32] provided by Lumerical Inc. (Vancouver, Canada) is used to facilitate FDTD simulations. EF is calculated for a photovoltaic cell structure in Figure 1 for $t_1=33 \mathrm{nm}$, $t_2=20 \mathrm{nm}$, $r=5 \mathrm{nm}$, $s=11.5 \mathrm{nm}$ and for different $P$. Computed EF values are compared with Finite Element Method (FEM) simulations by Shen et al. [30] in Figure 2.

Despite these powerful solution techniques and parallelization options, the numerical solution of Maxwell’s equations for nano-structures is very time-consuming and can be an obstruction for direct optimization. Surrogate modeling can be used to approximate the absorptivity as a function of the inputs, namely OPV geometry and source properties. In the sequel, we explain the use of NNs as a surrogate model and describe the procedures for training and validation data generation, model fitting and validation along with necessary mathematical backgrounds.

3. Surrogate-Based Modeling and Optimization

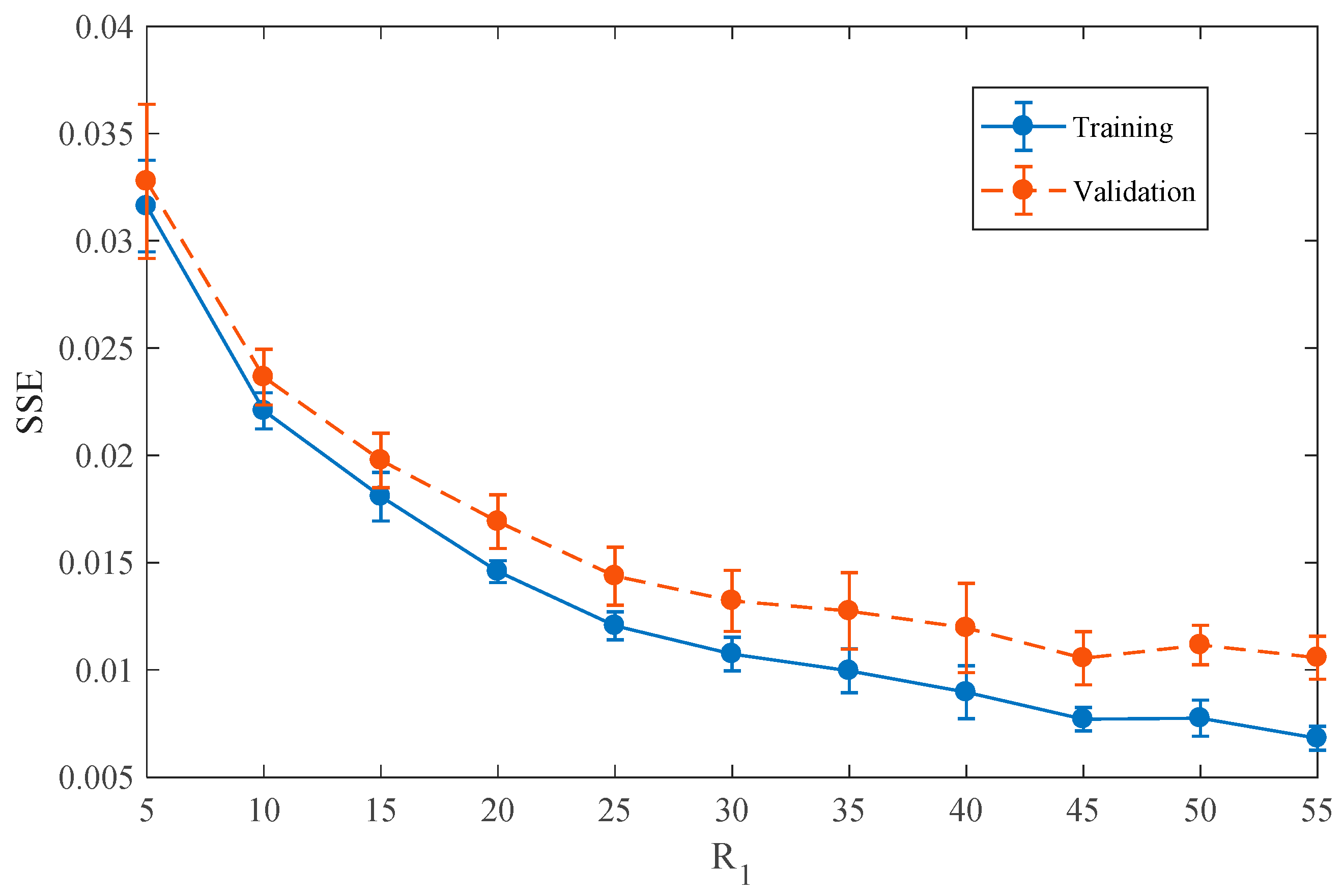
Surrogate modeling starts with a proper sampling scheme (also known as design of experiments). After sampling points in the input space are collected, they are used in the forward problem to obtain an input–output set of data for training. This set is used for determining the corresponding parameters of the surrogate model [33]. This procedure is called model training (fitting). An additional set of input–output pairs (validation set) is used to validate the trained surrogate model. Cross validation (CV) [33] is often used as a reliable technique due to the intuitive solution and unbiased estimation. In CV, data is divided into $N$ folds, and training is repeated $N$ times, where ($N-1$) of the folds are used as training and one fold is left out and used for validation each time. The training-validation set can be sampled in various ways such as Uniform Sampling (US), Latin Hypercube Sampling (LHS) and Orthogonal Arrays (OA) [33]. The purpose of sampling is to represent the input space in the best way, while making sure that the number of sample points is kept at a minimum, in order to reduce the computational forward problem cost.

3.1. Neural Network Model of Absorptivity

NN is a well-established regression tool which can approximate almost every function regardless of the degree of nonlinearity [34,35]. NN represents the relationship between input and output as a series of functions evaluated at the artificial neurons. The output of the NN model is

$$\begin{gathered} y_i=f_i\left(W_i{y}_{\mathrm{i}-1}\right), \forall 1\le i\le L, \\ {y}_{\mathbf{0}}={\left[{\overline{t}}_1,{\overline{t}}_2 , \overline{r},\overline{s},\overline{P},\overline{\theta },\overline{\lambda },1\right]}^T. \end{gathered}$$

(2)

where $y_i$ is the normalized output vector and $W_i$ is the coefficient matrix of the ith layer and $L$ is the number of layers. $y_{\mathbf{0}}$ is the input vector normalized to $\left[-1 1\right]$ range by ${\overline{z}}_1=2\left(z_1-z_{1,min}\right)/\left(z_{1,max}-z_{1,min}\right)-1$. The output is then renormalized to $\left[0 1\right]$ to obtain NN absorptivity, ${\alpha }_{NN}=f_{NN}\left(x,\theta ,\lambda \right)$ and $x={\left[t_1,r,s,P,t_2\right]}^T$.

$W_i$ is found as a result of NN training by minimizing the error between NN output and target. The details of NN training are not included here for the sake of brevity, but are presented in Appendix A. The interested readers are referred to [34,35] for further details. One of the advantages provided by the present NN model is modeling both plasmonic and bare structures in the same model, thus avoiding the additional computational cost.

3.2. Objective Function

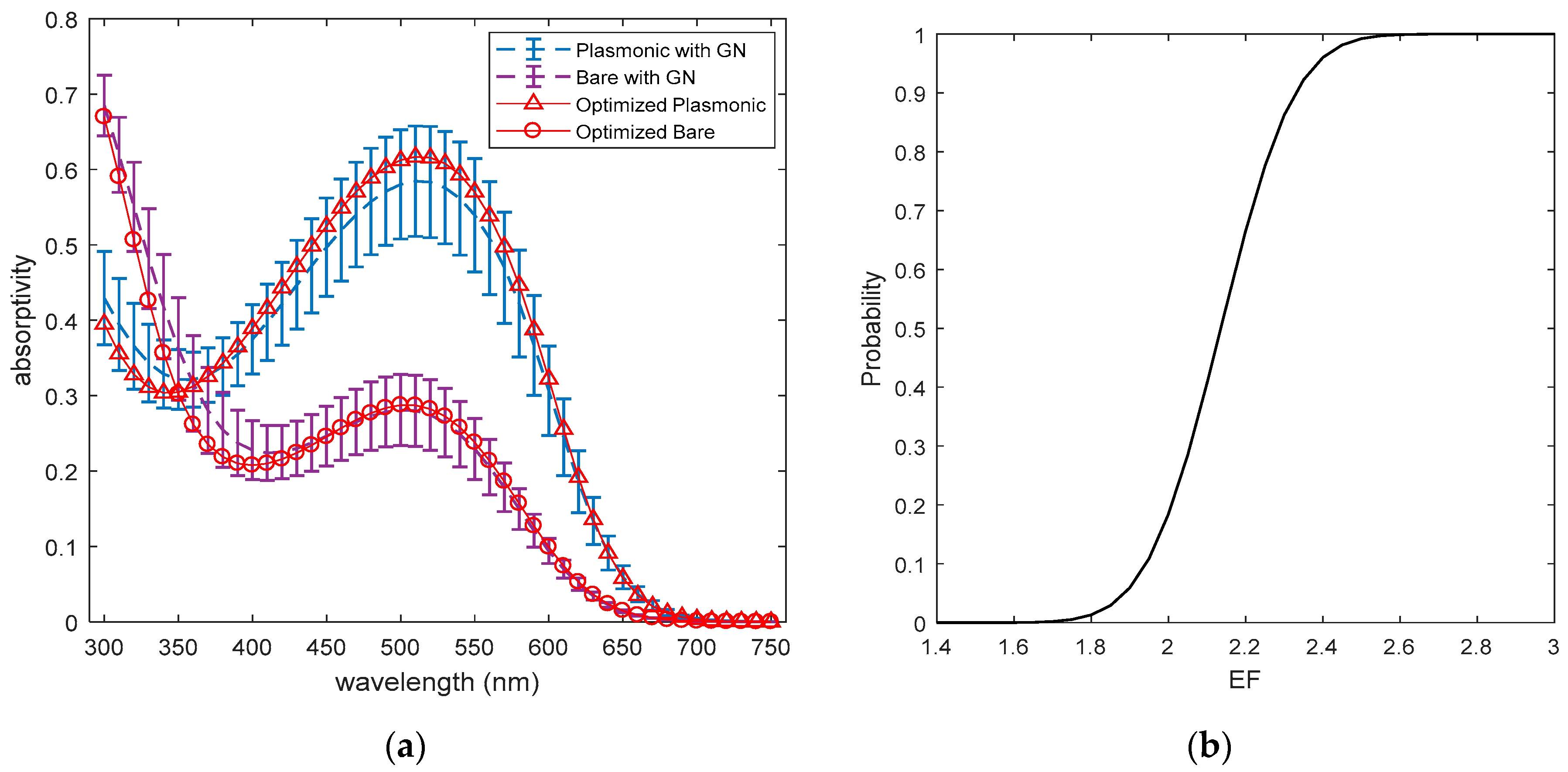
The objective of the present optimization problem is to maximize EF by modifying the cell geometry. One of the reasons for choosing EF as the objective function is that the algorithm tends to minimize the active layer thickness when the aim is to maximize EF, thus the possibility of recombination is also decreased although photocurrent is not considered as the objective.

Therefore, the present optimization problem can be formulated as

$$\begin{gathered} \underset{x}{\max } EF\left(x\right)=\left({\displaystyle \int }\lambda f_{NN}\left(x,\lambda , \theta \right)I\left(\lambda \right)d\lambda \right){\left({\displaystyle \int }\lambda f_{NN}\left(x_b,\lambda ,\theta \right)I\left(\lambda \right)d\lambda \right)}^{-1} \\ \mathrm{Subject} \mathrm{to}: x^{\left(\mathit{U}\right)}<x<x^{\left(\mathit{U}\right)}. \end{gathered}$$

(3)

where $x$ is the geometry vector with Ag nanoparticles and $x_b$ is the bare geometry without the nanoparticles, i.e., $x_b={\left[t_1,0,0,1,t_2\right]}^T$, and the lower and upper limits for the geometry vector are $x^{\left(\mathit{L}\right)}={\left[10,0,5,5,5\right]}^T\mathrm{nm}$ and $x^{\left(\mathit{U}\right)}={\left[100,t_1/2,t_1/2-r,200,100\right]}^T\mathrm{nm}$. The bounds are the same as the bounds of training and validation sets except the lower bound of $s$. $s^L=5\mathrm{nm}$ in order to avoid short-circuit possibility due to Ag–Al contact. $EF\left(x\right)$ is then calculated as the ratio of the integrals in the numerator and denominator of (16) which are calculated by using the trapezoidal method by evaluating the output of the surrogate model $f_{NN}\left(x,\lambda ,\theta \right)$ and $f_{NN}\left(x_b,\lambda ,\theta \right)$ for each wavelength increment (1 nm). The cost function in the optimization problem, however, is set to the inverse of EF and penalty terms are added [36] in order to obtain an unconstrained minimization problem:

$$\underset{x}{\min } C\left(x\right)=\frac{1}{EF\left(x\right)}+{\phi }_1{\displaystyle \sum }_{j=1}^{R_0}\max \left(x_j-x_j^U,0\right)+{\phi }_2{\displaystyle \sum }_{j=1}^{R_0}\max \left(x_j^L-x_j,0\right).$$

(4)

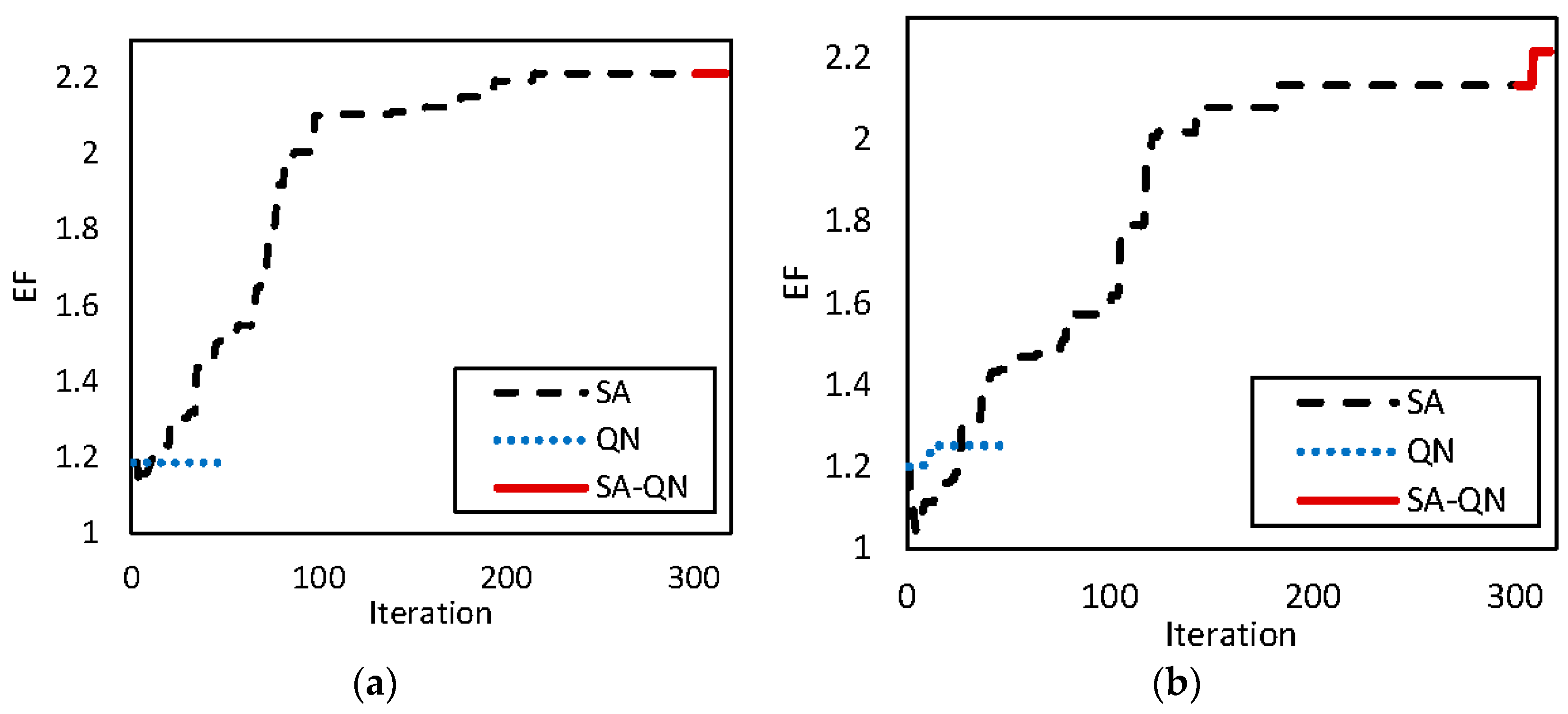
3.3. Optimization Algorithms

Numerical optimization methods can be classified as stochastic and deterministic [37]. In stochastic optimization, the next candidate search point is selected randomly based on a current selection distribution, while in deterministic search no randomness is involved. The most notable deterministic search methods are gradient-based algorithms, which rely on first and/or second order derivatives (i.e., gradient and Hessian) and use a line search approach based on those. Some examples of stochastic methods are nature-inspired algorithms, such as artificial bee colony [38], genetic algorithms [39], Tabu search [40] and Simulated Annealing [41]. Examples of Gradient-based optimization algorithms include Conjugate Gradient, Levenberg Marquardt and Quasi Newton methods [36]. We choose to work with a mixture of global Simulated Annealing (SA) and Quasi Newton (QN) techniques in the current work. The details of these algorithms can be found in reference [36,41]. For objective functions linked to NNs, the gradient can be computed directly using a back-propagation sensitivity quantity, which is elaborated in Appendix A.

4. Results and Discussion

4.1. Data Generation

In total, 6000 data points are generated using uniform random sampling from the ranges given in

Table 1. Lower (LB) and upper (UB) bounds of the input data for random data generation.

Input Name	${\mathit{t}}_1$	$\mathit{r}$	$\mathit{s}$	$\mathit{P}$	${\mathit{t}}_2$	$\mathit{\theta }$	$\mathit{\lambda }$
Lower Bound	10	5	0	2$r$	5	0	300
Upper Bound	100	$t_1/2$	$t_1-2r$	200	100	89	900

.

Once the random set of input data is generated, FDTD simulations are done to gather input–output pairs. Output values are normalized before being used in NN training. Details of normalization and training are outlined in the Appendix. Average duration for a single simulation (at a single wavelength) is 5 min. If EF in Equation (1) was desired to be evaluated using FDTD, 72 simulations were required using the solar spectrum of 300–650 nm with 10 nm increments (the absorbed power in P3HT: PCBM is almost zero at wavelengths larger than 650 nm). Therefore, 6000 simulations are equivalent to 83 iterations of direct simulations. This means that any efficient direct optimization should take less than 83 iterations to find a solution better than an optimization based on the surrogate model, which is practically impossible. All simulations in this study were performed using 20 cores on a 17,340-core IBM/Lenovo supercomputer provided by the Texas A&M High Performance Research Computing Center.

4.2. Results of Optimization

The optimized geometry obtained by the NN-based optimization procedure with QN and SA methods is presented in

Table 2. Optimized geometry of plasmonic OPV and corresponding enhancement factor (EF) values.

Method	${\left[{\mathit{t}}_1, \mathit{r}, \mathit{s}, \mathit{P},{\mathit{t}}_2\right]}^{\mathit{T}}{}_{\mathit{i}\mathit{n}\mathit{i}\mathit{t}.}$	${\left[{\mathit{t}}_1, \mathit{r}, \mathit{s}, \mathit{P},{\mathit{t}}_2\right]}^{\mathit{T}}{}_{\mathit{o}\mathit{p}\mathit{t}}$	EF
NN–QN	${\left[50 , 20 , 5 , 100 , 50\right]}^T$	${\left[46 , 20 , 5 , 99 , 50\right]}^T$	1.26
NN–SA	${\left[50 , 20 , 5 , 100 , 50\right]}^T$	${\left[24 , 9 , 6 , 51 , 87 \right]}^T$	2.21
NN–SA–QN	${\left[50 , 20 , 5 , 100 , 50\right]}^T$	${\left[24 , 9 , 6 , 51 , 87 \right]}^T$	2.21
NN–QN	${\left[40 , 11 , 15 , 80 , 20\right]}^T$	${\left[33, 10 , 16 , 82 , 14\right]}^T$	1.25
NN–SA	${\left[40 , 11 , 15 , 80 , 20\right]}^T$	${\left[26 , 10 , 6 , 51 , 87 \right]}^T$	2.14
NN–SA–QN	${\left[40 , 11 , 15 , 80 , 20\right]}^T$	${\left[24 , 9 , 6 , 51 , 89 \right]}^T$	2.22

for two different initial guesses. NN-SA-QN refers to the hybrid optimization algorithm in which QN is used after the SA algorithm to find the global optimum in the vicinity of the SA solution.

Note that the SA algorithm has a better performance for finding the global optimum and is less likely to get trapped in local optima, unlike QN. In Figure 3, the variation of EF during iterations is presented for these three algorithms and for the two different initial guesses.

4.3. Uncertainty Analysis

In order to quantify the uncertainty (sensitivity) of the optimized solution, an error vector $\mathit{\epsilon }$ is added to the optimized geometry, $x_{opt}={\left[24 , 9 , 6 , 51 , 89 \right]}^T$, and the performance probability distribution is measured by means of Monte Carlo method. In the optimized geometry, the Ag nanosphere is in contact with PEDOT:PSS and this condition ($s+2r=t_1$) is also preserved in the uncertainty analysis. Therefore, the error vector is $\mathit{\epsilon }={\left[{\epsilon }_{t_1},{\epsilon }_r,{\epsilon }_P,{\epsilon }_{t_2}\right]}^T$. The error vector is modeled as independent zero mean Gaussian elements with standard deviation equal to 10% of the corresponding geometry element.

$$\begin{gathered} x=x_{opt}+\mathit{\epsilon } \\ {\epsilon }_i=\mathcal{N}\left(0 , 0.1x_i\right) \end{gathered}$$

(5)

The variations of spectral absorptivity and EF are presented for 1000 randomly generated samples in Figure 4. According to the results, 90% of the samples result in EF between 1.9–2.4.

5. Conclusions

We demonstrated that design optimization of the plasmonic organic thin film photovoltaic cells can be efficiently done using a surrogate model, instead of solving costly Maxwell’s electromagnetic equations. The NN-based surrogate model replaced the optical absorptivity in the absorber layer. Consequently, the plasmonic contribution to the PV cell which can be quantified by optical enhancement factor can be efficiently estimated. We demonstrated that the model can be reliably used for an extremely fast optimization. The resulting enhancement factor is more than 200%. The required time to complete NN-based optimization is 5–10 times less than direct simulation optimization. We also demonstrated that NN can also be used to evaluate the uncertainty of the results to small changes in the inputs, which is another a computational burden with direct computations.