Applications of the Chaotic Quantum Genetic Algorithm with Support Vector Regression in Load Forecasting
Abstract
:1. Introduction
2. The Proposed SVRCQGA Model
2.1. Brief Description of the SVR Model
2.2. Chaotic Quantum Genetic Algorithm (CQGA)
2.2.1. Introduction of QGA
2.2.2. Quantum Computing Concepts
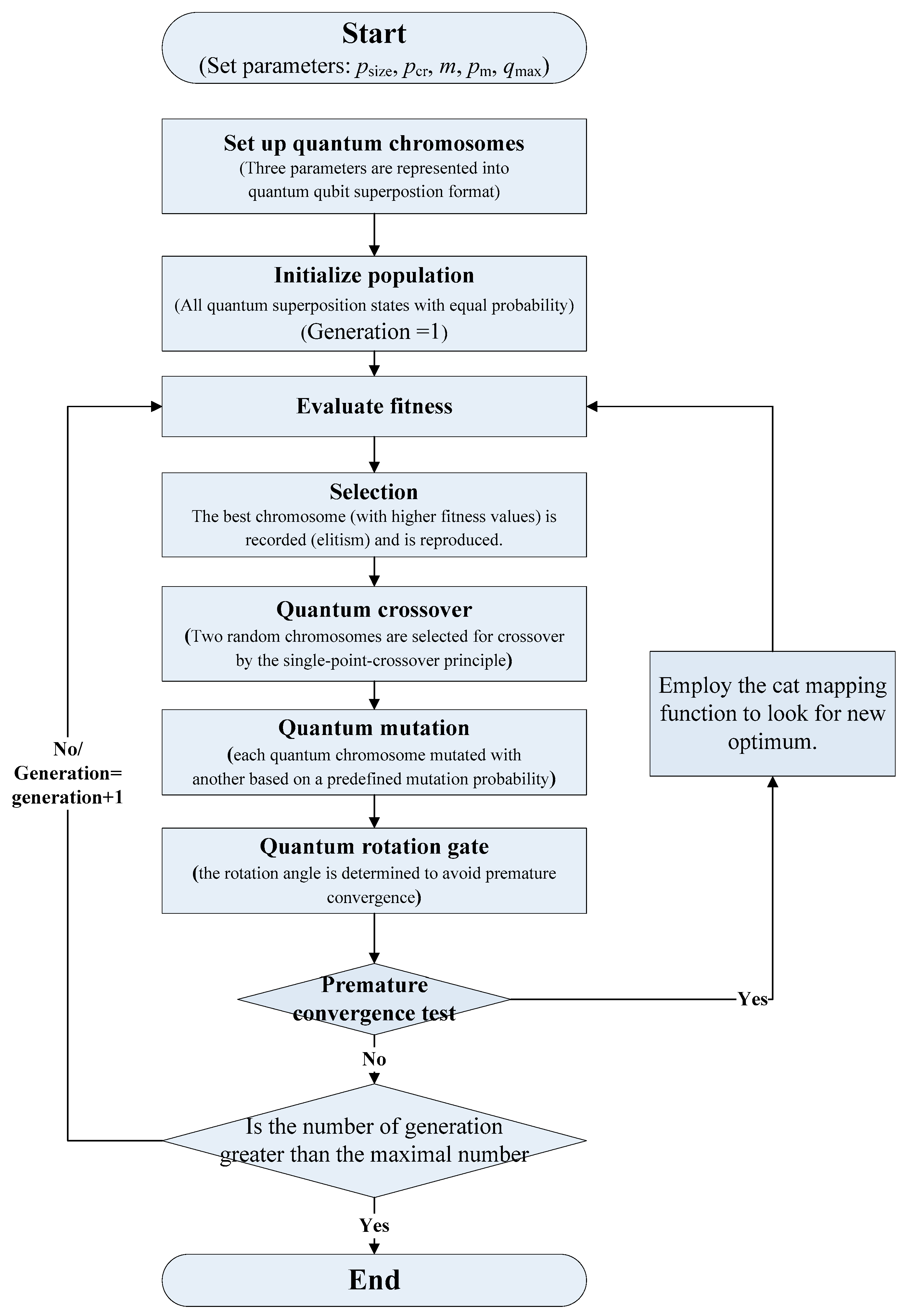
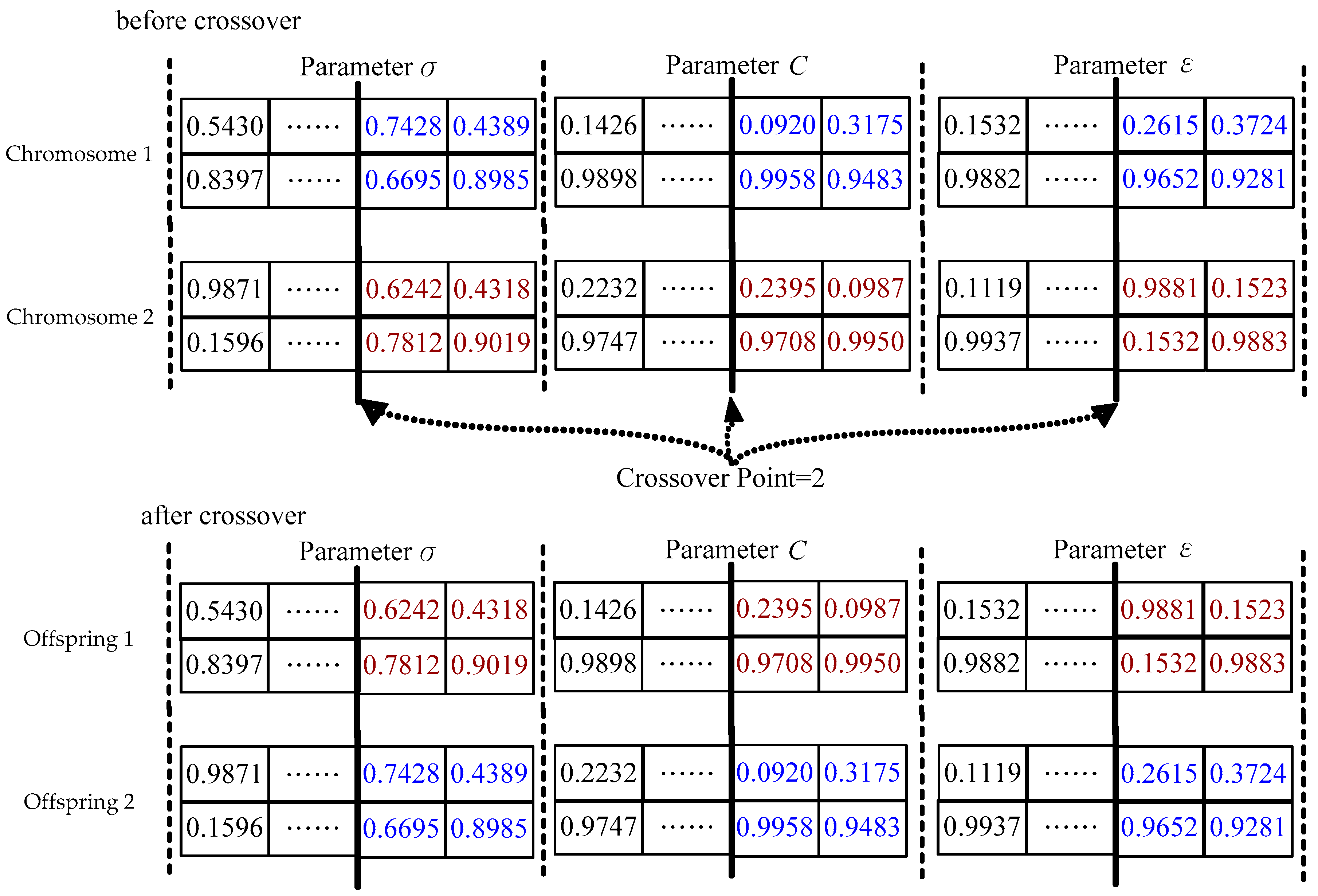
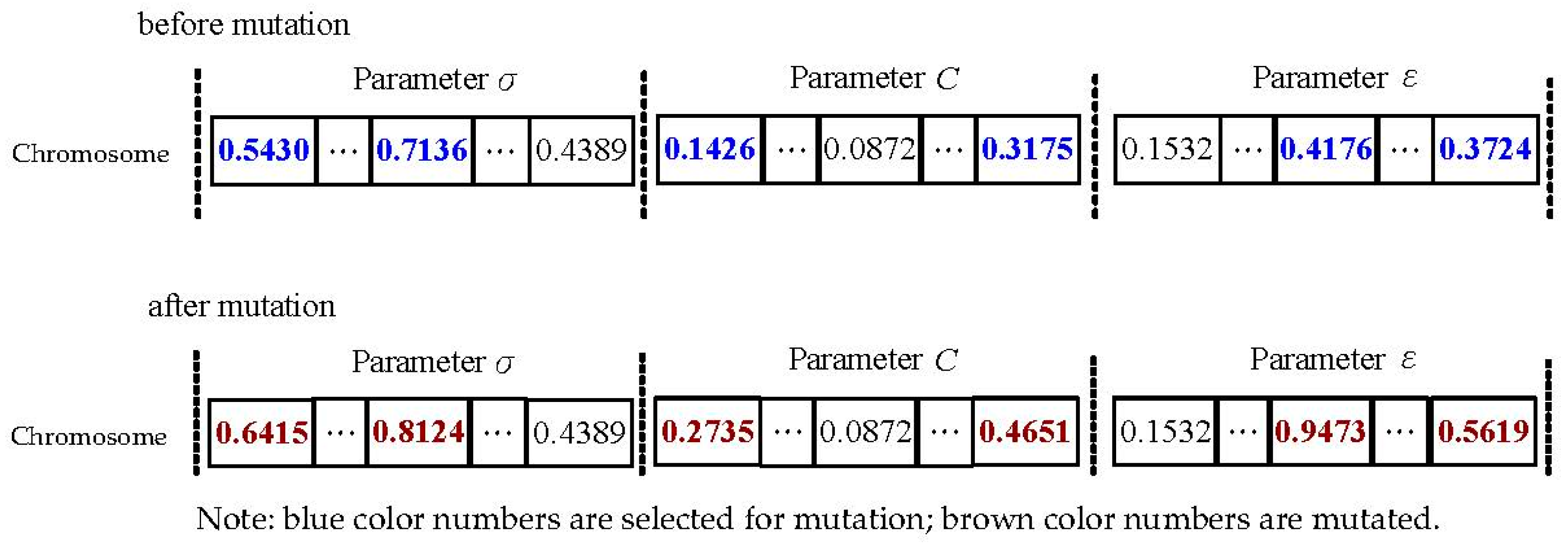
2.2.3. Implementation Steps of CQGA
3. Experimental Examples
3.1. Data Sets of Experimental Examples
3.1.1. Regional Electricity Load Data in Taiwan: Example 1
3.1.2. Annual Electricity Load Data in Taiwan: Example 2
3.1.3. 2014 Global Energy Forecasting Competition (GEFCOM 2014) Electricity Load Data: Example 3
3.2. Parameters Setting & Forecasting Results and Analysis
3.2.1. Setting the CQGA Parameters
3.2.2. Forecasting Accuracy Indexes
3.2.3. Forecasting Performance Superiority Tests
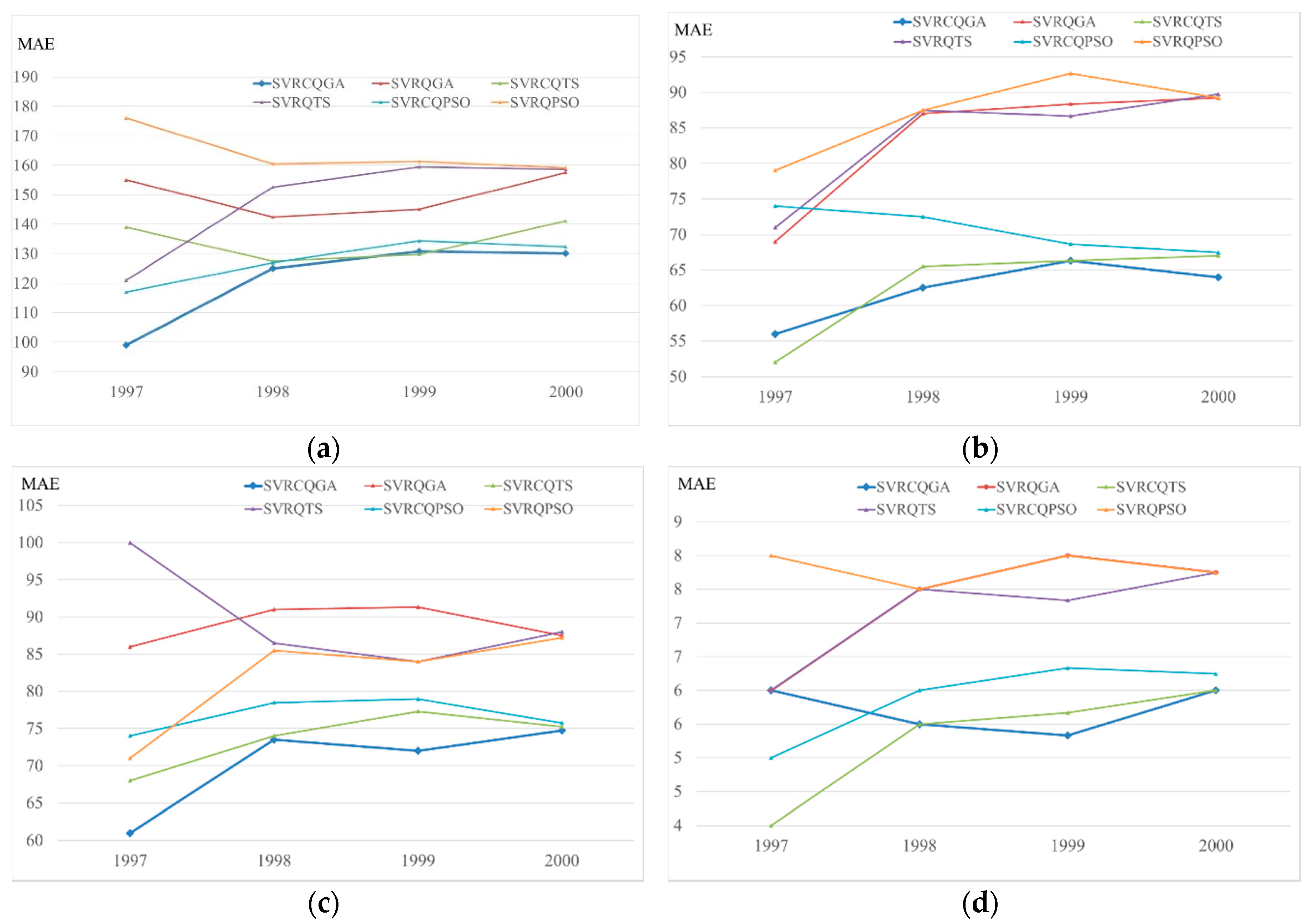
3.2.4. Results and Analysis: Example 1
3.2.5. Results and Analysis: Example 2
3.2.6. Results and Analysis: Example 3
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Xiao, L.; Shao, W.; Liang, T.; Wang, C. A combined model based on multiple seasonal patterns and modified firefly algorithm for electrical load forecasting. Appl. Energy 2016, 167, 135–153. [Google Scholar] [CrossRef]
- Fan, S.; Chen, L. Short-term load forecasting based on an adaptive hybrid method. IEEE Trans. Power Syst. 2006, 21, 392–401. [Google Scholar] [CrossRef]
- Cincotti, S.; Gallo, G.; Ponta, L.; Raberto, M. Modelling and forecasting of electricity spot-prices: Computational intelligence vs. classical econometrics. AI Commun. 2014, 27, 301–314. [Google Scholar]
- Amjady, N.; Keynia, F. Day ahead price forecasting of electricity markets by a mixed data model and hybrid forecast method. Int. J. Electr. Power Energy Syst. 2008, 30, 533–546. [Google Scholar] [CrossRef]
- Weron, R. Electricity price forecasting: A review of the state-of-the-art with a look into the future. Int. J. Forecast. 2014, 30, 1030–1081. [Google Scholar] [CrossRef]
- Fan, G.; Peng, L.-L.; Hong, W.-C.; Sun, F. Electric load forecasting by the SVR model with differential empirical mode decomposition and auto regression. Neurocomputing 2016, 173, 958–970. [Google Scholar] [CrossRef]
- Hussain, A.; Rahman, M.; Memon, J.A. Forecasting electricity consumption in Pakistan: The way forward. Energy Policy 2016, 90, 73–80. [Google Scholar] [CrossRef]
- Vu, D.H.; Muttaqi, K.M.; Agalgaonkar, A.P. A variance inflation factor and backward elimination based Robust regression model for forecasting monthly electricity demand using climatic variables. Appl. Energy 2015, 140, 385–394. [Google Scholar] [CrossRef]
- Maçaira, P.M.; Souza, R.C.; Oliveira, F.L.C. Modelling and forecasting the residential electricity consumption in Brazil with pegels exponential smoothing techniques. Procedia Comput. Sci. 2015, 55, 328–335. [Google Scholar] [CrossRef]
- Al-Hamadi, H.M.; Soliman, S.A. Short-term electric load forecasting based on Kalman filtering algorithm with moving window weather and load model. Electr. Power Syst. Res. 2004, 68, 47–59. [Google Scholar] [CrossRef]
- Hippert, H.S.; Taylor, J.W. An evaluation of Bayesian techniques for controlling model complexity and selecting inputs in a neural network for short-term load forecasting. Neural Netw. 2010, 23, 386–395. [Google Scholar] [CrossRef] [PubMed]
- Kelo, S.; Dudul, S. A wavelet Elman neural network for short-term electrical load prediction under the influence of temperature. Int. J. Electr. Power Energy Syst. 2012, 43, 1063–1071. [Google Scholar] [CrossRef]
- Lahouar, A.; Slama, J.B.H. Day-ahead load forecast using random forest and expert input selection. Energy Convers. Manag. 2015, 103, 1040–1051. [Google Scholar] [CrossRef]
- Chaturvedi, D.K.; Sinha, A.P.; Malik, O.P. Short term load forecast using fuzzy logic and wavelet transform integrated generalized neural network. Int. J. Electr. Power Energy Syst. 2015, 67, 230–237. [Google Scholar] [CrossRef]
- Zhai, M.-Y. A new method for short-term load forecasting based on fractal interpretation and wavelet analysis. Int. J. Electr. Power Energy Syst. 2015, 69, 241–245. [Google Scholar] [CrossRef]
- Coelho, V.N.; Coelho, I.M.; Coelho, B.N.; Reis, A.J.R.; Enayatifar, R.; Souza, M.J.F.; Guimarães, F.G. A self-adaptive evolutionary fuzzy model for load forecasting problems on smart grid environment. Appl. Energy 2016, 169, 567–584. [Google Scholar] [CrossRef]
- Bahrami, S.; Hooshmand, R.-A.; Parastegari, M. Short term electric load forecasting by wavelet transform and grey model improved by PSO (particle swarm optimization) algorithm. Energy 2014, 72, 434–442. [Google Scholar] [CrossRef]
- Aras, S.; Kocakoç, İ.D. A new model selection strategy in time series forecasting with artificial neural networks: IHTS. Neurocomputing 2016, 174, 974–987. [Google Scholar] [CrossRef]
- Kendal, S.L.; Creen, M. An Introduction to Knowledge Engineering; Springer: London, UK, 2007. [Google Scholar]
- Cherroun, L.; Hadroug, N.; Boumehraz, M. Hybrid approach based on ANFIS models for intelligent fault diagnosis in industrial actuator. J. Control Electr. Eng. 2013, 3, 17–22. [Google Scholar]
- Hahn, H.; Meyer-Nieberg, S.; Pickl, S. Electric load forecasting methods: Tools for decision making. Eur. J. Oper. Res. 2009, 199, 902–907. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Hong, W.C. Chaotic particle swarm optimization algorithm in a support vector regression electric load forecasting model. Energy Convers. Manag. 2009, 50, 105–117. [Google Scholar] [CrossRef]
- Hong, W.C. Electric load forecasting by seasonal recurrent SVR (support vector regression) with chaotic artificial bee colony algorithm. Energy 2011, 36, 5568–5578. [Google Scholar] [CrossRef]
- Bhunia, C.T. Quantum computing & information technology: A tutorial. IETE J. Educ. 2006, 47, 79–90. [Google Scholar]
- Dey, S.; Bhattacharyya, S.; Maulik, U. Quantum inspired genetic algorithm and particle swarm optimization using chaotic map model based interference for gray level image thresholding. Swarm Evol. Comput. 2014, 15, 38–57. [Google Scholar] [CrossRef]
- Huang, M.-L. Hybridization of chaotic quantum particle swarm optimization with SVR in electric demand forecasting. Energies 2016, 9, 426. [Google Scholar] [CrossRef]
- Lee, C.-W.; Lin, B.-Y. Application of hybrid quantum tabu search with support vector regression (SVR) for load forecasting. Energies 2016, 9, 873. [Google Scholar] [CrossRef]
- Shor, P.W. Algorithms for quantum computation: Discrete logarithms and factoring. In Proceedings of the 35th Annual Symposium on Foundations of Computer Science, Santa Fe, NM, USA, 20–22 November 1994; pp. 124–134. [Google Scholar]
- Han, K.-H. Quantum-inspired evolutionary algorithms with a new termination criterion, Hε gate, and two-phase scheme. IEEE Trans. Evol. Comput. 2004, 8, 156–169. [Google Scholar]
- Lahoz-Beltra, R. Quantum genetic algorithms for computer scientists. Computers 2016, 5, 24. [Google Scholar] [CrossRef]
- Chen, G.; Mao, Y.; Chui, C.K. Asymmetric image encryption scheme based on 3D chaotic cat maps. Chaos Solitons Fract. 2004, 21, 749–761. [Google Scholar] [CrossRef]
- Hang, B.; Jiang, J.; Gao, Y.; Ma, Y. A Quantum Genetic Algorithm to Solve the Problem of Multivariate. In Information Computing and Applications, Proceedings of the Second International Conference ICICA 2011, Qinhuangdao, China, 28–31 October 2011; Liu, C., Chang, J., Yang, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 308–314. [Google Scholar]
- Su, H. Chaos quantum-behaved particle swarm optimization based neural networks for short-term load forecasting. Procedia Eng. 2011, 15, 199–203. [Google Scholar] [CrossRef]
- 2014 Global Energy Forecasting Competition Site. Available online: http://www.drhongtao.com/gefcom/ (accessed on 9 November 2017).
- Diebold, F.X.; Mariano, R.S. Comparing predictive accuracy. J. Bus. Econ. Stat. 1995, 13, 134–144. [Google Scholar]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. Biom. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Friedman, M. A comparison of alternative tests of significance for the problem of m rankings. Ann. Math. Stat. 1940, 11, 86–92. [Google Scholar] [CrossRef]


| Examples | Data Type | Data Length | Data Size | Data Characteristics |
|---|---|---|---|---|
| Example 1 | Regional and annual | From 1981 to 2000 | 4 regions and 20 years | Increment with fluctuation caused by some accidental event (921 earthquake) |
| Example 2 | Annual | From 1945 to 2003 | 59 years | Increment with the continuous economic development in Taiwan |
| Example 3 | Hourly | From 1 December 2011 to 1 January 2012 | 744 h | Cyclic fluctuation |
| Regions | SVRCQGA Parameters | MAPE of Testing (%) | ||
| σ | C | ε | ||
| Northern | 4.0000 | 0.6500 | 1.0760 | |
| Central | 6.0000 | 0.3500 | 1.2130 | |
| Southern | 8.0000 | 0.4800 | 1.1650 | |
| Eastern | 12.0000 | 0.2800 | 1.5180 | |
| Regions | SVRQGA Parameters | MAPE of Testing (%) | ||
| σ | C | ε | ||
| Northern | 3.0000 | 0.3400 | 1.3150 | |
| Central | 10.0000 | 0.4800 | 1.6830 | |
| Southern | 6.0000 | 0.3500 | 1.3640 | |
| Eastern | 4.0000 | 0.6800 | 1.9680 | |
| Indexes | SVRCQGA | SVRQGA | SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO |
|---|---|---|---|---|---|---|
| Northern region | ||||||
| MAPE (%) | 1.0760 | 1.3150 | 1.0870 | 1.3260 | 1.1070 | 1.3370 |
| RMSE | 131.48 | 159.26 | 132.79 | 159.43 | 142.62 | 160.28 |
| MAE | 130.00 | 157.50 | 141.00 | 158.50 | 132.25 | 159.00 |
| Central region | ||||||
| MAPE (%) | 1.2130 | 1.6830 | 1.2650 | 1.6870 | 1.2840 | 1.6890 |
| RMSE | 64.46 | 90.18 | 67.69 | 90.67 | 67.70 | 89.87 |
| MAE | 64.00 | 89.25 | 67.00 | 89.75 | 67.50 | 89.25 |
| Southern region | ||||||
| MAPE (%) | 1.1650 | 1.3640 | 1.1720 | 1.3670 | 1.1840 | 1.3590 |
| RMSE | 75.44 | 87.82 | 75.57 | 88.84 | 76.03 | 88.05 |
| MAE | 74.75 | 87.50 | 75.25 | 88.00 | 75.75 | 87.25 |
| Eastern region | ||||||
| MAPE (%) | 1.5180 | 1.9680 | 1.5430 | 1.9720 | 1.5940 | 1.9830 |
| RMSE | 6.12 | 7.86 | 6.38 | 7.95 | 6.30 | 7.79 |
| MAE | 6.00 | 7.75 | 6.00 | 7.75 | 6.25 | 7.75 |
| Compared Models | Wilcoxon Signed-Rank Test α = 0.05; Wilcoxon W Statistic = 0 | Friedman Test α = 0.05 |
|---|---|---|
| Northern region | H0: e1 = e2 = e3 = e4 = e5 = e6 F = 12.46; p = 0.028 (reject H0) | |
| SVRCQGA vs. SVRQPSO | W = 0 * | |
| SVRCQGA vs. SVRCQPSO | W = 0 * | |
| SVRCQGA vs. SVRQTS | W = 0 * | |
| SVRCQGA vs. SVRCQTS | W = 1 | |
| SVRCQGA vs. SVRQGA | W = 0 * | |
| Central region | H0: e1 = e2 = e3 = e4 = e5 = e6 F = 13.43; p = 0.021 (reject H0) | |
| SVRCQGA vs. SVRQPSO | W = 0 * | |
| SVRCQGA vs. SVRCQPSO | W = 0 * | |
| SVRCQGA vs. SVRQTS | W = 0 * | |
| SVRCQGA vs. SVRCQTS | W = 1 | |
| SVRCQGA vs. SVRQGA | W = 0 * | |
| Southern region | H0: e1 = e2 = e3 = e4 = e5 = e6 F = 15.57; p = 0.013 (reject H0) | |
| SVRCQGA vs. SVRQPSO | W = 0 * | |
| SVRCQGA vs. SVRCQPSO | W = 0 * | |
| SVRCQGA vs. SVRQTS | W = 0 * | |
| SVRCQGA vs. SVRCQTS | W = 1 | |
| SVRCQGA vs. SVRQGA | W = 0 * | |
| Eastern region | H0: e1 = e2 = e3 = e4 = e5 = e6 F = 11.34; p = 0.035 (reject H0) | |
| SVRCQGA vs. SVRQPSO | W = 0 * | |
| SVRCQGA vs. SVRCQPSO | W = 0 * | |
| SVRCQGA vs. SVRQTS | W = 0 * | |
| SVRCQGA vs. SVRCQTS | W = 1 | |
| SVRCQGA vs. SVRQGA | W = 0 * |
| Optimization Algorithms | Parameters | MAPE of Testing (%) | ||
|---|---|---|---|---|
| σ | C | ε | ||
| QPSO algorithm [27] | 12.0000 | 0.380 | 1.3460 | |
| CQPSO algorithm [27] | 10.0000 | 0.560 | 1.1850 | |
| QTS algorithm [28] | 5.0000 | 0.630 | 1.3210 | |
| CQTS algorithm [28] | 6.0000 | 0.340 | 1.1540 | |
| QGA algorithm | 9.0000 | 0.480 | 1.3180 | |
| CQGA algorithm | 12.0000 | 0.650 | 1.1160 | |
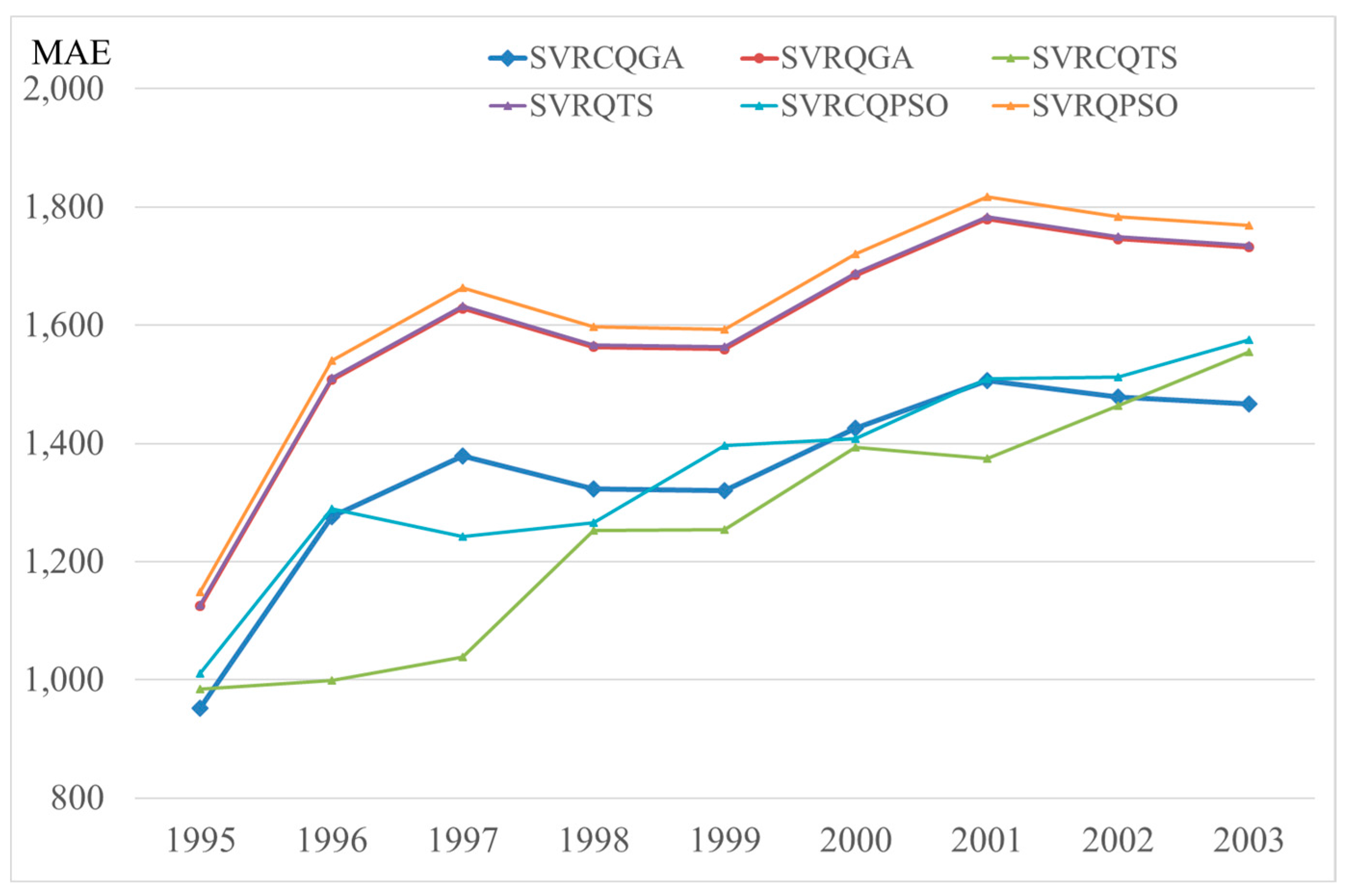
| Years | SVRCQGA | SVRQGA | SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO |
|---|---|---|---|---|---|---|
| MAPE (%) | 1.1160 | 1.3180 | 1.1540 | 1.3210 | 1.1850 | 1.3460 |
| RMSE | 1502.66 | 1774.62 | 1631.48 | 1778.74 | 1618.34 | 1812.51 |
| MAE | 1466.33 | 1731.78 | 1554.89 | 1735.78 | 1575.67 | 1768.78 |
| Compared Models | Wilcoxon Signed-Rank Test α = 0.05; Wilcoxon W Statistic = 8 | Friedman Test α = 0.05 |
|---|---|---|
| SVRCQGA vs. SVRQPSO | W = 4 * | H0: e1 = e2 = e3 = e4 = e5 = e6 F = 13.35; p = 0.022 (reject H0) |
| SVRCQGA vs. SVRCQPSO | W = 2 * | |
| SVRCQGA vs. SVRQTS | W = 4 * | |
| SVRCQGA vs. SVRCQTS | W = 4 * | |
| SVRCQGA vs. SVRQGA | W = 4 * |
| Optimization Algorithms | Parameters | MAPE of Testing (%) | ||
|---|---|---|---|---|
| σ | C | ε | ||
| QPSO algorithm [27] | 9.000 | 42.000 | 0.1800 | 1.9600 |
| CQPSO algorithm [27] | 19.000 | 35.000 | 0.8200 | 1.2900 |
| QTS algorithm [28] | 25.000 | 67.000 | 0.0900 | 1.8900 |
| CQTS algorithm [28] | 12.000 | 26.000 | 0.3200 | 1.3200 |
| QGA algorithm | 5.000 | 79.000 | 0.3800 | 1.7500 |
| CQGA algorithm | 6.000 | 54.000 | 0.6200 | 1.1700 |
| Indexes | SVRCQGA | SVRQGA | SVRCQTS | SVRQTS | SVRCQPSO | SVRQPSO |
|---|---|---|---|---|---|---|
| MAPE (%) | 1.1700 | 1.7500 | 1.3200 | 1.8900 | 1.2900 | 1.9600 |
| RMSE | 1.4927 | 1.6584 | 1.9909 | 2.8507 | 1.9257 | 2.9358 |
| MAE | 1.4522 | 1.6174 | 1.8993 | 2.7181 | 1.8474 | 2.8090 |
| Compared Models | Wilcoxon Signed-Rank Test | Friedman Test | |
|---|---|---|---|
| α = 0.05; Wilcoxon W Statistic = 2328 | p-Value | α = 0.05 | |
| SVRCQGA vs. SVRQPSO | W = 1278.0 * | 0.00012 | H0: e1 = e2 = e3 = e4 = e5 = e6 F = 71.266; p = 0.000 (reject H0) |
| SVRCQGA vs. SVRCQPSO | W = 1152.5 * | 0.00000 | |
| SVRCQGA vs. SVRQTS | W = 1256.0 * | 0.00000 | |
| SVRCQGA vs. SVRCQTS | W = 1263.0 * | 0.00010 | |
| SVRCQGA vs. SVRQGA | W = 2134.5 * | 0.00720 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, C.-W.; Lin, B.-Y. Applications of the Chaotic Quantum Genetic Algorithm with Support Vector Regression in Load Forecasting. Energies 2017, 10, 1832. https://doi.org/10.3390/en10111832
Lee C-W, Lin B-Y. Applications of the Chaotic Quantum Genetic Algorithm with Support Vector Regression in Load Forecasting. Energies. 2017; 10(11):1832. https://doi.org/10.3390/en10111832
Chicago/Turabian StyleLee, Cheng-Wen, and Bing-Yi Lin. 2017. "Applications of the Chaotic Quantum Genetic Algorithm with Support Vector Regression in Load Forecasting" Energies 10, no. 11: 1832. https://doi.org/10.3390/en10111832




