Dependency Relations among International Stock Market Indices
Abstract
:1. Introduction
2. The Data
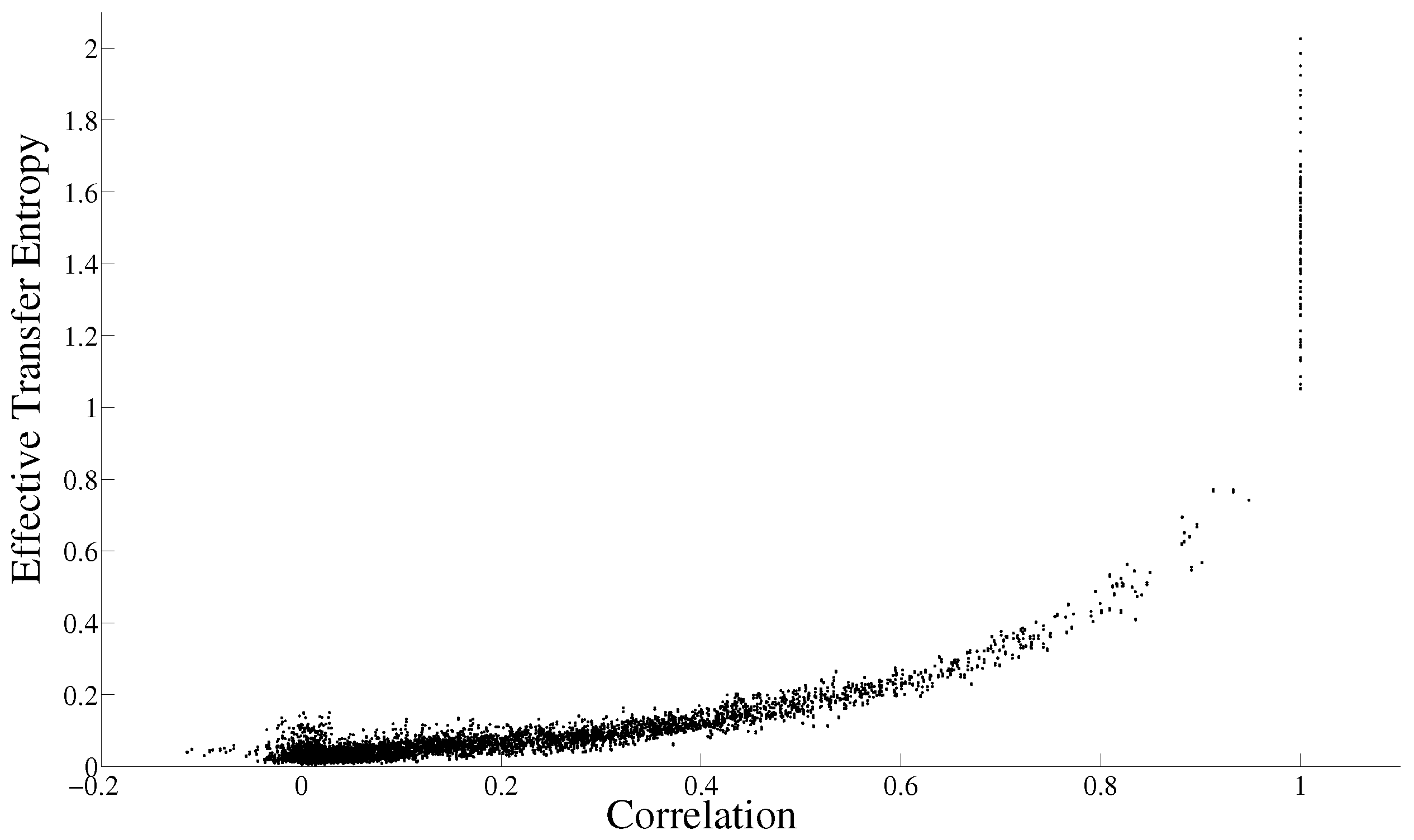
3. Correlation and Transfer Entropy
3.1. Correlation
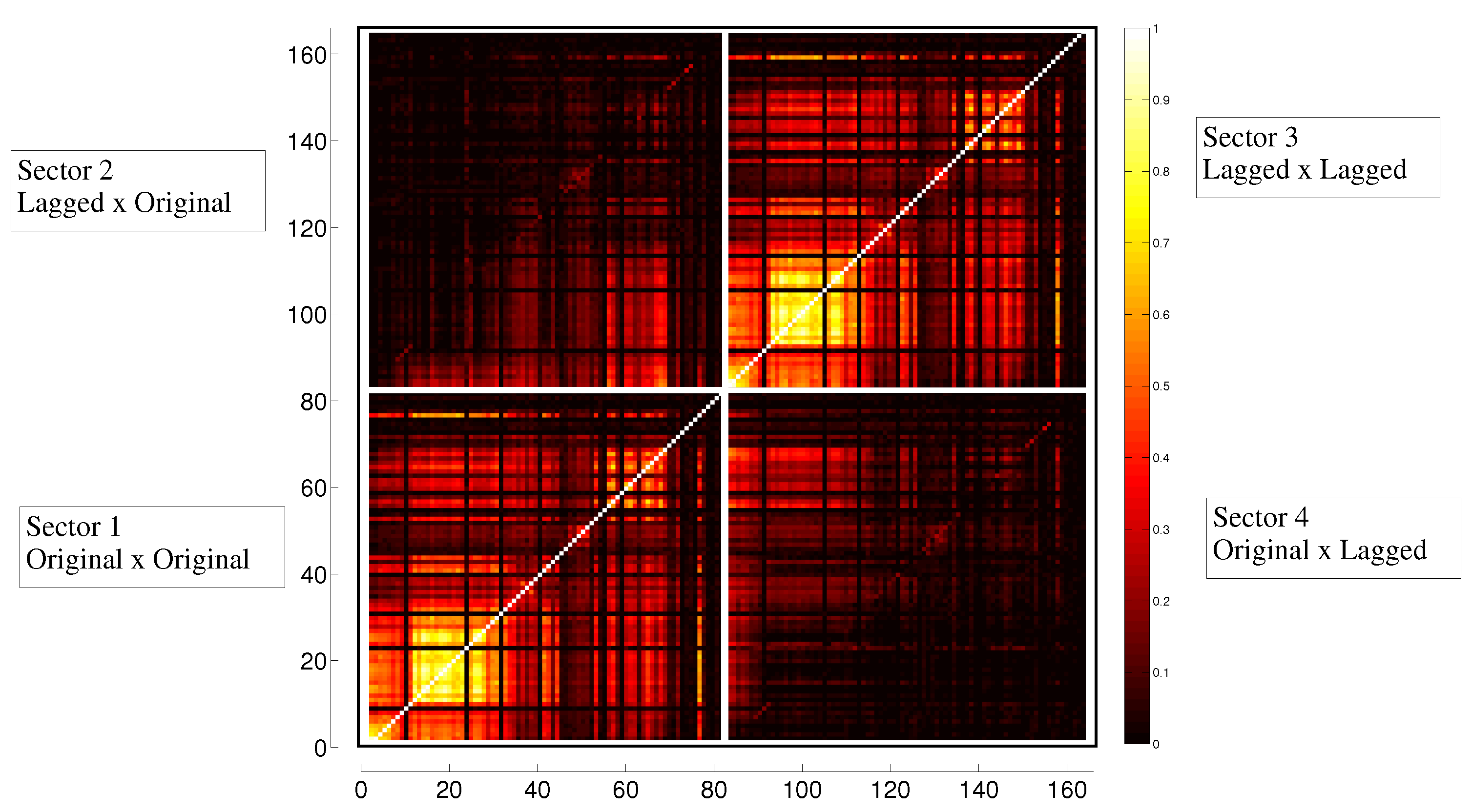
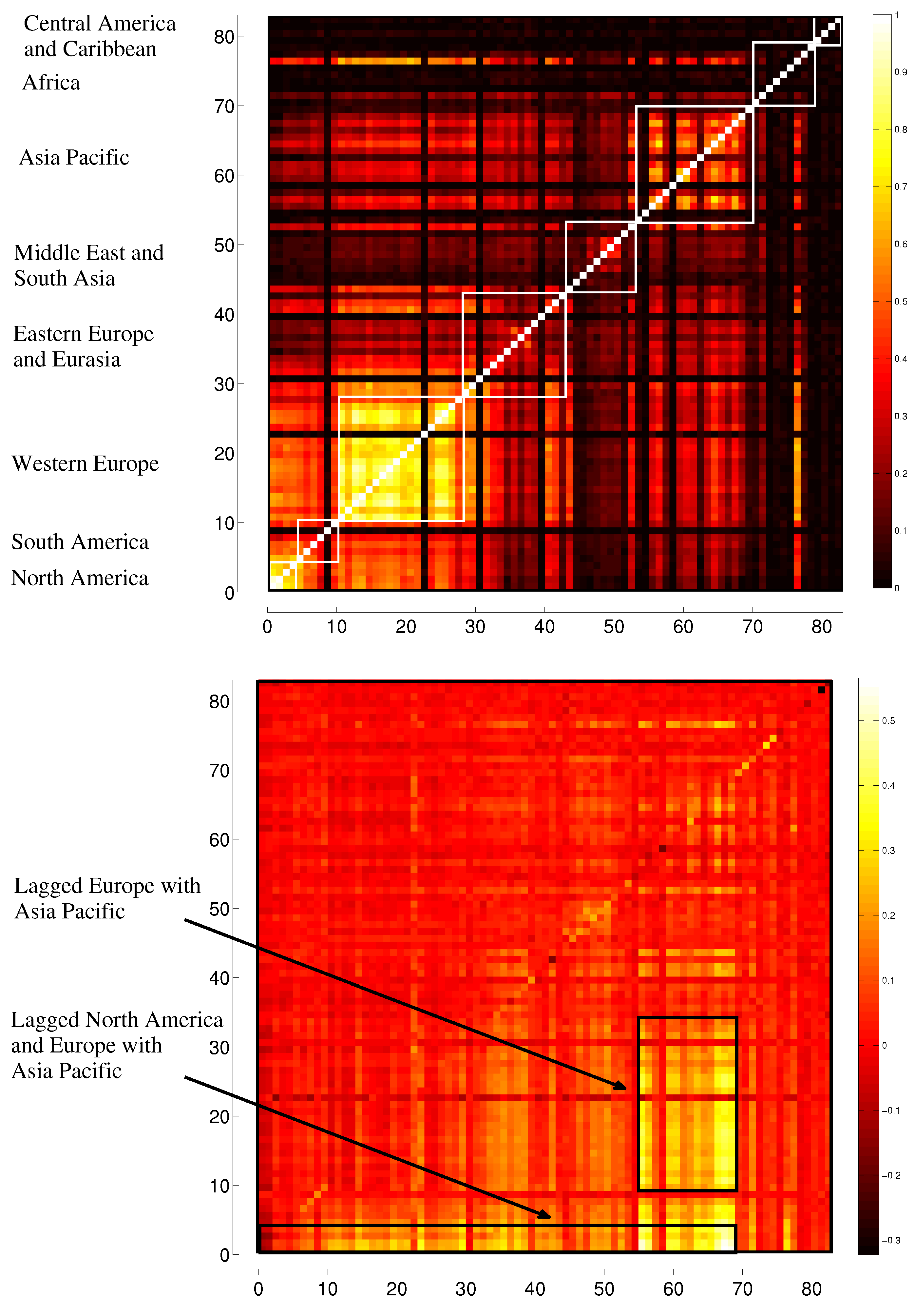
3.2. Transfer Entropy

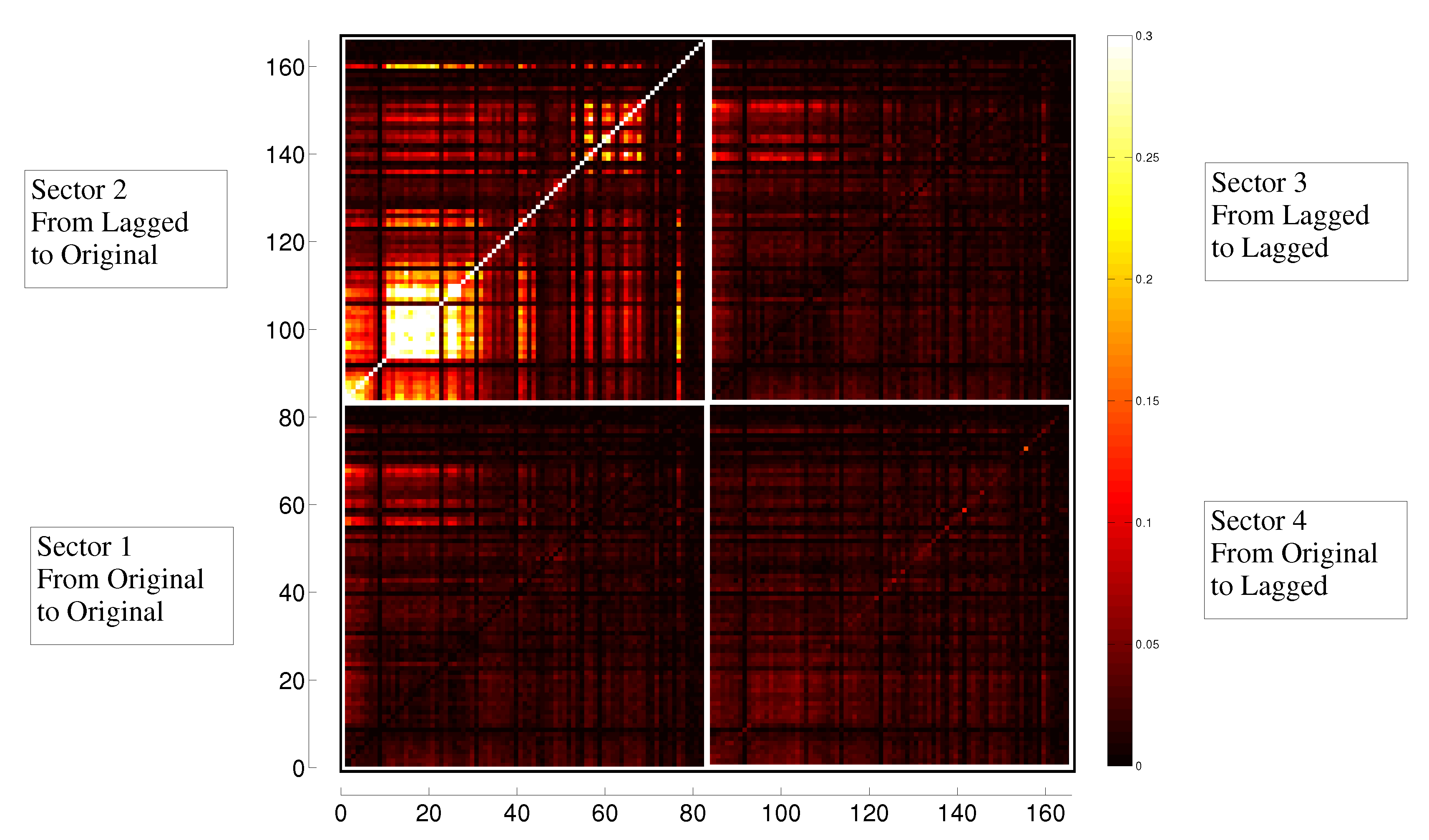

3.3. Evolution in Time
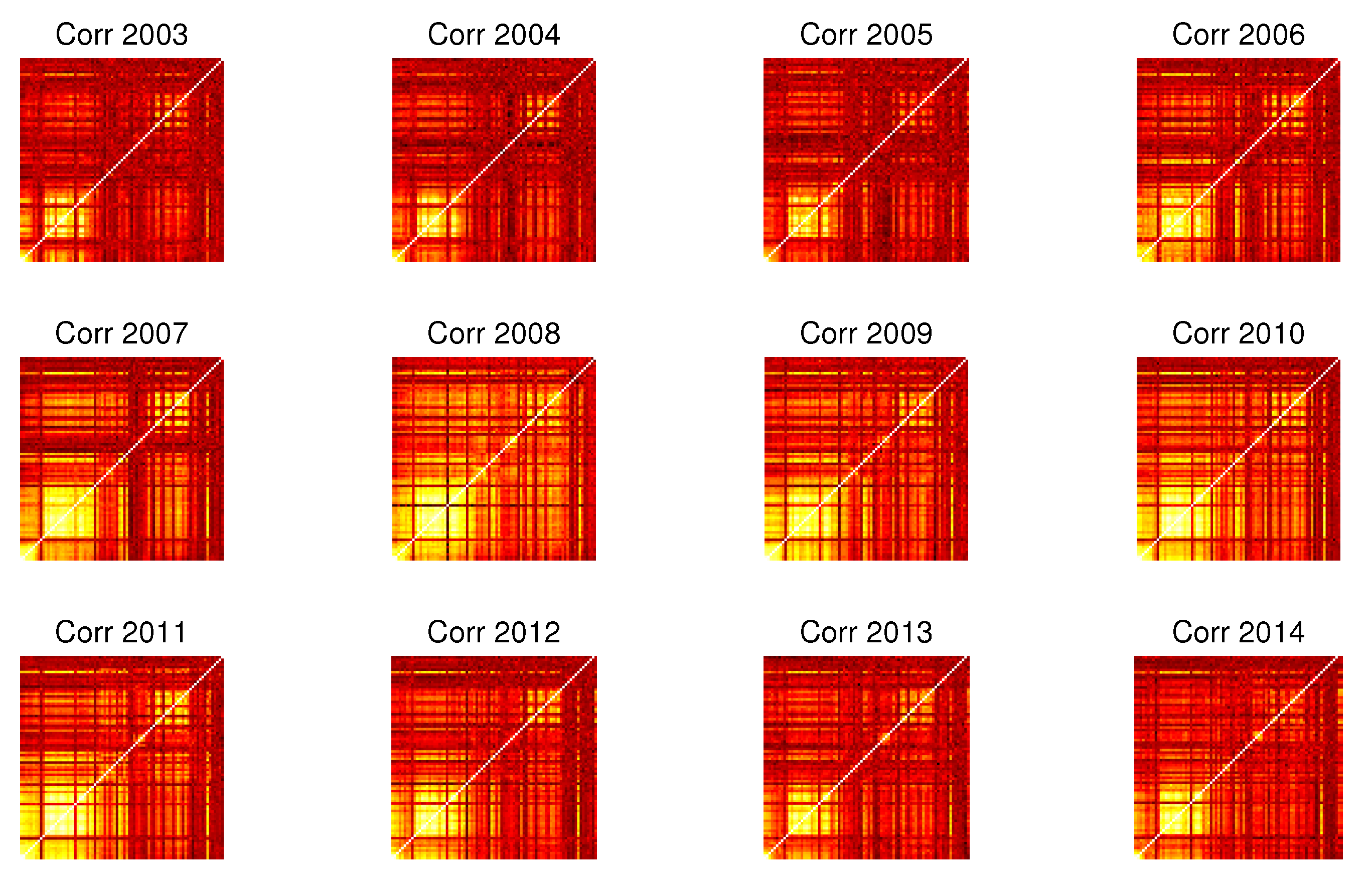
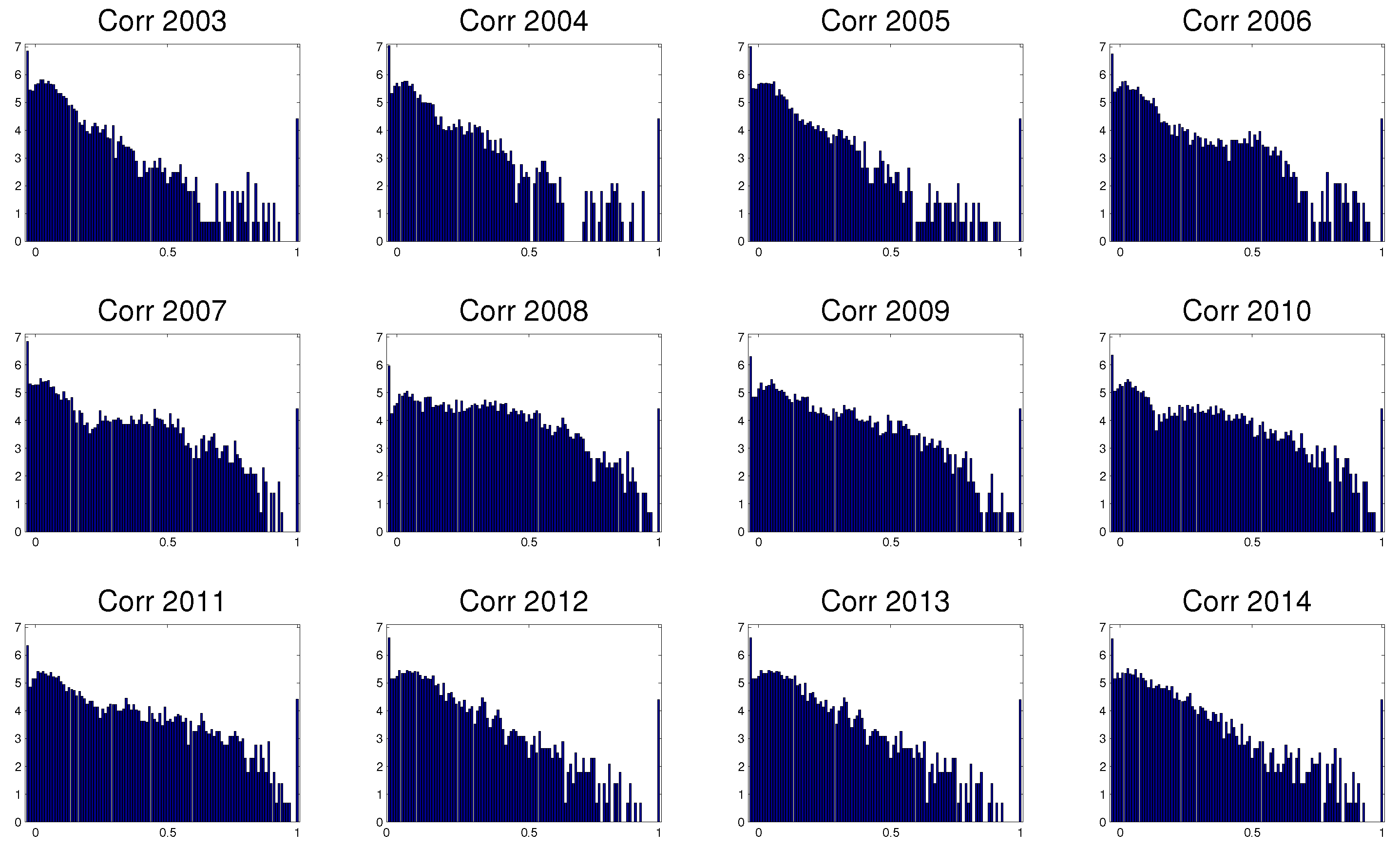
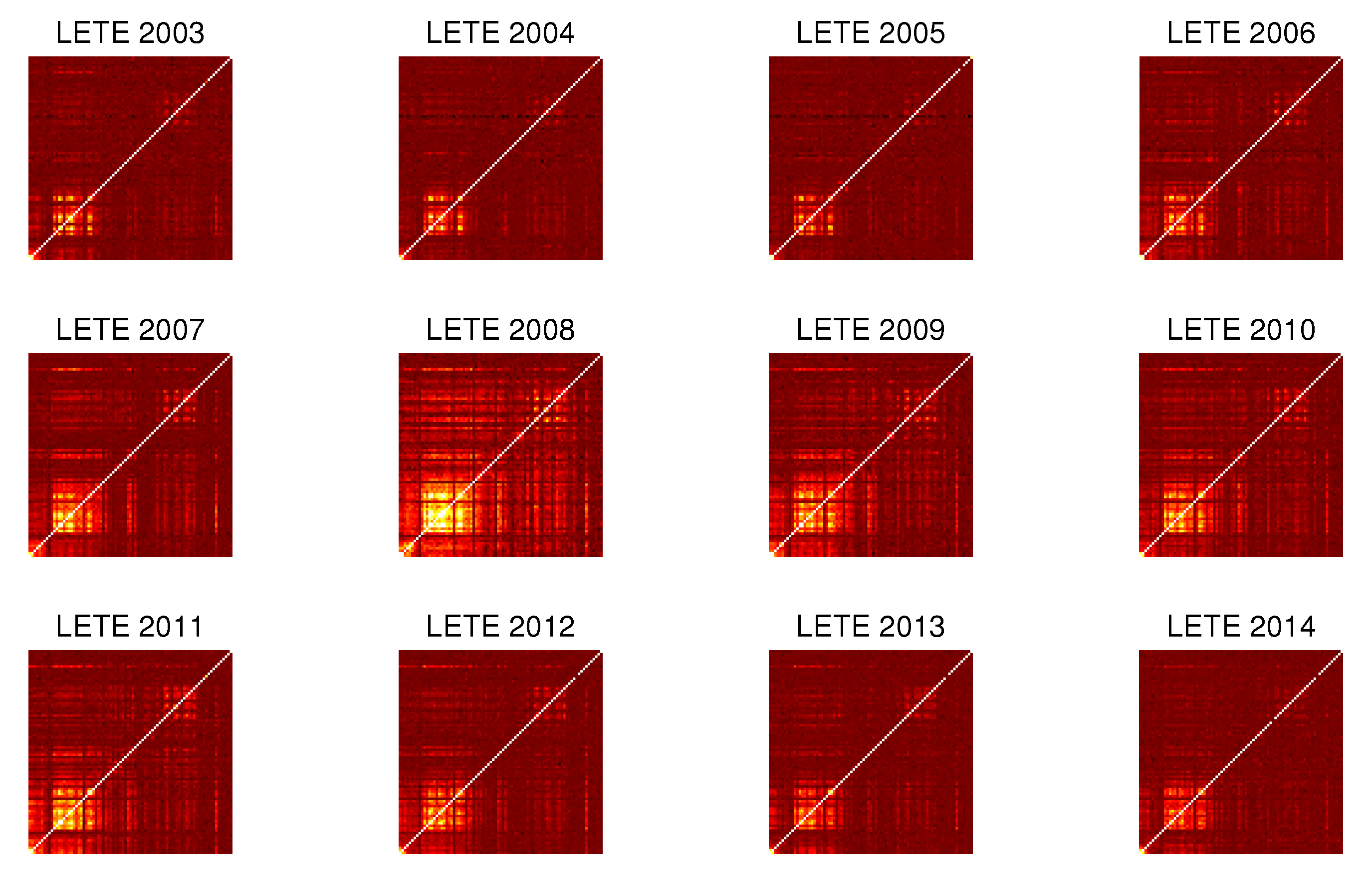

4. Dependency Networks and Node Influence

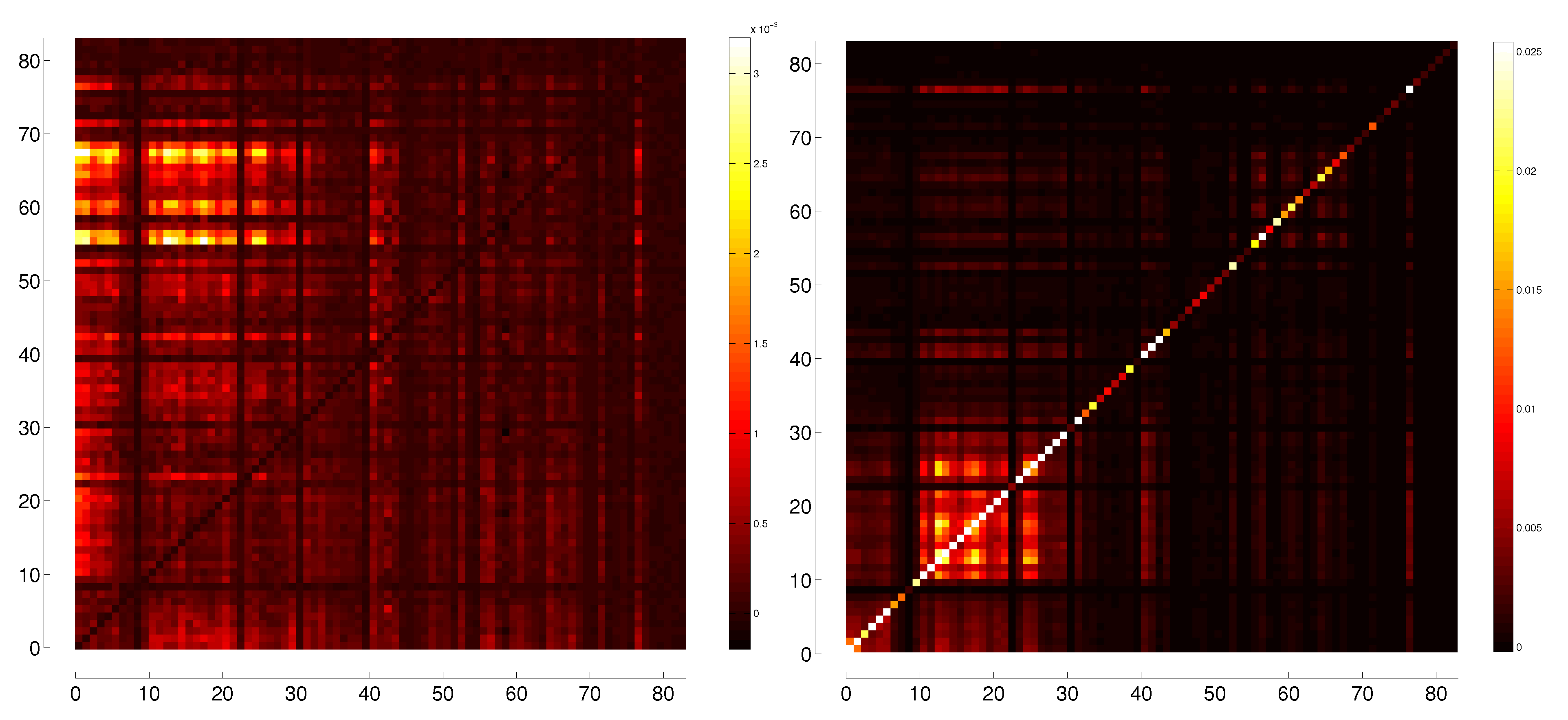
5. Representation of Correlation and Effective Transfer Entropy Dependency Networks

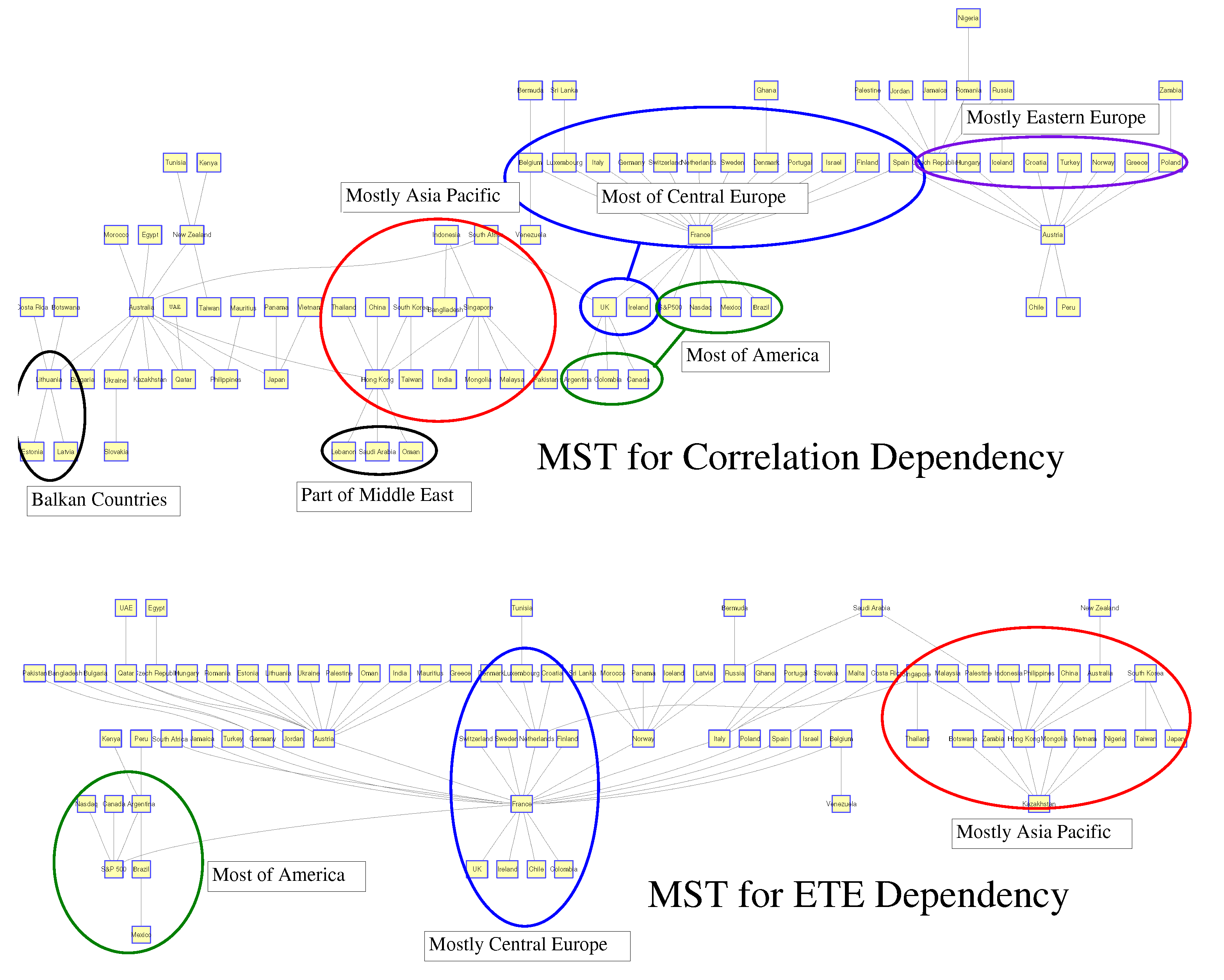
6. Centrality
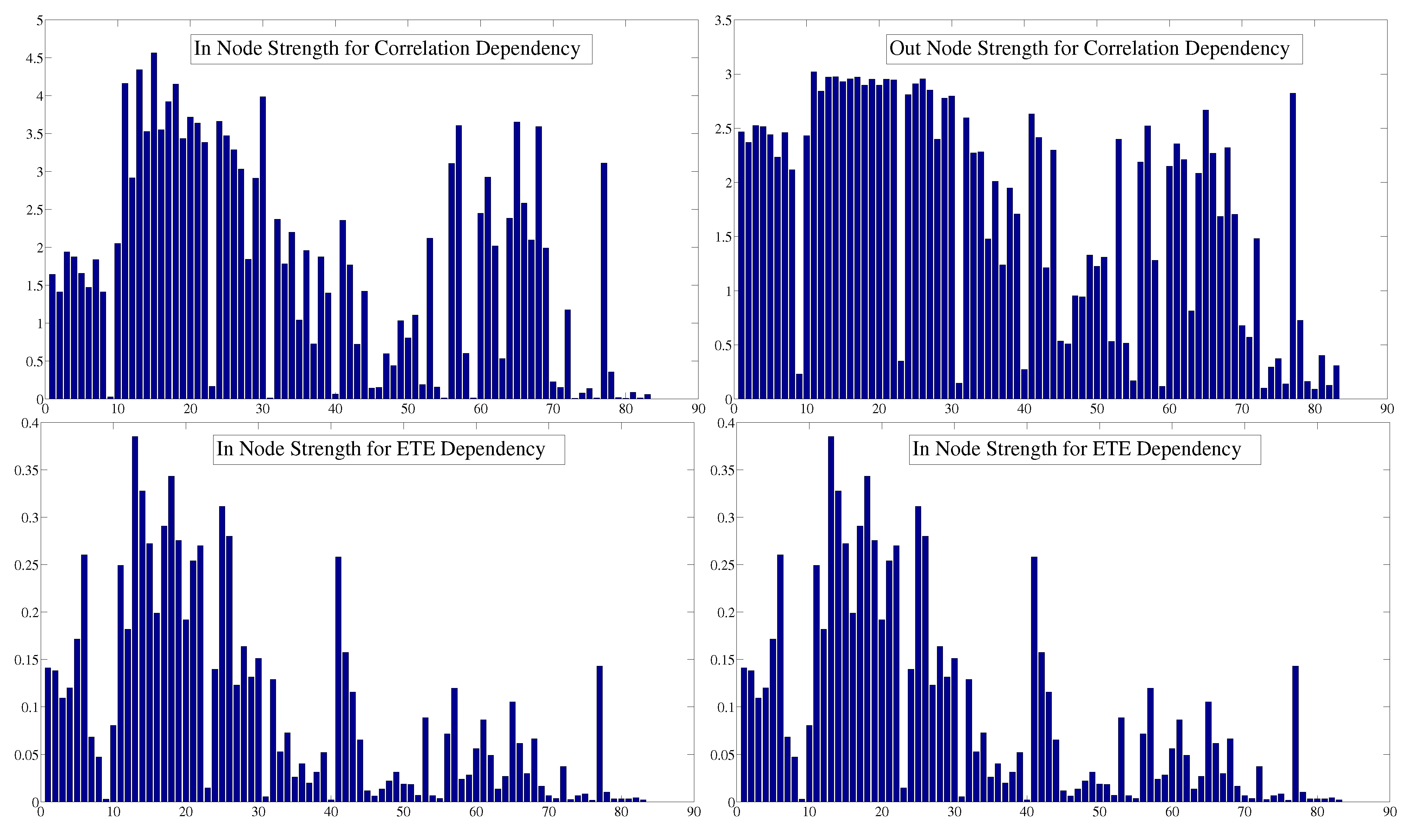
| Correlation Dependency | |||
|---|---|---|---|
| Index | In NS | Index | Out NS |
| Austria | 4.57 | UK | 3.02 |
| France | 4.35 | Germany | 2.98 |
| UK | 4.16 | France | 2.97 |
| Netherlands | 4.15 | Belgium | 2.97 |
| Czech Republic | 3.99 | Switzerland | 2.96 |
| Belgium | 3.93 | Spain | 2.96 |
| Denmark | 3.72 | Sweden | 2.95 |
| Luxembourg | 3.66 | Norway | 2.95 |
| Singapore | 3.66 | Finland | 2.95 |
| Norway | 3.63 | Austria | 2.93 |
| ETE Dependency | |||
|---|---|---|---|
| Index | In NS | Index | Out NS |
| France | 0.39 | France | 0.32 |
| Netherlands | 0.34 | Netherlands | 0.29 |
| Germany | 0.33 | Germany | 0.28 |
| Italy | 0.31 | Italy | 0.28 |
| Belgium | 0.29 | Spain | 0.26 |
| Spain | 0.28 | Belgium | 0.25 |
| Sweden | 0.28 | Sweden | 0.25 |
| Austria | 0.27 | Finland | 0.24 |
| Finland | 0.27 | UK | 0.23 |
| Argentina | 0.26 | Austria | 0.22 |
7. Dynamics
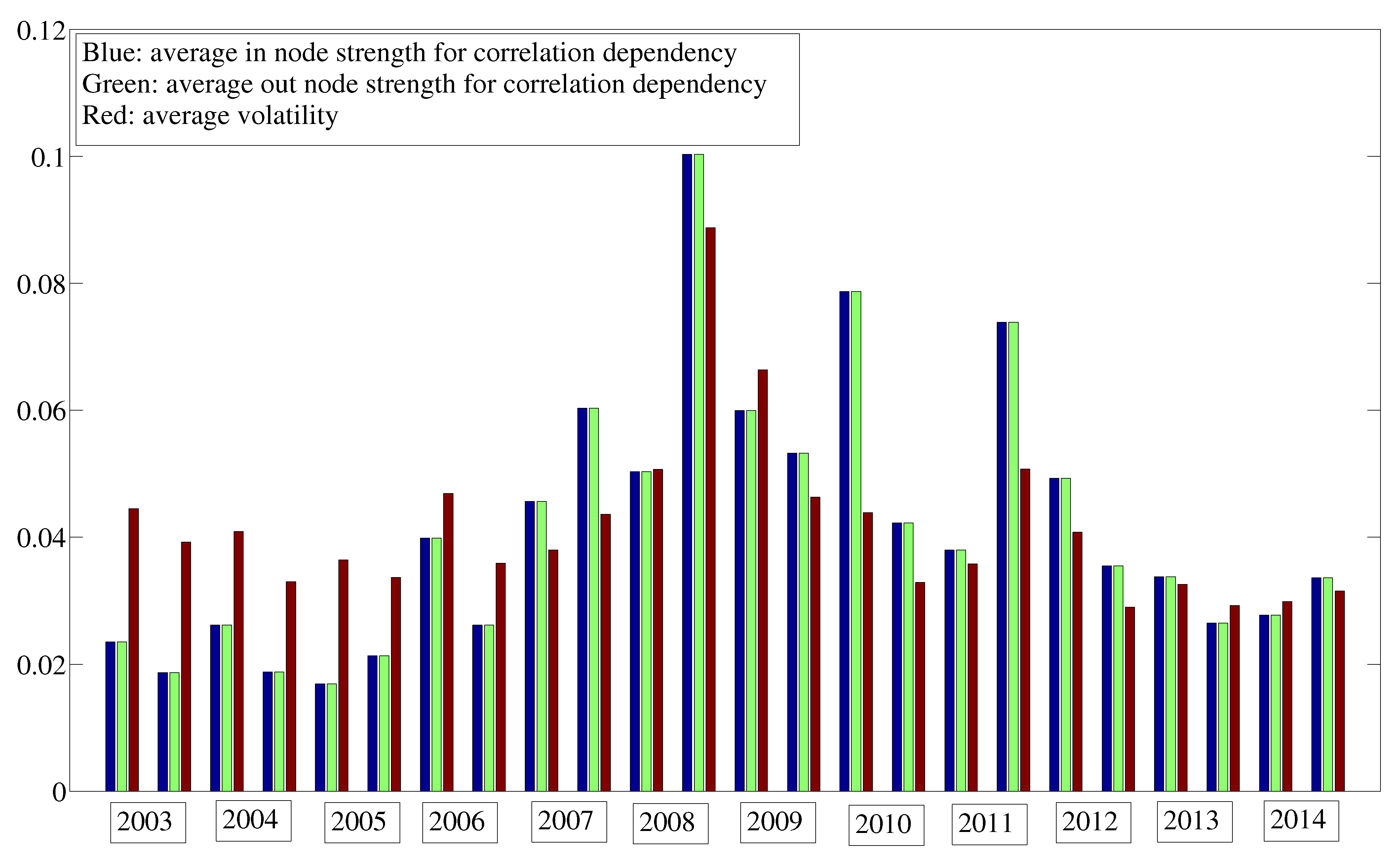


8. Dependencies for Volatility


| Mininum Value | Maximum Value | |
|---|---|---|
| Correlation of log-returns | –0.1143 | 1 (0.9485) |
| Correlation of volatility | –0.0890 | 1 (0.9236) |
| Lagged Correlation of log-returns | –0.3227 | 0.5657 |
| Lagged Correlation of volatility | –0.1106 | 0.4977 |
| ETE of log-returns | –0.0162 | 0.1691 |
| ETE of volatility | –0.0114 | 0.1899 |
| LETE of log-returns | 0.0040 | 2.0265 (0.7386) |
| LETE of volatility | –0.0105 | 1.4328 (0.4282) |
| Correlation Dependency of log-returns | 0 | 0.1454 |
| Correlation Dependency of volatility | 0 | 0.2774 |
| ETE Dependency of log-returns | –0.0002 | 0.1417 |
| ETE Dependency of volatility | 0 | 0.0064 |

8.1. Oil Producing Nations
| OIL PRODUCER | Most Influenced by | ||||
|---|---|---|---|---|---|
| Russia (Volatility Correlation) | Norway | Czech Republic | South Africa | Austria | UK |
| Russia (Volatility Dependence) | Norway | Czech Republic | Ukraine | Austria | South Africa |
| Saudi Arabia (Volatility Correlation) | Palestine | Oman | Indonesia | Qatar | Jordan |
| Saudi Arabia (Volatility Dependence) | Palestine | Indonesia | Russia | Canada | Qatar |
| USA (SP) (Volatility Correlation) | USA(Nas) | Canada | Mexico | Brazil | Germany |
| USA (SP) (Volatility Dependence) | USA(Nas) | Canada | Mexico | Germany | Brazil |
| USA (Nas) (Volatility Correlation) | USA(SP) | Canada | Mexico | Brazil | Germany |
| USA (Nas) (Volatility Dependence) | USA(SP) | Canada | Brazil | Germany | France |
| China (Volatility Correlation) | Hong Kong | Singapore | Taiwan | Australia | South Korea |
| China (Volatility Dependence) | Hong Kong | Taiwan | South Korea | Singapore | Vietnam |
| Canada (Volatility Correlation) | USA(SP) | USA(Nas) | Norway | Brazil | Mexico |
| Canada (Volatility Dependence) | USA(SP) | USA(Nas) | Brazil | Mexico | Argentina |
| UAE (Volatility Correlation) | Qatar | Oman | Jordan | Egypt | Czech Republic |
| UAE (Volatility Dependence) | Qatar | Oman | Palestine | Jordan | Saudi Arabia |
| Venezuela (Volatility Correlation) | Costa Rica | Colombia | Jamaica | Palestine | Chile |
| Venezuela (Volatility Dependence) | Colombia | Brazil | Argentina | Mongolia | Saudi Arabia |
| Mexico (Volatility Correlation) | USA(SP) | USA(Nas) | Brazil | Canada | UK |
| Mexico (Volatility Dependence) | Brazil | USA(SP) | USA(Nas) | Argentina | Norway |
| Brazil (Volatility Correlation) | USA(SP) | Mexico | USA(Nas) | Canada | Netherlands |
| Brazil (Volatility Dependence) | Mexico | Argentina | USA(Nas) | USA(SP) | Canada |
| Norway (Volatility Correlation) | UK | Netherlands | Sweden | France | Austria |
| Norway (Volatility Dependence) | Denmark | Austria | Sweden | Finland | Netherlands |
9. Conclusions
Acknowledgments
 , all figures were made using Matlab or PSTricks, and the calculations were made using Matlab and Excel. All data and codes used are freely available upon request on [email protected].
, all figures were made using Matlab or PSTricks, and the calculations were made using Matlab and Excel. All data and codes used are freely available upon request on [email protected].Author Contributions
A. Indices and Countries they Belong to
| Number | Country | Index |
| 1 | S& P 500 | S& P 500 Index |
| 2 | Nasdaq | Nasdaq Composite Index |
| 3 | Canada | S& P/TSX Composite Index |
| 4 | Mexico | Mexico Stock Exchange IPC Index |
| 5 | Brazil | Ivovespa São Paulo Stock Exchange Index |
| 6 | Argentina | Buenos Aires Stock Exchange Merval Index |
| 7 | Chile | Santiago Stock Exchange IPSA Index |
| 8 | Colombia | Indice IGBC |
| 9 | Venezuela | Caracas Stock Exchange Market Index |
| 10 | Peru | Bolsa de Valores de Lima General Sector Index |
| 11 | UK | FTSE 100 Index |
| 12 | Ireland | ISEQ Overall Index |
| 13 | France | CAC 40 Index |
| 14 | Germany | DAX Index |
| 15 | ATX | Austrian Traded Index |
| 16 | Switzerland | Swiss Market Index |
| 17 | Belgium | BEL 20 Index |
| 18 | Netherlands | AEX Index |
| 19 | Sweden | OMX Stockholm 30 Index |
| 20 | KFX | OMX Copenhagen 20 Index |
| 21 | Norway | OBX Oslo Index |
| 22 | Finland | OMX Helsinki All-Share Index |
| 23 | Iceland | OMX Iceland All-Share Index |
| 24 | Luxembourg | Luxembourg LuxX Index |
| 25 | Italy | FTSE MIB |
| 26 | Spain | IBEX 35 Index |
| 27 | Portugal | Portugal PSI 20 Index |
| 28 | Greece | Athens Stock Exchange General Index |
| 29 | Poland | Warsaw Stock Exchange WIG Index |
| 30 | Czech Republic | PX Index |
| 31 | Slovakia | Slovak Share Index |
| 32 | Hungary | Budapest Stock Exchange Index |
| 33 | Croatia | CROBEX |
| 34 | Romania | Bucharest Exchange Trading Index |
| 35 | Bulgaria | Bulgaria Stock Exchange Sofix Index |
| 36 | Estonia | OMX Tallinn |
| 37 | Latvia | OMX Riga |
| 38 | Lithuania | OMX Vilnius |
| 39 | Ukraine | Ukraine PFTS Index |
| 40 | Malta | Malta Stock Exchange Index |
| 41 | Russia | MICEX Index |
| 42 | Turkey | Borsa Istambul 100 |
| 43 | Kazakhstan | Kazakhstan Stock Exchange Index KASE |
| 44 | Israel | Tel Aviv 25 Index |
| 45 | Palestine | Palestine Al Quda Index |
| 46 | Lebanon | BLOM Stock Index |
| 47 | Jordan | ASE General Index |
| 48 | Saudi Arabia | Tadawul All Share Index |
| 49 | Qatar | QE Index |
| 50 | United Arab Emirates | ADX General Index |
| 51 | Oman | MSM Index |
| 52 | Pakistan | Karachi Stock Exchange KSE100 Index |
| 53 | India | S& P BSE Sensex Index |
| 54 | Sri Lanka | Sri Lanka Stock Market Colombo All-Share Index |
| 55 | Bangladesh | DSE General Index |
| 56 | Japan | Nikkei-225 Stock Average |
| 57 | Hong Kong | Hang Seng Index |
| 58 | China | Shanghai Stock Exchange Composite Index |
| 59 | Mongolia | MSE Top 20 Index |
| 60 | Taiwan | TWSE |
| 61 | South Korea | KOSPI Index |
| 62 | Thailand | Bangkok SET Index |
| 63 | Vietnam | Vietnam Stock Index |
| 64 | Malaysia | FTSE Bursa Malaysia KLCI Index |
| 65 | Singapore | Straits Times Index |
| 66 | Indonesia | Jakarta Stock Price Index |
| 67 | Philippnies | Philippine Stock Exchange PSEi Index |
| 68 | Australia | S& P/ASX 200 |
| 69 | New Zealand | New Zealand Exchange 50 Gross Index |
| 70 | Morocco | CFG 25 |
| 71 | Tunisia | Tunis Stock Exchange TUNINDEX |
| 72 | Egypt | EGX 30 Index |
| 73 | Ghana | GSE Composite Index |
| 74 | Nigeria | Nigerian Stock Exchange All Share Index |
| 75 | Kenya | Nairobi Securities Exchange Ltd 20 Share Index |
| 76 | Botswana | Botswana Domestic Companies Gaborone Index |
| 77 | South Africa | FTSE/JSE Africa All Shares Index |
| 78 | Mauritius | SEMDEX Index |
| 79 | Zambia | Lusaka Stock Exchange All Share Index |
| 80 | Bermuda | Bermuda Stock Exchange Index |
| 81 | Jamaica | Jamaica Stock Exchange Market Index |
| 82 | Costa Rica | BCT Corp Costa Rica Stock Market Index |
| 83 | Panama | Bolsa de Valores de Panama General Index |
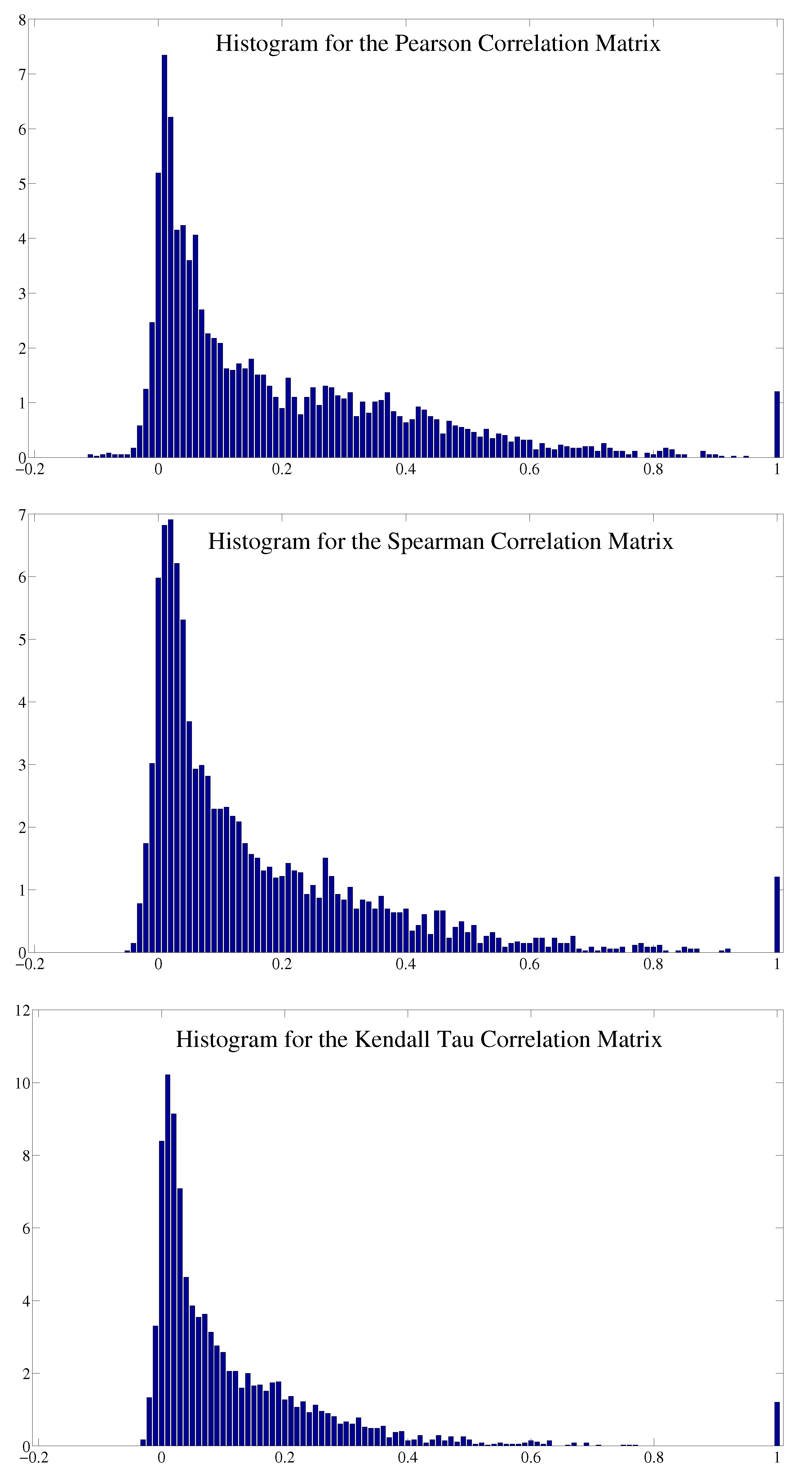
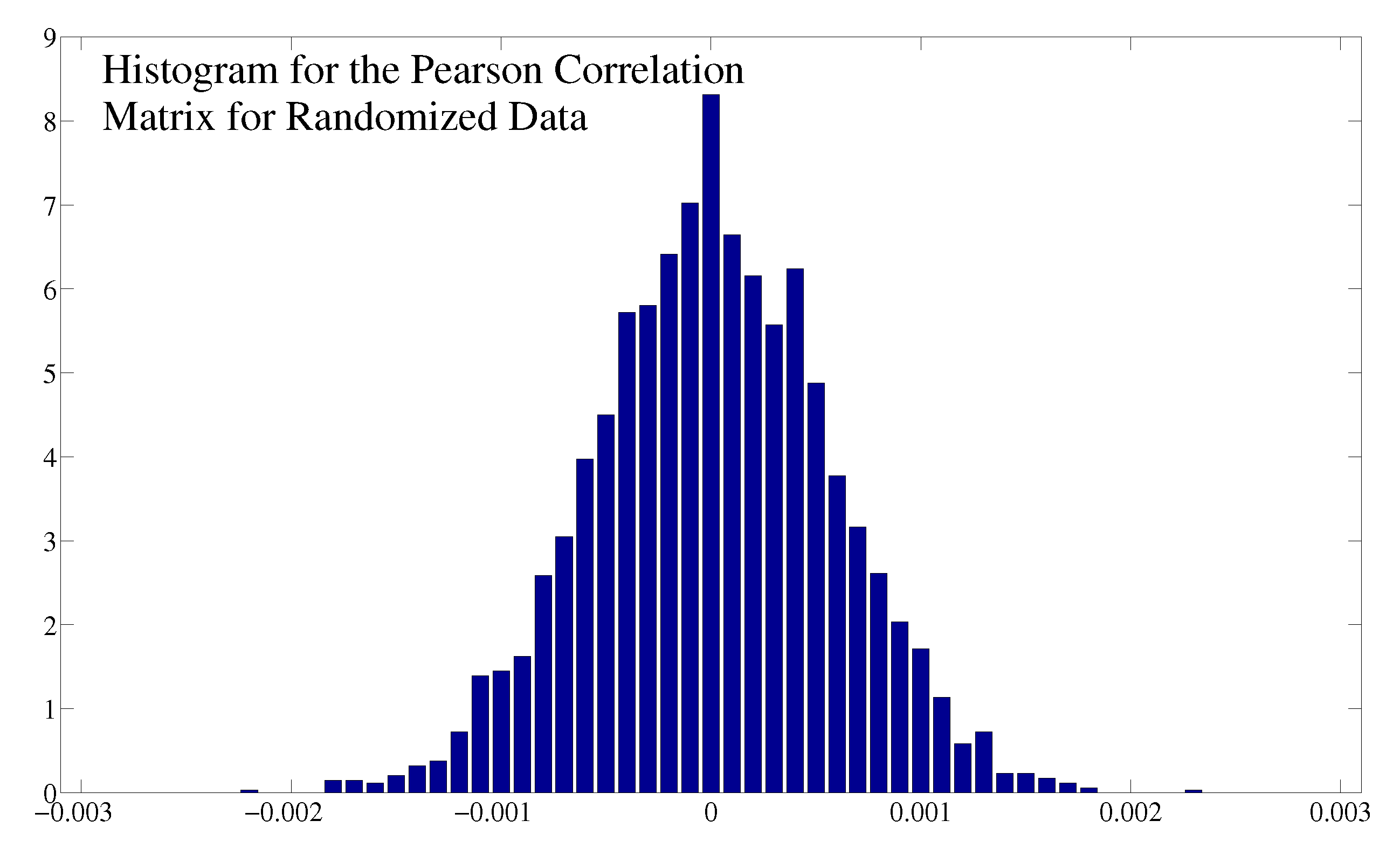
B. Comparison between Different Correlation Measures
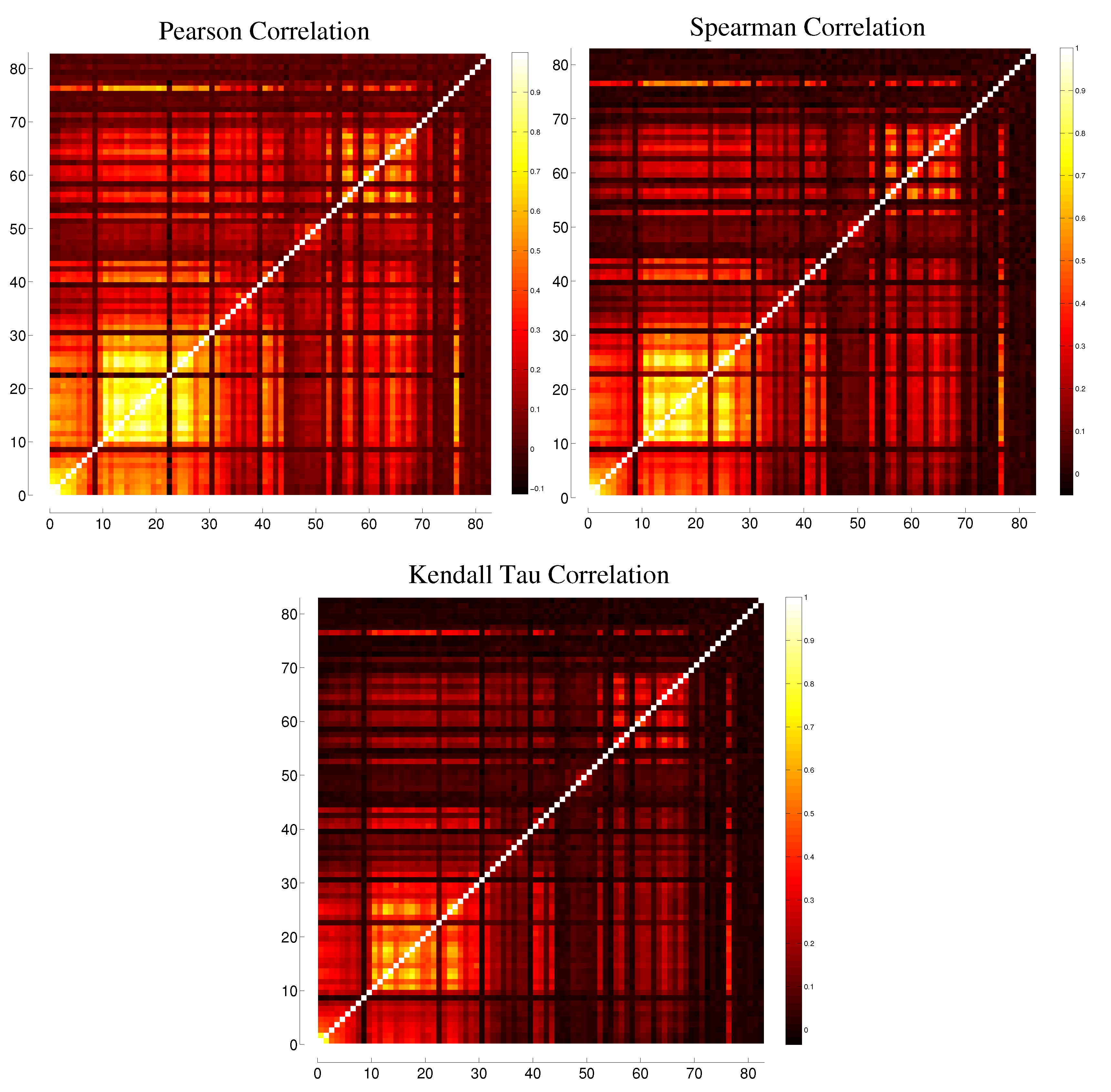
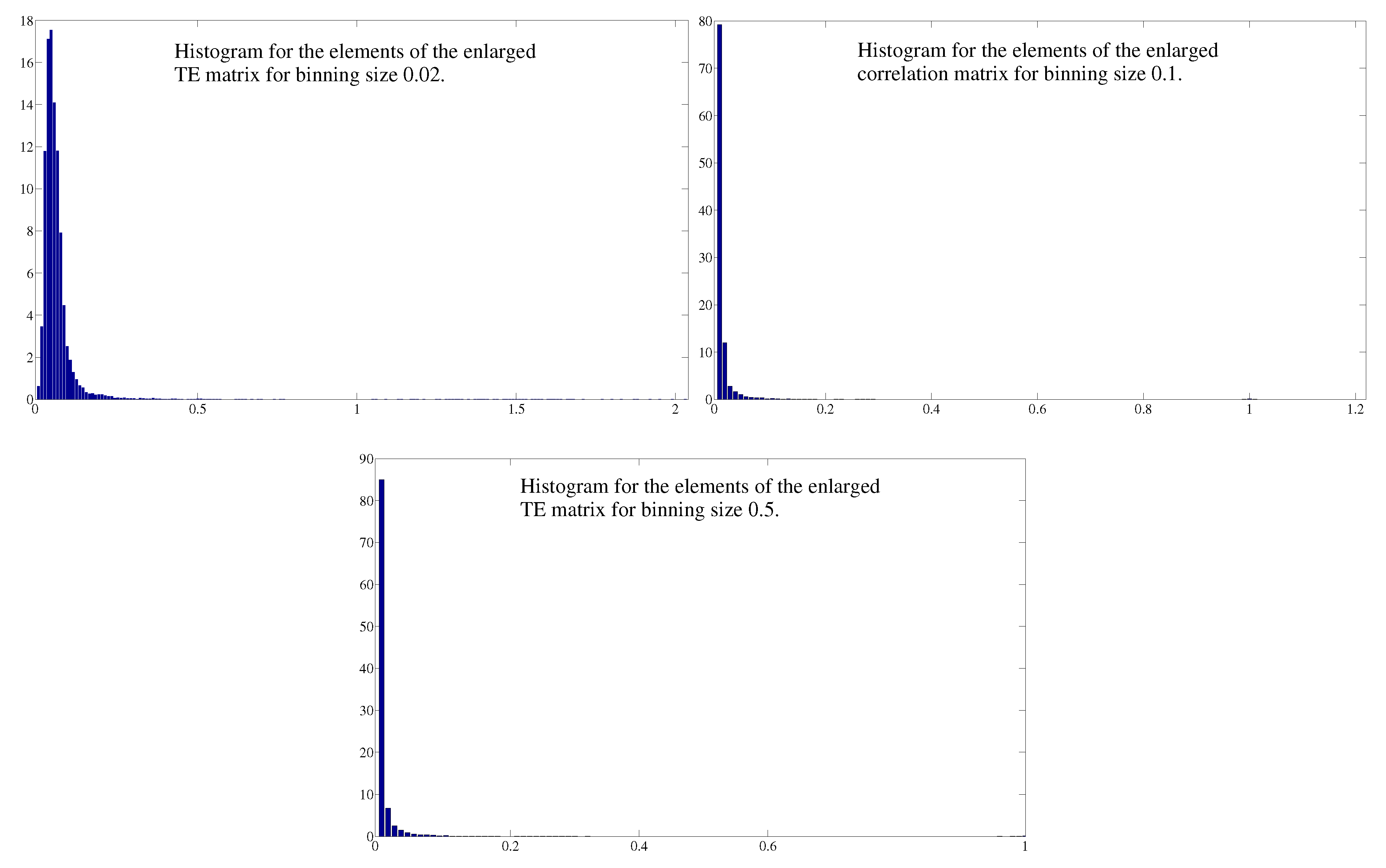
C. Comparison between Different Binnings for Transfer Entropy

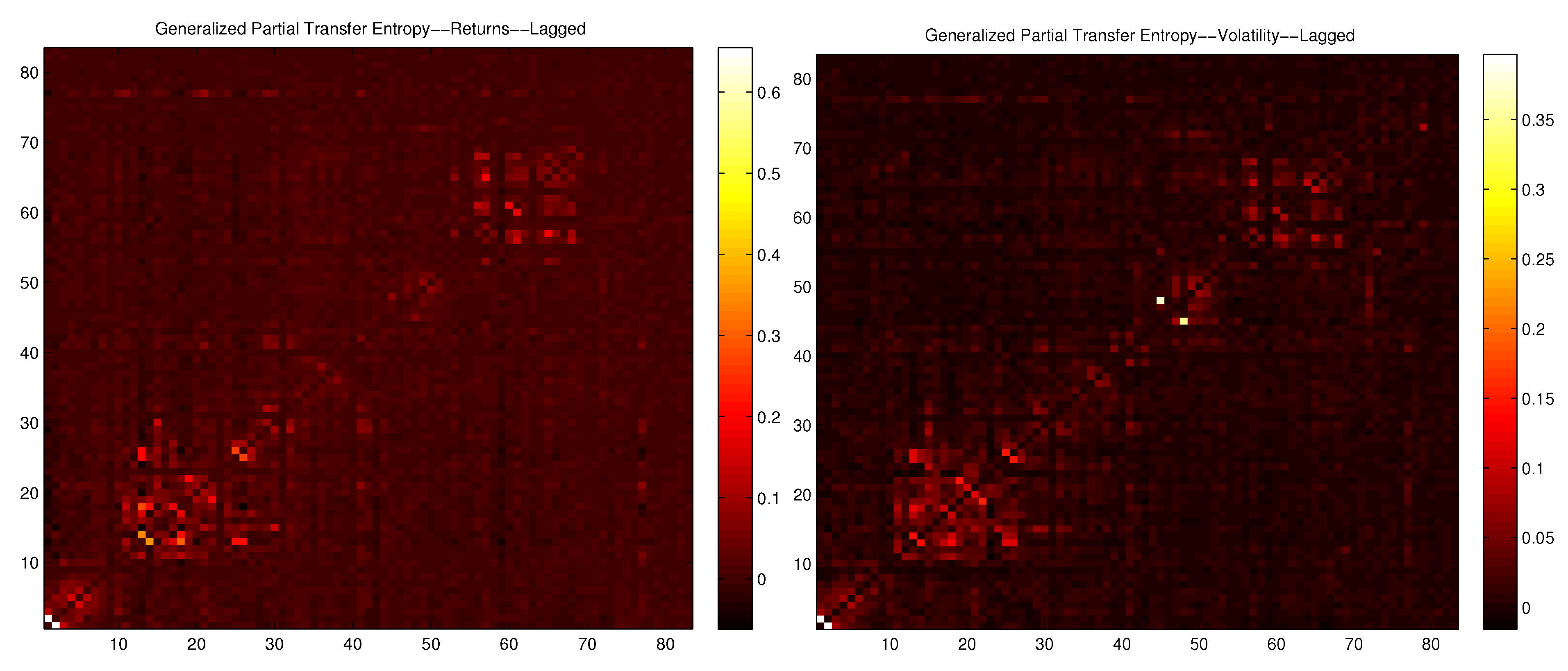
D. Partial Lagged ETE and Generalized Partial Lagged ETE
Conflicts of Interest
References
- F. Allen, and D. Gale. “Financial contagion.” J. Polit. Econ. 108 (2000): 1–33. [Google Scholar] [CrossRef]
- L. Sandoval Jr. “Structure of a Global Network of Financial Companies based on Transfer Entropy.” Entropy 16 (2014): 4443–4482. [Google Scholar] [CrossRef]
- L. Sandoval Jr., and I.D.P. Franca. “Correlation of financial markets in times of crisis.” Phys. A 391 (2012): 187–208. [Google Scholar]
- L. Sandoval Jr. “To lag or not to lag? How to compare indices of stock markets that operate at different times.” Phys. A 403 (2014): 227–243. [Google Scholar]
- D.Y. Kenett, M. Tumminello, A. Madi, G. Gur-Gershgoren, R.N. Mantegna, and E. Ben-Jacob. “Dominating clasp of the financial sector revealed by partial correlation analysis of the stock market.” PLoS ONE 5 (2010): e15032. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- T. Schreiber. “Measuring information transfer.” Phys. Rev. Lett. 85 (2000): 461–464. [Google Scholar] [CrossRef] [PubMed]
- C.W.J. Granger. “Investigating Causal Relations by Econometric Models and Cross-spectral Methods.” Econometrica 37 (1969): 424–438. [Google Scholar] [CrossRef]
- L. Barnett. “Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables.” Phys. Rev. Lett. 103 (2009): 238701. [Google Scholar] [CrossRef] [PubMed]
- R. Marschinski, and H. Kantz. “Analysing the information flow between financial time series-an improved estimator for Transfer Entropy.” Eur. Phys. J. B 30 (2002): 275–281. [Google Scholar] [CrossRef]
- S.K. Baek, W.-S. Jung, O. Kwon, and H.-T. Moon. “Transfer Entropy Analysis of the Stock Market.” 2005. ArXiv:physics/0509014v2. Available online: http://arxiv.org/abs/physics/0509014 (accessed on 27 May 2015).
- O. Kwon, and J.-S. Yang. “Information flow between composite stock index and individual stocks.” Phys. A 387 (2008): 2851–2856. [Google Scholar] [CrossRef]
- O. Kwon, and J.-S. Yang. “Information flow between stock indices.” Eur. Phys. Lett. 82 (2008): 68003. [Google Scholar] [CrossRef]
- Y.V. Reddy, and A. Sebastin. “Interaction Between Forex and Stock Markets in India: An Entropy Approach.” VIKALPA 33 (2008): 27–45. [Google Scholar]
- P. Jizba, H. Kleinert, and M. Shefaat. “Renyi’s information transfer between financial time series.” Phys. A 391 (2012): 2971–2989. [Google Scholar] [CrossRef]
- F.J. Peter, T. Dimpfl, and L. Huergo. “Using Transfer Entropy to measure information flows from and to the CDS market.” Midwest Finance Association 2012 Annual Meetings Paper. Available online: http://ssrn.com/abstract=1683948 or http://dx.doi.org/10.2139/ssrn.1683948 (accessed on 27 May 2015).
- T. Dimpfl, and F.J. Peter. “Using Transfer Entropy to measure information flows between financial markets.” Stud. Nonlinear Dyn. Econ. 17 (2012): 85–102. [Google Scholar] [CrossRef]
- J. Kim, G. Kim, S. An, Y.-K. Kwon, and S. Yoon. “Entropy-based analysis and bioinformatics-inspired integration of global economic information transfer.” PLoS ONE 8 (2013): e51986. [Google Scholar] [CrossRef] [PubMed]
- J. Li, C. Liang, X. Zhu, X. Sun, and D. Wu. “Risk contagion in Chinese banking industry: A Transfer Entropy-based analysis.” Entropy 15 (2013): 5549–5564. [Google Scholar] [CrossRef]
- T. Dimpfl, and F.J. Peter. “The impact of the financial crisis on transatlantic information flows: An intraday analysis.” J. Int. Financ. Mark. Inst. Money 31 (2014): 1–13. [Google Scholar] [CrossRef]
- A. Şensoy, C. Sobaci, S. Şensoy, and F. Alali. “Effective Transfer Entropy Approach To Information Flow Between Exchange Rates And Stock Markets.” Chaos Solitons Fractals 68 (2014): 180–185. [Google Scholar] [CrossRef]
- Y. Shapira, D.Y. Kenett, and E. Ben-Jacob. “The index cohesive effect on stock market correlations.” Eur. Phys. J. B-Condens. Matter Complex Syst. 72 (2009): 657–669. [Google Scholar] [CrossRef]
- D.Y. Kenett, M. Raddant, L. Zatlavi, T. Lux, and E. Ben-Jacob. “Correlations and Dependencies in the global financial village.” Int. J. Mod. Phys. Conf. Ser. 16 (2012): 13–28. [Google Scholar] [CrossRef]
- D.Y. Kenett, T. Preis, G. Gur-Gershgoren, and E. Ben-Jacob. “Dependency network and node influence: Application to the study of financial markets.” Int. J. Bifurc. Chaos 22 (2012): 1250181. [Google Scholar] [CrossRef]
- A. Madi, D.Y. Kenett, S. Bransburg-Zabary, Y. Merbl, F.J. Quintana, S. Boccaletti, and E. Ben-Jacob. “Analyses of antigen dependency networks unveil immune system reorganization between birth and adulthood.” Chaos Interdiscip. J. Nonlinear Sci. 21 (2011): 016109. [Google Scholar] [CrossRef] [PubMed]
- Y.N. Kenett, D.Y. Kenett, E. Ben-Jacob, and M. Faust. “Global and local features of semantic networks: Evidence from the Hebrew mental lexicon.” PLoS ONE 6 (2011): e23912. [Google Scholar] [CrossRef] [PubMed]
- D.A. Dickey, and W.A. Fuller. “Distribution of the Estimators for Autoregressive Time Series with a Unit Root.” J. Am. Stat. Assoc. 74 (1979): 427–431. [Google Scholar]
- P. Phillips, and P. Perron. “Testing for a Unit Root in Time Series Regression.” Biometrika 75 (1998): 335–346. [Google Scholar] [CrossRef]
- D. Kwiatkowski, P.C.B. Phillips, P. Schmidt, and Y. Shin. “Testing the Null Hypothesis of Stationarity against the Alternative of a Unit Root.” J. Econ. 54 (1992): 159–178. [Google Scholar] [CrossRef]
- J. Cochrane. “How Big is the Random Walk in GNP? ” J. Polit. Econ. 96 (1988): 893–920. [Google Scholar] [CrossRef]
- A.W. Lo, and A.C. MacKinlay. “Stock Market Prices Do Not Follow Random Walks: Evidence from a Simple Specification Test.” Rev. Financ. Stud. 1 (1988): 41–66. [Google Scholar] [CrossRef]
- A.W. Lo, and A.C. MacKinlay. “The Size and Power of the Variance Ratio Test.” J. Econ. 40 (1989): 203–238. [Google Scholar] [CrossRef]
- C.E. Shannon. “A mathematical theory of communication.” ACM SIGMOBILE Mob. Comput. Commun. Rev. 5 (2001): 3–55. [Google Scholar] [CrossRef]
- M. Wibral, N. Pampu, V. Priesemann, F. Siebenhühner, H. Seiwert, M. Lindner, J.T. Lizier, and R. Vicente. “Measuring Information-Transfer Delays.” PLoS ONE 8 (2013): e55809+. [Google Scholar] [CrossRef] [PubMed]
- J.T. Lizier. “JIDT: An information-theoretic toolkit for studying the dynamics of complex systems.” Front. Robot. AI 1 (2014): 11. [Google Scholar] [CrossRef]
- L. Sandoval Jr. “Cluster formation and evolution in networks of financial market indices.” Algorithm. Financ. 2 (2013): 3–43. [Google Scholar]
- I. Borg, and P. Groenen. Modern Multidimensional Scaling: Theory and Applications, 2nd ed. New York, NY: Springer, 2005. [Google Scholar]
- R.N. Mantegna. “Hierarchical structure in financial markets.” Eur. Phys. J. B 11 (1999): 193. [Google Scholar] [CrossRef]
- T.J. Flavin, M.J. Hurley, and F. Rousseau. “Explaining stock market correlation: A gravity model approach.” Manch. Sch. 70 (2002): 87–106. [Google Scholar] [CrossRef]
- G. Bonanno, G. Caldarelli, F. Lillo, S. Miccichè, N. Vandewalle, and R.N. Mantegna. “Networks of equities in financial markets.” Eur. Phys. J. B 38 (2004): 363–371. [Google Scholar] [CrossRef]
- Y.W. Goo, T.W. Lian, W.G. Ong, W.T. Choi, and S.A. Cheong. “Financial atoms and molecules.” 2009. ArXiv:0903.2009v1. Available online: http://arxiv.org/abs/0903.2099 (accessed on 27 May 2015).
- R. Coelho, C.G. Gilmore, B. Lucey, P. Richmond, and S. Hutzler. “The evolution of interdependence in world equity markets-evidence from minimum spanning trees.” Phys. A 376 (2007): 455–466. [Google Scholar] [CrossRef]
- C. Eom, G. Oh, W.-S. Jung, H. Jeong, and S. Kim. “Topological properties of stock networks based on minimal spanning tree and random matrix theory in financial time series.” Phys. A 388 (2009): 900–906. [Google Scholar] [CrossRef]
- M. Eryiǧit, and R. Eryiǧit. “Network structure of cross-correlations among the world market indices.” Phys. A 388 (2009): 3551–3562. [Google Scholar] [CrossRef]
- D.-M. Song, M. Tumminello, W.-X. Zhou, and R.N. Mantegna. “Evolution of worldwide stock markets, correlation structure and correlation based graphs.” Phys. Rev. E 84 (2011): 026108. [Google Scholar] [CrossRef]
- L. Sandoval Jr. “Prunning a Minimum Spanning Tree.” Phys. A 391 (2012): 2678–2711. [Google Scholar] [CrossRef]
- M.E.J. Newman. Networks, and Introduction. Oxford, United Kingdom: Oxford University Press, 2010. [Google Scholar]
- R.N. Mantegna, and H.E. Stanley. Introduction to Econophysics: Correlations and Complexity in Finance. Cambridge, United Kingdom: Cambridge University Press, 2005. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Junior, L.S.; Mullokandov, A.; Kenett, D.Y. Dependency Relations among International Stock Market Indices. J. Risk Financial Manag. 2015, 8, 227-265. https://doi.org/10.3390/jrfm8020227
Junior LS, Mullokandov A, Kenett DY. Dependency Relations among International Stock Market Indices. Journal of Risk and Financial Management. 2015; 8(2):227-265. https://doi.org/10.3390/jrfm8020227
Chicago/Turabian StyleJunior, Leonidas Sandoval, Asher Mullokandov, and Dror Y. Kenett. 2015. "Dependency Relations among International Stock Market Indices" Journal of Risk and Financial Management 8, no. 2: 227-265. https://doi.org/10.3390/jrfm8020227





