2.1. Soil Sampling and Analysis
To investigate the pollution status of heavy metals in Beijing agricultural areas, a large-scale soil sampling project was conducted after the crop harvest in the autumn of 2006. According to the agricultural land distribution and land use type maps of Beijing, a non-uniform distribution of the stratified sampling technique was adopted to collect samples and ensure the representativeness of samples. The sampling strategy was divided into three steps to collect a total of 1,018 samples. First, 231 soil samples were collected from the entire study area, with uniform sampling being the low sampling density (C). Secondly, another 360 soil samples were added from areas with more agricultural soils to create the medium sampling density (M). Third, 427 soil samples were further collected on the basis of the two previous samplings and the agricultural soils to make a high sampling density (F).
Figure 1 shows the distribution of soil samples at the three sampling densities.
Figure 1.
The distribution of soil samples at three levels.
Figure 1.
The distribution of soil samples at three levels.
For each sample, five surface soil (0~20 cm) sites were sampled within 10 × 10 m square areas and then mixed. A Global Positioning System was used to precisely locate each sampling position (latitude and longitude); and a total of 1 kg of mixed soil per sample was collected. All soil samples were collected using a stainless steel spade and a scoop made from bamboo and then stored in polyethylene bags. The soil samples were air-dried, crushed in an agate mortar, and then passed through a 100-mesh nylon sieve. The concentrations of eight heavy metals, including Cr, Ni, Cu, Zn, As, Cd, Pb, and Hg, were analyzed in the soil samples following the Chinese Environmental Quality Standard for Soils (GB15618-1995). After digesting the samples with a mixture of HCl, HNO3 and HClO4, the Cr, Ni, Cu, and Zn concentrations were analyzed by flame atomic absorption spectrophotometry, Pb and Cd were analyzed by graphite furnace atomic absorption spectrophotometry, and the As concentration was determined by potassium borohydride-silver nitrate spectrophotometry. In addition, the Hg concentration was analyzed by cold atomic absorption spectrophotometry after the samples were digested with a mixture of H2SO4, HNO3 and KMnO4. During processing, all samples were handled carefully to avoid input or loss of trace elements during preparation and analysis.
2.2. Spatial Autocorrelation
Spatial autocorrelation is an assessment of the correlation of a variable in reference to spatial location of the variable, which is a match between location similarity and attribute similarity [
13]. Moran’s I is the more popular test statistic for spatial autocorrelation. Global Moran’s I examines whether spatial correlation exists or not over an entire region, and it is calculated as follow as [
14]:
where
![Ijerph 09 00995 i003]()
is the number of observations of the whole region,
![Ijerph 09 00995 i004]()
and
![Ijerph 09 00995 i005]()
are the observations at locations of
![Ijerph 09 00995 i006]()
and
![Ijerph 09 00995 i007]()
,
![Ijerph 09 00995 i008]()
is the mean of
![Ijerph 09 00995 i009]()
, and
![Ijerph 09 00995 i010]()
, an element of spatial weights matrix
![Ijerph 09 00995 i011]()
, is the spatial weight between locations of
![Ijerph 09 00995 i006]()
and
![Ijerph 09 00995 i007]()
. The value of Moran’s I generally varies between 1 and −1. Positive autocorrelation in the data translates into positive values of Moran’s I; negative autocorrelation produces negative values. No autocorrelation results in a value close to 0 [
11].
The selection of neighbors is formally specified in the weights matrix
![Ijerph 09 00995 i011]()
, which depicts the relationship between an element and its surrounding elements. A distance-based weight matrix was adopted in this study, and each distance class is specified as a threshold distance, such that all locations within the given distance are considered to be “neighbors” (the value not equal to zero in the matrix) in the distance-based weight matrix. Usually, normal approximation as a precondition, global Moran’s I can be standardized to
![Ijerph 09 00995 i012]()
, and
![Ijerph 09 00995 i012]()
is calculated as [
14,
15]:
where
![Ijerph 09 00995 i019]()
is the sum of all weights located in the row
![Ijerph 09 00995 i006]()
,
![Ijerph 09 00995 i020]()
is the sum of all weights in the column
![Ijerph 09 00995 i006]()
. The threshold of 1.96 was applied to test the significance level of
![Ijerph 09 00995 i012]()
. If
![Ijerph 09 00995 i012]()
was greater than 1.96 or smaller than −1.96, it implied that the spatial autocorrelation was significant [
7].
The spatial correlogram is a graph where the Moran’s I is plotted in ordinate, against distances among localities (in abscissa). According to Legendre and Fortin, the spatial correlogram can be standardized into a standardized correlogram, in which the ordinate is the standardized Moran’s I,
Z(I) [
16]. The shape of the standardized correlogram provides indications about the spatial pattern (spatial clusters and spatial outliers) and spatial correlation distance of a variable [
9,
16]. However, the standardized correlogram often has one or more positive correlation ranges. Zhang
et al. explained that the closer positive correlation range represents the average size of the zone of spatial clusters, that is, the spatial correlation distance [
17].
Local Moran’s I is a local test statistic for spatial autocorrelation, which is used to identify the locations of spatial clusters and spatial outliers. It is computed as follows:
The notations in Equation (3) are as described for Equation (1), but the corresponding values are from the local neighboring region. For more details of Moran’s I principles and methods, see the references [
12,
14]. With the local Moran’s I statistic analysis, five categories of local spatial autocorrelation can be distinguished. Two of these are spatial clusters, including high values surrounded by high values (High-high), and low values surrounded by low values (Low-low) types. Two are spatial outliers, including high values surrounded by low values (High-low) and low values surrounded by high values (Low-high). The last type is the spatial randomness that is without significant spatial patterns at corresponding weight matrix.
2.3. Geostatistics Method
Geostatistics uses the technique of semivariance to measure the spatial variability of a regionalized variable, and provides input parameters for the spatial interpolation of kriging [
18]. It relates the semivariance,
γ(h), which is computed as half the average squared difference between the components of data pairs [
19]:
where
![Ijerph 09 00995 i024]()
is the number of data pairs separated by a distance
![Ijerph 09 00995 i025]()
, and
![Ijerph 09 00995 i026]()
is the measured value of the variable
![Ijerph 09 00995 i027]()
at location of
![Ijerph 09 00995 i028]()
, and
![Ijerph 09 00995 i029]()
is the measured value of the variable
Z at location
![Ijerph 09 00995 i030]()
. For irregular sampling, it is rare for the distance between the sample pairs to be exactly equal to
h, therefore, the lag distance
h is often represented by a distance band.
A variogram plot can be acquired by calculating variogram at different lags. Data pairs were grouped into lag “bins” and Equation (4) was used to calculate the variogram for that bin. The mean lag of all the pairs in a particular bin was used as the representative lag for that bin.
The variogram plot is fitted with a theoretical model, such as spherical, exponential, Gaussian, linear and power models. In this study, the exponential model was selected.
The exponential function is:
where
![Ijerph 09 00995 i033]()
is the nugget variance (
![Ijerph 09 00995 i034]()
), represents the experimental error and field variation within the minimum sampling spacing. Typical, the semivariance increase with increasing lag distances to approach or attain a maximum value or still (
![Ijerph 09 00995 i035]()
) equivalent to the population variance.
C is the structural variance and
a is the spatial range across which the data exhibit spatial correlation.
Due to the complexity of spatial data, its spatial variability usually needs be described using two or more theoretical semivariances. This is the so-called nested model, which is described by the following equation [
20]:
where
![Ijerph 09 00995 i037]()
is the nugget value of the nested model, which is usually considered to be the spatial variability that cannot be described at the smallest sampling scale, and
![Ijerph 09 00995 i038]()
is the semivariance at different scales.
The fitted model provides information about the spatial structure as well as input parameters for kriging interpolation. Kriging is a linear interpolation technique that provides a linear unbiased estimate for spatial variables, which can be depicted as follows:
where
![Ijerph 09 00995 i040]()
is the predicted value at location of
![Ijerph 09 00995 i041]()
,
![Ijerph 09 00995 i042]()
is the measured value at location of
![Ijerph 09 00995 i028]()
,
![Ijerph 09 00995 i003]()
is the number of sites within the search neighborhood used for the estimation. Contrary to other methods (such as inverse distance weighted), the weighting function
![Ijerph 09 00995 i043]()
is no longer arbitrary; rather, it is calculated based on the parameters of the semivariogram model. To ensure that the estimate is unbiased, the weights need to sum to one:
and the estimation errors (or kriging variances) need to be minimized.
With wide and increasing applications of spatial interpolation methods, there is a growing concern about their accuracy and precision. Accuracy of spatial interpolation was evaluated through cross-validation approach. Commonly used error measures include: mean error (ME), mean absolute error (MAE), mean squared error (MSE) and root mean squared error (RMSE). Willmott suggests that MAE and RMSE are among the “best” overall measures of model performance [
21]. RMSE provides a measure of error size, but it is sensitive to outliers as it places a lot of weight on large errors [
22]. MAE provides an absolute measure of the size of the error, and it is less sensitive to extreme values [
23].
MAE is calculated as:
RMSE can be calculated as:
Because MAE does not reveal the magnitude of error that might occur at any point, MSE will be calculated [
24] as:
where
![Ijerph 09 00995 i042]()
,
![Ijerph 09 00995 i048]()
is the observed and predicted value at location of
![Ijerph 09 00995 i006]()
, respectively. Smaller MAE values indicate few errors. The RMSE can be used to compare different methods by seeing how closely predicted values match the observed values, the smaller the RMSE the better. Squaring the difference at any point gives an indication of the magnitude. Smaller MSE values indicate more accurate point-by-point estimation.
2.4. Data Treatment with Computer Software
Soil samples were stored using the ArcView 3.2 software to create a spatial database. The spatial autocorrelation analysis was conducted using Geoda095i software. The experimental semivariance models were constructed using GS+5.3, while kriging was performed using the geostatistical analyst extension of ArcGIS 8.3.
As in conventional statistics, a normal distribution for the variable under study is desirable in linear geostatistics. Even though normality may not be strictly required, serious violation of normality, such as too high skewness and outliers, can impair the variorum structure and the kriging results. It is often observed that environmental variables are lognormal [
1], and data transformation is necessary to normalize such data sets.
The normality tests of the eight heavy metals for the 1,018 samples were performed as described by Huo
et al. [
25]. Compared with the raw data sets, the log-transformation significantly reduced the skewness values of data sets towards “0”. However, because of data sets with many duplicate values or multi-modals, Cu, As, Cd, and Pb still cannot pass the Kolmogorov-Smirnov test for normality (K-S p) after log-transformation. As a result, further analysis focused on Cr, Ni, Zn, and Hg. In order to compare with geostatistics, the data after log-transformation were used in the Moran’s I analysis.

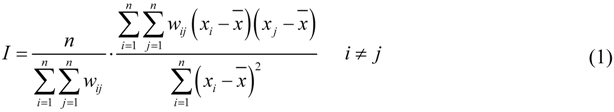
 is the number of observations of the whole region,
is the number of observations of the whole region,  and
and  are the observations at locations of
are the observations at locations of  and
and  ,
,  is the mean of
is the mean of  , and
, and  , an element of spatial weights matrix
, an element of spatial weights matrix  , is the spatial weight between locations of
, is the spatial weight between locations of  and
and  . The value of Moran’s I generally varies between 1 and −1. Positive autocorrelation in the data translates into positive values of Moran’s I; negative autocorrelation produces negative values. No autocorrelation results in a value close to 0 [11].
. The value of Moran’s I generally varies between 1 and −1. Positive autocorrelation in the data translates into positive values of Moran’s I; negative autocorrelation produces negative values. No autocorrelation results in a value close to 0 [11]. , which depicts the relationship between an element and its surrounding elements. A distance-based weight matrix was adopted in this study, and each distance class is specified as a threshold distance, such that all locations within the given distance are considered to be “neighbors” (the value not equal to zero in the matrix) in the distance-based weight matrix. Usually, normal approximation as a precondition, global Moran’s I can be standardized to
, which depicts the relationship between an element and its surrounding elements. A distance-based weight matrix was adopted in this study, and each distance class is specified as a threshold distance, such that all locations within the given distance are considered to be “neighbors” (the value not equal to zero in the matrix) in the distance-based weight matrix. Usually, normal approximation as a precondition, global Moran’s I can be standardized to  , and
, and  is calculated as [14,15]:
is calculated as [14,15]:
 is the sum of all weights located in the row
is the sum of all weights located in the row  ,
,  is the sum of all weights in the column
is the sum of all weights in the column  . The threshold of 1.96 was applied to test the significance level of
. The threshold of 1.96 was applied to test the significance level of  . If
. If  was greater than 1.96 or smaller than −1.96, it implied that the spatial autocorrelation was significant [7].
was greater than 1.96 or smaller than −1.96, it implied that the spatial autocorrelation was significant [7].

 is the number of data pairs separated by a distance
is the number of data pairs separated by a distance  , and
, and  is the measured value of the variable
is the measured value of the variable  at location of
at location of  , and
, and  is the measured value of the variable Z at location
is the measured value of the variable Z at location  . For irregular sampling, it is rare for the distance between the sample pairs to be exactly equal to h, therefore, the lag distance h is often represented by a distance band.
. For irregular sampling, it is rare for the distance between the sample pairs to be exactly equal to h, therefore, the lag distance h is often represented by a distance band.
 is the nugget variance (
is the nugget variance (  ), represents the experimental error and field variation within the minimum sampling spacing. Typical, the semivariance increase with increasing lag distances to approach or attain a maximum value or still (
), represents the experimental error and field variation within the minimum sampling spacing. Typical, the semivariance increase with increasing lag distances to approach or attain a maximum value or still (  ) equivalent to the population variance. C is the structural variance and a is the spatial range across which the data exhibit spatial correlation.
) equivalent to the population variance. C is the structural variance and a is the spatial range across which the data exhibit spatial correlation. 
 is the nugget value of the nested model, which is usually considered to be the spatial variability that cannot be described at the smallest sampling scale, and
is the nugget value of the nested model, which is usually considered to be the spatial variability that cannot be described at the smallest sampling scale, and  is the semivariance at different scales.
is the semivariance at different scales.
 is the predicted value at location of
is the predicted value at location of  ,
,  is the measured value at location of
is the measured value at location of  ,
,  is the number of sites within the search neighborhood used for the estimation. Contrary to other methods (such as inverse distance weighted), the weighting function
is the number of sites within the search neighborhood used for the estimation. Contrary to other methods (such as inverse distance weighted), the weighting function  is no longer arbitrary; rather, it is calculated based on the parameters of the semivariogram model. To ensure that the estimate is unbiased, the weights need to sum to one:
is no longer arbitrary; rather, it is calculated based on the parameters of the semivariogram model. To ensure that the estimate is unbiased, the weights need to sum to one:



 ,
,  is the observed and predicted value at location of
is the observed and predicted value at location of  , respectively. Smaller MAE values indicate few errors. The RMSE can be used to compare different methods by seeing how closely predicted values match the observed values, the smaller the RMSE the better. Squaring the difference at any point gives an indication of the magnitude. Smaller MSE values indicate more accurate point-by-point estimation.
, respectively. Smaller MAE values indicate few errors. The RMSE can be used to compare different methods by seeing how closely predicted values match the observed values, the smaller the RMSE the better. Squaring the difference at any point gives an indication of the magnitude. Smaller MSE values indicate more accurate point-by-point estimation.

 and
and  represented the distance where the Moran’s I and the standardized Moran’s I,
represented the distance where the Moran’s I and the standardized Moran’s I,  reached maximum, respectively.
reached maximum, respectively.  was the maximal positive correlation distance for Cr, Ni, Zn, and Hg, and
was the maximal positive correlation distance for Cr, Ni, Zn, and Hg, and  was the sum distance of the positive and negative correlation. Table 4 lists these characteristic distances. There was no
was the sum distance of the positive and negative correlation. Table 4 lists these characteristic distances. There was no  for Ni because no distinct negative correlation range was found between the two positive correlation ranges.
for Ni because no distinct negative correlation range was found between the two positive correlation ranges. 



 ,
,  ,
,  ,
,  , respectively. Because the Moran’s I analysis based on
, respectively. Because the Moran’s I analysis based on  and
and  can highlight the local (often the spatial outliers) and major spatial structure and the complexity of spatial variables, the nested model of
can highlight the local (often the spatial outliers) and major spatial structure and the complexity of spatial variables, the nested model of  and
and  was used to describe the spatial variability of heavy metals at local and global scales. It is worth noting that model
was used to describe the spatial variability of heavy metals at local and global scales. It is worth noting that model  was the traditional geostatistics model in the following.
was the traditional geostatistics model in the following. was generated. The different theoretical semivariance models were used to try with the best fitting value. The smallest nugget values of mean prediction error (ME) close to 0 and root-mean-square standardized prediction errors (RMSSE) close to 1 were selected. Figure 4 presents the scatter plots and fitted model based on the traditional geoststistics model and model
was generated. The different theoretical semivariance models were used to try with the best fitting value. The smallest nugget values of mean prediction error (ME) close to 0 and root-mean-square standardized prediction errors (RMSSE) close to 1 were selected. Figure 4 presents the scatter plots and fitted model based on the traditional geoststistics model and model  . According to the scatter plots, the values ME and RMSSE were calculated. The ME values of traditional geostatistics model and model
. According to the scatter plots, the values ME and RMSSE were calculated. The ME values of traditional geostatistics model and model  were 0.234, 0.1015, and the RMSSE were 1.119 and 1.075, respectively. Therefore, the theoretical semivariance of model
were 0.234, 0.1015, and the RMSSE were 1.119 and 1.075, respectively. Therefore, the theoretical semivariance of model  was better than traditional geostatistics model. For Ni, Zn, and Hg, The selection of the semivariance were similar to Cr.
was better than traditional geostatistics model. For Ni, Zn, and Hg, The selection of the semivariance were similar to Cr. (b) (distance, m).
(b) (distance, m).
 (b) (distance, m).
(b) (distance, m).
 ,
,  ,
,  ,
,  ,
,  , and the nested model of
, and the nested model of  and
and  . The cross-validation method was used to validate the parameters of these models. Evaluation indices from cross-validation of spatial maps of the four heavy metals are given in Table 5. For Cr, Ni, Zn, and Hg, except for the nested model of
. The cross-validation method was used to validate the parameters of these models. Evaluation indices from cross-validation of spatial maps of the four heavy metals are given in Table 5. For Cr, Ni, Zn, and Hg, except for the nested model of  and
and  , the MAE, RMSE, and MAE values of model
, the MAE, RMSE, and MAE values of model  and model
and model  were the smallest, which indicated that semivariance parameters obtained from fitting of experimental semivariogram values were reasonable and spatial prediction using semivariogram parameters is better than other models. The values of model
were the smallest, which indicated that semivariance parameters obtained from fitting of experimental semivariogram values were reasonable and spatial prediction using semivariogram parameters is better than other models. The values of model  and
and  were close and the largest, implying unsuitable semivariogram parameters. The values of model
were close and the largest, implying unsuitable semivariogram parameters. The values of model  were close to the values of model
were close to the values of model  , which were the third smallest. This suggested that the dominant spatial pattern can be captured through traditional geostatistics. Compared with model
, which were the third smallest. This suggested that the dominant spatial pattern can be captured through traditional geostatistics. Compared with model  , the values of the MAE, RMSE, and MAE of the nested model of
, the values of the MAE, RMSE, and MAE of the nested model of  and
and  were smaller, which indicated that the nested model can further improve the global prediction. It may be caused by the model
were smaller, which indicated that the nested model can further improve the global prediction. It may be caused by the model  being able to highlight local spatial patterns while the model
being able to highlight local spatial patterns while the model  focuses on the global dominant spatial pattern. Thus, their coupling may allow fusion of the details and the dominating spatial patterns of heavy metals. Table 5 shown that the best model was the nested model of
focuses on the global dominant spatial pattern. Thus, their coupling may allow fusion of the details and the dominating spatial patterns of heavy metals. Table 5 shown that the best model was the nested model of  and
and  , followed by model
, followed by model  ,
,  ,
,  . Therefore, the Moran’s I analysis can help to provide the better semivariogram parameters and improve estimation accuracy.
. Therefore, the Moran’s I analysis can help to provide the better semivariogram parameters and improve estimation accuracy. and the nested model
and the nested model  plus
plus  were used, the data ranges were wider, and the standard deviations and CVs were larger than when other models were used. This indicated that the model
were used, the data ranges were wider, and the standard deviations and CVs were larger than when other models were used. This indicated that the model  and the nested model
and the nested model  plus
plus  can reduce the smoothing effect of kriging and improve the estimatiom accuracy, especially the nested model of
can reduce the smoothing effect of kriging and improve the estimatiom accuracy, especially the nested model of  and
and  .
.




 plus
plus 



 plus
plus 



 plus
plus 



 plus
plus 



 plus
plus 
 ,
,  , the nested model of
, the nested model of  and
and  , and the traditional geostatistics model
, and the traditional geostatistics model  , the pollution status of both measured and predicted values of the samples were assessed. In Table 7, the rows are the pollution status based on predicted values, while the columns are the pollution status based on measured values. Thus, in each block composed by heavy metal and prediction model, data in the left diagonal present the agreement in pollution status between the measured and predicted values, while those in the right diagonal present the disagreement in pollution status between the measured and predicted values.
, the pollution status of both measured and predicted values of the samples were assessed. In Table 7, the rows are the pollution status based on predicted values, while the columns are the pollution status based on measured values. Thus, in each block composed by heavy metal and prediction model, data in the left diagonal present the agreement in pollution status between the measured and predicted values, while those in the right diagonal present the disagreement in pollution status between the measured and predicted values. and
and  improved the Zn global prediction accuracy (Table 7). For Cr, 0.69% of measured values were in pollution status, and these samples were underestimated and became unpolluted after interpolation using models
improved the Zn global prediction accuracy (Table 7). For Cr, 0.69% of measured values were in pollution status, and these samples were underestimated and became unpolluted after interpolation using models  and traditional geostatistics model
and traditional geostatistics model  . However, after interpolation using model
. However, after interpolation using model  and the nested model of
and the nested model of  and
and  , there were still 0.10% of samples remained pollution status. Before and after interpolation, the changes of samples pollution status were more complicated for Ni and Hg, as there was not only an underestimation effect, but also an overestimation effect. These two effects were severe after interpolation using models
, there were still 0.10% of samples remained pollution status. Before and after interpolation, the changes of samples pollution status were more complicated for Ni and Hg, as there was not only an underestimation effect, but also an overestimation effect. These two effects were severe after interpolation using models  and
and  (Table 7). For Ni, 3.93% of measured samples were in pollution status. After spatial interpolation, the model
(Table 7). For Ni, 3.93% of measured samples were in pollution status. After spatial interpolation, the model  avoided the overestimation effect and reduced the underestimation effect from 3.44% to 1.57% compared with the model
avoided the overestimation effect and reduced the underestimation effect from 3.44% to 1.57% compared with the model  . The nested model of
. The nested model of  and
and  showed that there were still 3.05% of samples remained pollution status, but only 0.88% of samples were changed from polluted to unpolluted status after interpolation.
showed that there were still 3.05% of samples remained pollution status, but only 0.88% of samples were changed from polluted to unpolluted status after interpolation. , the percent of samples remained pollution status increased from 1.96% to 3.05% after interpolation using the model
, the percent of samples remained pollution status increased from 1.96% to 3.05% after interpolation using the model  , and the percent of samples changed from polluted to unpolluted reduced from 4.32% to 3.24%. Thus, it avoided designating 1.08% of polluted samples wrongly as unpolluted. Models
, and the percent of samples changed from polluted to unpolluted reduced from 4.32% to 3.24%. Thus, it avoided designating 1.08% of polluted samples wrongly as unpolluted. Models  and
and  also had the overestimation effect, the percent of samples changed unpolluted to polluted were 0.39% and 0.49%, respectively, therefore, 0.10% of unpolluted samples were wrongly identified as polluted. Compared with model
also had the overestimation effect, the percent of samples changed unpolluted to polluted were 0.39% and 0.49%, respectively, therefore, 0.10% of unpolluted samples were wrongly identified as polluted. Compared with model  , the percent of samples remained pollution status increased by 0.19%, and the percent of samples changed from unpolluted to polluted increased by 0.10% after interpolaton using the nested model of
, the percent of samples remained pollution status increased by 0.19%, and the percent of samples changed from unpolluted to polluted increased by 0.10% after interpolaton using the nested model of  and
and  .
. , the method combining geostatistics with Moran’s I analysis (models
, the method combining geostatistics with Moran’s I analysis (models  ,
,  ) can avoid effectively the underestimation and overestimation effect so that more samples remain original pollution status.
) can avoid effectively the underestimation and overestimation effect so that more samples remain original pollution status.  ) was used to optimize the semivariance, this underestimation effect can be slightly reduced. With the increase of the polluted samples and a significant local spatial pattern appeared, the effect of reducing underestimation was more significant, such as Ni and Hg in this study. If the distances where the Moran’s I and the standardized Moran’s I,
) was used to optimize the semivariance, this underestimation effect can be slightly reduced. With the increase of the polluted samples and a significant local spatial pattern appeared, the effect of reducing underestimation was more significant, such as Ni and Hg in this study. If the distances where the Moran’s I and the standardized Moran’s I,  reached maximum (
reached maximum (  and
and  ) were combined to optimize the semivariance, the underestimation effect can be reduced further. The reason for this may be that the optimality of semivariance using
) were combined to optimize the semivariance, the underestimation effect can be reduced further. The reason for this may be that the optimality of semivariance using  can highlight the most significant local spatial patterns and reflects the more abnormal information of the polluted samples. Thus, the nested model would better balance the details and dominating spatial patterns. But, there also was an overestimation effect. Because most of the overestimation errors happened near actual polluted samples, making the potentially high-risk areas, in terms of soil heavy metal pollution, a little overestimation may be better than more underestimation. By comparing all the models
can highlight the most significant local spatial patterns and reflects the more abnormal information of the polluted samples. Thus, the nested model would better balance the details and dominating spatial patterns. But, there also was an overestimation effect. Because most of the overestimation errors happened near actual polluted samples, making the potentially high-risk areas, in terms of soil heavy metal pollution, a little overestimation may be better than more underestimation. By comparing all the models  ,
,  ,
,  , the nested model of
, the nested model of  and
and  , the nested model was defined as the optimality model.
, the nested model was defined as the optimality model. and
and  . Heavy metals concentrations are separated into classes according to the background values of soil heavy metals of Beijing and their multiples to highlight the spatial differences of different classes.
. Heavy metals concentrations are separated into classes according to the background values of soil heavy metals of Beijing and their multiples to highlight the spatial differences of different classes. and
and  (a) Cr, (b) Ni, (c) Zn, (d) Hg.
(a) Cr, (b) Ni, (c) Zn, (d) Hg.
 and
and  (a) Cr, (b) Ni, (c) Zn, (d) Hg.
(a) Cr, (b) Ni, (c) Zn, (d) Hg.




