Spatial Pattern Analysis of Heavy Metals in Beijing Agricultural Soils Based on Spatial Autocorrelation Statistics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
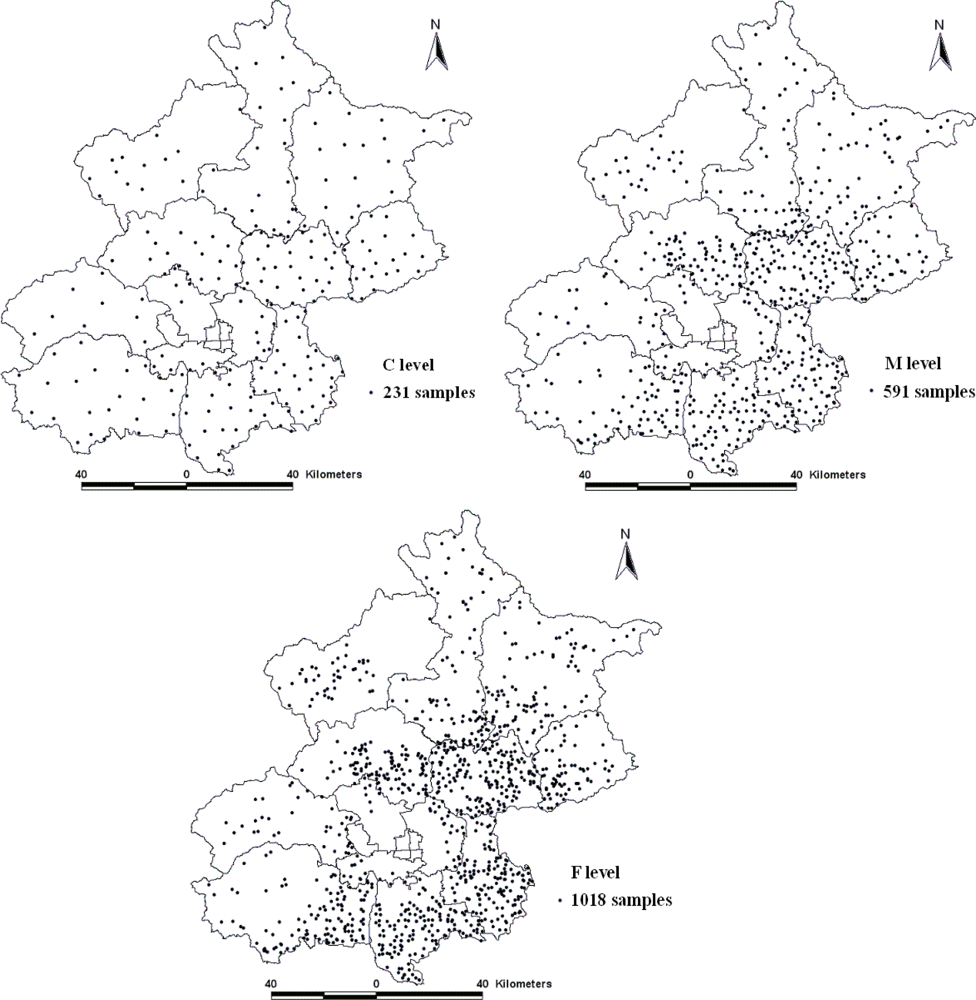
2.2. Soil Sampling and Analysis
2.3. Global Spatial Autocorrelation
2.4. Local Spatial Autocorrelation
2.5. Data Treatment with Computer Software
3. Results and Discussion
3.1. Influence of Different Weight Matrixes on Spatial Autocorrelation
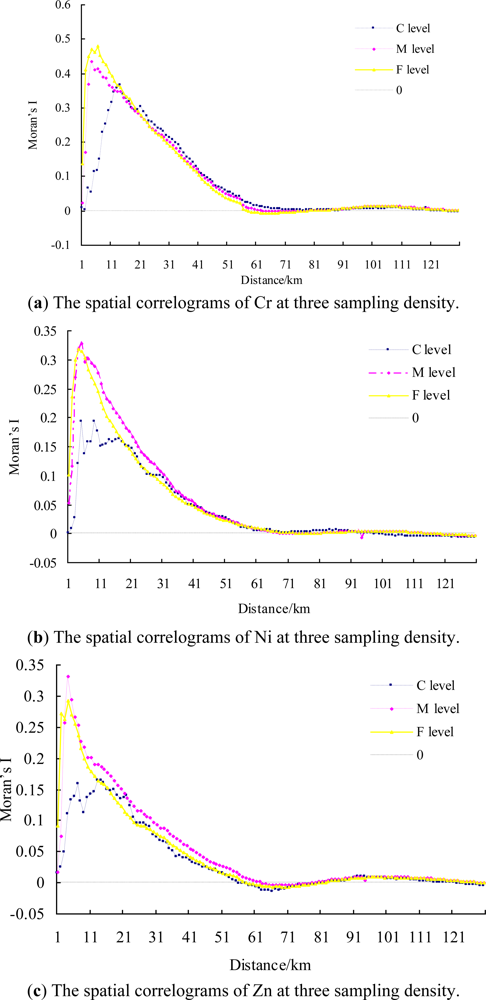
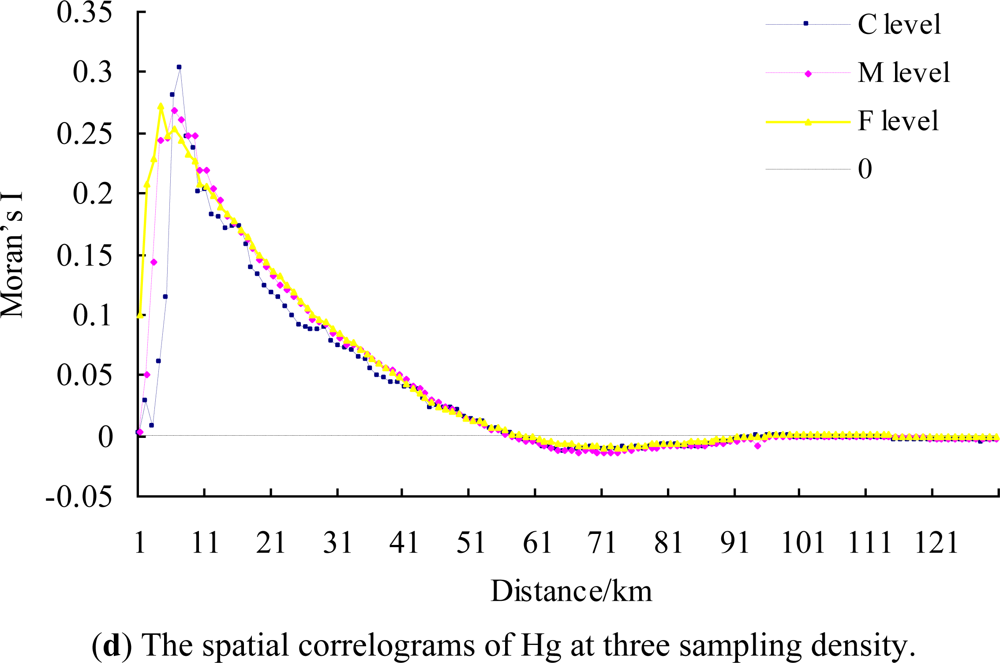
3.2. The Effect of Sampling Density on Spatial Autocorrelation
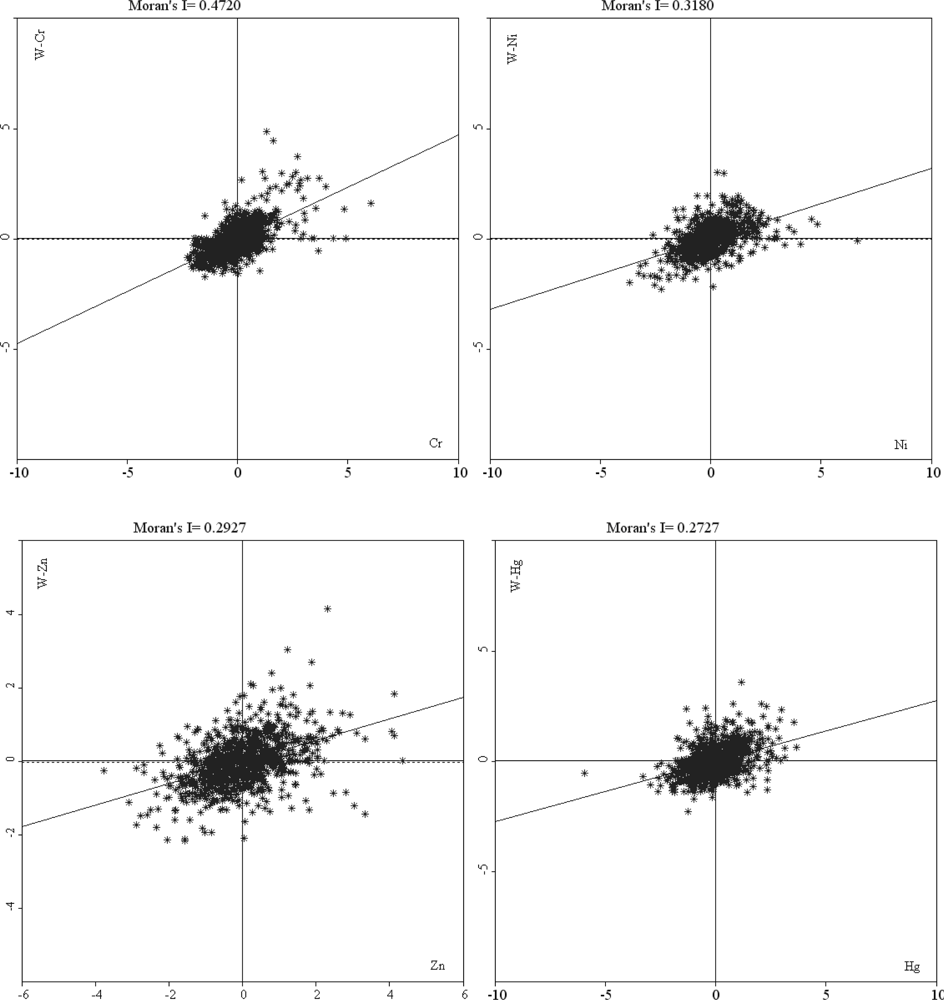
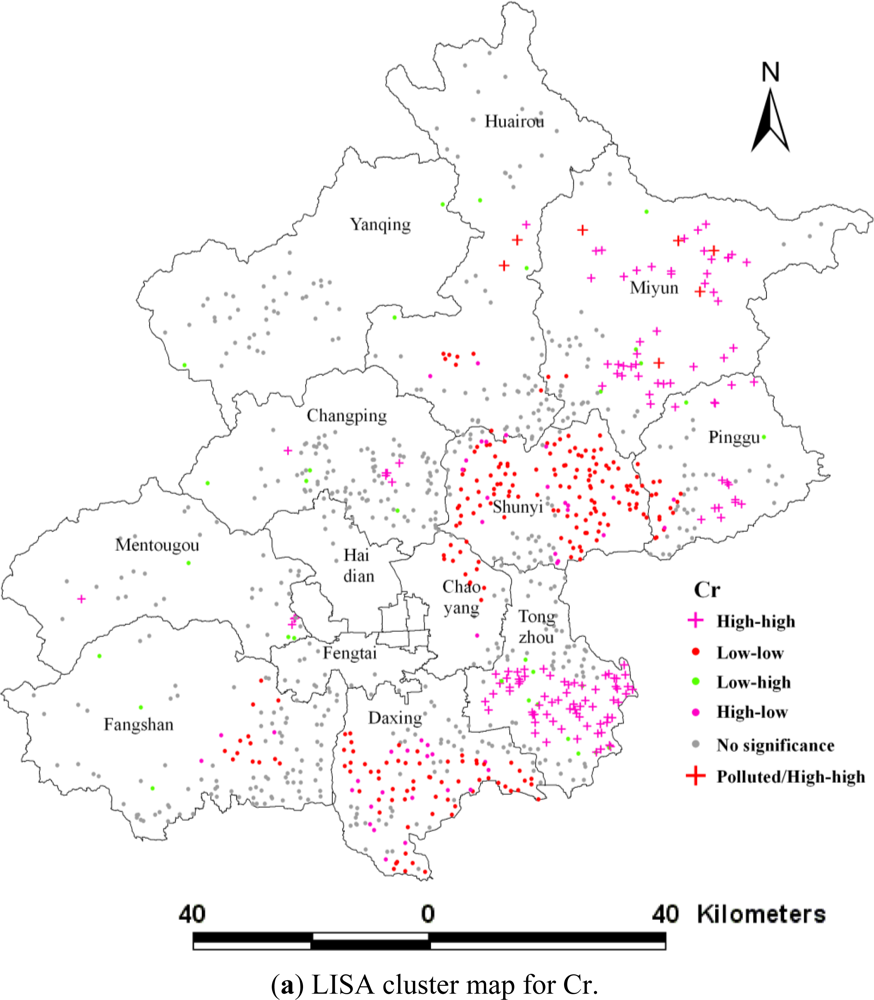
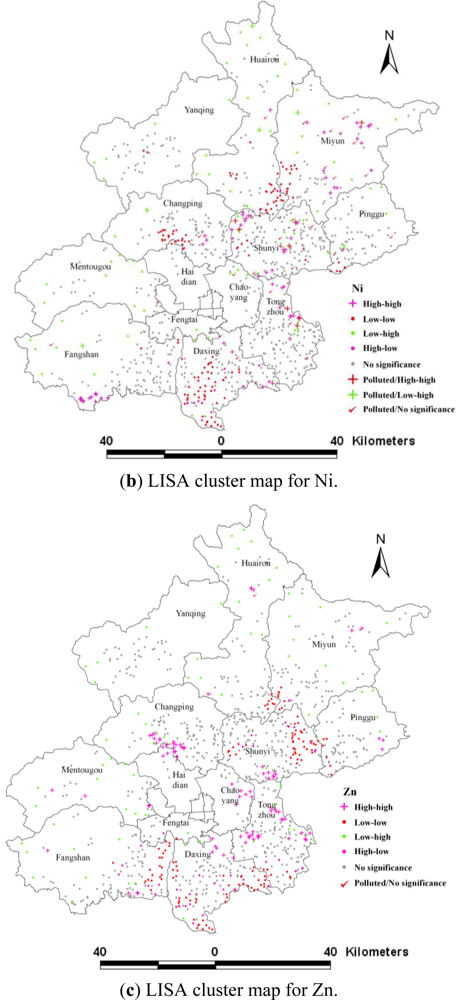
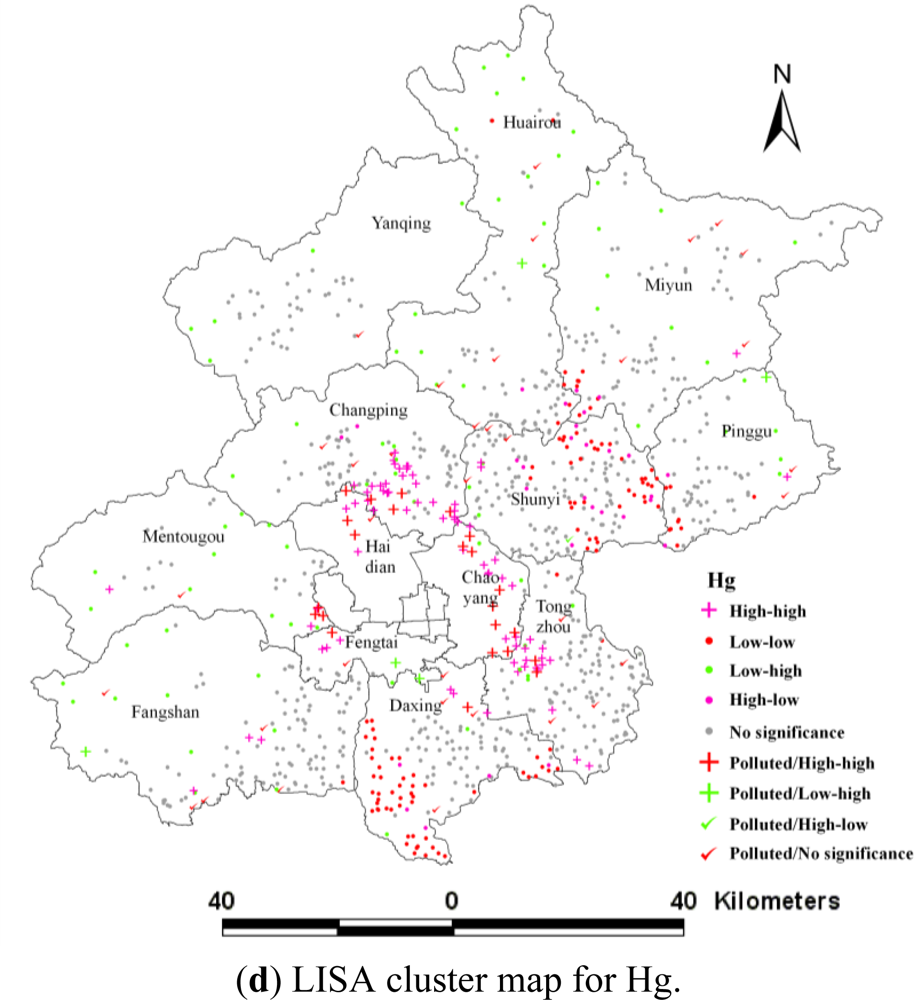
3.3. Local Indicators of Spatial Association (LISA)
4. Conclusions
Acknowledgments
References
- McGrath, D; Zhang, CS; Carton, OW. Geostatistical analyses and hazard assessment on soil lead in Slivermines areas, Ireland. Environ. Pollut 2004, 127, 239–248. [Google Scholar]
- Franco, C; Soares, A; Delgado, J. Geostatistical modelling of heavy metal contamination in the topsoil of Guadiamar river margins (S Spain) using a stochastic simulation technique. Geoderma 2006, 136, 852–864. [Google Scholar]
- Liu, XM; Wu, JJ; Xu, JM. Characterizing the risk assessment of heavy metals and sampling uncertainty analysis in paddy field by geostatistics and GIS. Environ. Pollut 2006, 141, 257–264. [Google Scholar]
- Hu, KL; Li, H; Li, BG; Huang, YF. Spatial and temporal patterns of soil organic matter in the urban-rural transition zone of Beijing. Geoderma 2007, 141, 302–310. [Google Scholar]
- Anselin, L. Local indicators of association-LISA. Geogr. Anal 1995, 27, 93–115. [Google Scholar]
- Boots, B. Local measures of spatial association. Ecoscience 2002, 9, 168–176. [Google Scholar]
- Dale, MR; Fortin, MJ. Spatial autocorrelation and statistical tests in ecology. Ecoscience 2002, 9, 162–167. [Google Scholar]
- Overmars, KP; de Koning, GHJ; Veldkamp, A. Spatial autocorrelation in multi-scale land use models. Ecol. Model 2003, 164, 257–270. [Google Scholar]
- Zhang, CS; McGrath, D. Geostatistical and GIS analyses on soil organic carbon concentrations in grassland of southeastern Ireland from two different periods. Geoderma 2004, 119, 261–275. [Google Scholar]
- Zhang, CS; Zhang, S; He, JB. Spatial distribution characteristics of heavy metals in the sediments of Changjiang River system-Spatial autocorrelation and fractal methods. Acta Geogr Sinica 1998, 53, 87–96. (in Chinese). [Google Scholar]
- Anselin, L. Spatial effects in econometric practice in environmental and resource economics. Am. J. Agric. Econ 2001, 83, 705–710. [Google Scholar]
- Hu, KL; Zhang, FR; Li, H; Huang, F; Li, BG. Spatial patterns of soil heavy metals in urban-rural transition zone of Beijing. Pedosphere 2006, 16, 690–698. [Google Scholar]
- Tan, MZ; Xu, FM; Chen, J; Zhang, XL; Chen, JZ. Spatial prediction of heavy metal pollution for soils in pre-urban Beijing, China based on fuzzy set theory. Pedosphere 2006, 16, 545–554. [Google Scholar]
- Wu, S; Xia, XH; Lin, CY; Chen, X; Zhou, CH. Levels of arsenic and heavy metals in the rural soils of Beijing and their changes over the last two decades (1985–2008). J. Hazar. Mater 2010, 179, 860–868. [Google Scholar]
- Huo, XN; Li, H; Sun, DF; Zhou, LD; Li, BG. Multi-scale spatial structure of heavy metals in agricultural soils in Beijing. Environ. Monit. Assess 2010, 164, 605–616. [Google Scholar]
- Goodchild, MF. Spatial Autocorrelation; CATMOG 47; Geobooks: Norwich, UK, 1986; pp. 6–25. [Google Scholar]
- Cliff, AD; Ord, JK. Spatial Processes: Models and Applications; Pion: London, UK, 1981. [Google Scholar]
- Anselin, L; Syabri, I; Kho, Y. GeoDa: An Introduction to spatial data Analysis. Geogr. Anal 2006, 38, 5–22. [Google Scholar]
- Khan, S; Cao, Q; Zheng, YM; Huang, YZ; Zhu, YG. Health risks of heavy metals in contaminated soils and food crops irrigated with wastewater in Beijing, China. Environ. Pollut 2008, 152, 686–692. [Google Scholar]
- Miller, JR; Lechler, PJ; Bridge, G. Mercury contamination of alluvial sediments within the Essequibo and Mazaruni river basins, Guyana. Water Air Soil Pollut 2003, 148, 139–166. [Google Scholar]
- Engle, MA; Gustin, MS; Lindberg, SE; Gertler, AW; Ariya, PA. The influence of ozone on atmospheric emissions of gaseous elemental mercury and relative gaseous mercury from substrates. Atmos. Environ 2005, 39, 7506–7517. [Google Scholar]

| Spatial weights | Cr | Ni | Cu | Zn | As | Cd | Pb | Hg |
|---|---|---|---|---|---|---|---|---|
| First order rook contiguity | 0.495 * | 0.317 * | 0.026 | 0.282 * | 0.077 * | 0.119 * | 0.051 * | 0.290 * |
| First order queen contiguity | 0.495 * | 0.317 * | 0.026 | 0.282 * | 0.077 * | 0.119 * | 0.051 * | 0.290 * |
| 4-nearest neighbors | 0.541 * | 0.327 * | 0.006 | 0.287 * | 0.071 * | 0.124 * | 0.036 | 0.283 * |
| 5-nearest neighbors | 0.521 * | 0.320 * | 0.018 | 0.277 * | 0.080 * | 0.125 * | 0.047 * | 0.275 * |
| 6-nearest neighbors | 0.513 * | 0.321 * | 0.018 | 0.265 * | 0.084 * | 0.122 * | 0.049 * | 0.271 * |
| 7-nearest neighbors | 0.498 * | 0.315 * | 0.018 | 0.253 * | 0.078 * | 0.118 * | 0.045 * | 0.263 * |
| 8-nearest neighbors | 0.486 * | 0.309 * | 0.018 | 0.246 * | 0.073 * | 0.119 * | 0.047 * | 0.258 * |
| 4km distance band | 0.472 * | 0.318 * | 0.024 | 0.293 * | 0.090 * | 0.127 * | 0.056 * | 0.272 * |
| Types of spatial autocorrelation | Cr | Ni | Zn | Hg |
|---|---|---|---|---|
| No significance | 56.09 | 69.94 | 66.70 | 67.78 |
| High-high | 14.34 | 7.07 | 8.74 | 9.63 |
| Low-low | 22.20 | 12.48 | 13.46 | 11.30 |
| Low-high | 3.05 | 7.96 | 7.56 | 8.35 |
| High-low | 4.32 | 2.55 | 3.54 | 2.95 |
| Heavy metals | Pollution status | Types of spatial autocorrelation | ||||
|---|---|---|---|---|---|---|
| No significance | High-high | Low-low | Low-high | High-low | ||
| Cr | Polluted | 0.69 | ||||
| Unpolluted | 56.09 | 13.65 | 22.20 | 3.05 | 4.32 | |
| Ni | Polluted | 2.65 | 0.79 | 0.49 | ||
| Unpolluted | 67.29 | 6.29 | 12.48 | 7.47 | 2.55 | |
| Zn | Polluted | 0.10 | ||||
| Unpolluted | 66.60 | 8.74 | 13.46 | 7.56 | 3.54 | |
| Hg | Polluted | 3.44 | 2.26 | 0.49 | 0.10 | |
| Unpolluted | 64.34 | 7.37 | 11.30 | 7.86 | 2.85 | |
© 2011 by the authors; licensee MDPI, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Huo, X.-N.; Zhang, W.-W.; Sun, D.-F.; Li, H.; Zhou, L.-D.; Li, B.-G. Spatial Pattern Analysis of Heavy Metals in Beijing Agricultural Soils Based on Spatial Autocorrelation Statistics. Int. J. Environ. Res. Public Health 2011, 8, 2074-2089. https://doi.org/10.3390/ijerph8062074
Huo X-N, Zhang W-W, Sun D-F, Li H, Zhou L-D, Li B-G. Spatial Pattern Analysis of Heavy Metals in Beijing Agricultural Soils Based on Spatial Autocorrelation Statistics. International Journal of Environmental Research and Public Health. 2011; 8(6):2074-2089. https://doi.org/10.3390/ijerph8062074
Chicago/Turabian StyleHuo, Xiao-Ni, Wei-Wei Zhang, Dan-Feng Sun, Hong Li, Lian-Di Zhou, and Bao-Guo Li. 2011. "Spatial Pattern Analysis of Heavy Metals in Beijing Agricultural Soils Based on Spatial Autocorrelation Statistics" International Journal of Environmental Research and Public Health 8, no. 6: 2074-2089. https://doi.org/10.3390/ijerph8062074




