A Methodological Approach to Assessing the Health Impact of Environmental Chemical Mixtures: PCBs and Hypertension in the National Health and Nutrition Examination Survey
Abstract
:1. Introduction
2. Experimental Section
3. Results and Discussion
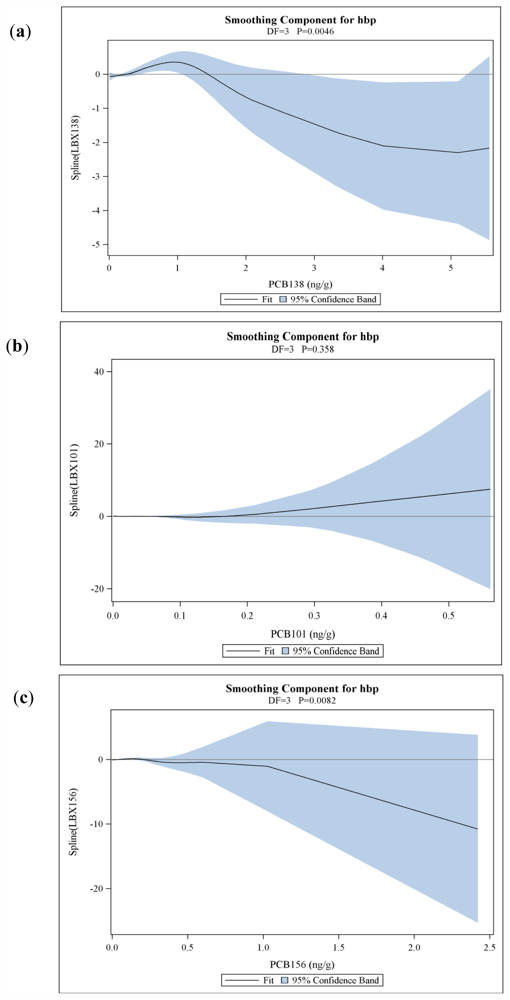
3.1. Results
3.2. Discussion
4. Conclusions
- Conflict of InterestThe authors declare no conflict of interest.
- DisclaimerThis manuscript has been reviewed by the U.S. Environmental Protection Agency and approved for publication. The views expressed in this manuscript are those of the authors and do not necessarily reflect the views or policies of the U.S. Environmental Protection Agency.
References
- Phthalates and Cumulative Risk Assessment: The Task Ahead; Committee on the Health Risks of Phthalates, National Research Council: Washington, DC, USA, 2008.
- Everett, C.J.; Frithsen, I.; Player, M. Relationship of polychlorinated biphenyls with type 2 diabetes and hypertension. J. Environ. Monit. 2011, 13, 241–251. [Google Scholar]
- Wang, S.L.; Tsai, P.-C.; Yang, C.-Y.; Guo, Y.L. Increased risk of diabetes and polychlorinated biphenyls and dioxins: A 24-year follow-up study of the Yucheng cohort. Diabetes Care 2008, 31, 1574–1579. [Google Scholar]
- Goncharov, A.; Pavuk, M.; Foushee, H.R.; Carpenter, D.O. Blood pressure in relation to concentrations of PCB congeners and chlorinated pesticides. Environ. Health Perspect. 2011, 119, 319–325. [Google Scholar]
- Centers for Disease Control and Prevention (CDC). National Center for Health Statistics (NCHS). National Health and Nutrition Examination Survey Data for 1999–2004; Department of Health and Human Services, Centers for Disease Control and Prevention: Hyattsville, MD, USA, 2005. Available online: http://www.cdc.gov/nchs/nhanes/nhanes_questionnaires.htm accessed on 3 September 2010.
- CDC. National Health and Nutrition Examination Survey; Centers for Disease Control and Prevention: Atlanta, GA, USA, 2010. Available online: http://www.cdc.gov/nchs/nhanes.htm accessed on 7 September 2010.
- Gaskins, A.J.; Schisterman, E.F. The effect of lipid adjustment on the analysis of environmental contaminants and the outcome of human health risks. Methods Mol. Biol. 2009, 580, 371–381. [Google Scholar]
- Schisterman, E.F.; Whitcomb, B.W.; Louis, G.M.; Louis, T.A. Lipid adjustment in the analysis of environmental contaminants and human health risks. Environ. Health Perspect. 2005, 113, 853–857. [Google Scholar]
- Gennings, C.; Sabo, R.; Carney, E. Identifying subsets of complex mixtures most associated with complex diseases: Polychlorinated biphenyls and endometriosis as a case study. Epidemiology 2010, 21, S77–S84. [Google Scholar]
- Chevrier, J.; Dewailly, E.; Ayotte, P.; Mauriège, P.; Després, J.P.; Tremblay, A. Body weight loss increases plasma and adipose tissue concentrations of potentially toxic pollutants in obese individuals. Int. J. Obes. Relat. Metab. Disord. 2000, 24, 1272–1278. [Google Scholar]
- Glynn, A.W.; Granath, F.; Aune, M.; Atuma, S.; Darnerud, P.O.; Bjerselius, R.; Vainio, H.; Weiderpass, E. Organochlorines in Swedish women: Determinants of serum concentrations. Environ. Health Perspect. 2003, 111, 349–355. [Google Scholar]
- Pelletier, C.; Doucet, E.; Imbeault, P.; Tremblay, A. Associations between weight loss-induced changes in plasma organochlorine concentrations, serum T-3 concentration, and resting metabolic rate. Toxicol. Sci. 2002, 67, 46–51. [Google Scholar]
- Walford, R.L.; Mock, D.; MacCallum, T.; Laseter, J.L. Physiologic changes in humans subjected to severe, selective calorie restriction for two years in biosphere 2: Health, aging, and toxicological perspectives. Toxicol. Sci. 1999, 52, 61–65. [Google Scholar]
- Everett, C.J.; Mainous, A.G., 3rd; Frithsen, I.L.; Player, M.S.; Matheson, E.M. Association of polychlorinated biphenyls with hypertension in the 1999–2002 National Health and Nutrition Examination Survey. Environ. Res. 2008, 108, 94–97. [Google Scholar]
- Goncharov, A.; Bloom, M.; Pavuk, M.; Birman, I.; Carpenter, D.O. Blood pressure and hypertension in relation to levels of serum polychlorinated biphenyls in residents of Anniston, Alabama. J. Hypertens. 2010, 28, 2053–2060. [Google Scholar]
- Guidance for Data Quality Assessment: Practical Methods for Data Analysis 25 EPA QA/G9, QA-97 Version; EPA/600/R-96/084; Office of Research and Development, US Environmental Protection Agency: Washington, DC, USA, 2000.
| Characteristic | N (%) | ||
|---|---|---|---|
| Total | Normotensive | Hypertensive | |
| Total | 4,119 (100) | 2,311 (56.1) | 1,808 (43.9) |
| Gender | |||
| Male | 1,943 (47.2) | 1,066 (46.1) | 877 (48.5) |
| Female | 2,176 (52.8) | 1,245 (53.9) | 931 (51.5) |
| Age group | |||
| 20–39 years | 1,511 (36.7) | 1,274 (55.1) | 237 (13.1) |
| 40–49 years | 664 (16.1) | 442 (19.1) | 222 (12.3) |
| 50–59 years | 541 (13.1) | 268 (11.6) | 273 (15.1) |
| 60–69 years | 627 (15.2) | 185 (8.0) | 442 (24.5) |
| 70+ years | 776 (18.8) | 142 (6.1) | 634 (35.1) |
| Race/ethnicity | |||
| NH White | 2,124 (51.6) | 1,135 (49.1) | 989 (54.7) |
| NH Black | 739 (17.9) | 358 (15.5) | 381 (21.1) |
| Mexican-American | 902 (21.9) | 583 (25.2) | 319 (17.6) |
| Other Hispanic | 192 (4.7) | 119 (5.2) | 73 (4.0) |
| Other/Mixed/Missing | 162 (3.9) | 116 (5.0) | 46 (2.5) |
| BMI | |||
| Underweight | 71 (1.8) | 50 (2.2) | 21 (1.2) |
| Normal weight | 1,250 (31.3) | 855 (37.6) | 395 (22.9) |
| Overweight | 1,419 (35.5) | 805 (35.4) | 614 (35.6) |
| Obese | 1,257 (31.5) | 563 (24.8) | 694 (40.3) |
| Whole weight concentration (ng/g) | Total | Normotensive | Hypertensive |
|---|---|---|---|
| ∑PCBs | |||
| Geometric Mean | 1.10 | 0.83 | 1.61 |
| 25th percentile | 0.66 | 0.56 | 1.01 |
| 50th percentile | 1.10 | 0.78 | 1.68 |
| 75th percentile | 1.94 | 1.34 | 2.60 |
| ∑estrogenic PCBs | |||
| Geometric Mean | 0.13 | 0.10 | 0.18 |
| 25th percentile | 0.09 | 0.08 | 0.11 |
| 50th percentile | 0.12 | 0.10 | 0.18 |
| 75th percentile | 0.21 | 0.15 | 0.29 |
| ∑mono-ortho sub. PCBs | |||
| Geometric Mean | 0.23 | 0.18 | 0.33 |
| 25th percentile | 0.16 | 0.15 | 0.20 |
| 50th percentile | 0.22 | 0.18 | 0.33 |
| 75th percentile | 0.38 | 0.25 | 0.52 |
| ∑di-ortho sub. PCBs | |||
| Geometric Mean | 0.75 | 0.55 | 1.12 |
| 25th percentile | 0.42 | 0.34 | 0.70 |
| 50th percentile | 0.75 | 0.51 | 1.16 |
| 75th percentile | 1.38 | 0.96 | 1.84 |
| ∑tri/tetra-ortho sub. PCBs | |||
| Geometric Mean | 0.11 | 0.09 | 0.16 |
| 25th percentile | 0.08 | 0.08 | 0.11 |
| 50th percentile | 0.11 | 0.09 | 0.15 |
| 75th percentile | 0.18 | 0.13 | 0.24 |
| ∑dioxin-like PCBs | |||
| Geometric Mean | 0.38 | 0.27 | 0.58 |
| 25th percentile | 0.20 | 0.17 | 0.36 |
| 50th percentile | 0.39 | 0.25 | 0.62 |
| 75th percentile | 0.72 | 0.49 | 0.96 |
| PCB 138&158 | |||
| % < LOD | 17.0 | 23.2 | 9.2 |
| Geometric Mean | 0.14 | 0.10 | 0.22 |
| 25th percentile | 0.08 | 0.06 | 0.12 |
| 50th percentile | 0.14 | 0.09 | 0.23 |
| 75th percentile | 0.29 | 0.18 | 0.40 |
| PCB 153 | |||
| % < LOD | 13.8 | 19.4 | 6.6 |
| Geometric Mean | 0.20 | 0.14 | 0.32 |
| 25th percentile | 0.10 | 0.08 | 0.19 |
| 50th percentile | 0.21 | 0.13 | 0.35 |
| 75th percentile | 0.41 | 0.28 | 0.57 |
| PCB 180 | |||
| % < LOD | 15.1 | 21.7 | 6.6 |
| Geometric Mean | 0.15 | 0.10 | 0.24 |
| 25th percentile | 0.06 | 0.05 | 0.15 |
| 50th percentile | 0.17 | 0.09 | 0.28 |
| 75th percentile | 0.33 | 0.23 | 0.44 |
| Categorical exposure OR (95% CI) | Continuous exposure | Continuous exposure, natural log transform | Continuous exposure, centered | GAM–linear component | GAM–spline component | |||
|---|---|---|---|---|---|---|---|---|
| Quartile 2 vs. 1 | Quartile 3 vs. 1 | Quartile 4 vs. 1 | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | Chi-square p | |
| ∑PCBs (all non missing values) | 1.05 (0.83–1.34) | 1.09 (0.84–1.43) | 1.38 (1.02–1.87) | 0.0689 (0.0360) 0.0553 | 0.1579 (0.0727) 0.0299 | 0.1099 (0.0573) 0.0553 | − −± | − −± |
| ∑estrogenic PCBs† | 0.92 (0.74–1.16) | 1.05 (0.84–1.32) | 1.42 (1.10–1.84) | 0.7637 (0.3172) 0.0161 | 0.1838 (0.0678) 0.0067 | 0.1375 (0.0573) 0.0164 | 0.8378 (0.2536) 0.0010 | 0.0411 |
| ∑mono-ortho sub. PCBs† | 0.92 (0.73–1.16) | 1.13 (0.89–1.42) | 1.60 (1.22–2.10) | 0.4014 (0.1665) 0.0159 | 0.2044 (0.0686) 0.0029 | 0.1420 (0.0593) 0.0166 | 0.4795 (0.1337) 0.0003 | 0.0141 |
| ∑di-ortho sub. PCBs† | 1.07 (0.83–1.36) | 1.06 (0.81–1.40) | 1.34 (0.98–1.82) | 0.0777 (0.0490) 0.1131 | 0.1321 (0.0712) 0.0637 | 0.0877 (0.0553) 0.1131 | 0.0974 (0.0407) 0.0169 | 0.9438 |
| ∑tri/tetra-ortho sub. PCBs† | 1.01 (0.79–1.28) | 1.05 (0.82–1.36) | 1.29 (0.97–1.71) | 0.7817 (0.3537) 0.0271 | 0.0966 (0.0651) 0.1378 | 0.1257 (0.0575) 0.0287 | 1.1294 (0.3447) 0.0011 | 0.6920 |
| ∑dioxin-like PCBs† | 1.01 (0.79–1.29) | 1.05 (0.80–1.39) | 1.26 (0.91–1.74) | 0.1725 (0.0986) 0.0803 | 0.1439 (0.0710) 0.0429 | 0.0922 (0.0574) 0.0837 | − −± | − −± |
| Individual congeners | ||||||||
| Tertile 1 vs. <LOD | Tertile 2 vs. <LOD | Tertile 3 vs. <LOD | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | Chi-square p | |
| PCB 52 | 0.85 (0.66–1.08) | 0.77 (0.60–0.98) | 0.87 (0.68–1.12) | 4.2542 (2.0166) 0.0349 | 0.1083 (0.0674) 0.1081 | 0.0996 (0.0469) 0.0337 | 4.0520 (2.0305) 0.0461 | 0.7483 |
| PCB 66 | 0.95 (0.74–1.21) | 0.77 (0.60–0.97) | 1.13 (0.88–1.45) | 8.6799 (2.4294) 0.0004 | 0.1539 (0.0566) 0.0065 | 0.2330 (0.0650) 0.0003 | 8.8179 (2.4416) 0.0003 | 0.4479 |
| PCB 74 | 1.03 (0.81–1.29) | 1.20 (0.94–1.54) | 1.61 (1.21–2.15) | 1.5528 (0.6253) 0.0130 | 0.2002 (0.0631) 0.0015 | 0.1402 (0.0578) 0.0154 | 2.0481 (0.5724) 0.0004 | 0.0232 |
| Quartile 2 vs. 1 | Quartile 3 vs. 1 | Quartile 4 vs. 1 | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | Chi-square p | |
| PCB 99 | 0.88 (0.71–1.10) | 0.90 (0.72–1.12) | 1.05 (0.82–1.35) | 0.6639 (0.6115) 0.2776 | 0.0799 (0.0593) 0.1781 | 0.0516 (0.0490) 0.2924 | 1.4130 (0.6007) 0.0187 | 0.0111 |
| PCB 101 | 0.77 (0.59–0.99) | 0.90 (0.70–1.16) | 0.71 (0.55–0.92) | 4.3306 (1.8184) 0.0172 | 0.0588 (0.0492) 0.2323 | 0.1059 (0.0444) 0.0172 | 3.6032 (2.0645) 0.0810 | 0.3580 |
| PCB 105 | 0.87 (0.69–1.11) | 0.90 (0.72–1.13) | 1.25 (0.97–1.62) | 4.4674 (1.7956) 0.0128 | 0.1488 (0.0530) 0.0050 | 0.1634 (0.0664) 0.0139 | 4.4639 (1.4354) 0.0019 | 0.1009 |
| PCB 118 | 1.00 (0.79–1.27) | 1.12 (0.86–1.44) | 1.63 (1.23–2.17) | 1.1521 (0.3925) 0.0033 | 0.2206 (0.0547) <0.0001 | 0.1841 (0.0643) 0.0042 | 1.2740 (0.3047) <0.0001 | 0.0175 |
| PCB 128 | 0.79 (0.50–1.25) | 0.82 (0.52–1.27) | 0.87 (0.55–1.37) | 10.5785 (3.4915) 0.0024 | 0.0631 (0.0237) 0.0077 | 0.1190 (0.0393) 0.0025 | 11.0304 (3.5228) 0.0018 | 0.3670 |
| PCB 138&158 | 1.11 (0.86–1.44) | 1.08 (0.83–1.41) | 1.21 (0.90–1.61) | 0.2080 (0.1833) 0.2567 | 0.0922 (0.0597) 0.1224 | 0.0609 (0.0518) 0.2398 | 0.3630 (0.1587) 0.0223 | 0.0046 |
| PCB 146 | 1.01 (0.81–1.26) | 1.06 (0.84–1.32) | 1.48 (1.15–1.91) | 2.3435 (1.0986) 0.0329 | 0.0903 (0.0611) 0.1393 | 0.1219 (0.0566) 0.0312 | 3.4321 (1.0103) 0.0007 | 0.0257 |
| PCB 153 | 1.05 (0.79– 1.39) | 1.26 (0.94–1.68) | 1.42 (1.03–1.95) | 0.2321 (0.1457) 0.1112 | 0.1199 (0.0609) 0.0489 | 0.0903 (0.0552) 0.1021 | 0.3631 (0.1221) 0.0030 | 0.0183 |
| PCB 156 | 1.00 (0.80–1.25) | 1.00 (0.79–1.28) | 1.24 (0.94–1.62) | −0.2324 (0.6936) 0.7376 | 0.0282 (0.0587) 0.6308 | −0.0183 (0.0421) 0.6627 | 2.2396 (0.9765) 0.0219 | 0.0082 |
| PCB 157 | 1.01 (0.78–1.32) | 0.74 (0.57–0.95) | 0.81 (0.61–1.07) | −1.7276 (2.7168) 0.5249 | 0.0136 (0.0430) 0.7512 | −0.0264 (0.0382) 0.4895 | 3.9313 (3.6762) 0.2850 | 0.0610 |
| PCB 167 | 0.91 (0.70–1.19) | 0.71 (0.55–0.92) | 1.31 (0.96–1.78) | 2.8837 (2.9219) 0.3237 | 0.0449 (0.0380) 0.2377 | 0.0453 (0.0470) 0.3350 | 3.9883 (2.6270) 0.1290 | 0.0593 |
| Quartile 2 vs. 1 | Quartile 3 vs. 1 | Quartile 4 vs. 1 | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | β (SE) Wald test p | Chi-square p | |
| PCB 170 | 1.07 (0.83–1.38) | 1.14 (0.86–1.51) | 1.36 (0.99–1.86) | 0.8607 (0.5392) 0.1104 | 0.1117 (0.0662) 0.0913 | 0.0729 (0.0547) 0.1826 | 1.2980 (0.4727) 0.0061 | 0.0764 |
| PCB 172 | 0.90 (0.70–1.15) | 0.83 (0.65–1.05) | 1.17 (0.90–1.54) | 6.2173 (2.9162) 0.0330 | 0.0433 (0.0456) 0.3425 | 0.1052 (0.0506) 0.0378 | 8.0991 (2.9156) 0.0055 | 0.6976 |
| PCB 177 | 0.93 (0.72–1.19) | 0.85 (0.67–1.06) | 0.95 (0.73–1.24) | 2.0869 (2.2230) 0.3479 | 0.0126 (0.0548) 0.8184 | 0.0428 (0.0487) 0.3794 | 3.2771 (2.0929) 0.1175 | 0.0700 |
| PCB 178 | 0.92 (0.72–1.17) | 0.87 (0.69–1.10) | 1.21 (0.93–1.58) | 4.6817 (2.5458) 0.0659 | 0.0401 (0.0520) 0.4405 | 0.0925 (0.0508) 0.0683 | 6.1459 (2.7717) 0.0267 | 0.2531 |
| PCB 180 | 0.95 (0.72–1.25) | 1.06 (0.79–1.44) | 1.22 (0.86–1.72) | 0.2610 (0.2019) 0.1960 | 0.0864 (0.0617) 0.1617 | 0.0664 (0.0542) 0.2210 | 0.4762 (0.1874) 0.0111 | 0.3838 |
| PCB 183 | 1.01 (0.81–1.26) | 0.95 (0.76–1.18) | 1.02 (0.80–1.31) | 3.5053 (1.9062) 0.0659 | 0.0439 (0.0578) 0.4470 | 0.0933 (0.0520) 0.0729 | 4.8404 (1.9036) 0.0110 | 0.2414 |
| PCB 187 | 1.12 (0.89–1.42) | 1.16 (0.89–1.50) | 1.25 (0.93–1.67) | 1.4990 (0.5978) 0.0122 | 0.1178 (0.0603) 0.0510 | 0.1517 (0.0598) 0.0111 | 2.1694 (0.5855) 0.0002 | 0.5394 |
| Analytic approach | Results |
|---|---|
| Collinearity | Collinearity present between: PCBs 157 and 167; PCBs 170 and 180; PCBs 146 and 153 |
| Cluster analysis | 4 clusters identified: PCBs 138, 146, 153, 170, 172, 177, 178, 180, 183, and 187; PCBs 52, 66, 101 and 128; PCBs 74, 99, 105 and 118; PCBs 156, 157 and 167 |
| Discriminant analysis | Most strongly associated PCBs are: 66, 74, 99, 105, 118, 128, 156, 157, 167, 178, 180 and 187 |
| Principal component analysis | 4 components with eigenvalues >1.0 |
| Optimization of weighted sum | PCBs 66 (weight = 0.3163), 101 (weight = 0.0819), 118 (weight = 0.2183), 128 (weight = 0.0856) and 187 (weight = 0.2979) |
© 2011 by the authors; licensee MDPI, Basel, Switzerland This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Christensen, K.L.Y.; White, P. A Methodological Approach to Assessing the Health Impact of Environmental Chemical Mixtures: PCBs and Hypertension in the National Health and Nutrition Examination Survey. Int. J. Environ. Res. Public Health 2011, 8, 4220-4237. https://doi.org/10.3390/ijerph8114220
Christensen KLY, White P. A Methodological Approach to Assessing the Health Impact of Environmental Chemical Mixtures: PCBs and Hypertension in the National Health and Nutrition Examination Survey. International Journal of Environmental Research and Public Health. 2011; 8(11):4220-4237. https://doi.org/10.3390/ijerph8114220
Chicago/Turabian StyleChristensen, Krista L. Yorita, and Paul White. 2011. "A Methodological Approach to Assessing the Health Impact of Environmental Chemical Mixtures: PCBs and Hypertension in the National Health and Nutrition Examination Survey" International Journal of Environmental Research and Public Health 8, no. 11: 4220-4237. https://doi.org/10.3390/ijerph8114220




