Fast Inverse Distance Weighting-Based Spatiotemporal Interpolation: A Web-Based Application of Interpolating Daily Fine Particulate Matter PM2.5 in the Contiguous U.S. Using Parallel Programming and k-d Tree
Abstract
:1. Introduction
1.1. Background
- IDW interpolation is simple and intuitive.
- IDW interpolation is fast to compute the interpolated values.
- The choice of IDW interpolation parameters are empirical (i.e., based on, concerned with or verifiable by observation or experience rather than theory or pure logic).
- The IDW interpolation is always exact (i.e., no smoothing).
- The IDW interpolation has sensitivity to outliers and sampling configuration (i.e., clustered and isolated points).
1.2. Literature Review on Interpolation in GIS
2. Methods
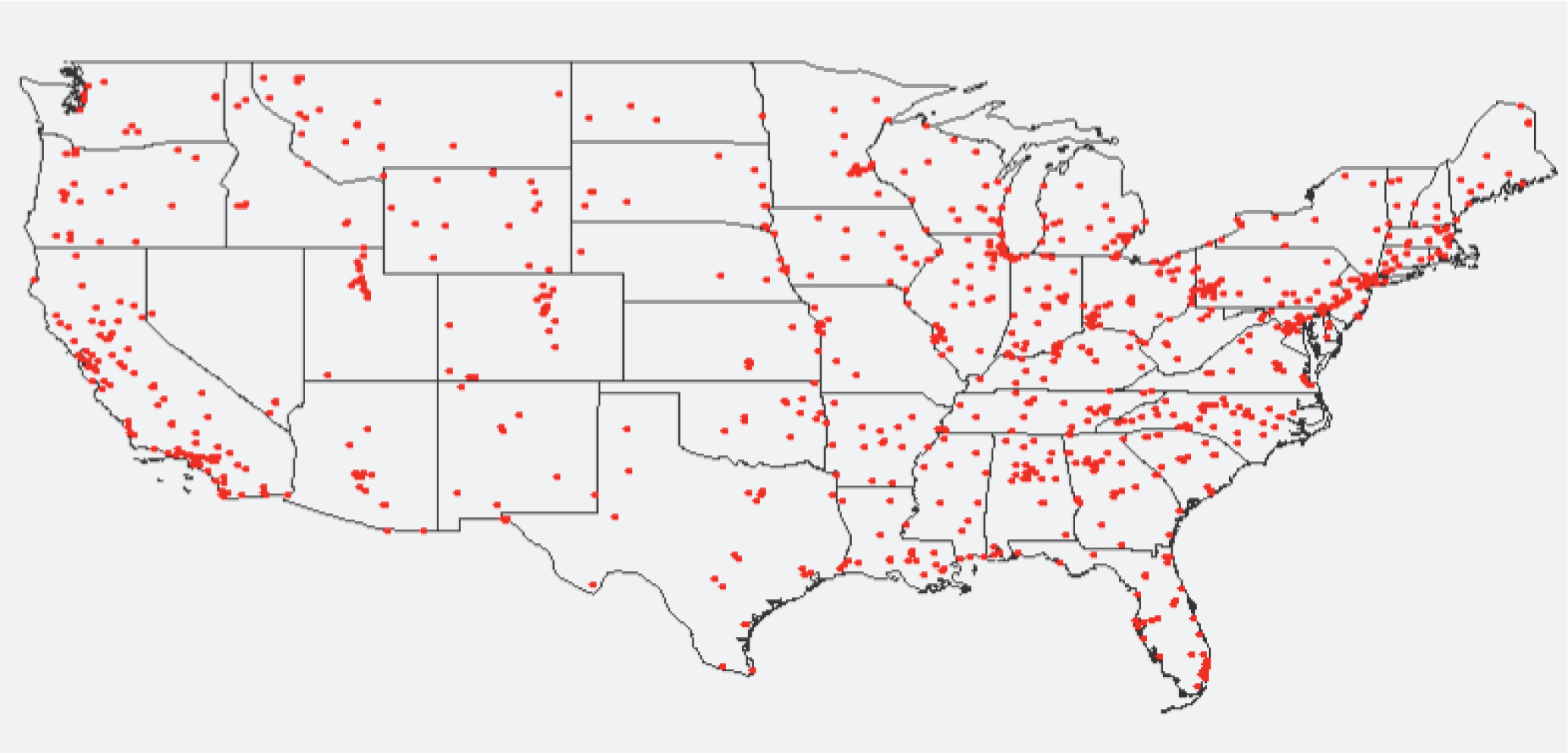
2.1. Experimental PM2.5 Data
2.2. IDW-Based Spatiotemporal Interpolation Method Using the Extension Approach
2.2.1. Original IDW-Based Spatiotemporal Interpolation Method Using the Extension Approach
| Day | t | c * t |
|---|---|---|
| 1 January 2009 | 1 | 0.1086 |
| 2 January 2009 | 2 | 0.2172 |
| 3 January 2009 | 3 | 0.3258 |
| 4 January 2009 | 4 | 0.4344 |
| ... | ... | ... |
| 31 December 2009 | 365 | 39.6390 |
2.2.2. Improved IDW-Based Spatiotemporal Interpolation Method Using the Extension Approach
2.2.3. Discussion of the Methods
2.3. Applying Parallel Computing Techniques
2.3.1. Motivation of Using Parallel Computing
2.3.2. Implementation of Parallel Computing
2.4. k-d Tree Data Structure
2.4.1. Motivation of Using k-d Tree
2.4.2. Properties of a k-d Tree
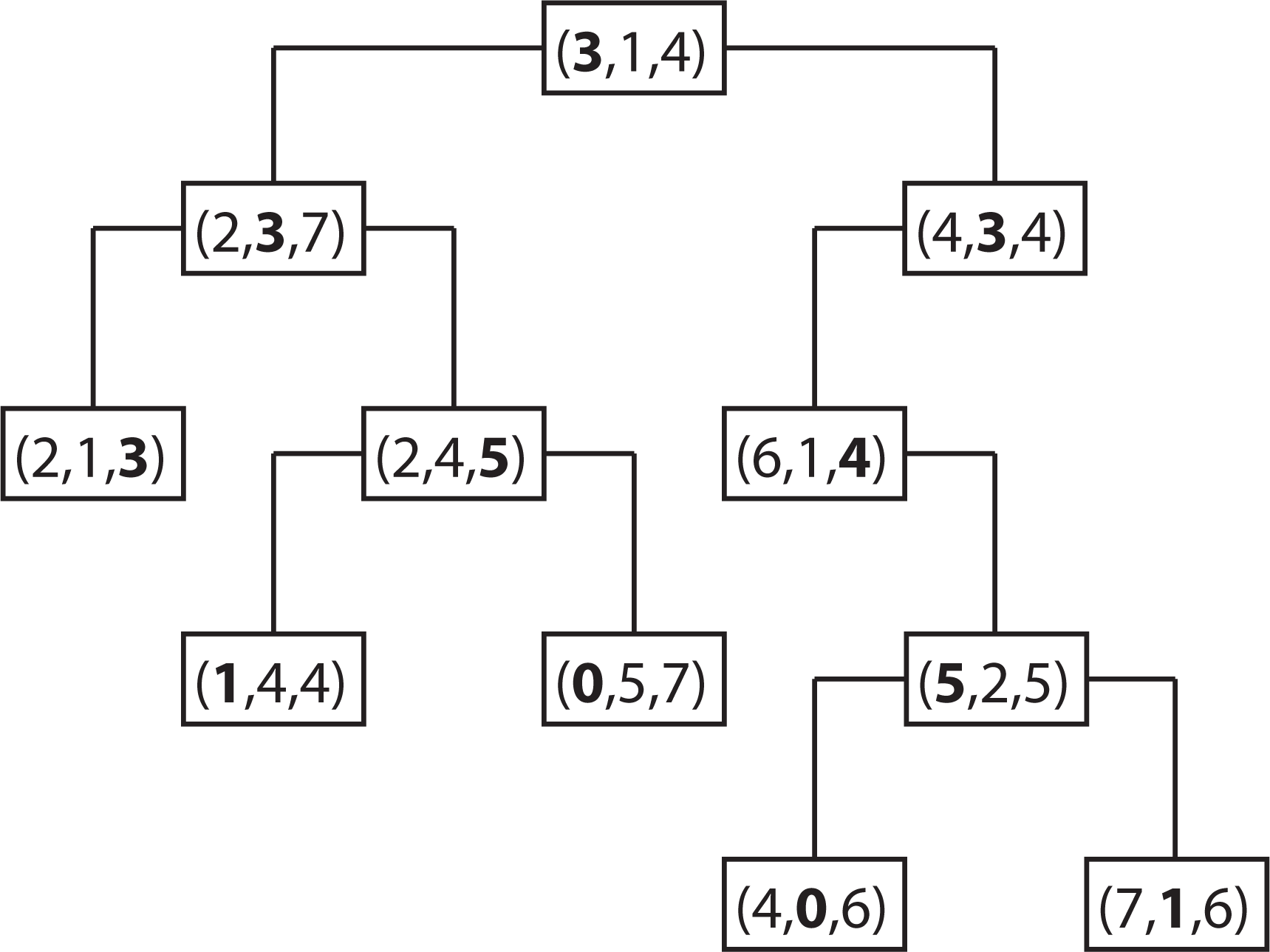
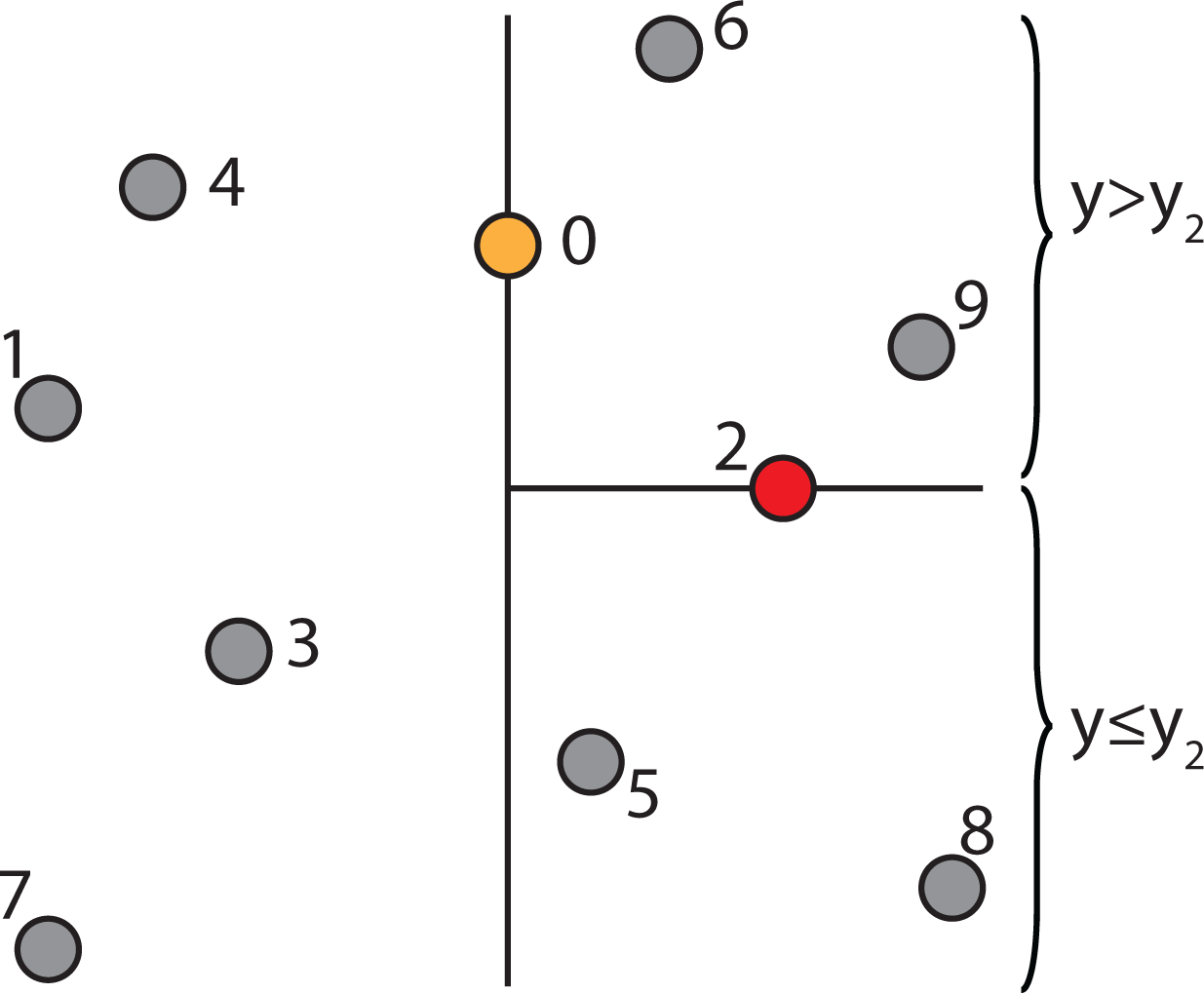
2.4.3. Constructing a k-d Tree


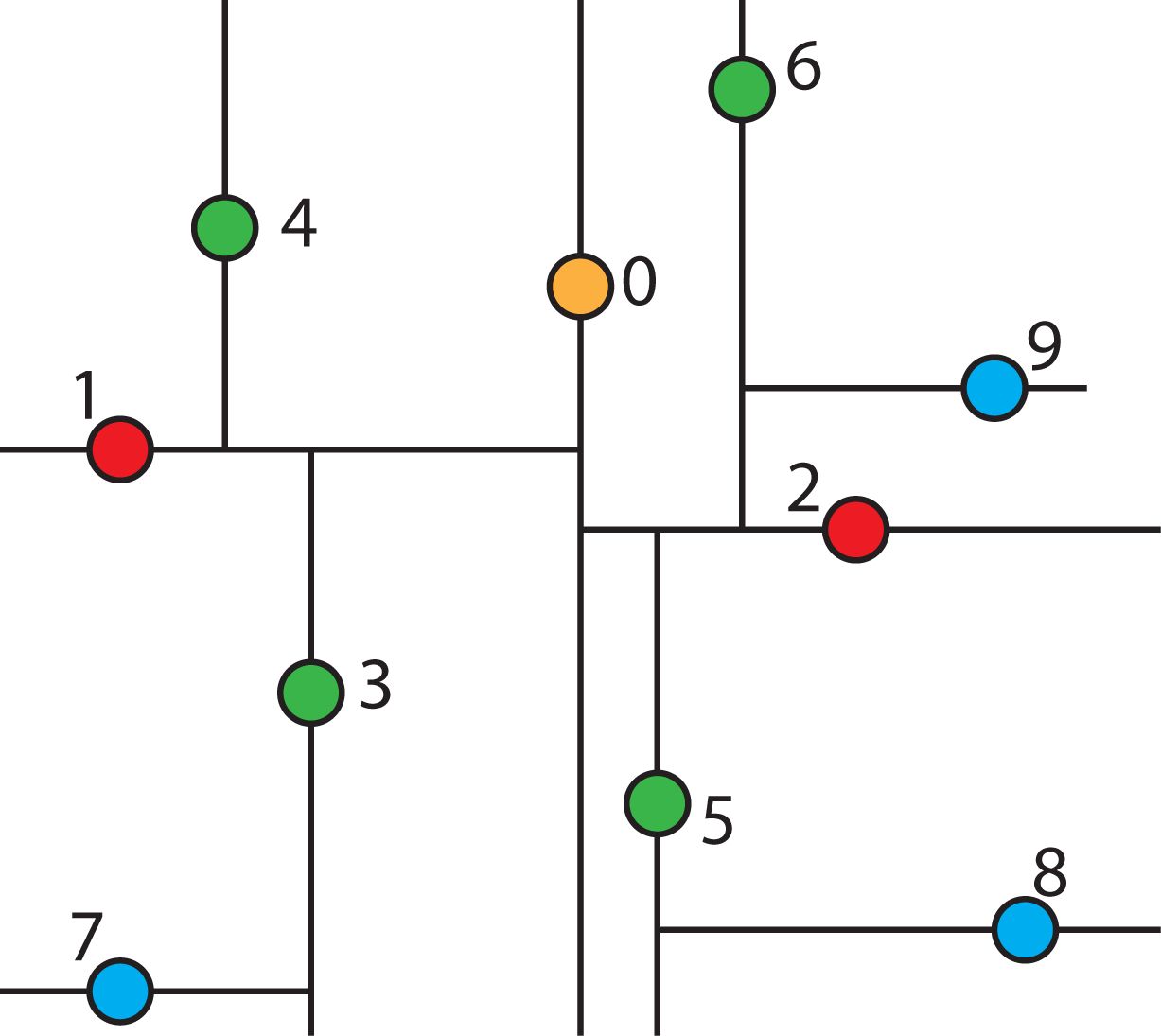

2.4.4. Searching a k-d Tree
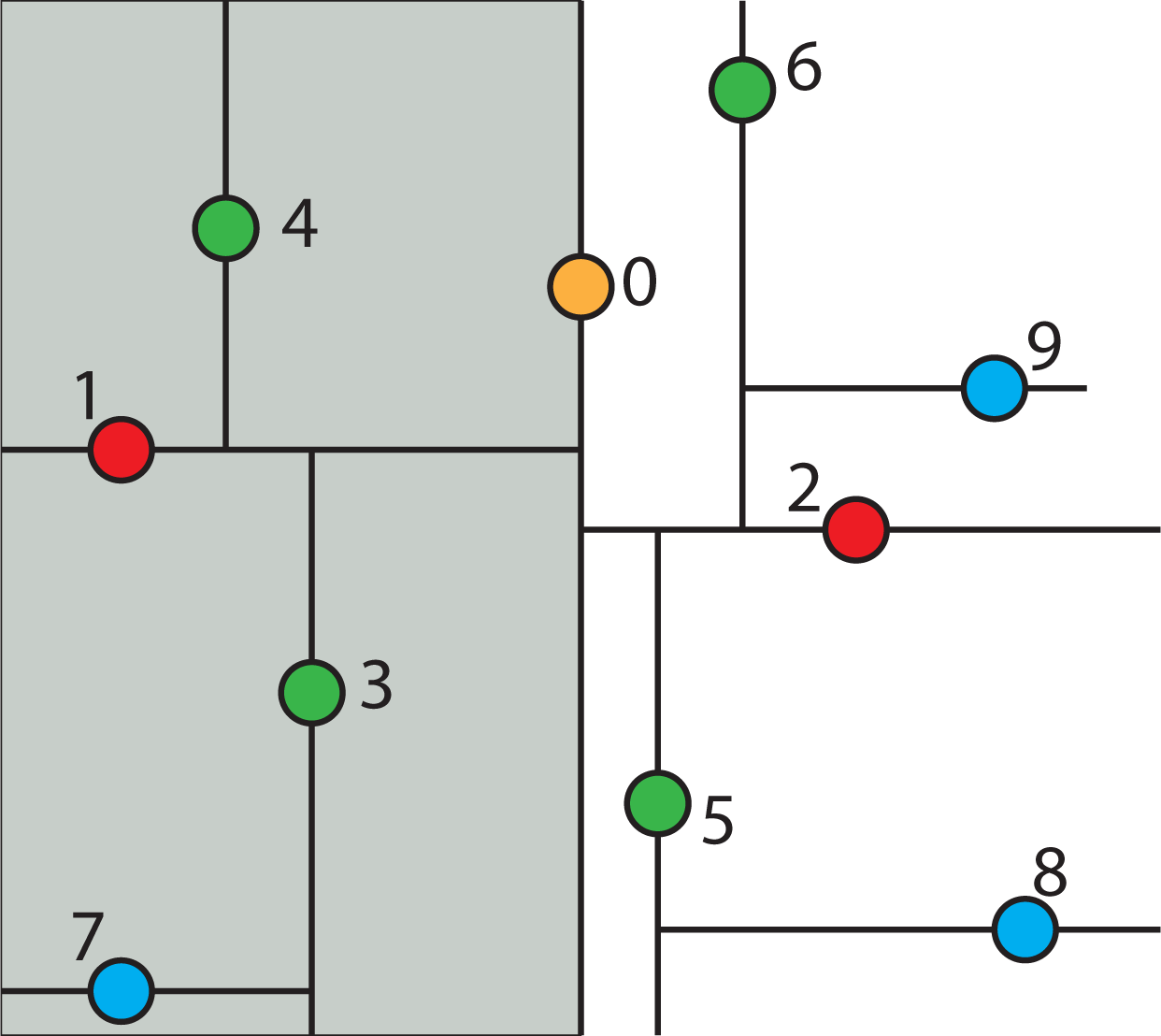


2.4.5. Nearest Neighbor Search Algorithm using k-d Tree to Find One Nearest Neighbor
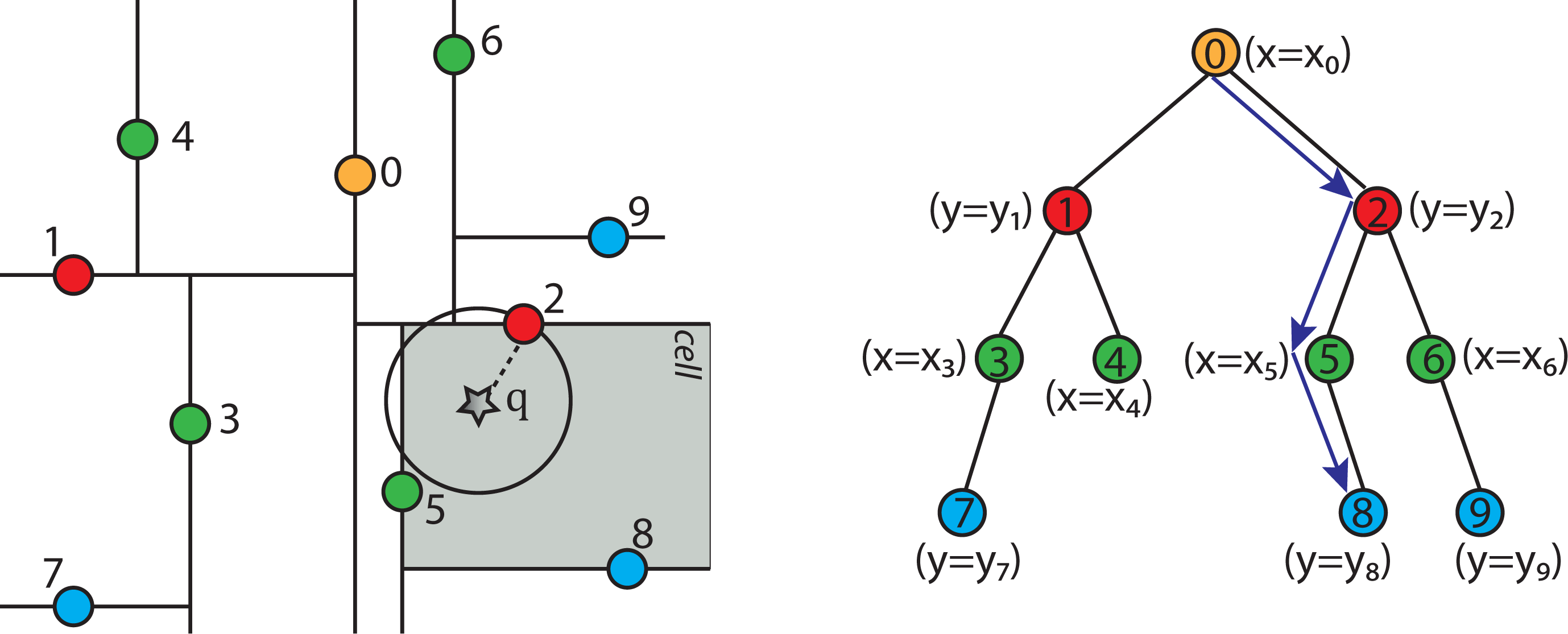
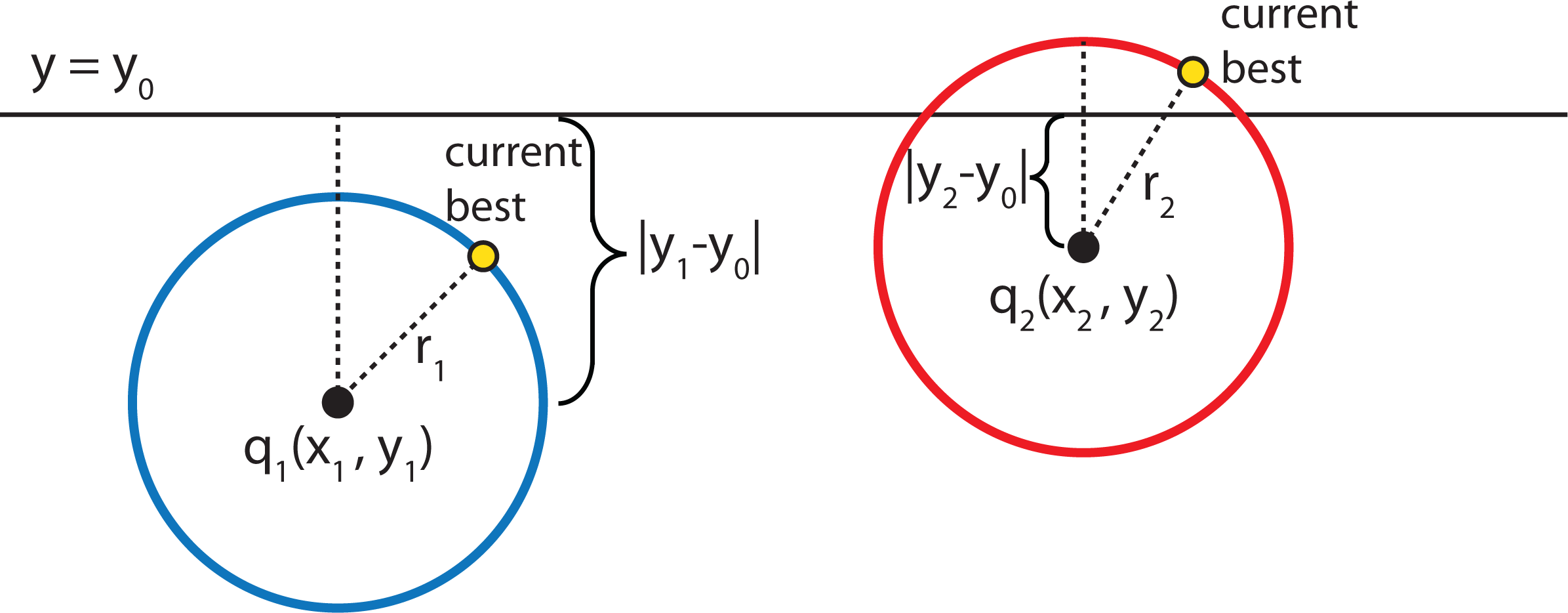
- Given a current best estimate of the node that may be the nearest neighbor, a candidate hyper-sphere can be constructed that is centered at the query point q(q0, q1, q2,...,qk−1) and running through the current best node point. The nearest neighbor to the query point must lie inside the hyper-sphere.
- If the hyper-sphere is fully to one side of a splitting hyper-plane, then all points on the other side of the splitting hyper-plane cannot be contained in the sphere and, thus, cannot be the nearest neighbor.
- To determine whether the candidate hyper-sphere crosses the splitting hyper-plane that compares coordinate at dimension i, check whether |qi − ai| < r.
2.4.6. Adapted Neighbor Search Algorithm Using a k-d Tree to Find Multiple Nearest Neighbors

| Algorithm 1: getNearestNeighbors(k, value) k-nearest neighbor search in a k-d tree |
 |
| Algorithm 2: searchNode(value, curr, k, neighborList, examined), Part I moving up the k-d tree to look for better nearest neighbors |
 |
| Algorithm 3: searchNode(value, curr, k, neighborList, examined), Part II |
 |
2.5. Cross-Validation
2.5.1. K-Fold Cross-Validation Method
2.5.2. Leave-One-Out Cross-Validation Method
2.5.3. Error Statistics
3. Results
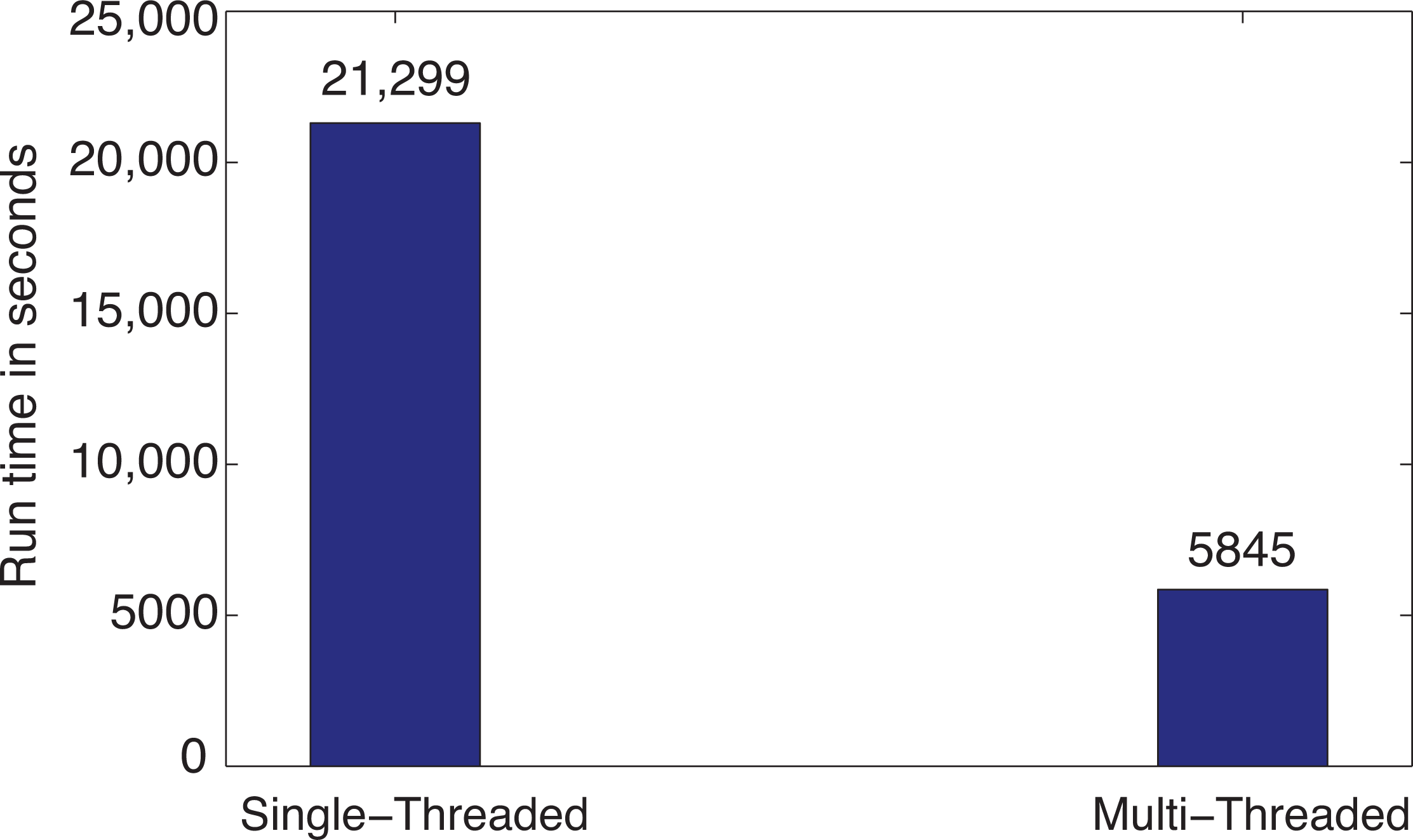
3.1. Computational Performance Improvement by Using Parallel Computing
3.2. Computational Performance Improvement of by Using k-d Tree
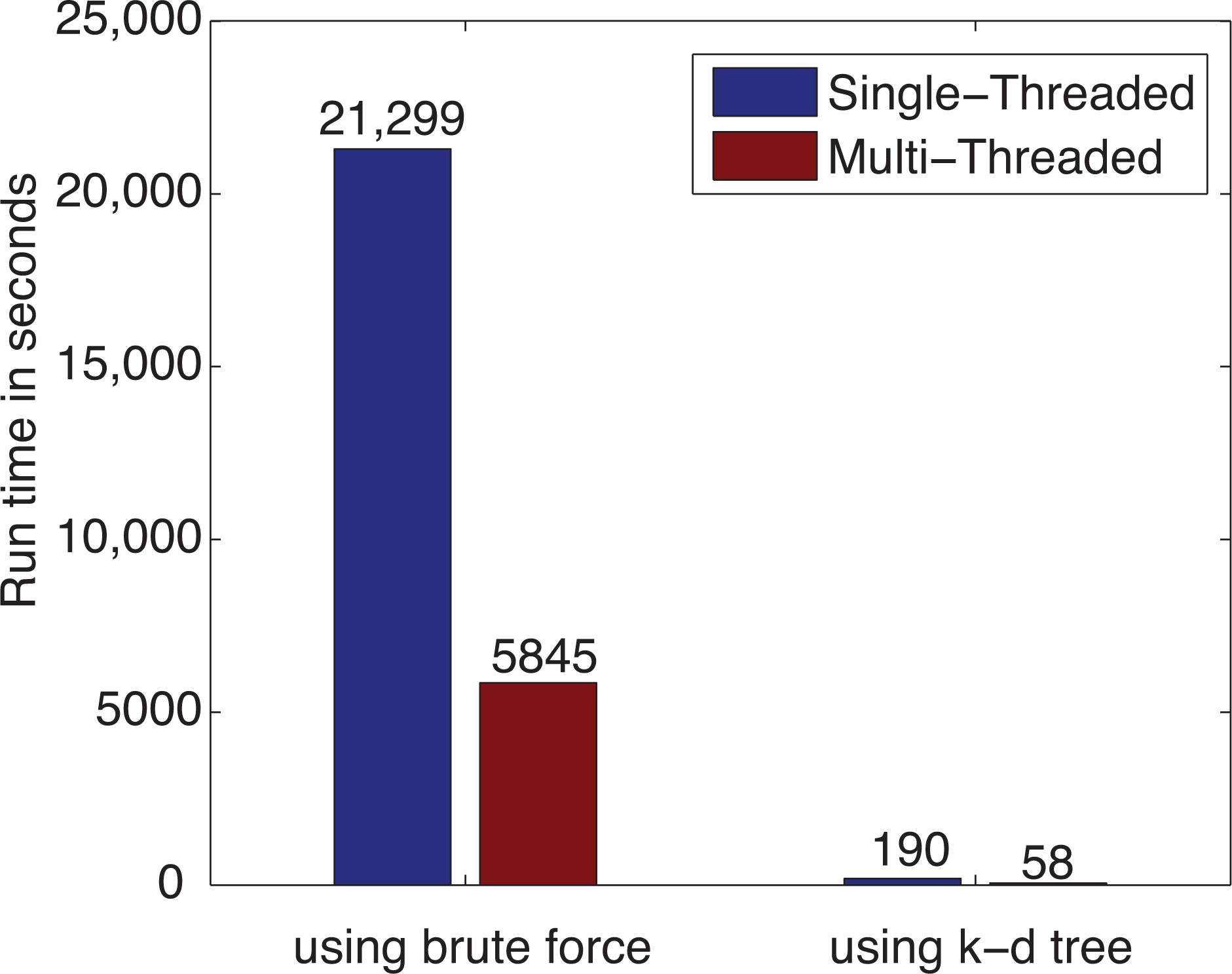
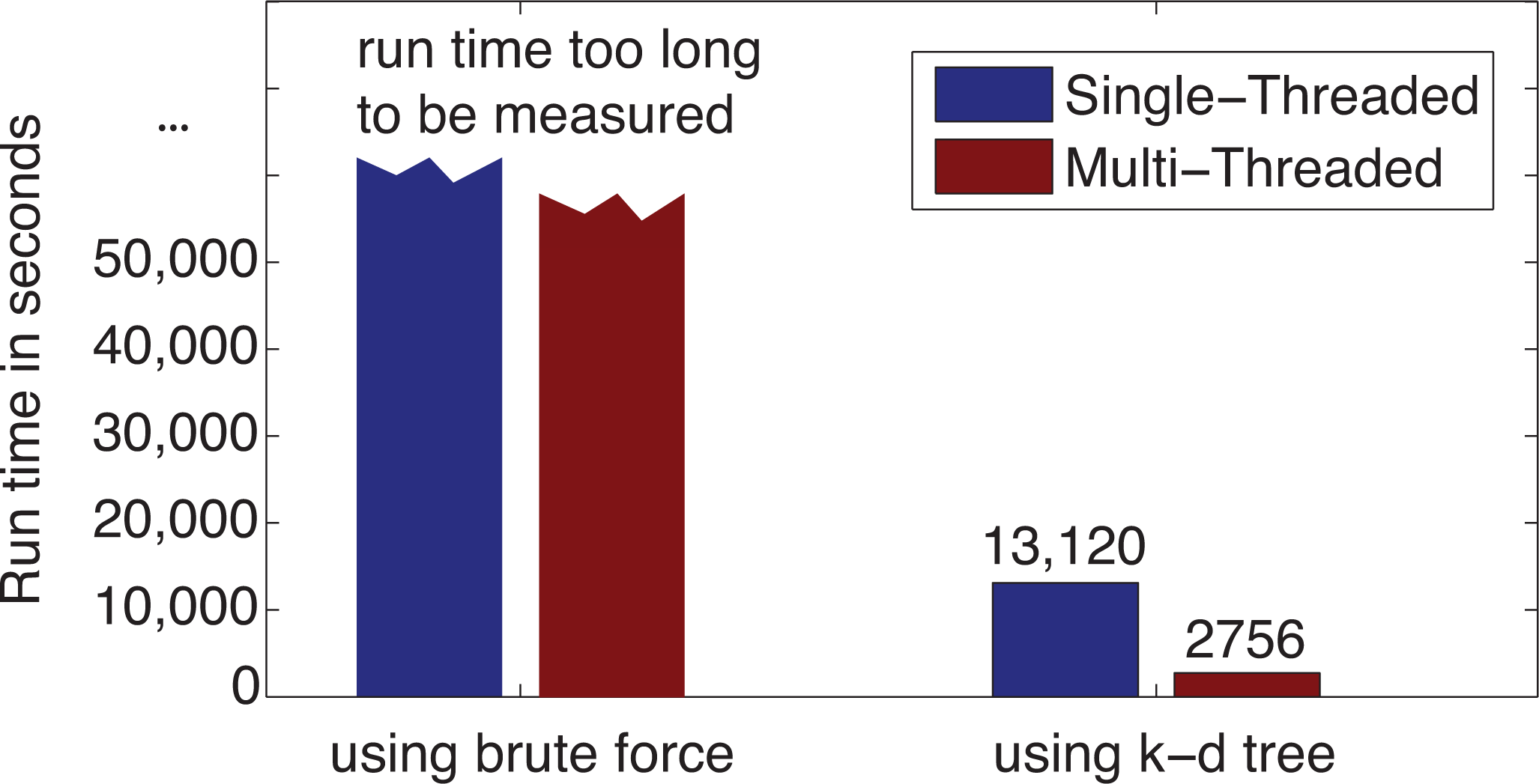
3.3. Leave-One-Out Cross-Validation Results for the Original IDW-Based Method

| Neighbors | Exponent | MARE |
|---|---|---|
| 3 | 1.0 | 0.54797 |
| 3 | 1.5 | 0.54301 |
| 3 | 2.0 | 0.54012 |
| 3 | 2.5 | 0.53849 |
| 3 | 3.0 | 0.53768 |
| 3 | 3.5 | 0.53739 |
| 3 | 4.0 | 0.53742 |
| 3 | 4.5 | 0.53768 |
| 3 | 5.0 | 0.53807 |
3.4. Cross-Validation Results for the Improved IDW-Based Method
3.4.1. Leave-One-Out Cross-Validation Results


| Exponent | MARE: n = 3 | MARE:n=4 | RMSPE:n=3 | RMSPE:n=4 |
|---|---|---|---|---|
| 1.0 | 0.37027 | 0.38444 | 242.1428 | 279.8240 |
| 1.5 | 0.36641 | 0.37664 | 210.7435 | 241.7803 |
| 2.0 | 0.36423 | 0.37154 | 185.4772 | 208.6938 |
| 2.5 | 0.36302 | 0.36816 | 167.2276 | 182.7473 |
| 3.0 | 0.36240 | 0.36595 | 155.4234 | 164.5911 |
| 3.5 | 0.36214 | 0.36454 | 148.5401 | 153.2638 |
| 4.0 | 0.36209 | 0.36367 | 144.8794 | 146.9017 |
| 4.5 | 0.36219 | 0.36317 | 143.0899 | 143.6380 |
| 5.0 | 0.36237 | 0.36294 | 142.2915 | 142.0947 |
3.4.2. Ten-Fold Cross-Validation Results
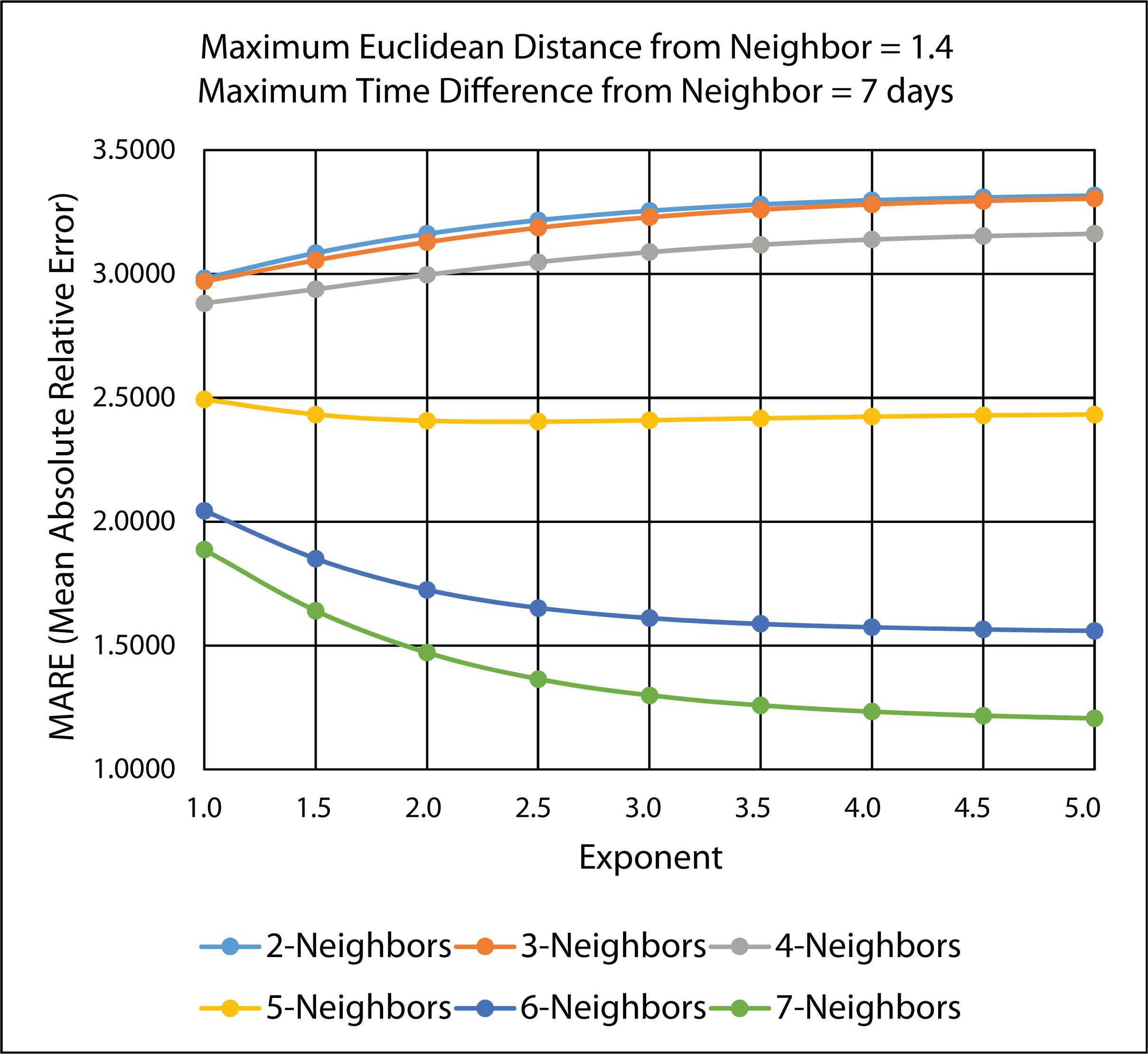
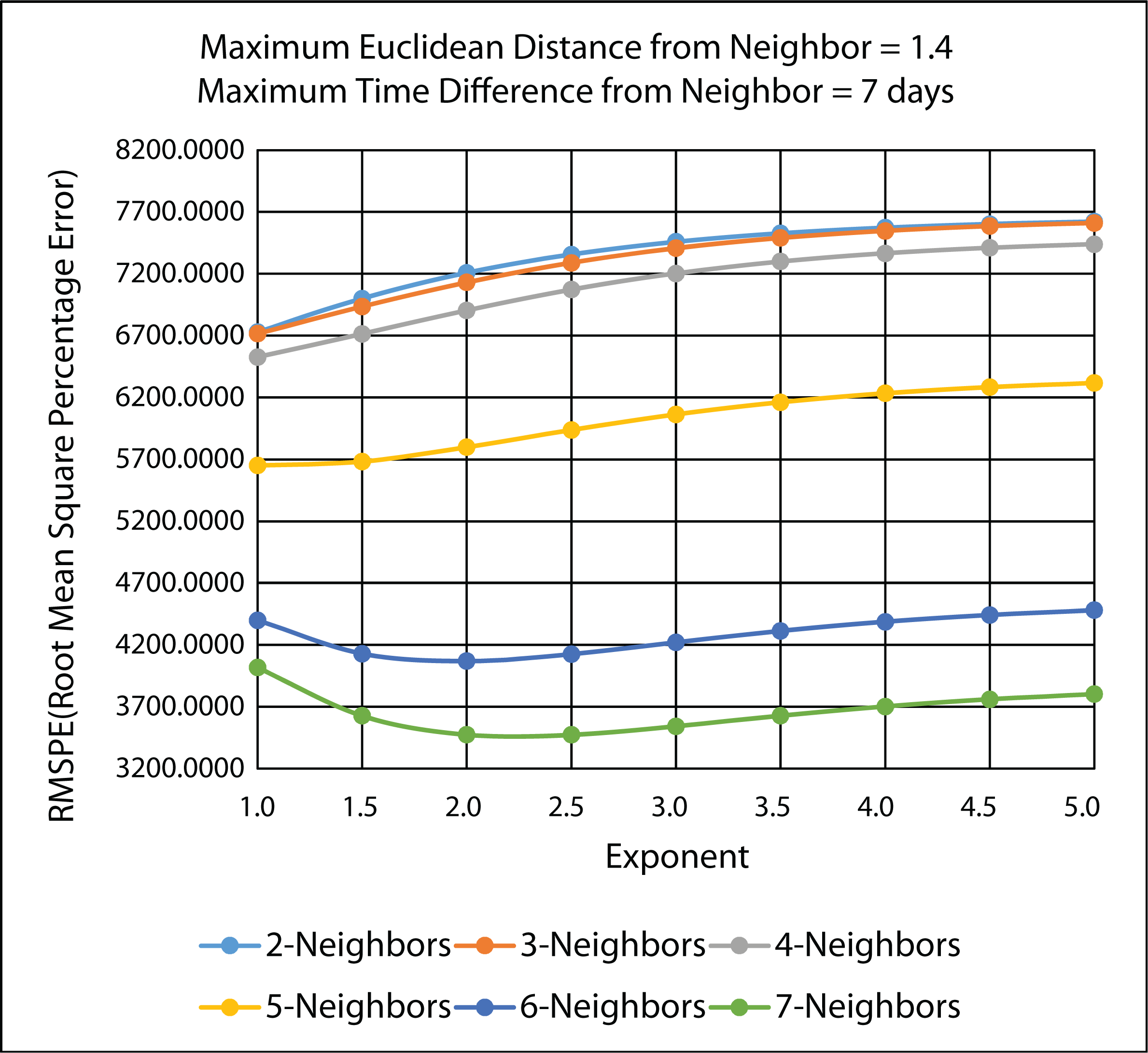
| Exponent | MARE: n = 7 | RMSPE: n = 7 |
|---|---|---|
| 1.0 | 1.88664 | 4016.4020 |
| 1.5 | 1.64071 | 3626.1590 |
| 2.0 | 1.47143 | 3472.6450 |
| 2.5 | 1.36437 | 3472.7490 |
| 3.0 | 1.29870 | 3542.2100 |
| 3.5 | 1.25827 | 3627.0180 |
| 4.0 | 1.23285 | 3702.0150 |
| 4.5 | 1.21648 | 3759.8730 |
| 5.0 | 1.20577 | 3801.4410 |
3.4.3. Comparison of Leave-One-Out and 10-Fold Cross-Validation Results
3.5. A Web-Based Spatiotemporal IDW Interpolation Application
3.5.1. Interpolation and Cross-Validation

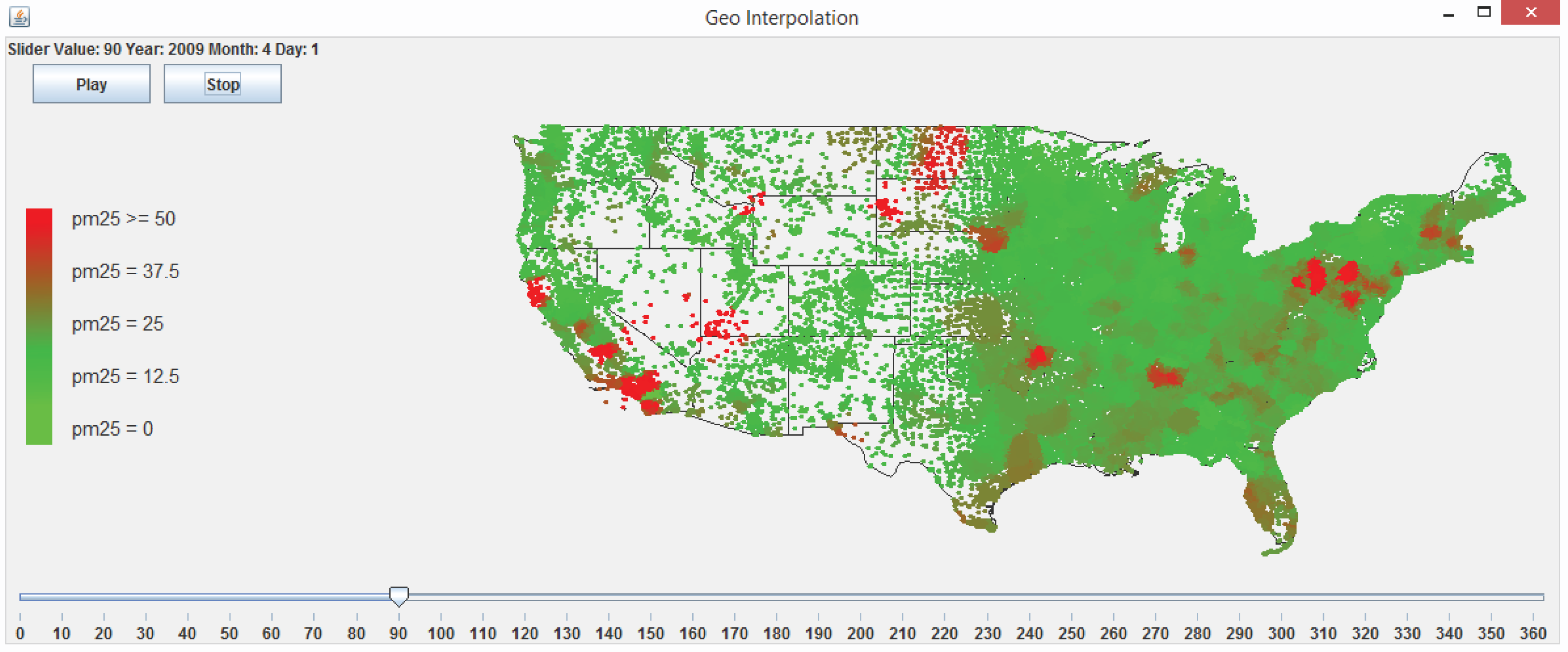
3.5.2. Visualization and Animation

4. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zou, B.; Wilson, J.G.; Zhan, F.B.; Zeng, Y. Air pollution exposure assessment methods utilized in epidemiological studies. J. Environ. Monit 2011, 11, 475–490. [Google Scholar]
- Ahmed, S.; Gan, H.T.; Lam, C.S.; Poonepalli, A.; Ramasamy, S.; Tay, Y.; Tham, M.; Yu, Y.H. Transcription factors and neural stem cell self-renewal, growth and differentiation. Cell Adhes. Migr 2009, 3, 412–424. [Google Scholar]
- Rehman, A.; Pandey, R.K.; Dixit, S.; Sarviya, R.M. Performance and emission evaluation of diesel engine fueled with vegetable oil. Int. J. Environ. Res 2009, 3, 463–470. [Google Scholar]
- Bell, M.L.; Ebisu, K.; Leaderer, B.P.; Gent, J.F.; Lee, H.J.; Koutrakis, P.; Wang, Y.; Dominici, F.; Peng, R.D. Associations of PM2.5 Constituents and sources with hospital admissions: Analysis of four counties in connecticut and Massachusetts (USA) for persons ≥ 65 years of age. Environ. Health Perspect 2014, 122, 138–144. [Google Scholar]
- Brunekreef, B.; Holgate, S.T. Air pollution and health. Lancet 2002, 360, 1233–1242. [Google Scholar]
- Pope, C.A.; Burnett, R.T.; Thurston, G.D.; Thun, M.J.; Calle, E.E.; Krewski, D.; Godleski, J.J. Cardiovascular mortality and long-term exposure to particulate air pollution: Epidemiological evidence of general pathophysiological pathways of disease. Circulation 2004, 109, 71–77. [Google Scholar]
- Pope, C.A.; Dockery, D.W. Health effects of fine particulate air pollution: Lines that connect. J. Air Waste Manag. Assoc 2006, 56, 709–742. [Google Scholar]
- Krall, J.R.; Anderson, G.B.; Dominici, F.; Bell, M.L.; Peng, R.D. Short-term exposure to particulate matter constituents and mortality in a national study of U.S. urban communities. Environ. Health Perspect 2013, 121, 1111–1119. [Google Scholar]
- Waller, L.A.; Louis, T.A.; Carlin, B.P. Environmental justice and statistical summaries of differences in exposure distributions. J. Expo. Anal. Environ. Epidemiol 1999, 9, 56–65. [Google Scholar]
- Ryan, P.H.; Lemasters, G.K.; Biswas, P.; Levin, L.; Hu, S.; Lindsey, M.; Bernstein, D.I.; Lockey, J.; Villareal, M.; Hershey, G.K.K.; Grinshpun, S.A. A comparison of proximity and land use regression traffic exposure models and wheezing in infants. Environ. Health Perspect 2007, 115, 278–284. [Google Scholar]
- Silverman, K.C.; Tell, J.G.; Sargent, E.V.; Qiu, Z. Comparison of the industrial source complex and AERMOD dispersion models: Case study for human health risk assessment. J. Air Waste Manag. Assoc 2007, 57, 1439–1446. [Google Scholar]
- Salehi, F.; Monavari, S.M.; Arjomandi, R.; Dabiri, F.; Samadi, R. Approach towards environmental monitoring plan in steam power plants. Int. J. Environ. Res 2010, 4, 433–438. [Google Scholar]
- Bell, M.L.; Belanger, K.; Ebisu, K.; Gent, J.F.; Lee, H.J.; Koutrakis, P.; Leaderer, B.P. Prenatal exposure to fine particulate matter and birth weight. Epidemiology 2010, 21, 884–891. [Google Scholar]
- Mulholland, J.A.; Butler, A.J.; Wilkinson, J.G.; Russell, A.G.; Tolbert, P.E. Temporal and spatial distributions of ozone in Atlanta: Regulatory and epidemiologic implications. J. Air Waste Manag. Assoc 1998, 48, 418–426. [Google Scholar]
- Jerrett, M.; Arain, A.; Kanaroglou, P.; Beckerman, B.; Potoglou, D.; Sahsuvaroglu, T.; Morrison, J.; Giovis, C. A review and evaluation of intraurban air pollution exposure models. J. Expo. Anal. Environ. Epidemiol 2005, 15, 185–204. [Google Scholar]
- Maheswaran, R.; Elliott, P. Stroke mortality associated with living near main roads in England and wales: A geographical study. Stroke 2003, 34, 2776–2780. [Google Scholar]
- Brender, J.D.; Zhan, F.B.; Langlois, P.H.; Suarez, L.; Scheuerle, A. Residential proximity to waste sites and industrial facilities and chromosomal anomalies in offspring. Int. J. Hyg. Environ. Health 2008, 211, 50–58. [Google Scholar]
- Rogers, J.F.; Thompson, S.J.; Addy, C.L.; McKeown, R.E.; Cowen, D.J.; Decouflé, P. Association of very low birth weight with exposures to environmental sulfur dioxide and total suspended particulates. Am. J. Epidemiol 2000, 151, 602–613. [Google Scholar]
- Bellander, T.; Berglind, N.; Gustavsson, P.; Jonson, T.; Nyberg, F.; Pershagen, G.; Järup, L. Using geographic information systems to assess individual historical exposure to air pollution from traffic and house heating in Stockholm. Environ. Health Perspect 2001, 109, 633–639. [Google Scholar]
- de Mesnard, L. Pollution models and inverse distance weighting: Some critical remarks. Comput. Geosci 2013, 52, 459–469. [Google Scholar]
- Shepard, D. A two-dimensional interpolation function for irregularly spaced data. Proceedings of the 23nd National Conference ACM, Las Vegas, NV, USA, 27–29 August 1968; ACM: New York, USA, 1968; pp. 517–524. [Google Scholar]
- Krige, D.G. A Statistical Approach to Some Mine Valuations and Allied Problems at the Witwatersrand.
- Zienkiewics, O.C.; Taylor, R.L. Finite Element Method, Volume 1, The Basis; Butterworth Heinemann: London, UK, 2000. [Google Scholar]
- de Boor, C. A Practical Guide to Splines; Springer: Berlin/Heidelberg, Germany, 2001; Volume 27. [Google Scholar]
- Zurflueh, E.G. Applications of two-dimensional linear wavelength filtering. Geophysics 1967, 32, 1015–1035. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr 1970, 46, 234–240. [Google Scholar]
- Murphy, R.; Curriero, F.; Ball, W. Comparison of spatial interpolation methods for water quality evaluation in the Chesapeake Bay. J. Environ. Eng 2010, 136, 160–171. [Google Scholar]
- Rahman, H.; Alireza, K.; Reza, G. Application of artificial neural network, kriging, and inverse distance weighting models for estimation of scour depth around bridge pier with bed sill. J. Softw. Eng. Appl 2010, 3, 944–964. [Google Scholar]
- Eldrandaly, K.A.; Abu-Zaid, M.S. Comparison of six GIS-based spatial interpolation methods for estimating air temperature in Western Saudi Arabia. J. Environ. Inf 2011, 18, 38–45. [Google Scholar]
- Xie, Y.; Chen, T.; Lei, M.; Yang, J.; Guo, Q.; Song, B.; Zhou, X. Spatial distribution of soil heavy metal pollution estimated by different interpolation methods: Accuracy and uncertainty analysis. Chemosphere 2011, 82, 468–476. [Google Scholar]
- Ninyerola, M.; Pons, X.; Roure, J.M. Objective air temperature mapping for the Iberian Peninsula using spatial interpolation and GIS. Int. J. Clim 2007, 27, 1231–1242. [Google Scholar]
- Luo, W.; Taylor, M.C.; Parker, S.R. A comparison of spatial interpolation methods to estimate continuous wind speed surfaces using irregularly distributed data from England and Wales. Int. J. Clim 2008, 28, 947–959. [Google Scholar]
- Miller, E.J. Towards a 4D GIS: Four-dimensional Interpolation Utilizing Kriging. In Innovations in GIS 4: Selected Papers from the Fourth National Conference on GIS Research U.K, Ch. 13; Taylor & Francis: London, UK, 1997; pp. 181–197. [Google Scholar]
- Li, L.; Revesz, P. A. Comparison of Spatio-Temporal Interpolation Methods. In Proceedings of the Second International Conference on GIScience 2002, Boulder, CO, USA, 25–28 September 2002; Springer: Berlin/Heidelberg, Germany, 2002; 2478, pp. 145–160. [Google Scholar]
- Li, L.; Li, Y.; Piltner, R. A. New Shape Function Based Spatiotemporal Interpolation Method. In Proceedings of the First International Symposium on Constraint Databases 2004, Paris, France, 12–13 June 2004; Springer: Berlin/Heidelberg, Germany, 2004; 3074, pp. 25–39. [Google Scholar]
- Revesz, P.; Wu, S. Spatiotemporal reasoning about epidemiological data. Artif. Intell. Med 2006, 38, 157–170. [Google Scholar]
- Li, L. Constraint Databases and Data Interpolation. In Encyclopedia of Geographic Information System; Shekhar, S., Xiong, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 144–153. [Google Scholar]
- Hussain, I.; Spöck, G.; Pilz, J.; Yu, H.L. Spatio-temporal interpolation of precipitation during monsoon periods in Pakistan. Adv. Water Resour 2010, 33, 880–886. [Google Scholar]
- Yu, H.L.; Wang, C.H. Quantile-based Bayesian maximum entropy approach for spatiotemporal modeling of ambient air quality levels. Environ. Sci. Technol 2013, 47, 1416–1424. [Google Scholar]
- Li, L.; Revesz, P. Interpolation methods for spatio-temporal geographic data. J. Comput. Environ. Urban Syst 2004, 28, 201–227. [Google Scholar]
- Liao, D.; Peuquet, D.J.; Duan, Y.; Whitsel, E.A.; Dou, J.; Smith, R.L.; Lin, H.M.; Chen, J.C.; Heiss, G. GIS Approaches for the estimation of residential-level ambient PM concentrations. Environ. Health Perspect 2006, 114, 1374–1380. [Google Scholar]
- Li, L.; Zhang, X.; Holt, J.B.; Tian, J.; Piltner, R. Estimating population exposure to fine particulate matter in the conterminous U.S. using shape function-based spatiotemporal interpolation method: A county level analysis. GSTF: Int. J. Comput 2012, 1, 24–30. [Google Scholar]
- Li, L. Spatiotemporal Interpolation Methods in GIS—Exploring Data for Decision Making; VDM Verlag Dr. Müller: Saarbrücken, Germany, 2009. [Google Scholar]
- Revesz, P. Introduction to Databases: From Biological to Spatio-Temporal; Springer: New York, NY, USA, 2010. [Google Scholar]
- Li, L.; Zhang, X.; Piltner, R. A Spatiotemporal Database for Ozone in the Conterminous U.S. Proceedings of the IEEE Thirteenth International Symposium on Temporal Representation and Reasoning, Budapest, Hungary, 15–17 June 2006; pp. 168–176.
- Li, L.; Zhang, X.; Piltner, R. An application of the shape function based spatiotemporal interpolation method on ozone and population exposure in the contiguous U.S. J. Environ. Inf 2008, 12, 120–128. [Google Scholar]
- Mueller, T.G.; Pusuluri, N.B.; Mathias, K.K.; Cornelius, P.L.; Barnhisel, R.I.; Shearer, S.A. Map Quality for ordinary kriging and inverse distance weighted interpolation. Soil Sci. Soc. Am. J 2004, 68, 2042–2047. [Google Scholar]
- Li, J.; Heap, A.D. A review of comparative studies of spatial interpolation methods in environmental sciences: Performance and impact factors. Ecol. Inf 2011, 6, 228–241. [Google Scholar]
- Akhtari, R.; Morid, S.; Mahdian, M.H.; Smakhtin, V. Assessment of areal interpolation methods for spatial analysis of SPI and EDI drought indices. Int. J. Clim 2009, 29, 135–145. [Google Scholar]
- Lu, G.Y.; Wong, D.W. An adaptive inverse-distance weighting spatial interpolation technique. Comput. Geosci 2008, 34, 1044–1055. [Google Scholar]
- Hayhoe, H.N.; Lapen, D.R.; Andrews, C.J. Using weather indices to predict survival of winter wheat in a cool temperate environment. Int. J. Biometeorol 2003, 47, 62–72. [Google Scholar]
- Kravchenko, A.; Bullock, D.G. A comparative study of interpolation methods for mapping soil properties. Agron. J 1999, 91, 393–400. [Google Scholar]
- Weber, J.; Adamek, H.E.; Riemann, J.F. Extracorporeal piezoelectric lithotripsy for retained bile duct stones. Endoscopy 1992, 24, 239–243. [Google Scholar]
- Childs, C. Interpolating surfaces in ArcGIS spatial analyst. ArcUser. 2004. Available onine: http://webapps.fundp.ac.be/geotp/SIG/interpolating.pdf (accessed on 1 September 2014).
- Hoek, G.; Fischer, P.; Van Den Brandt, P.; Goldbohm, S.; Brunekreef, B. Estimation of long-term average exposure to outdoor air pollution for a cohort study on mortality. J. Expo. Anal. Environ. Epidemiol 2001, 11, 459–469. [Google Scholar]
- Bell, M.L. The use of ambient air quality modeling to estimate individual and population exposure for human health research: A case study of ozone in the Northern Georgia Region of the United States. Environ. Int 2006, 32, 586–593. [Google Scholar]
- Kan, H.; Heiss, G.; Rose, K.M.; Whitsel, E.; Lurmann, F.; London, S.J. Traffic exposure and lung function in adults: The atherosclerosis risk in communities study. Thorax 2007, 62, 873–879. [Google Scholar]
- Brauer, M.; Lencar, C.; Tamburic, L.; Koehoorn, M.; Demers, P.; Karr, C. A cohort study of traffic-related air pollution impacts on birth outcomes. Environ. Health Perspect 2008, 116, 680–686. [Google Scholar]
- Wikipedia. Census Block Group. 2013. Available online: http:\\en.wikipedia.org\wiki\Census_block_group (accessed on 1 September 2014).
- Clemons, W.; Grecol, M.; Losser, T.; Yorke, C. Monitoring Pollution Trend in the Course of the Year Using Inverse Distance Weighting Spatio-Temporal Interpolation. Technical Report at Department of Computer Sciences; Georgia Southern University: Statesboro, GA, USA, 2013. [Google Scholar]
- Fasshauer, G.E. Meshfree Approximation Methods with MATLAB; World Scientific Publishing: Singapore, 2007. [Google Scholar]
- Wendland, H. Scattered Data Approximation; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Kurniawan, B. Java 7: A Beginner’s Tutorial, 3rd ed.; BrainySoftware: Quebec, Canada, 2011. [Google Scholar]
- Bentley, J.L. Multidimensional binary search trees used for associative searching. Commun. ACM 1975, 18, 509–517. [Google Scholar]
- Heineman, G.; Pollice, G.; Selkow, S. Algorithms in a Nutshell; O’Reilly Media: Sebastopol, CA, USA, 2008. [Google Scholar]
- Friedman, J.H.; Bentley, J.L.; Finkel, R.A. An Algorithm for finding best matches in logarithmic expected time. ACM Trans. Math. Softw 1977, 3, 209–226. [Google Scholar]
- Refaeilzadeh, P.; Tang, L.; Liu, H. Cross Validation. In Encyclopedia of Database Systems; Özsu, M.T., Liu, L., Eds.; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Vural, R.A.; Özyilmaz, L.; Yildirim, T. A comparative study on computerised diagnostic performance of hepatitis disease using ANNs. Proceedings of the 2006 International Conference on Intelligent Computing, Kunming, China, 16–19 August 2006; pp. 1177–1182.
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, L.; Losser, T.; Yorke, C.; Piltner, R. Fast Inverse Distance Weighting-Based Spatiotemporal Interpolation: A Web-Based Application of Interpolating Daily Fine Particulate Matter PM2.5 in the Contiguous U.S. Using Parallel Programming and k-d Tree. Int. J. Environ. Res. Public Health 2014, 11, 9101-9141. https://doi.org/10.3390/ijerph110909101
Li L, Losser T, Yorke C, Piltner R. Fast Inverse Distance Weighting-Based Spatiotemporal Interpolation: A Web-Based Application of Interpolating Daily Fine Particulate Matter PM2.5 in the Contiguous U.S. Using Parallel Programming and k-d Tree. International Journal of Environmental Research and Public Health. 2014; 11(9):9101-9141. https://doi.org/10.3390/ijerph110909101
Chicago/Turabian StyleLi, Lixin, Travis Losser, Charles Yorke, and Reinhard Piltner. 2014. "Fast Inverse Distance Weighting-Based Spatiotemporal Interpolation: A Web-Based Application of Interpolating Daily Fine Particulate Matter PM2.5 in the Contiguous U.S. Using Parallel Programming and k-d Tree" International Journal of Environmental Research and Public Health 11, no. 9: 9101-9141. https://doi.org/10.3390/ijerph110909101





