Stereochemistry of Complex Marine Natural Products by Quantum Mechanical Calculations of NMR Chemical Shifts: Solvent and Conformational Effects on Okadaic Acid
Abstract
:1. Introduction

2. Results and Discussion
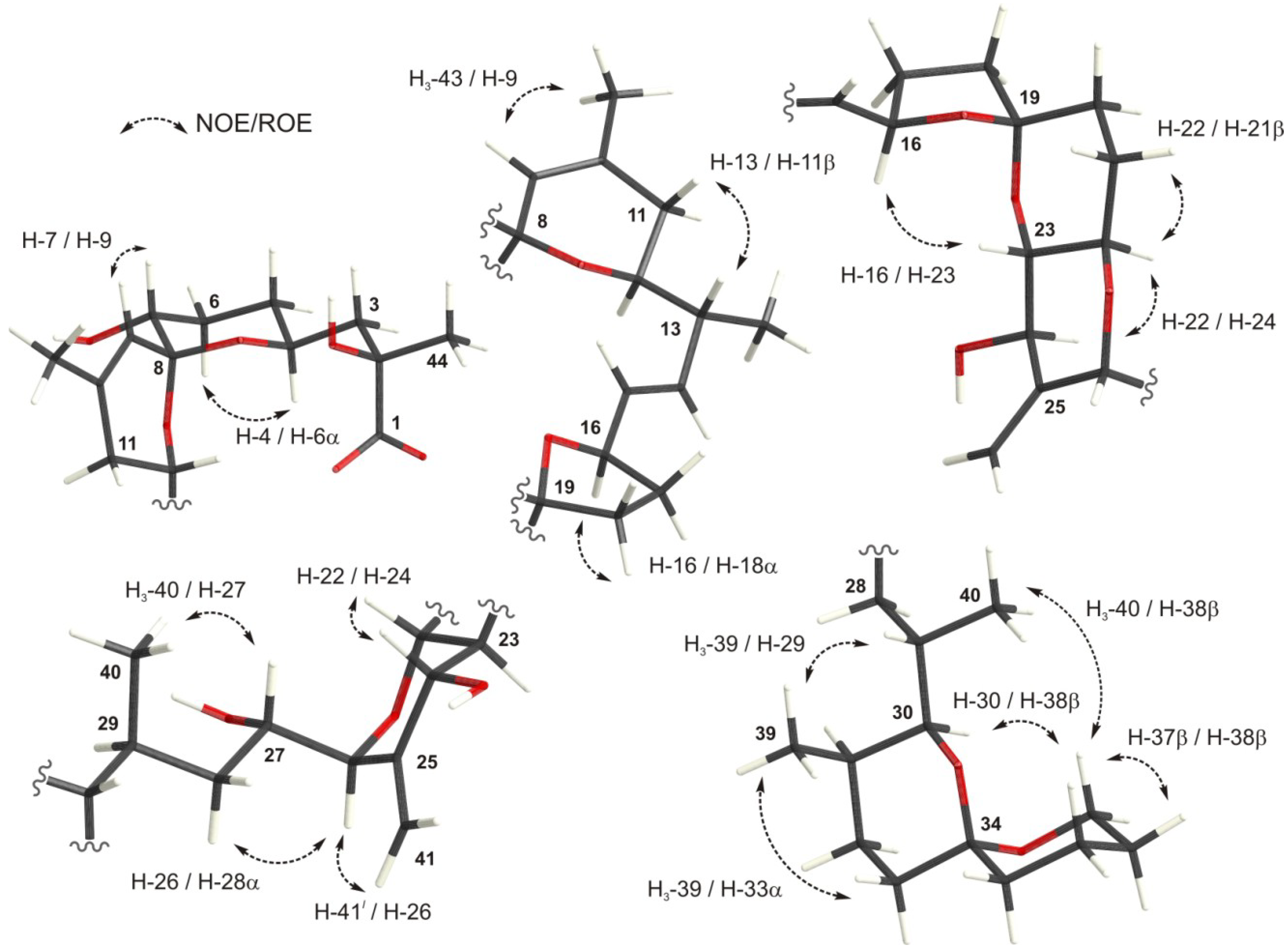
2.1. Crystallographic Structure of Okadaic Acid
2.2. Experimental NMR Data of Okadaic Acid
| C | δC | δH | 3JH,H | C | δC | δH | 3JH,H |
|---|---|---|---|---|---|---|---|
| 1 | 182.2 | - | - | 23 | 78.1 | 3.28 | 9.8, 9.8 |
| 2 | 76.0 | - | - | 24 | 71.8 | 3.92 | 9.8 |
| 3 | 46.1 | 1.79S | 2.0, 12.0 | 25 | 146.7 | - | - |
| 1.65R | 11.0, 12.0 | ||||||
| 4 | 68.2 | 3.92 | 2.0, 2.5, 9.0, 11.0 | 26 | 86.2 | 3.80 | 8.8 |
| 5 | 33.1 | (β) 1.72R | 4.0, 9.0, 10.0, 13.0 | 27 | 65.8 | 3.94 | 2.0, 8.8, 10.0 |
| (α) 1.30S | 2.5, 2,5, 5.0, 13.0 | ||||||
| 6 | 28.2 | (α) 1.82R | 4.0, 4.8, 5.0, 13.0 | 28 | 36.3 | 1.28R | 2.6, 10.0, 12.0 |
| (β) 1.51S | 2.5, 9.5, 10.0, 13.0 | 0.82S | 2.0, 11.0, 12.0 | ||||
| 7 | 73.2 | 3.22 | 4.8, 9.5 | 29 | 32.0 | 1.78 | 2.6, 6.4, 10.5, 11.0 |
| 8 | 97.1 | - | - | 30 | 76.7 | 3.13 | 2.2, 10.5 |
| 9 | 123.5 | 5.13 | - | 31 | 28.5 | 1.69 | 2.2, 2.5, 6.5, 6.9 |
| 10 | 138.8 | - | - | 32 | 27.5 | (α) 1.88S | 2.5, 2.5, 12.0, 12.0 |
| (β) 1.25R | 2.0, 6.5, 6.5, 12.0 | ||||||
| 11 | 33.4 | (β) 1.90R | 11.0, 16.0 | 33 | 30.6 | 1.22(2H) | - |
| (α) 1.69S | 4.0, 16.0 | ||||||
| 12 | 71.4 | 3.71 | 4.0, 8.0, 11.0 | 34 | 96.5 | - | |
| 13 | 42.9 | 2.20 | 7.0, 8.0, 8.5 | 35 | 36.6 | (β) 1.49R | 2,5, 4.3, 13.0 |
| (α) 1.26S | 2.5, 13.0, 13.0 | ||||||
| 14 | 137.2 | 5.81 | 8.5, 15.4 | 36 | 19.4 | (α) 1.79S | 2.5, 2.5, 4.3, 4.3, 13.0 |
| (β) 1.40R | 2.5, 2.5, 13.0, 13.0, 13.0 | ||||||
| 15 | 131.9 | 5.34 | 7.9, 15.4 | 37 | 26.1 | 1.37(2H) | - |
| 16 | 80.2 | 4.52 | 7.5, 7.5, 7.9 | 38 | 60.9 | (β) 3.57S | 3.0, 11.5, 12.0 |
| (α) 3.39R | 2.5, 3.0, 12.0 | ||||||
| 17 | 31.0 | (α) 2.04R | 6.2, 7.5, 9.5, 12.0 | 39 | 10.6 | 0.79 | 6.9 |
| (β) 1.43S | 5.0, 5.5, 7.5, 12.0 | ||||||
| 18 | 37.7 | (α) 1.88S | 5.0,9.5, 12.5 | 40 | 16.8 | 0.91 | 6.4 |
| (β) 1.72R | 5.5, 6.2, 12.5 | ||||||
| 19 | 106.5 | - | - | 41 | 112.6 | 5.25 | - |
| 4.91 | |||||||
| 20 | 33.4 | 1.75 (2H) | - | 42 | 16.9 | 0.98 | 7.0 |
| 21 | 27.5 | (α) 1.75R | 4.0, 13.0 | 43 | 22.9 | 1.59 | - |
| (β) 1.65S | 10.0, 13.0 | ||||||
| 22 | 71.1 | 3.50 | 4.0, 9.8, 10.0 | 44 | 27.5 | 1.16 | - |
2.3. Diasteroisomeric Structure of Okadaic Acid
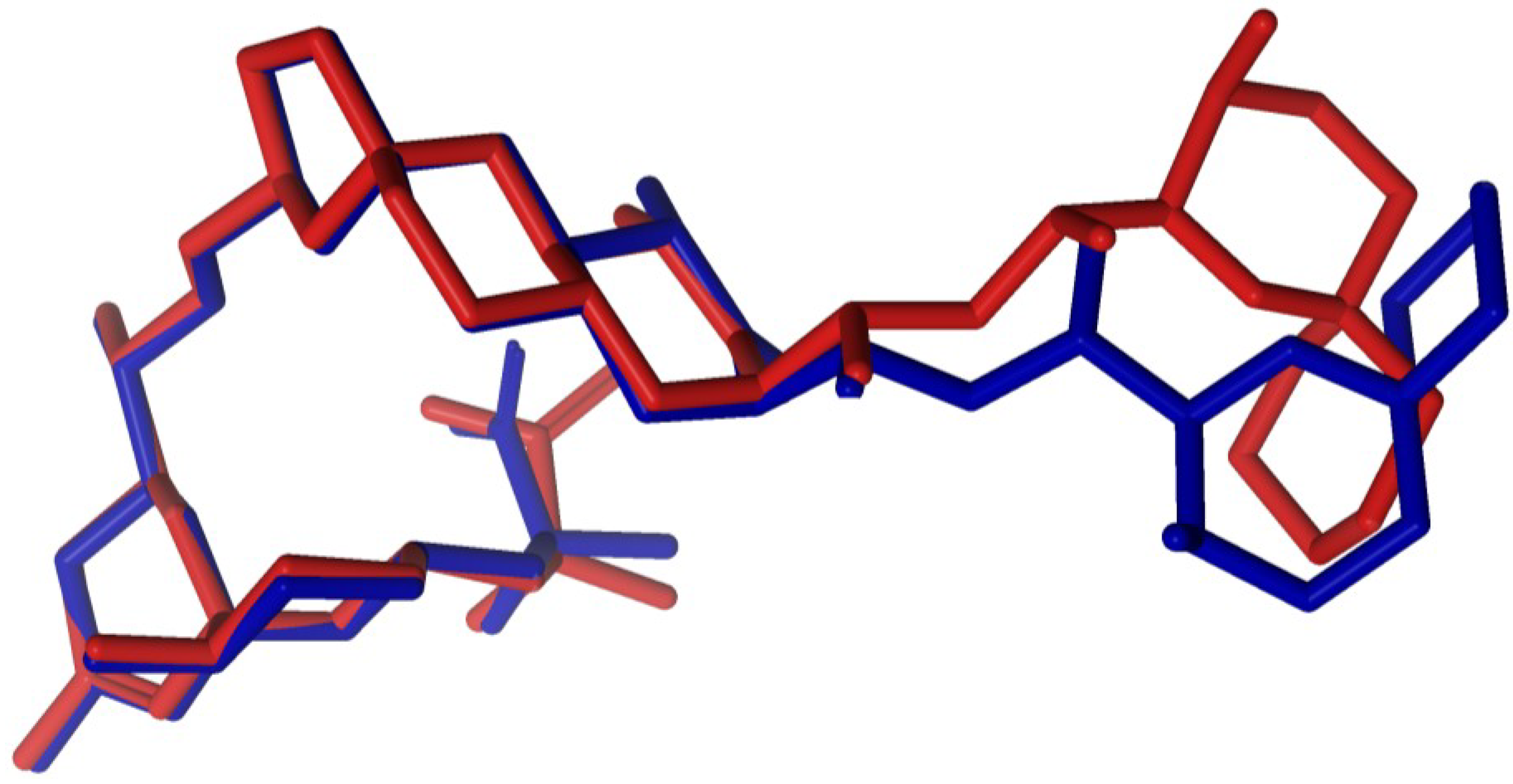
2.4. Conformational Searches
2.5. Calculation of NMR Chemical Shifts
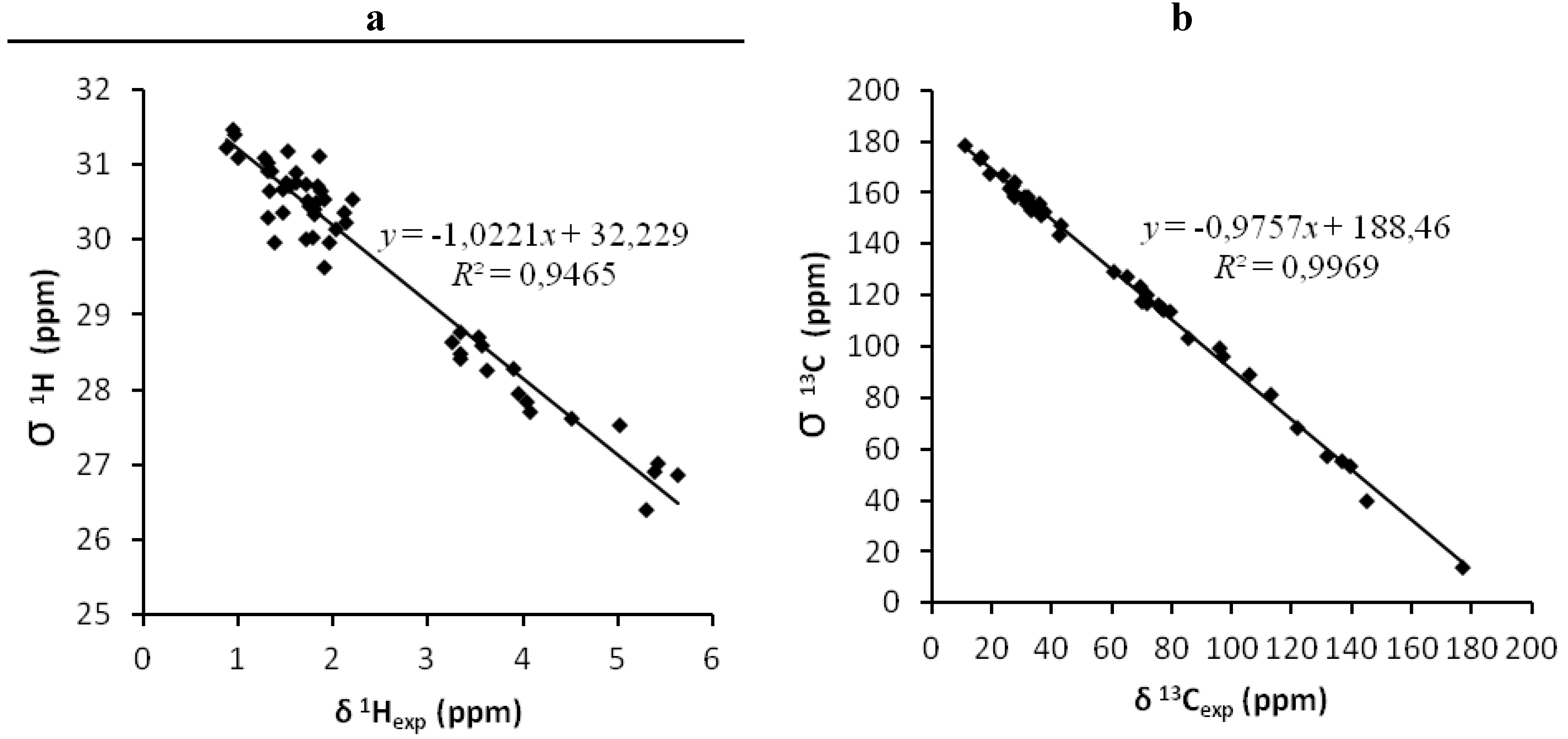
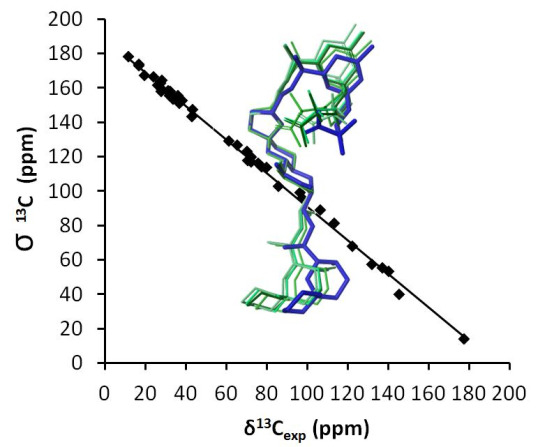
| C | 1-Gas (CDCl3) | 1-CHCl3 (CDCl3) | 2-Gas (CDCl3) | 2-CHCl3 (CDCl3) | Expt (CDCl3) | Expt (CD3OD) | 1-Gas (CD3OD) | 1-CH3OH (CD3OD) | 2-Gas (CD3OD) | 2-CH3OH (CD3OD) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 178.7 | 179.5 | 172.9 | 172.5 | 177.1 | 182.2 | 180.2 | 180.7 | 174.3 | 176.0 |
| 2 | 76.2 | 76.5 | 73.9 | 74.8 | 77.0 | 76.0 | 76.8 | 77.1 | 74.5 | 75.8 |
| 3 | 42.1 | 42.1 | 43.2 | 43.0 | 42.8 | 46.1 | 42.4 | 42.2 | 43.4 | 43.0 |
| 4 | 66.8 | 67.6 | 68.3 | 68.0 | 69.8 | 68.2 | 67.3 | 68.1 | 68.8 | 67.8 |
| 5 | 31.1 | 31.3 | 30.9 | 30.7 | 32.0 | 33.1 | 31.3 | 31.4 | 31.1 | 30.9 |
| 6 | 31.2 | 31.3 | 35.3 | 35.7 | 27.5 | 28.2 | 31.4 | 31.5 | 35.5 | 35.9 |
| 7 | 73.1 | 72.4 | 71.4 | 71.0 | 72.0 | 73.2 | 73.7 | 72.8 | 71.9 | 71.2 |
| 8 | 94.8 | 94.4 | 94.5 | 93.6 | 97.0 | 97.1 | 95.6 | 95.1 | 95.2 | 93.0 |
| 9 | 123.5 | 120.2 | 123.3 | 120.2 | 121.9 | 123.5 | 124.5 | 119.7 | 124.3 | 118.7 |
| 10 | 138.3 | 140.9 | 138.4 | 141.7 | 139.9 | 138.8 | 139.4 | 143.9 | 139.5 | 144.0 |
| 11 | 34.5 | 34.6 | 31.6 | 31.3 | 33.6 | 33.4 | 34.7 | 35.0 | 31.8 | 31.6 |
| 12 | 70.1 | 69.7 | 67.5 | 68.3 | 72.0 | 71.4 | 70.7 | 70.5 | 68.0 | 67.5 |
| 13 | 46.3 | 45.9 | 46.2 | 45.7 | 42.6 | 42.9 | 46.6 | 46.2 | 46.5 | 46.1 |
| 14 | 136.3 | 136.8 | 134.0 | 135.0 | 136.9 | 137.2 | 137.4 | 139.1 | 135.1 | 135.3 |
| 15 | 134.2 | 133.4 | 139.6 | 138.5 | 131.8 | 131.9 | 135.3 | 133.6 | 140.8 | 138.2 |
| 16 | 76.6 | 76.5 | 74.9 | 75.2 | 79.6 | 80.2 | 77.2 | 76.8 | 75.5 | 75.3 |
| 17 | 30.6 | 30.6 | 29.0 | 28.9 | 31.1 | 31.0 | 30.8 | 30.6 | 29.2 | 29.0 |
| 18 | 36.7 | 36.9 | 33.1 | 33.3 | 37.7 | 37.7 | 36.9 | 37.3 | 33.3 | 33.5 |
| 19 | 101.9 | 101.8 | 104.1 | 103.4 | 106.1 | 106.5 | 102.7 | 102.6 | 104.9 | 104.2 |
| 20 | 35.9 | 35.6 | 35.7 | 35.6 | 33.2 | 33.4 | 36.1 | 35.8 | 36.0 | 35.8 |
| 21 | 26.3 | 26.2 | 26.5 | 26.6 | 27.0 | 27.5 | 26.5 | 26.3 | 26.6 | 26.9 |
| 22 | 72.4 | 72.5 | 72.9 | 70.1 | 70.2 | 71.1 | 72.9 | 72.8 | 73.5 | 70.3 |
| 23 | 75.5 | 75.3 | 73.1 | 72.5 | 76.9 | 78.1 | 76.1 | 75.9 | 73.7 | 73.4 |
| 24 | 72.7 | 72.4 | 72.9 | 72.7 | 71.6 | 71.8 | 73.3 | 73.0 | 73.4 | 73.8 |
| 25 | 152.3 | 151.4 | 148.8 | 149.8 | 145.2 | 146.7 | 153.5 | 151.9 | 150.0 | 152.6 |
| 26 | 87.6 | 87.0 | 90.9 | 89.6 | 85.3 | 86.2 | 88.3 | 87.5 | 91.6 | 90.9 |
| 27 | 63.0 | 63.1 | 72.3 | 71.1 | 65.0 | 65.8 | 63.5 | 63.5 | 72.8 | 71.8 |
| 28 | 33.9 | 34.1 | 38.5 | 39.9 | 35.7 | 36.3 | 34.1 | 34.4 | 38.7 | 40.9 |
| 29 | 33.7 | 33.8 | 41.9 | 41.6 | 31.5 | 32.0 | 33.9 | 34.3 | 42.2 | 41.9 |
| 30 | 74.1 | 74.4 | 72.5 | 74.6 | 75.5 | 76.7 | 74.7 | 74.9 | 73.1 | 75.3 |
| 31 | 29.9 | 29.9 | 34.3 | 34.6 | 27.8 | 28.5 | 30.1 | 30.0 | 34.5 | 34.9 |
| 32 | 26.6 | 26.8 | 23.5 | 24.9 | 26.8 | 27.5 | 26.8 | 27.0 | 23.6 | 25.1 |
| 33 | 31.8 | 32.0 | 29.4 | 29.4 | 30.8 | 30.6 | 32.0 | 32.2 | 29.5 | 29.8 |
| 34 | 91.6 | 92.2 | 93.6 | 93.9 | 96.0 | 96.5 | 92.3 | 93.0 | 94.3 | 94.8 |
| 35 | 38.2 | 38.6 | 37.5 | 37.7 | 36.3 | 36.6 | 38.4 | 39.0 | 37.7 | 38.2 |
| 36 | 21.7 | 21.8 | 21.1 | 22.0 | 19.2 | 19.4 | 21.8 | 22.0 | 21.2 | 22.2 |
| 37 | 27.3 | 27.9 | 25.3 | 26.4 | 25.9 | 26.1 | 27.5 | 28.1 | 25.5 | 26.7 |
| 38 | 60.7 | 60.7 | 58.2 | 58.5 | 60.8 | 60.9 | 61.1 | 61.3 | 58.6 | 59.3 |
| 39 | 10.6 | 10.5 | 12.0 | 12.3 | 11.1 | 10.6 | 10.6 | 10.5 | 12.0 | 12.4 |
| 40 | 15.1 | 14.8 | 13.0 | 12.4 | 16.6 | 16.6 | 15.2 | 14.7 | 13.0 | 12.7 |
| 41 | 109.8 | 110.4 | 117.5 | 118.3 | 113.0 | 112.6 | 110.7 | 111.8 | 118.5 | 118.8 |
| 42 | 15.9 | 15.6 | 12.4 | 11.9 | 16.3 | 16.9 | 16.0 | 15.6 | 12.4 | 12.2 |
| 43 | 22.3 | 22.1 | 20.3 | 20.0 | 23.5 | 22.9 | 22.4 | 22.1 | 20.4 | 20.1 |
| 44 | 24.6 | 25.1 | 20.3 | 19.8 | 27.7 | 27.5 | 24.7 | 25.3 | 20.4 | 19.2 |
| C | 1-Gas (CDCl3) | 1-CHCl3 (CDCl3) | 2-Gas (CDCl3) | 2-CHCl3 (CDCl3) | Expt (CDCl3) | Expt (CD3OD) | 1-Gas (CD3OD) | 1-CH3OH (CD3OD) | 2-Gas (CD3OD) | 2-CH3OH (CD3OD) |
|---|---|---|---|---|---|---|---|---|---|---|
| H3 * | 1.43 | 1.54 | 1.59 | 1.56 | 1.62 | 1.65 | 1.35 | 1.49 | 1.52 | 1.35 |
| H3 † | 1.83 | 1.83 | 1.46 | 1.61 | 2.12 | 1.79 | 1.75 | 1.75 | 1.39 | 1.86 |
| H4 | 4.20 | 4.24 | 3.71 | 3.95 | 3.96 | 3.92 | 4.15 | 4.16 | 3.63 | 3.62 |
| H5 † | 1.45 | 1.36 | 1.21 | 1.35 | 1.31 | 1.30 | 1.37 | 1.25 | 1.14 | 1.14 |
| H5 * | 1.17 | 1.36 | 1.96 | 1.94 | 1.72 | 1.72 | 1.08 | 1.34 | 1.89 | 1.84 |
| H6 † | 1.69 | 1.66 | 1.86 | 1.59 | 1.83 | 1.51 | 1.62 | 1.54 | 1.80 | 1.41 |
| H6 * | 2.16 | 2.08 | 1.87 | 2.06 | 1.79 | 1.82 | 2.09 | 1.93 | 1.80 | 1.71 |
| H7 | 3.38 | 3.65 | 3.10 | 3.21 | 3.34 | 3.22 | 3.32 | 3.65 | 3.03 | 3.00 |
| H9 | 5.71 | 5.60 | 5.50 | 5.51 | 5.29 | 5.13 | 5.68 | 5.41 | 5.42 | 5.22 |
| H11 * | 1.54 | 1.61 | 1.71 | 1.80 | 1.87 | 1.90 | 1.46 | 1.65 | 1.64 | 1.89 |
| H11 † | 1.66 | 1.80 | 1.45 | 1.76 | 1.91 | 1.69 | 1.58 | 1.80 | 1.38 | 1.45 |
| H12 | 3.72 | 3.37 | 3.97 | 4.03 | 3.35 | 3.71 | 3.67 | 3.29 | 3.89 | 4.09 |
| H13 | 1.65 | 1.85 | 1.51 | 2.16 | 2.21 | 2.20 | 1.57 | 1.88 | 1.44 | 1.65 |
| H14 | 5.26 | 5.23 | 5.37 | 5.29 | 5.63 | 5.81 | 5.23 | 5.24 | 5.29 | 5.13 |
| H15 | 5.10 | 5.17 | 5.60 | 5.70 | 5.42 | 5.34 | 5.06 | 5.15 | 5.52 | 5.22 |
| H16 | 4.52 | 4.48 | 4.14 | 4.03 | 4.51 | 4.52 | 4.47 | 4.31 | 4.06 | 3.90 |
| H17 | 1.48 | 1.61 | 1.91 | 1.92 | 1.54 | 1.43 | 1.40 | 1.51 | 1.84 | 1.73 |
| H17 * | 1.96 | 2.01 | 1.30 | 1.48 | 2.14 | 2.04 | 1.89 | 1.89 | 1.23 | 1.42 |
| H18 † | 2.05 | 1.95 | 1.96 | 1.99 | 2.04 | 1.88 | 1.98 | 1.78 | 1.89 | 1.82 |
| H18 * | 1.85 | 1.95 | 1.76 | 1.90 | 1.80 | 1.72 | 1.77 | 1.91 | 1.69 | 1.95 |
| H20 * | 1.84 | 1.87 | 1.75 | 1.75 | 1.47 | 1.75 | 1.76 | 1.83 | 1.68 | 1.70 |
| H20 † | 1.90 | 1.96 | 1.74 | 1.70 | 1.32 | 1.75 | 1.83 | 1.84 | 1.67 | 1.60 |
| H21 † | 1.78 | 1.82 | 1.78 | 1.55 | 1.81 | 1.65 | 1.70 | 1.78 | 1.71 | 1.35 |
| H21 * | 2.17 | 2.05 | 2.28 | 1.99 | 1.72 | 1.75 | 2.10 | 1.89 | 2.21 | 1.82 |
| H22 | 3.56 | 3.55 | 4.58 | 4.17 | 3.57 | 3.50 | 3.51 | 3.57 | 4.50 | 4.15 |
| H23 | 3.68 | 3.70 | 3.77 | 3.62 | 3.35 | 3.28 | 3.62 | 3.60 | 3.70 | 3.62 |
| H24 | 4.43 | 4.36 | 4.07 | 4.00 | 4.07 | 3.92 | 4.38 | 4.36 | 4.00 | 4.15 |
| H26 | 3.87 | 3.93 | 4.16 | 4.34 | 3.90 | 3.80 | 3.82 | 3.97 | 4.08 | 4.71 |
| H27 | 4.30 | 4.35 | 5.77 | 5.48 | 4.04 | 3.94 | 4.25 | 4.32 | 5.69 | 5.61 |
| H28 * | 1.11 | 1.08 | 1.83 | 1.63 | 1.28 | 1.28 | 1.03 | 1.07 | 1.76 | 1.64 |
| H28 † | 0.75 | 0.60 | 0.84 | 1.08 | 0.95 | 0.82 | 0.66 | 0.53 | 0.78 | 1.19 |
| H29 | 2.55 | 2.24 | 1.59 | 1.61 | 1.91 | 1.78 | 2.49 | 2.06 | 1.52 | 1.65 |
| H30 | 3.52 | 3.49 | 3.22 | 3.45 | 3.25 | 3.13 | 3.46 | 3.42 | 3.15 | 3.38 |
| H31 | 1.75 | 1.72 | 1.40 | 1.57 | 1.75 | 1.69 | 1.67 | 1.68 | 1.34 | 1.49 |
| H32 * | 1.10 | 1.18 | 1.68 | 1.64 | 1.86 | 1.25 | 1.01 | 1.12 | 1.61 | 1.30 |
| H32 † | 2.22 | 2.05 | 0.84 | 1.05 | 1.96 | 1.88 | 2.15 | 1.88 | 0.77 | 0.84 |
| H33 * | 1.54 | 1.63 | 0.51 | 0.90 | 1.34 | 1.22 | 1.46 | 1.56 | 0.45 | 0.67 |
| H33 † | 1.03 | 1.13 | 1.50 | 1.58 | 1.52 | 1.22 | 0.94 | 1.02 | 1.43 | 1.53 |
| H35 † | 1.53 | 1.50 | 2.04 | 1.74 | 1.31 | 1.26 | 1.45 | 1.39 | 1.97 | 1.68 |
| H35 * | 1.28 | 1.44 | 0.69 | 1.07 | 1.48 | 1.49 | 1.20 | 1.38 | 0.63 | 0.95 |
| H36 † | 1.30 | 1.32 | 1.56 | 1.42 | 1.61 | 1.79 | 1.21 | 1.26 | 1.49 | 1.35 |
| H36 * | 2.21 | 2.03 | 2.62 | 2.29 | 1.39 | 1.40 | 2.14 | 1.89 | 2.55 | 2.24 |
| H37 † | 1.44 | 1.33 | 1.17 | 1.49 | 1.51 | 1.37 | 1.36 | 1.27 | 1.11 | 1.30 |
| H37 * | 1.47 | 1.58 | 1.50 | 1.35 | 1.84 | 1.37 | 1.39 | 1.48 | 1.44 | 1.26 |
| H38 † | 3.88 | 3.75 | 3.72 | 3.53 | 3.62 | 3.57 | 3.83 | 3.67 | 3.65 | 3.49 |
| H38 * | 3.44 | 3.54 | 2.65 | 3.14 | 3.53 | 3.39 | 3.39 | 3.49 | 2.58 | 3.10 |
| H39 | 0.99 | 0.92 | 1.22 | 1.20 | 0.88 | 0.79 | 0.90 | 0.81 | 1.16 | 1.12 |
| H40 | 1.11 | 0.95 | 2.08 | 1.61 | 1.01 | 0.91 | 1.02 | 0.88 | 2.01 | 1.55 |
| H41 | 4.60 | 4.81 | 4.34 | 4.44 | 5.02 | 4.91 | 4.56 | 4.87 | 4.26 | 4.67 |
| H41 | 5.22 | 5.11 | 5.23 | 5.19 | 5.39 | 5.25 | 5.18 | 5.07 | 5.16 | 5.08 |
| H42 | 0.80 | 0.82 | 0.90 | 0.73 | 0.97 | 0.98 | 0.71 | 0.76 | 0.83 | 0.91 |
| H43 | 1.68 | 1.70 | 1.65 | 1.77 | 1.73 | 1.59 | 1.61 | 1.64 | 1.58 | 1.64 |
| H44 | 1.28 | 1.28 | 1.51 | 1.40 | 1.36 | 1.16 | 1.20 | 1.18 | 1.44 | 1.29 |
| Structure | 13C B3LYP | 1H B3LYP | 13C mPW1PW91 | 1H mPW1PW91 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| CMAD | R2 | DP4 | CMAD | R2 | DP4 | CMAD | R2 | DP4 | CMAD | R2 | DP4 | |
| CHCl3 as Solvent | ||||||||||||
| 1gas (A) | 1.89 | 0.9969 | - | 0.25 | 0.9465 | - | 1.81 | 0.9969 | - | 0.24 | 0.9499 | - |
| 2gas (B) | 3.29 | 0.9907 | - | 0.38 | 0.8677 | - | 3.18 | 0.9917 | - | 0.35 | 0.8904 | - |
| A vs. B | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| 1CHCl3 (C) | 1.80 | 0.9972 | - | 0.22 | 0.9598 | - | 1.67 | 0.9973 | - | 0.21 | 0.9623 | - |
| 2CHCl3 (D) | 3.21 | 0.9909 | - | 0.28 | 0.9222 | - | 3.10 | 0.9916 | - | 0.26 | 0.9346 | - |
| C vs. D | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| 1CH3OH (E) | 1.89 | 0.9972 | - | 0.22 | 0.9539 | - | 1.78 | 0.9971 | - | 0.23 | 0.9565 | - |
| 2CH3OH (F) | 3.31 | 0.9903 | - | 0.34 | 0.9170 | - | 3.09 | 0.9908 | - | 0.27 | 0.9300 | - |
| E vs. F | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| CS I (G) | 2.08 | 0.9958 | 0.31 | 0.9268 | 1.95 | 0.9961 | - | 0.27 | 0.9365 | - | ||
| G vs. B | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| CS II (H) | 2.35 | 0.9914 | - | 0.32 | 0.9229 | - | 2.22 | 0.9923 | - | 0.31 | 0.9365 | - |
| H vs. B | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| CH3OH as solvent | ||||||||||||
| 1gas (I) | 1.84 | 0.9970 | - | 0.24 | 0.9415 | - | 1.78 | 0.997 | - | 0.24 | 0.9445 | - |
| 2gas (J) | 3.32 | 0.9904 | - | 0.34 | 0.8893 | - | 3.22 | 0.9914 | - | 0.30 | 0.9099 | - |
| I vs. J | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| 1CH3OH (K) | 1.94 | 0.9969 | - | 0.21 | 0.9596 | 1.88 | 0.997 | - | 0.21 | 0.9589 | - | |
| 2CH3OH (L) | 3.51 | 0.9899 | - | 0.29 | 0.9163 | - | 3.28 | 0.9909 | - | 0.21 | 0.9513 | - |
| K vs. L | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| 1CHCl3 (M) | 1.93 | 0.9971 | - | 0.23 | 0.9639 | - | 1.81 | 0.9973 | - | 0.22 | 0.9626 | - |
| 2CHCl3 (N) | 3.43 | 0.9903 | - | 0.25 | 0.9039 | - | 3.32 | 0.9917 | - | 0.23 | 0.9389 | - |
| M vs. N | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| CS I (O) | 1.75 | 0.9971 | - | 0.30 | 0.9299 | - | 1.68 | 0.9973 | - | 0.27 | 0.9396 | - |
| O vs. J | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
| CS II (P) | 2.58 | 0.9913 | - | 0.30 | 0.9201 | - | 2.46 | 0.9921 | - | 0.27 | 0.9329 | - |
| P vs. J | - | - | 100 | - | - | 100 | - | - | 100 | - | - | 100 |
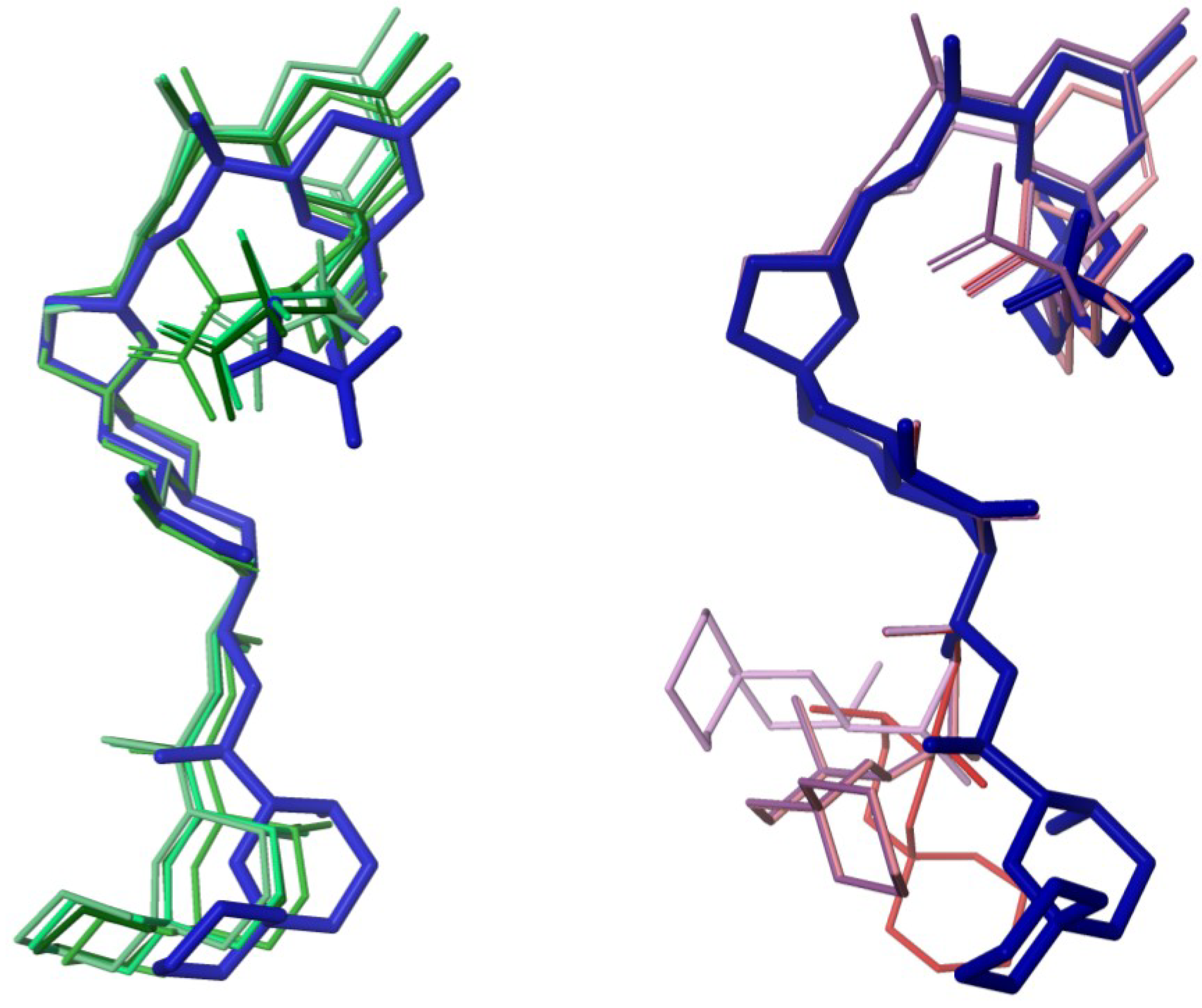
3. Experimental Section
3.1. Instrumentation and General Methods
3.2. Prorocentrum Belizeanum Cultures
3.3. Extraction and Isolation of Okadaic Acid
3.4. Computational Methods
4. Conclusions
Acknowledgments
Conflicts of Interest
References
- Blunt, J.W.; Copp, B.R.; Keyzers, R.A.; Munro, M.H.G.; Prinsep, M.R. Marine natural products. Nat. Prod. Rep. 2013, 30, 237–323. [Google Scholar] [CrossRef]
- Molinski, T.F.; Dalisay, D.S.; Lievens, S.L.; Saludes, J.P. Drug development from marine natural products. Nat. Rev. Drug Discov. 2009, 8, 69–85. [Google Scholar] [CrossRef]
- Breton, R.C.; Reynolds, W.F. Using NMR to identify and characterize natural products. Nat. Prod. Rep. 2013, 30, 501–524. [Google Scholar] [CrossRef]
- Matsumori, N.; Kaneno, D.; Murata, M.; Nakamura, H.; Tachibana, K. Stereochemical determination of acyclic structures based on carbon-proton spin-coupling constants. A method of configuration analysis for natural products. J. Org. Chem. 1999, 64, 866–876. [Google Scholar] [CrossRef]
- Bifulco, G.; Dambruoso, P.; Gomez-Paloma, L.; Riccio, R. Determination of relative configuration in organic compounds by NMR spectroscopy and computational methods. Chem. Rev. 2007, 107, 3734–3779. [Google Scholar]
- Smith, S.G.; Goodman, J.M. Assigning stereochemistry to single diastereoisomers by GIAO NMR calculation: The DP4 probability. J. Am. Chem. Soc. 2010, 132, 12946–12959. [Google Scholar] [CrossRef]
- Saielli, G.; Nicolaou, K.C.; Ortiz, A.; Zhang, H.; Bagno, A. Addressing the stereochemistry of complex organic molecules by density functional theory-NMR: Vannusal B in retrospective. J. Am. Chem. Soc. 2011, 133, 6072–6077. [Google Scholar] [CrossRef]
- Lodewyk, M.W.; Siebert, M.R.; Tantillo, D.J. Computational prediction of 1H and 13C chemical shifts: A useful tool for natural product, mechanistic, and synthetic organic chemistry. Chem. Rev. 2012, 112, 1839–1862. [Google Scholar] [CrossRef]
- Jain, R.; Bally, T.; Rablen, P.R. Calculating accurate proton chemical shifts of organic molecules with density functional methods and modest basis sets. J. Org. Chem. 2009, 74, 4017–4023. [Google Scholar] [CrossRef]
- Helgaker, T.; Jaszunski, M.; Ruud, K. Ab initio methods for the calculation of NMR shielding and indirect spin–spin coupling constants. Chem. Rev. 1999, 99, 293–352. [Google Scholar] [CrossRef]
- Dračínský, M.; Bouř, P. Computational analysis of solvent effects in NMR spectroscopy. J. Chem. Theory Comput. 2010, 6, 288–299. [Google Scholar] [CrossRef]
- Bagno, A.; Ratrelli, F.; Saielli, G. Toward the complete prediction of the 1H and 13C NMR spectra of complex organic molecules by DFT methods: Application to natural substances. Chem. Eur. J. 2006, 12, 5514–5525. [Google Scholar] [CrossRef]
- Bagno, A.; Ratrelli, F.; Saielli, G. Prediction of the 1H and 13C NMR spectra of α-d-glucose in water by DFT methods and MD simulations. J. Org. Chem. 2007, 72, 7373–7381. [Google Scholar] [CrossRef]
- Giesen, D.J.; Zumbulyadis, N. A hybrid quatum mechanical and empirical model for the prediction of isotropic 13C shielding constans of organic molecules. Phys. Chem. Chem. Phys. 2002, 4, 5498–5507. [Google Scholar] [CrossRef]
- Smith, S.G.; Channon, J.A.; Paterson, I.; Goodman, J.M. The stereochemical assignment of acyclic polyols: A computational study of the NMR data of a library of stereopentad sequences from polyketide natural products. Tetrahedron 2010, 66, 6437–6444. [Google Scholar] [CrossRef]
- Casanovas, J.; Namba, A.M.; León, S.; Aquino, G.L.B.; da Silva, G.V.J.; Alemán, C. Calculated and experimental NMR chemical shifts of p-menthane-3,9-diols. A combination of molecular dynamics and quantum mechanics to determine the structure and the solvent effects. J. Org. Chem. 2001, 66, 3775–3782. [Google Scholar] [CrossRef]
- Daranas, A.H.; Norte, M.; Fernández, J.J. Toxic marine microalgae. Toxicon 2001, 39, 1101–1132. [Google Scholar] [CrossRef]
- Dominguez, H.J.; Paz, B.; Daranas, A.H.; Norte, M.; Franco, J.M.; Fernández, J.J. Dinoflagellate polyether within the yessotoxin, pectenotoxin and okadaic acid toxin groups: Characterization, analysis and human health implications. Toxicon 2010, 56, 191–217. [Google Scholar] [CrossRef]
- Napolitano, J.G.; Daranas, A.H.; Norte, M.; Fernández, J.J. Marine macrolides, a promising source of antitumor compounds. Anticancer Agents in Med. Chem. 2013, 2, 122–137. [Google Scholar]
- Tachibana, K.; Scheuer, P.J.; Tsukitani, Y.; Kikuchi, H.; van Engen, D.; Clardy, J.; Gopichand, Y.; Schmitz, F.J. Okadaic acid, a cytotoxic polyether from two marine sponges of the genus Halinchondria. J. Am. Chem. Soc. 1981, 103, 2469–2471. [Google Scholar] [CrossRef]
- Norte, M.; González, R.; Fernández, J.J.; Rico, M. Okadaic acid: A proton and carbón NMR study. Tetrahedron 1991, 47, 7437–7446. [Google Scholar] [CrossRef]
- Matsumori, N; Murata, M.; Tachibana, K. Conformation analysis of natural products using long range carbón-proton coupling constants: Three-dimensional structure of okadaic acid in solution. Tetrahedron 1995, 51, 12229–12238. [Google Scholar] [CrossRef]
- Kita, M.; Kuramoto, M.; Chiba, T.; Yamada, A.; Yamada, N.; Ishida, T.; Haino, T.; Yamada, K.; Ijuin, Y.; Ohno, O.; et al. Structure-activity relationship of okadaic acid, a potent protein phosphatases PP1 and PP2A inhibitor: 24-Epi-okadaic acid and a 18-membered lactone analog. Heterocycles 2008, 76, 1033–1042. [Google Scholar] [CrossRef]
- Cen-Pacheco, F.; Rodriguez, J.; Norte, M.; Fernández, J.J.; Hernández, D.A. Connecting discrete stereoclusters by using DFT and NMR spectroscopy: The case of nivariol. Chem. Eur. J. 2013, 19, 8525–8532. [Google Scholar]
- Cambridge Crystallographic Data Centre. Available online: http://www.ccdc.cam.ac.uk/data_request/cif (accessed on 30 September 2013).
- Napolitano, J.G.; Norte, M.; Fernández, J.J.; Hernández, D.A. Corozalic acid: A key biosynthetic precursor with phosphatase inhibition activity. Chem. Eur. J. 2010, 16, 11576–11579. [Google Scholar] [CrossRef]
- Thrippleton, M.J.; Keeler, J. Elimination of zero-quantum interference in two-dimensional NMR spectra. Angew. Chem. Int. Ed. 2003, 42, 3938–3941. [Google Scholar] [CrossRef]
- Banks, J.L.; Beard, H.S.; Cao, Y.; Cho, A.E.; Damm, W.; Farid, R.; Felts, A.K.; Halgren, T.A.; Mainz, D.T.; Maple, J.R.; et al. Integrated modeling program, applied chemical theory (IMPACT). J. Comput. Chem. 2005, 26, 1752–1780. [Google Scholar] [CrossRef]
- Mohamadi, F.; Richards, N.G.J.; Guida, W.C.; Liskamp, R.; Lipton, M.; Caufield, C.; Chang, G.; Hendrickson, T.; Still, W.C. Macromodel, an integrated software system for modeling organic and bioorganic molecules using molecular mechanics. J. Comput. Chem. 1990, 11, 440–467. [Google Scholar] [CrossRef]
- Kolossváry, I.; Guida, W.C. Low-mode conformational search elucidated: Application to C39H80 and flexible docking of 9-deazaguanine inhibitors into PNP. J. Comput. Chem. 1999, 20, 1671–1684. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the colle-savetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Stephens, P.J.; Devlin, F.J.; Chabalowski, C.F.; Frisch, M.J. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. J. Phys. Chem. 1994, 98, 11623–11627. [Google Scholar] [CrossRef]
- Adamo, C.; Barone, V. Exchange functionals with improved long-range behavior and adiabatic connection methods without adjustable parameters. J. Chem. Phys. 1998, 108, 664–675. [Google Scholar] [CrossRef]
- CHESHIRE CCAT. Available online: http://www.cheshirenmr.info/ (accessed on 20 December 2013).
- Smith, S.G.; Goodman, J.M. Assigning the stereochemistry of pairs of diastereoisomers using GIAO NMR shift calculation. J. Org. Chem. 2009, 74, 4597–4607. [Google Scholar] [CrossRef]
- Poza, J.J.; Jiménez, C.; Rodríguez, J. J-based analysis and DFT-NMR assignments of natural complex molecules: Application to 3β,7-dihydroxy-5,6-epoxycholestanes. Eur. J. Org. Chem. 2008, 2008, 3960–3969. [Google Scholar]
- Wolinski, K.; Hinton, J.F.; Pulay, P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J. Am. Chem. Soc. 1990, 112, 8251–8260. [Google Scholar] [CrossRef]
Supplementary Files
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Domínguez, H.J.; Crespín, G.D.; Santiago-Benítez, A.J.; Gavín, J.A.; Norte, M.; Fernández, J.J.; Daranas, A.H. Stereochemistry of Complex Marine Natural Products by Quantum Mechanical Calculations of NMR Chemical Shifts: Solvent and Conformational Effects on Okadaic Acid. Mar. Drugs 2014, 12, 176-192. https://doi.org/10.3390/md12010176
Domínguez HJ, Crespín GD, Santiago-Benítez AJ, Gavín JA, Norte M, Fernández JJ, Daranas AH. Stereochemistry of Complex Marine Natural Products by Quantum Mechanical Calculations of NMR Chemical Shifts: Solvent and Conformational Effects on Okadaic Acid. Marine Drugs. 2014; 12(1):176-192. https://doi.org/10.3390/md12010176
Chicago/Turabian StyleDomínguez, Humberto J., Guillermo D. Crespín, Adrián J. Santiago-Benítez, José A. Gavín, Manuel Norte, José J. Fernández, and Antonio Hernández Daranas. 2014. "Stereochemistry of Complex Marine Natural Products by Quantum Mechanical Calculations of NMR Chemical Shifts: Solvent and Conformational Effects on Okadaic Acid" Marine Drugs 12, no. 1: 176-192. https://doi.org/10.3390/md12010176