1. Introduction
The performance of an integrated Global Positioning System (GPS)/Inertial Navigation System (INS) is mainly characterised by the ability of the INS to bridge GPS outages. In recent years, a promising technology namely, Micro-Electro-Mechanical Systems (MEMS)-based inertial sensors, has been developed, which can provide a low-cost navigation solution when integrated with GPS. MEMS systems are commonly fabricated using silicon, which possesses significant electrical and mechanical advantages over other materials [
1]. However, due to the small size and weight of the MEMS-based inertial units, their performance characteristics are highly dependent on the temperature variations. Since these errors accumulate over time, the navigation solution degrades if the temperature effects on both, accelerometer and gyroscope (biases and scale factors) are not modelled and compensated [
2]. Hence, there is a need for the development of accurate, reliable rigorous thermal models to reduce the effect of these temperature variations on the inertial sensor errors.
The inertial sensor errors can be divided into two types: deterministic (systematic) errors and random errors [
3]. If not treated, such errors cause a rapid degradation in the INS navigation solution during the GPS outage period. In order to integrate MEMS inertial sensors with GPS, and to provide a continuous and reliable integrated navigation solution, the characteristics of different error sources and the understanding of the stochastic characteristics of these errors are of significant importance [
4].
The deterministic error sources include bias and scale factor errors, which can be removed by specific calibration procedures in a laboratory environment. Park and Gao [
4] discussed the laboratory calibration procedure for MEMS units, whereas Shin and El-Sheimy [
5] developed field calibration procedures. Abdel-Hamid [
6] implemented the deterministic error (bias and scale factor) to MEMS IMU at different temperature points and demonstrated that the deterministic error is temperature-dependent. Aggarwal
et al., [
7] investigated the use of a simple polynomial temperature model to compensate for the inertial bias and scale factor deterministic errors and concluded that the inertial navigation solution was significantly improved.
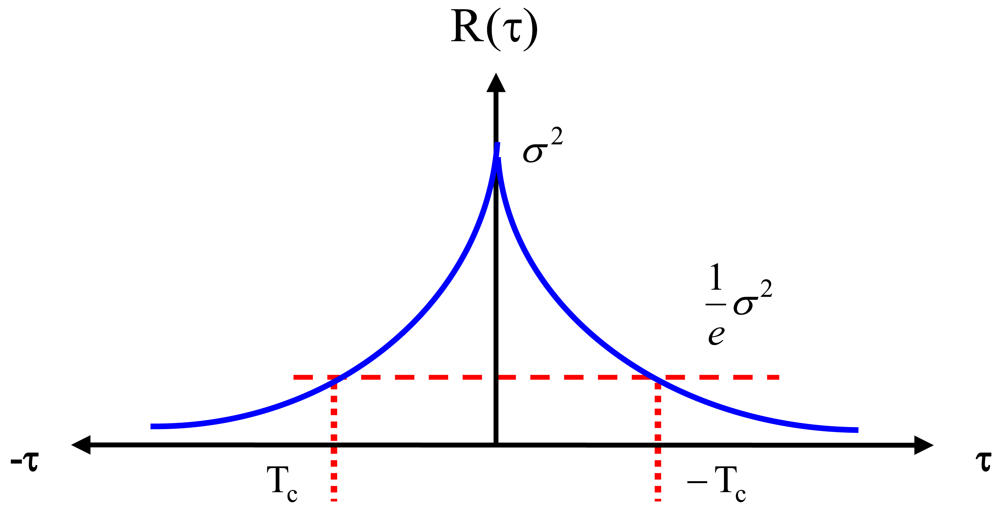
On the other hand, the inertial sensor random errors primarily include the sensor noise, which consists of two parts, a high and a low frequency component. The high frequency component has white noise characteristics, while the low-frequency component is characterised by correlated noise [
8]. A de-noising methodology is required to filter out the high frequency noise of the inertial sensor measurements prior to processing, using a low pass filter or a wavelet de-noising technique [3-6-8-9]. However, the low frequency noise component (correlated noise) can be modelled with sufficient accuracy using random processes [
3] such as, random constant (random bias), random walk, Gauss-Markov or periodic random processes. Details of these stochastic models can be found in Nassar [
3] and Gelb [
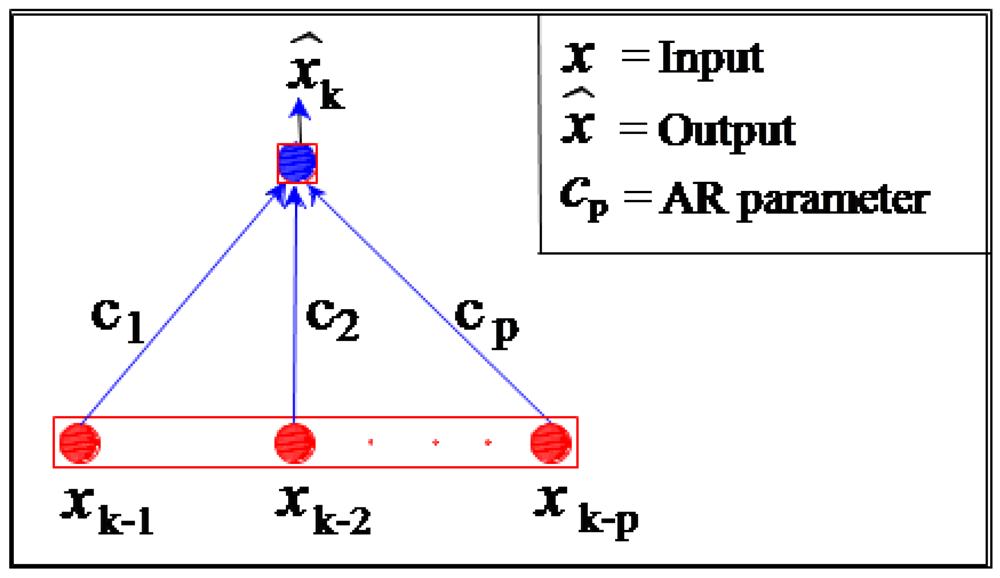
10]. The most commonly used process is the first order Gauss-Markov process, whereas more recently, the use of Auto-Regressive (AR) modelling methods on low cost sensors were tested (e.g., Nassar, [
3]; Park and Gao, [
4]). Moreover, Hou and El-Sheimy [
11] used Allan variance to study the random error of MEMS-based IMU, and demonstrated that the most dominant error has random walk characteristics.
A specific shortcoming in most of the above investigations is the disregard of the stochastic variation of these errors, which is of significant importance, and has not yet been investigated at different temperature points. The GPS/INS integrated system accuracy is significantly affected by the stochastic characteristics of the inertial navigation system [
12]. Traditionally, the inertial navigation error model consists of three position errors, three velocity errors, and three attitude errors in addition to the, three gyro and three accelerometer bias errors. The process of understanding the stochastic variation of the errors at different temperature points is one of the most important steps for developing a reliable low-cost integrated navigation system. The reason is that a low-cost IMU accumulates relatively large navigation errors in a small time interval. Unless an accurate temperature-dependent stochastic model is developed, the mechanisation parameters will possess larger errors that could significantly degrade the system performance. Therefore, there is a need for the development of accurate, reliable and rigorous stochastic models, which can be used in the INS/GPS filter to provide an accurate navigation solution [
3-
12].
This paper examines the effect of changing the temperature points on the MEMS inertial sensor noise models using for the first time a rigorous Autoregressive-based Gauss-Markov process (AR-based GM). In this work we collect static data sets under different temperature points using a MEMS-based IMU, namely the ADIS16364 [
13] and we use them to develop AR-based GM stochastic models at different temperature points. In addition, field kinematic test data collected at about 17 °C are used to test the performance of the stochastic models at different temperature points in the filtering stage when using Unscented Kalman Filter (UKF) with GPS position and heading updates. It should be noted that the focus of this paper is to investigate the effect of the IMU temperature variations on the navigation solution and therefore either UKF or Extended-KF (EKF) can be used. It has been demonstrated in the scientific literature (see Wendel
et. al. [
14] for example) that the UKF and EKF show very similar performance and thus, testing UKF and EKF algorithms is not of concern in this paper.
3. Test Description
Figure 4 shows pictures of the static test setup. The data were collected at the Space Instrumentation Laboratory (SIL) of York University, which, among others, is equipped with a thermal/vacuum chamber. Static data sets were collected under different temperature points using the ADIS16364 inertial measurement unit (IMU) from Analog Devices Inc. [
13] (see
Table 1 for the specifications of the ADIS16364 IMU). The ADIS16364 IMU static data were collected with a sampling rate of 200 Hz at different temperature points in the range −40 °C to +60 °C with 20 °C step. Thus, the performed test covers the operational temperature of the ADIS16364 IMU.
To examine the performance of the six stochastic models to be developed from the above static tests at different temperature points, dual frequency GPS data from a Trimble BD950 receiver and inertial data from the ADIS16364 IMU were collected on July 15, 2008 in Hamilton Harbour, Ontario, onboard the hydrographic surveying vessel “Merlin”, owned by the Canadian Hydrographic Service of the Department of Fisheries and Oceans. The kinematic test temperature was about 17 °C during the entire test time span.
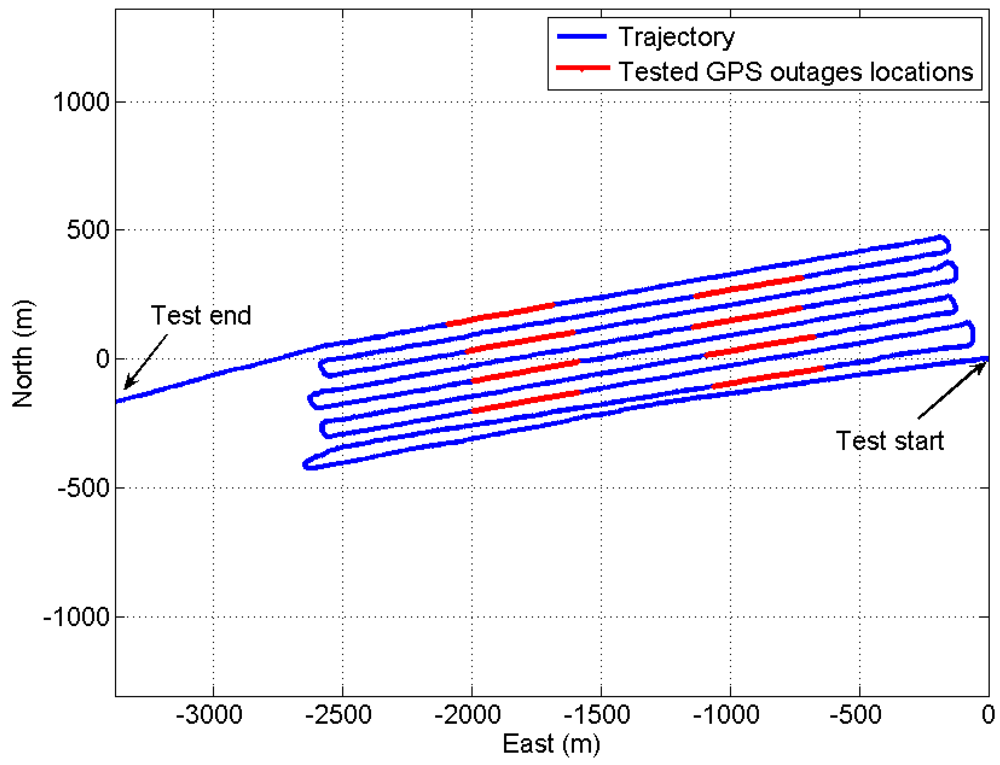
Figure 5 shows the vessel configuration. The test trajectory (blue line) with eight (8) artificial outages (each of 100 s length—red lines) is shown in
Figure 6. It should be noted that two GPS antennas are used to estimate the GPS heading in addition to the GPS position solution to update the MEMS IMU navigation solution to provide accurate INS/GPS navigation solution.
4. Data Analysis and Results
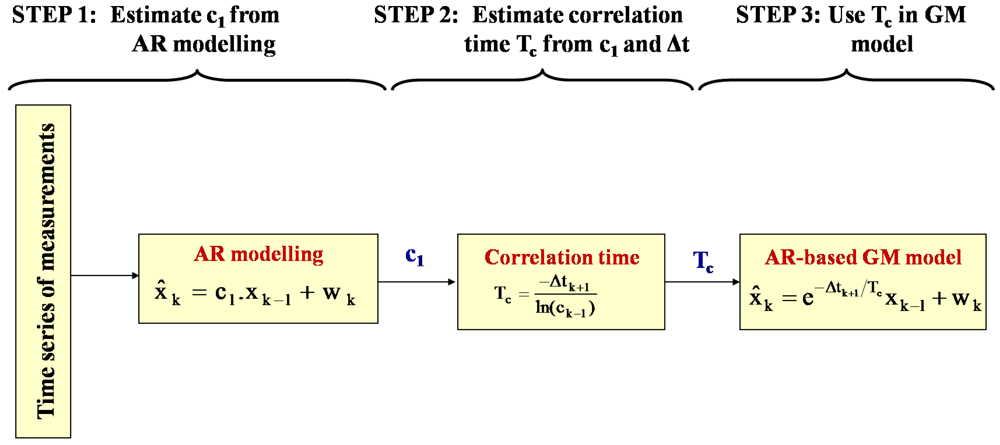
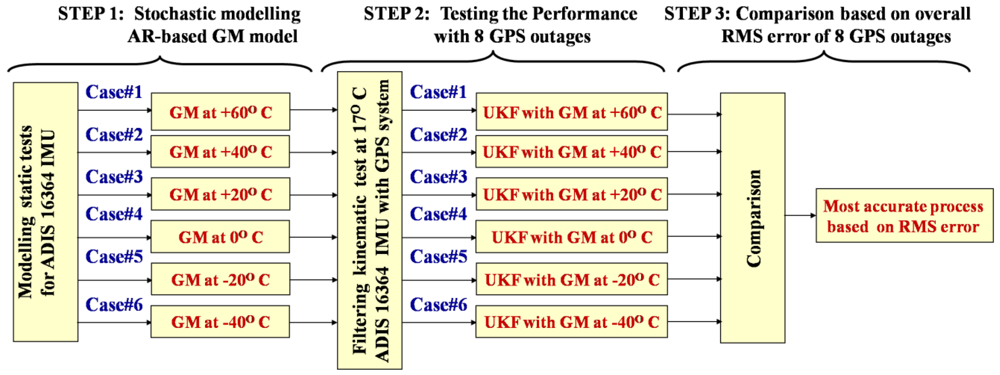
Figure 7 shows the three steps followed in this paper to develop one AR-based GM model per temperature point. In Step 1, static data sets are collected at different temperature points (from −40 °C to +60 °C, at 20 °C intervals) using the ADIS16364 MEMS-based IMU. In step 2, the test data collected in the kinematic mode at the specific temperature point of 17 °C are used to test the performance of the six stochastic models developed in Step 1. The integrated navigation solution from the INS/GPS is obtained using the UKF estimator. The GPS position solution from the rover GPS antenna and GPS heading solution from the two GPS antennas (vessel equipped by two GPS antennas onboard separated by 2.37 m) are employed to update the UKF filter every 1 s. UKF [also called Sigma-point KF (SPKF) in the literature such as, Wendel
et al. [
14] is used in this paper simply because the linearisation of dynamic and observation equations is not needed and the two navigation solutions of UKF and EKF are not significantly different [
14]. In UKF, we use 21 inertial states (three components of each: position, velocity, attitude, gyro bias, accelerometer bias, gyro scale, and accelerometer scale errors) to develop the INS system state-space equations. Along with the state-space equations, we use the GPS positions and heading solution, and estimated INS positions and heading to develop the INS/GPS system observation equations. Then, we apply eight artificial 100 s GPS outages to test the INS-only navigation solution. In Step 3, we estimate the overall root-mean-square (RMS) error of the INS-only 3D positions and 3D orientations using the eight artificial 100 s GPS outages. Then, out of the six possible stochastic models (one for each temperature point), we select the best model, i.e., the model that exhibits the lowest RMS error, that should be applied in the UKF estimator to provide the most accurate navigation solution. It should be noted that due to the existence of high level white noise in the collected MEMS-based static and kinematic data in Steps 1 and 2, respectively, the Kaiser FIR low pass filter [
8], with appropriate cut-off frequency is used to suppress this white noise. The following sub-sections show the results of the three steps shown in
Figure 7 and described above.
4.1. Step1: AR-based GM Modelling at Different Temperature Points
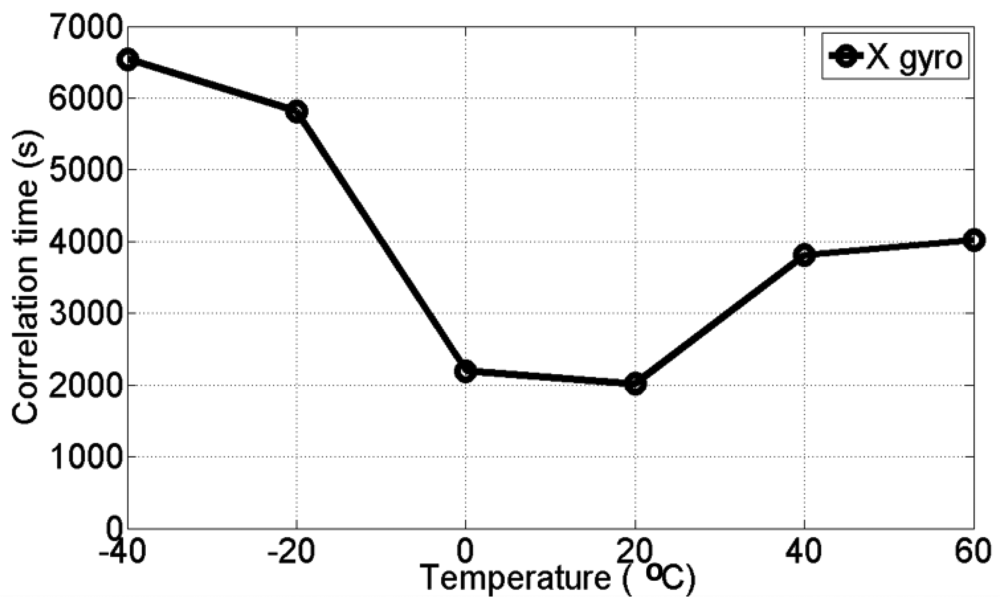
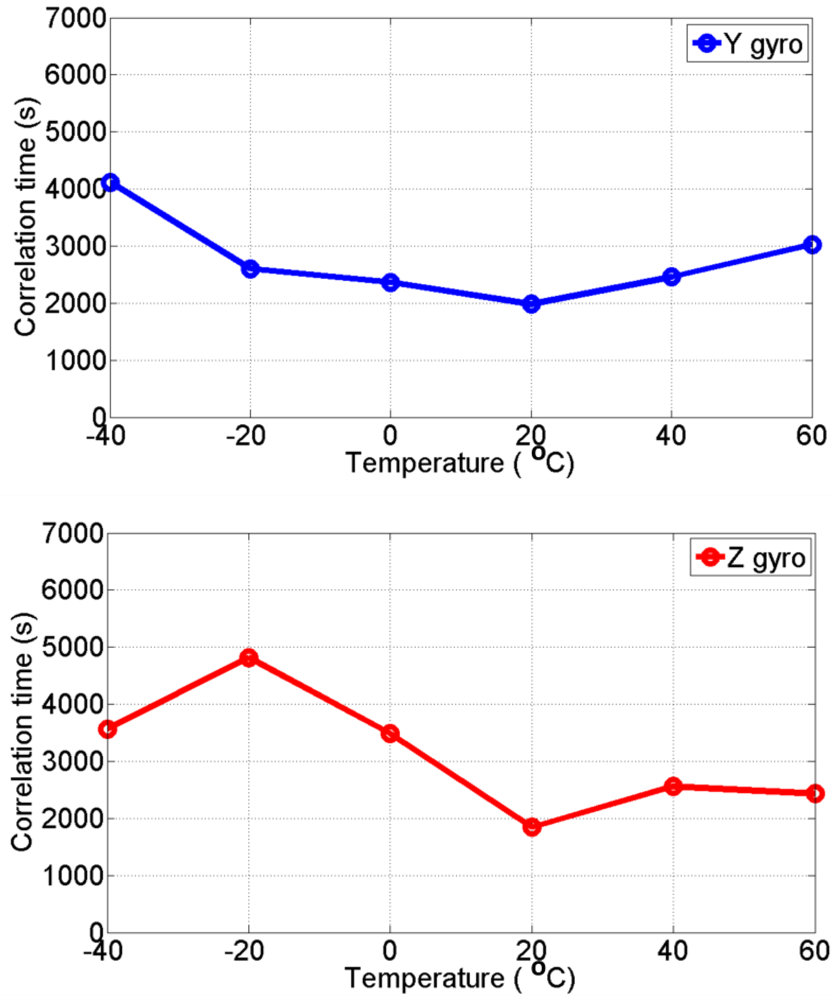
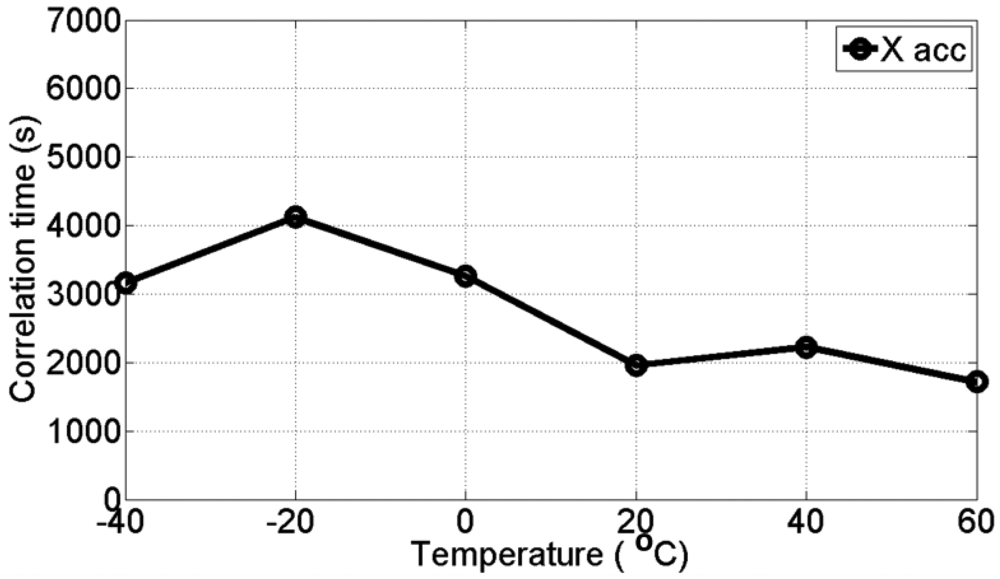
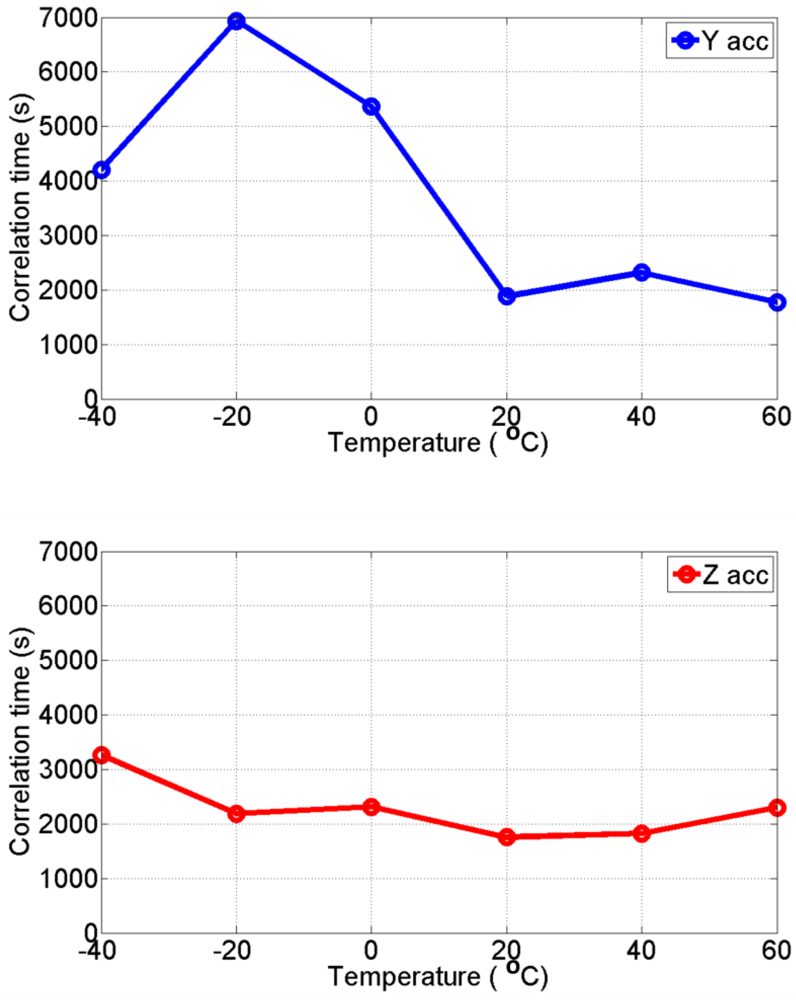
The six static data sets were collected at a sampling rate of about 200 Hz at six different temperature points ranging from −40 °C to 60 °C for a period of 3 hours, which were then used to develop the six AR-based GM stochastic models (i.e., AR-based GM at −40 °C, −20 °C, 0 °C, +20 °C, +40 °C, and +60 °C) described in Section 3, for three gyro and three accelerometer bias errors. The correlation times for the AR-based GM model were estimated using
Equation (10).
Figures 8 and
9 show the estimated correlation times for the three gyro and the three accelerometer channels, respectively at all different temperature points. It is clear that the correlation time is temperature dependent and therefore, it is concluded that the stochastic models for MEMS-based ADIS16364 inertial sensor errors are temperature-dependent.
4.3. Step3: Comparison Based on Overall Root-Mean-Square Error
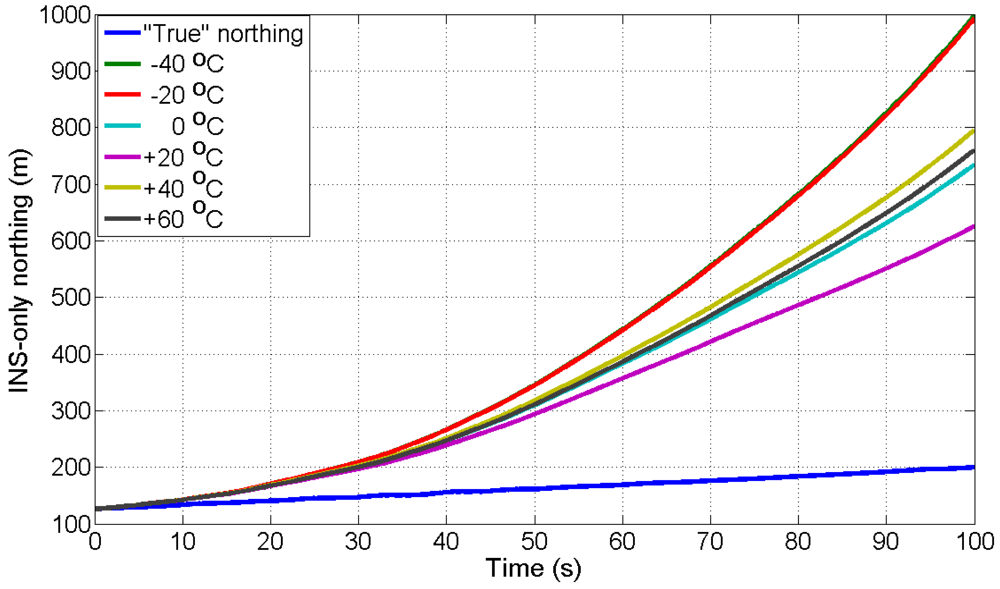
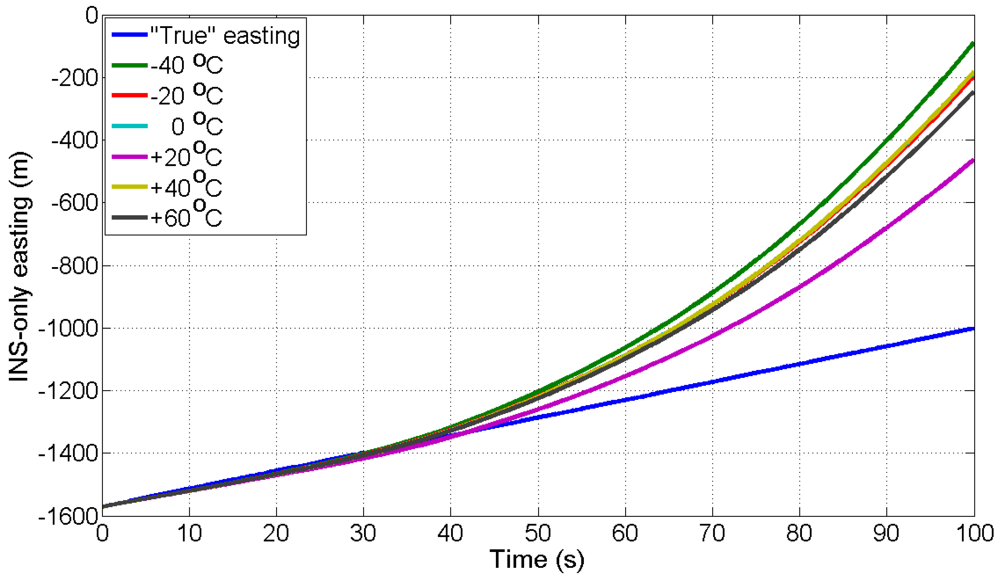
Now, we estimate the overall root-mean-square (RMS) error for northing and easting for all eight, 100 s GPS outages.
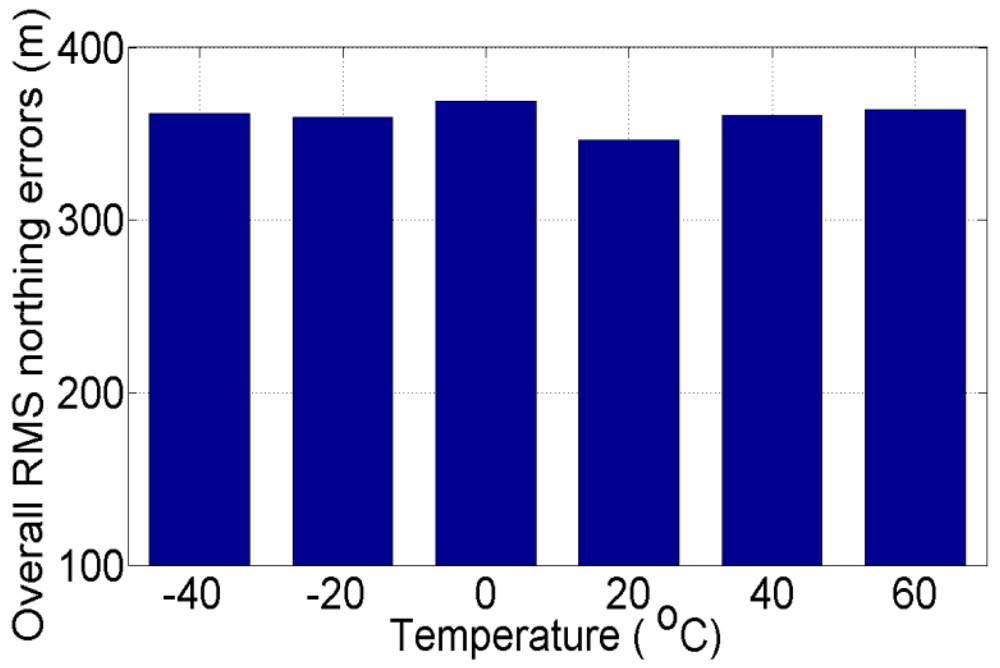
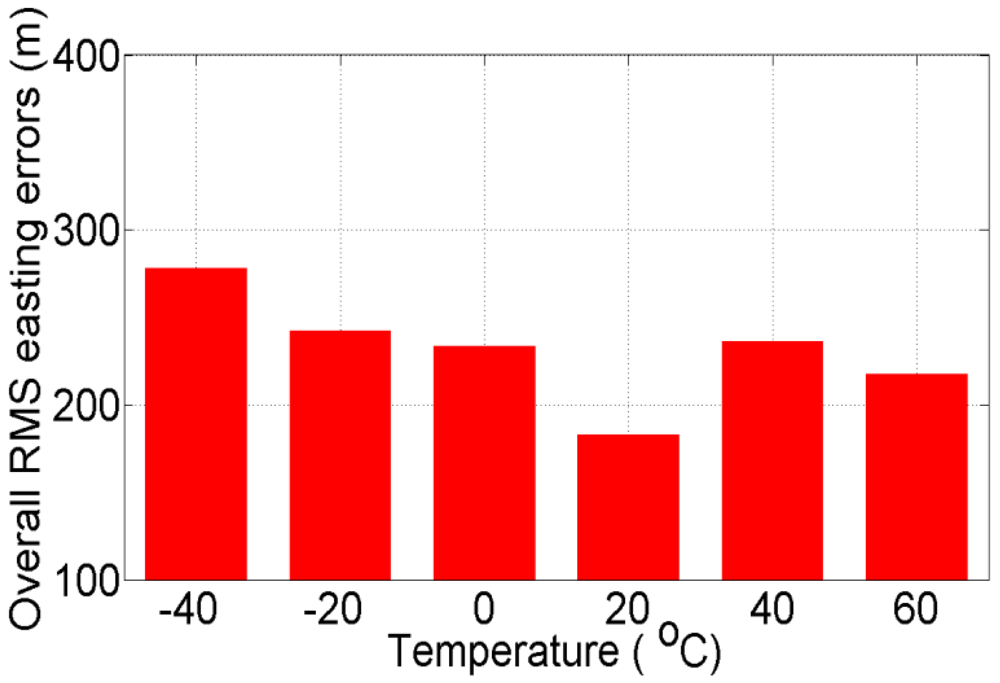
Figures 13 and
14 show the overall (average of eight GPS outages) RMS error of northing and easting respectively at different temperature points, when compared with “true” GPS-based positions.
In
Figures 13 and
14, the overall RMS error at +20 °C is found to be ±346.40 m and ±182.80 m for northing and easting, respectively, which is lower than the overall RMS error at all other temperature points.
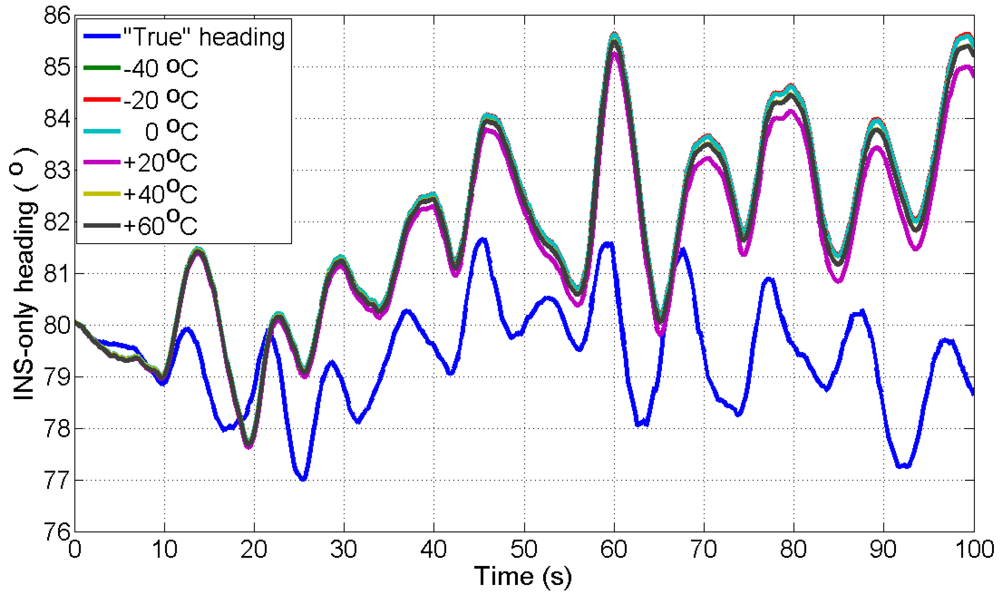
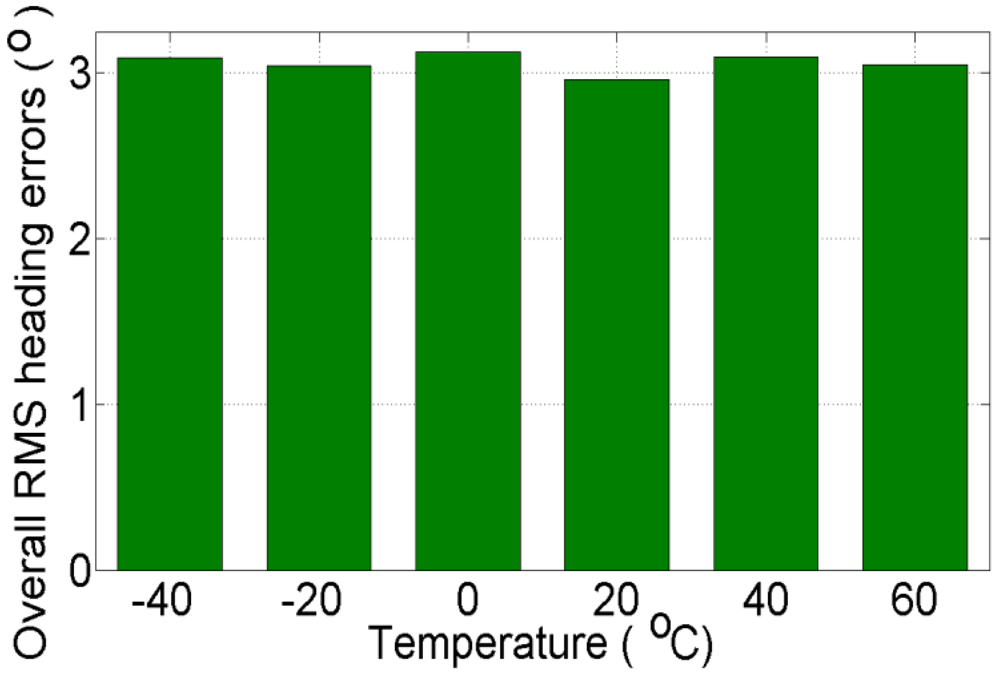
Figure 15 shows the overall (average of eight GPS outages) RMS error of heading at different temperature points, when compared with “true” GPS-based heading. In
Figure 15 it can be seen that the overall RMS error is found to be 2.95 °C at +20 °C, which is lower than the overall RMS error of the eight GPS outages estimated with the AR-based GM model at all other temperature points.
To this end, we conclude that in order to have an optimal navigation solution, we should include in the processing stage of MEMS-based INS/GPS integration different stochastic model parameters at different temperature points with +20 °C interval and we should use the temperature-dependent stochastic model nearest to the real sensor temperature during the test.