1. Introduction
Wireless Sensor Networks (WSNs) hold the promise of many new applications in the area of environment surveillance and target tracking. In such applications, the user is interested only in the occurrence of a certain event, such as target appearances or status changes. Due to the random distribution or mobility of the targets, a certain level of sensing coverage over the field of interest should be maintained to guarantee that events of interest will be captured with minimal delay. The sensing area of a sensor node is often assumed to be a disk bound by a sensing circle of fixed radius
r centered at the node. The field is said to be
k-covered or have a coverage degree of
k if any point contained in it is within the sensing area of at least
k sensors [
1]. In general, coverage degree can be considered as a measure of quality of service (QoS) of a wireless sensor network [
2]. The higher the coverage degree is, the better the field is monitored. However, the constrained power supply of sensors cannot justify the scheme in which all sensors are put on duty to achieve a high coverage degree. Continuous working leads to the quick depletion of battery power and this shortens the overall network lifetime. Moreover, sensors have limited processing ability and storage capacity due to low cost and small size [
3]. Therefore, power-efficient and lightweight designs to prolong network lifetime without sacrificing the coverage degree are one of the fundamental concerns for wireless sensor networks.
In WSNs, unattended deployment usually causes asymmetric node density in the field. In some sub-areas of the field, the sensing areas of neighboring nodes might overlap with each other, which results in coverage redundancy. This redundancy can be exploited to design energy-efficient coverage control protocols [
4-
10]. In a
k-covered field, a node is said to be redundant if each point within its sensing area is already
k-covered by other active nodes [
5]. The main mechanism of the coverage control protocols is to turn off the redundant nodes, which are also called eligible nodes to sleep. Since the coverage degree is maintained by the other on-duty nodes, unnecessary power consumption of eligible nodes is saved to a significant extent. An off-duty eligibility rule to identify eligible nodes is critical to the accuracy and efficiency of coverage control protocols. The two most well-known protocols in literature, the Ottawa protocol [
4] and CCP protocol [
5], adopt either unnecessary or insufficient rules and as a result, redundancy still exists in the Ottawa protocol and blind points might exist with the CCP protocol. Moreover, the centralized algorithms proposed in [
9] and [
10] can incur expensive communication overhead in a large scale wireless sensor network, due to information exchange. Given the multi-hop and unattended deployment of wireless sensor networks, a localized protocol is more adaptive to large and dynamic network topology which is expected to be quite frequent in mobile and ubiquitous scenarios.
In this paper, we propose a sufficient and necessary condition for a redundant node, Eligibility Rule based on Perimeter Coverage (ERPC). The concept of perimeter coverage was first proposed in [
11] to determine whether a field is
k-covered by sensor networks. Perimeter coverage provides an efficient approach to the complicated coverage problem by simple geometrical calculation. Based on ERPC, a localized Coverage Preserving Protocol (CPP) is presented to maintain network coverage by scheduling the sleep and active states of eligible nodes. Here we summarize the advantages of CPP over previous studies, i.e., the main contribution of this paper as follows.
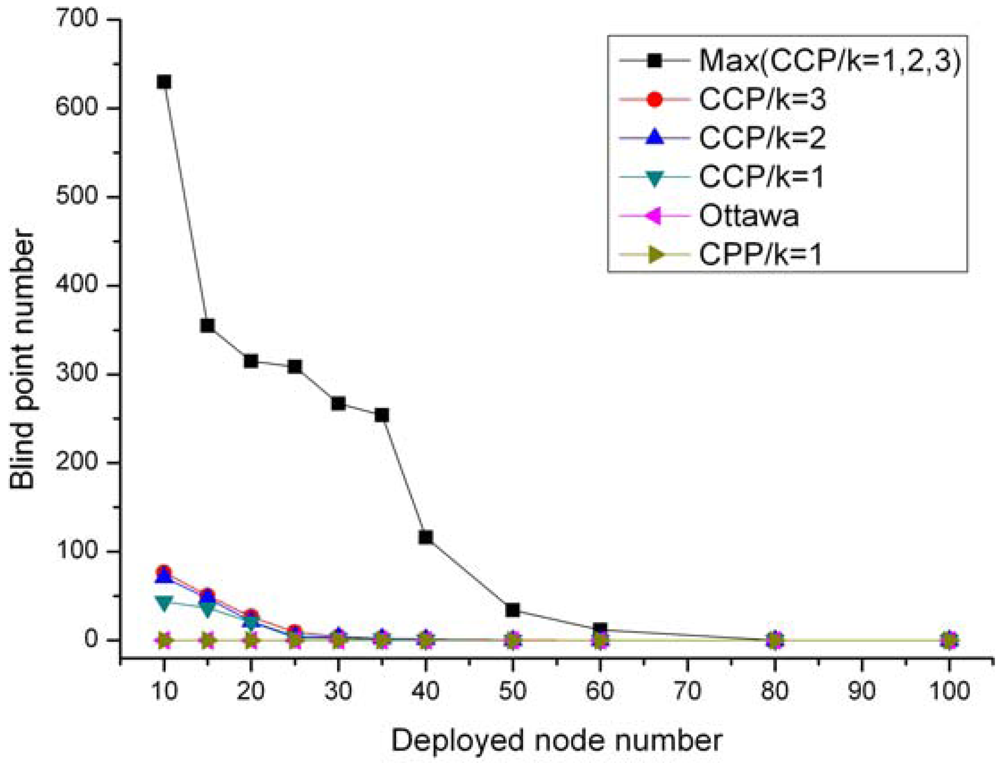
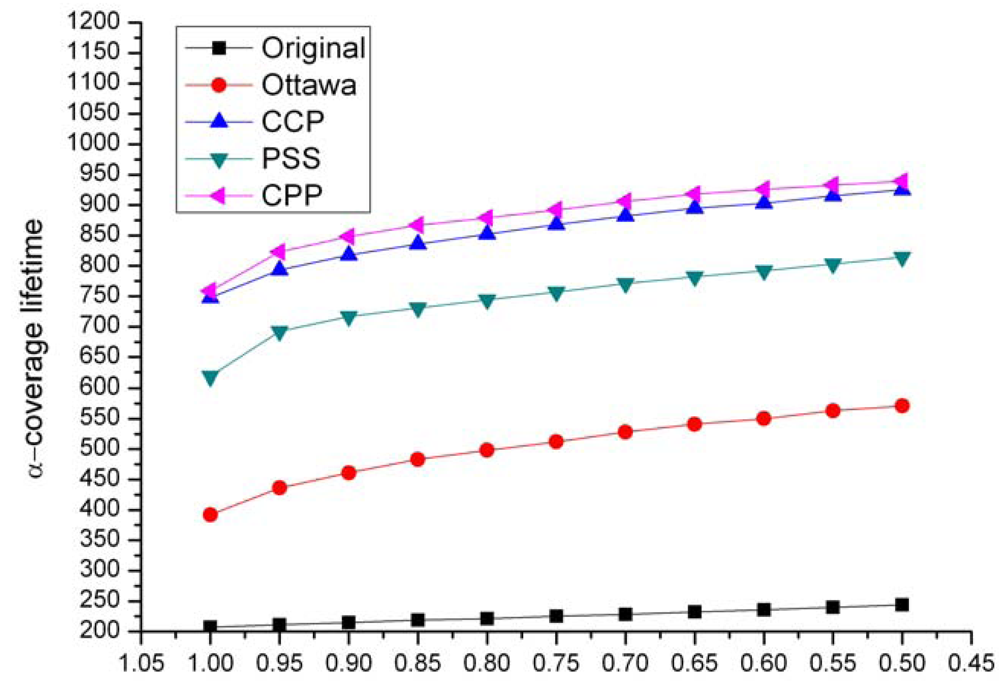
Since our ERPC is a complete condition to determine an eligible node, the ERPC-based CPP not only eliminates the coverage redundancy completely, but also identifies all the eligible nodes exactly. Therefore, CPP can maximize network lifetime without sacrificing system QoS.
Based merely on local information, CPP is more cost-effective, especially in large scale and multi-hop networks, than the centralized protocols described in [
9-
10]. Although [
11] presented a power saving scheme (we denote it by PSS) as a possible extension to the perimeter coverage problem, PSS requires much more information exchange and computation time than our work.
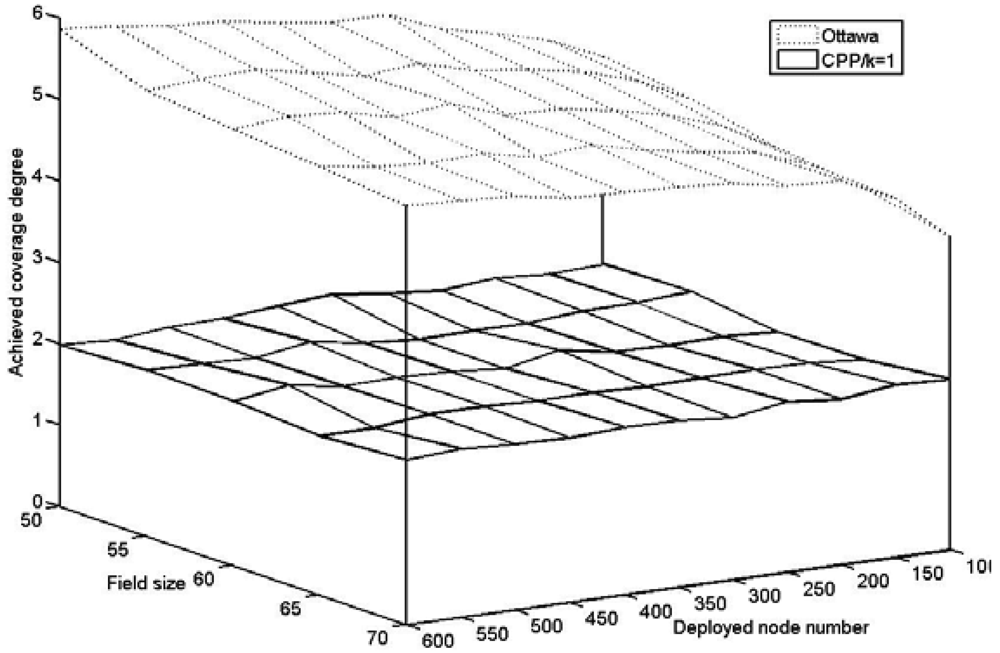
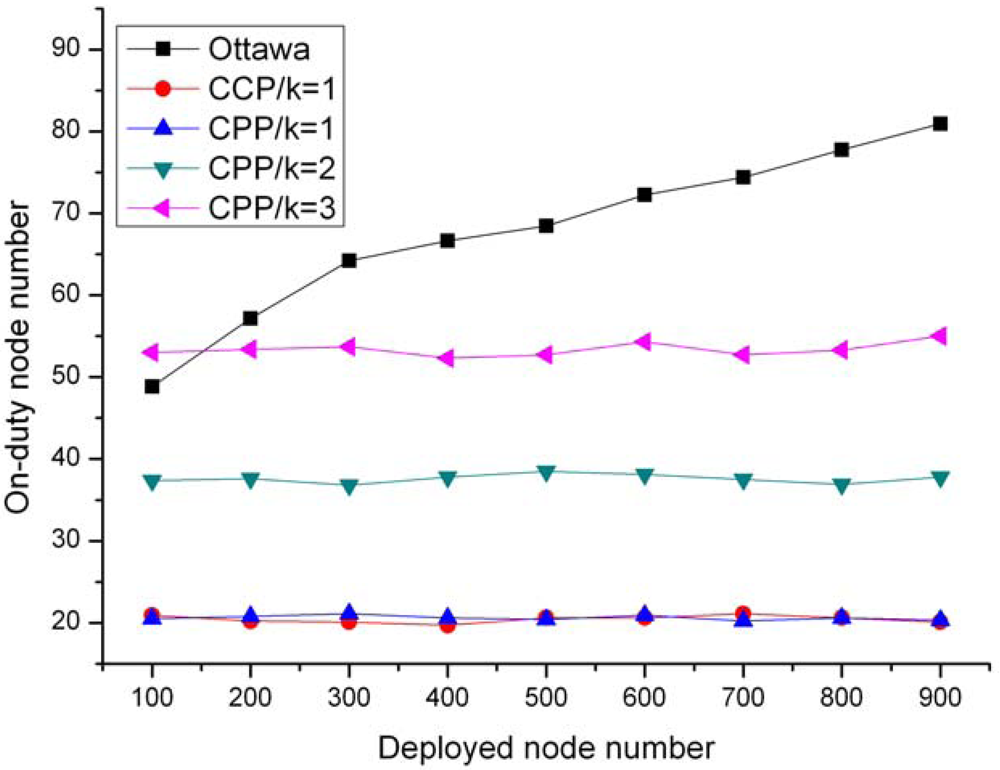
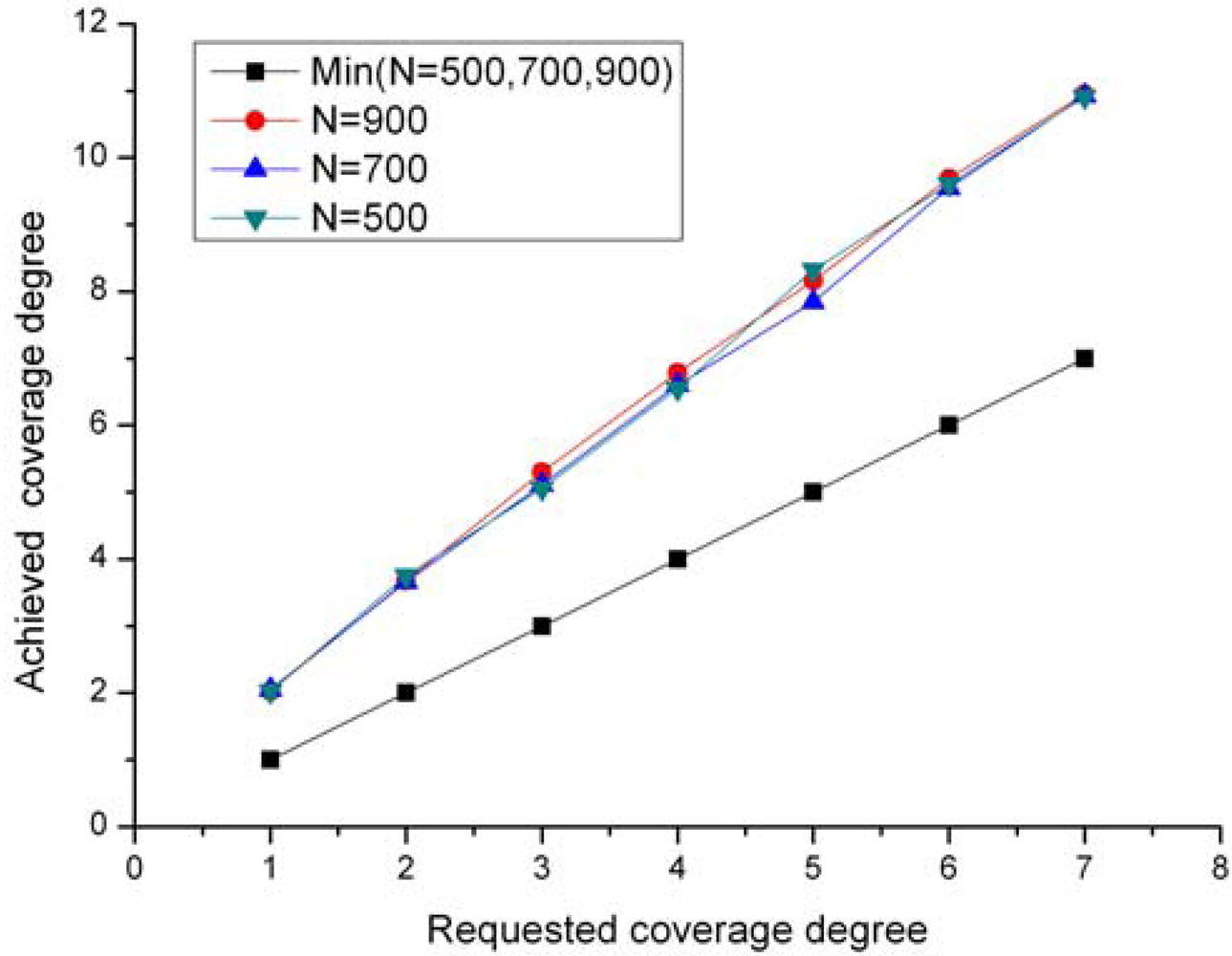
CPP is capable of maintaining the network to the specific coverage degree requested by an application, while the Ottawa protocol does not support a configurable coverage degree.
The computational complexity of ERPC is O(N2log(N)), where N is the number of neighboring nodes. Comparing with CCP whose eligibility rule has a complexity of O(N3), CPP is a more lightweight protocol and more suitable for sensors whose computation and storage capabilities are harshly constrained.
The rest of this paper is organized as follows. Section 2 surveys the related work in literature. In Section 3, we describe the network model and problem formulation. Section 4 proposes our method to identify an eligible node and clarifies our advantages over the eligibility rule proposed by [
11]. Section 5 introduces our coverage control protocol. In Section 6, we present the simulation results. Section 7 concludes this paper.
2. Related Work
The most discussed coverage problems in the literature can be classified into two categories: barrier coverage and full coverage. The barrier coverage problem aims to minimize the probability of undetected intrusion through the barrier formed by sensor networks. There has been substantial research on the barrier coverage problem, for example, in [
2,
12-
15]. In [
2] one kind of barrier coverage problem is addressed to determine the least and most covered paths by which an intruder moves through a field given a set of the initial and final locations. Another kind of barrier coverage is introduced in [
13] to determine a path with minimal exposure which reflects the time for a sensor to detect a target. Unlike the rectangular or circular field studied in the prior work, the barrier coverage problem in a thin belt field is extensively researched in [
12,
14-
15].
In this paper, we focus on another type of coverage problem, the so-called full coverage. Full coverage provides the QoS of minimizing the probability of undetected events in the full range of the field. Instrumented with full coverage, the sensor network is vigilant to capture any interested events which take place any time and anywhere. To minimize the power consumption and deployment cost, one kind of energy-efficient full coverage problem is to derive critical conditions for
k-coverage. In [
16], the authors address the problem of determining the relationship among network parameters to guarantee that the probability of
k-covered approaches 1 as the number of deployed sensors approaches infinity. A mathematical model is proposed in [
17] to calculate the minimal number of sensors needed to reach
k-coverage given the ratio of the sensing range to the range of the field. In [
11], the authors suggest that, given a set of sensors, the whole area is
k-covered if and only if the perimeter of each sensor' sensing area is covered by at least
k neighboring sensors. All these research efforts indicate that
k-coverage can be preserved with only a minimal number of deployed sensors. In fact, due to unattended deployment and physical frangibility, more sensors than this minimal number must be deployed, therefore, turning off some redundant sensors can prolong the network lifetime.
Many energy-efficient protocols have been proposed to ensure a desired node density by exploiting deployment redundancy. In [
7], a Geographical Adaptive Fidelity (GAF) algorithm is proposed to reduce overall energy consumption, while maintaining a constant level of routing fidelity. A probing-based density control algorithm called PEAS is proposed in [
6] to ensure prolonged network lifetime and sensing coverage. Some functional nodes in PEAS continue working until they drain down the battery energy or fail physically, which might reduce network connectivity. In order to balance energy consumption among the network, the ALUL protocol is presented in [
8]. None of all the works above, however, derive complete conditions for redundant nodes for coverage. In fact, their main purpose is to maintain network connectivity, which in most cases does not guarantee coverage.
In [
9] and [
10], the authors propose coverage control algorithms to extend network lifetime for target tracking sensor networks. The algorithms aim to divide the sensor nodes into a maximum number of disjoint sets, each of which can completely cover all the targets. By activating these sets successively, unnecessary energy can be saved to a maximum extent. The authors prove that determining sum maximum sets is an NP-complete problem. Two heuristic algorithms are presented to approximately address the problem. The major limitation of the centralized algorithms, however, is that heavy communication overhead is introduced due to much information exchange, especially in a mobile and multi-hop sensor network. Hence, there is a strong need to develop localized protocols while preserving the desired coverage.
Localized protocols have recently been presented to provide coverage control while maintaining network longevity. One of the most representative protocols is Optimal Geographical Density Control (OGDC) in [
18]. OGDC first computes the position where each active node should locate if a full coverage is achieved. Then OGDC picks the nodes closest to these positions-should-be as active node set and put all the other nodes into sleep to conserve energy. This optimal approach by OGDC is built under an assumption that the network density is high enough that a node can be found at any desirable position. Moreover, OGDC assumes that the field is large enough that the nodes near the boundary of the field can be ignored. However, the two assumptions do not necessarily hold true for most sensor networks. Hence, this paper will discuss the localized coverage control problem while relaxing the assumptions about network density and field range.
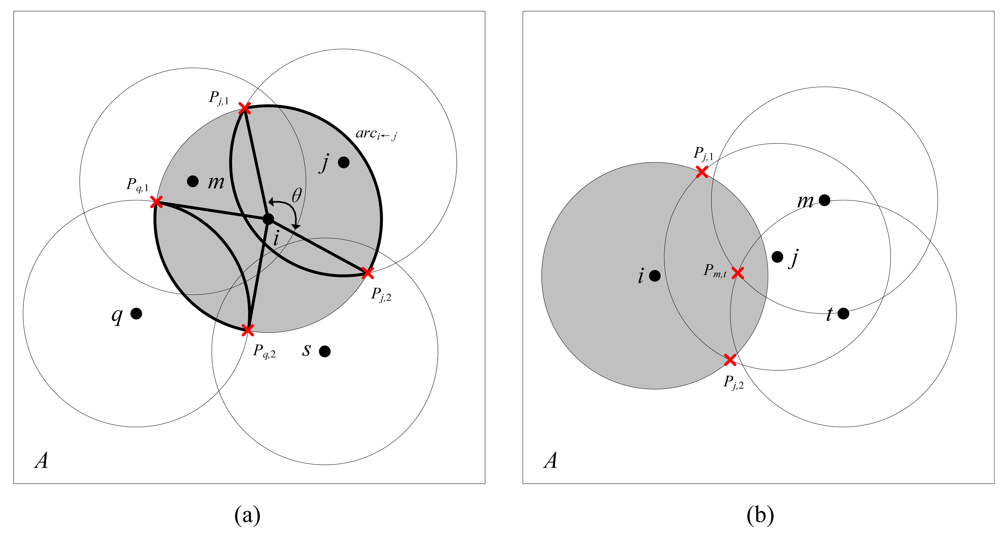
The works most relevant to our approach are the Ottawa protocol in [
4] and CCP in [
5]. Their main approaches are to derive off-duty eligibility rules for redundant nodes and then schedule the work status of these eligible nodes. The off-duty eligibility rule for a sensor to determine whether it is redundant is critical to such protocols. The Ottawa protocol uses a sector to approximately calculate node
i's sensing area covered by node
j as illustrated in
Figure 1(a). The sector corresponds to the angle of
θ and is bounded by radius
iPj,1,
iPj,2 and
arci←j. In the eligibility rule of Ottawa protocol, node
i is said to be eligible for turning off if the sum of the angles created by all of its neighboring nodes are larger than 2π. However, this rule only takes the neighbors within a node's sensing area into account, bypassing the nodes outside the sensing area but still contributing to coverage sponsorship. In the scenario shown in
Figure 1(a), the eligible node
i is considered ineligible by the Ottawa protocol since nodes
q and
s are ignored. Therefore, as a sufficient but unnecessary condition, the Ottawa protocol can result in redundancy after turning off only a subset of eligible nodes. An extension to the Ottawa protocol is proposed as the Optimal Coverage-Preserving Scheme (OCoPS) in [
19] to provide more accurate coverage control. However, both Ottawa protocol and OCoPS only support 1-coverage and can not meet the requirements of some applications such as target localization or tracking which requires at least 3-coverage[
20].
In CCP, a coverage-configurable off-duty rule is adopted to determine node eligibility. The CCP rule considers a node to be eligible if all the intersection points inside its sensing area are
k-covered. An intersection point is defined as the intersection point of the sensing circles of two nodes or that of the sensing circle of one node with the boundary of the field. The CCP protocol outperforms the Ottawa protocol in coverage efficiency. In the CCP rule, however, the rule does not test the intersection points on a node's sensing circle. As shown in
Figure 1(b), the CCP considers node
i eligible mistakenly based on the assumption that all the inner intersection (i.e.
Pm,t) is covered by node
j. Therefore, the CCP rule is a necessary but insufficient condition for an eligible node and blind points might be incurred, which is verified in our experiment. In this paper, we extend the perimeter coverage lemma in [
11] to propose a sufficient and necessary condition for eligible nodes. Based on this complete eligibility rule, our CPP protocol exhibits higher efficiency and accuracy than the two counterparts, the Ottawa and CCP protocols. Moreover, the complexity of our eligibility rule is
O(
N2log(
N)), lower than that of CCP rule,
O(
N3), where
N is the total number of neighboring nodes. To validate the analysis above, we will integrate the Ottawa and CCP protocols in our simulation and provide a comparative study.
3. Network Model and Problem Description
3.1. Network Model and Basic Definitions
Consider a square field A with side length L. Although the field is assumed square in our discussion and simulation, our approach can work in rectangular and circular fields too. We are given a set of sensor nodes, S={i|1,2,…,N} and each node i (i∈S) is located at a known coordinate (xi,yi) inside A. Each node has a fixed sensing range of r. Moreover, no two nodes are located in the same position.
To better state the coverage problem, we give some basic definitions as follows.
Definition 1
The sensing area of node i (i∈S) is defined as a set of points: D(i)={p(x,y)|p(x,y)∈A ∧ (x-xi)2+(y-yi)2≤r2}.
Definition 2
A location point p(x,y) (p(x,y)∈A) is said to be covered by node i (i∈S) if (x-xi)2+(y-yi)2≤r2 is true.
Definition 3
A location point p(x,y) (p(x,y)∈A) is said to be k-covered or have a coverage degree of k if it is covered by at least k nodes in S.
Definition 4
The field A is said to be k-covered or have a coverage degree of k if for any location point p(x,y) (∀p(x,y)∈A), its coverage degree is no lower than k. For a specific application, the sensor network is expected to achieve a given coverage degree which is defined as the requested coverage degree.
Definition 5
For a sensor network with a requested coverage degree of k, a location point p(x,y) (p(x,y)∈A) is said to be a blind point if this point is less than k-covered.
Unlike the Ottawa protocol, we consider all the nodes with a distance within 2r to a node since all theses nodes contribute to coverage sponsorship.
Definition 6
The neighboring nodes of node i (i∈S) are defined as: N(i)={j|j∈S ∧ (xi-xj)2+(yi-yj)2≤(2r)2, i≠j}.
Moreover, we assume a simple communication model adopted by [
5] as follows.
Definition 7
For any two nodes i and j (∀i, j∈S), they can communicate with each other if and only if (xi-xj)2+(yi-yj)2≤R2 is true, where R is the communication radius of each node.
In order to minimize energy consumption caused by communication, we employ a communication radius of
R=2
r to ensure that only the neighboring nodes can hear each other (The Micaz[
21] sensor platform by Crossbow supports adjustable transmission control scheme.).
The overlapped sensing areas can result in redundant nodes which are defined in [
5] as follows.
Definition 8
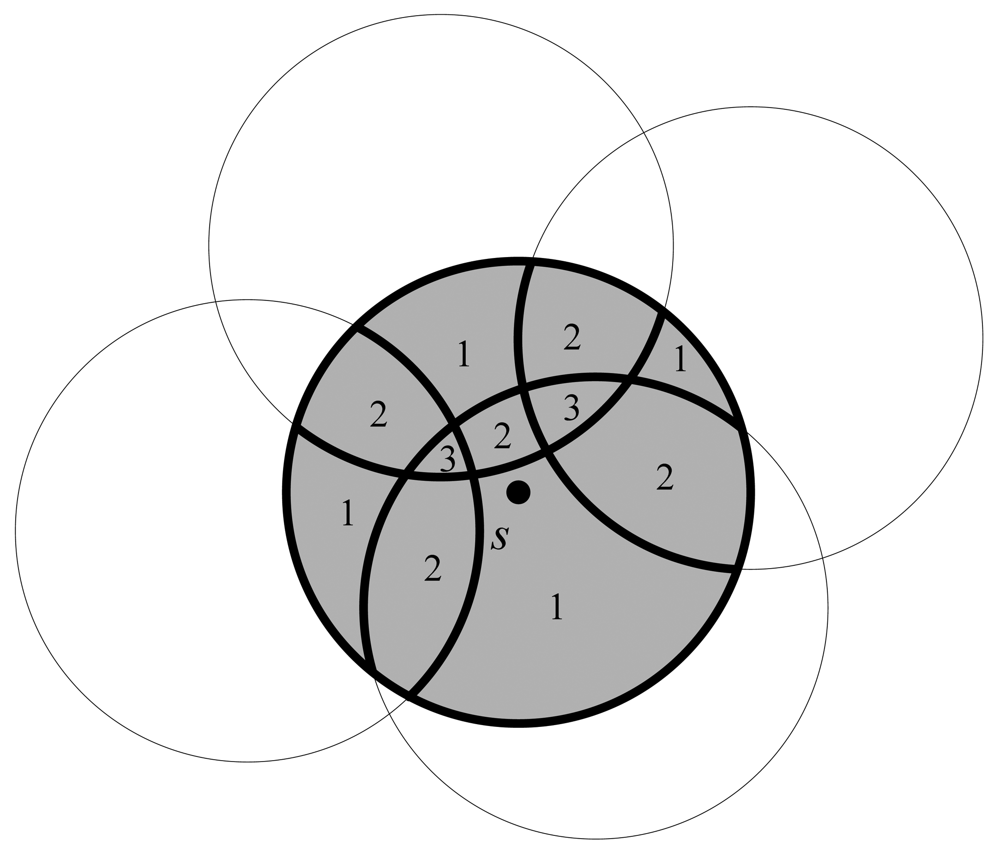
Node i (i∈S) is said to be a redundant node if and only if each point within its sensing area is at least k-covered by other active nodes.
As illustrated in
Figure 2, the sensing area of node
i is completely covered by its neighboring nodes, by Definition 8, node
i is a redundant node. Turning off redundant nodes can save unnecessary power consumption. Hence, a redundant node is also called an off-duty eligible node.
3.2. Problem Description
As shown in
Figure 2, one direct solution to determine a redundant node is to find out all sub-regions divided by the sensing circles of all neighboring nodes and check if each sub-region is
k-covered or not. However, calculating the concave or convex shaped sub-regions might be a highly computation- intensive task for a resource-constrained sensor [
11].
Therefore, the energy-efficient coverage problem to be addressed in this paper is formulated as follows:
Given a field A(L×L), a set of sensors S, a sensing radius r and a requested coverage degree k, propose an off-duty eligibility rule for a node i (i∈S) to determine whether it is a redundant node. It is required that such an eligibility rule be a sufficient and necessary condition for an eligible node and can be executed at a low computational complexity. Moreover, for all the eligible nodes identified by ERPC, a sleep scheduling protocol is needed to balance energy consumption among all the nodes in the network.
4. Off-duty ERPC Approach
In this section, we describe our novel localized approach to identify redundant nodes, denoted as Eligibility Rule based on Perimeter Coverage (ERPC). Each node runs ERPC locally to compute the coverage degree of each neighbor's sensing circle within the node's sensing area. By checking such information of all the neighboring nodes, the eligibility of a particular node can be determined.
4.1. ERPC Theorem
Definition 9
The sensing circle of node i (i∈S) is called the perimeter of the node and is defined as a set of points: P(i)={p(x,y)|p(x,y)∈A ∧ (x-xi)2+(y-yi)2=r2}; An arc segment of the perimeter of node i is denoted as arc(i) and called an arc segment of node i. Obviously, arc(i)⊆P(i) holds.
Definition 10
Suppose a point p(x,y) (p(x,y)∈P(i), i∈S), p(x,y) is said to be perimeter covered by node j (j∈S) if (x-xj)2+(y-yj)2≤r2 is true. If p(x,y) is covered by at least k nodes except node i, we say that the perimeter coverage degree of p(x,y) is k or p(x,y) is k-perimeter-covered.
Definition 11
Node i (i∈S) is said to be k-perimeter-covered if for any point p(x,y) (∀p(x,y)∈P(i)), it is perimeter covered by at least k nodes other than node i. Similarly, an arc segment of node i, arc(i) (arc(i)⊆P(i)), is said to be k-perimeter-covered if for any point p(x,y) (∀p(x,y)∈ arc(i)), its perimeter-coverage is no smaller than k.
A perimeter coverage lemma is proposed in [
11] to determine whether a field
A instrumented with a sensor network
S is sufficiently
k-covered. They can be stated as follows.
Lemma 1[11]
Any arc segment of node i' (i∈S) sensing circle divides two sub-regions in the field A. If this arc segment is k-perimeter-covered, the sub-region that is outside node i's sensing area is k-covered and the sub-region that is inside node i's sensing area (k+1)-covered.
Based on Lemma 1, we can obtain the following lemma.
Lemma 2
In a sensor network S with a requested coverage degree k, node i (i∈S) is a redundant node if and only if any neighboring node j (j∈N(i)) is k-perimeter-covered when node i is ignored.
Proof
For the “if” part, each sub-region inside the sensing area of node i is bounded by at least one arc segment of a neighbor's sensing circle. Since the perimeter coverage degree of each neighboring node is still k after the removal of node i, by Lemma 1, each sub-region inside the sensing area of node i is either k-covered or (k+1)-covered, which means the sensing area of the absent node i is sufficiently compensated by its neighboring nodes. Hence proves the “if” part.
For the “only if” part, we prove by contradiction. Suppose there exists a neighboring node m (m∈N(i)) whose perimeter coverage degree drops from k to km (km<k) due to node i's absence. Consider the arc segment of node m's sensing circle within node i's sensing area. There are two sub-regions divided by this arc segment. According to Lemma 1, the sub-region outside the sensing area of node m but inside the sensing area of node i is km-covered. This contradicts the assertion that any point in the sensing area of node i is k-covered by its neighboring nodes since node i is redundant, hence proved.
Lemma 2 justifies that a node is redundant if and only if no neighboring node is less than k-perimeter-covered due to its absence. However, using Lemma 2 as an eligibility rule requires collecting the perimeter coverage degrees from all the neighboring nodes, which can result in much message exchange among nodes. From Lemmas 1 and 2, we derive a more localized approach called Eligibility Rule based on Perimeter Coverage (ERPC) as follows.
Theorem 1
In a sensor network S with a requested coverage degree k, node i (i∈S) is said to be eligible for turning off if and only if for each neighboring node j (j∈N(i)) of node i, the arc segment of node j's sensing circle within the sensing area of node i is k-perimeter-covered other than node i.
Proof
The proof is directly from Lemma 2. For the “if” part, since the arc segment of each neighboring node j's sensing circle within the sensing area of node i is still k-perimeter-covered when excluding node i, the perimeter coverage of each node j remains k. By Lemma 2, node i is an eligible node, which proves the “if” part. For the “only if” part, we prove by contradiction. Let node m (m∈N(i)) be the neighboring node whose arc segment covered by node i is km-perimeter-covered (km<k) after node i is turned off. Since node i is redundant, all its neighboring nodes are k-perimeter-covered, which is contradictory with the assertion that there exists a neighboring node m that is km-perimeter-covered. Hence proves the “only if” part.
For the case in which some nodes' sensing areas may exceed the boundary of the field
A, ERPC also holds since the sensing area of a node is defined as the intersection area of the disk area of the node and the field
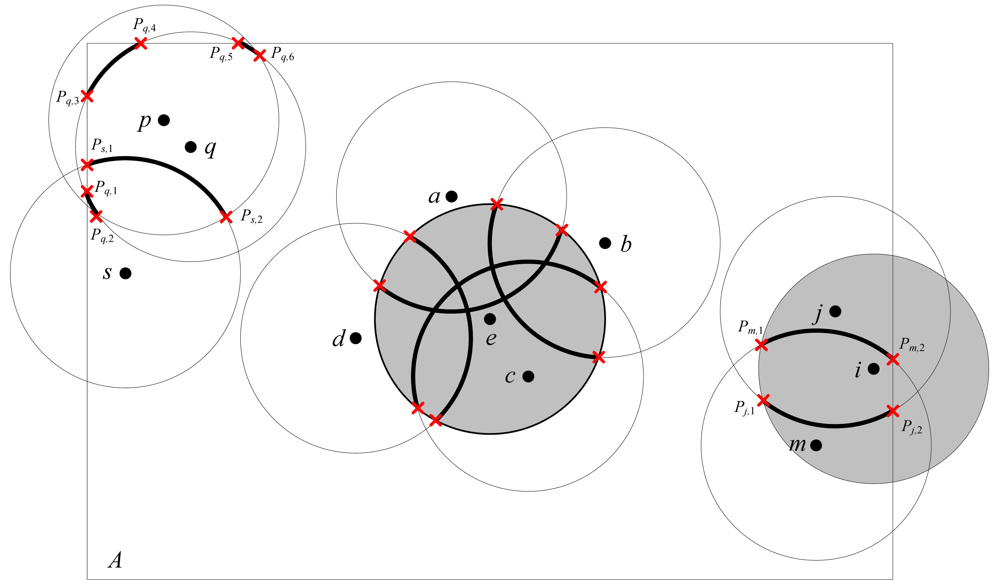
A in Definition 1. As illustrated in
Figure 3, node
e and
i are identified as eligible nodes for 1-coverage by ERPC. The node
p is not eligible since the arc segments [
Pq,3,
Pq,4] and [
Pq,5,
Pq,6] within node
p's sensing area are not perimeter covered by any nodes other than node
p.
By running ERPC locally, a node can identify its off-duty eligibility only based on the location information of its neighboring nodes. Therefore, ERPC is a localized approach and incurs limited communication overhead to the network.
4.2. Differences between ERPC and [11]
In [
11], Huang
et al. proposed the use of perimeter coverage to address the problem of how to determine if an area is sufficiently
k-covered by a given sensor network. According to their solution, the overall system cost can be minimized significantly by periodically examining the network coverage during the deployment process. For a senor network already redundantly deployed, however, [
11] does not derive an eligibility rule by which eligible nodes can be identified and then turned off to avoid unnecessary energy drain. The authors of [
11] pointed out that a power saving scheme (PSS) might be an extension of perimeter coverage to schedule the sleep and wakeup of nodes. PSS adopts an eligibility rule derived straightforwardly from Lema1[
11]:
In a sensor network S with a requested coverage degree k, node i (i∈S) is said to be eligible for turning off if and only if each neighboring node j (j∈N(i)) of node i is still k-perimeter-covered after node i is removed.
However, this eligibility rule, denoted as PSS-ER, does not follow a distributed fashion completely. PSS-ER requires excessive collaborations and communications among neighboring nodes, which is more time-consuming and energy-expensive than ERPC only based on limited local information. The two main advantages of ERPC over PSS-ER are detailed as follows.
In each round of PSS-ER, each node has to evaluate its perimeter coverage for two times: the first time evaluation filters out the candidates of eligible nodes; and then, for the second time, each neighbor of any candidate node i re-evaluates its perimeter coverage by skipping node i. Since the computational complexity of calculating perimeter coverage is as high as O(N2log(N)), the two-phase evaluation in PSS-ER takes more time than the one-off judgment used in ERPC.
ERPC and PSS-ER share one thing in common at that both of them require information exchange with neighbors when collecting neighbor information and announcing eligibility. Apart from such communication cost, however, each candidate node in PSS-ER has to broadcast its candidacy to all of its neighbors after the first evaluation phase ends. Therefore, PSS-ER incurs much more communication overhead into the network than ERPC does.
In a word, compared with the macro view of the work in [
11], ERPC solves the coverage problem from a micro prospective, which identifies an individual redundant node rather than the redundant network as a whole. The issue addressed by ERPC is more significant and challenging for a large-scaled and redundant-deployed sensor network. Moreover, as a completely distributed scheduling scheme, ERPC presents to be more time-saving and power-efficient than PSS-ER proposed by [
11], which will be validated in our simulations in Section 6.
4.3. ERPC Algorithm
The main part of the ERPC algorithm is to determine the perimeter coverage degree of the arc segment of each neighboring node within a node's sensing area. The whole algorithm of ERPC that runs at node
i is detailed as follows:
For a node
j (
j∈
N(
i)), let
d(
i,j) be the distance between node
i and
j. Then, calculate the length of the segment of node
j covered by node
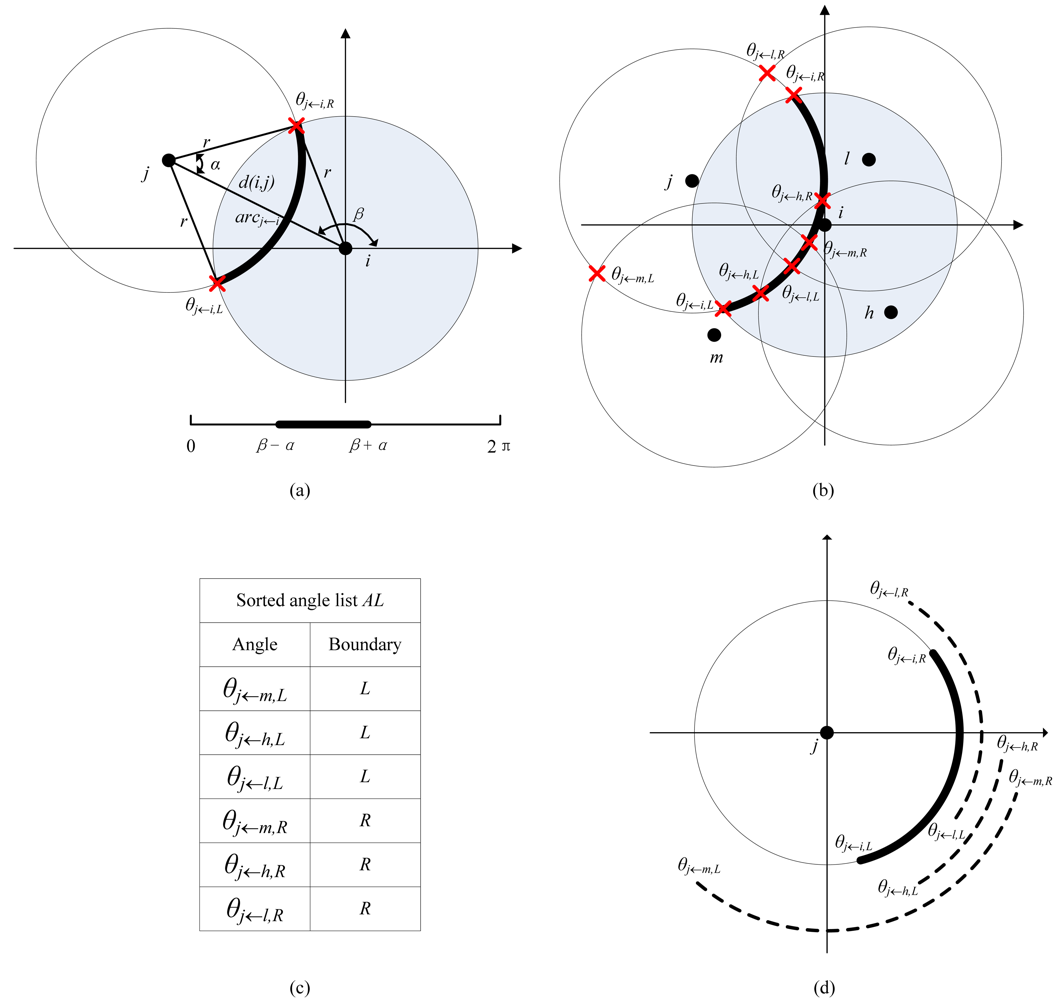
i. As shown in
Figure 4.(a), the
arcj←i can be measured by its central angle: [
θj←i,L, θj←i,R]=[
β-α, β+
α], where
α=
arccos(
d(
i,j)/2
r),
β=
arctg((
yi-yj)/(
xi-xj)).
For node
j's each neighboring node
m (
m∈
N(
i)∧
m≠
i), calculate node
j's arc segment covered by node
m, denoted by [
θj←m,L, θj←m,R], as illustrated in
Figure 4(b).
Add all the points
θj←m,L and
θj←m,R generated by last step to an angle list
AL and then sort AL in an ascending order. Meanwhile, mark each point as a left or right boundary of each covered arc segment, as shown in
Figure 4(c).
As demonstrated in
Figure 4(d), first calculate the perimeter coverage degree of the start point of
arcj←i, denoted as
ktemp. Then, scan the arc segment [
θj←i,L, θj←i,R] by visiting each point in the sorted
AL: whenever a start point is visited,
ktemp is increased by one; whenever an end point is visited,
ktemp is decreased by one. Finally, the perimeter coverage degree of
arcj←i should be the minimal value of
ktemp during the scanning process.
For each node j (j∈N(i)), check the perimeter coverage degree of its arc segment within node i's sensing area by running the above 4 steps. If there exists a node whose arc segment covered by node i is less than k-perimeter-covered, node i considers itself ineligible. If no such a node is found, node i determines it is eligible.
4.4. Complexity Analysis
Consider the algorithm in Section 4.2. In a network with N nodes, the maximum number of nodes that are neighboring to a node is N. The first four steps of the ERPC algorithm are performed to determine the perimeter coverage degree of a covered arc segment. In the second step, calculating all the arc segments of all the neighbors has a complexity of O(N). The complexity of the quick sort algorithm in the third step is O(Nlog(N)). In the fourth step, the scanning process has a complexity of O(N). Hence, the complexity to calculate an arc's perimeter coverage degree is O(Nlog(N)). Since the fifth step tests all the N neighboring nodes to draw a final decision, the overall complexity for the ERPC algorithm is O(N2log(N)). The rule used in the CPP protocol checks whether all the intersection points between nodes' sensing circles are k-covered to identify an eligible node. Since the number of the intersection points between N nodes is O(N2) and the complexity to calculate the coverage of an intersection point is O(N), the overall complexity of CCP rule is O(N3). Therefore, ERPC is a more lightweight off-duty eligibility rule than CCP rule.
5. Coverage Preserving Protocol
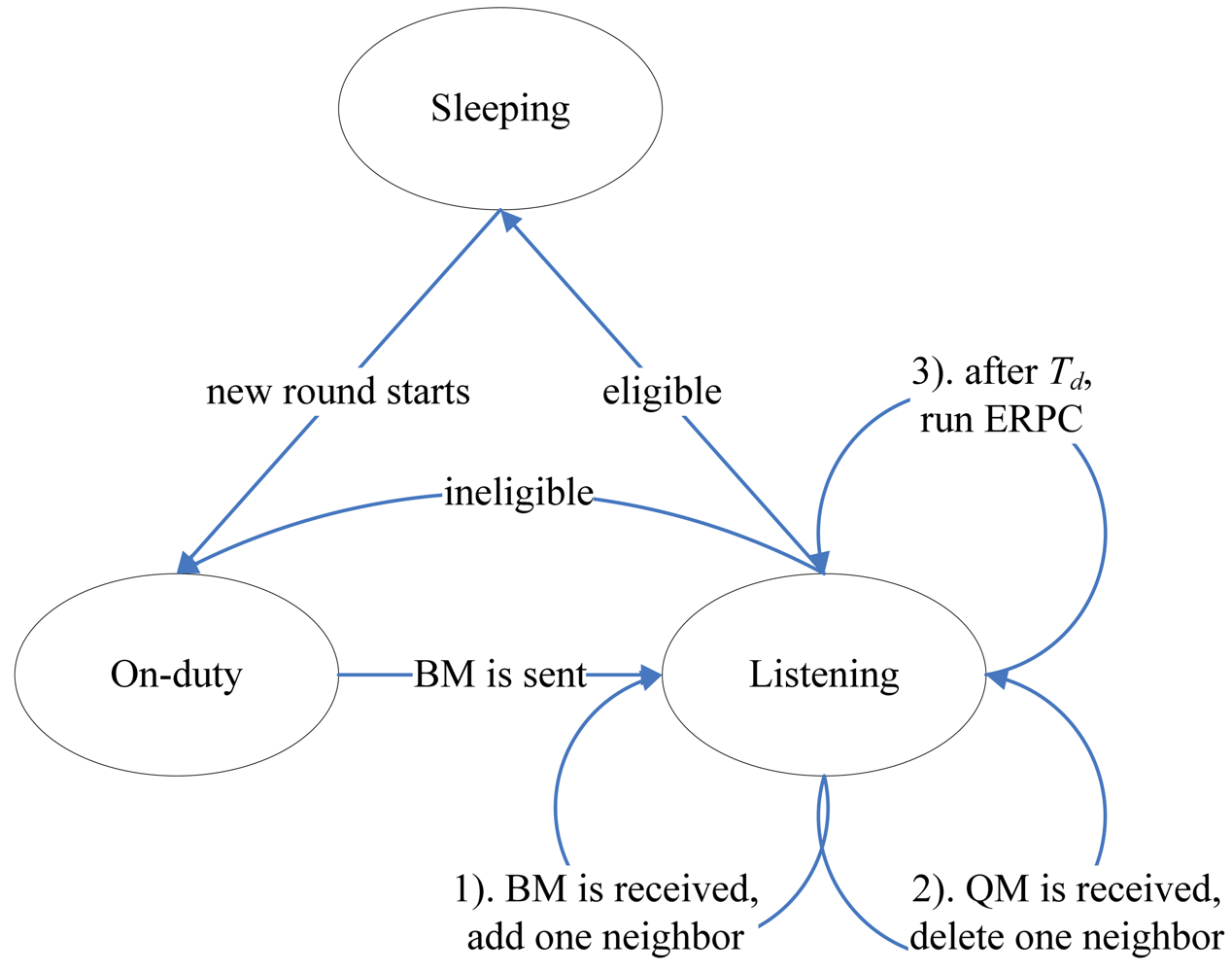
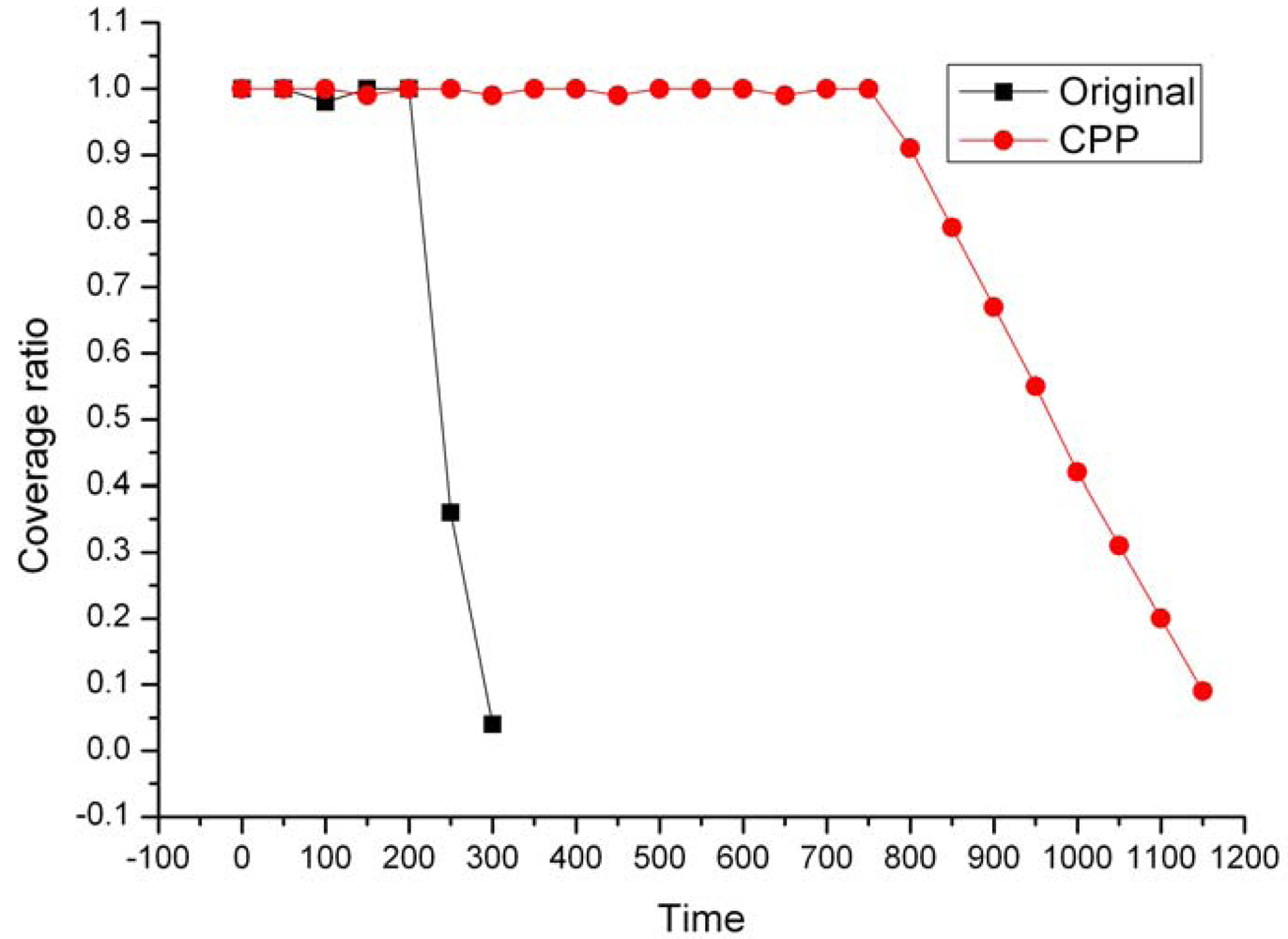
After turning off the eligible nodes filtered out by ERPC, the network coverage degree can be preserved by the remaining active nodes. If these on-duty nodes continuously work, however, they may soon run out of battery energy. This working model might not be desirable since the failure of some functional nodes can result in partitioning of the network or isolation of nodes. In this section, we propose a Coverage Preserving Protocol (CPP) to balance energy consumption among the neighboring nodes while maintaining the requested coverage degree. In CPP, a node can work at one of three states: Sleeping (Off-duty), Active (On-duty) and Listening. The operation of each node is divided into rounds. Each round takes the same period of time (Tr) and consists two steps detailed as follows.
5.2. Back-off based Eligibility Evaluation
After collection of neighbor information, each node evaluates its eligibility by ERPC. However, blind points may occur due to some neighboring nodes' dependency on each other, as shown in [
4]. CPP adopts the back-off scheme in [
4] to avoid blind points. In this scheme, each node runs ERPC after a random delay timer
Td. The node with the shortest
Td evaluates its eligibility earliest. If a node considers itself eligible by ERPC, it broadcasts a Quit Message (QM) to declare that it enters Sleeping state. The neighboring nodes with longer
Td receive the QM and remove the sleeping node from their neighbor lists. Thus, a node with a longer
Td will evaluate its eligibility without taking the sleeping nodes into account. Furthermore, by the back-off scheme, the candidate nodes that dependent on each other compete to be eligible by rounds in a random fashion, which evenly spreads the energy consumption around all nodes.
In Sleeping state, the eligible node is turned off to save battery energy. In On-duty state, the node performs the normal sensing and processing tasks. In Listening state, the node 1). first adds one neighbor in case that a BM is received, and then 2). deletes one neighbor upon QM and finally 3). evaluates its eligibility by ERPC after
Td. The state transition in CPP can be illustrated as
Figure 5.
5.3. Discussion about Tr and Td
The back-off scheme in CPP employs a randomized delay timer
Td to avoid blind points caused by multiple eligible nodes. When deciding
Tr, we mainly consider two factors: message exchange delay and remained energy. First, to bound the delay within a reasonable interval, we suggest that
Td should be a fraction of the sum of the round-trip delays among neighborhood. Therefore, we derive a back-off delay in the form as
where
RNDM(0,1) represents a random value uniformly distributed between [0,1],
Nd indicates node density defined as π
r2N/L2, and
Trt is the round-trip delay for a QM packet to travel over the wireless link. In a scenario where the wireless bandwidth is 256 kbps and the packet length of QM is 32 bytes,
Trt is typically 2 ms.
Moreover, we take the remained energy at each node into account. Suppose that all nodes have different energy levels at the very beginning. Let
Er denote the amount of energy at a node that remains and
Em denote the amount of initial energy. A fair consideration is to ensure that a node with a lower
Er/Em should be more likely eligible for sleep than the node with a larger
Er/Em. As a result, the energy consumption can be evenly spread around all the nodes. Therefore, combining with
Equation 5.1, the final form of the delay timer can be stated as:
As for the length of each round, it has little impact on the total working time of each node in all rounds. However, frequent round switch would result in much energy drain. Hence, Tr≫Ti,d is generally enough. In the simulation we choose 100 s as Tr for a 1000-second-long running process if not specified otherwise.