Kernel Based Nonlinear Dimensionality Reduction and Classification for Genomic Microarray
Abstract
:1 Introduction
 ⊆ ℜn onto feature space ℍ ⊆ ℜN, φ:
⊆ ℜn onto feature space ℍ ⊆ ℜN, φ:
 ⊆ ℜn → ℍ ⊆ ℜN. The kernel method provides a powerful and principled way of detecting nonlinear relations using well-understood linear algorithms in an appropriate feature space. This approach decouples the design of the algorithm from specification of the feature space. Most importantly, based on the kernel method, the kernel matrix is guaranteed to be positive semi-definite, convenient for the learning algorithm receiving information about the feature space and input data, and projects data onto an associated manifold, such as PCA. In addition, to solve KNN's parameter problems, fuzzy KNN adopts the theory of fuzzy sets to KNN, and fuzzy KNN assigns fuzzy membership as a function of the object's distance from its K-nearest neighbors and the memberships in the possible classes. This combination has two advantages. Firstly, fuzzy KNN can denoise training datasets. And secondly, the number of nearest neighbors selection, though not the most important, can consider the neighbor's fuzzy membership value.
⊆ ℜn → ℍ ⊆ ℜN. The kernel method provides a powerful and principled way of detecting nonlinear relations using well-understood linear algorithms in an appropriate feature space. This approach decouples the design of the algorithm from specification of the feature space. Most importantly, based on the kernel method, the kernel matrix is guaranteed to be positive semi-definite, convenient for the learning algorithm receiving information about the feature space and input data, and projects data onto an associated manifold, such as PCA. In addition, to solve KNN's parameter problems, fuzzy KNN adopts the theory of fuzzy sets to KNN, and fuzzy KNN assigns fuzzy membership as a function of the object's distance from its K-nearest neighbors and the memberships in the possible classes. This combination has two advantages. Firstly, fuzzy KNN can denoise training datasets. And secondly, the number of nearest neighbors selection, though not the most important, can consider the neighbor's fuzzy membership value.2 Summary of Kernel Method
 (the input space) to a vector space ℍ (the feature space) via a nonlinear mapping ψ:
(the input space) to a vector space ℍ (the feature space) via a nonlinear mapping ψ:
 ⊆ ℜn → ℍ ⊆ ℜN, the kernel function is the form K(xi, xj) = 〈ψ (xi), ψ (xj)〉, and the kernel matrix is K = (Kij) = (K(xi, xj)), respectively. Then, linear algorithms may be applied to the vector representation ψ(x) of the data, which performs nonlinear analysis of data by linear method. In other words, the kernel method is an attractive computational shortcut, the purpose of the mapping ψ(·) is to translate nonlinear structures of data into new linear representation in ℍ.
⊆ ℜn → ℍ ⊆ ℜN, the kernel function is the form K(xi, xj) = 〈ψ (xi), ψ (xj)〉, and the kernel matrix is K = (Kij) = (K(xi, xj)), respectively. Then, linear algorithms may be applied to the vector representation ψ(x) of the data, which performs nonlinear analysis of data by linear method. In other words, the kernel method is an attractive computational shortcut, the purpose of the mapping ψ(·) is to translate nonlinear structures of data into new linear representation in ℍ.3 Kernel Method based LLE Algorithm for Dimensionality Reduction
3.1 Locally Linear Embedding
3.2 Fuzzy K-Nearest Neighbor Algorithms
3.3 Kernel Method based LLE Algorithm
- Step 1.
- Mapping. Let
= {x1, x2, …, xn} be a set of n points in a high-dimensional data space ℜD. Suppose that the space
is mapped into a Hilbert space ℍ through a nonlinear mapping function ψ:
⊆ ℜD → ℍ ⊆ ℜN.
- Step 2.
- The fuzzy neighborhood for each point. Assign neighbors to each data point ψ(xi) using the Fuzzy KNN algorithm. The k̅ closest neighbors are selected using the new define fuzzy Euclidean distance measure , as follows:where Vi is a fuzzy covariance matrix of the point xi, and Vi is a symmetric and positive definite matrix, which specifies the shape of the clusters. The matrix Vi is commonly selected as the identity matrix, leading to Euclidean distance and, consequently, to spherical clusters, and and Vi is defined as
- Step 3.
- The kernel method based manifold reconstruction error. The KLLE's reconstruction error is similar to those of LLE, which is measured by cost function:Considering reconstruction weights , the reconstruction error can be rewritten bywhere ; it is obvious that QTQ is a positive semi-definite matrix. Then K = QTQ is defined as a kernel matrix. Hence Eq.(7) which is subjected to can be cast as the following Lagrange formulationwhere the solution of Eq.(8) is , K is a positive definite matrix, the eigendecomposition of K is of the form K = UTΛU, then Wi = UTΛ−1U1/1TUTΛ−1U1. Hence, the reconstruction weights W are computed by kernel matrix's eigenvalues and eigenvectors.
- Step 4.
- The kernel method computes low-dimensional embedding Y. In this step, KLLE is used to compute the best low-dimensional embedding Y based on the weight matrix W obtained.subject to the constraints and . Where M = (I − W)T(I − W), in LLE algorithm, the LLE embedding is given by the d eigenvectors correspond to the d smallest non-zero eigenvalues of matrix M [18].
4 Kernel Method based SVM Classifier
5 Performance Evaluation
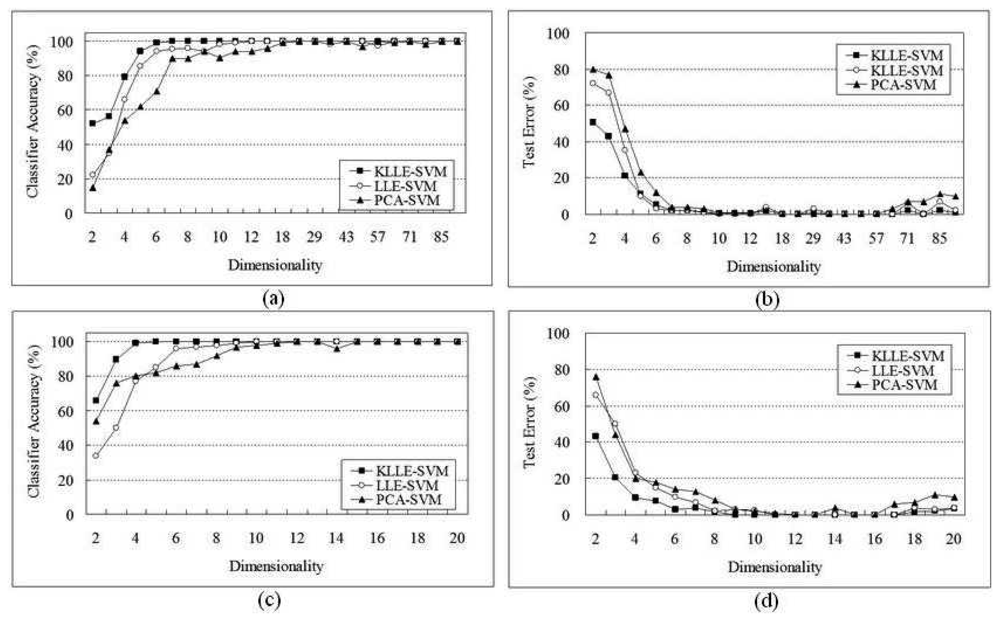
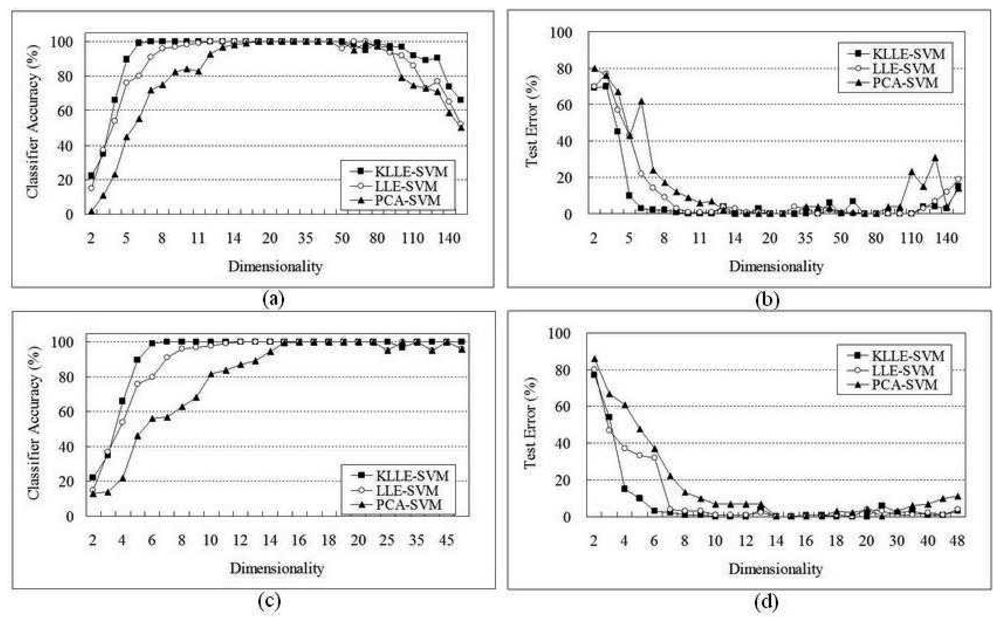
5.1 SRBCT Data
5.2 Lymphoma Data
6 Conclusion
Acknowledgments
References
- Shalon, D.; Smith, S.J.; Brown, P.O. A DNA microarray system for analyzing complex DNA samples using two-color fluorescent probe hybridization. Genome Research. 1996, 6(7), 639–45. [Google Scholar]
- Tenenbaum, J.B.; Silva, V.de; Langford, J.C. A global geometric framework for. nonlinear dimensionality reduction. Science. 2000, 260, 2319–2323. [Google Scholar]
- Roweis, S.T.; Saul, L.K. Nonlinear Dimensionality Reduction by Locally Linear Embedding. Science. 2000, 290, 2323–2326. [Google Scholar]
- Zhang, C.; Wang, J.; Zhao, N.; Zhang, D. Reconstruction and analysis of multi-pose face images based on nonlinear dimensionality reduction. Pattern Recognition. 2004, 37(2), 325–336. [Google Scholar]
- Elgammal, A.M.; Lee, C.S. Separating style and content on a nonlinear manifold. IEEE Computer Society Conference on Computer Vision and Pattern Recognition. 2004, 478–485. [Google Scholar]
- Mekuz, N.; Bauckhage, C.; Tsotsos, J.K. Face recognition with weighted locally linear embedding. The Second Canadian Conference on Computer and Robot Vision. 2005, 290–296. [Google Scholar]
- Schölkopf, B.; Smola, A.; Müller, K.R. Nonlinear component analysis as a kernel eigenvalue problem. Neural Computation. 1998, 10(5), 1299–1319. [Google Scholar]
- Shawe-Talyor, J.; Cristianini, N. Kernel Methods for Pattern Analysis.; Cambridge; Cambridge Uninversity Press, 2004. [Google Scholar]
- Young, R.A. Biomedical discovery with DNA arrays. Cell. 2000, 102, 9–15. [Google Scholar]
- Brown, M.P.; Grundy, W.N.; Lin, D.; Cristianini, N.; Sugnet, C.W.; Furey, T.S.; Ares, M.J.; Haussler, D. Knowledge-based analysis of microarray gene expression data by using support vector machines. Proc. Natl Acad. Sci. 2000, 97, 262–267. [Google Scholar]
- Lee, Y.; Lee, C.K. Classification of multiple cancer types by multicategory support vector machines using gene expression data. Bioinformatics. 2003, 19(9), 1132–1139. [Google Scholar]
- Wang, X.C.; Paliwal, K.K. Feature extraction and dimensionality reduction algorithms and their applications in vowel recognition, Pergamon. The Journal of the Pattern Recognition Society. 2003, 36, 2429–2439. [Google Scholar]
- Haykin, S. Neural networks: A Comprehensive Foundation; New Jersey; Practice-Hall Press, 1999; pp. 330–332. [Google Scholar]
- Marina, M.; Shi, J.b. Learning segmentation by random walks.; Cambridge, Advances in NIPS 13; 2001; pp. 873–879. [Google Scholar]
- Kouropteva, O.; Okun, O.; Pietikainen, M. Selection of the optimal parameter value for the locally linear embedding algorithm. Proc of the 1st International Conference on Fuzzy Systems and Knowledge Discovery, Singapore 2002, 359–363. [Google Scholar]
- Cover, T.M.; Hart, P.E. Nearest neighbour pattern classification. IEEE Trans. Inform. Theory. 1967, IT-13, 21–27. [Google Scholar]
- Keller, J.M.; Gray, M.R.; Givens, J.A. A fuzzy k-nearest neighbours algorithm. IEEE Transactions on Systems, Man, and Cybernetics. 1985, 15, 580–585. [Google Scholar]
- Saul, L.; Roweis, S. Think globally, fit locally: unsupervised learning of nonlinear manifolds. In Technical Report MS CIS-02-18; University of Pennsylvania, 2002; Volume 37, pp. 134–135. [Google Scholar]
- Vapnik, V.N. Statistical Learning Theory; John Wiley: New York, 1998; pp. 157–169. [Google Scholar]
- Vapnik, V.N. The nature of statistical learning theory.; NY; Springer-Verlag, 1995. [Google Scholar]
- Qian, Z.; Cai, Y.D.; Li, Y. A novel computational method to predict transcription factor DNA binding preference. Biochem. Biophys. Res. Commun. 2006, 348, 1034–1037. [Google Scholar]
- Vapnik, V.N. An Overview of Statistical Learning Theory. IEEE Transactions on Neural Networks. 1999, 10(5), 988–999. [Google Scholar]
- Cristianini, N.; Shawe-Talyor, J. An introduction to support vector Machines; Cambridge; Cambridge Uninversity Press, 2000; pp. 96–98. [Google Scholar]
- Du, P.F.; He, T.; Li, Y.D. Prediction of C-to-U RNA editing sites in higher plant mitochondria using only nucleotide sequence features. Biochemical and Biophysical Research Communications. 2007, 358, 336–341. [Google Scholar]
- Ellis, M.; Davis, N.; Coop, A.; Liu, M.; Schumaker, L.; Lee, R.Y.; et al. Development and validation of a method for using breast core needle biopsies for gene expression microarray analyses. Clin. Cancer Res. 2002, 8(5), 1155–1166. [Google Scholar]
- Orr, M.S.; Scherf, U. Large-scale gene expression analysis in molecular target discovery. Leukemia. 2002, 16(4), 473–477. [Google Scholar]
- Khan, J.; Wei, J.S.; Ringner, M.; Saal, L.H.; Ladanyi, M.; Westermann, F.; et al. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat Med. 2001, 7(6), 673–9. [Google Scholar]
- Nikhil, R.P.; Kripamoy, A.; Animesh, S.; Amari, S.I. Discovering biomarkers from gene expression data for predicting cancer subgroups using neural networks and relational fuzzy clustering. BMC Bioinformatics. 8(5).
- Yeo, G.; Poggio, T. Multiclass classification of SRBCTs. Technical Report AI Memo 2001-018 CBCL Memo 206, MIT. 2001. [Google Scholar]Alizadeh, A.A.; Eisen, M.B.; et al. Distinct types of diffuse large b-cell lymphoma identified by gene expression profiling. Nature 2000, 403, 503–511. [Google Scholar]
- Troyanskaya, O.; Cantor, M.; et al. Missing value estimation methods for DNA microarrays. Bioin-formatics. 2001, 17, 520–525. [Google Scholar]
- Tusher, V.G.; Tibshirani, R.; Chu, G. Significance analysis of microarrays applied to the ionizing radiation response. Proc. Natl. Acad. Sci. USA. 2001, 98, 5116–5121. [Google Scholar]
- Tibshirani, R.; Hastie, T.; Narasimhan, B.; Chu, G. Class predicition by nearest shrunken centroids with applications to DNA microarrays. Statistical Science. 2003, 18, 104–117. [Google Scholar]
| Algorithms | 96 genes | 20 genes | ||||
|---|---|---|---|---|---|---|
| Dimensional | Support vectors | Time(sec) | Dimensional | Support vectors | Time(sec) | |
| SVM | 96 | - | - | 20 | 106 | 4127 |
| PCA-SVM | 29 | 87 | 2672 | 11 | 64 | 1933 |
| LLE-SVM | 14 | 63 | 2102 | 9 | 42 | 1743 |
| KLLE-SVM | 7 | 42 | 1934 | 5 | 31 | 1307 |
| Algorithms | 165 genes | 48 genes | ||||
|---|---|---|---|---|---|---|
| Dimensional | Support vectors | Time(sec) | Dimensional | Support vectors | Time(sec) | |
| SVM | 165 | - | - | 48 | 124 | 5343 |
| PCA-SVM | 18 | 104 | 2672 | 22 | 83 | 3105 |
| LLE-SVM | 15 | 74 | 2133 | 9 | 56 | 2247 |
| KLLE-SVM | 7 | 56 | 1934 | 5 | 41 | 1766 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative CommonsAttribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Li, X.; Shu, L. Kernel Based Nonlinear Dimensionality Reduction and Classification for Genomic Microarray. Sensors 2008, 8, 4186-4200. https://doi.org/10.3390/s8074186
Li X, Shu L. Kernel Based Nonlinear Dimensionality Reduction and Classification for Genomic Microarray. Sensors. 2008; 8(7):4186-4200. https://doi.org/10.3390/s8074186
Chicago/Turabian StyleLi, Xuehua, and Lan Shu. 2008. "Kernel Based Nonlinear Dimensionality Reduction and Classification for Genomic Microarray" Sensors 8, no. 7: 4186-4200. https://doi.org/10.3390/s8074186




