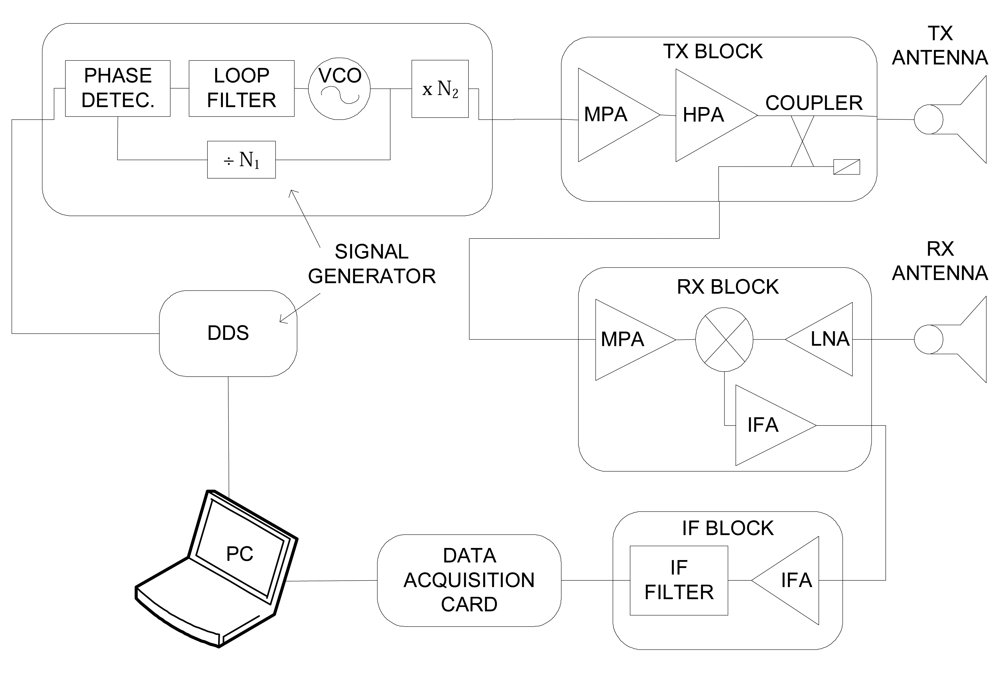
4.1. Phase Gradient Autofocus (PGA)
This subsection only shows an overview of the PGA algorithm. The detailed description can be found in [
5,
6,
7]. PGA is able to estimate and remove arbitrary phase errors in SAR images. The right operation of spotlight PGA is based on three hypotheses:
- -
The phase error must be spatially invariant over the entire image, that is, all the scatters in a scene must share the same phase error history.
- -
Targets must exist with phase error information over the entire data set.
- -
The raw data signal must be related to the SAR image by means of a two-dimensional Fourier Transform. This condition is always fulfilled in spotlight SAR, because the data are usually motion compensated to a point. However, our radar is going to operate at stripmap-mode to maximize the coverage of the scene.
The next four points summarize spotlight PGA:
Circular shifting: The input to PGA is the complex SAR image. The first step is to choose the strongest target for each range bin and circularly shift it to the azimuthal origin. This shift removes the Doppler frequency offset of these scatters. Therefore, PGA can not estimate linear phase errors in the Doppler history.
Windowing: Each selected scatter is windowed azimuthally. Windowing isolates the phase error information contained at the dominant scatter from other scatters at the same range bin that could interfere with the phase error estimation.
Phase gradient estimation: The circular shifted and windowed data are inversely Fourier transformed along azimuth to the range-compressed domain. Let us denote
S(m,n) as the signal associated with the windowed target from the
nth range bin, i.e., the windowed and shifted Fourier transform across the columns of
s(m,n):
where Φ
err(
m) is the phase error (spatially invariant) and
θ(
m,
n) is the scatter-dependent phase function for the chosen target in the
nth range bin. The linear unbiased minimum variance estimate of the gradient phase error is given by:
where
S′(
m,
n) is the first derivative along columns of
S(m,n).
There are other phase gradient estimators that produce good results in combination with circular shifting and windowing [
5,
7,
16].
Iterative phase correction: The estimated phase gradient has to be integrated to obtain the phase error. Any constant or linear term of the phase error is removed. After the integration, the phase error is corrected multiplying the range-compressed data with a complex exponential function whose phase is the inverse of the phase error estimate. Then the corrected data are Fourier transformed to the image domain, leading to a more focused image. All the described steps are iteratively repeated until some convergence criterion is reached [
5,
7].
Basic spotlight PGA is based on the three fundamental hypotheses that have been explained above. The proposed SAR signal processing chain implements a stripmap-mode with motion compensation to a line. The first difference is referred to the azimuthal resolution limit and the scene coverage. In stripmap-mode, the antenna beamwidth limits the azimuthal resolution, and data collection length determines azimuthal scene size. However, in spotlight-mode, data collection length determines azimuthal resolution and antenna beamwidth limits the azimuthal scene size.
Both modes usually use the same transmitted signal and a dechirp-on receive procedure [
7]. However, the second difference is the reference signal used for dechirping. Stripmap-mode uses compensation to a line that preserves the azimuthal chirp, while spotlight-mode uses motion compensation to a point that removes this azimuthal chirp [
7].
The proposed stripmap PGA implements different strategies to fulfill these PGA hypotheses. The implemented algorithm is described in the next subsections. The movement error that has been estimated by PGA is used in a two step correction method: a coarse correction that removes the range shift, and a fine correction that focuses the target within the resolution cell.
4.2. Stripmap to spotlight conversion
Spotlight PGA needs a raw signal data that can be compressed by means of a two dimensional Fourier transform to form a SAR image. However, stripmap data preserve the azimuthal chirp and a linear range migration, that is, a single scatter is detected at different range bins for each pulse of the data set. These stripmap characteristics do not allow compression of the image using a two-dimensional Fourier transform. To solve this problem, the proposed algorithm converts stripmap data to spotlight data. The conversion consists of a change of the reference signal. Stripmap data have been motion compensated with a fixed reference range
R0, while spotlight data were motion compensated with a different reference range
Rc(m) for each pulse. The stripmap to spotlight conversion removes the stripmap motion compensation and applies motion compensation to the scene center. This is equivalent to multiply each pulse with a complex exponential given by
equation. (13):
where
λ is the wavelength.
This conversion removes the azimuthal chirp without modifying the phase error that must be estimated [
7]. PGA needs targets with phase error information over the entire data collection range. In spotlight-mode, the phase history of any point covers the entire data set. However, in stripmap-mode the phase history of any scatter is limited by the antenna beamwidth and is contained only in a portion of the data set. A solution was proposed in [
17]. It consists of dividing the complete data collection into azimuthal data segments. Our proposed PGA uses this philosophy and independently converts each segment from stripmap to spotlight mode. Furthermore, this minimizes range migration even in the case of squinted stripmap data.
Both spotlight and stripmap data with dechirp-on receive have a RVP term. In both modes, RVP can be removed using the range deskew filter given by
Equation (14) [
7].
4.3. Range alignment previous to the phase estimation
For each azimuthal data segment, some prominent scatters must be selected to estimate the phase error due to the non-ideal movement. This selection can be done in the range compressed domain. Several methods to choose prominent scatters in the range compressed domain have been proposed in the specialized literature about ISAR [
19,
20]. For our purpose, the most appropriate algorithm is based on the minimal normalized variance criteria. It computes the normalized variance for each range bin (column of the range compressed map). The range bin
n̂ with the minimal normalized variance is chosen. The formulation is given by
Equation (15):
where
S(m,n) is the range compressed map, with
M azimuthal cells (rows), and
N range bins (columns).
In this way, we achieve selected targets that are located in an azimuthal coordinate quite centered respect to the middle of the azimuthal data segment. Taking short enough azimuthal data segments, we can avoid the linear range migration due to the ideal motion of the platform. It means that a selected target has remained in the same range cell for the major part of the azimuthal data segment and, therefore, this range column is the most appropriate to extract the movement error.
Unfortunately, the range migration cell due to non-ideal motion is still present in the range compressed domain. The selected range column could be processed by the typical PGA to extract the movement error. However, the range column does not have information in zones where the movement error was larger than the range resolution, because the target has suffered a range shift. One way to overcome this drawback is range aligning the history of the target in the range compressed domain. There are several ISAR techniques that make this correction. Also, we have to take into account that this range alignment is usually the first step for motion compensation in ISAR. For example, EC [
8,
9] or GRA [
10] are robust techniques for aligning the history of a target in the same range column in presence of noise and clutter.
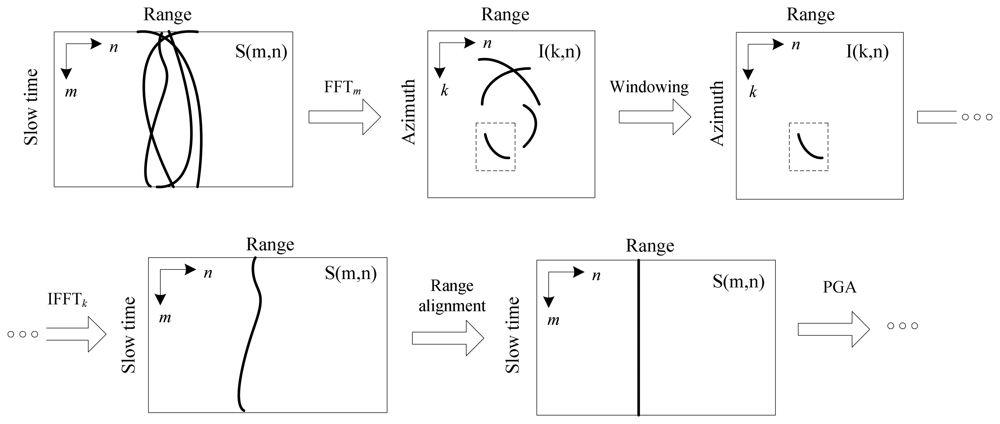
To avoid the interference of other targets in the range compressed domain, we can compress the image azimuthally via a Fourier transform and isolate the selected prominent scatter in the image domain using a window. This technique is used in ISAR processing [
21]. The complete procedure is illustrated in
Figure 4.
After the range alignment, the column can be processed by the basic PGA to estimate the phase error due to non-ideal motion.
4.4. Phase gradient estimation
Only the scatters that are illuminated during all the acquisition time have complete phase error information. The geometry of stripmap-mode does not allow collection of data from the same scatter all the time. Returns from a target are only received for a limited number of pulses. The number of received pulses is determined by the antenna beamwidth. This is a drawback, because PGA needs targets with phase error information over the entire data set.
The solution proposed in [
17] consists of dividing the data set into shorter azimuthal data segments. After this division, each azimuthal data segment is independently converted from stripmap to spotlight-mode in the manner described above. Each segment is range compressed via a Fourier transform. For each segment, several columns containing prominent targets are selected using minimal normalized variance. The history of these targets is range aligned as previously explained. Then, basic spotlight PGA is independently applied to each column to obtain a phase error estimate. Final phase error of the segment will be an average of these independent estimations.
It is known that PGA can not estimate linear phase errors. Thus, the phase error estimation of each segment could exhibit a different linear component. To avoid discontinuities in the phase error estimation between consecutive segments, in [
17] it is proposed to remove the mean of the phase gradient before combining and integrating the phase error segments. However, this procedure leads to large errors because the segments are small, and the linear component of the actual phase error is, in fact, different from zero and also different from one segment to another.
An estimate of the second derivative of the phase error has the advantage of forcing the mathematical continuity between consecutive segment estimations. The second derivative estimate of the phase error from all the segments is integrated together yielding the phase error gradient without any discontinuity over the complete data set. The mean of the whole phase gradient was then removed before integrating again to get the complete phase error.
The first hypothesis of PGA is that the phase error must be spatially invariant over the entire image, i.e. all the scatters in a scene must share the same phase error. Traditional PGA algorithm assumes that the phase error is constant with range. However, with wide swaths or short ranges, the incidence angle is highly varied and the phase error due to the movement exhibits range dependence. Two alternatives have been proposed:
The first one consists of dividing the data set into narrow range subswaths. The subswath width has to be chosen to guarantee high correlation of the phase error within the subswath. The division is carried out with the range compressed data, after azimuthal segmentation and stripmap to spotlight conversion. The previously described PGA procedure is independently applied to each subswath. The selected targets of one subswath will have very similar phase errors, and the PGA correction will be appropriate to all the targets within the subswath.
The second alternative is to estimate the range dependence of the error to correlate different subswaths. This method is based on the Phase Weighted Estimation PGA (PWE-PGA) described in [
18]. This method improves the performance of PGA, but increases its computational complexity.
4.5. Coarse movement correction
Once the phase error due to non-ideal motion has been estimated, the movement error can be extracted using the phase information. Usually
t0 is negligible in comparison with
and, therefore,
Rerr(
m) can be approximated by:
where Φ
err(
m) is the estimated phase error and
Rerr(
m) is the estimated motion error on the slant plane.
This estimate is valid to correct the range shifts due to the movement errors. The range shift can be removed using the original stripmap raw data. The procedure consists of shifting each received pulse the quantity given by Rerr(m). The shift can be performed by multiplying each mth pulse of the raw matrix s(m,n) with a complex exponential given by (17).
After this correction, the movement errors that are larger than the resolution cell have been compensated, i.e. the range shift due to non-ideal motion has been removed. However, the range curvature due to ideal motion that is different for each scatter still remains. This range curvature will be compensated using RMA [
7,
15].
The range error estimated by (16) is extracted from the phase information. This range information is only valid if the estimated phase error can be unwrapped, i.e. if the phase difference between two consecutive pulses is lower than
π radians:
Equation (18) imposes a limit for the maximum instantaneous radial velocity error (projected over slant plane velocity) that can be corrected. Using
Equation (19), for our system the instantaneous maximum radial velocity error will be 11 m/s, which is a high value.
4.6. Fine movement correction
The coarse correction removes the range shift, but a fine correction is still necessary, i.e. the typical phase correction of PGA. Once the phase error component has been estimated and the range shift removed, the corrected stripmap data set can be Fourier transformed to the range domain, and the phase error estimation can be removed for each range bin. Let
S(m,n) be the range compressed data of
s(m,n). The correction consists of multiplying each column (range bin) of the matrix
S(m,n) with a complex exponential given by
Equation (20):
Finally, the range compressed data are inversely Fourier transformed again to the time domain. This data matrix contains the stripmap signal in the format required by RMA, without motion error and without RVP.
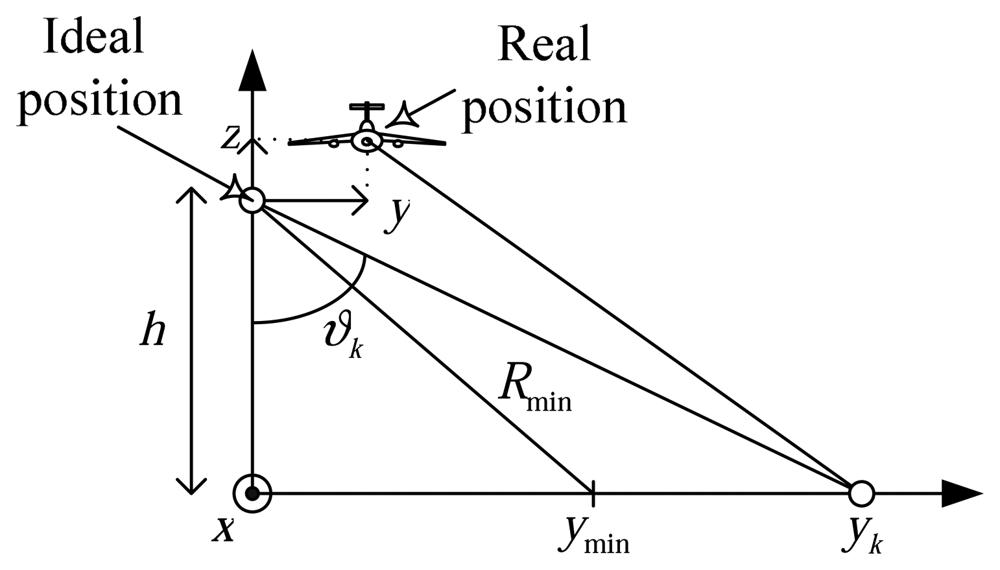
4.7. Movement error analysis
Let there be a trajectory error with
z and
y direction components, see
Figure 5. These movements,
y(m) and
z(m), induce a phase error and a range shift on the slant plane that depends on the range to the targets
yk. The proposed algorithm can correct range dependencies due to non-planar movement of the platform.
The phase error can be written as:
For a target located in the center of the
kth range bin the incidence angle
ϑk is:
where
δR is the range resolution of the image
The Φ
y(
m) and Φ
z(
m) phase error components do not depend on
ϑk and, therefore, they are the same for all the range bins. This is exploited by PWE-PGA, described in [
18]. Therefore, this non-ideal motion can be compensated by the proposed autofocus algorithm described above.
Variations in along-track speed result in non-uniform spacing of the radar pulses. This non-uniform sampling of the Doppler spectrum results in erroneous calculations of the Doppler phase history. Traditionally, the data are interpolated in the azimuthal direction to correct the velocity variations across the synthetic aperture [
2]. This interpolation is based on the measured data of an IMU. Our system does not have an available IMU, therefore, this kind of error can not be compensated. However, our autofocus is able to correct constant deviations respect to the nominal velocity, that is, the mean velocity error.
A constant deviation of the speed generates a phase error that produces defocus and distortion in the image. An analytic study of this phase error can be obtained with a simple geometrical development.
Suppose a target located on the ground in a position with coordinates (
xp,
yp). The phase of the received signal for each pulse is directly proportional to the distance between the platform and the target
Rp(
t̂):
where
t̂ is the slow time and
λ is the wavelength of the transmitted signal.
The range between the platform and the target varies for each pulse if the platform moves at different speed from the nominal one. Suppose a nominal velocity of the platform,
Va, this range is given by:
where
is the distance between platform and target projected over the
y-z plane.
Supposing
xp and
Va ·
t̂ <
rp,
Equation (24) can be approximated by:
Now, suppose that the platform moves with a constant deviation velocity, Δ
Va, over the nominal speed
Va. The new range between the platform and the target,
Rbias(
t̂), is given by:
Supposing
xp and (
Va + Δ
Va)·
t̂ ≪
rp,
Equation (26) can be approximated by:
Using
Equation (23) that relates range with phase, the phase error due to a non-zero mean velocity error is given by:
The phase error consists of two different components. The first term is a quadratic error. This error produces a loss of resolution. The second term is a linear error which produces an azimuthal shift of the image.
The quadratic error depends on the projected distance over the
y-z plane,
rp. Therefore, this error is different for each range bin, because it depends on the position of the target in
z and
y. However, this kind of error can be compensated by the autofocus, because it perfectly matches with the error model of the method PWE-PGA described in [
18].
The linear phase error cannot be corrected. It is space variant because depends on the projected distance over the y-z plane, rp, and the azimuthal coordinate of the target xp. Therefore, this error distorts the image. The permitted distortion gives the maximum allowed velocity deviation, ΔVa.
4.8. Simulated results
The algorithm was tested with simulated stripmap-mode data. The simulated system has the same parameters as our real LFM-CW SAR system. The nominal resolution cell chosen for this experiment is 15 cm (24 cm with windowing). The simulation evaluated the degradation of the impulse response of the SAR system. The measured parameters were azimuth and slant range resolution at -3 dB and -9 dB respect to the main lobe level, and azimuth and slant range PSLR (Peak Side-Lobe Ratio) with respect to the main lobe level.
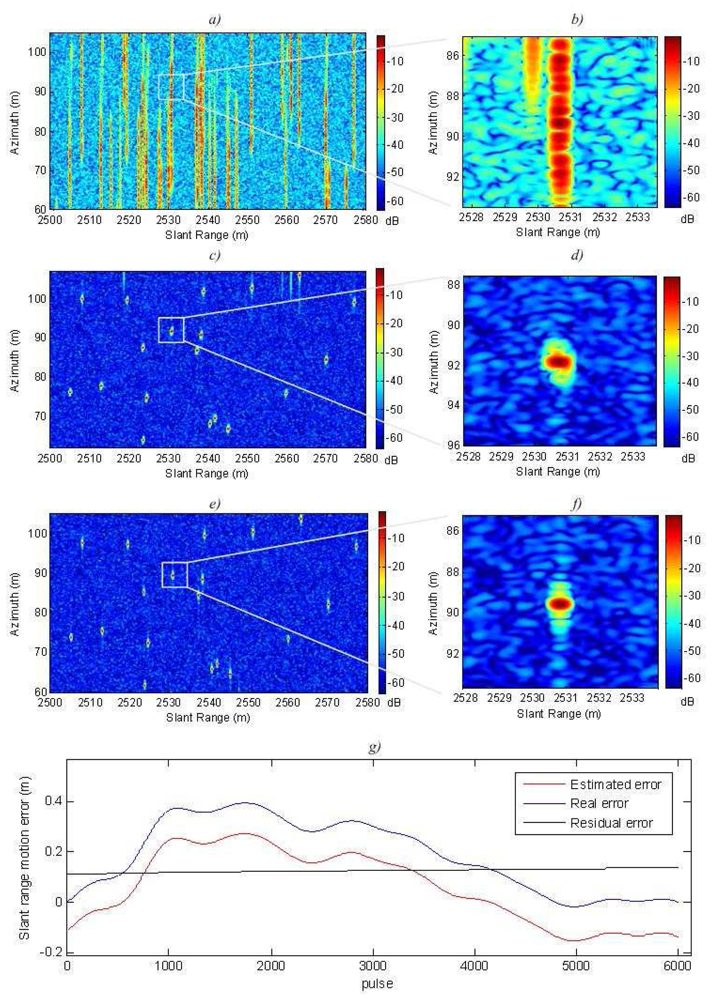
The simulated scene consists of several corner reflectors uniformly distributed in a swath of 45×80 m. The swath is 2500 m away from the radar. The movement error consists of random shifts in the
y-z plane, see
Figure 5. The combination of these errors generated a range shift in the slant plane larger than the range resolution. This motion error is shown in
Figure 6g. Also, the estimated motion error by the autofocus is shown in
Figure 6g. Our algorithm appears to have good accuracy. The residual error is linear and can not be compensated by the autofocus. However, it is not important because these errors do not result in image defocusing [
7].
Figure 6a shows the SAR image and
Figure 6b shows the detail of the system impulse response without applying any autofocus technique. The image is completely defocused.
Figure 6c illustrates a more focused SAR image. This is the result of applying the autofocus only with fine correction, without coarse correction. The detail of the system impulse response can be seen in
Figure 6d.
Figure 6e and 6f respectively show the SAR image and the detailed system impulse response applying the complete autofocus. Thanks to the novel coarse compensation we can appreciate a resolution improvement of 7 % in slant range, and 11 % in azimuth. Also a slight increment of the PSLR is achieved.
Table 2 gives the exact measured values.