Estimation of the Total Atmospheric Water Vapor Content and Land Surface Temperature Based on AATSR Thermal Data
Abstract
:1. Introduction
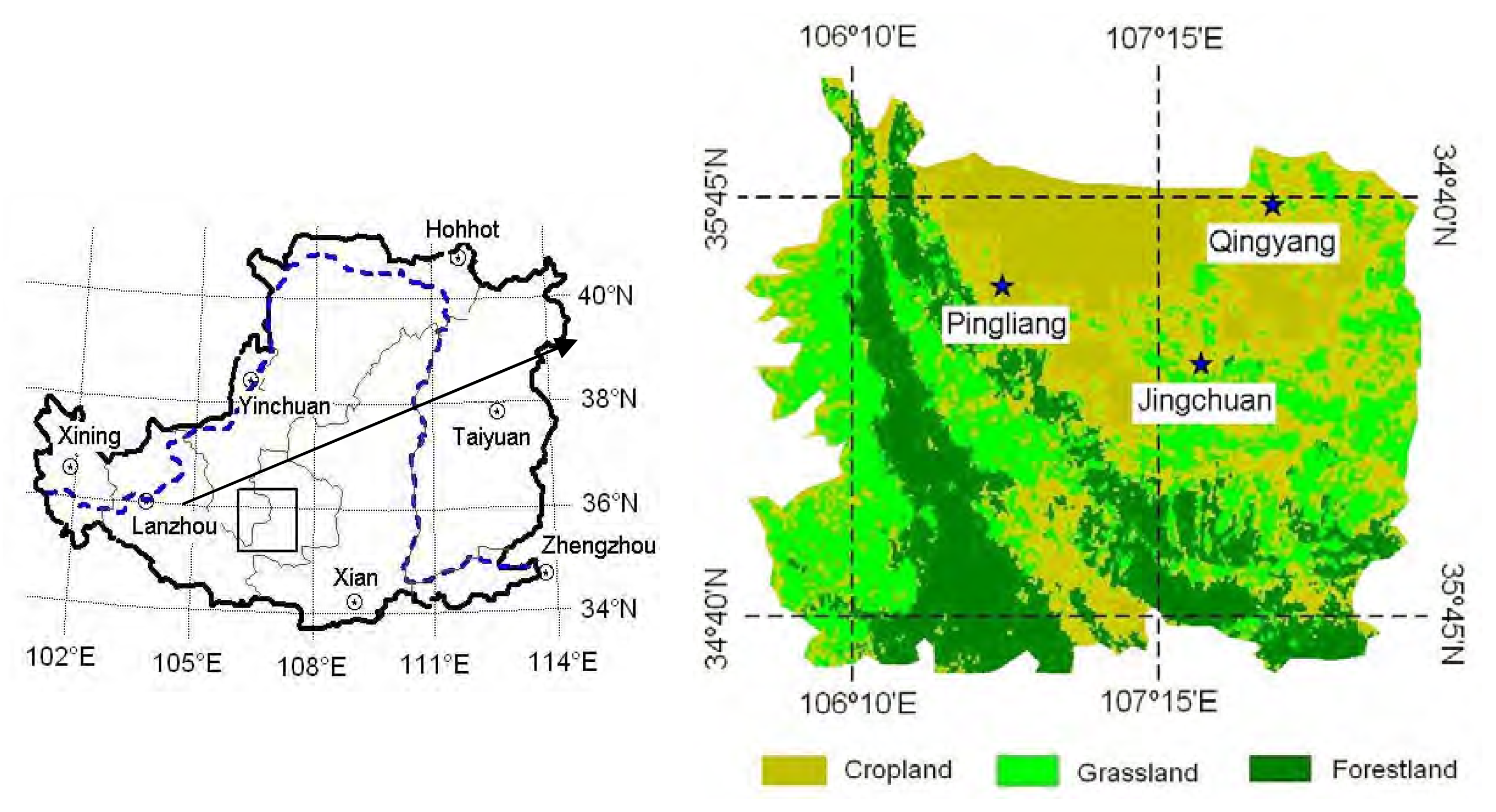
2. The Loess Plateau and the field campaigns
2.1 The Loess Plateau
2.2 The field campaigns
2.3 The AATSR data
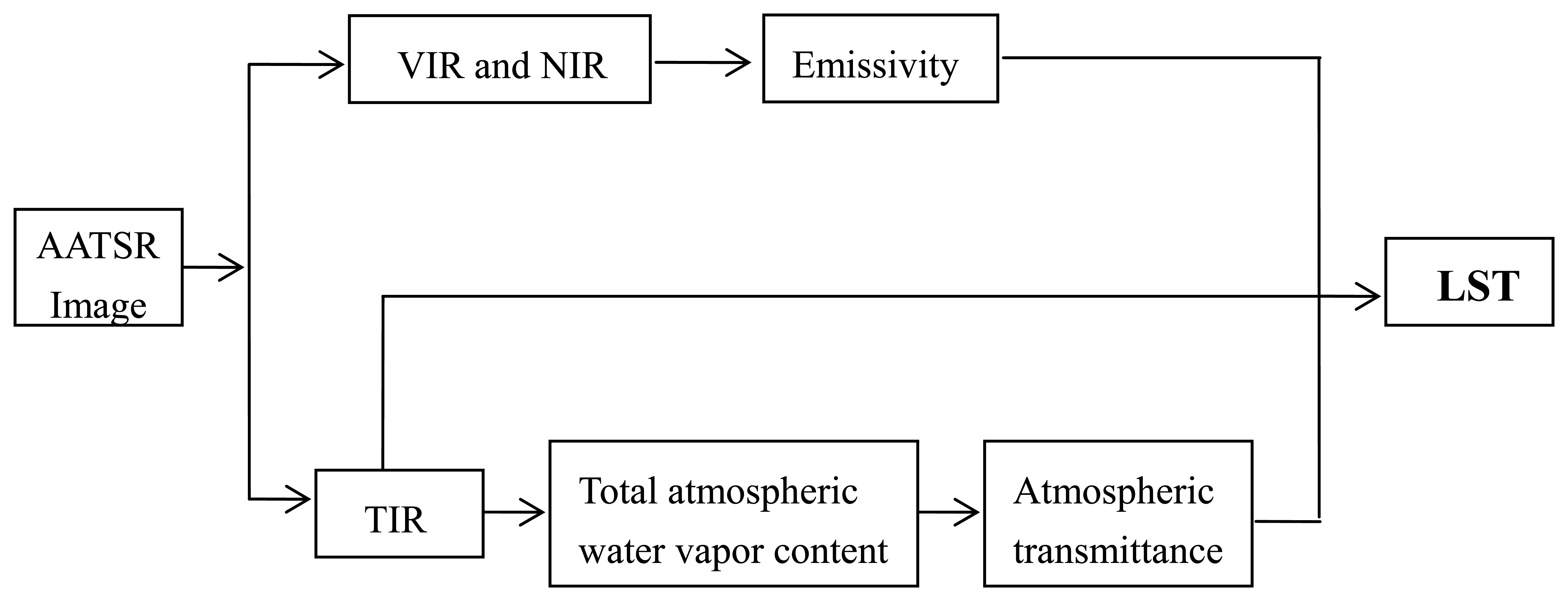
3. Algorithm for TAWV and LST retrievals
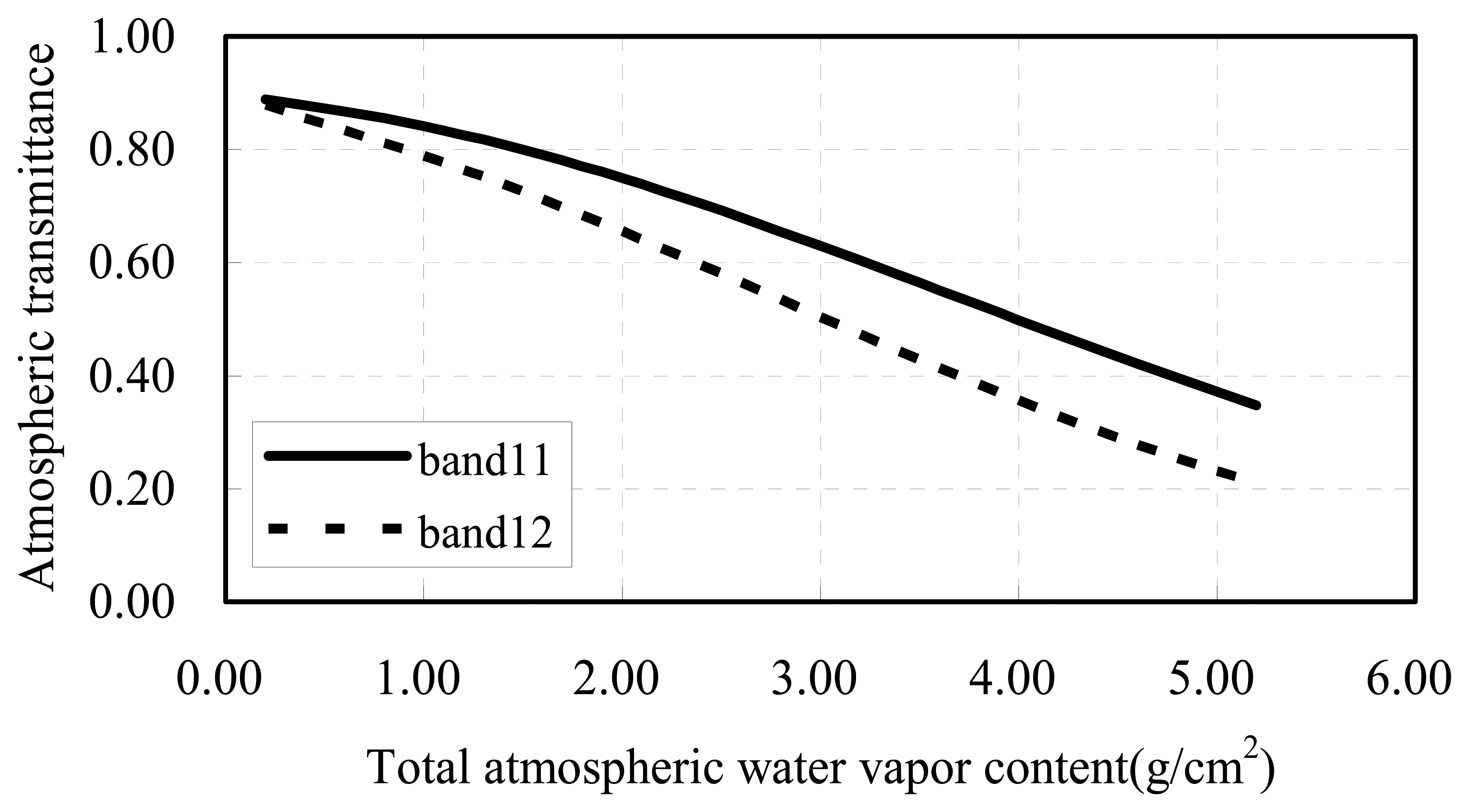
3.1 Determination of the total atmospheric water vapor content
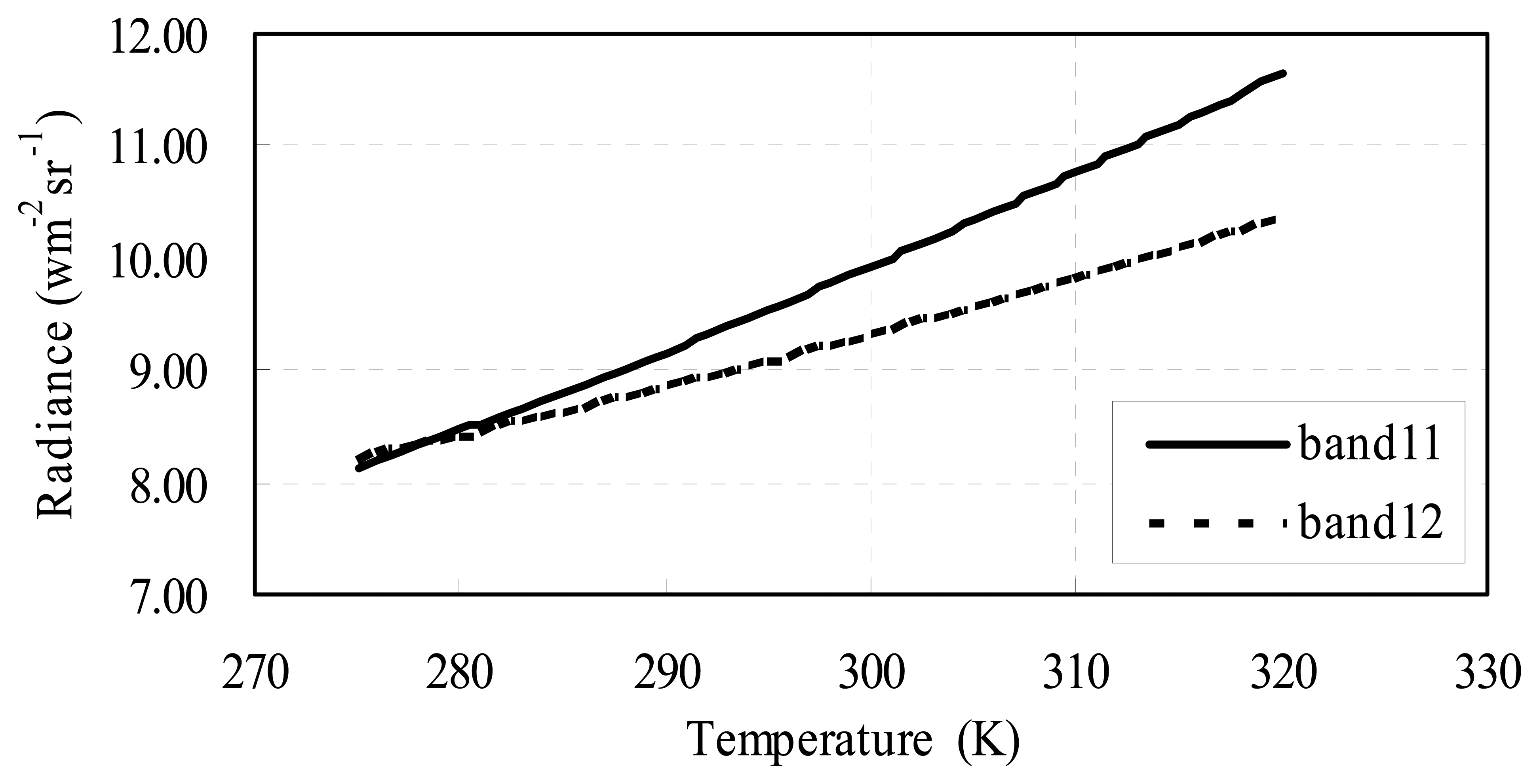
3.2 The thermal radiative transfer equation
3.3 Calculation of atmospheric transmittance
3.4 Estimation of land surface emissivity
3.5 Land surface temperature retrieval
4. Results and Validation
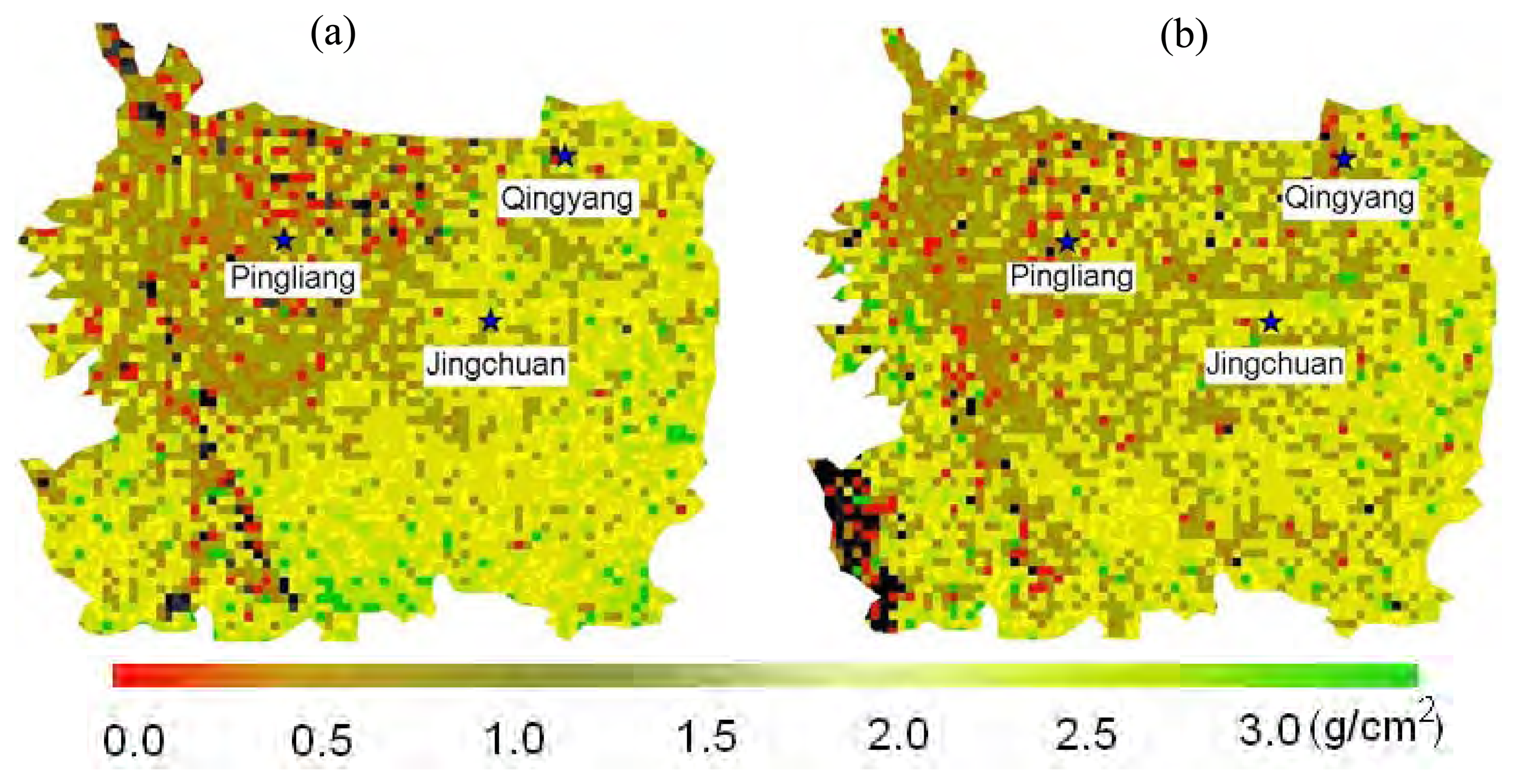
4.1 Mapping of total atmospheric water vapor content
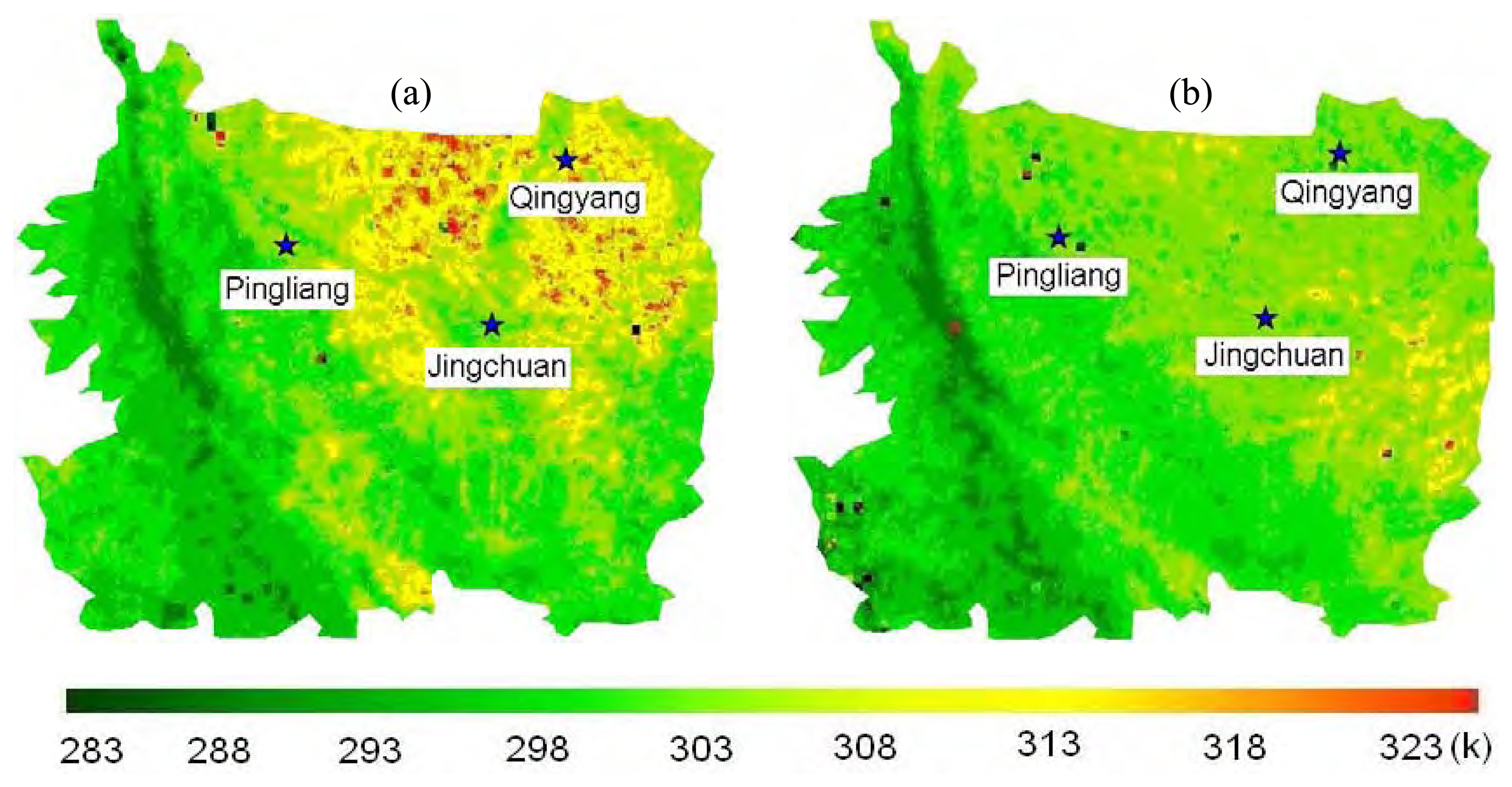
4.2 Validation of land surface temperature
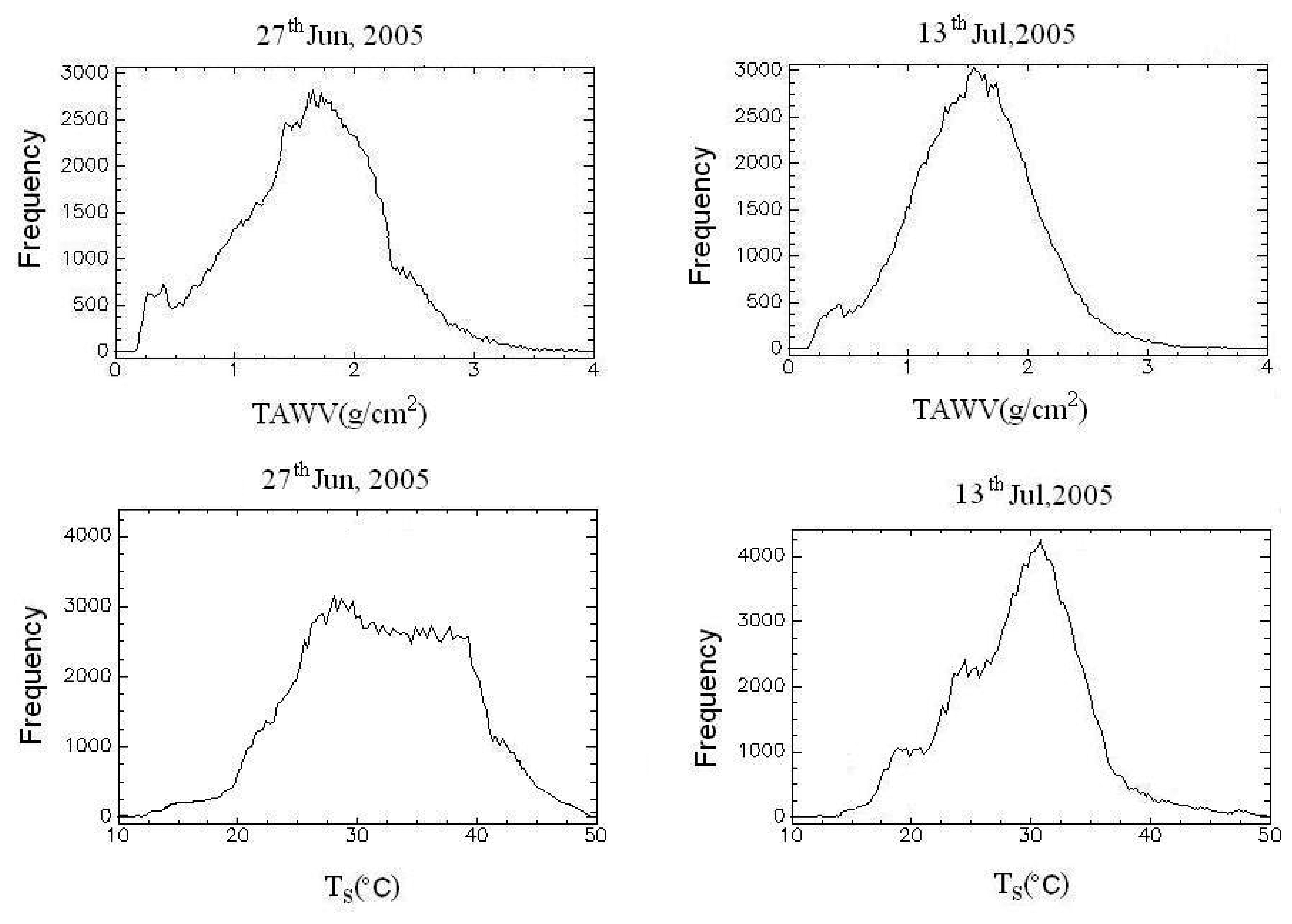
4.3 Analysis on the TAWV and the LST
5. Discussions
Acknowledgments
References
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Sellers, P. J.; Hall, F. G.; Asrar, G.; Strebel, D. E.; Murphy, R. E. The first ISLSCP Field Experiment (FIFE). B. Am. Meteorol. Soc. 1988, 69, 22–27. [Google Scholar]
- Running, S.W.; Justice, C.; Salomonson, V.; Hall, D.; Braker, J.; Kaufman, Y.; Strahler, A.; Huete, A.; Muller, J. P.; Vanderbilt, V.; Wan, Z.; Teillet, P. Terrestrial remote sensing science and algorithms planned for EOS/MODIS. Int. J. Remote Sensing 1994, 15, 3587–2620. [Google Scholar]
- Becker, F. L.; Li, Z. L. Towards a local split window method over land surface. Int. J. Remote Sensing 1990, 11, 369–393. [Google Scholar]
- Sobrino, J. A.; Coll, C.; Caselles, V. Atmospheric corrections for land surface temperature using AVHRR channel 4 and 5. Remote Sens. Environ. 1991, 38, 19–34. [Google Scholar]
- Franca, G. B.; Cracknell, A. P. Retrieval of land and sea surface temperature using NOAA-11 AVHRR data in northeastern Brazil. Int. J. Remote Sensing 1994, 15, 1695–1712. [Google Scholar]
- Stroeve, J.; Haefliger, M.; Steffen, K. Surface temperature from ERS-1 ATSR infrared thermal satellite data in polar regions. J. Appl. Meteor. 1996, 35(8), 1231–1239. [Google Scholar]
- Key, J. R.; Collins, J. B.; Fowler, C.; Stone, R. S. High-latitude surface temperature estimates from thermal satellite data. Remote Sens. Environ. 1997, 61(2), 302–309. [Google Scholar]
- Wan, Z.; Li, Z. L. A Physics-based algorithm for retrieving land-surface emissivity and temperature from EOS/MODIS data. IEEE Trans. Geosci. Remote Sensing 1997, 35, 980–996. [Google Scholar]
- Gillespie, A. R.; Rokugawa, S.; Matsunaga, T.; Cothern, J. S.; Hook, S.; Kahle, A. B. A temperature and emissivity separation algorithm for Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) images. IEEE Trans. Geosci. Remote Sensing 1998, 36, 1113–1126. [Google Scholar]
- Qin, Z. H.; Giorgio, D. O.; Arnon, K. Derivation of split window algorithm and its sensitivity analysis for retrieving land surface temperature from NOAA-advanced very high resolution radiometer data. J. Geophys. Res. 2001, 105, 22655–22670. [Google Scholar]
- Mao, K.B.; Qin, Z.H.; Shi, J.C.; Gong, P. A practical split-window algorithm for retrieving land surface temperature from MODIS data. Int. J. Remote Sensing 2004, 26(15), 3181–3204. [Google Scholar]
- Smith, D. L.; Delderfield, J.; Drummond, D.; Edwards, T.; Mutlow, C. T.; Read, P. D.; Toplis, G. M. Calibration of the AATSR Instrument. Adv. Space Res. 2001, 28(1), 31–39. [Google Scholar]
- Kimura, R.; Bai, L.; Fan, J.; Takayama, N.; Hinokidani, O. Evapo-transpiration estimation over the river basin of the Loess Plateau of China based on remote sensing. J. Arid Environ. 2006, 68, 53–65. [Google Scholar]
- Chen, L.D.; Huang, Z. L.; Gong, J.; Fu, B.J.; Huang, Y.L. The effect of land cover/vegetation on soil water dynamic in the hilly area of the loess plateau, China. Catena 2007, 70, 200–208. [Google Scholar]
- Liu, J.G. Advances in Modern Ecology; China Science and Technology Press: Beijing, 1992; pp. 69–76. [Google Scholar]
- Wen, J. An overview of the Loess Plateau mesa region land surface process field experiment 2005 (LOPEX05). ISPMSRS Conference Proceeding 2005, 402–404. [Google Scholar]
- Wen, J.; Wei, Z.G.; Lu, S.H.; Chen, S.Q.; Ao, Y.H.; Liang, L. The Characteristics of Land Surface Energy and Water Exchange over the Loess Plateau Mesa in China. Adv. Atmos. Sci. 2007, 24(2), 301–310. [Google Scholar]
- Chesters, D.; Uccellini, L.W.; Robinson, W.D. Low level water vapor fields from the VISSR atmospheric sounder (VAS) split window channels. J. Clim. Appl. Meteor. 1983, 22, 725–743. [Google Scholar]
- Fraser, R. S.; Kaufman, Y. F. The relative importance of aerosol scattering and absorption in remote sensing. IEEE Trans. Geosci. Remote Sens. 1985, 23, 625–633. [Google Scholar]
- Grant, W.B. Water vapor absorption coefficient in the 8-13 mm spectral region: a critical review. Appl Optics. 1990, 29, 451–462. [Google Scholar]
- Kaufman, Y. J.; Gao, B.C. Remote sensing of water vapor in the near IR from EOS/MODIS. IEEE Trans. Geosci. Remote Sens. 1992, 30, 871–884. [Google Scholar]
- King, M. D.; Kaufman, Y. J.; Menzel, W. P.; Tanre, D. Remote sensing of cloud, aerosol and water vapor. properties from the Moderate Resolution Imaging. Spectrometer (MODIS). IEEE Trans. Geosci. Remote. Sens. 1992, 30(1), 2–27. [Google Scholar]
- Czajkowski, K. P.; Goward, S. N.; Shirey, D.; Walz, A. Thermal remote sensing of near surface water vapor. Remote Sens. Environ. 2002, 79, 253–265. [Google Scholar]
- Li, Z. L.; Jia, L.; Su, Z.; Wan, Z.; Zhang, R.; H. A new approach for retrieving precipitable water from ATSR2 split-window channel data over land area. Int. J. Remote Sensing 2003, 24, 5059–5117. [Google Scholar]
- Berk, A.; Bernstein, L.S.; Robertson, D.C. Modtran: A Moderate Resolution Model for LOWTRAN 7. In Technical Report GL-TR-89-0122; Geophys. Lab: Bedford, MA, 1989. [Google Scholar]
- Jia, L.; Li, Z. L.; Menenti, M.; Su, Z.; Verhoef, W.; Wan, Z. A practical algorithm to infer soil and foliage component temperatures from bi-angular ATSR-2 data. Int. J. Remote Sensing 2003, 24, 4739–4760. [Google Scholar]
| Date | Retr(K) | Meas(K) | RD(%) | AD(K) |
|---|---|---|---|---|
| 27th Jun, 2005 | 306.03 | 305.02 | 3.17 | 1.01 |
| 305.99 | 304.84 | 3.63 | 1.15 | |
| 305.09 | 303.37 | 5.69 | 1.72 | |
| 13th Jul, 2005 | 311.05 | 307.06 | 11.80 | 4.0 |
| 304.06 | 304.67 | 1.93 | 0.61 | |
| 305.5 | 304.28 | 3.92 | 1.22 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Zhang, T.; Wen, J.; Van der Velde, R.; Meng, X.; Li, Z.; Liu, Y.; Liu, R. Estimation of the Total Atmospheric Water Vapor Content and Land Surface Temperature Based on AATSR Thermal Data. Sensors 2008, 8, 1832-1845. https://doi.org/10.3390/s8031832
Zhang T, Wen J, Van der Velde R, Meng X, Li Z, Liu Y, Liu R. Estimation of the Total Atmospheric Water Vapor Content and Land Surface Temperature Based on AATSR Thermal Data. Sensors. 2008; 8(3):1832-1845. https://doi.org/10.3390/s8031832
Chicago/Turabian StyleZhang, Tangtang, Jun Wen, Rogier Van der Velde, Xianhong Meng, Zhenchao Li, Yuanyong Liu, and Rong Liu. 2008. "Estimation of the Total Atmospheric Water Vapor Content and Land Surface Temperature Based on AATSR Thermal Data" Sensors 8, no. 3: 1832-1845. https://doi.org/10.3390/s8031832




