Temporal Stability of Soil Moisture and Radar Backscatter Observed by the Advanced Synthetic Aperture Radar (ASAR)
Abstract
:1. Introduction
2. Theory
2.1. Temporal Stability of Soil Moisture
 with coordinates (xi, yi). The measurement scale of the in-situ sensors is denoted here as point scale because the measurements are only representative of a small area ranging from about 0.1 to 10 dm2 depending on the employed measurement technique (see [15] for a discussion of different in-situ measurement techniques). For identifying the most representative soil moisture stations [7] used the relative difference between point scale and regional scale soil moisture
with coordinates (xi, yi). The measurement scale of the in-situ sensors is denoted here as point scale because the measurements are only representative of a small area ranging from about 0.1 to 10 dm2 depending on the employed measurement technique (see [15] for a discussion of different in-situ measurement techniques). For identifying the most representative soil moisture stations [7] used the relative difference between point scale and regional scale soil moisture
 within a measurement network, it is now applied to any arbitrary point (x, y) situated within a region of size Ar:
within a measurement network, it is now applied to any arbitrary point (x, y) situated within a region of size Ar:
2.2. Temporal Stability of Radar Backscatter
2.3. Estimation of Soil Moisture Scaling Coefficients
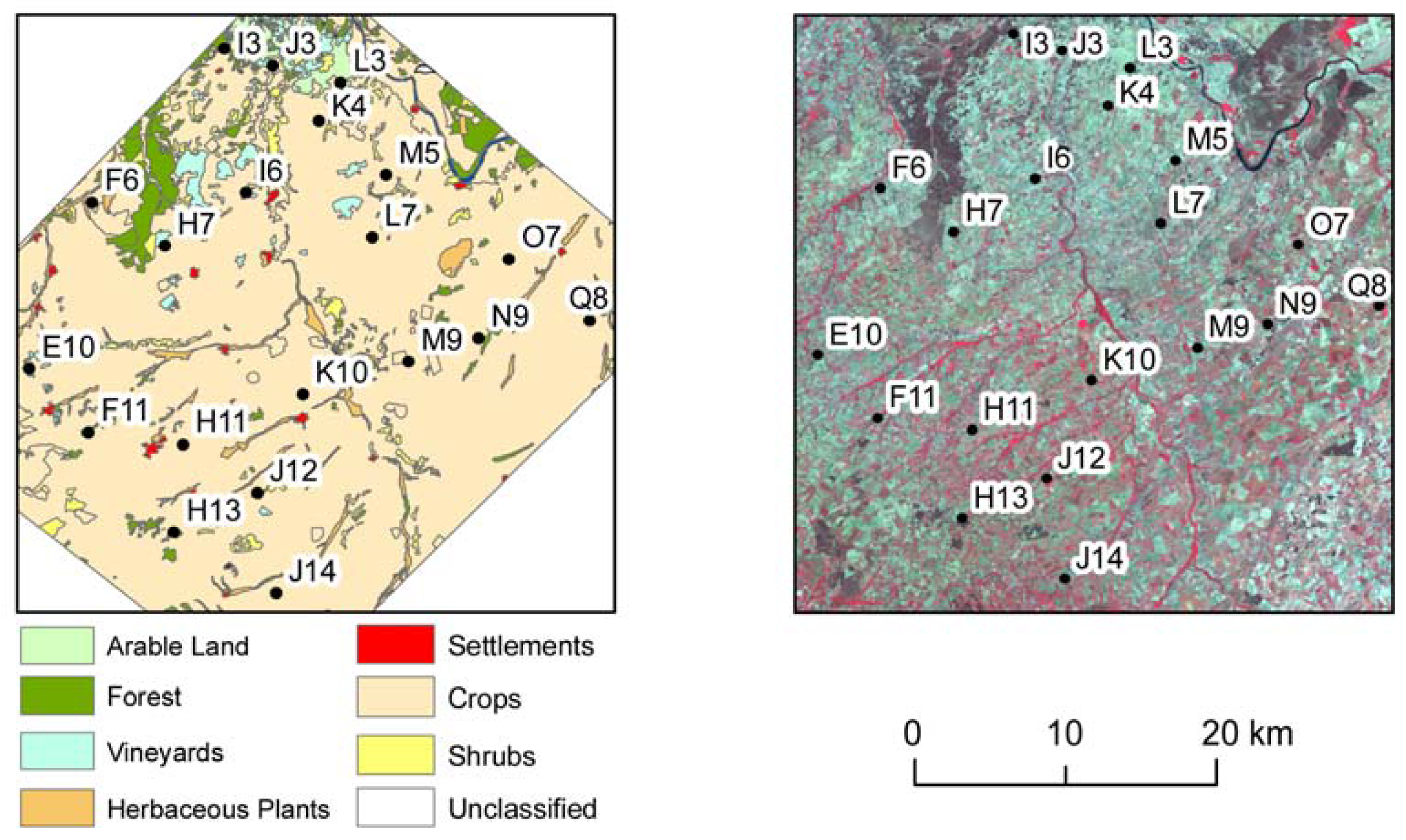
3. Test Site and Satellite Data
3.1. Test Site
3.2. Satellite Data
4. Methods
4.1. Pre-Processing of ASAR Data
4.2. Analysis of Soil Moisture Scaling Properties
4.3. Analysis of Backscatter Scaling Properties
4.4. Estimation of Soil Moisture Scaling Properties from ASAR
5. Results and Discussion
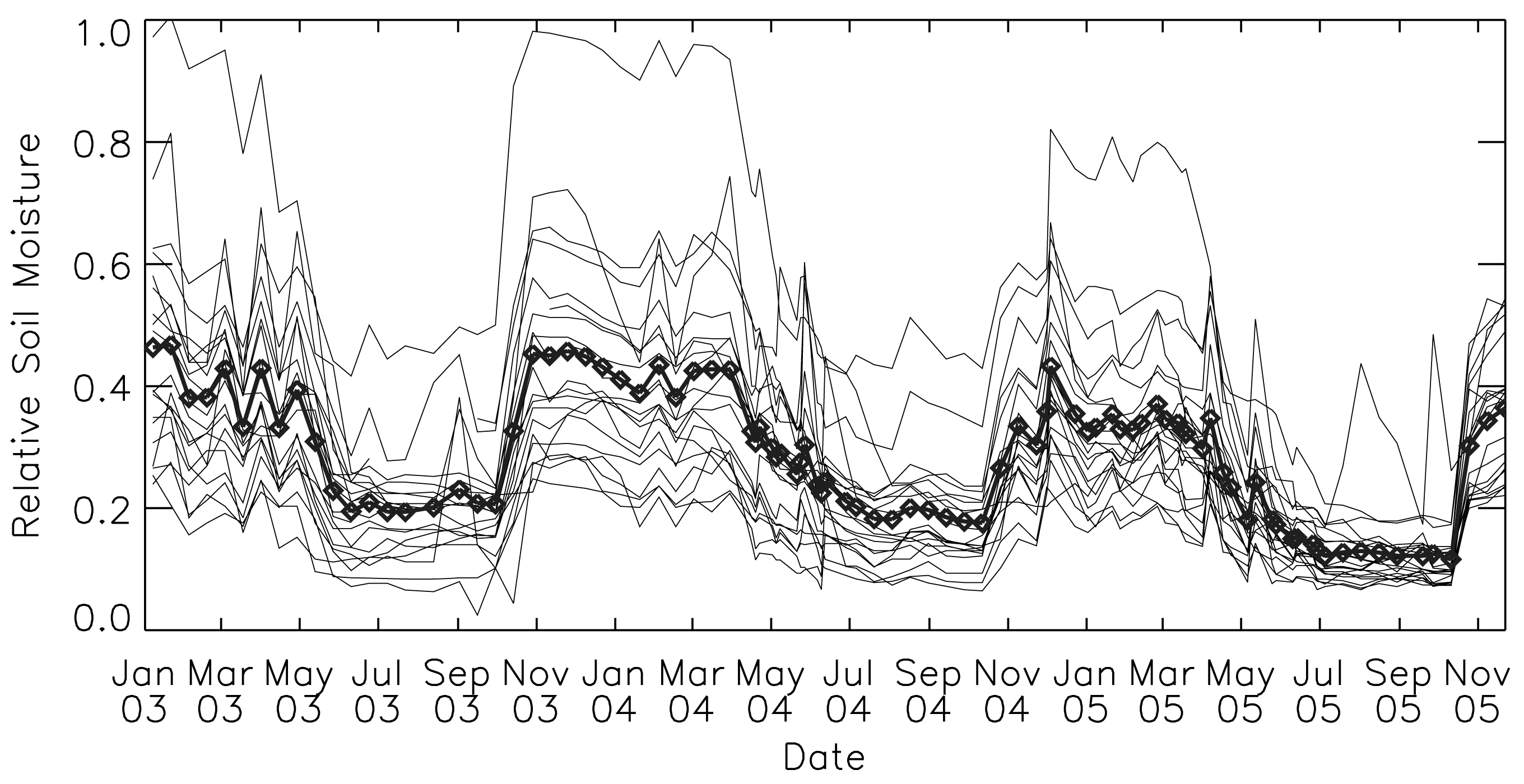
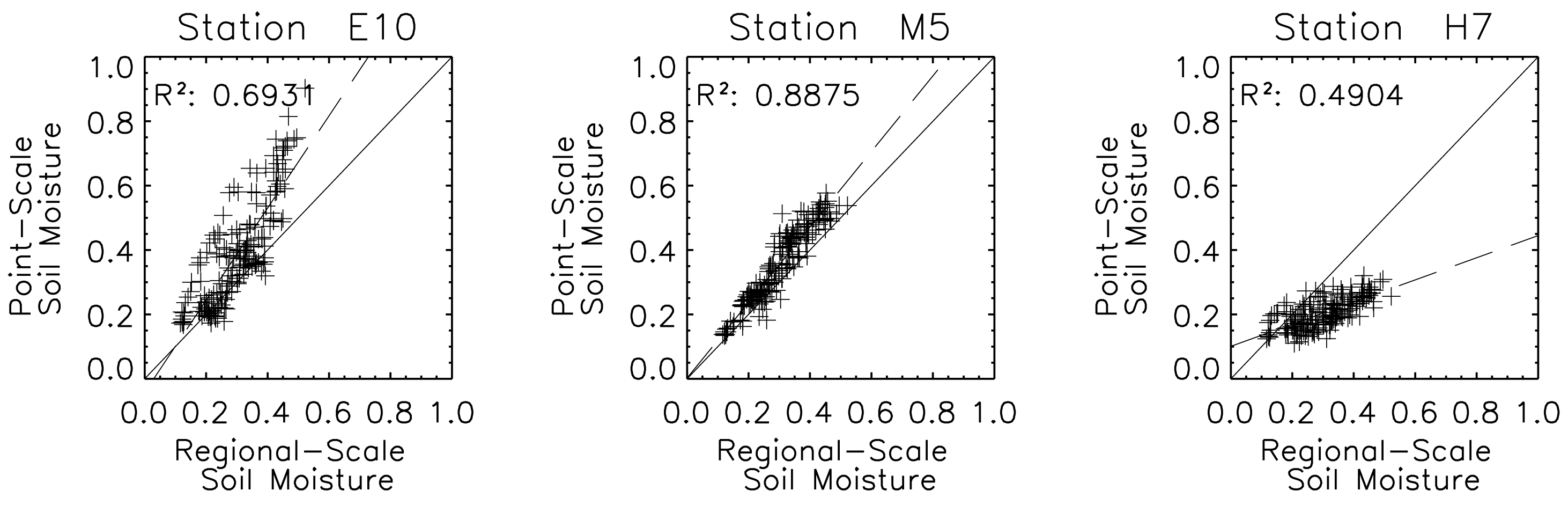
5.1. Soil moisture scaling properties from in-situ measurements
 to the regional scale . By mathematical deduction it is also possible to confirm the suitability of Equation (13) to connect the local () and regional () scale (section 2.2.).
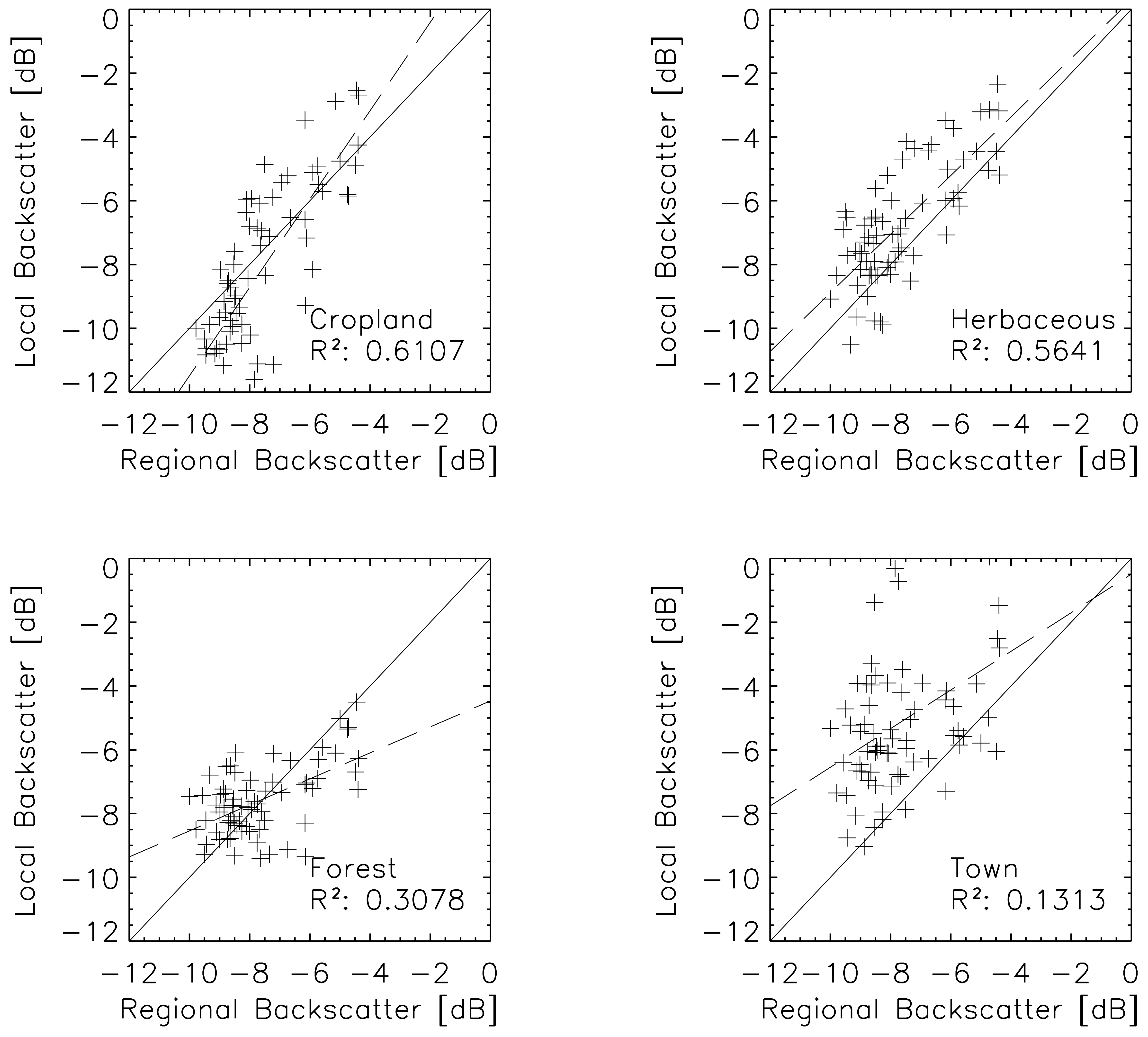
to the regional scale . By mathematical deduction it is also possible to confirm the suitability of Equation (13) to connect the local () and regional () scale (section 2.2.).5.2. Backscatter scaling properties observed by ASAR
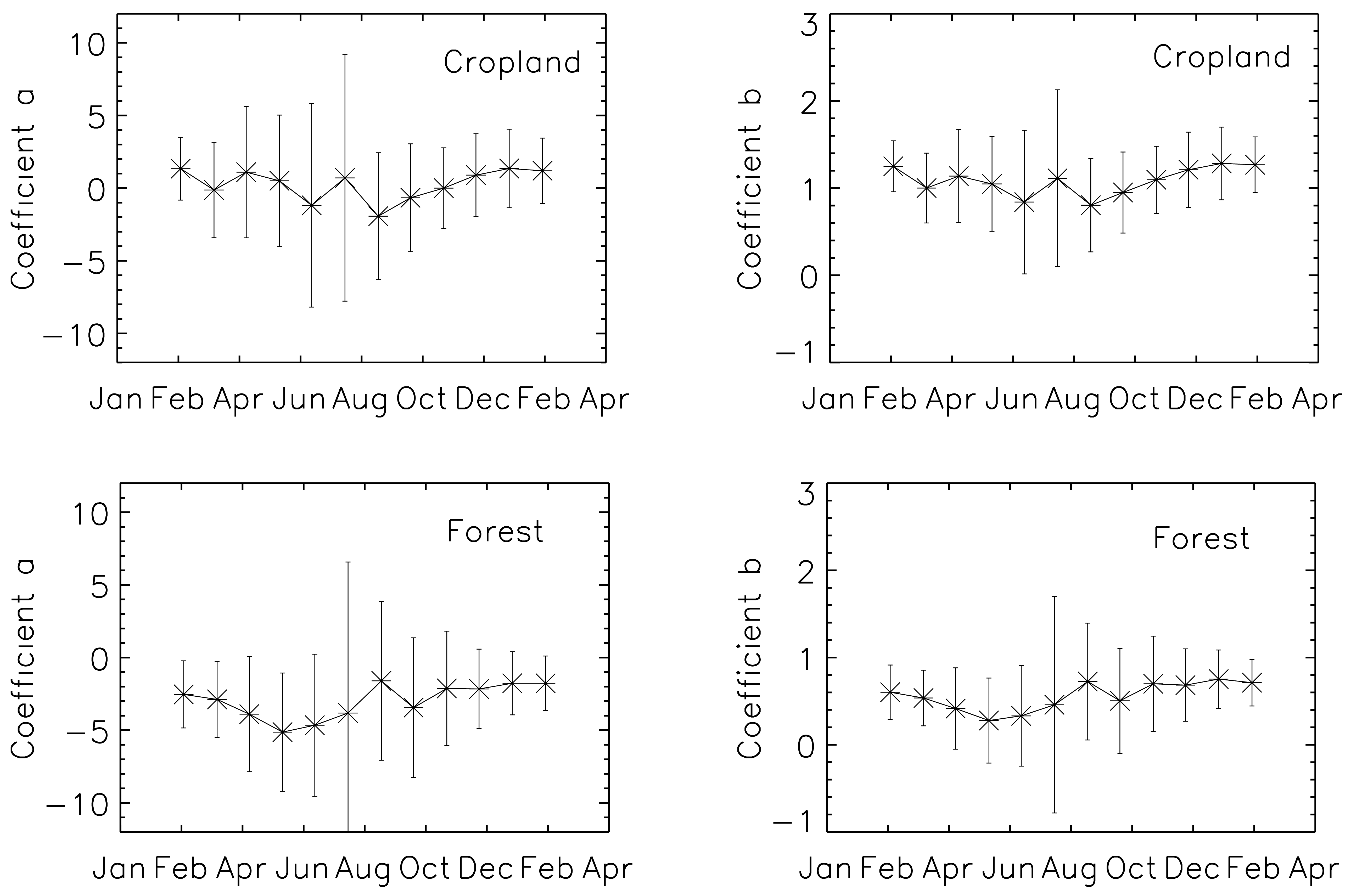
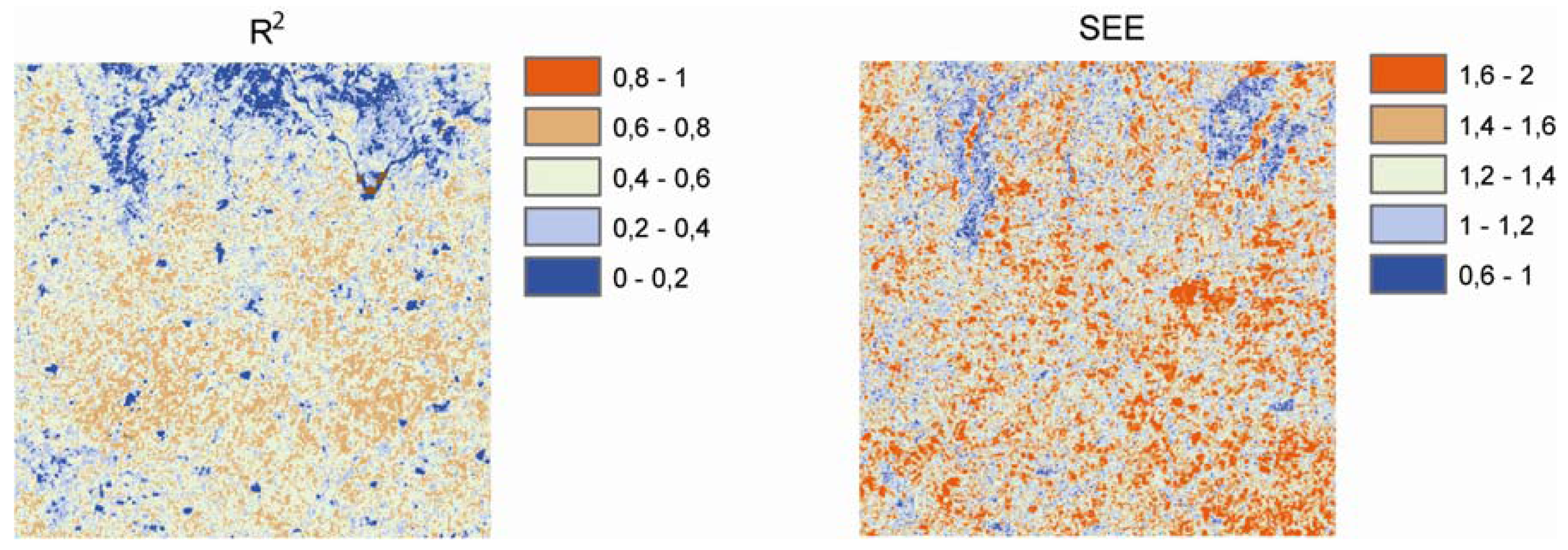
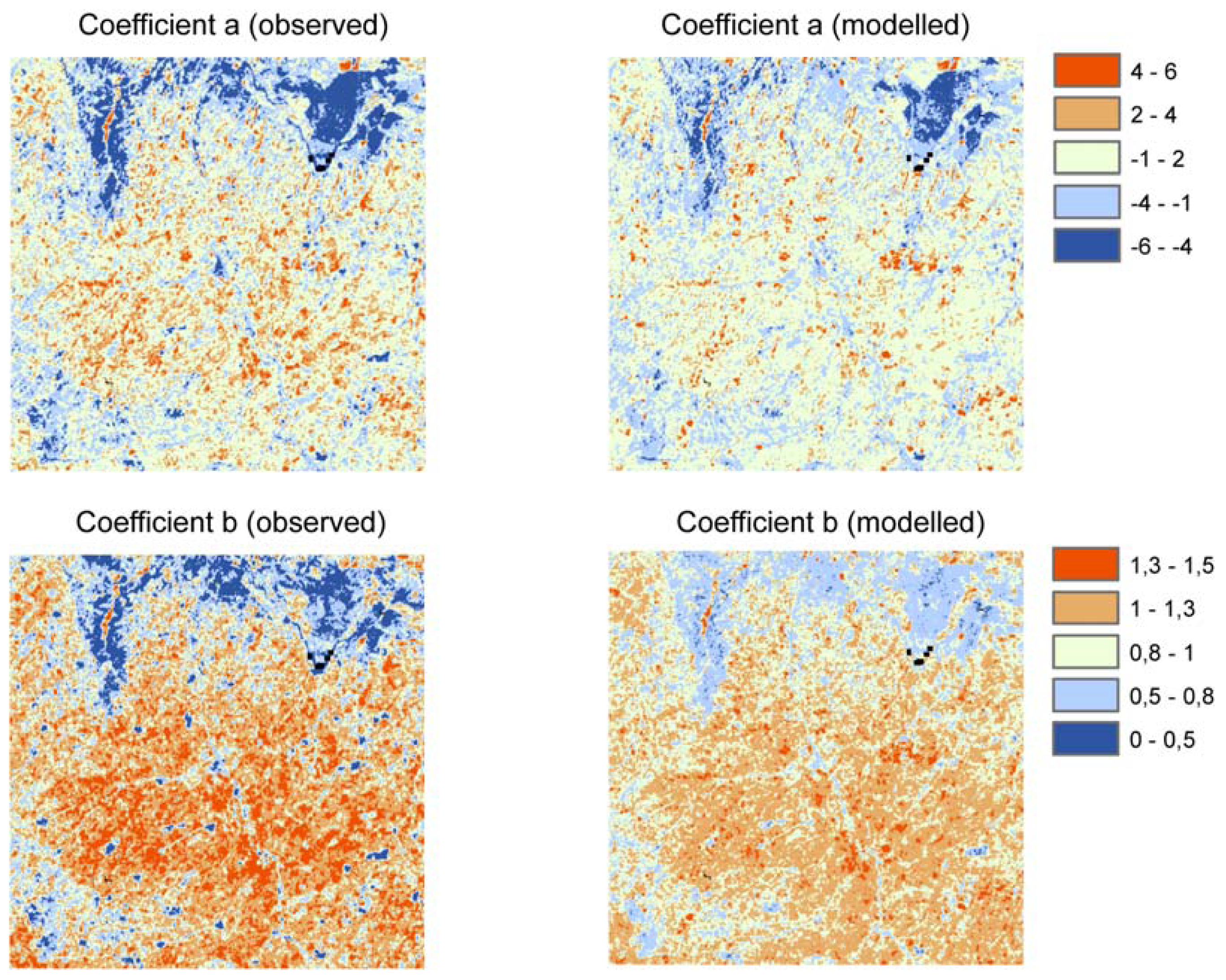
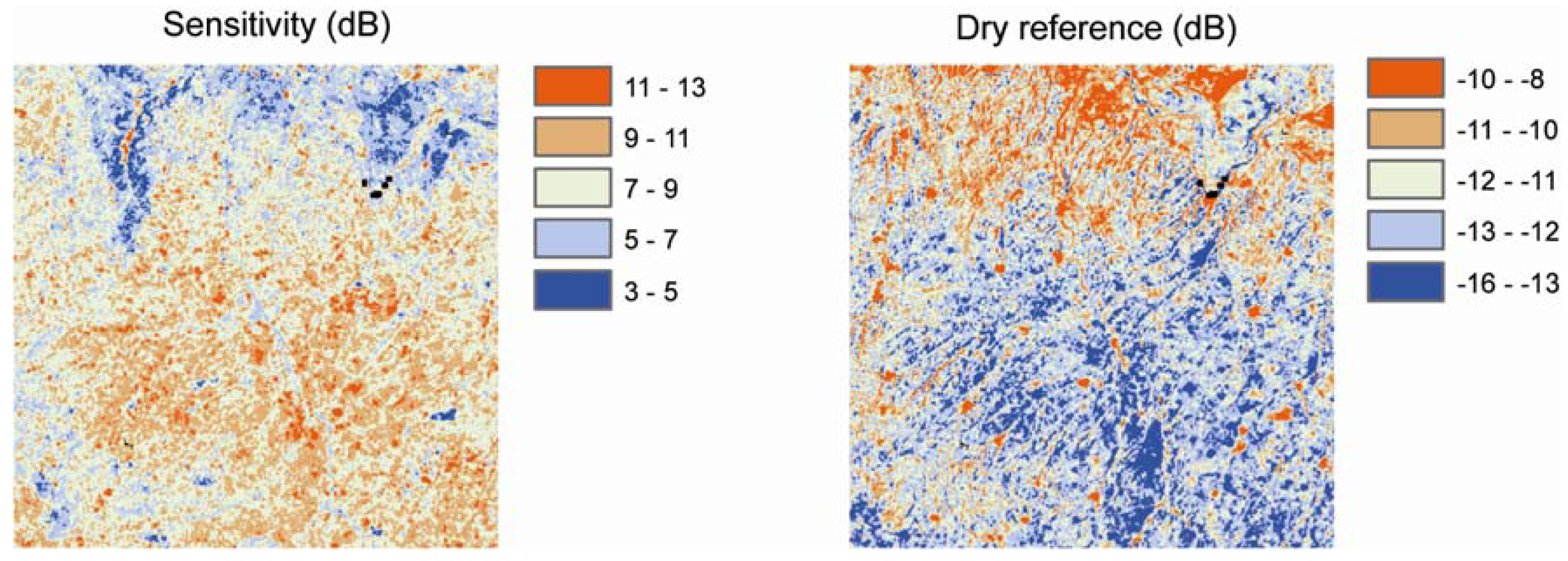
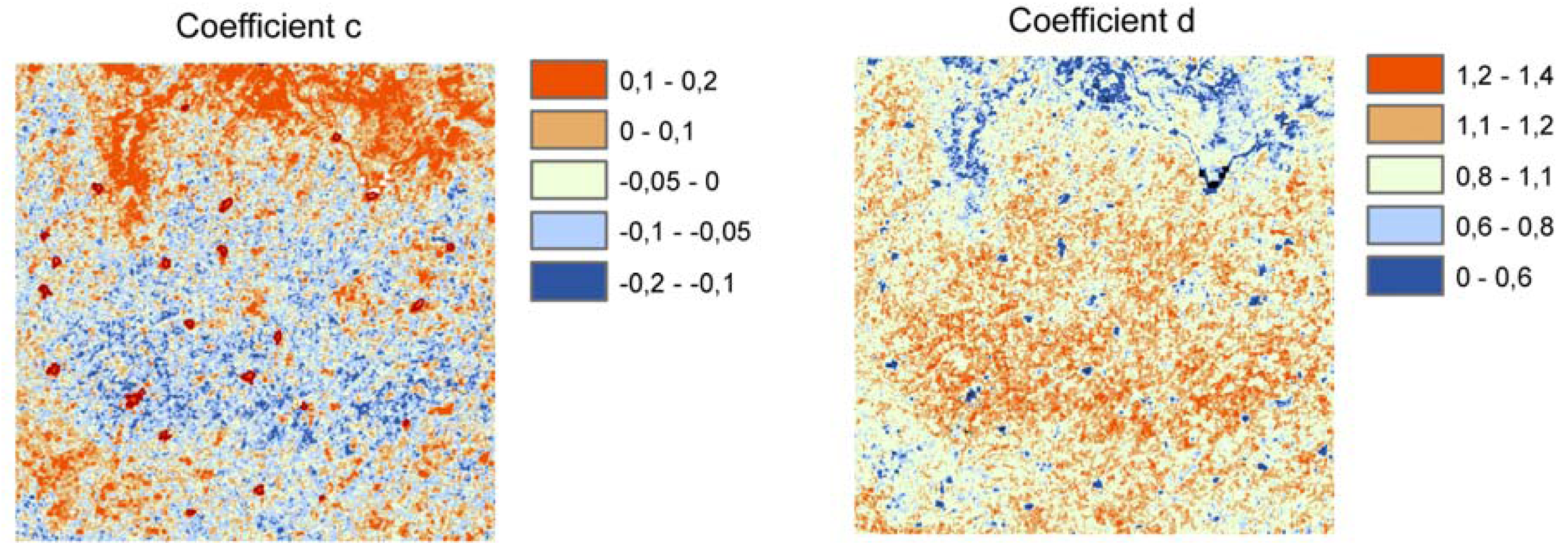
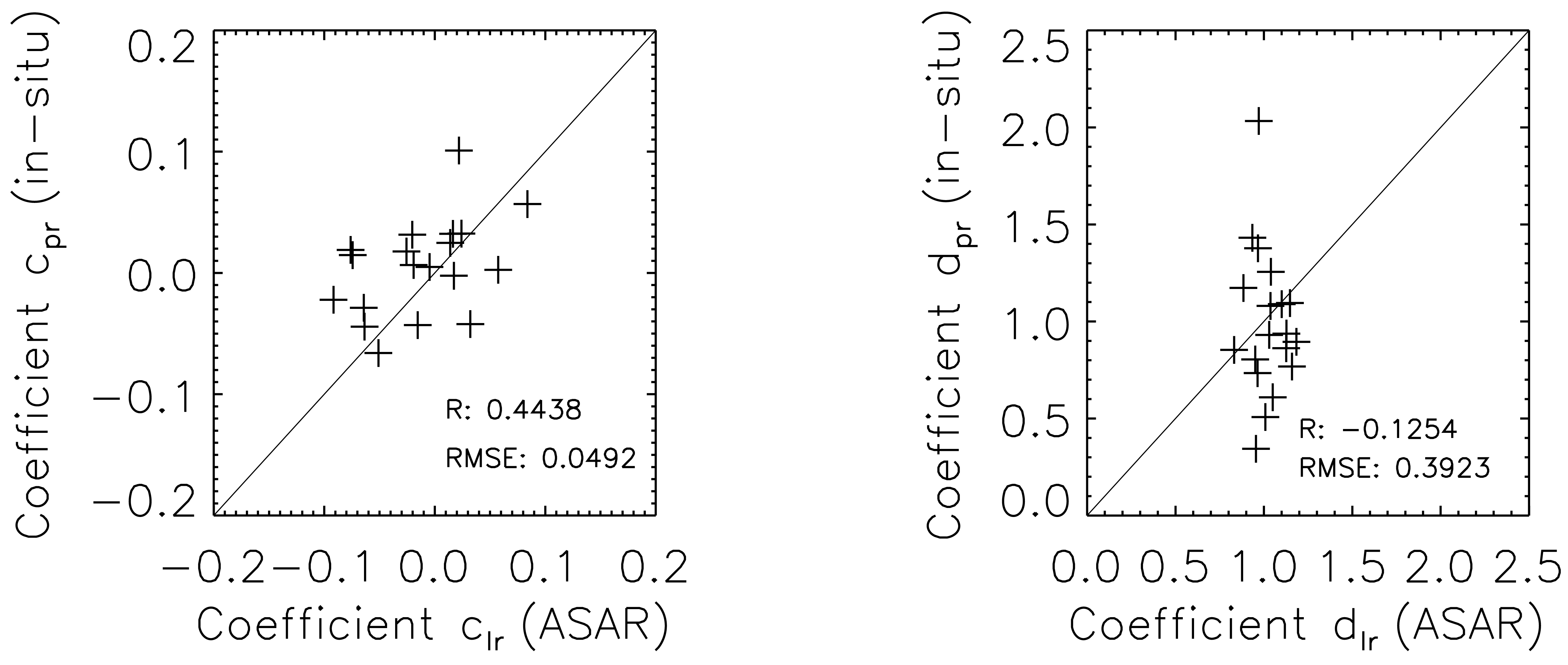
5.3. Backscatter scaling coefficients
5.4. Soil moisture scaling parameters derived from ASAR
6. Conclusions
Acknowledgments
References and Notes
- Western, A. W.; Blöschl, G. On the spatial scaling of soil moisture. Journal of Hydrology. 1999, 217, 203–224. [Google Scholar]
- Dubayah, R.; Wood, E. F.; Lavallée, D. Multiscaling Analysis in Distributed Modelling and Remote Sensing: An Application Using Soil Moisture. In Scale in Remote Sensing and GIS; Quattrochi, D. A., Goodchild, M. F., Eds.; Boca Raton, Boston, London, New York, Washington, D.C.; Lewis Publishers, 1997. [Google Scholar]
- Raju, S.; Chanzy, A.; Wigneron, J.; Calvet, J.; Kerr, Y.; Laguerre, L. Soil moisture and temperature profile effects on microwave emission at low frequencies. Rem. Sens. Environ. 1995, 54, 85–97. [Google Scholar]
- Entin, J. K.; Robock, A.; Vinnikov, K. Y.; Hollinger, S. E.; Liu, S.; Namkhai, A. Temporal and spatial scales of observed soil moisture variations in the extratropics. Journal of Geophysical Research. 2000, 105(D9), 11865–11877. [Google Scholar]
- Western, A. W.; Zhou, S.-L.; Grayson, R. B.; McMahon, T. A.; Blöschl, G.; Wilson, D. J. Spatial correlation of soil moisture in small catchments and its relationship to dominant spatial hydrological processes. Journal of Hydrology 2004, 286(1-4), 113–134. [Google Scholar]
- Vinnikov, K. Y.; Robock, A.; Speranskaya, N. A.; Schlosser, C. A. Scales of temporal and spatial variability of mitlatitude soil moisture. J. Geophys. Res. 1996, 101(D3), 7163–7174. [Google Scholar]
- Vachaud, G.; Passerat de Silans, A.; Balabanis, P.; Vauclin, M. Temporal Stability of Spatially Measured Soil Water Probability Density Function. Soil Sci. Soc. Am. J. 1985, 49, 822–828. [Google Scholar]
- Wagner, W.; Naeimi, V.; Scipal, K.; de Jeu, R.; Martinez-Fernandez, J. Soil moisture from operational meteorological satellites. Hydrogeology Journal. 2007, 15(1), 121–131. [Google Scholar]
- Njoku, E. G.; Jackson, T. J.; Lakshmi, V.; Chan, T. K.; Nghiem, S. V. Soil moisture retrieval from AMSR-E. IEEE Transactions on Geoscience and Remote Sensing. 2003, 41(2), 215–229. [Google Scholar]
- Bartalis, Z.; Wagner, W.; Naeimi, V.; Hasenauer, S.; Scipal, K.; Bonekamp, H.; Figa, J.; Anderson, C. Initial soil moisture retrievals from the METOP-A Advanced Scatterometer (ASCAT). Geophysical Research Letters. 2007, 34, L20401. [Google Scholar]
- Kerr, Y. H. Soil moisture from space: Where are we? Hydrogeology Journal. 2007, 15(1), 117–120. [Google Scholar]
- Wagner, W.; Blöschl, G.; Pampaloni, P.; Calvet, J.-C.; Bizzarri, B.; Wigneron, J.-P.; Kerr, Y. Operational readiness of microwave remote sensing of soil moisture for hydrologic applications. Nordic Hydrology. 2007, 38(1), 1–20. [Google Scholar]
- Cosh, M. H.; Jackson, T. J.; Starks, P.; Heathman, G. Temporal stability of surface soil moisture in the Little Washita River watershed and its applications in satellite soil moisture product validation. Journal of Hydrology. 2006, 323, 168–177. [Google Scholar]
- Grayson, R.; Western, A. W. Towards areal estimation of soil water content from point measurements: time and space stability of mean response. Journal of Hydrology. 1998, 207, 68–82. [Google Scholar]
- Walker, J. P.; Willgoose, G. R.; Kalma, J. D. In situ measurement of soil moisture: a comparison of techniques. Journal of Hydrology. 2004, 293(1-4), 85–99. [Google Scholar]
- Cosh, M. H.; Jackson, T. J.; Bindlish, R.; Prueger, J. H. Watershed scale temporal and spatial stability of soil moisture and its role in validating satellite estimates. Remote Sensing of Environment. 2004, 92(4), 427–435. [Google Scholar]
- Chen, D.; Engman, E. T.; Brutsaert, W. Spatial distribution and pattern persistence of surface soil moisture and temperature over prairie from remote sensing. Remote Sensing of Environment. 1997, 61, 347–360. [Google Scholar]
- De Lannoy, G. J. M.; Houser, P. R.; Verhoest, N. E. C.; Pauwels, V. R. N.; Gish, T. J. Upscaling of point scale measurements to field averages at the OPE3 test site. Journal of Hydrology. 2007, 343(1-2), 1–11. [Google Scholar]
- Baup, F.; Mougin, E.; de Rosnay, P.; Timouk, F.; Chênere, I. Surface soil moisture estimation over the AMMA Sahelian site in Mali using ENVISAT/ASAR data. Rem. Sens. Environ. 2007, 109, 473–481. [Google Scholar]
- Loew, A.; Mauser, W. On the dissagregation of passive microwave data using priori knowledge on temporal persistent soil moisture fields. IEEE Transactions on Geoscience and Remote Sensing. 2008, in press. [Google Scholar]
- Ulaby, F. T.; Moore, R. K.; Fung, A. K. Microwave Remote Sensing: Active and Passive. Volume 2: Radar Remote Sensing and Surface Scattering and Emission Theory; Addison-Wesley Advanced Book Program: Reading, Massachusetts, 1982; p. 609. [Google Scholar]
- Fung, A. K. Microwave scattering and emission models and their applications.; Artech House: Boston, 1994. [Google Scholar]
- Ulaby, F. T.; Sarabandi, K.; McDonald, K.; Whitt, M.; Dobson, M. C. Michigan Microwave Canopy Scattering Model (MIMICS). International Journal of Remote Sensing. 1990, 11(7), 1223–1253. [Google Scholar]
- Baghdadi, N.; Zribi, M. Evaluation of radar backscatter models IEM, OH and DUBOIS using experimental observations. International Journal of Remote Sensing. 2006, 27(18-20), 3831–3852. [Google Scholar]
- Walker, J.; Houser, P.; Willgoose, G. Active microwave remote sensing for soil moisture measurement: a field evaluation using ERS-2. Hydrological Processes. 2004, 18(11), 1975–1997. [Google Scholar]
- Davidson, M.; Le Toan, T.; Mattia, F.; Satalino, G.; Manninen, T.; Borgeaud, M. On the characterisation of agricultural soil roughness for radar remote sensing studies. IEEE Transactions on Geoscience and Remote Sensing. 2000, 38(2), 630–640. [Google Scholar]
- Moran, M. S.; Hymer, D. C.; Qi, J.; Sano, E. E. Soil moisture evaluation using multi-temporal synthetic aperture radar (SAR) in semiarid rangeland. Agricultural and Forest Meteorology. 2000, 105, 69–80. [Google Scholar]
- Engman, E. T. Soil moisture. In Remote Sensing in Hydrology and Water Management; Schultz, G. A., Engman, E. T., Eds.; Berlin; Springer, 2000; pp. 197–216. [Google Scholar]
- Wagner, W.; Lemoine, G.; Borgeaud, M.; Rott, H. A Study of Vegetation Cover Effects on ERS Scatterometer Data. IEEE Transactions on Geoscience and Remote Sensing. 1999, 37(2), 938–948. [Google Scholar]
- Hillel, D. Introduction to Soil Physics; Academic Press: San Diego, 1982. [Google Scholar]
- Wagner, W.; Scipal, K.; Pathe, C.; Gerten, D.; Lucht, W.; Rudolf, B. Evaluation of the agreement between the first global remotely sensed soil moisture data with model and precipitation data. Journal of Geophysical Research D: Atmospheres. 2003, 108(D19). Art. No. 4611. [Google Scholar]
- Pellarin, T.; Calvet, J.-C.; Wagner, W. Evaluation of ERS scatterometer soil moisture products over a half-degree region in southwestern France. Geophysical Research Letters. 2006, 33(17). Art. No. L17401. [Google Scholar]
- Crow, W.; Zhan, X. Continental-scale evaluation of remotely sensed soil moisture products. IEEE Geoscience and Remote Sensing Letters. 2007, 4(3), 451–455. [Google Scholar]
- Dirmeyer, P. A.; Guo, Z. C.; Gao, X. Comparison, validation, and transferability of eight multiyear global soil wetness products. Journal of Hydrometeorology. 2004, 5(6), 1011–1033. [Google Scholar]
- Zhao, D.; Künzer, C.; Fu, C.; Wagner, W. Evaluation of the ERS Scatterometer derived Soil Water Index to monitor water availability and precipitation distribution at three different scales in China. Journal Of Hydrometeorology. in press.
- Wagner, W.; Pathe, C.; Sabel, D.; Bartsch, A.; Künzer, C.; Scipal, K. Experimental 1 km soil moisture products from ENVISAT ASAR for Southern Africa, Proceedings of ENVISAT Symposium 2007, Montreux, Switzerland; 2007; p. SP-636.
- Njoku, E. G.; Wilson, W. J.; Yueh, S. H.; Dinardo, S. J.; Li, F. K.; Jackson, T. J.; Lakshmi, V.; Bolten, J. Observations of soil moisture using a passive and active low-frequency microwave airborne sensor during SGP99. IEEE Transactions on Geoscience and Remote Sensing. 2002, 40(2), 2659–2673. [Google Scholar]
- Narayan, U.; Lakshmi, V.; Jackson, T. J. High-resolution change estimation of soil moisture using L-band radiometer and radar observations made during the SMEX02 experiments. IEEE Transactions on Geoscience and Remote Sensing. 2006, 44(6), 1545–1554. [Google Scholar]
- Ceballos, A.; Martinez-Fernandez, J.; Santos, F.; Alonso, P. Soil-water behaviour of sandy soils under semi-arid conditions in the Duero Basin (Spain). Journal of Arid Environments. 2002, 51, 501–519. [Google Scholar]
- Martinez-Fernandez, J.; Ceballos, A. Mean soil moisture estimation using temporal stability analysis. Journal of Hydrology. 2005, 312, 28–38. [Google Scholar]
- Ceballos, A.; Scipal, K.; Wagner, W.; Martínez-Fernández, J. Validation of ERS scatterometer-derived soil moisture data in the central part of the Duero Basin, Spain. Hydrological Processes. 2005, 19(8), 1549–1566. [Google Scholar]
- Kerr, Y. H.; Waldteufel, P.; Wigneron, J.-P.; Martinuzzi, J.; Font, J.; Berger, M. Soil moisture retrieval from space: the Soil Moisture and Ocean Salinity (SMOS) mission. IEEE Transactions on Geoscience and Remote Sensing. 2001, 39(8), 1729–1735. [Google Scholar]
- Bamler, R.; Eineder, M. ScanSAR Processing Using Standard High Precission SAR Algorithms. IEEE Transactions on Geoscience and Remote Sensing. 1996, 34(1), 212–218. [Google Scholar]
- Zink, M.; Buck, C.; Suchail, J.-L.; Torres, R.; Bellini, A.; Closa, J.; Desnos, Y.-L.; Rosich, B. The radar imaging instrument and its applications: ASAR. ESA Bulletin. 2001, 106, 46–55. [Google Scholar]
- Meier, E.; Frei, U.; Nüesch, D. Precise Terrain corrected Geocoded Images. In SAR processing: data and systems; Schreier, G., Ed.; Karlsruhe: Wichmann, 1993; pp. 173–185. [Google Scholar]
- van Zyl, J.; Chapman, B. D.; Dubois, P. C.; Shi, J. The Effect of Topography on SAR Calibration. IEEE Transactions on Geoscience and Remote Sensing. 1993, 31(5), 1036–1043. [Google Scholar]
- Gauthier, Y.; Bernier, M.; Fortin, J.-P. Aspect and incidence angle sensitivity in ERS-1 SAR data. International Journal of Remote Sensing. 1998, 19(10), 2001–2006. [Google Scholar]
- Mäkynen, M. P.; Manninen, T.; Similä, M. H.; Karvonen, J. A.; Hallikainen, M. T. Incidence Angle Dependence of the Statistical Properties of C-Band HH-Polarization Backscattering Signatures of the Baltic Sea Ice. IEEE Transactions on Geoscience and Remote Sensing. 2002, 40(12), 2593–2609. [Google Scholar]
- Martinez-Fernandez, J.; Ceballos, A. Temporal Stability of Soil Moisture in a Large-Field Experiment in Spain. Soil Sci. Soc. Am. J. 2003, 67, 1647–1656. [Google Scholar]
- Schanda, E. Physical fundamentals of remote sensing; Springer Verlag: Berlin Heidelberg New York Tokyo, 1986; p. 187. [Google Scholar]

| In-situ | ASAR | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Station | Sand (%) | Silt (%) | Clay (%) | δi,j [%] | Stdev (δi,j) | cpr | dpr | R2 | SEE | clr | dlr |
| E10 | 75.1 | 16.4 | 8.5 | -47.50 | 9.26 | -0.04 | 1.43 | 0.69 | 0.09 | 0.03 | 0.93 |
| F6 | 67.2 | 13.7 | 19.1 | -32.60 | 18.32 | 0.02 | 2.03 | 0.79 | 0.10 | 0.01 | 0.97 |
| F11 | 81.5 | 12.0 | 6.5 | -29.89 | 18.13 | -0.04 | 0.93 | 0.89 | 0.03 | -0.02 | 1.03 |
| H7 | 85.1 | 9.6 | 5.3 | -27.76 | 26.17 | 0.10 | 0.34 | 0.49 | 0.03 | 0.02 | 0.96 |
| H11 | 79.7 | 10.2 | 10.1 | -27.13 | 27.17 | 0.03 | 1.26 | 0.75 | 0.07 | -0.02 | 1.04 |
| H13 | 70.4 | 11.5 | 18.2 | -22.98 | 14.88 | 0.02 | 0.77 | 0.69 | 0.05 | -0.08 | 1.16 |
| I3 | 90.2 | 6.3 | 3.5 | -18.28 | 15.37 | 0.01 | 1.08 | 0.78 | 0.05 | -0.02 | 1.04 |
| I6 | 89.8 | 5.9 | 4.3 | -16.38 | 37.73 | 0.06 | 0.85 | 0.73 | 0.05 | 0.08 | 0.83 |
| J3 | 85.1 | 11.3 | 3.7 | -16.27 | 20.45 | 0.00 | 0.73 | 0.57 | 0.06 | 0.02 | 0.96 |
| J12 | 60.9 | 16.9 | 22.2 | -14.99 | 20.66 | 0.03 | 1.38 | 0.85 | 0.05 | 0.02 | 0.97 |
| J14 | 66.8 | 21.0 | 12.2 | -12.12 | 23.17 | -0.02 | 0.90 | 0.84 | 0.04 | -0.09 | 1.18 |
| K4 | 87.1 | 9.3 | 3.6 | -8.48 | 19.47 | 0.02 | 0.61 | 0.65 | 0.04 | -0.03 | 1.05 |
| K10 | 91.2 | 5.7 | 3.1 | 5.54 | 22.37 | -0.04 | 0.86 | 0.77 | 0.04 | -0.06 | 1.13 |
| L3 | 82.3 | 6.4 | 11.3 | 9.85 | 25.04 | 0.03 | 0.80 | 0.77 | 0.04 | 0.02 | 0.95 |
| L7 | 46.8 | 20.8 | 32.4 | 14.79 | 12.17 | -0.03 | 0.94 | 0.49 | 0.09 | -0.06 | 1.13 |
| M5 | 81.6 | 8.3 | 10.1 | 18.02 | 16.12 | 0.00 | 1.17 | 0.89 | 0.04 | 0.06 | 0.88 |
| M9 | 49.8 | 24.9 | 25.3 | 29.04 | 39.59 | 0.01 | 1.10 | 0.92 | 0.03 | -0.07 | 1.15 |
| N9 | 62.5 | 16.8 | 20.8 | 38.26 | 43.75 | -0.07 | 1.09 | 0.82 | 0.05 | -0.05 | 1.10 |
| O7 | 78.8 | 13.5 | 7.7 | 48.70 | 25.93 | 0.00 | 0.51 | 0.84 | 0.02 | 0.00 | 1.01 |
| Q8 | 86.1 | 5.7 | 8.3 | 110.78 | 46.90 | -0.10 | 1.22 | 0.81 | 0.06 | 0.28 | 0.44 |
| Mean | 75.9 | 12.3 | 11.8 | 0.03 | 24.13 | 0.00 | 1.00 | 0.75 | 0.05 | 0.00 | 1.00 |
| Stdev | 13.1 | 5.6 | 8.4 | 36.41 | 10.40 | 0.05 | 0.37 | 0.12 | 0.02 | 0.08 | 0.16 |
© 2008 by MDPI Reproduction is permitted for noncommercial purposes.
Share and Cite
Wagner, W.; Pathe, C.; Doubkova, M.; Sabel, D.; Bartsch, A.; Hasenauer, S.; Blöschl, G.; Scipal, K.; Martínez-Fernández, J.; Löw, A. Temporal Stability of Soil Moisture and Radar Backscatter Observed by the Advanced Synthetic Aperture Radar (ASAR). Sensors 2008, 8, 1174-1197. https://doi.org/10.3390/s80201174
Wagner W, Pathe C, Doubkova M, Sabel D, Bartsch A, Hasenauer S, Blöschl G, Scipal K, Martínez-Fernández J, Löw A. Temporal Stability of Soil Moisture and Radar Backscatter Observed by the Advanced Synthetic Aperture Radar (ASAR). Sensors. 2008; 8(2):1174-1197. https://doi.org/10.3390/s80201174
Chicago/Turabian StyleWagner, Wolfgang, Carsten Pathe, Marcela Doubkova, Daniel Sabel, Annett Bartsch, Stefan Hasenauer, Günter Blöschl, Klaus Scipal, José Martínez-Fernández, and Alexander Löw. 2008. "Temporal Stability of Soil Moisture and Radar Backscatter Observed by the Advanced Synthetic Aperture Radar (ASAR)" Sensors 8, no. 2: 1174-1197. https://doi.org/10.3390/s80201174





