Assessment of Polarimetric SAR Interferometry for Improving Ship Classification based on Simulated Data
Abstract
:1. Introduction
2. GRECOSAR
2.1. Overall description
- Physical Optics (PO) for perfectly conducting surfaces.
- Method of Equivalent Currents (MEC) with Ufimtsev's Physical Theory of Diffraction (PTD) coefficients or Mitzner's Incremental Length Diffraction Coefficients (ILDC) for perfectly conducting edges.
- Multiple reflection analysis by a Geometrical Optics (GO) + PO ray-tracing algorithm. Bi-static GO is used for all reflections except the last one, for which PO is used. GO divergence factors for curved surfaces are computed approximately.
2.2. Main Simulation Steps
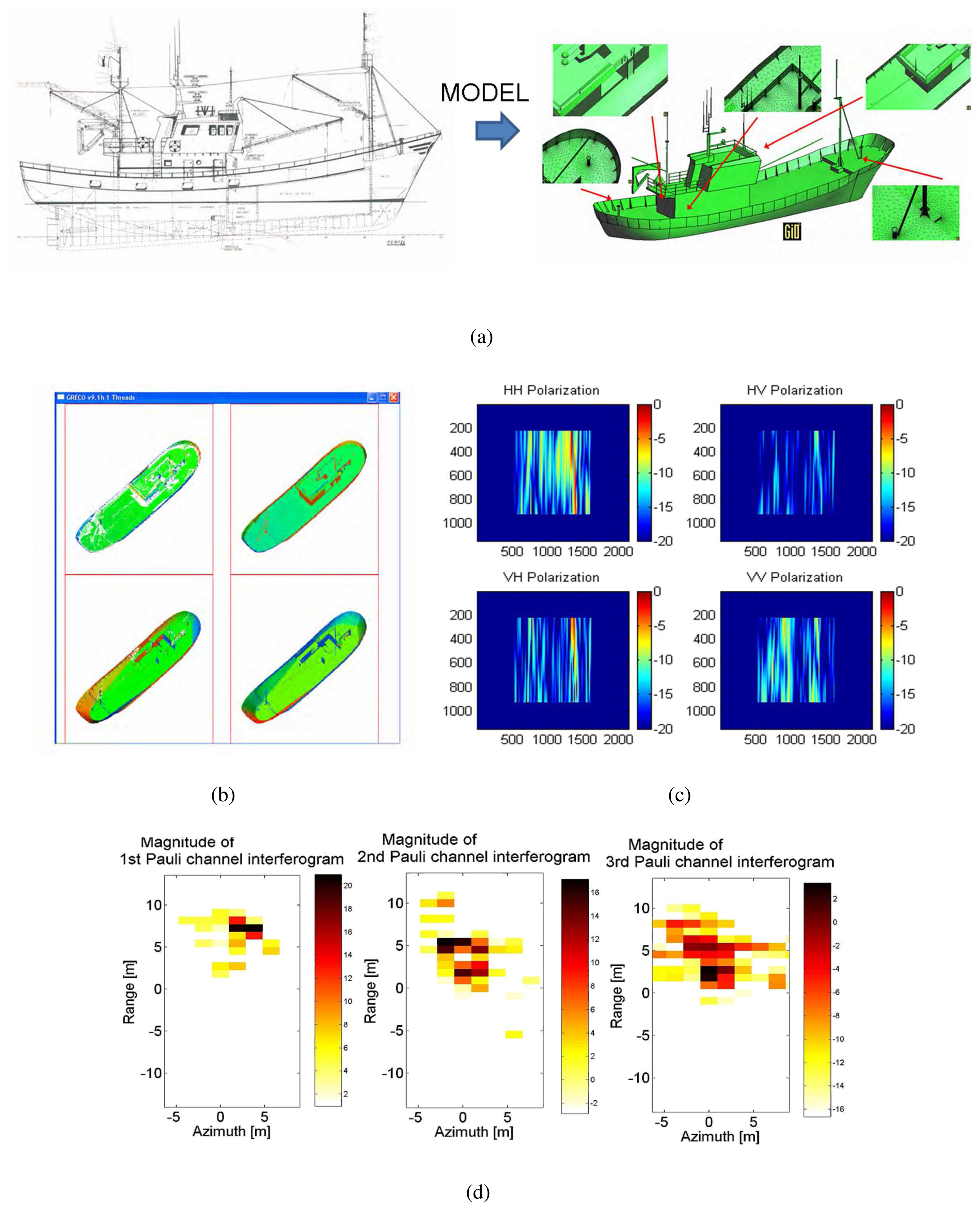
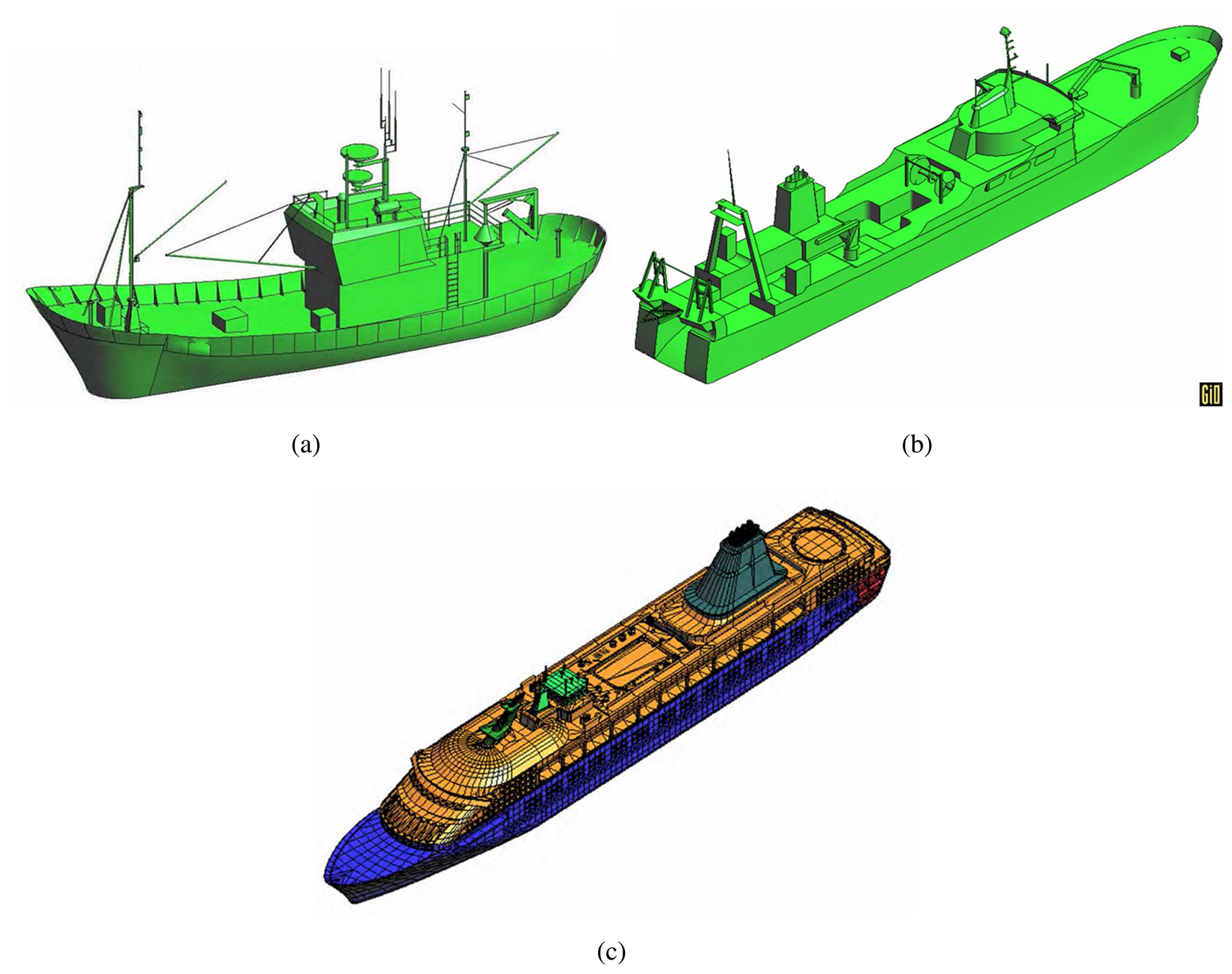
- Target modeling.
- This stage is devoted to manually build a parametric version of the model from hard or digital blueprints. Once finished, the parametric geometry is discretized into planar facets by the commented tessellation procedure. Several tests have shown that a facet length of 1 cm provides an efficient trade-off between the degree of detail and computational efforts. The total number of facets in a model depends, besides facet length, in the chordal error, which fixes the minimum distance between a curved surface and the planar one discretizing it. For ship models around 70 m long, more than 4 · 105 facets are managed with a chordal error below 3 mm.
- Pre-Processing.
- This stage simulates the sensor point of view and the transmitted chirp signal. For the former, the platform path (both orbital or airborne), antenna pointing and target environment (location, orientation and dynamics) are considered. The result is a file defining the radar aspect angle at each synthetic aperture position via two view angles.† For the latter, the chirp signal is simulated at base band in time domain. As GRECO® works in the frequency domain, the chirp frequency samples are computed, and the related amplitude and phase terms of the chirp spectrum stored in a file for raw data synthesizing.
- GRECO.
- This stage corresponds to EM simulation. According to the user-defined radar aspect angle, GRECO estimates the mono-static polarimetric EM field scattered by the input geometry for each of the frequency samples related to the chirp signal. It provides the value normalized to the incident field and takes both far- and near-field regimes according to the scenario configuration. In order to make this step faster, GRECO® applies an additional discretizing step consisting on generating a bitmap of the input meshed target. The PC graphic workstation performs all the intense operation tasks and generates a bitmap image of the visible entities according to a user-defined pixel size value. Several tests have shown that a value of 1 cm provides an efficient tradeoff between model realism and processing time, despite in some cases lower values are mandatory (specially when sea surface is adopted in the scene).
- Post-Processing.
- This stage synthesizes the raw data in time domain from the contribution of the different magnitude and phase terms at each frequency. The complete SAR signal as received at the antenna is emulated by properly adding the complex chirp spectrum samples, the magnitude and phase terms due to target scattering (GRECO® EM fields), the phase term due to the two-way signal propagation and the azimuth-dependent phase terms due to Range Cell Migration. The resulting raw data is windowed in the Doppler domain according to the azimuth antenna radiation pattern. In GRECOSAR, the temporal window is fixed by the time extend in which the signal impinges the target and, hence, the antenna radiation pattern can be assumed constant along range due to the reduced dimension of the scene.
- SAR Processing.
- This stage focuses the raw data as done for real images. An efficient and platform-independent code of the Extended Chirp Scaling Algorithm (ECSA) is used [24].
- Data Interpretation.
- GRECOSAR provides some utilities for data interpretation as CTD polari-metric processing, 3D image formation or zero-padding interpolation for analysis purposes.
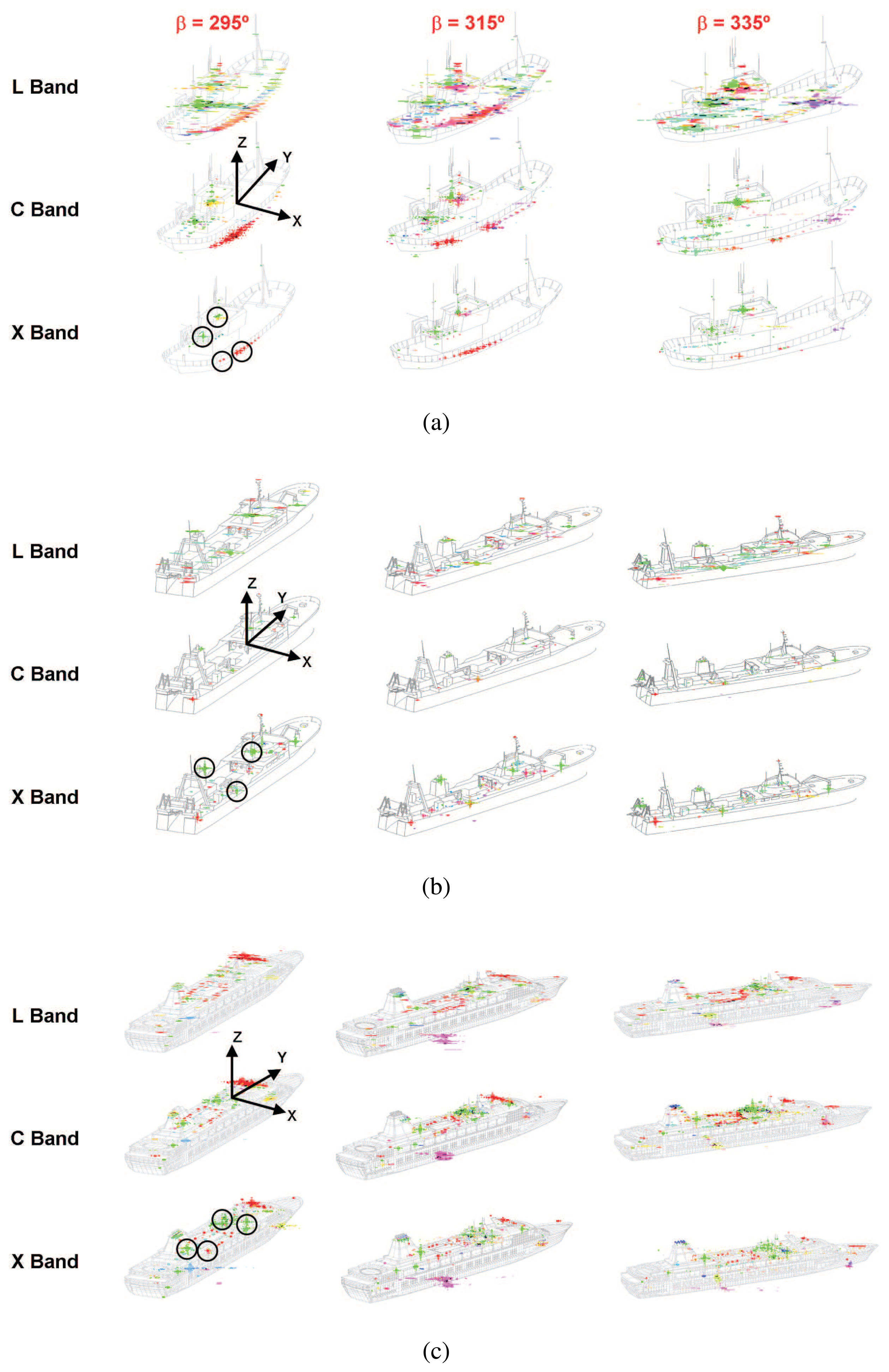
3. Scattering Study
4. PePS-based feature set
5. Vessel Classification Algorithm
- Coregistrate single-pass interferometric pairs and generate Pauli interferograms.
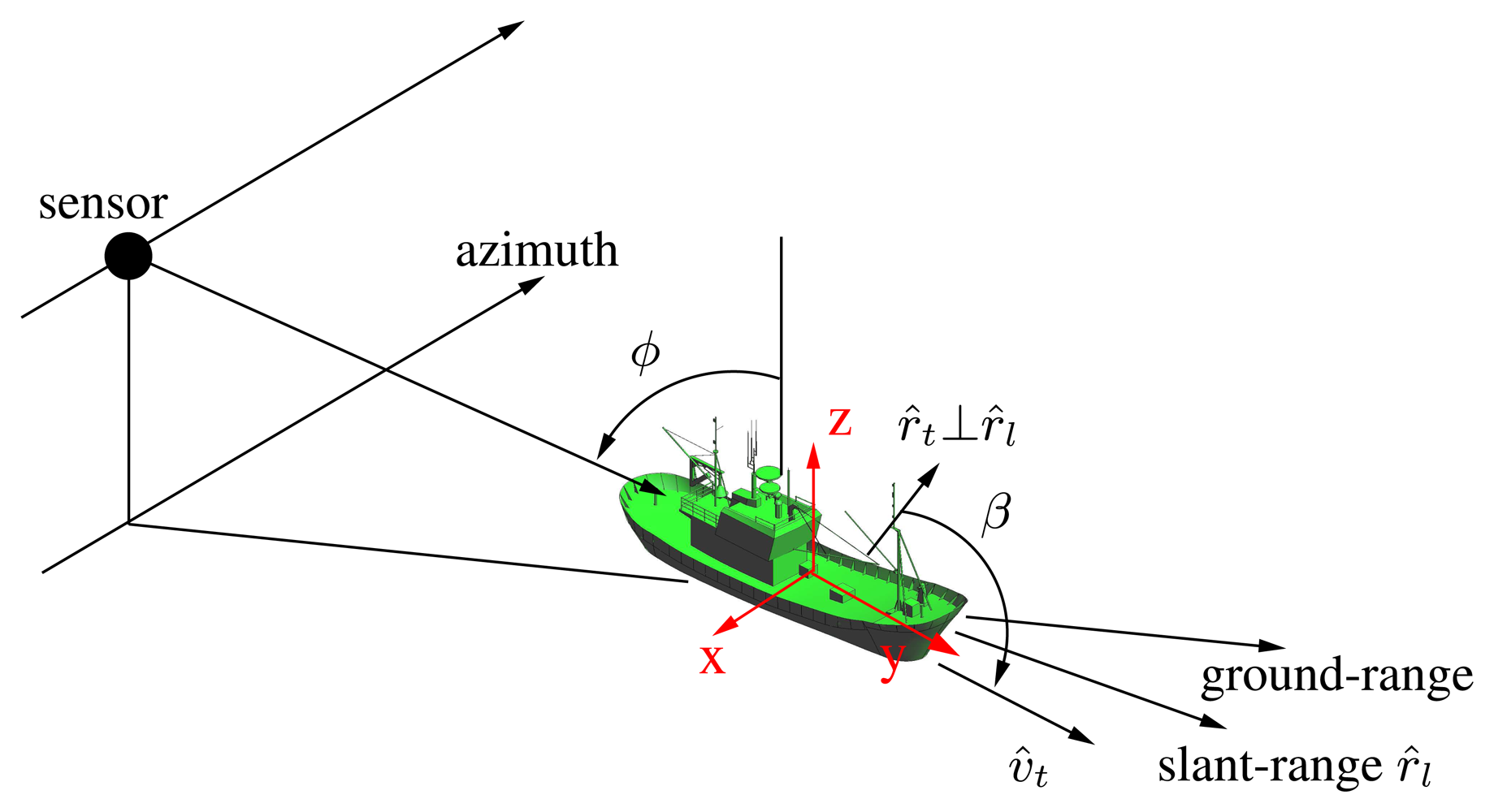
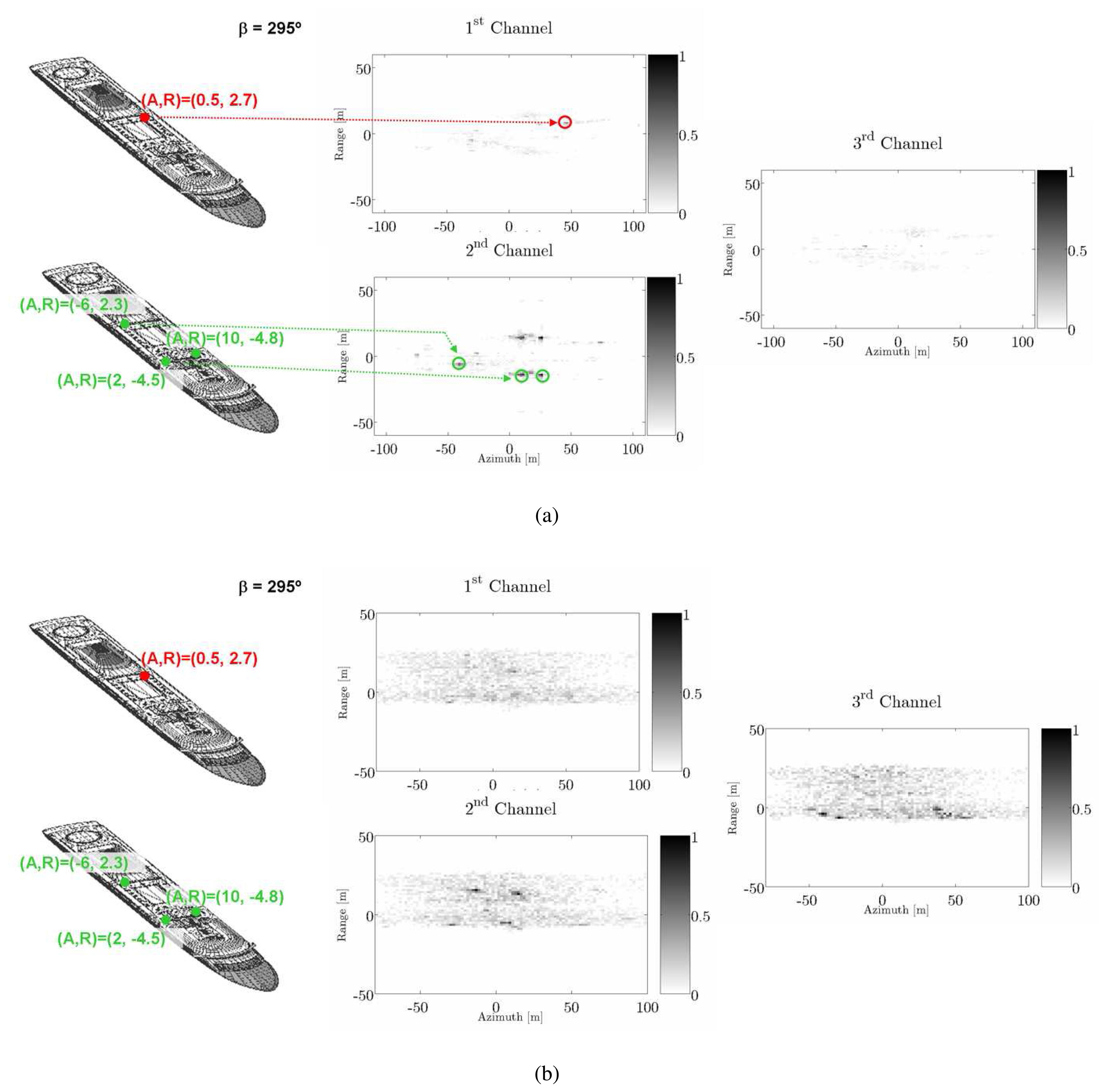
- Isolate all the local maxima (m) present in all the three Pauli interferograms for a fixed dynamic range (DRi) and find the values of the four components defining the feature set. In this step, a ship bearing estimation methodology based on the Radon transform has been used for making the required coordinate system transformation (see Section 4. Equation 8).
- For each pattern with M PePS, test the similarity of the permutations possible. Here, the formulation from Equation 9 to 14 applies with the suitability scatter step. This implies that, for a permutation κ, r could be lower than M if exists one or more local maxima that present, in at least two of the four components of the feature set vector, errors equal to 1.
- That pattern with that permutation providing the highest similarity value is selected to classify the observed ship for the dynamic range DRi.
- Repeat steps 2-4 for different dynamic ranges in order to reach the maximum similarity and/or the best discrimination among the different models. The model which feature set has been selected the highest number of times to classify the observed ship becomes the final decision of the algorithm. The final similarity value is the value providing the best discrimination among models.
6. VCA Performance evaluation
7. Requirements for Real Scenarios
8. Conclusions
Acknowledgments
References and Notes
- Margarit, G.; Mallorqui, J. J.; Rius, J. M.; Sanz-Marcos, J. On the usage of GRECOSAR, an orbital polarimetric SAR simulator of complex targets, for vessel classification studies. IEEE Trans. Geosci. Remote Sensing 2006, 44, 3517–3526, 1., 2., 5. [Google Scholar]
- Margarit, G. Marine Applications of SAR Polarimetry. PhD thesis, Remote Sensing Laboratory (RSLab), Universitat Politécnica de Catalunya (UPC), Barcelona, Spain, July 2007. 1., 2., 3., 5., 6. [Google Scholar]
- IMPAST consortium, DG-FISH. IMPAST project final report with reference (IMPAST/D 1.4/2.0) and under contract nr: Q5RS-2001--02266. 1.
- Joint Research Center, EC. DECLIMS project [Online]. Available at; In DECLIMS Web page.; 1.
- Krogager, E. New decomposition of the radar target scattering matrix. IEEE Electronic Letters 1990, 26, 1525–1527, 1., 3. [Google Scholar]
- Cameron, W. L.; Youssef, N. N.; Leung, L. L. Simulated polarimetric signatures of primitive geometrical shapes. IEEE Trans. Geosci. Remote Sensing 1996, 34, 793–803, 1., 3. [Google Scholar]
- Margarit, G.; Mallorqui, J. J.; Fabregas, X. Single-pass polarimetric SAR interferometry for vessel classification. IEEE Trans. Geosci. Remote Sensing 2007, 45, 3494–3502, 1., 5., 6. [Google Scholar]
- Margarit, G.; Mallorqui, J. J. Scattering-based model of the SAR signatures of complex targets for classification applications. Int. J. Navig. Observ. 2008, 2008, 426267:1–426267:11, 1., 2.1., 2.1., 4., 4., 4., 5. [Google Scholar]
- Musman, S.; Kerr, D.; Bachmann, C. Automatic recognition of ISAR ship images. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 1392–1404, 1., 4., 4. [Google Scholar]
- Osman, H.; Blostein, S. D. Probabilistic winner-take-all segmentation of images with application to ship detection. IEEE Trans. Syst., Man, Cybern. B 2000, 30, 485–490, 1. [Google Scholar]
- Rius, J.; Ferrando, M.; Jofre, L. High frequency RCS of complex radar targets in real time. IEEE Trans. Antennas Propagat. 1993, 41, 1308–1319, 2., 2.1. [Google Scholar]
- Rius, J.; Ferrando, M.; Jofre, L. GRECO: Graphical electromagnetic computing for RCS prediction in real time. IEEE Antennas Propagat. Mag. 1993, 35, 7–17, 2.1. [Google Scholar]
- International Center for Numerical Methods in Engineering (CIMNE). GID - The personal pre and post processor (Software). Available online at: GID web page. 2.1.
- Hesany, V.; Plant, W.J.; Keller, W. C. The normalized radar cross section of the sea at 10 incidence. IEEE Trans. Geosci. Remote Sensing 2000, 38, 64–72, 2.1., 2.1. [Google Scholar]
- Blanch, S.; Aguasca, A. Dielectric permittivity measurements of sea water. Proc. of the ESA EuroSTARRS, WISE and LOSAC Campaign Workshop, ESA:SP525; 2003. 2.1. [Google Scholar]
- Harger, R. O. A sea surface height estimator using synthetic aperture radar complex imagery. IEEE Journal of Oceanic Engineering 1983, 8, 71–78, 2.1., 2.1. [Google Scholar]
- Plant, W. J.; Keller, W. C.; Hayes, K. Measurement of river surface currents with coherent microwave systems. IEEE Trans. Geosci. Remote Sensing 2005, 43, 1242–1257, 2.1., 2.1. [Google Scholar]
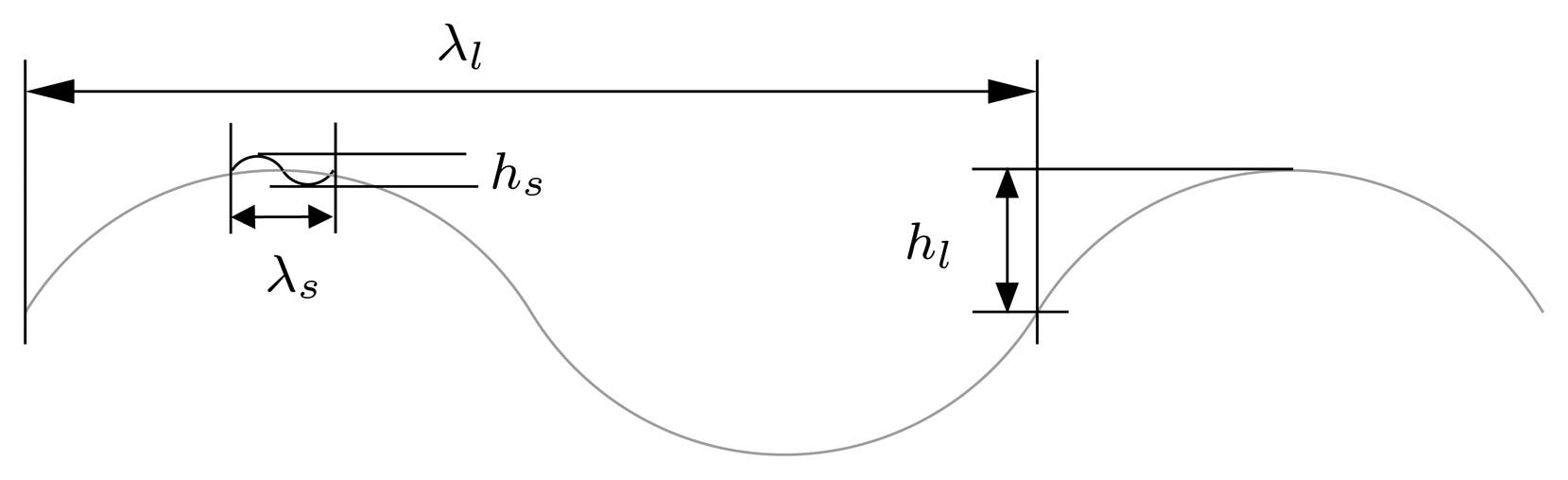
- Elfouhaily, T.; Chapron, B.; Katsaros, K.; Vandemark, D. A unified directional spectrum for long and short wind-driven waves. J. Geophys. Res. 1997, 102, 15781–15796, 2.1. [Google Scholar]
- Durden, S. L.; Vesecky, J. F. A physical radar cross-section model for a wind-driven sea with swell. IEEE J. Oceanic Eng. 1985, 10, 445–451, 2.1. [Google Scholar]
- Margarit, G.; Mallorqui, J. J. Discretization effects in sea surface simulation applied to ship classification studies. Proc. ESA of SEASAR workshop; 2008. 2.1. [Google Scholar]
- Bao, M.; Brüning, C.; Alpers, W. Simulation of ocean waves imaging by an along-track interfero-metric synthetic aperture radar. IEEE Trans. Geosci. Remote Sensing 1997, 35, 618–631, 2.1. [Google Scholar]
- Toporkov, J. V.; Sletten, M. A. Statistical properties of low-grazing range-resolved sea surface backscatter generated through two-dimensional direct numerical simulations. IEEE Trans. Geosci. Remote Sensing 2007, 45, 1181–1197, 2.1., 6. [Google Scholar]
- Migliaccio, M.; Ferrara, G.; Gambardella, A.; Nunziata, F.; Sorrentino, A. A physically consistent speckle model for marine SLC SAR images. IEEE J. Oceanic Eng. 2007, 32, 839–837, 2.1. [Google Scholar]
- Sanz, J.; Prats, P.; Mallorqui, J. Platform and mode independent sar data processor based on the extended chirp scaling algorithm. Proc. IEEE International Geoscience and Remote Sensing Symposium (IGARSS'03); 2003; Vol. 6, pp. 4086–4088, 5. [Google Scholar]
- Margarit, G.; Mallorqui, J. J.; Lopez-Martinez, C.; Fortuny-Guasch, J. Phenomenological vessel scattering study based on simulated inverse SAR imagery. IEEE Trans. Geosci. Remote Sensing 2008. (accepted for publication). 3., 3. [Google Scholar]
- Berizzi, F.; Mese, E. D.; Diani, M.; Martorella, M. High-resolution ISAR imaging of maneuvering targets by means of the range instantaneous doppler technique: Modeling and performance analysis. IEEE Trans. Image Processing 2001, 10, 1880–1890, 3. [Google Scholar]
- Krattenthaler, W.; Hlawatsch, F. Time frequency design and processing of signals via smoothed wigner distributions. IEEE Trans. Signal Processing 1993, 41, 288–295, 3. [Google Scholar]
- Cloude, S. R.; Pottier, E. A review of target decomposition theorems in radar polarimetry. IEEE Trans. Geosci. Remote Sensing 1996, 34, 498–518, 3. [Google Scholar]
- Zilman, G.; Zapolski, A.; Marom, M. The speed and beam of a ship from its wake's SAR images. IEEE Trans. Geosci. Remote Sensing 2004, 42, 2335–2343, 4. [Google Scholar]
- Rosen, P. A.; Hensley, S.; Joughin, I. R.; Li, F. K.; Madsen, S. N.; Rodriguez, E.; Goldstein, R. M. Synthetic aperture radar interferometry. Proc. of IEEE 2000, Vol. 88, 333–382, 4. [Google Scholar]
- Madsen, S. N. Syntehtic Aperture Radar Interferometry: Principles and Applications; Artech House: Boston, MA, 1999; 4. [Google Scholar]
- Ouchi, K.; Iehara, M.; Morimura, K.; Kumano, S.; Takami, I. Nonuniform azimuth image shift observed in the radarsat images of ships in motion. IEEE Trans. Geosci. Remote Sensing 2002, 40, 2188–2195, 5. [Google Scholar]
- Margarit, G.; Mallorqui, J. J.; Lopez-Martinez, C.; Fortuny-Guasch, J. Exploitation of ship scattering in polarimetric SAR for improved classification under high clutter conditions. IEEE Trans. Geosci. Remote Sensing 2008. (accepted for publication). 6., 7. [Google Scholar]
- Touzi, R.; Lopes, A.; Bruniquel, J.; Vachon, P. W. Coherence estimation for SAR imagery. IEEE Trans. Geosci. Remote Sensing 1999, 37, 135–149, 6. [Google Scholar]
- Werner, M. Shuttle radar topography mission (srtm): experience with the X-band SAR interferometer. Proc. of the CIE International Conference on Radar; 2001; pp. 634–638, 7. [Google Scholar]
- Souyris, J.-C.; Imbo, P.; Fjørtoft, R.; Mingot, S.; Lee, J.-S. Compact polarimetry based on symmetry properties of geophysical media: The PI/4 mode. IEEE Trans. Geosci. Remote Sensing 2005, 43, 634–645, 7. [Google Scholar]
- Raney, K. Hybrid-polarity SAR architecture. IEEE Trans. Geosci. Remote Sensing 2007, 45, 3397–3404, 7. [Google Scholar]
- Margarit, G.; Mallorqui, J. J. Discretization effects in sea surface simulation applied to ship classification studies. Proc. European Conference on Synthetic Aperture Radar (EUSAR'08) 2008, Vol. 2, 136–139, 7. [Google Scholar]
- Manual of; Deutsche Forschungsanstalt fur Luft- und Raumfahrt (DLR). Airborne sensor, FSAR. [Online] Available at: DLR web page. 7.
- Ferro-Famil, L.; Reigber, A.; Pottier, E. Scene characterization using sub-aperture polarimetric interferometric SAR data. Proc. IEEE International Geoscience and Remote Sensing Symposium (IGARSS'03); 2003; Vol. 2, pp. 702–704, 7. [Google Scholar]
- Zandona, R.; Papathanassiou, K. P.; Hajnsek, I.; Moreira, A. Polarimetric and interferometric characterization of coherent scatters in urban areas. IEEE Trans. Geosci. Remote Sensing 2006, 44, 971–984, 7. [Google Scholar]
- *Small facets are selected for modeling sea surface in order to meet the criteria followed with ships and allow accurate sea-ship interaction evaluation.
- †For interferometric simulations the slave image have the same information than the master one, but compensated by the baseline vector.
- ‡This is the solid angle subtended by a cone of 30° of aperture.
- §Due to the Pauli decomposition is a complete representation, the same simple mechanisms are isolated in any basis, for instance linear or circular.
- ¶Main specifications are accurate ground-truth, maritime scenario with different known vessels, fine resolution and fine radiometric calibration

| ΘSPA | ΘICE | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| xi | yi | zi | pi | xi | yi | hi | pi | ||
| 1 | 3.5 | -10 | 0 | 0 | 1 | 3 | -2 | 0 | 1 |
| 2 | 3.5 | -5 | 0 | 0 | 2 | -6 | -14 | 6.5 | 1 |
| 3 | -0.5 | -8 | 2.5 | 1 | 3 | -1 | 1 | 6.5 | 1 |
| 4 | -0.5 | -2 | 4.5 | 1 | - | - | - | - | - |
| ΘFER | - | ||||||||
| xi | yi | zi | pi | - | |||||
| 1 | 12 | -25 | 0 | 0 | - | ||||
| 2 | 10 | -25 | 0.5 | 1 | - | ||||
| 3 | 9 | 8 | 2.5 | 1 | - | ||||
| 4 | 9 | -8 | 2.5 | 1 | - | ||||
| ϕ [°] | 20 | ro [Km] | 550 | PRF [Hz] | 3630 |
|---|---|---|---|---|---|
| f [GHz] | 9.65 | BW [MHz] | 135 | τ[μs] | 25 |
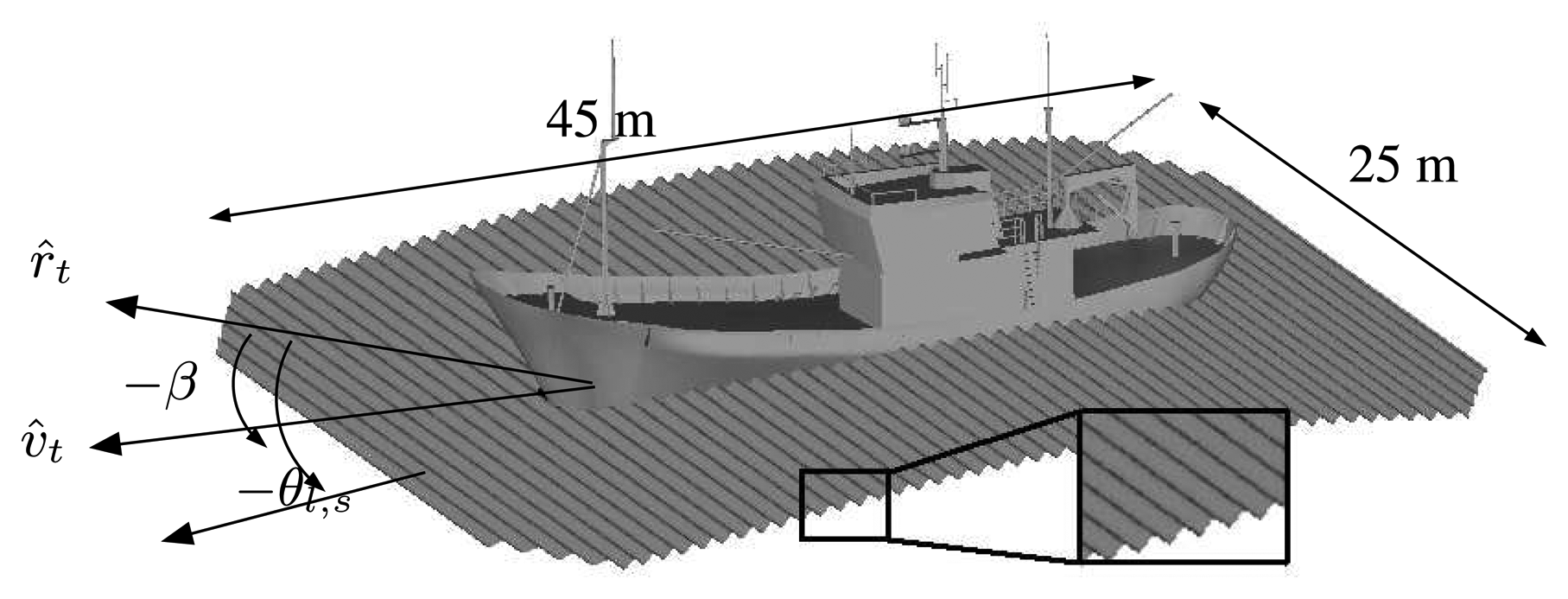
| Scenario | Bearings | Motions | Sea surface | β | δ̇roll | δ̇pitch | β | δ̇roll | δ̇pitch |
|---|---|---|---|---|---|---|---|---|---|
| 0 | [295:10:355]° | No | No | 295 | -1.56 | -0.26 | 335 | -0.98 | -1.16 |
| 1 | [295:10:355]° | Right Side | No | 305 | -1.43 | -0.52 | 345 | -0.76 | -1.32 |
| 2 | [295:10:355]° | No | 2 scale | 315 | -1.32 | -0.76 | 355 | -0.52 | -1.43 |
| 3 | [295:10:355]° | Right Side | 2 scale | 325 | -1.16 | -0.98 | - | - | - |
| β = 295° | β = 315° | ΘSPA | ΘICE | ΘFER | β = 295° | β = 315° | ΘSPA | ΘICE | ΘFER |
|---|---|---|---|---|---|---|---|
| Processing SPA | 0.82 | 0.8 | 0.31 | 0.47 | 0.3 | 0.32 | Processing SPA | 0.76 | 0.71 | 0.22 | 0.11 | 0.22 | 0.4 |
| Processing ICE | 0.08 | 0.0 | 0.56 | 0.82 | 0.08 | 0.28 | Processing ICE | 0.0 | 0.32 | 0.7 | 0.76 | 0.08 | 0.45 |
| Processing FER | 0.1 | 0.11 | 0.19 | 0.0 | 0.7 | 0.6 | Processing FER | 0.34 | 0.1 | 0.26 | 0.0 | 0.74 | 0.76 |
| β = 295° | β = 315° | ΘSPA | ΘICE | ΘFER | β = 295° | β = 315° | ΘSPA | ΘICE | ΘFER |
| Processing SPA | 0.62 | 0.63 | 0.26 | 0.22 | 0.31 | 0.21 | Processing SPA | 0.57 | 0.44 | 0.15 | 0.0 | 0.0 | 0.25 |
| Processing ICE | 0.0 | 0.17 | 0.33 | 0.45 | 0.0 | 0.08 | Processing ICE | 0.1 | 0.7 | 0.8 | 0.44 | 0.1 | 0.25 |
| Processing FER | 0.11 | 0.0 | 0.33 | 0.0 | 0.5 | 0.57 | Processing FER | 0.21 | 0.0 | 0.3 | 0.0 | 0.69 | 0.56 |
| β = 295° | β = 315° | SPApat | ICEpat | FERpat |
|---|---|---|---|
| Processing SPA | 0.0 | 0.0 | 0.1 | 0.35 | 0.0 | 0.0 |
| Processing ICE | 0.38 | 0.0 | 0.0 | 0.0 | 0.0 | 0.21 |
| Processing FER | 0.1 | 0.13 | 0.0 | 0.1 | 0.0 | 0.0 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Margarit, G.; Mallorqui, J.J. Assessment of Polarimetric SAR Interferometry for Improving Ship Classification based on Simulated Data. Sensors 2008, 8, 7715-7735. https://doi.org/10.3390/s8127715
Margarit G, Mallorqui JJ. Assessment of Polarimetric SAR Interferometry for Improving Ship Classification based on Simulated Data. Sensors. 2008; 8(12):7715-7735. https://doi.org/10.3390/s8127715
Chicago/Turabian StyleMargarit, Gerard, and Jordi J. Mallorqui. 2008. "Assessment of Polarimetric SAR Interferometry for Improving Ship Classification based on Simulated Data" Sensors 8, no. 12: 7715-7735. https://doi.org/10.3390/s8127715




