Effect of External Vibration on PZT Impedance Signature
Abstract
:1. Introduction
2. EMI Model
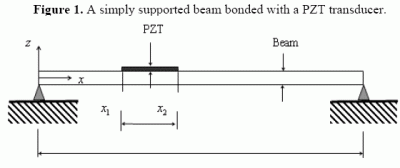
3. Experimental Setup
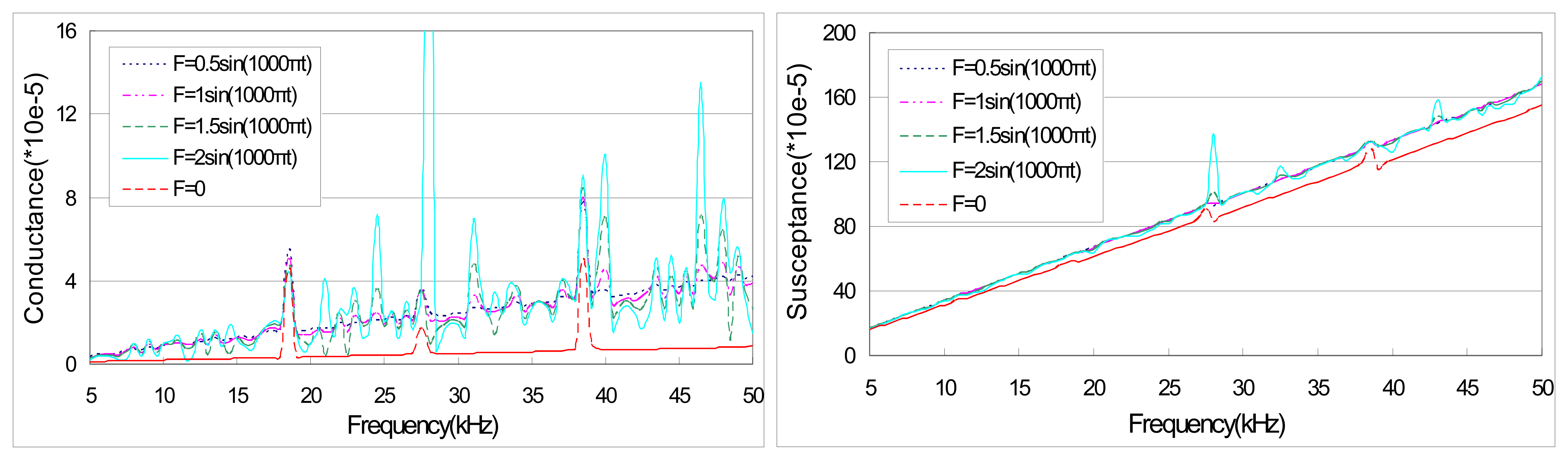
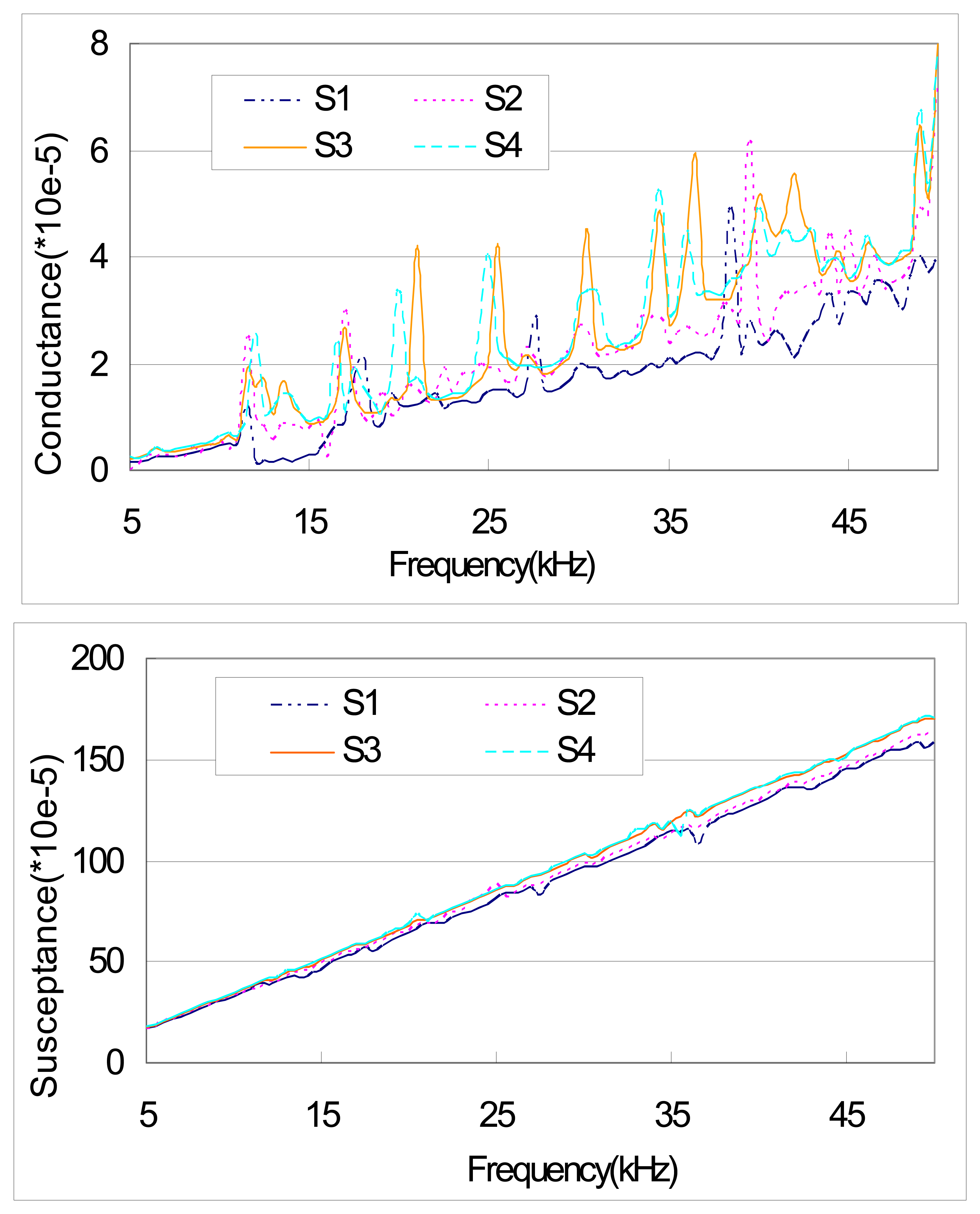
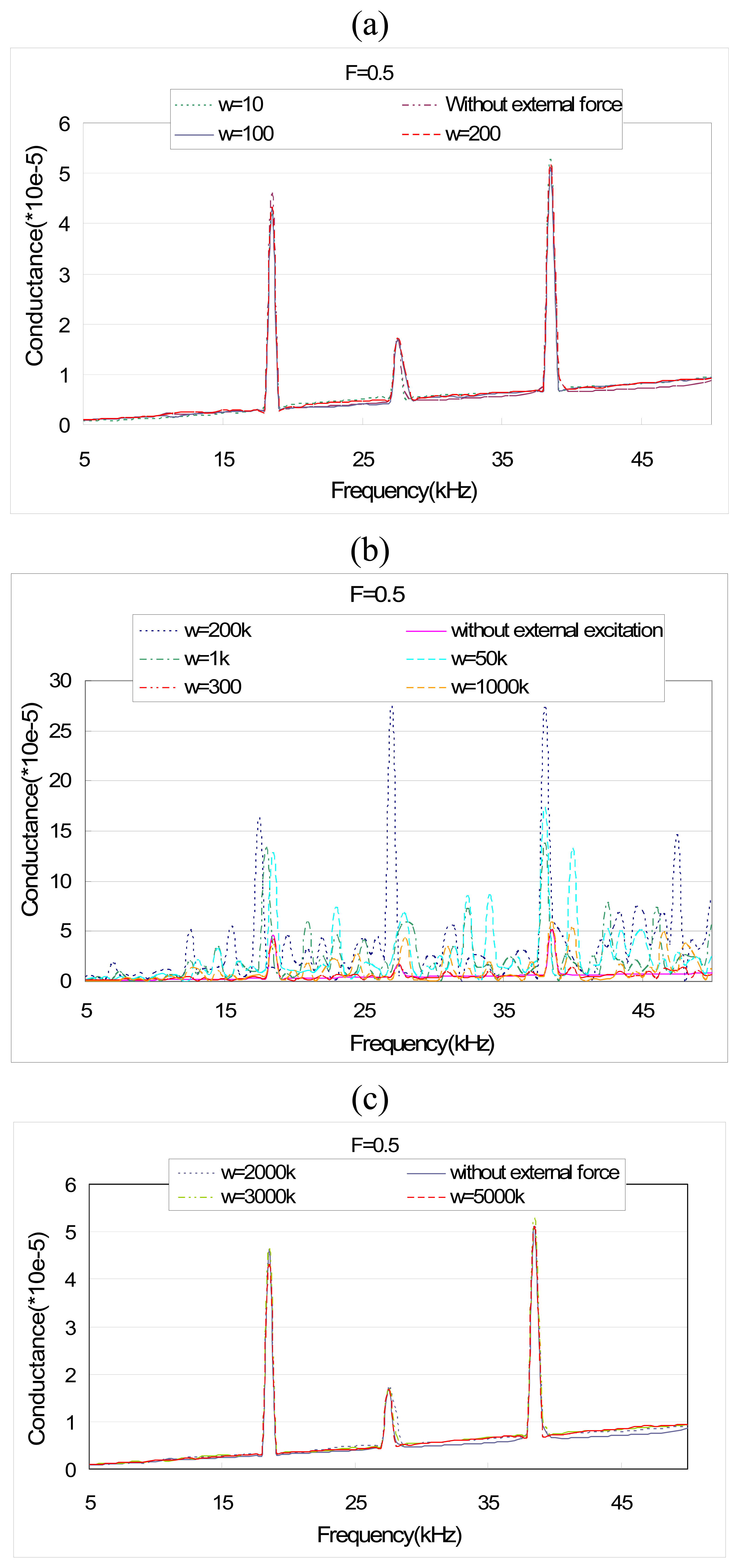
4. Results and Discussion
4. Conclusions
References
- Liang, C.; Sun, F.P.; Rogers, C.A. Coupled Electro-Mechanical Analysis of Adaptive Material System – Determination of the Actuator Power Consumption and System Energy Transfer. J. Intell. Mater. Syst. Struct. 1994, 5, 12–20. [Google Scholar]
- Liang, C.; Sun, F.P.; Rogers, C.A. Electromechanical Impedance Modeling of Active Material Systems. Smart Mater. Struct. 1996, 5, 171–186. [Google Scholar]
- Yang, Y.W.; Xu, J.F.; Soh, C.K. Generic Impedance-Based Model for Structure-Piezoceramic Interacting System. J. Aerospace Eng. 2005, 18, 93–101. [Google Scholar]
- Hu, Y.H.; Yang, Y.W. Wave Propagation Modeling of PZT Sensing Region for Structural Health Monitoring. Smart Mater. Struct. 2007, 16, 706–716. [Google Scholar]
- Annamdas, V.G.M.; Yang, Y.W.; Soh, C.K. Influence of Loading on Electromechanical Admittance of Piezoceramic Sensors. Smart Mater. Struct. 2007, 16, 1888–1897. [Google Scholar]
- Yang, Y.W.; Hu, Y.H. Electromechanical Impedance Modeling of PZT Sensors for Health Monitoring of Cylindrical Shell Structures. Smart Mater. Struct. 2008, 17, 015005. [Google Scholar]
- Sun, F.P.; Liang, C.; Rogers, C.A. Experimental Model Testing Using Piezoceramic Patches as Collocated Sensors-Actuators. Proceedings of 1994 SEM Spring Conference & Exhibits, Baltimore MD, June6 – 8, 1994.
- Zhou, S.; Liang, C.; Rogers, C.A. Integration and Design of Piezoceramic Elements in Intelligent Structures. J. Intell. Mater. Syst. Struct. 1995, 6, 733–743. [Google Scholar]
- Sun, F.P.; Chaudhry, Z.; Liang, C.; Rogers, C.A. Truss Structure Integrity Identification Using PZT Sensor-Actuator. J. Intell. Mater. Syst. Struct. 1995, 6, 134–139. [Google Scholar]
- Ayres, J.W.; Lalande, F.; Chaudhry, Z.; Rogers, C.A. A Vibrational Technique for Non-Destructively Assessing the Integrity of Structures. J. Mech. Eng. Sci. 1998, 20, 93–100. [Google Scholar]
- Giurgiutiu, V.; Zagrai, A.N.; Bao, J.J. Piezoelectric Wafer Embedded Active Sensors for Aging Aircraft Structural Health Monitoring. Struct. Health Monit. 2002, 1, 41–61. [Google Scholar]
- Xu, J.F.; Yang, Y.W.; Soh, C.K. Electromechanical Impedance-Based Structural Health Monitoring with Evolutionary Programming. J. Aerospace Eng. 2004, 17, 182–193. [Google Scholar]
- Ayres, J.W.; Lalande, F.; Chaudhry, Z.; Rogers, C.A. Qualitative Impedance-Based Health Monitoring of Civil Infrastructures. Smart Mater. Struct. 1998, 7, 599–605. [Google Scholar]
- Park, G.; Cudney, H.; Inman, D.J. Impedance-Based Health Monitoring of Civil Structural Components. J. Infrastruct. Syst. 2000, 6, 153–160. [Google Scholar]
- Park, G.; Cudney, H.H.; Inman, D.J. Feasibility of Using Impedance-Based Damage Assessment for Pipeline Structures. Earthquake Eng. Struct. Dyn. 2001. [Google Scholar]
- Park, S.; Ahmad, S.; Yun, C.-B.; Roh, Y. Multiple Crack Detection of Concrete Structures Using Impedance-Based Structural Health Monitoring Techniques. Exp. Mech. 2006, 46, 609–618. [Google Scholar]
- Yang, Y.W.; Bhalla, S.; Wang, C.; Soh, C.K.; Zhao, J. Monitoring of Rocks Using Smart Sensors. Tunnell. Underground Space Technol. 2007, 22, 206–221. [Google Scholar]
- Yang, Y.W.; Annamdas, V.G.M.; Wang, C.; Zhou, Y.X. Application of multiplexed FBG and PZT impedance sensors for health monitoring of rocks. Sensors 2008, 8, 271–289. [Google Scholar]
- Yang, Y.W.; Hu, Y.H.; Lu, Y. Sensitivity of PZT Impedance Sensors for Damage Dection of Concrete Structures. Sensors 2008, 8, 327–346. [Google Scholar]
- Yang, Y.W.; Lim, Y.Y.; Soh, C.K. Practical Issues Related to the Application of EMI Technique in SHM of Civil Structures: Part I – Experiment. Smart Mater. Struct. 2008, 17, 035008. [Google Scholar]
- Yang, Y.W.; Lim, Y.Y.; Soh, C.K. Practical Issues Related to the Application of EMI Technique in SHM of Civil Structures: Part I – Numerical Verification. Smart Mater. Struct. 2008, 17, 035009. [Google Scholar]
- Giurgiutiu, V.; Reynolds, A.; Rogers, C.A. Experimental investigation of E/M Impedance Health Monitoring for Spot-Welded Structural Joints. J. Intell. Mater. Syst. Struct. 1998, 10, 802–812. [Google Scholar]
- Ong, C.W.; Yang, Y.W.; Naidu, A.S.K.; Lu, Y.; Soh, C.K. Application of the electro-mechanical impedance method for the identification of in-situ stress in structures. Proc. SPIE 2002, 4935, 503–14. [Google Scholar]
- Providakis, C.P.; Kontoni, D.-P.N.; Voutetaki, M.E. Development of an Electromechanical Admittance Approach for Application in the Vibration Control of Intelligent Structures. Smart Mater. Struct. 2007, 16, 275–281. [Google Scholar]
- Hewlett Packard. HP LF 4192A impedance analyzer operation manual.; Hewlett Packard: Japan, 1996. [Google Scholar]







| Young's ModulusY(GPa) | Loss Factor | Mass Density ρ(kg/m3) | Strain Constant d d31(m/volt) | Permittivity (farad/m) | Dielectric Loss Factorδ | Dimension (mm) | Location (mm) |
|---|---|---|---|---|---|---|---|
| 68.9 | 0.001 | 7800 | -2.10E-10 | 2.36E-08 | 1.47E-02 | l=b=10 h=0.2 | 100 mm from both ends |
| Length (mm) | width (mm) | Thickness (mm) | Thickness Young's Modulus (GPa) | Poisson's Ratio | Mass Density (kg / m3 ) | Damping Ratio |
|---|---|---|---|---|---|---|
| 200 | 30 | 2 | 68.9 | 0.3 | 2700 | 0.005 |
| F=1.5 sin (1000πt) | F=1.6 sin (100πt) | ||||
|---|---|---|---|---|---|
| Peak locations (kHz) | Peak locations (kHz) | ||||
| Theoretical predictions | Experimental results | Errors | Theoretical predictions | Experimental results | Errors |
| 12.25 | 11.80 | -0.45 | 12.10 | 11.95 | -0.15 |
| 13.75 | 14.25 | +0.50 | 14.60 | 14.60 | 0 |
| 18.50 | 17.00 | -1.50 | 15.90 | 16.50 | +0.60 |
| 21.30 | 20.50 | -0.80 | 21.15 | 20.55 | -0.60 |
| 24.75 | 25.20 | +0.55 | 25.60 | 25.35 | -0.25 |
| 27.25 | 27.00 | -0.25 | 26.70 | 26.70 | 0 |
| 30.55 | 30.15 | -0.40 | 30.25 | 30.30 | +0.05 |
| 34.55 | 34.75 | +0.20 | 32.40 | 32.35 | -0.05 |
| 37.40 | 36.00 | -1.40 | 34.85 | 34.75 | -0.10 |
| 38.50 | 38.30 | -0.20 | 36.90 | 36.65 | -0.25 |
| 40.00 | 39.85 | -0.15 | 38.25 | 38.25 | 0 |
| 43.40 | 42.50 | -0.90 | 40.95 | 40.00 | -0.95 |
| 44.50 | 43.75 | -0.75 | 42.45 | 43.65 | +1.20 |
| 45.55 | 45.00 | -0.55 | 44.10 | 44.10 | 0 |
| 46.70 | 46.70 | 0 | 45.00 | 45.00 | 0 |
| 47.75 | 46.50 | -1.25 | |||
| Cases | Peak locations and peak shifts | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| S1 | 11.5 | 18 | 22 | 27.5 | 30 | 34 | 35 | 38.5 | 41 |
| S2 | 11.5 | 17 | 21.5 | 27 | 30 | 33.5 | 35.5 | 39.5 | 42.5 |
| S3 | 12.5 | 17 | 21 | 25.5 | 30.5 | 34.5 | 36.3 | 39.5 | 42 |
| S4 | 12.3 | 16.2 | 20.2 | 25 | 30.5 | 34.2 | 36.3 | 40.2 | 43.5 |
| S2–S1 | 0 | -1 | -0.5 | -0.5 | 0 | -0.5 | +0.5 | +1 | +1.5 |
| S3–S1 | +1 | -1 | -1 | -2 | +0.5 | +0.5 | +1.3 | +1 | +1 |
| S4–S2 | +0.8 | -0.8 | -1.3 | -2 | +0.5 | +0.7 | +0.8 | +0.7 | +1 |
© 2008 by the authors; licensee Molecular Diversity Preservation International, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Yang, Y.; Miao, A. Effect of External Vibration on PZT Impedance Signature. Sensors 2008, 8, 6846-6859. https://doi.org/10.3390/s8116846
Yang Y, Miao A. Effect of External Vibration on PZT Impedance Signature. Sensors. 2008; 8(11):6846-6859. https://doi.org/10.3390/s8116846
Chicago/Turabian StyleYang, Yaowen, and Aiwei Miao. 2008. "Effect of External Vibration on PZT Impedance Signature" Sensors 8, no. 11: 6846-6859. https://doi.org/10.3390/s8116846