Intelligent Fiber Optic Sensor for Estimating the Concentration of a Mixture-Design and Working Principle
Abstract
: This paper presents the construction and working principles of an intelligent fiber-optic intensity sensor used for examining the concentration of a mixture in conjunction with water. It can find applications e.g. in waste-water treatment plant for selection of a treatment process. The sensor head is the end of a large core polymer optical fiber, which constitutes one arm of an asymmetrical coupler. The head works on the reflection intensity basis. The reflected signal level depends on the Fresnel reflection from the air and from the mixture examined when the head is immersed in it. The sensor head is mounted on a lift. For detection purposes the signal can be measured on head submerging, submersion, emerging and emergence. Therefore, the measured signal depends on the surface tension, viscosity, turbidity and refraction coefficient of the solution. The signal coming from the head is processed electrically in an opto-electronic interface. Then it is fed to a neural network. The novelty of the proposed sensor lies in that it contains an asymmetrical coupler and a neural network that works in the generalization mode. The sensor resolution depends on the efficiency of the asymmetrical coupler, the precision of the opto-electronic signal conversion and the learning accuracy of the neural network. Therefore, the number and quality of the points used for the learning process is very important. By way of example, the paper describes a sensor intended for examining the concentration of liquid soap in water.1. Introduction
Irrespective of the type of the fiber sensor, whether extrinsic or intrinsic, and of the core/cladding materials of the optical fiber, the operating principle is similar: an environmental signal or an external perturbation modulates the light by varying its frequency/color, phase, intensity or polarization. In the recent years, with the progress in polymer fiber technologies, there has been great interest in the use of plastic optical fibers (POF) for local area network (LAN), vision, illumination and alarm systems, [1, 2]. The POF are large-size cores multimode fibers with a small minimum bend radius, inexpensive, resistant to water and oil damage under normal ambient conditions, [3]. They are easy to install thanks to the simple and fast preparation of the fiber facet for the connection, the efficient coupling of the light source radiation to the fiber. However the specific properties of large – molecules thermoplastics do not permit substituting automatically silica glass fibers by POF. In designing the sensors and examining their models that contain plastic fibers, special attention should be paid to certain factors that are less important in devices with silica glass fibers.
2. Sensor scheme
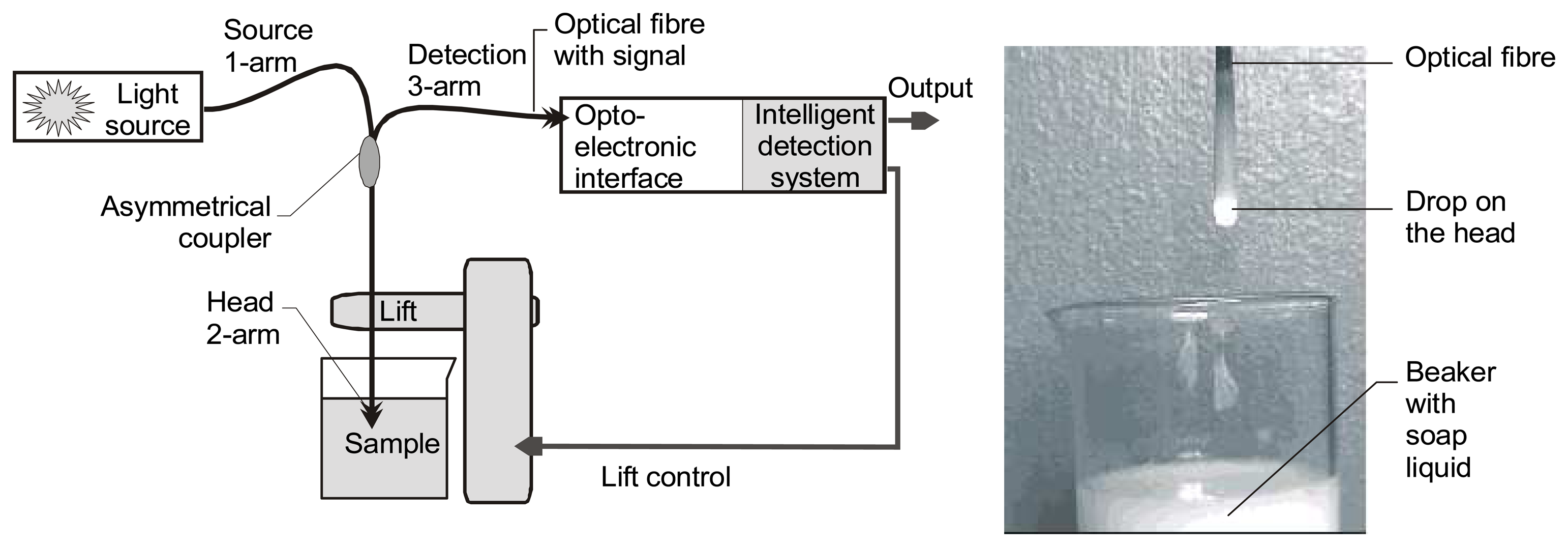
The sensor consists of a light source, asymmetrical fiber coupler, an optic head, a mini lift and a computer-aided measuring system with a detection block, Figure 1. We assume that in the constructed sensor a multimode laser diode or LED diode is used. In contrast to well-known fiber optical intelligent sensors which use information of various optical wavelengths, [4], the proposed construction uses time-dependant information. The sensor operates according to a stepwise measuring procedure which includes head submerging, submersion, emerging and emergence from the examined medium, [5]. The variation of the amplitude of the measured signal versus time provides information about the type of the liquid.
The resolution of the detection system mostly depends on the quality of the optical signal passed to the detection unit. This is related with the power budget which in turn depends on the power of the light source, the efficiency of the coupler and the sensitivity of the opto-electronic conversion. The power budget can be improved by increasing the power of the source and using a large core optical fiber. The signal quality can be improved by using the light source with signal modulation. Moreover, the construction of the detection block with the possibility of modulation enables detecting properly low power signals of e.g. tens of nW, [6]. The signal quality also depends on the degree of the stabilization of the sample position and on the lift movement.
3. Design of sensor optical path
3.1. The simulation fundamentals
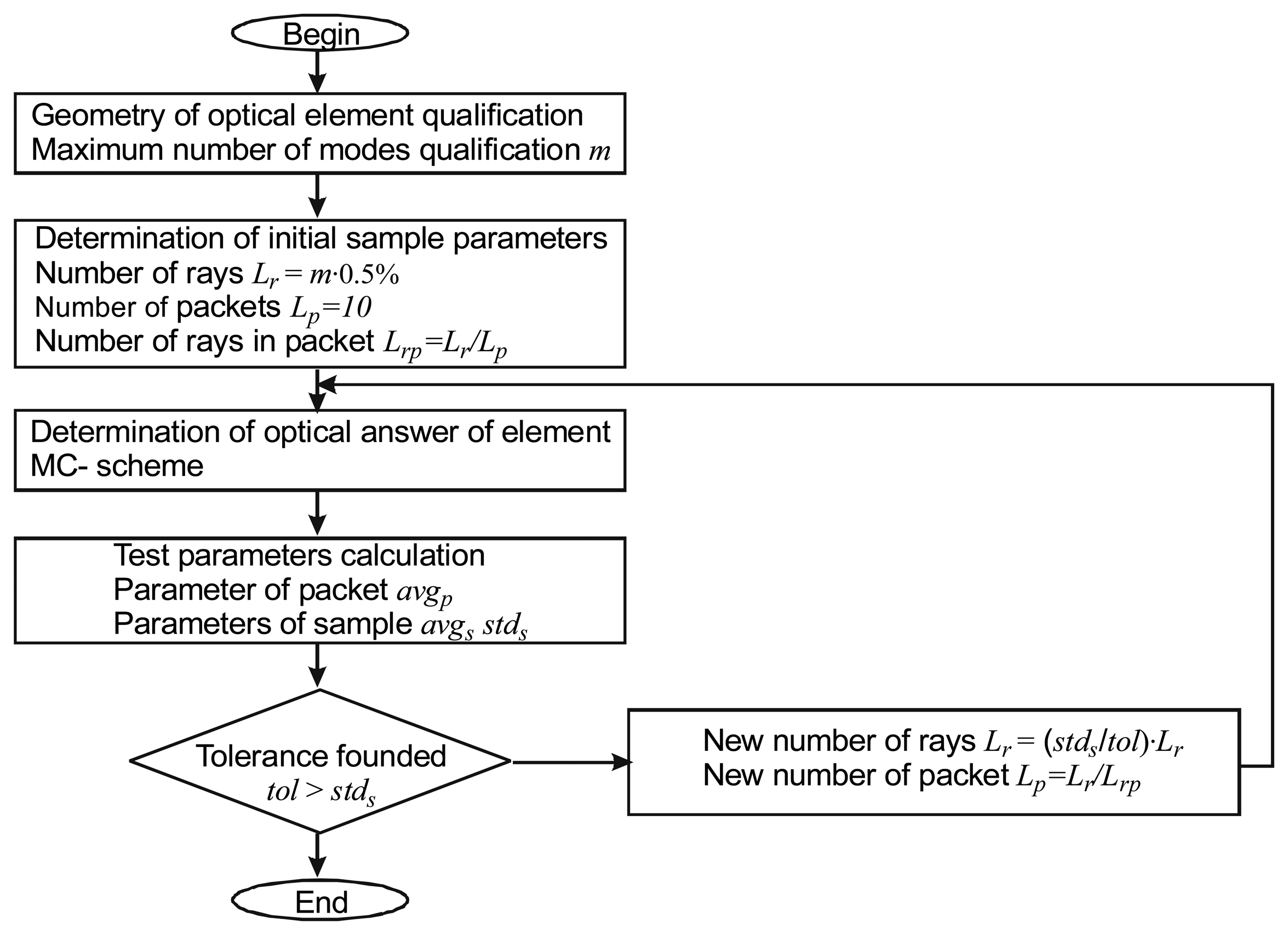
We assume that the optical path is a large core optical fiber. Such a fiber has a core diameter much greater than the wavelength of the light. Therefore, the non-sequential ray tracing method can be used for designing the sensor optical path, [7]. In practical cases, the individual path components are analyzed separately. The first design step in the implementation of this method consists of describing virtual light sources. The virtual light source can be represented by the intensity patterns in a cross-section of the optical fiber. These patterns are composed of the surface- and angular light intensity distributions. The second step includes a description of the material and the geometrical parameters of the components. Next, the optical parameters are calculated and,, the power budget is estimated.
The light surface intensity pattern in a cross-section of a large core polymer fiber is shown in Figure 2, for three different sources: an He-Ne laser, a multimode semiconductor laser and a light emitting diode. A chaotic interference pattern on a core cross-section can only be obtained when using a single mode source.
Therefore, the intensity version of the non- sequential ray tracing can be used, [8], for a design of the optical components or the sub-systems that utilize large core fibers and a multimode source. In this work we assume that, inside the fiber, the surface intensity distribution on a cross-section of the input tip of the optical components is uniform and the angular distribution is Gaussian [9]. Based on this information, meridional, skew and clad rays were generated. For the simulation purposes, we assumed that the initial number of rays is equal to 0.5% of the number of fiber modes. The proposed method utilizes the ray refraction and reflection according to the Fresnel phenomenon. The attenuation of the media was assumed to be constant. The internal light scattering in the fibers was neglected, but that in the liquid media was taken into account, [10]. The flow chart of the intensity method, which involves the estimation of the calculation tolerance aimed at reducing the simulation time, is shown in Figure 3.
We used this method for designing the asymmetric coupler and for analyzing the head working conditions. The constructional parameters of these units can be calculated using the transmission coefficients and the light intensity patterns calculated as a function of their geometry and optical parameters. The geometry of the optical components and sub-components were described by interpolation and approximation techniques. The proper selection of the approximation point is a complex task, because an erroneous selection can result in nooses in the modeled shape. A solution to this problem was given by Kushkuley and Rosenberg in [11]. The idea of this solution lies in that the path length is maintained constant during curve fitting:
In the simulation of the light transmission in the coupler arm, the fiber core path is divided into straight segments that are connected at a certain angle. The lengths of these segments and angle at which they are connected result from the number of divisions of the Bezier curve (2). In the simulation of the head working condition, the drop shape was described using the Bezier curve (2). The description of the shape of the drop while it was being formed was an interesting problem. The reduction of the shape quantity parameters was achieved by assuming that the drop is axially symmetric, Figure 10.
3.2. Asymmetrical coupler
One of the important optical path components is the asymmetrical coupler. The well-known transfer matrix describes its operation:
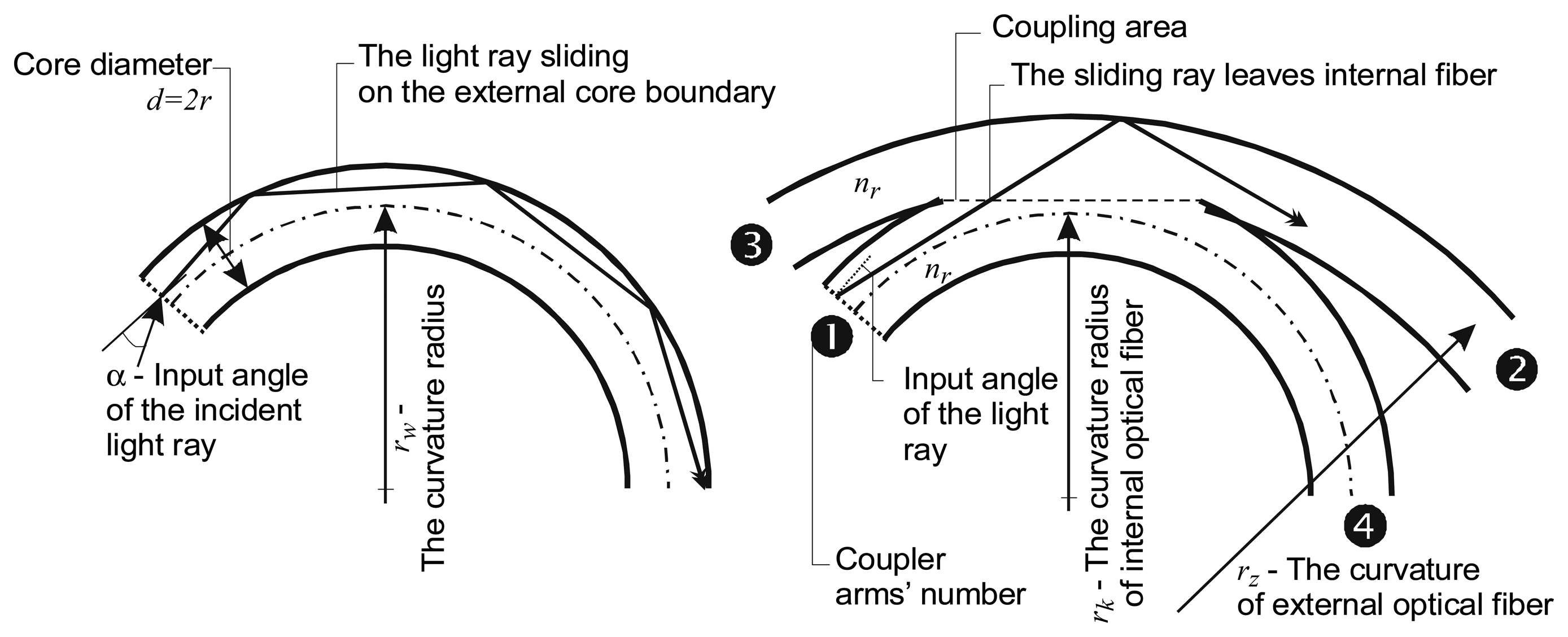
The major requirement of the sensor coupler is its maximum efficiency (4). The minor requirement is that the transmission from arm 1 to 3 should be at a minimum. Classical couplers do not meet these requirements and thus, we designed an appropriate coupler. The results reported in [9] allow us to conclude that, in a bent optical fiber, the light rays play along the external core wall. Sometimes, these rays are called the sliding rays. This phenomenon is illustrated schematically in Figure 4.
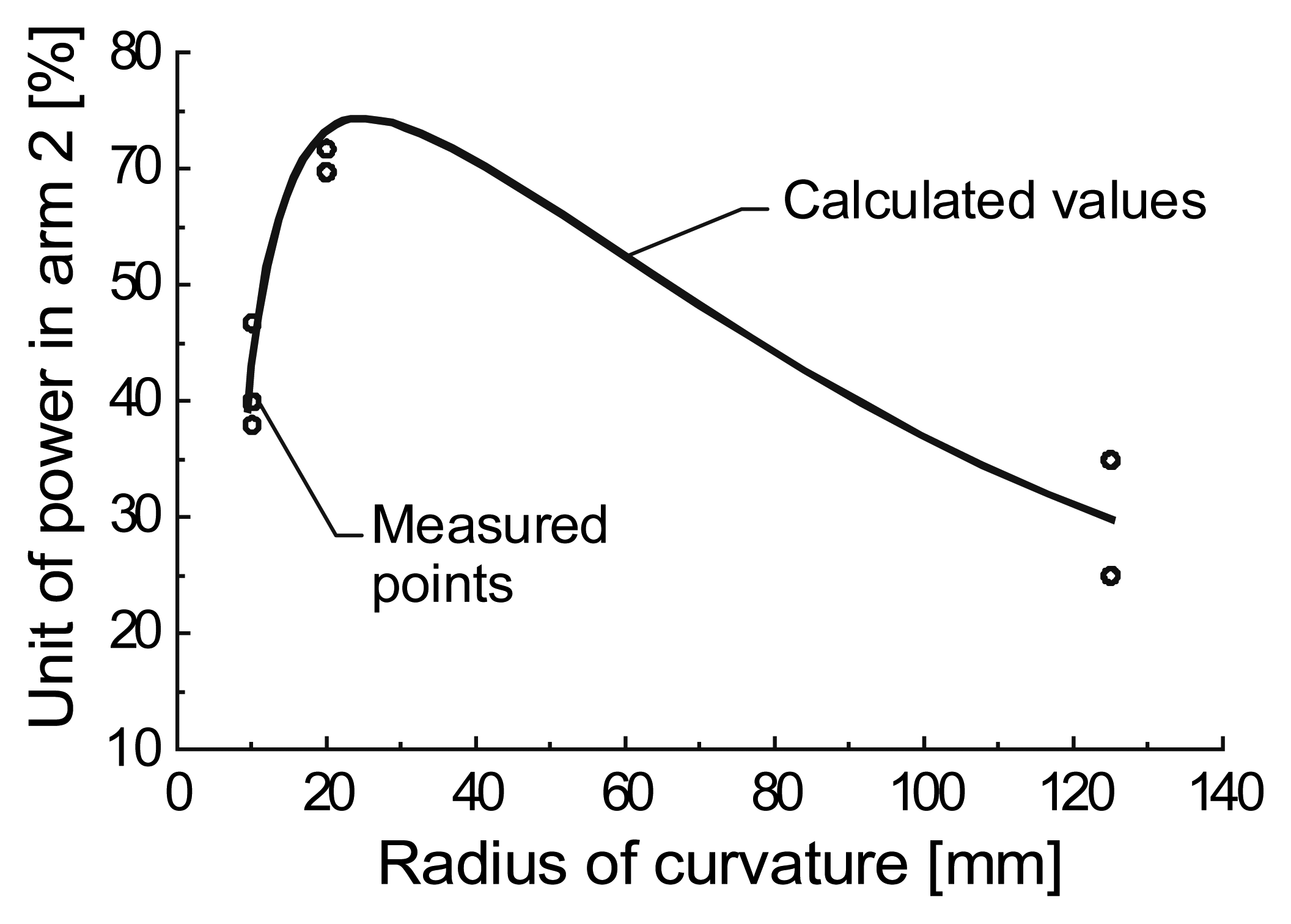
The coupler constructional parameters are the curvature radius, and the length and the depth of the coupling area. We assume that our sensor is equipped with the polymer optical fiber PFU-CD 751-22-E. The core of this fiber has a diameter of 750μm and its allowable radius of repeatable bend is 40mm. The variation of the light transmission coefficient of a fiber bend in the form of a half-circle as a function of the curvature radius is shown in Figure 5, [13].
It can be seen that, with bends of the curvature radius above 20mm, the power transmission coefficient exceeds 0.75. However the curvature radius of the arms of the proposed coupler must exceed 30mm so as to fulfill the small insertion loss condition. The light intensity patterns at the tip of the fiber core cross-section for deformations by “half of the ring” and “one fourth of the ring” are illustrated in the Figure 6, [13].
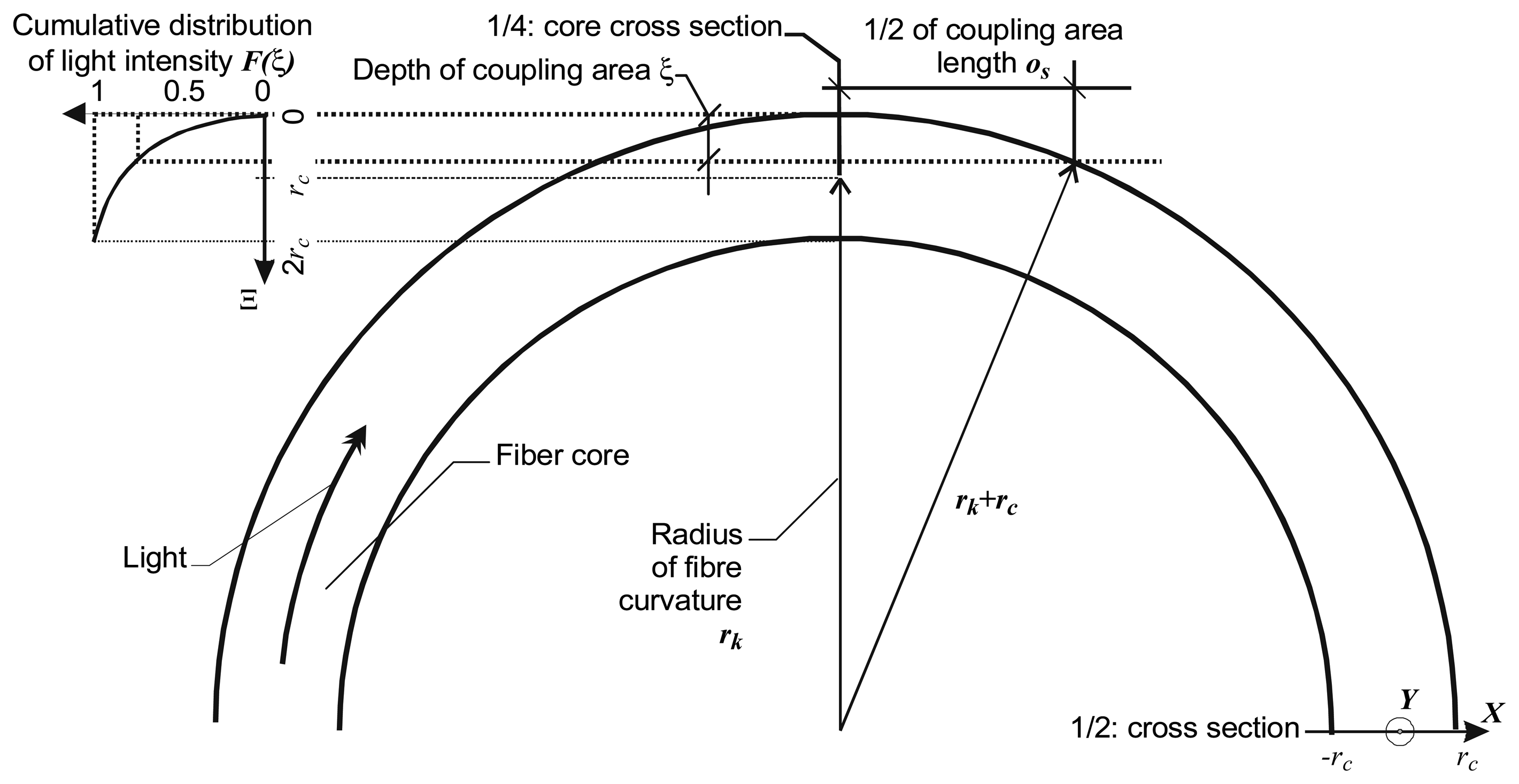
In the fiber examined, the external core boundary corresponds to the co-ordinate x that is equal to 325μm. The outer half surface area of the core cross-section is represented by the co-ordinate x greater than 0. We calculate a set of intensity patterns for various curvature radii. It can be seen from Figure 6 that, at the 33mm radius, the transmitted light intensity pattern changes significantly, but no light transmission losses occur. At greater curvature radii, the light intensity tends to form a uniform pattern, whereas at smaller radii, the total light transmission coefficient decreases, Figure 5. The situation shown in Figure 6 corresponds to the optimum state in which the transmitted light moves into the outer half portion of the core. The knowledge of the light intensity pattern permits estimating the coupling length and depth of the fiber core that should be removed from the coupler arms, as shown schematically in Figures 4 and 7.
The coupling depth and length are interrelated by the relationship:
The cumulative distribution determines the level of coupling. At constant depth of the coupling area the m12 coefficient has a maximum value in its dependence of the inner fiber curvature radius (rk). In our case, at a coupling depth equal 375μm, the m12 has maximum of 0.75 for the curvature radius of 33mm. The 3-2 arms of the coupler should have the same open core area. When the radius of curvature of the inner arms and the external fiber curvature radius are 33mm and 40mm respectively, the insertion losses for arms 2 and 3 are relatively small i.e. m23=0.72. This means that, theoretically, asymmetric constructions have better efficiency than symmetric. In the case discussed, the maximum useful power in the arm 3 can be 54% of the input power. This is much more than the useful output power from symmetric structures where it does not exceed a value of 25%.
Examples of the thus-designed asymmetrical coupler were made manually by stripping off the polyethylene jacket, forming the curvature and polishing fibers. Then the fibers were positioned, etched and clamped. The relative coupling efficiency was:
The figure shows the power distribution between the coupler arms and compares it with that predicted by mathematical modeling, but the efficiency of the coupler is e=0.4. The proposed device is characterized by high insertion losses caused by coupling area defects. It was found that the insertion losses in asymmetric and symmetric couplers are similar if the devices are made using the same manual technological procedure.
3.3. The head
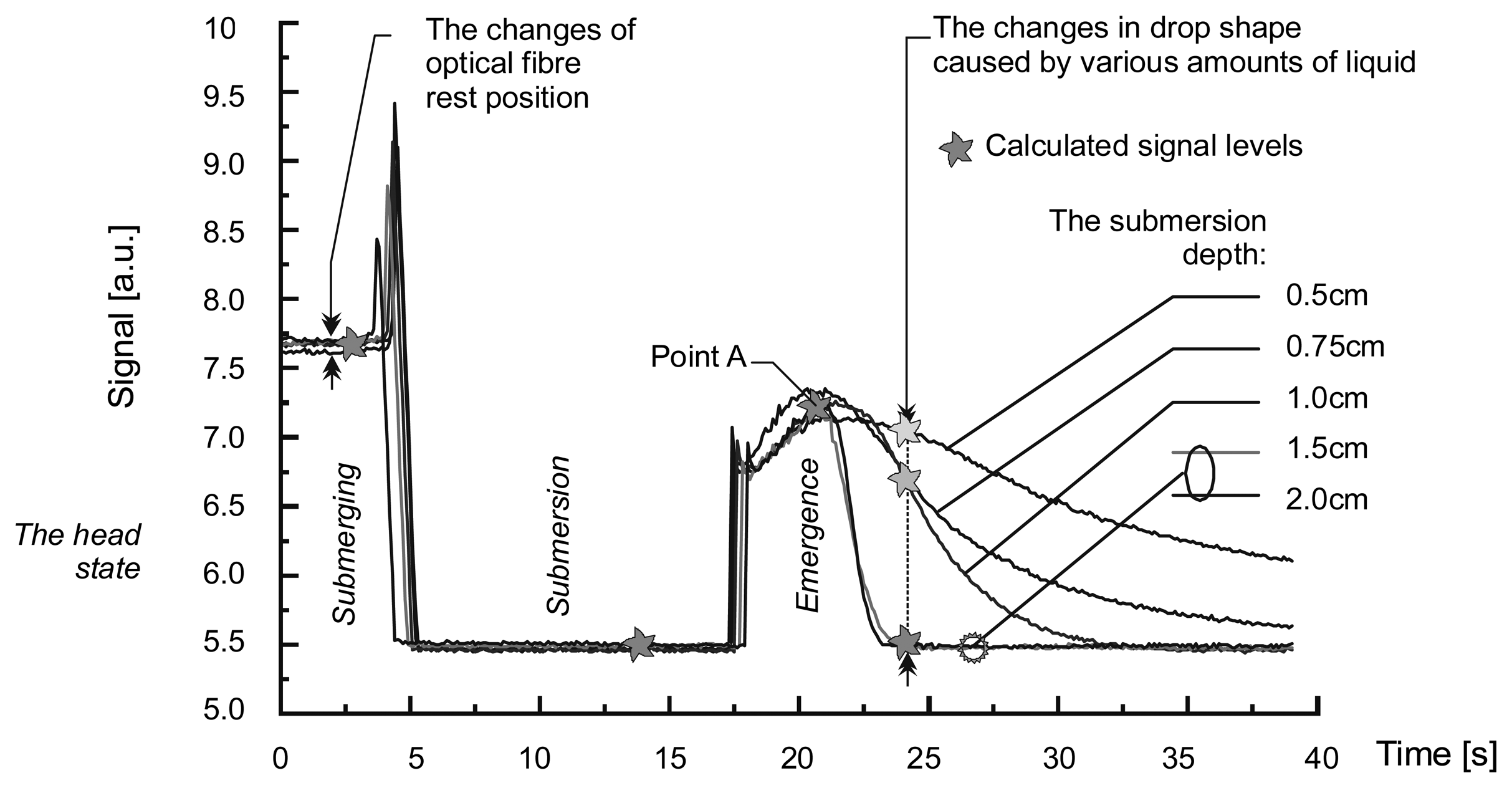
Compared to other advanced reflectometric systems, [14], the studied head is characterized by an extremely low-cost and simple construction. The head is formed by the end of the polymer optical fiber. It is mounted on a mini-lift, so that the speed of its movement and its submersion depth are constant and repeatable in time. Thus, the optical signal is related to the measuring time. The test signal obtained in examining edible oil, at various submersion depths of the head, is shown in Figure 9.
Figure 10 shows the shape of the liquid drop formed at the fiber tip which was used for calculating the measurement point marked with A in Figure 9.
The depth of submersion should be such that the liquid will not drop from the head in the emerging and emergence states. If the depth at which the head is submerged is too great, the liquid will drop down from the head, thereby disturbing the optical signal. I should be noted that, once the optimum depth is established, it is easy to maintain, since as found experimentally, the sufficient tolerance is ±1mm.
During the experiment the head was subjected to a three-step washing process: flannel dampened in a water wipe, a dry lint-free kim wipe and a lint-free kim dampened in a methanol wipe. The sensor has been tested in room temperature (19-23C) and under atmospheric pressure. The samples of mixture were prepared with an electromagnetic rabble. Under these conditions, the measured characteristics were reproducible, (Figure 12 and 13).
3.4. Opto-electronic signal processing
The next design step consists of determining the minimum level of the received optical signal. We assume that the reflection from the medium examined is 2% and that one tenth of its changes should be distinguished. Our opto-electronic interface has a 20nW resolution. Therefore, we need at least 200nW at its input. Taking into account the coupler efficiency, medium reflection, and the input beam coupling conditions we found that 1.4% of the source power is transmitted. The source should thus give 280μW. We used a standard semiconductor laser as the light source. Its wavelength was 670nm and stabilized power was 2mW. The laser beam was modulated with a frequency of 1kHz at a ½ filling factor.
The optical signal was processed in two steps: at first, electronically in the opto-electronic interface and then digitally in the detection block equipped with a neural network. The opto-electronic interface comprised an integrated opto-electronic detector, a band-pass filter, an amplifier and a peak detector. The opto-electronic detector was equipped with a dark current compensation circuit. The band-width of the band-pass filter was 1kHz ± 10Hz. The amplifier had a linear and step-wise gain control. The peak detector contained an initial rectifier and a right peak detector. The memory capacitor of this detector was charged through a resistor and discharged thorough an additional current source. The opto-electronic interface is able to convert an optical signal of the order of nano-Watts. The output interface signal is a voltage ranging from 0 to 10V with maximum noise of 20mV. The speed of the interface reaction at its output is 10V/s. This means that, at a noise of 20mV, the time of reaction is 2ms, which is the maximum sensible sampling speed.
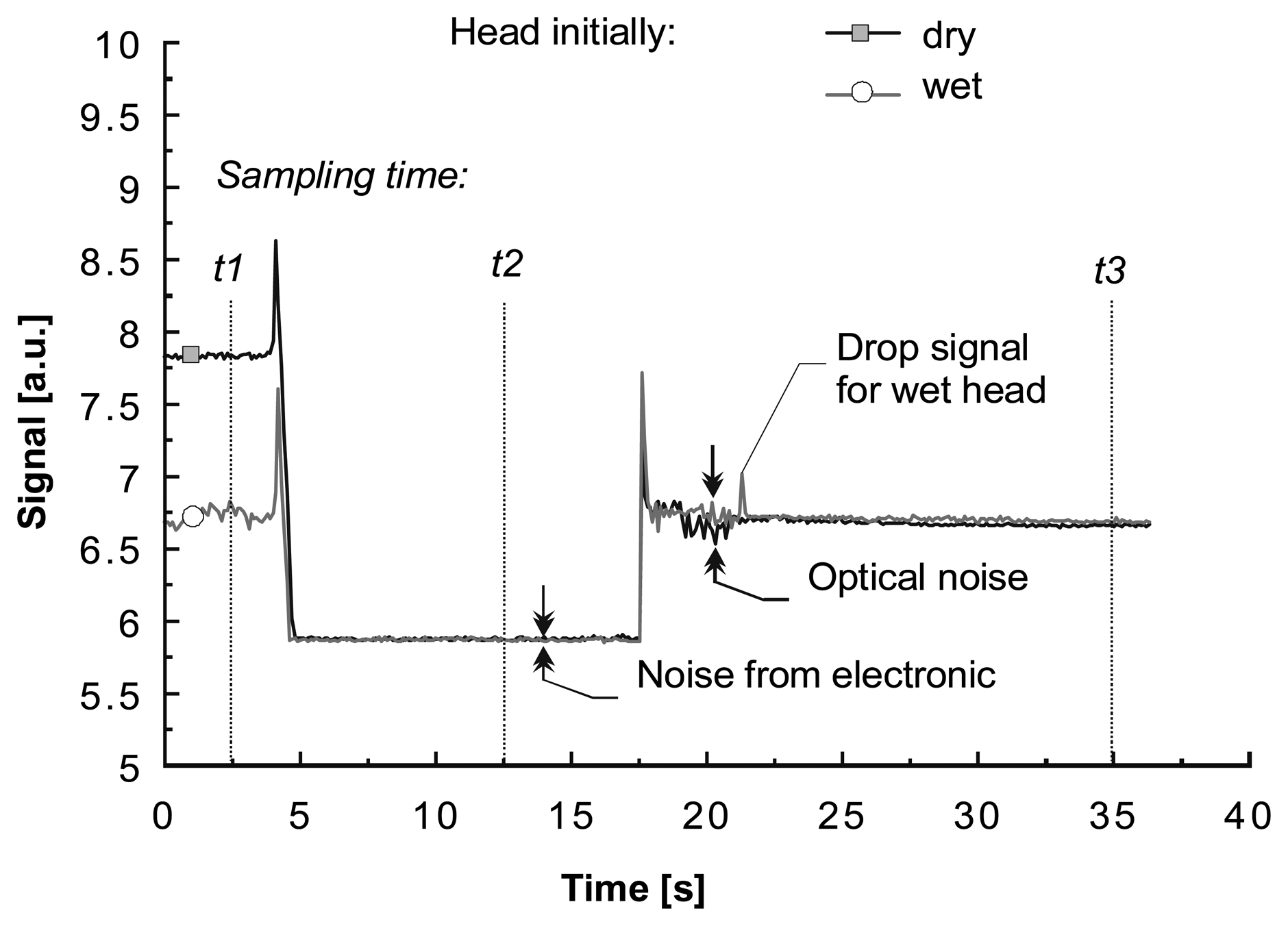
The signal from the interface is sampled, scaled and locally averaged on the cycle time information basis, and fed to the neural network inputs. The signal is scaled since the initial signal level changes due to the variations in the rest position of the optical fiber. This scaling enables rejecting signals whose initial levels differ too much from the reference level, Figure 11. Therefore, at the beginning of each measurement, the initial signal value is always the same.
The signal is averaged when the noise level is too high to accept. In our case the duration of the measurement cycle is about 30s. On the other hand, the number of transitory process characteristic points in analogical recognition situations, reported in the literature, is below 10, [15]. The number of neural network inputs is equal to the number of the characteristic points. This means that the average time of reading of the characteristic points is about 3.5s. As a result, the resolution can be increased because the time of reading the characteristic points is significantly greater than the time of sampling the data received from the head, Figure 11.
In response, the network can indicate the concentration of the solution or detect the type of the liquid, according to its training process. The network can be implemented in the software of a PC or a micro controller. The proposed sensor has been designed to co-operate with a PC equipped with acquisition and control cards such as the PCL818HG and the PCLD885, both delivered by the Advantech. The software for cards has been written in the Genie environment and the neural network has been developed in the Qnet software. The interprocess communication between the neural network and the acquisition software uses the DDE channels from the Windows system.
4. The Neural network training
The signal amplitude registered during each measuring cycle should be processed in order to get a desired information. Optical signal after digital processing was sent to a selected and trained neural network. For purposes of the experiment an architecture of a multilayer perceptron neural network with use of a hyperbolic tangent transfer function was chosen. An initial test has been done to investigate differences of head response under influence of selected liquids, Figure 12.
The differences were significant during the head emergence. An information obtained during the submersion phase is also visible. Formation and displacement of a drop of a liquid caused by emergence is highly repeatable for specified medium. It has to be noticed, that within one media the characteristic values of signal waveforms of the consecutive measuring cycles are well repeatable. Thus, I postulate that the information defining the type of the liquid is generated in submersion and emergence of the head. Therefore, the characteristic features of the particular signal collected and analyzed using a neural network model can be used for the recognition of the type of liquid. For the liquid identification several signal values were assumed in the data model: the starting value, value accorded to submersion and the values collected after the emergence in 15, 20 and 25 seconds, Figure 12. For each liquid 30 data models were measured. As the neural network the multilayer perceptron with two hidden layers was selected [15]. The learning error for 1000 iterations of the back propagation algorithm was 0.012%. It means that the network parameters were well selected and the learning process of the desired features has taken place. The results of neural network analysis are presented in Table 1.
As can be seen, the answers of the neural network to the test data are consistent with assumptions. The network analysis show that over 60% of essential information comes from the emergence of the sensor head from the liquid.
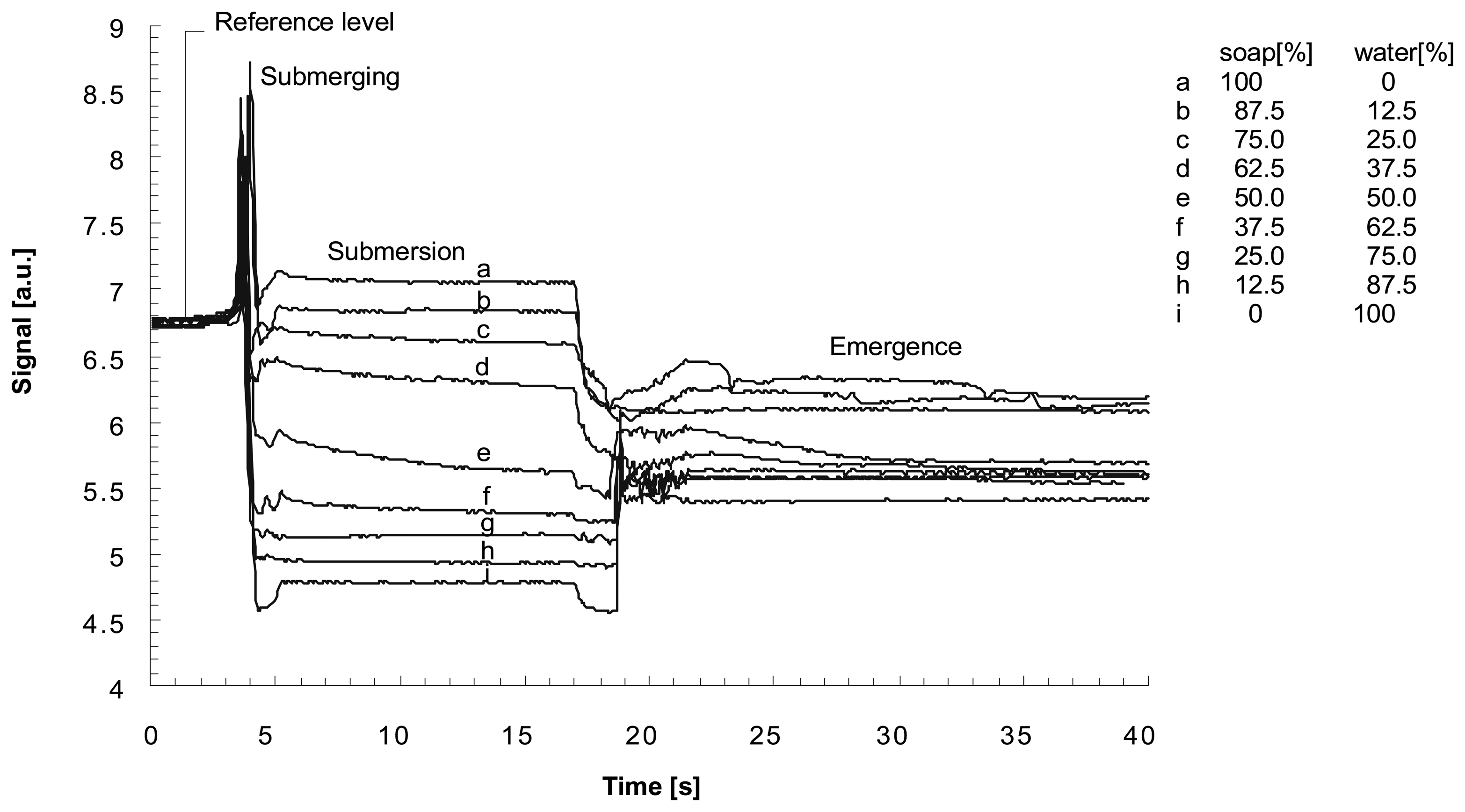
Fundamental test for presented sensor is examination of a mixture concentration. As a mixture the liquid soap (Palmolive Nourishing Liquid Hand wash Almond Milk) diluted with water was chosen. It consists of: water, Sodium C12-13, Pareth Sulfate, Cocamidopropyl Betaine, Sodium Chloride, Lauryl Polyglucose, Styrene/Acrylates Copolymer, Parfum, Glycol, Laureth-4, Polyquaternium,-7, Glyceryn, DMDM Hydantoin, Sodium Sulfate, Tetrasodium EDTA, Citric Acid, Prunus Dulcis, Sine Adipe Lac, Benzyl Benzonate, Hexyl Cinnamal, Hydroxyisohexyl 3-Cyclohexene Carboxaldehyde, Linalool. The data relevant to each mixture were collected and presented in Figure 13.
The characteristics clearly show that the signal level depends on the water concentration for the submersed head. This is in agreement with expectations, since the liquid is almond milk which dissipates light and its turbidity may be changed when water is added. When the head is in the emergence state, this effect is not so evident but it's present. The signal in emergence stabilizes in 35th second. Figure 14 shows the variation of the signal versus the concentration sampled in the submersion state at the 12th second of measuring procedure and in the emergence state at 35th second.
It can be seen in Figure 14 that the signal varies with the concentration in both states, but its dynamics is just the opposite than for previous example. Further experiments have shown that for constant concentration of water the formation of a drop and the dropping effect for various head submersion depth slightly but visible affects the measured signal. This leads us to the conclusion that, with the mixture examined, the light reflected from the almond suspension predominates over the optical signal reflected from the drop/air interface (boundary of the drop and the air).
According to previous example the light reflection intensity depends on a liquid drop dimensions that are correlated to density and surface tension of a liquid. In this case for purpose of identification of submersion and emergence head states influence, the architecture of the neural network was chosen to be as simple as possible, Figure 15.
The proposed network has two data inputs: submersion and emergence. The almost stable signals received at 12s and 35s are assumed to be the data pattern. The network has been trained to recognize the solutions with the concentrations: 0, 12.5, 25.0, 37.5, 50.0, 62.5, 75.0, 87.5 and 100%. The network answer is assumed to correspond to the soap concentration. Five independent data patterns determined for each solution concentration were used for the training process. The RMS error at the output, incurred in the training patterns, versus the tested data is 0.056. The correlation factor for all the network transfer functions is 0.93. The first hidden layer process gave 62.5% of the signal and the output layer gave 37.5%, so that additional layers are not necessary. The network and the trained weight factors wij and wwk are shown in Figure 15. The variation of the network output signal versus the inputs is shown in Figure 16. The average effect of inputs upon the output can be estimated to be 25% in the emergence and 75% in the submersion.
The network was tested 10 times using a solution composed of 20% of soap and 80% of water. The network has answered with absolute accuracy 0.1% and relative accuracy 0.5%. Further experiments and tests for example with mixtures 45% and 60% of water have confirmed that, proposed sensor achieved mentioned relative accuracy.
5. Summary
The design of the proposed intelligent sensor was concentrated on the fiber optic components and the method of signal processing. We used large-core polymer fibers, since they are elastic, can be plastically machined, and are resistant to the degradating effects of oils. The technique employed in designing of the optical path made of polymer light-guides appear to be effective. Using this technique, we developed and constructed the asymmetrical coupler and the head. During the simulation process, we observed that the optical parameters of the sub-assemblies depend strongly on their geometry. The coupler improved the power budget of the system and thereby the sensitivity of the sensor. The proposed construction of the sensor head is extremely simple. In addition, thanks to the large diameter of the fiber core, the sensor is resistant to endangerment during the head washing operation. Therefore, the sensor can be used for examining viscous liquids. The sensor takes about 40 seconds to collect the data and process them in the neural network. The data are collected during the head submerging, submersion, emerging and emergence from the examined medium. Presented time domain method for recognition of liquids and mixtures concentration gives more information about the liquid compared to that obtained from a static immersion of the head. Detection of liquids with similar refraction coefficients can be done when they differ in viscosity, surface tension, turbidity or rate of evaporation. The signal in emergence state is repeatable and can be use for improvement of liquid detection. The implementation of a neural network allows adopting of the elaborated construction to specific measurements. Thus, presented sensor is more accurate and universal. It can find applications e.g. in waste-water treatment plant. The analysed sensor model has passed two group of tests: first for identification of selected liquid and second for detection of mixture concentration. The concentration has been detected in by-chance tests with the relative accuracy of 0.5%.
References
- Marcou, J. Plastic optical fibers; John Wiley and Sons: New York, 1997. [Google Scholar]
- Polishuk, P. Automotive Fiber, Plastic optical fiber builds on MOST success. Laser Focus World 2006, 42, 57–60. [Google Scholar]
- López-Higuera, J.M.; Cobo, A.; Conde, O.M.; Lomer, M.; Madruga, F.J.; Quintela, M.; Quintela, A.; González, D. A.; Mirapeix, J.M.; García-Allende, P.B. Selected R&D results of PEG-UC and trends of Photonics Sensing Technology. Proc. of the Symposium on Photonics Technologies for 7th Framework Program, Wroclaw; 2006; pp. 72–77. [Google Scholar]
- Mignani, A.G.; Mencaglia, A.A.; Ciaccheri, L. Fiber optic system for colorimetry and scattered colorimetry. Proc. of SPIE Optical Fibers: Applications 2005. [Google Scholar]
- Borecki, M.; Kruszewski, J. Intelligent high resolution sensor for detecting of liquid mediums. Optica Applicata 2001, XXXI, 691–699. [Google Scholar]
- Novak, L.; Neuzil, P.; Pipper, J.; Zhang, Y.; Lee, S. An integrated fluorescence detection system for lab-on-a-chip applications. The Royal Society of Chemistry, Lab Chip 2007, 7, 27–29. [Google Scholar]
- Saleh Bahaa, E.A.; Teich, M.C. Fundamentals of Photonics; John Wiley & Sons: New York, Chichester, Brisbane, Toronto, Singapore, 1991. [Google Scholar]
- Klein, James E. Challenges and problems in nonsequential ray tracing. Proceedings of SPIE Novel Optical Systems Design and Optimization IV 2001. [Google Scholar]
- Borecki, M. Light behavior in polymer optical fiber bend – a new analysis method. Optica Applicata 2003, XXXIII, 191–204. [Google Scholar]
- Wilson, M.J.; Wang, R.K. A path-integral model of light scattered by turbid media. Journal of Physics B: Molecular and Optical Physics 2001, 34, 1453–1472. [Google Scholar]
- Kushkuley, A.; Rosenberg, S. Length function on parametric family of curves. In Latvian Math. Ezhegodnik; Riga, 1983; Volume 27, pp. 154–159. (in Russian) http://www.mathcad.com/library/LibraryContent/MathML/complex_splines.htm (in English). [Google Scholar]
- Curtis, F.G.; Wheatley, P.O. Applied Numerical Analysis, Fifth Edition ed; Addison Wesley Publishing: New York, 1994. [Google Scholar]
- Kruszewski, J.; Borecki, M.; Bebłowska, M. Designing and performance of the asymmetrical coupler of plastic optical fibers. In Proceedings of SPIE Lightguides and Their Applications II; 2004. [Google Scholar]
- Korwin-Pawlowski, M.L.; Dabek-Zlotorzynska, E.; Bock, W.J. Application of photonic band gap fibres in capillary electrophoresis systems. Proc. of SPIE Optical Fibers: Applications 2005. [Google Scholar]
- Bose Nirmal, K. Liang Ding, Neural network fundamentals with graphs, algorithms and applications; Mac Graw-Hill: New York, 1996. [Google Scholar]








| Liquid | Test sample no. | Output no. | |||||
|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | |||||
| Assumption | Answer | Assumption | Answer | Assumption | Answer | ||
| Domestic oil | 1 | 1 | 0.986 | 0 | 0.075 | 0 | -0.051 |
| 2 | 1.001 | 0.052 | -0.048 | ||||
| Water | 3 | 0 | 0.005 | 1 | 1.005 | 0 | -0.012 |
| 4 | 0.001 | 1.013 | -0.015 | ||||
| Alcohol | 5 | 0 | -0.008 | 0 | -0.011 | 1 | 1.016 |
| 6 | -0.007 | -0.012 | 1.016 | ||||
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Borecki, M. Intelligent Fiber Optic Sensor for Estimating the Concentration of a Mixture-Design and Working Principle. Sensors 2007, 7, 384-399. https://doi.org/10.3390/s7030384
Borecki M. Intelligent Fiber Optic Sensor for Estimating the Concentration of a Mixture-Design and Working Principle. Sensors. 2007; 7(3):384-399. https://doi.org/10.3390/s7030384
Chicago/Turabian StyleBorecki, Michal. 2007. "Intelligent Fiber Optic Sensor for Estimating the Concentration of a Mixture-Design and Working Principle" Sensors 7, no. 3: 384-399. https://doi.org/10.3390/s7030384




