Studying the Effect of Deposition Conditions on the Performance and Reliability of MEMS Gas Sensors
Abstract
:1. Introduction
2. Gas Sensor Case Study
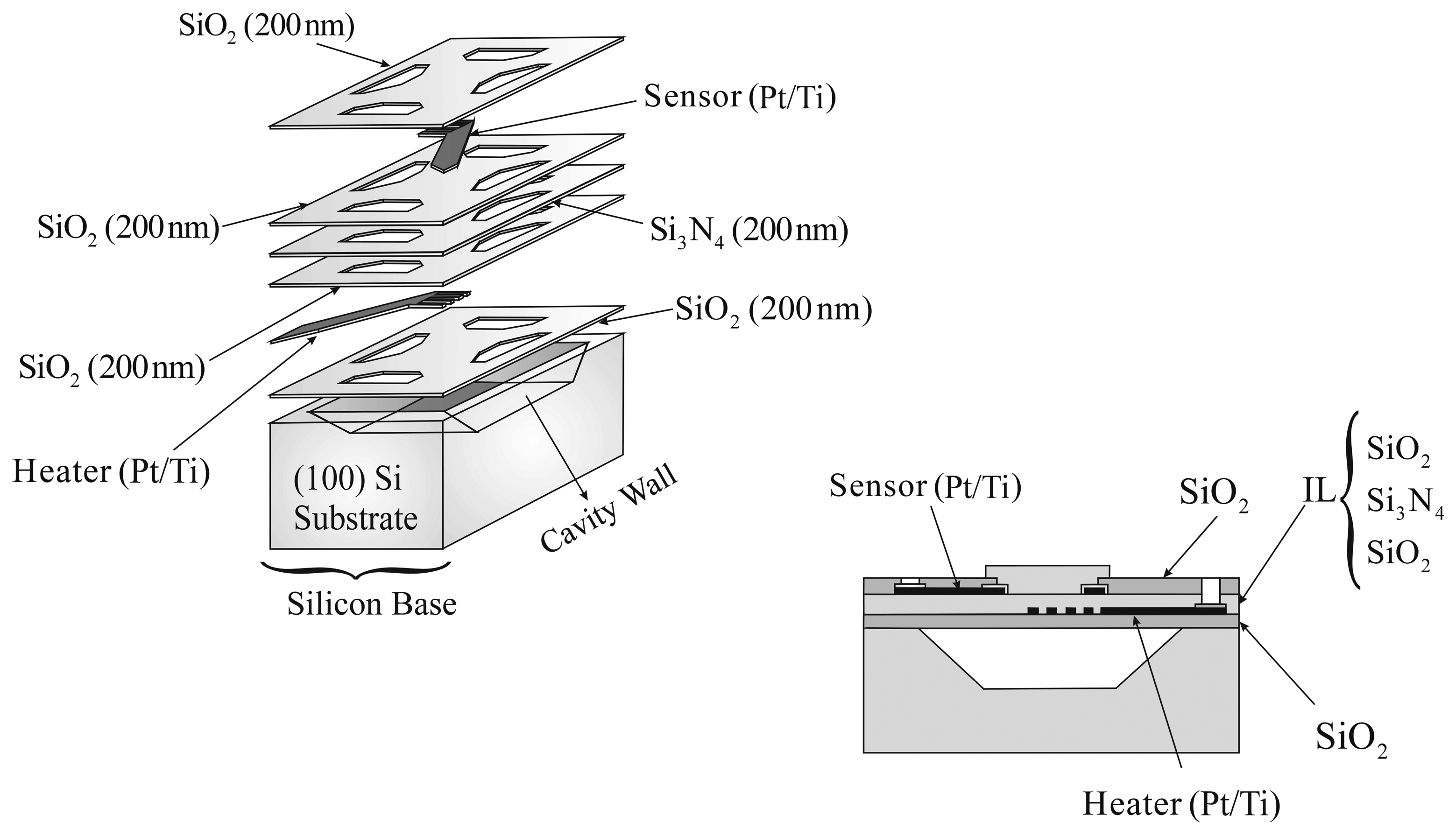
2.1 Device Description
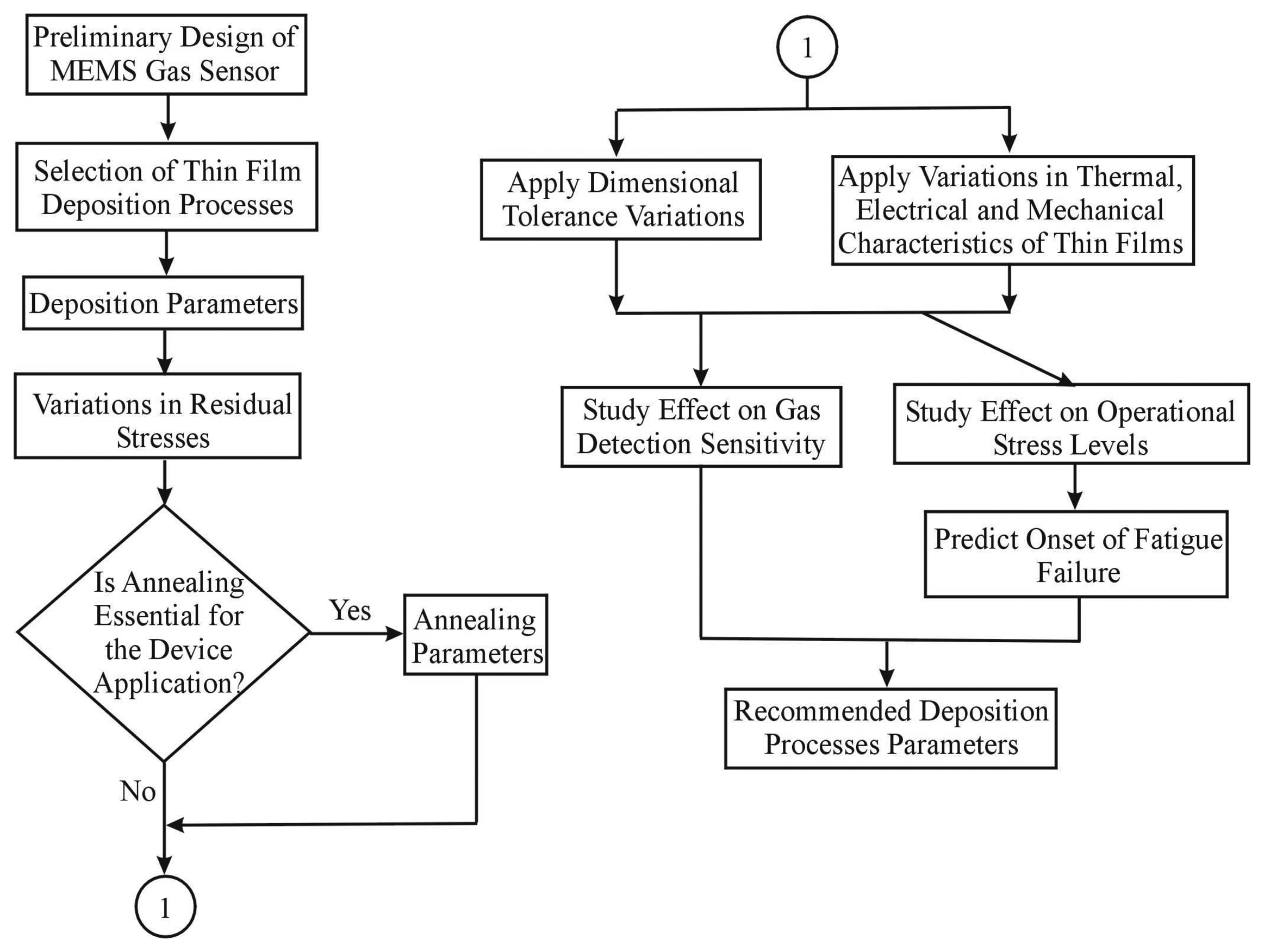
3. Design/Modeling Framework of the MEMS-Based Gas Sensor
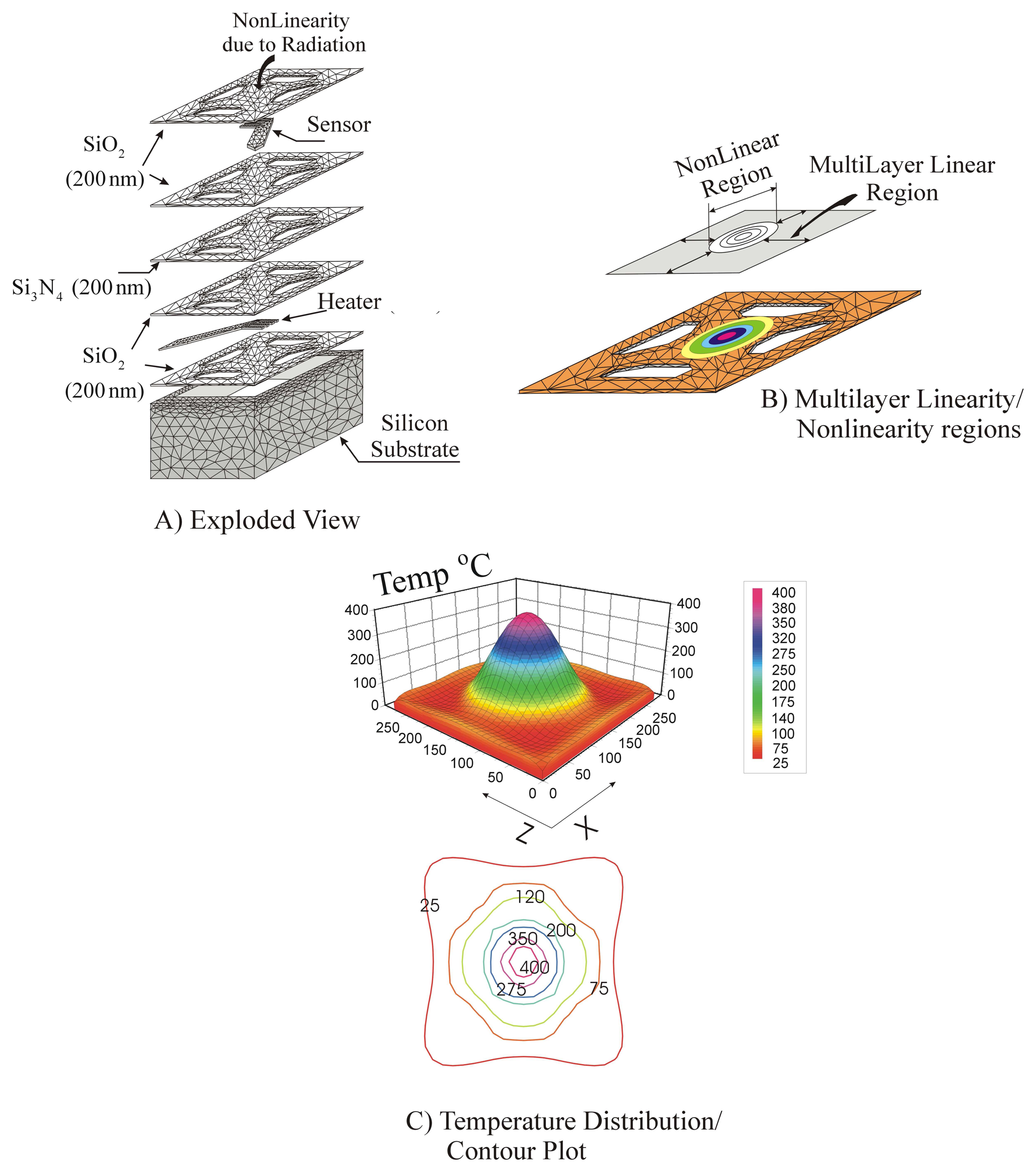
4. Thermal Fatigue Analysis of the MEMS-Based Gas Sensor
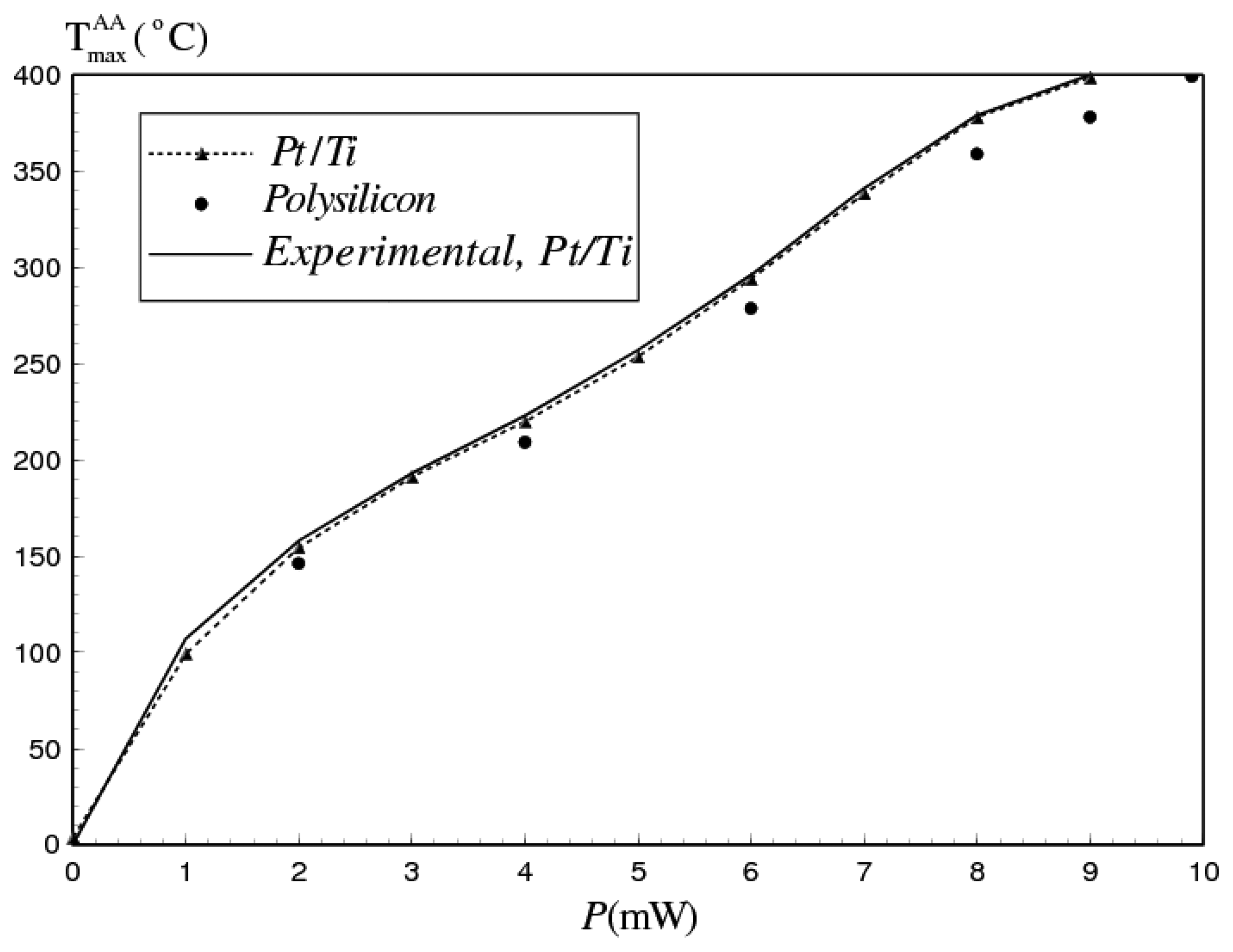
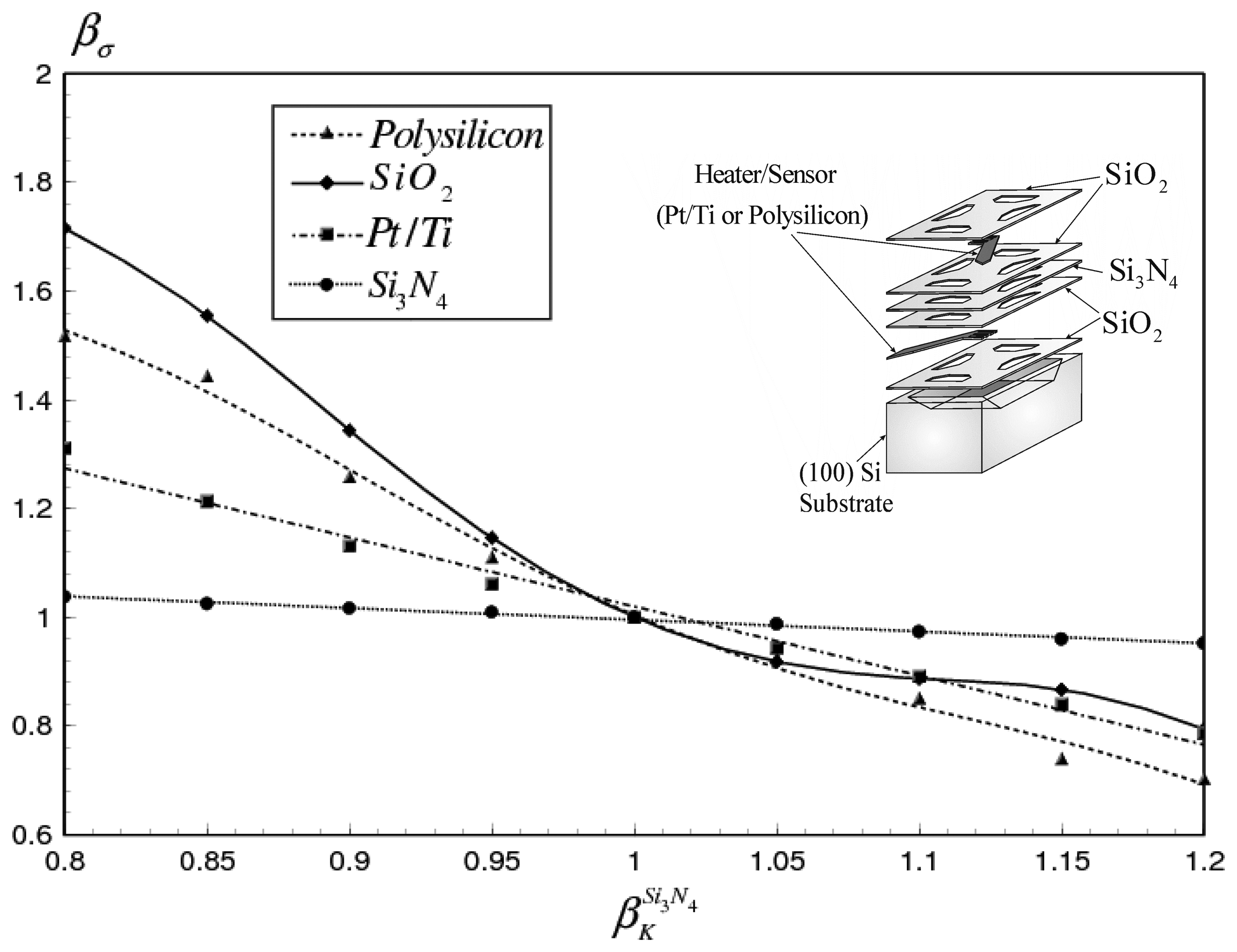
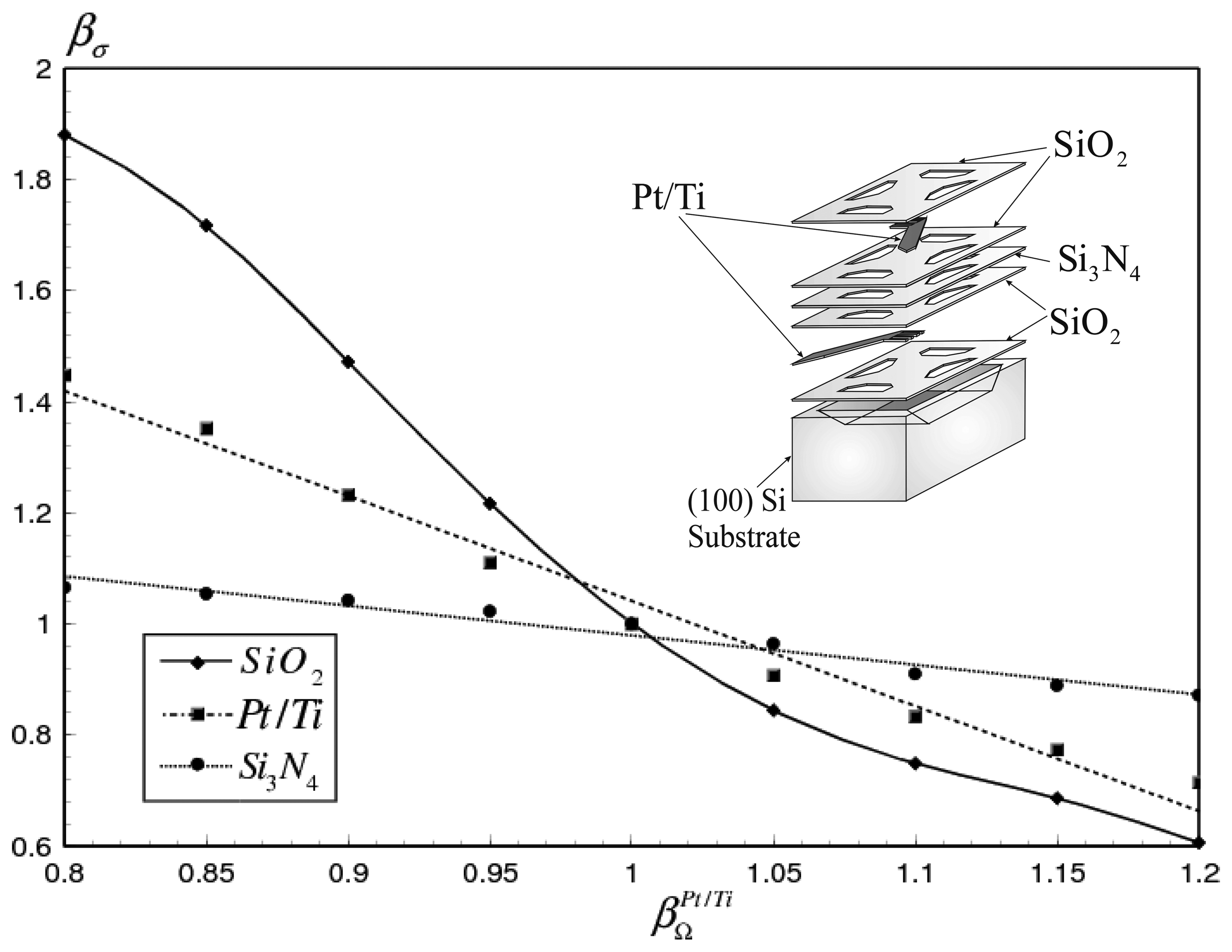
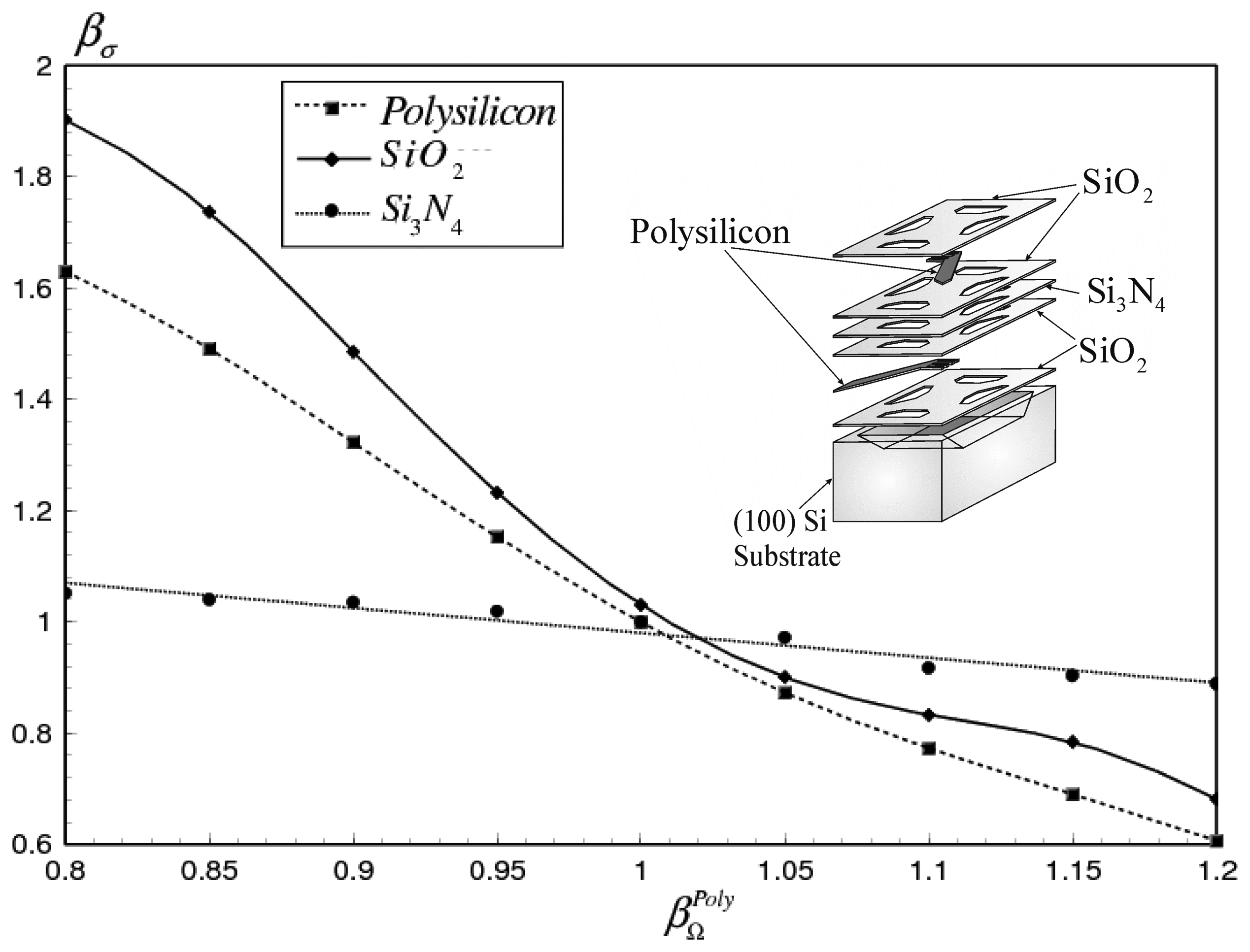
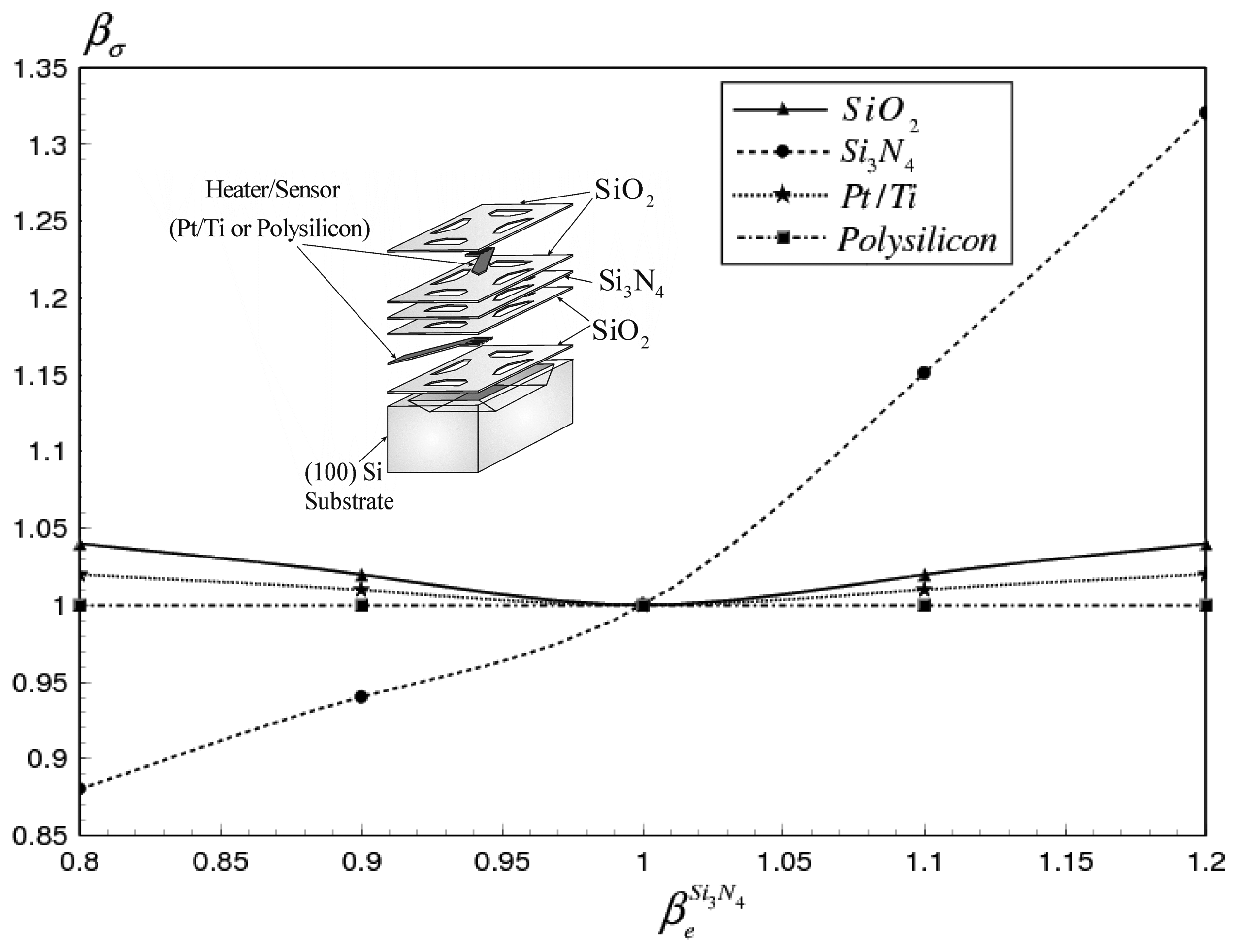
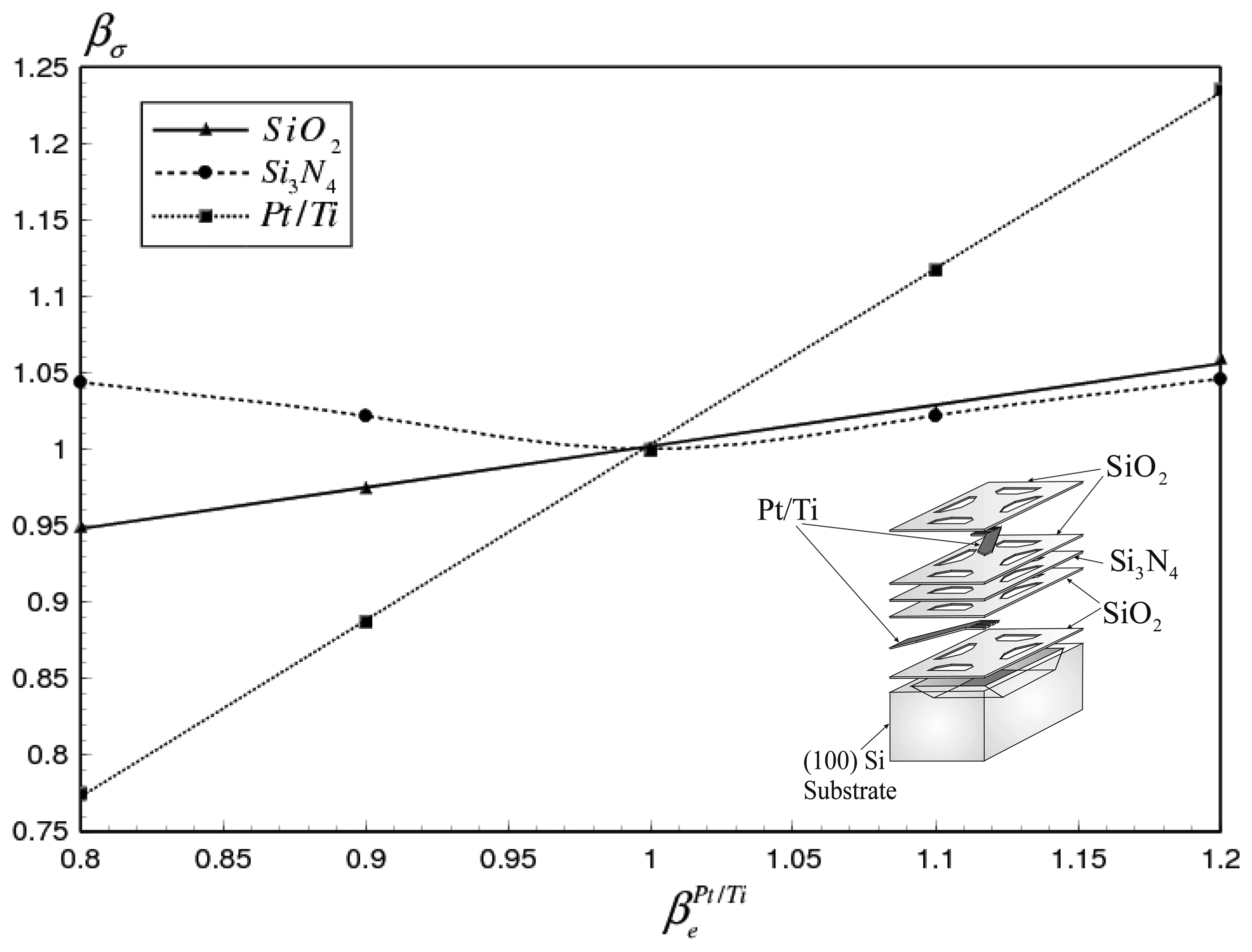
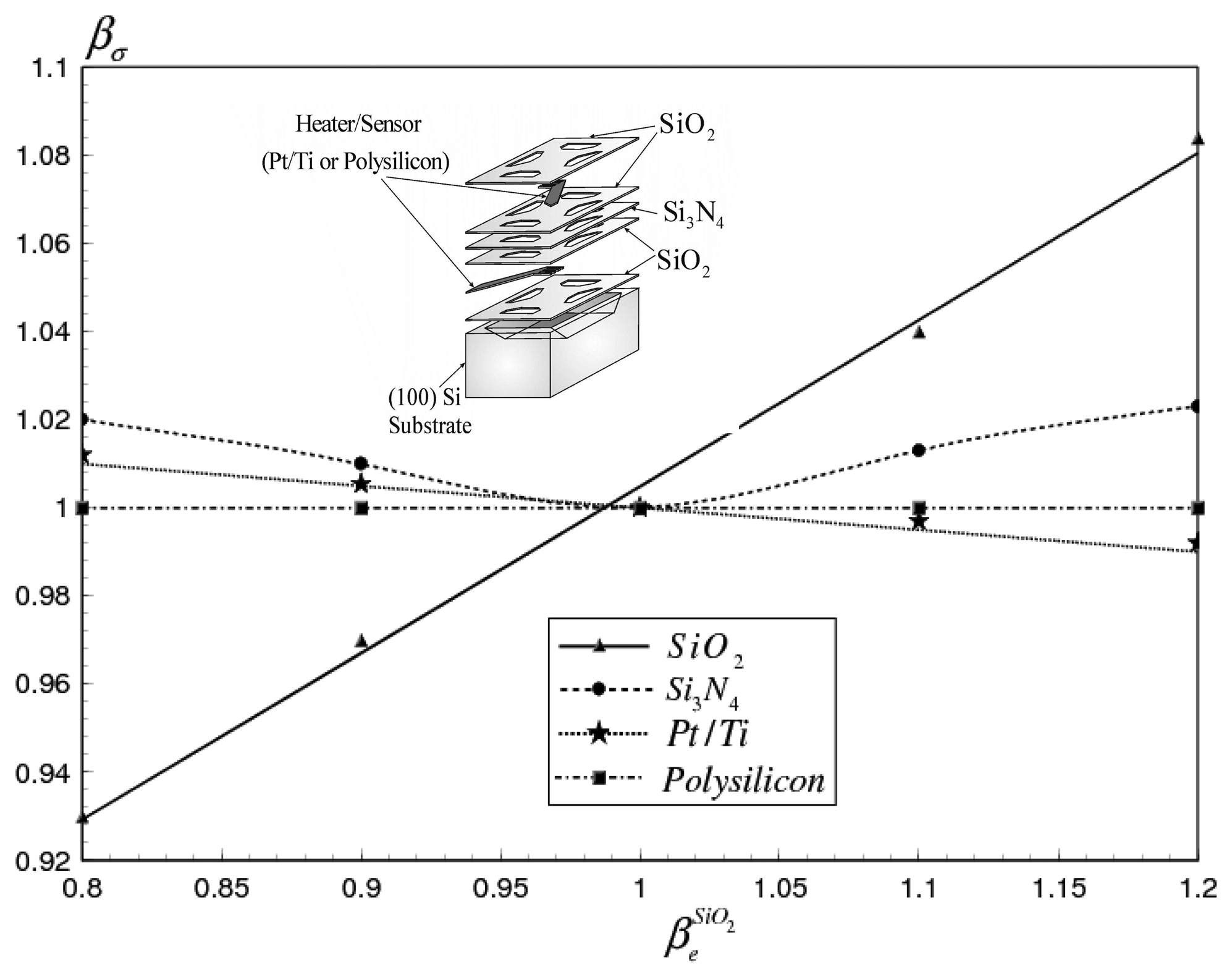
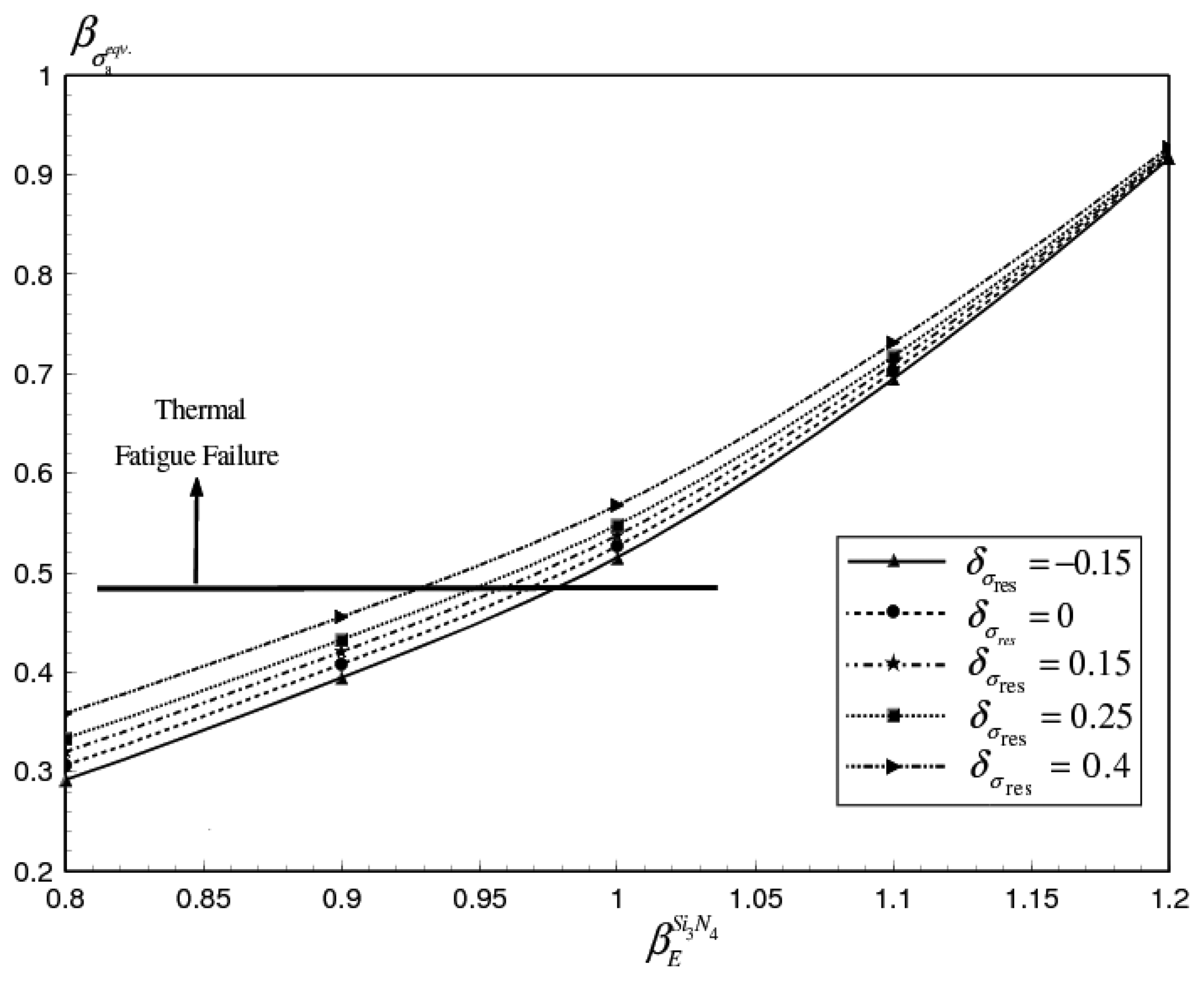
4.1. Maximum stress variation with the thermal, electrical and mechanical properties
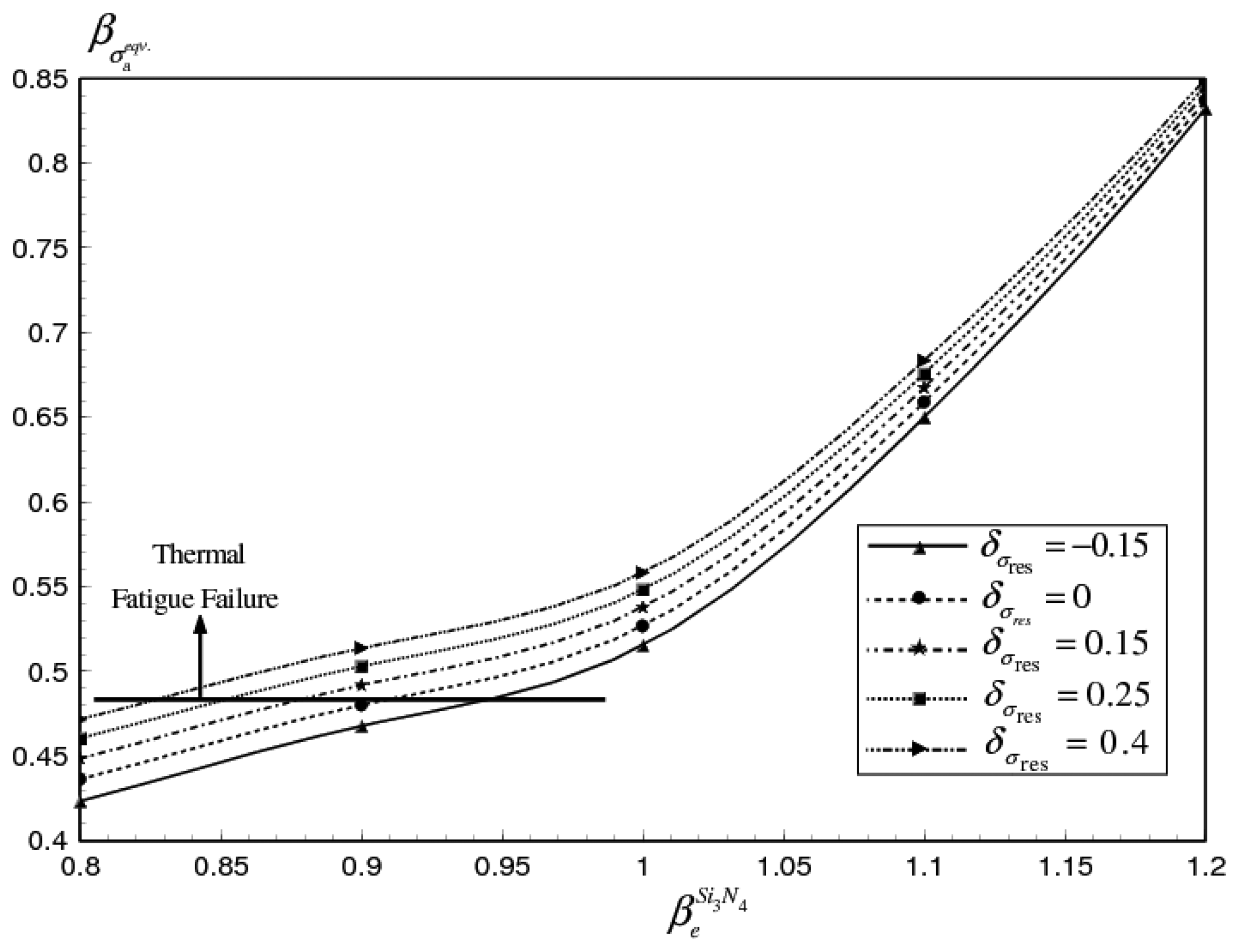
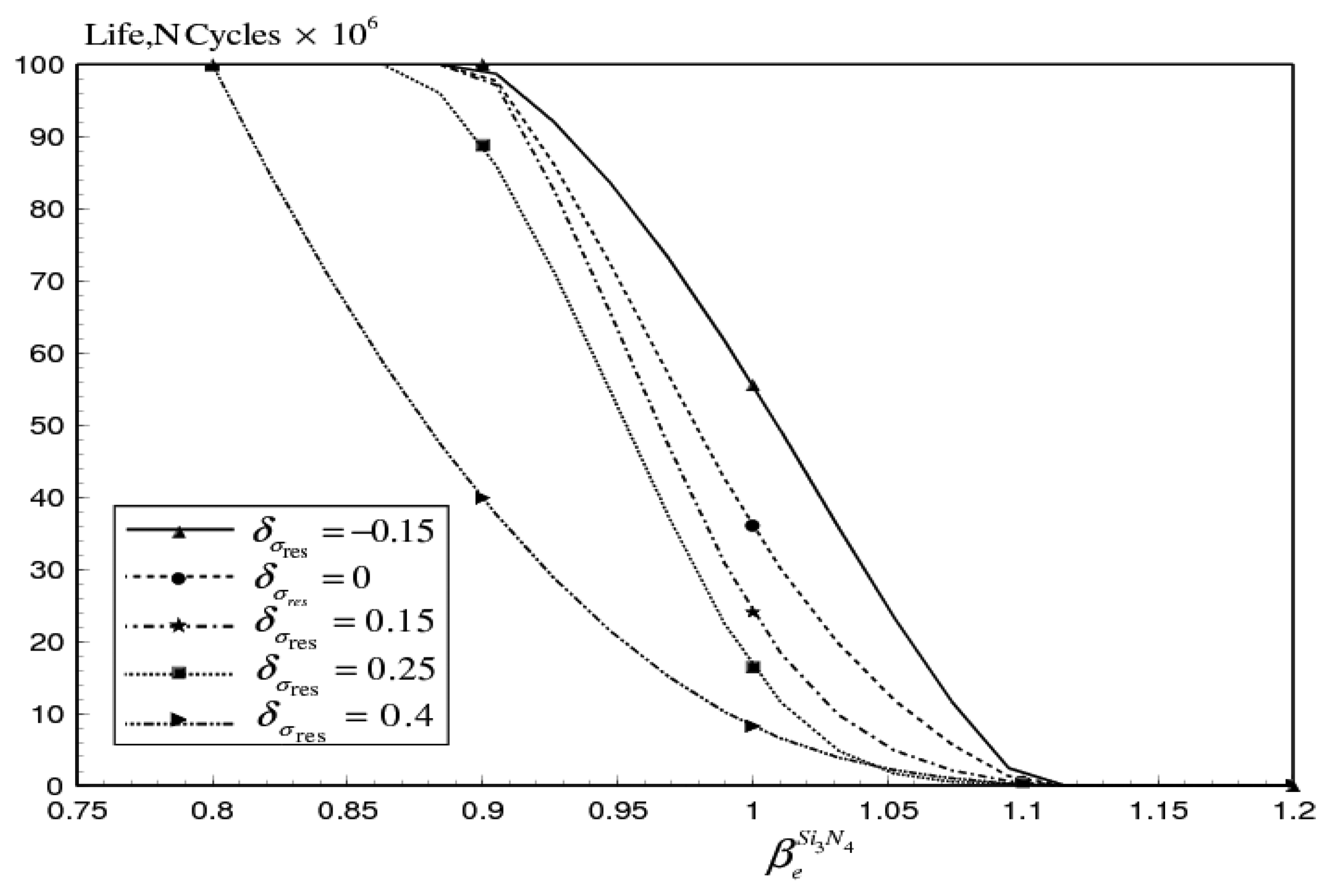
4.2 Fatigue life of the MEMS-based gas sensor
5. Conclusions
Acknowledgments
References
- Giridharan, M.G.; Stout, P.; Yang, H.Q.; Athavale, M.; Dionne, P.; Przekwas, A. Multi-Disciplinary CAD Systems for MEMS. Journal of Modeling and Simulations of Microsystems 2001, 2, 43–50. [Google Scholar]
- Judy, J.W. Microelectromechanical Systems (MEMS): Fabrication, Design and Applications. Smart Materials and Structures 2001, 10, 1115–1134. [Google Scholar]
- Lin, L.Y.; Goldstein, E.L. Opportunities and Challenges for MEMS in Lightwave Communications. IEEE Journal on Selected Topics in Quantum Electronics 2002, 8, 163–172. [Google Scholar]
- Sadek, K.; Moussa, W. Investigating the Effect of Deposition Variation on the Performance Sensitivity of Low-Power Gas Sensors. Sensors and Actuators B 2005, 107, 497–508. [Google Scholar]
- Chen, S.; Baughn, T.V.; Yao, Z. J.; Goldsmith, C.L. A New In Situ Residual Stress Measurement Method for a MEMS Thin Fixed-Fixed Beam Structure. Journal of Microelectromechanical Systems 2002, 11, 309–316. [Google Scholar]
- Doerner, M.; Nix, W. Stresses and Deformation Processes in Thin Films on Substrates. CRC Circuit. Rev. Solid States Material Science 1998, 14, 225–268. [Google Scholar]
- Stadtmueller, M. Mechanical Stress of CVD-Dielectrics. Journal of Electrochemical Society 1992, 139, 3269–3274. [Google Scholar]
- Belendez, T.; Neipp, C.; Belendez, A. Large and Small Deflections of a Cantilever Beam. European Journal of Physics 2002, 23, 371–379. [Google Scholar]
- Pamidighantam, S.; Puers, R.; Baert, K.; Tilmans, H.A.C. Pull-in Voltage Analysis of Electrostatically Actuated Beam Structures with Fixed-Fixed and Fixed-Free end conditions. Journal of Micromechanics and Microengineering 2002, 12, 458–464. [Google Scholar]
- Leplan, H.; Geenen, B.; Robic, J.Y.; Pauleau, Y. Residual Stresses in Evaporated Silicon Dioxide Thin Films: Correlation with Deposition Parameters and Aging Behavior. Journal of Applied Physics 1995, 78, 962–968. [Google Scholar]
- Wan, K.T.; Kogut, L. The Coupling Effect of Interfacial Adhesion and Tensile Residual Stress on a Thin Membrane Adhered to a Flat Punch. Journal of Micromechanics and Microengineering 2005, 15, 778–784. [Google Scholar]
- Mo, Y.; Okawa, Y.; Tajima, M.; Nakai, T.; Natukawa, K. Micro-machined Gas Sensor Array Based on Metal film Microheater. Sensors and Actuators B 2001, 79, 175–181. [Google Scholar]
- Paul, O.; Baltes, H. Thermal conductivity of CMOS Materials for the Optimization of Microsensors. Journal of Micromechanics and Microengineering 1993, 3, 110–112. [Google Scholar]
- Uma, S.; McConnell, A.D.; Asheghi, M.; Kurabayashi, K.; Goodson, K.E. Temperature-Dependent Thermal Conductivity of Undoped Polycrystalline Silicon Layers. International Journal of Thermophysics 2001, 22, 605–616. [Google Scholar]
- Pan, C.H. A Simple Method for Determining Linear Thermal Expansion Coefficients of Thin Films. Journal of Micromechanics and Microengineering 2002, 12, 548–555. [Google Scholar]
- Sharpe, W.N.; Turner, K.T.; Edwards, R.L. Tensile Testing of polysilicon. Experimental Mechanics 1999, 39, 162–170. [Google Scholar]
- Yi, T.; Kim, C.J. Measurement of Mechanical Properties for MEMS Materials. Measurement Science and Technology 1999, 10, 706–716. [Google Scholar]
- Sharpe, W.N.; Yaun, B.; Vaidyanathan, R. Measurements of Young's Modulus, Poisson's Ratio and Tensile Strength of polysilicon. Proceedings of the Tenth IEEE International Workshop on Microelectromechanical Systems, Nagoya, Japan; 1997; pp. 424–429. [Google Scholar]
- Denhoff, M.W. A Measurement of Young's Modulus and Residual Stress in MEMS Bridges using a Surface Profiler. Journal of Micromechanics and Microengineering 2003, 13, 686–692. [Google Scholar]
- Chaung, W.H.; Luger, T.; Fettig, R.K.; Ghodssi, R. Mechanical Property Characterization of LPCVD Silicon Nitride Thin Films at Cryogenic Temperatures. Journal of Microelectromechanical Systems 2004, 13, 870–879. [Google Scholar]
- Seok, S.; Lee, B.; Chun, K. A New Electrical Residual Stress Characterization Using Bent Beam Actuators. Journal of Micromechanics and Microengineering 2002, 12, 562–566. [Google Scholar]
- Min, Y.H.; Kim, Y.K. In Situ Measurement of Residual Stresses in Micromachined Thin films Using a Specimen with Composite-Layered Cantilevers. Journal of Micromechanics and Microengineering 2000, 10, 314–321. [Google Scholar]
- Kim, Y.J.; Allen, M.G. In Situ Measurement of Mechanical Properties of Polyimide Films Using Micromachined Resonant String Structures. IEEE Transactions on Components and Packaging Technology 1999, 22, 282–290. [Google Scholar]
- Madou, M. Fundamentals of Microfabrication; CRC Press LLC: USA, 1997. [Google Scholar]
- Noor, A.K.; Kamel, H.A.; Fulton, R.E. Substructuring Techniques Status and Projections. Computers & Structures 1978, 8, 621–632. [Google Scholar]
- Owen, D.R.; Goncalves, O.J.A. Substructuring Techniques in Material Non-Linear Analysis. Computers & Structures 1982, 15, 205–313. [Google Scholar]
- Thouless, M. D. Fracture Mechanics for Thin-Film Adhesion. IBM Journal of Resources Development 1994, 38, 367–377. [Google Scholar]
- Wrbanek, J.D.; Laster, K.L. Preparation and Analysis of Platinum Thin Films for High Temperature Sensor applications. NASA/TM-2005-213433 2005, 1–19. [Google Scholar]
- Branger, V.; Pelosin, V.; Badawi, K.F.; Goudeau, P. Study of Mechanical and Microstructural State of Platinum Thin Films. Thin solid Films 1996, 275, 22–24. [Google Scholar]
- Firebaugh, S. L.; Jensen, K.F.; Schmidt, M.A. Investigation of High-Temperature Degradation of Platinum Thin Films with an In Situ Resistance Measurement Apparatus. Journal of Microelectromechanical Systems 1998, 7, 128–135. [Google Scholar]
- Schneider, D.M.; Maibach, J.; Obermeier, E.; Schneider, D. Variations in Young's Modulus and Intrinsic Stress of LPCVD-Polysilicon due to High- Temperature Annealing. Journal of Micromechanics and Microengineering 1995, 5, 121–124. [Google Scholar]
- Muhlstein, C.L.; Ritchie, R.O. High-Cycle Fatigue of Micron-Scale Polycrystalline Silicon Films: Fracture Mechanics Analyses of the Role of Silica/Silicon Interface. International Journal of Fracture 2003, 119/120, 449–474. [Google Scholar]
- Mönig, R.; Keller, R.R.; Volkert, C.A. Thermal Fatigue Testing of Thin Metal Films. Review of Scientific Instruments 2004, 75, 4997–5004. [Google Scholar]
- Gad El Hak, M. The MEMS Handbook.; CRC Press: USA, 2001. [Google Scholar]
- Stark, B. MEMS Reliability Assurance Guidelines for Space Applications. JPL Publication, 99-1, USA 1999. [Google Scholar]
- Srikar, V.T.; Spearing, S.M. Materials Selection in Micromechanical Design: An Application of the Ashby Approach. Journal of Microelectromechanical Systems 2003, 12, 3–10. [Google Scholar]
- Biggs, T.; Taylor, S. S.; Van der Lingen, E. The Hardening of Platinum Alloys for Potential Jewellery Application. Platinum Metals Review 2005, 49, 2–15. [Google Scholar]
- Puigcorbé, J.; Vogel, D.; Michel, B.; Vilà, A.; Gràcia, I.; Cané, C. High Temperature Degradation of Pt/Ti Electrodes in Micro-Hotplate Gas Sensors. Journal of Micromechanics and Microengineering 2003, 13, 119–124. [Google Scholar]



| Coefficient of Thermal expansion (α) (°C-1) | Young's Modulus (E) (GPa) | Residual Stresses (σres) (GPa) | Major Contributing Deposition Parameters | |
|---|---|---|---|---|
| SiO2 | 7×10−6 ±18% | 75 ± 7.8 | −0.3 → 0.3 | f (p,T) |
| Si3N4 | 3.3×10−6 ±18% | 310 ± 32 | −0.2 → 0.8 | f (T, G) |
| Pt/Ti | 0.97×10−5 ±18% | 140 ± 16 | 0.2 → 0.9 | f (DR) |
| Polysilicon | 2.7×10−6 ±18% | 162 ± 14 | −0.4 →0.3 | f (p,T) |
| σNmax (MPa) | σNmax/Sut | |
|---|---|---|
| SiO2 | 343 | < 0.3 |
| Si3N4 | 265 | ∼ 0.7 |
| Pt/Ti | 478 | ∼ 2 |
| Polysilicon | 341 | ∼0.08 |
| Equation | Material | ao | a1 | RMS |
|---|---|---|---|---|
| 2 | Si3N4 | 1.21 | -0.22 | 0.02 |
| 2 | Pt/Ti | 2.3 | -1.27 | 0.04 |
| 4 | Si3N4 | 1.51 | -0.53 | 0.02 |
| 4 | Pt/Ti | 2.93 | -1.90 | 0.05 |
| 6 | Si3N4 | 1.43 | -0.45 | 0.02 |
| 9 | Pt/Ti | -0.15 | 1.15 | 0.001 |
| 9 | Polysilicon | 0.78 | 0.23 | 0.001 |
| 9 | SiO2 | 0.62 | 0.38 | 0.005 |
| 10 | Si3N4 | -0.68 | 1.7 | 0.05 |
| 10 | SiO2 | -0.002 | 1.001 | 0.02 |
| 10 | Pt/Ti | -0.005 | 1.002 | 0.01 |
| Equation | Material | bo | b1 | b2 | b3 | b4 | RMS |
|---|---|---|---|---|---|---|---|
| 3 | SiO2 | -155.3 | -660 | -1019.5 | 690 | -172.4 | 0.02 |
| 3 | Polysilicon | -72.1 | 307.21 | -470.81 | 314.5 | -77.8 | 0.04 |
| 5 | SiO2 | -162 | 674.1 | -1020.4 | 674.9 | -165 | 0.001 |
| 7 | SiO2 | -199.2 | 833.6 | -1247.7 | 852.7 | -211.4 | 0.001 |
| 7 | Polysilicon | -59.3 | 254.24 | -386.8 | 255.1 | -62.2 | 0.001 |
| 8 | Si3N4 | -46 | 192 | -292.6 | 196.4 | -48.7 | 0.002 |
© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Sadek, K.; Moussa, W. Studying the Effect of Deposition Conditions on the Performance and Reliability of MEMS Gas Sensors. Sensors 2007, 7, 319-340. https://doi.org/10.3390/s7030319
Sadek K, Moussa W. Studying the Effect of Deposition Conditions on the Performance and Reliability of MEMS Gas Sensors. Sensors. 2007; 7(3):319-340. https://doi.org/10.3390/s7030319
Chicago/Turabian StyleSadek, Khaled, and Walied Moussa. 2007. "Studying the Effect of Deposition Conditions on the Performance and Reliability of MEMS Gas Sensors" Sensors 7, no. 3: 319-340. https://doi.org/10.3390/s7030319




