Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest
Abstract
:1. Introduction
2. Methodology
2.1. Definition of EVI and NDVI
2.2. Non-Lambertian model for topographic effect
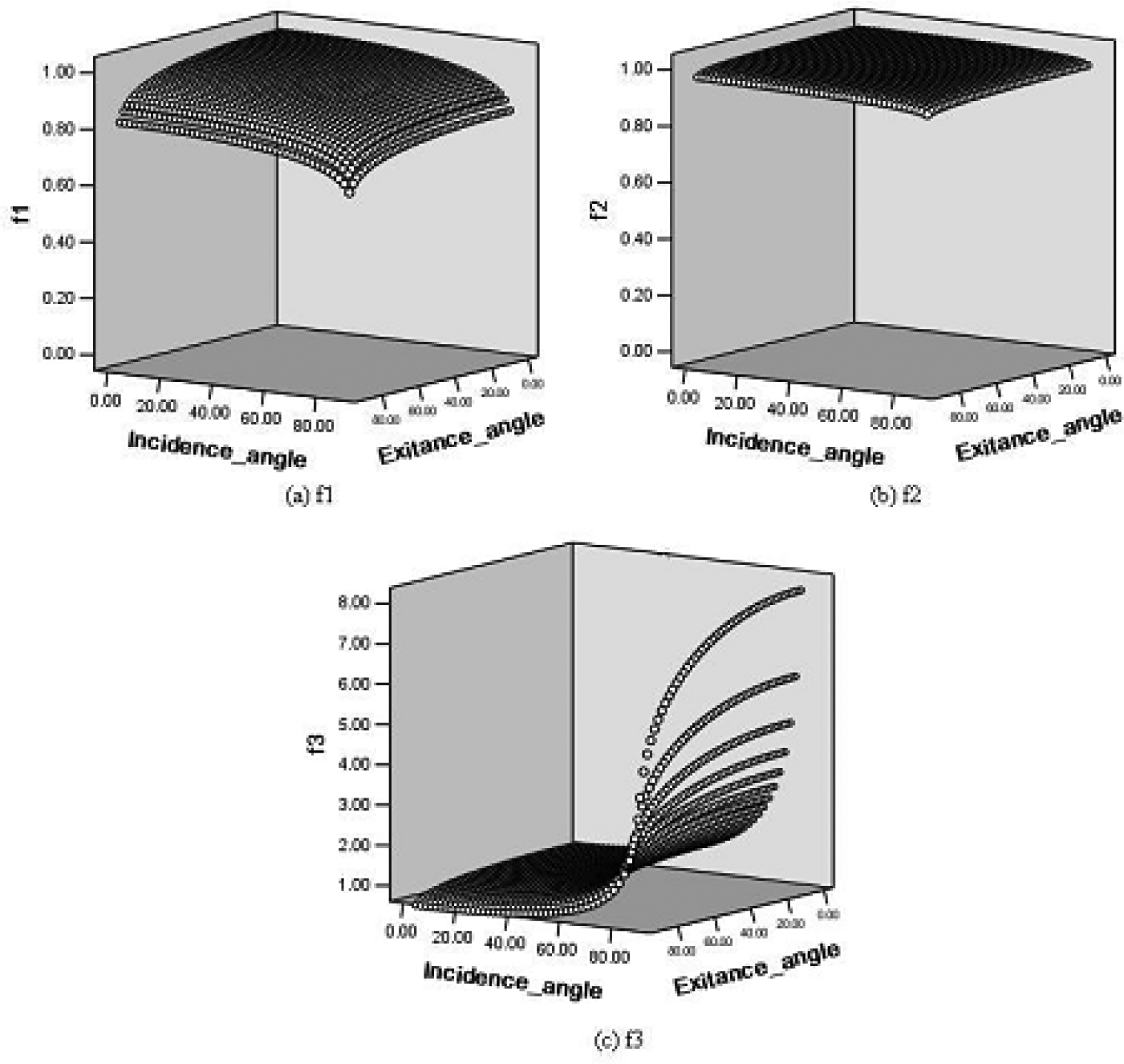
3. Theoretical analysis of topographic effects on EVI and NDVI
4. A case study for testing topographic effects on EVI and NDVI
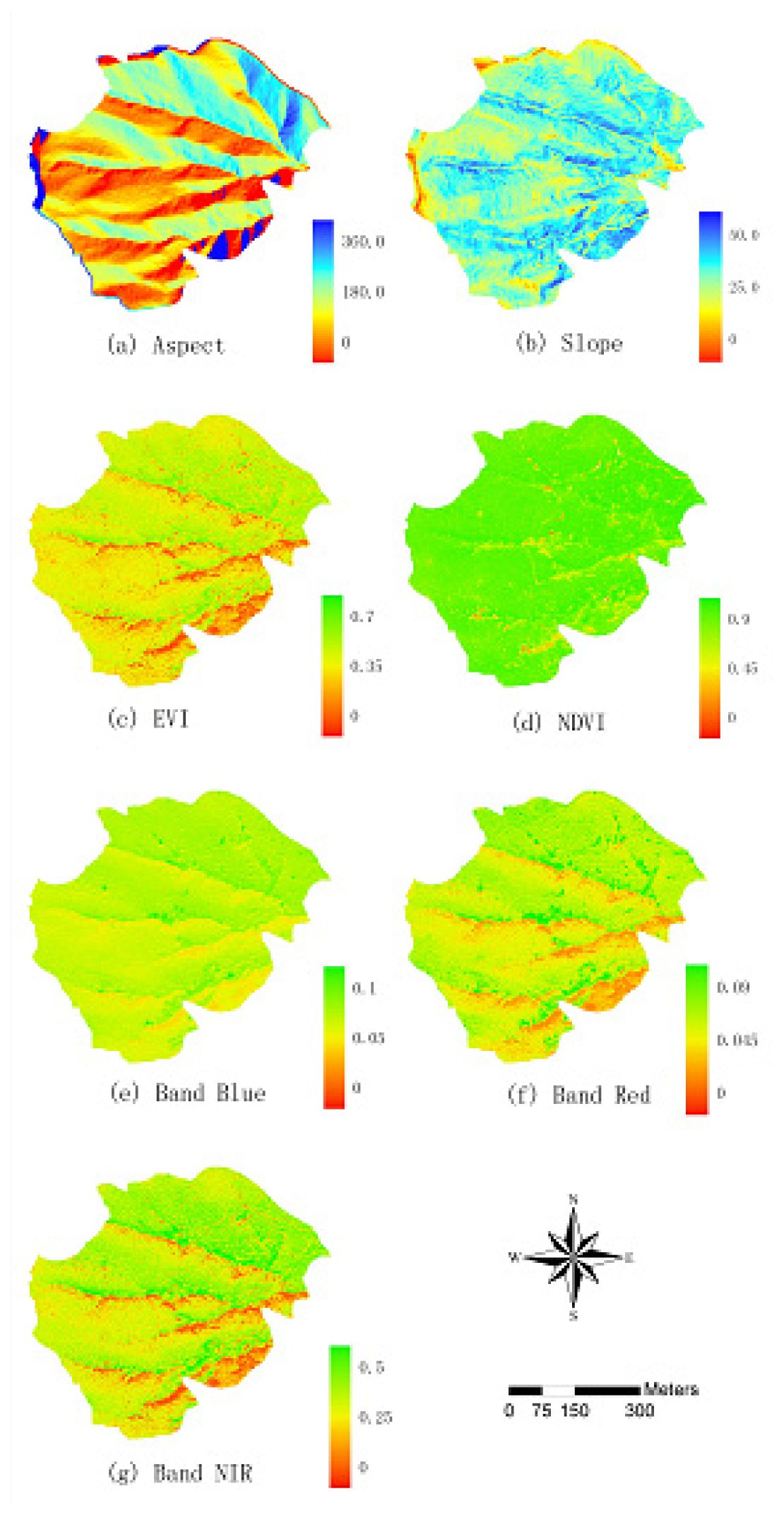
4.1. Study area and data processing
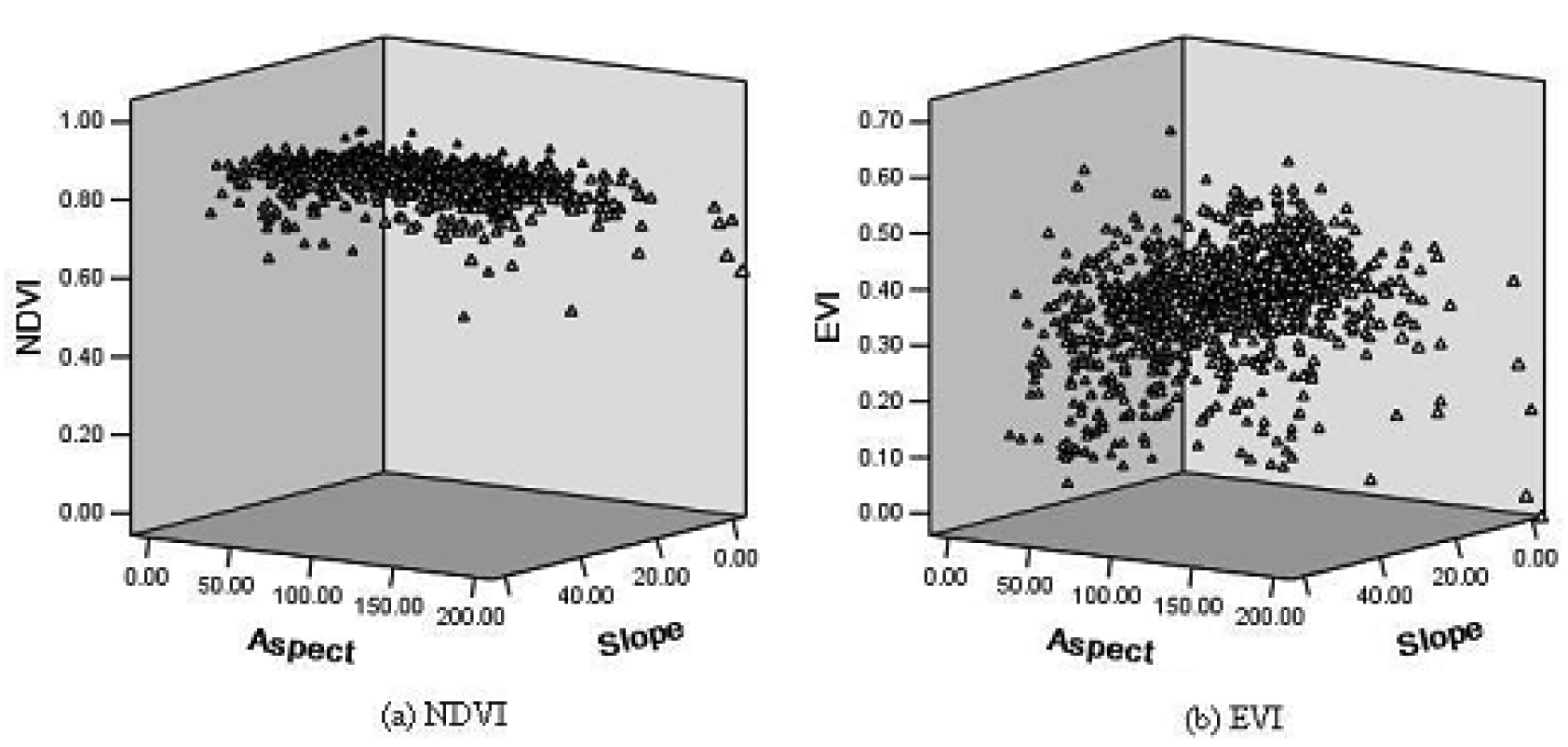
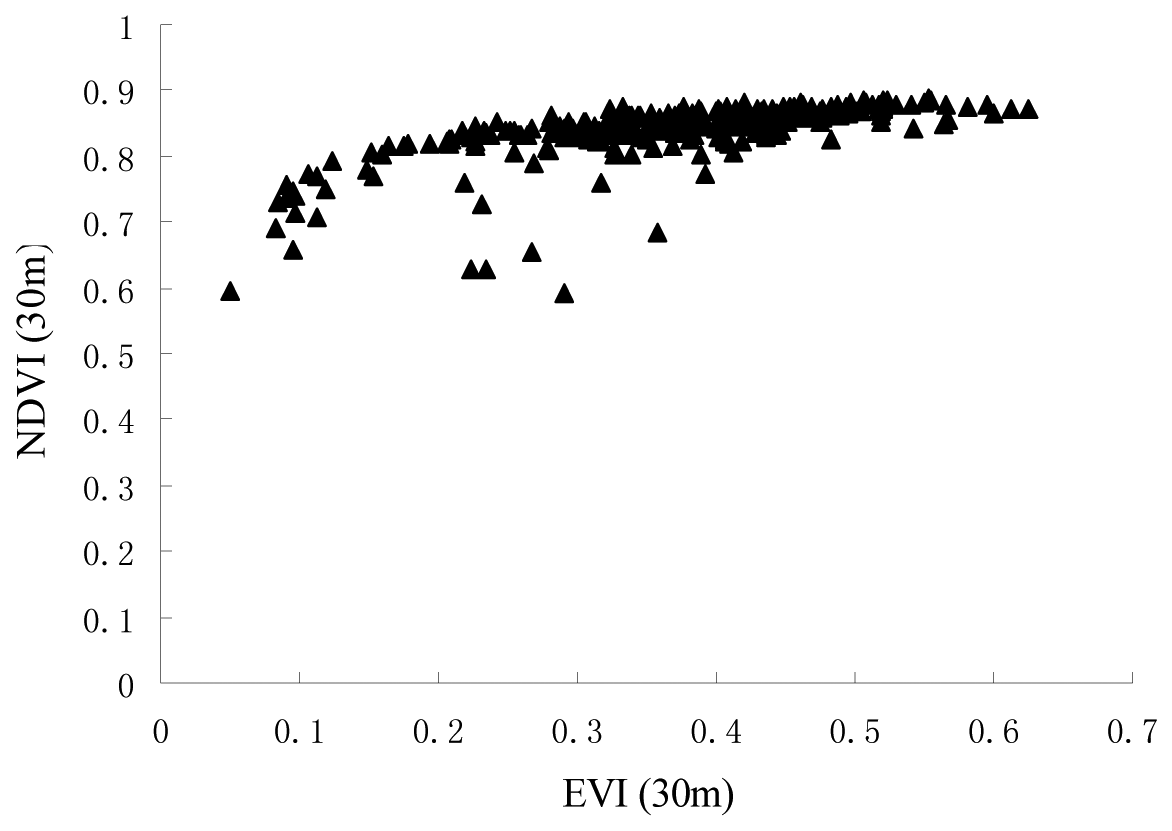
4.2. Results
5. Conclusions
Acknowledgments
References and Notes
- Huete, A.R.; Justice, C. MODIS vegetation index (MOD13) algorithm theoretical basis document. Ver. 3 1999. [Google Scholar]
- Liu, H.Q.; Huete, A.R. A feedback based modification of the NDV I to minimize canopy background and atmospheric noise. IEEE Transactions on Geoscience and Remote Sensing 1995, 33, 457–465. [Google Scholar]
- Gao, B.C. NDWI - A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sensing of Environment 1996, 58, 257–266. [Google Scholar]
- Soudani, K.; Francois, C.; le Maire, G.; Le Dantec, V.; Dufrene, E. Comparative analysis of IKONOS, SPOT, and ETM+ data for leaf area index estimation in temperate coniferous and deciduous forest stands. Remote Sensing of Environment 2006, 102, 161–175. [Google Scholar]
- Nagler, P.L.; Scott, R.L.; Westenburg, C.; Cleverly, J.R.; Glenn, E.P.; Huete, A.R. Evapotranspiration on western US rivers estimated using the Enhanced Vegetation Index from MODIS and data from eddy covariance and Bowen ratio flux towers. Remote Sensing of Environment 2005, 97, 337–351. [Google Scholar]
- Boles, S.H.; Xiao, X.M.; Liu, J.Y.; Zhang, Q.Y.; Munkhtuya, S.; Chen, S.Q.; Ojima, D. Land cover characterization of Temperate East Asia using multi-temporal VEGETATION sensor data. Remote Sensing of Environment 2004, 90, 477–489. [Google Scholar]
- Xiao, X.; Zhang, Q.; Braswell, B.; Urbanski, S.; Boles, S.; Wofsy, S.; Moore, B.; Ojima, D. Modeling gross primary production of temperate deciduous broadleaf forest using satellite images and climate data. Remote Sensing of Environment 2004, 91, 256–270. [Google Scholar]
- Waring, R.H.; Coops, N.C.; Fan, W.; Nightingale, J.M. MODIS enhanced vegetation index predicts tree species richness across forested ecoregions in the contiguous USA. Remote Sensing of Environment 2006, 103, 218–226. [Google Scholar]
- Holben, B.N.; Justice, C.O. An examination of spectral band ratioing to reduce the topographic effect on remotely sensed data. International Journal of Remote Sensing 1981, 2, 115–133. [Google Scholar]
- Smith, J.A.; Tzeu, L.L.; Ranson, K.J. The Lambertian Assumption and Landsat Data. Photogrammetric Engineering and Remote Sensing 1980, 46, 1183–1189. [Google Scholar]
- Meyer, P.; Itten, K.I.; Kellenberger, T.; Sandmeier, S.; Sandmeier, R. Radiometric corrections of topographically induced effects on Landsat TM data in an alpine environment. ISPRS Journal of Photogrammetry and Remote Sensing 1993, 48, 17–28. [Google Scholar]
- Trotter, C.M. Characterising the topographic effect at red wavelengths using juvenile conifer canopies. International Journal of Remote Sensing 1998, 19, 2215–2221. [Google Scholar]
- Dymond, J.R.; Shepherd, J.D. Correction of the topographic effect in remote sensing. IEEE Transactions on Geoscience and Remote Sensing 1999, 37(2), 2618–2620. [Google Scholar]
- Lee, T.Y.; Kaufman, Y.J. Non-lambertian effects on remote sensing of surface reflectance and vegetation index. IEEE Transactions on Geoscience and Remote Sensing 1986, 24, 699–707. [Google Scholar]
- Minnaert, M. The Reciprocity Principle in Lunar Photometry. Astrophys Journal 1941, 93, 403–410. [Google Scholar]
- Minnaert, M. The Solar System; Kuiper, G.P., Ed.; University of Chicago Press: Chicago, IL, 1961; Volume 3, pp. 213–249. [Google Scholar]
- Huete, A.R.; Liu, H.Q.; Batchily, K.; YanLeeuwen, W. A comparison of vegetation indices global set of TM images for EOS-MODIS. Remote Sensing of Environment 1997, 59, 440–451. [Google Scholar]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation system in the great plains with ERTS. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium; Greenbelt, USA; NASASP-351, 1974; pp. 3010–3017. [Google Scholar]
- Fukuyama, T.; Takenaka, C. Upward mobilization of 137Cs in surface soils of Chamaecyparis obtusa Sieb. Et Zucc. (hinoki) plantation in Japan. The Science of the Total Environment 2004, 318, 187–195. [Google Scholar]
- Onda, Y.; Tsujimura, M.; Nonoda, T.; Takenaka, C. Methods for measuring infiltration rate in forest floor in Hinoki plantations. J. Japan Soc. Hydrol. & Water Resour 2005, 18. [Google Scholar]
- Hattori, S.; Abe, T.; Kobayashi, C.; Tamai, K. Effect of forest floor coverage on reduction of soil erosion in hinoki plantations. Bull. For. Prod. Res. Inst 1992, 362, 1–34, (in Japanese, with English summary).. [Google Scholar]
- Matsushita, B.; Onda, Y.; Xu, M.; Toyota, M. Detecting forest degradation in Kochi, Japan: Combining in situ field measurements with remote sensing techniques. In IEEE International Geoscience and Remote Sensing Symposium; 2005; 3WE095A_29; pp. 1–4. [Google Scholar]
- Mäkisara, K.; Meinander, M.; Rantasuo, M.; Okkonen, J.; Aikio, M.; Sipola, K.; Pylkkö, P.; Braam, B. Airborne imaging spectrometer for applications (AISA). In IGARSS Digest; Tokyo; IGARSS, 1993; pp. 479–481. [Google Scholar]
- Mäkisara, K.; AISA Data User's Guide. Technical Research Centre of Finland. Research Note 1894 1998, 1–54. [Google Scholar]
- Roberts, D.A.; Green, R.O.; Adams, J.B. Temporal and spatial patterns in vegetation and atmospheric properties from AVIRIS. Remote Sensing of Environment 1997, 62, 223–240. [Google Scholar]
- Justice, C.O.; Wharton, S.W.; Holben, B.N. Application of digital terrain data to quantify and reduce the topographic effect on Landsat Data. International Journal of Remote Sensing 1981, 2, 213–230. [Google Scholar]
- Carpenter, G.A.; Gopal, S.; Macomber, S.; Martens, S.; Woodcock, C.E. A Neural Network Method for Mixture Estimation for Vegetation Mapping. Remote Sensing of Environment 1999, 70, 139–152. [Google Scholar]
- Baret, F.; Guyot, G. Potentials and limits of vegetation indices for LAI and APAR assessment. Remote Sensing of Environment 1991, 35, 161–173. [Google Scholar]
- Huete, A.R. A soil adjusted vegetation index (SAVI). Remote sensing of Environment 1988, 25, 295–309. [Google Scholar]

© 2007 by MDPI ( http://www.mdpi.org). Reproduction is permitted for noncommercial purposes.
Share and Cite
Matsushita, B.; Yang, W.; Chen, J.; Onda, Y.; Qiu, G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest. Sensors 2007, 7, 2636-2651. https://doi.org/10.3390/s7112636
Matsushita B, Yang W, Chen J, Onda Y, Qiu G. Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest. Sensors. 2007; 7(11):2636-2651. https://doi.org/10.3390/s7112636
Chicago/Turabian StyleMatsushita, Bunkei, Wei Yang, Jin Chen, Yuyichi Onda, and Guoyu Qiu. 2007. "Sensitivity of the Enhanced Vegetation Index (EVI) and Normalized Difference Vegetation Index (NDVI) to Topographic Effects: A Case Study in High-density Cypress Forest" Sensors 7, no. 11: 2636-2651. https://doi.org/10.3390/s7112636



