A Multi-Model Combined Filter with Dual Uncertainties for Data Fusion of MEMS Gyro Array
Abstract
:1. Introduction
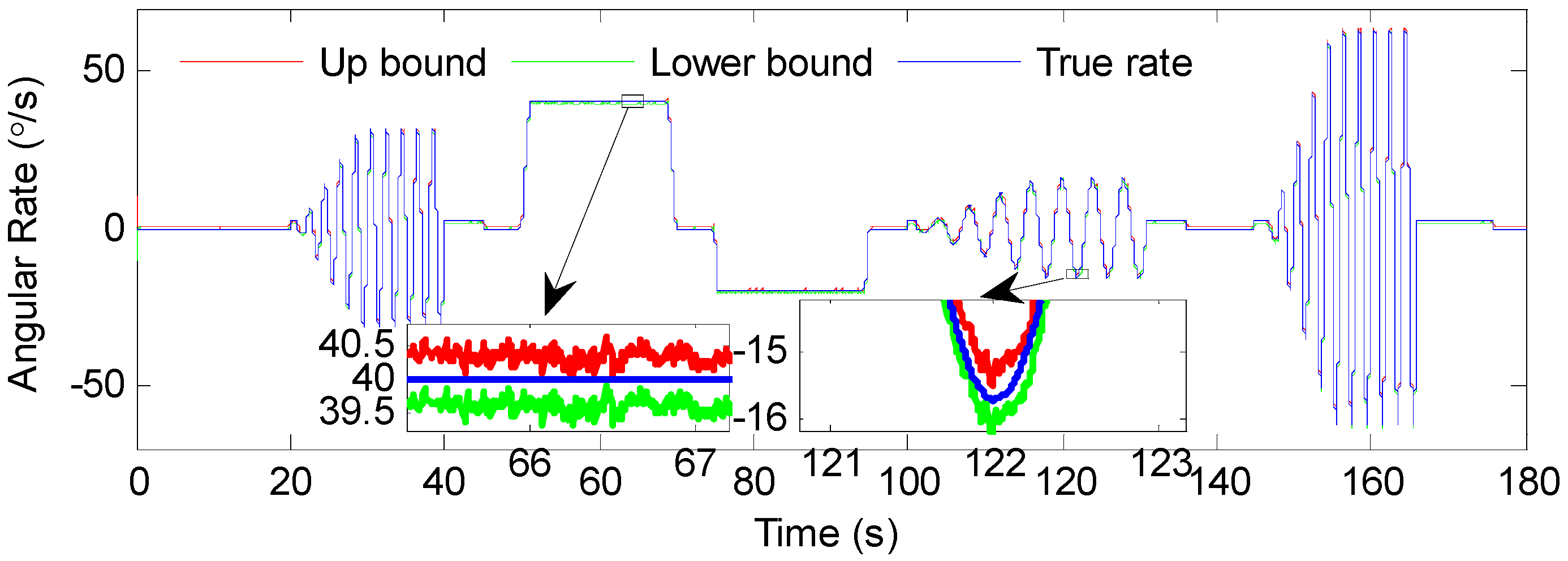
2. The Dual Uncertainties Model of a Gyro Array
3. Ellipsoidal Set and Relevant Properties
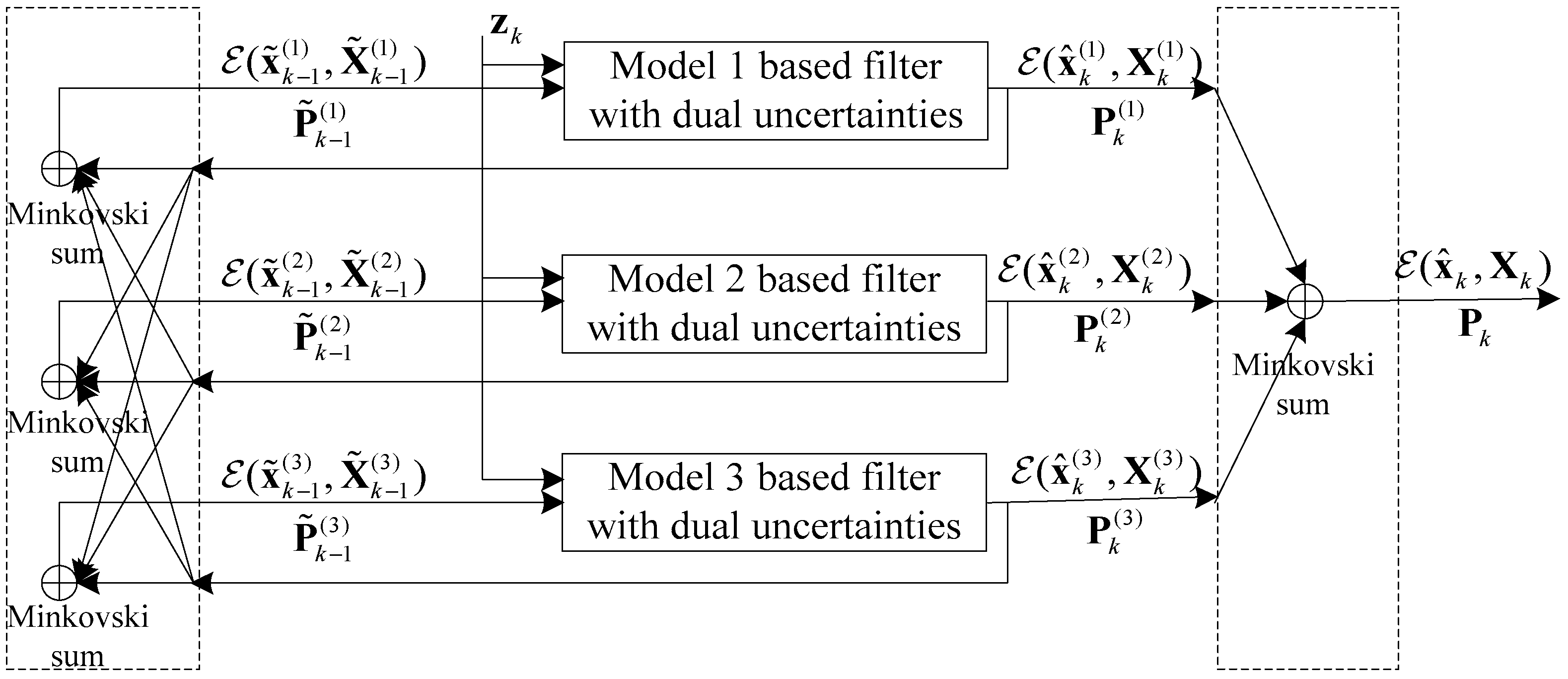
4. Multi-Model Combined Filtering with Dual Uncertainties (MMCF)
4.1. Model-Conditioned Reinitialization
4.2. Model-Conditioned Filtering
4.3. Mode Probability Update
4.4. Estimation Fusion
5. Experiments and Results
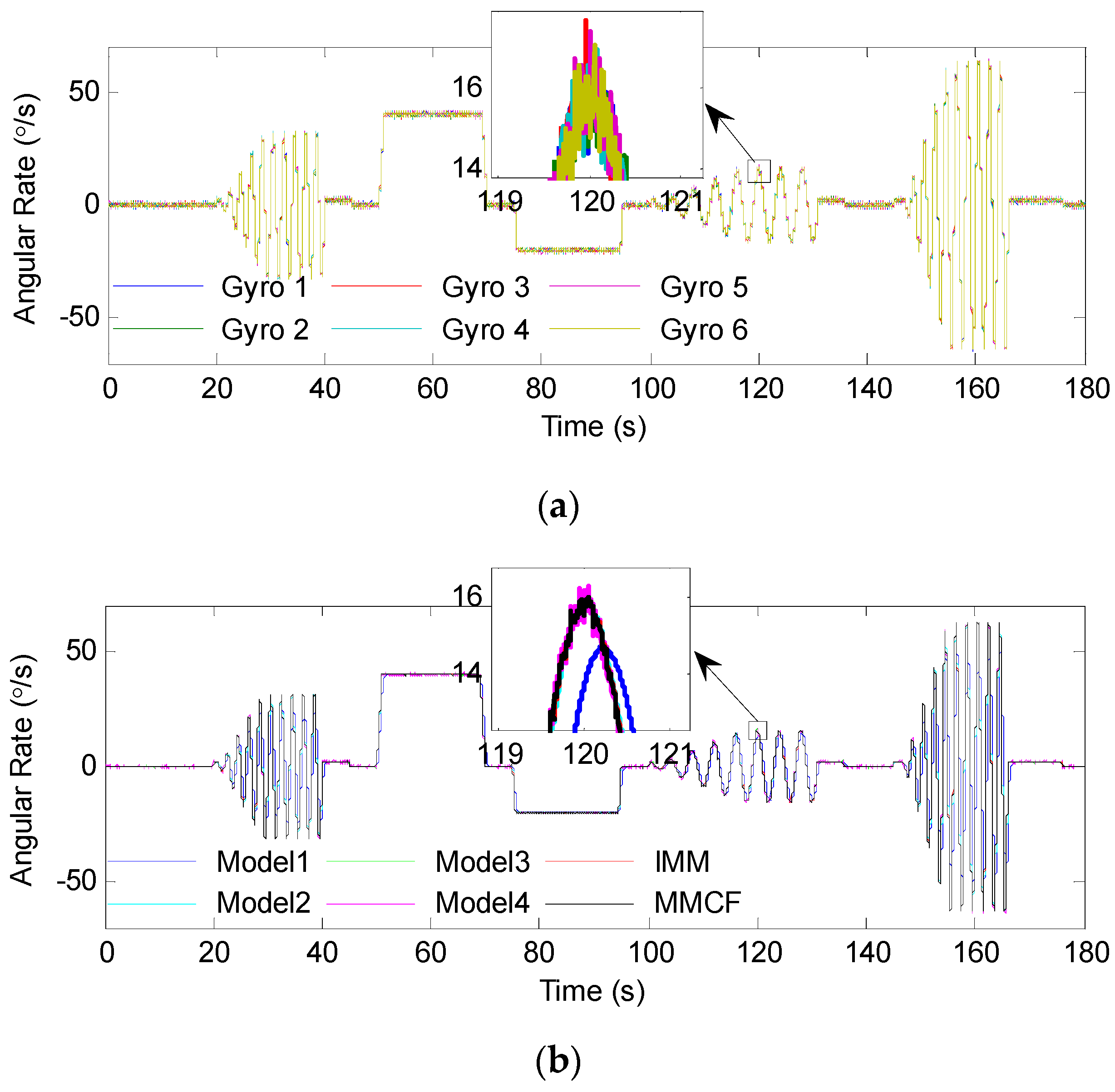
5.1. Experimental Setup
- 15–40 s: Swing with 10° angle amplitude and 0.5 Hz frequency;
- 45–65 s: Rotate with a 40°/s constant rate;
- 70–90 s: Rotate with a −20°/s constant rate;
- 100–136 s: Swing with 10° angle amplitude and 0.25 Hz frequency;
- 145–172 s: Swing with 20° angle amplitude and 0.5 Hz frequency.
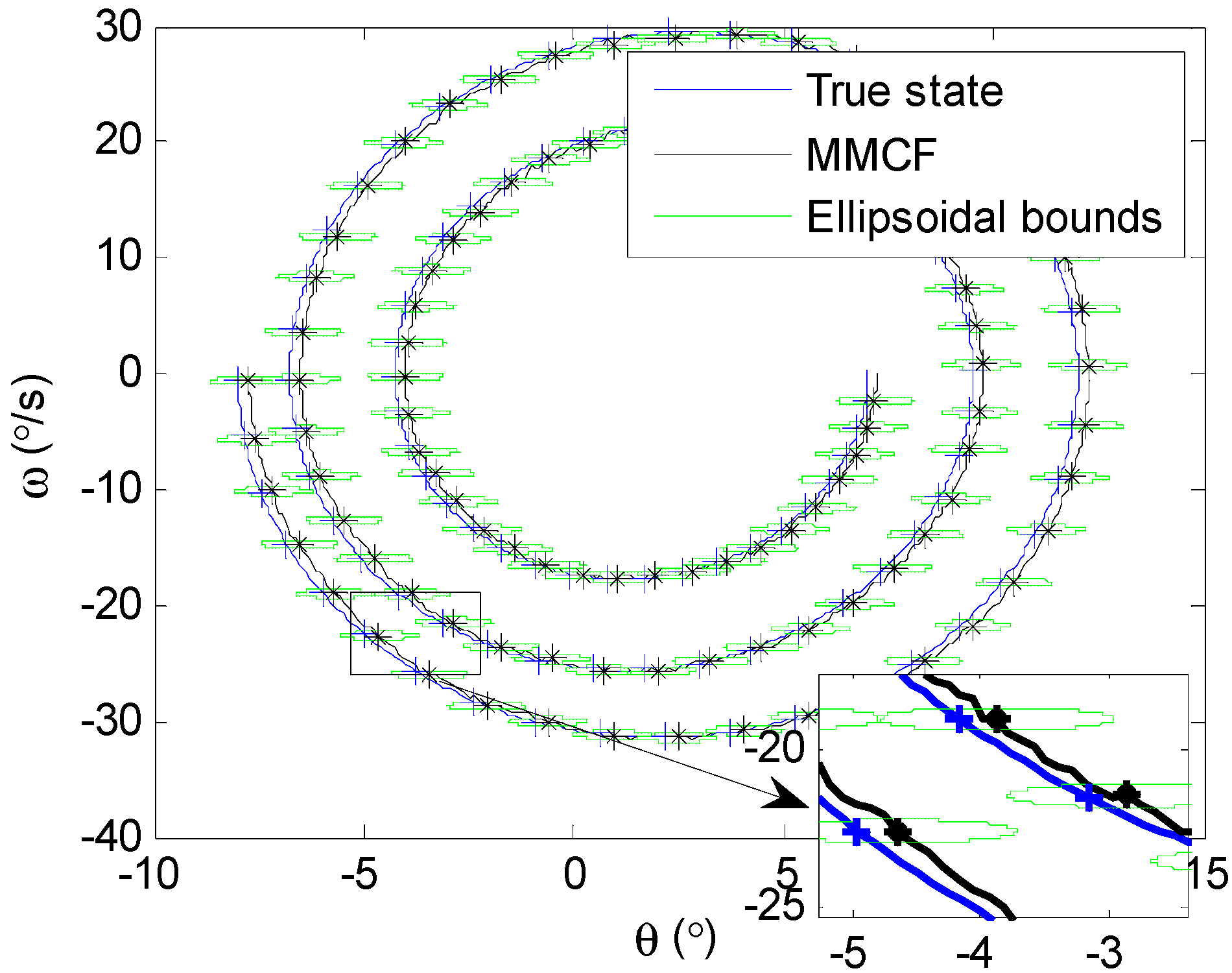
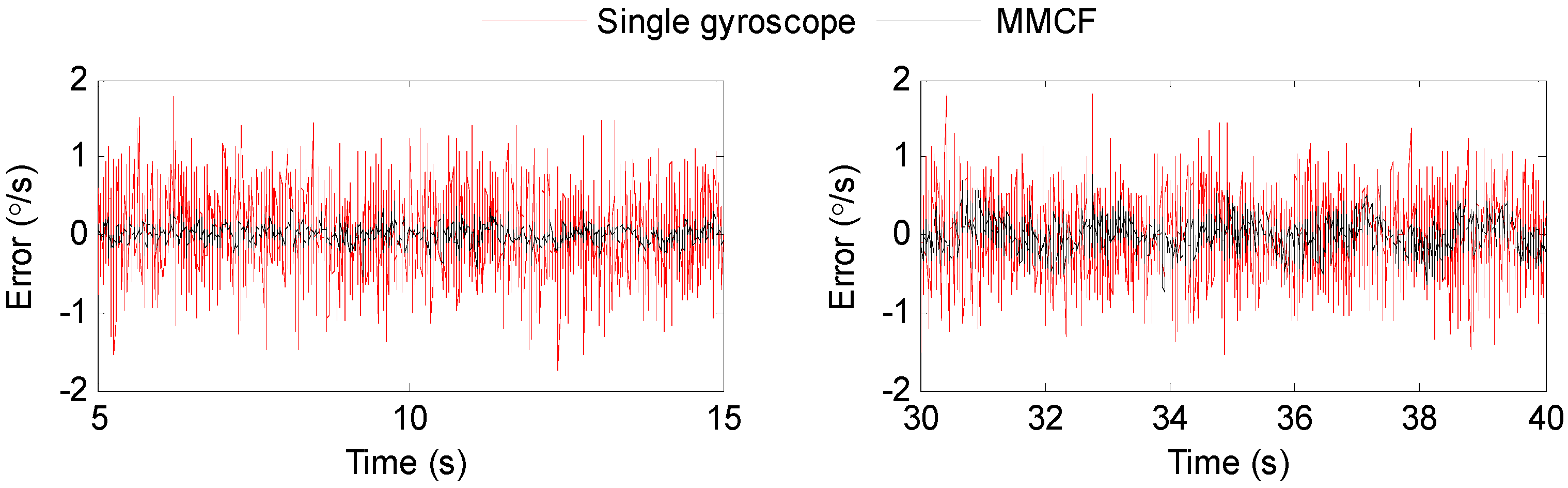
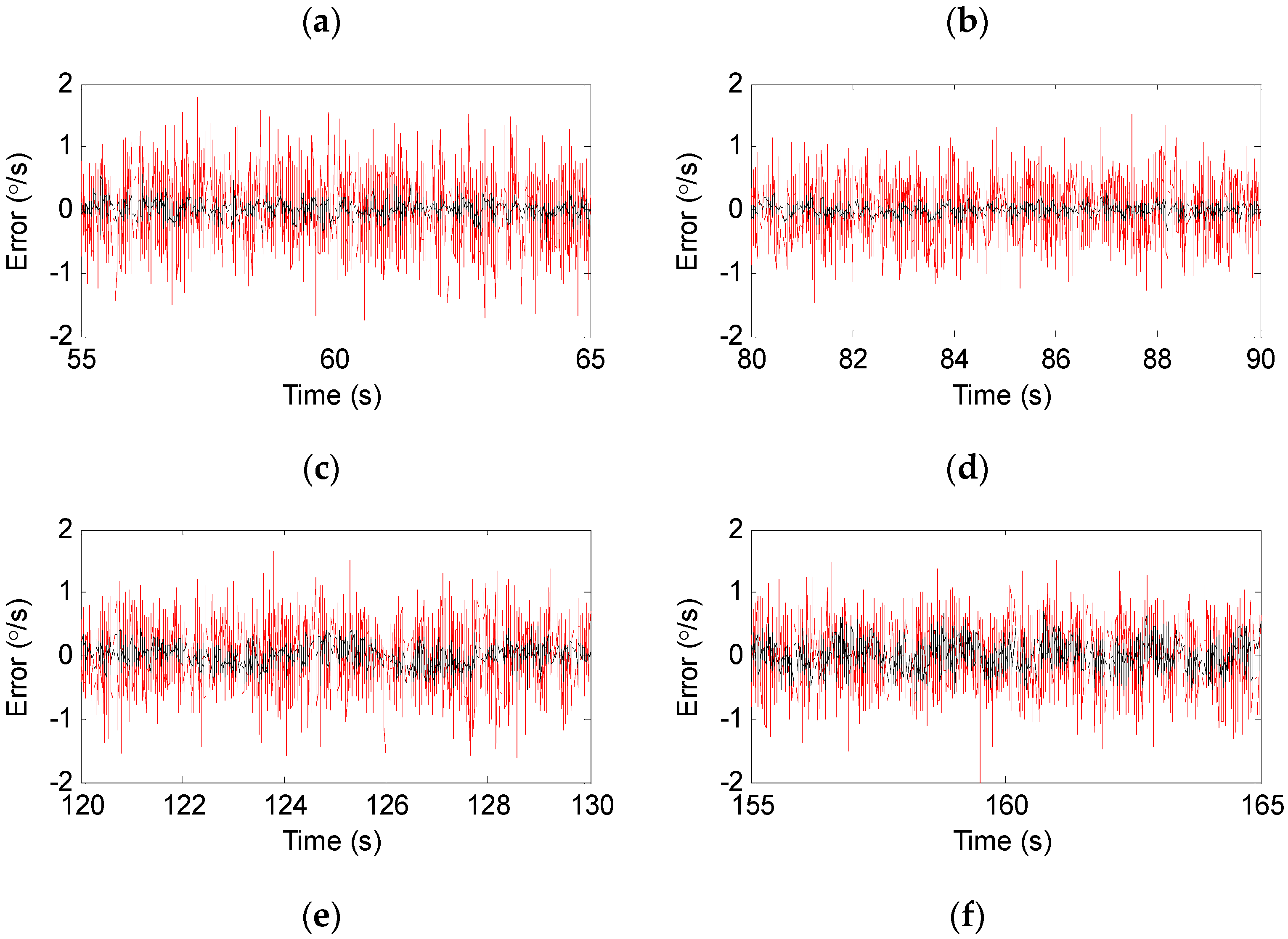
5.2. Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yang, C.; Tang, S.; Tavassolian, N. Utilizing gyroscopes towards the automatic annotation of seismocardiograms. IEEE Sens. J. 2017, 17, 2129–2136. [Google Scholar] [CrossRef]
- Li, Y.; Georgy, J.; Niu, X.; EI-Sheimy, N. Autonomous calibration of MEMS gyros in consumer portable devices. IEEE Sens. J. 2015, 15, 4062–4072. [Google Scholar] [CrossRef]
- Passaro, V.M.N.; Cuccovillo, A.; Vaiani, L.; Campanella, C.E. Gyroscope technology and applications: A review in the industrial perspective. Sensors 2017, 17, 2284. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Yang, J.; Tang, J.; Liu, J.; Cao, H. Note: Parallel processing algorithm of temperature and noise error for micro-electro-mechanical system gyroscope based on variational mode decomposition and augmented nonlinear differentiator. Rev. Sci. Instrum. 2018, 89, 076107. [Google Scholar] [CrossRef] [PubMed]
- Shen, C.; Song, R.; Li, J.; Zhang, X.; Tang, J.; Shi, Y.; Liu, J.; Cao, H. Temperature drift modeling of MEMS gyroscope based on genetic-Elman neural network. Mech. Syst. Signal Pr. 2016, 72–73, 897–905. [Google Scholar]
- Norouzpour-Shirazi, A.; Ayazi, F. A dual-mode actuation and sensing scheme for in-run calibration of bias and scale factor errors in axisymmetric resonant gyroscopes. IEEE Sens. J. 2018, 18, 1993–2005. [Google Scholar] [CrossRef]
- Marx, M.; Dorigo, D.D.; Nessler, S.; Rombanch, S.; Manoli, Y. A 27 μW 0.06 mm² background resonance frequency tuning circuit based on noise observation for a 1.71 mW CT-ΔΣ MEMS gyroscope readout system with 0.9 °/h bias instability. IEEE J. Solid-St. Circ. 2017, 53, 174–186. [Google Scholar] [CrossRef]
- Bayard, D.S.; Ploen, S.R. High Accuracy Inertial Sensors from Inexpensive Components. U.S. Patent US20030187623A1, 2 October 2003. [Google Scholar]
- Nilsson, J.O.; Skog, I. Inertial sensor arrays? A literature review. In Proceedings of the 2016 European Navigation Conference (ENC), Helsinki, Finland, 30 May–2 June 2016; pp. 1–10. [Google Scholar]
- Zhang, L.; Liu, C.; Yu, S.; Zhang, S.; Liu, S. Design and analysis of a novel virtual gyroscope with muti-gyroscope and accelerometer array. Rev. Sci. Instrum. 2016, 87, 1593–1608. [Google Scholar]
- Liu, J.Y.; Shen, Q.; Qin, W.W. Signal processing technique for combining numerous MEMS gyroscopes based on dynamic conditional correlation. Micromachines 2015, 6, 684–698. [Google Scholar] [CrossRef]
- Stubberud, P.A.; Stubberud, A.R. A signal processing technique for improving the accuracy of MEMS inertial sensors. In Proceedings of the 19th International Conference on Systems Engineering, Las Vegas, NV, USA, 19–21 August 2008; pp. 13–18. [Google Scholar]
- Xue, L.; Jiang, C.Y.; Chang, H.L.; Yang, Y.; Qin, W.; Yuan, W.Z. A novel Kalman filter for combining outputs of MEMS gyroscope array. Measurement 2012, 12, 745–754. [Google Scholar] [CrossRef]
- Jiang, C.Y.; Xue, L.; Chang, H.L.; Yuan, G.M.; Yuan, W.Z. Signal processing of MEMS gyroscope arrays to improve accuracy using a 1st order Markov for rate signal modeling. Sensors 2012, 12, 1720–1737. [Google Scholar] [CrossRef] [PubMed]
- Xue, L.; Jiang, C.Y.; Wang, L.X.; Liu, J.Y.; Yuan, W.Z. Noise reduction of MEMS gyroscope based on direct modeling for an angular rate signal. Micromachines 2015, 6, 266–280. [Google Scholar] [CrossRef]
- Chang, H.L.; Xue, L.; Jiang, C.Y.; Kraft, W.; Yuan, W.Z. Combining numerous uncorrelated MEMS gyroscopes for accuracy improvement based on an optimal Kalman filter. IEEE Trans. Instrum. Meas. 2012, 61, 3084–3093. [Google Scholar] [CrossRef]
- Heera, M.M.; Divya, J.K.; Varma, M.S.; Divya, R.A.; Agrawal, D.V.K. Minimum variance optimal filter design for a 3x3 MEMS gyroscope cluster configuration. IFAC-PapersOnLine 2016, 49, 639–645. [Google Scholar] [CrossRef]
- Richard, J.V.; Ahmed, S.Z. Reduced-drift virtual gyro from an array of low-cost gyros. Sensors 2017, 17, 352. [Google Scholar] [CrossRef]
- Fernández-Cantí, R.M.; Blesa, J.; Puig, V. Set-membership identification and fault detection using a Bayesian framework. Int. J. Syst. Sci. 2014, 47, 1710–1724. [Google Scholar] [CrossRef]
- Shen, Q.; Liu, J.; Zhou, X.; Zhao, Q.; Wang, Q. Low-complexity ISS state estimation approach with bounded disturbances. Int. J. Adapt. Control. 2018, 32, 1473–1488. [Google Scholar] [CrossRef]
- Yu, W.; Zamora, E.; Soria, A. Ellipsoid SLAM: A novel set membership method for simultaneous localization and mapping. Auton. Robot. 2016, 40, 125–137. [Google Scholar] [CrossRef]
- Maksarov, D.G.; Norton, J.P. State bounding with ellipsoidal set description of uncertainty. Int. J. Control. 1996, 65, 847–866. [Google Scholar] [CrossRef]
- Durieu, C.; Walter, E. Multi-input multi-output ellipsoidal state bounding. J. Optimiz. Theory Appl. 2001, 111, 273–303. [Google Scholar] [CrossRef]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part I. Dynamic models. IEEE Trans. Aero Electr. Syst. 2004, 39, 1333–1364. [Google Scholar]
- Noack, B.; Pfaff, F.; Hanebeck, U.D. Combined stochastic and set-membership information filtering in multisensor systems. In Proceedings of the 2012 15th International Conference on Information Fusion (FUSION), Singapore, 9–12 July 2012; pp. 1218–1224. [Google Scholar]
- Li, X.R.; Jilkov, V.P. Survey of maneuvering target tracking. Part V. Multiple-model methods. IEEE Trans. Aero Electr. Syst. 2005, 41, 1255–1321. [Google Scholar]
- Analog Devices. ADXRS300. Available online: http://www.analog.com/static/imported-files/data_sheets/ADXRS300.pdf (accessed on 20 January 2015).
- Xue, L.; Wang, X.; Yang, B.; Yuan, W.; Yuan, G. Analysis of correlation in MEMS gyroscope array and its influence on accuracy improvement for the combined angular rate signal. Micromachines 2018, 9, 22. [Google Scholar] [CrossRef] [PubMed]

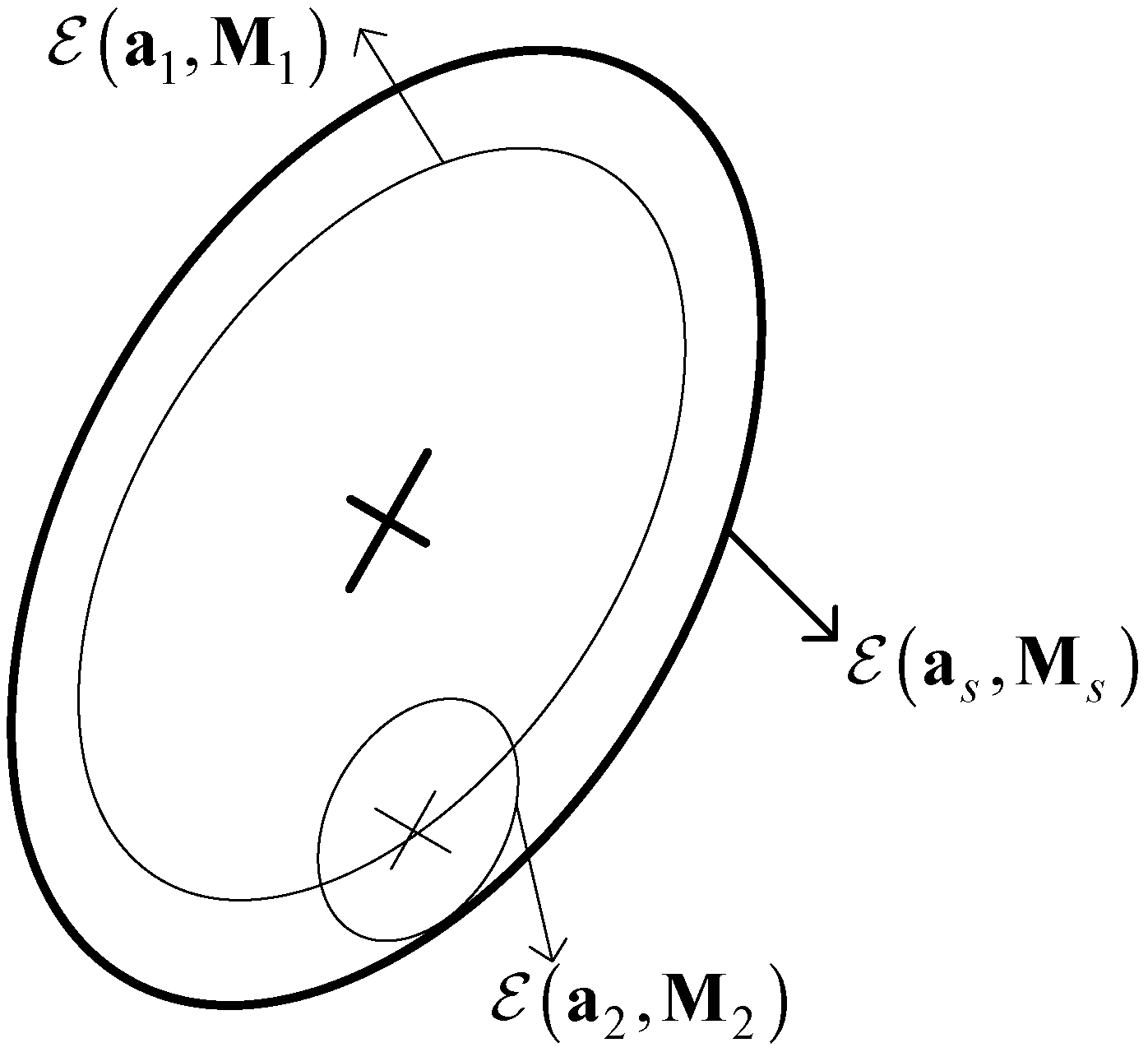




| Gyro 1 | Gyro 2 | Gyro 3 | Gyro 4 | Gyro 5 | Gyro 6 | |
|---|---|---|---|---|---|---|
| Gyro 1 | 1.0000 | 0.0016 | −0.0047 | 0.0297 | 0.0467 | 0.0451 |
| Gyro 2 | 0.0016 | 1.0000 | 0.0595 | −0.0095 | 0.0591 | 0.0542 |
| Gyro 3 | −0.0047 | 0.0595 | 1.0000 | −0.0939 | −0.0381 | −0.0688 |
| Gyro 4 | 0.0297 | −0.0095 | −0.0939 | 1.0000 | 0.0169 | 0.0946 |
| Gyro 5 | 0.0467 | 0.0591 | −0.0381 | 0.0169 | 1.0000 | 0.0501 |
| Gyro 6 | 0.0451 | 0.0542 | −0.0688 | 0.0946 | 0.0501 | 1.0000 |
| Models | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| Parameters |
| Terms | Single Gyroscope | Model 1 | Model 2 | Model 3 | Model 4 | IMM | MMCF |
|---|---|---|---|---|---|---|---|
| RMSE (°/s) | 0.4916 | 8.3886 | 0.9663 | 0.1828 | 0.2009 | 0.1628 | 0.1478 |
| IF | 1 | 0.0586 | 0.5087 | 2.6893 | 2.4470 | 3.0197 | 3.3261 |
| ARW () | 11.4362 | / | / | 4.8251 | 4.8458 | 4.0748 | 3.4395 |
| RRW () | 435.2964 | / | / | 192.5314 | 198.8246 | 178.2495 | 156.2842 |
| BI () | 63.2521 | / | / | 41.5448 | 33.1668 | 28.9512 | 21.0312 |
| Time (s) | Input (°/s) | Single Gyroscope | Gyro Array | |
|---|---|---|---|---|
| RMSE (°/s) | RMSE (°/s) | IF | ||
| 5–15 | 0 | 0.4939 | 0.1120 | 4.4098 |
| 30–40 | 0.4775 | 0.2081 | 2.2946 | |
| 55–65 | 40 | 0.5190 | 0.1212 | 4.2822 |
| 80–90 | −20 | 0.4320 | 0.0850 | 5.0824 |
| 120–130 | 0.4778 | 0.1686 | 2.8339 | |
| 155–165 | 0.4797 | 0.2200 | 2.1805 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, Q.; Liu, J.; Zhou, X.; Wang, L. A Multi-Model Combined Filter with Dual Uncertainties for Data Fusion of MEMS Gyro Array. Sensors 2019, 19, 85. https://doi.org/10.3390/s19010085
Shen Q, Liu J, Zhou X, Wang L. A Multi-Model Combined Filter with Dual Uncertainties for Data Fusion of MEMS Gyro Array. Sensors. 2019; 19(1):85. https://doi.org/10.3390/s19010085
Chicago/Turabian StyleShen, Qiang, Jieyu Liu, Xiaogang Zhou, and Lixin Wang. 2019. "A Multi-Model Combined Filter with Dual Uncertainties for Data Fusion of MEMS Gyro Array" Sensors 19, no. 1: 85. https://doi.org/10.3390/s19010085




