Perturbation Theory for Scattering from Multilayers with Randomly Rough Fractal Interfaces: Remote Sensing Applications
Abstract
:1. Introduction
2. Methods
2.1. Normalized Radar Cross Section (NRCS)
2.2. Interface Roughness Description: 2-D fBm
2.3. Validity Limits
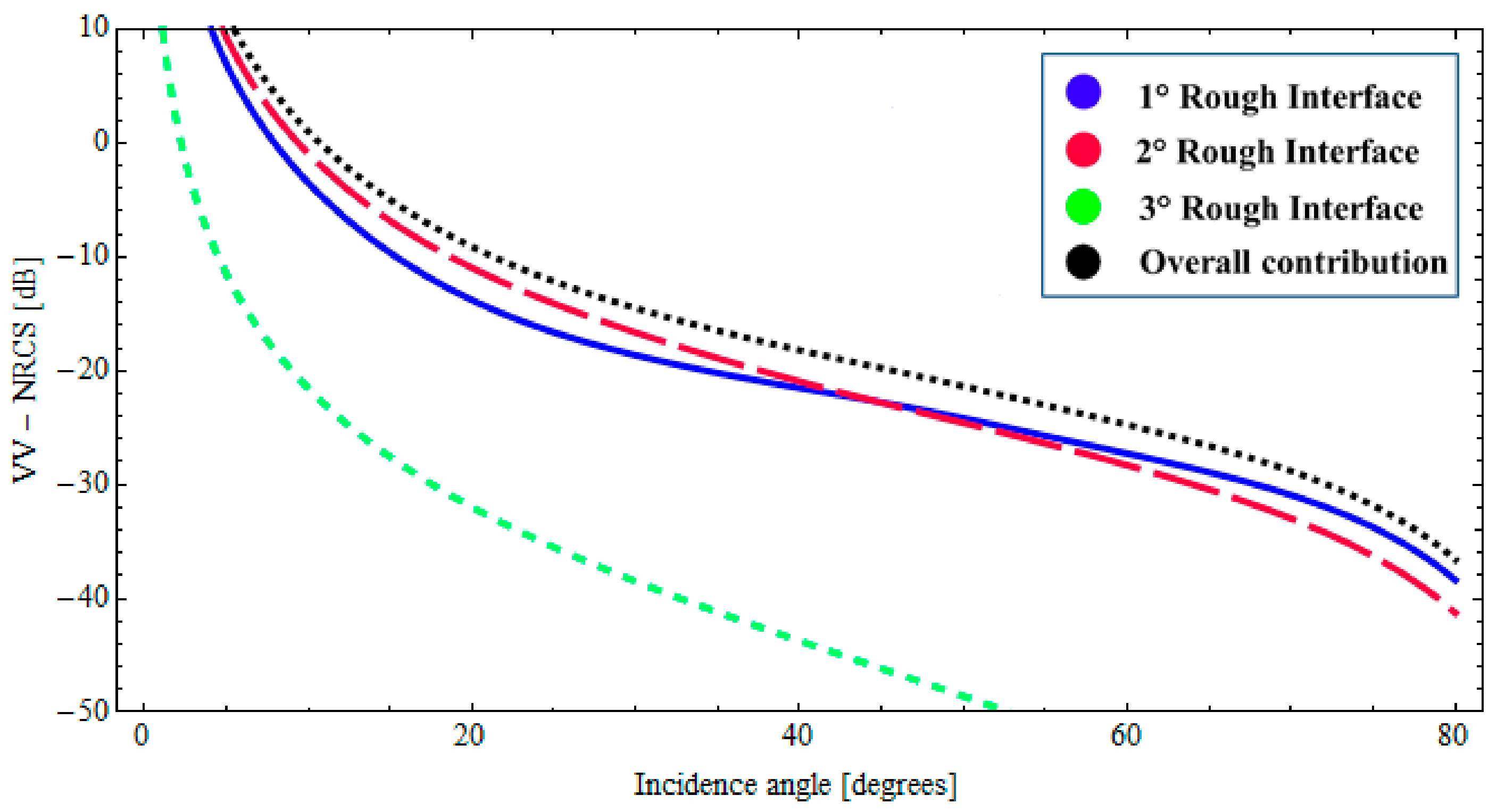
3. Results and Discussion
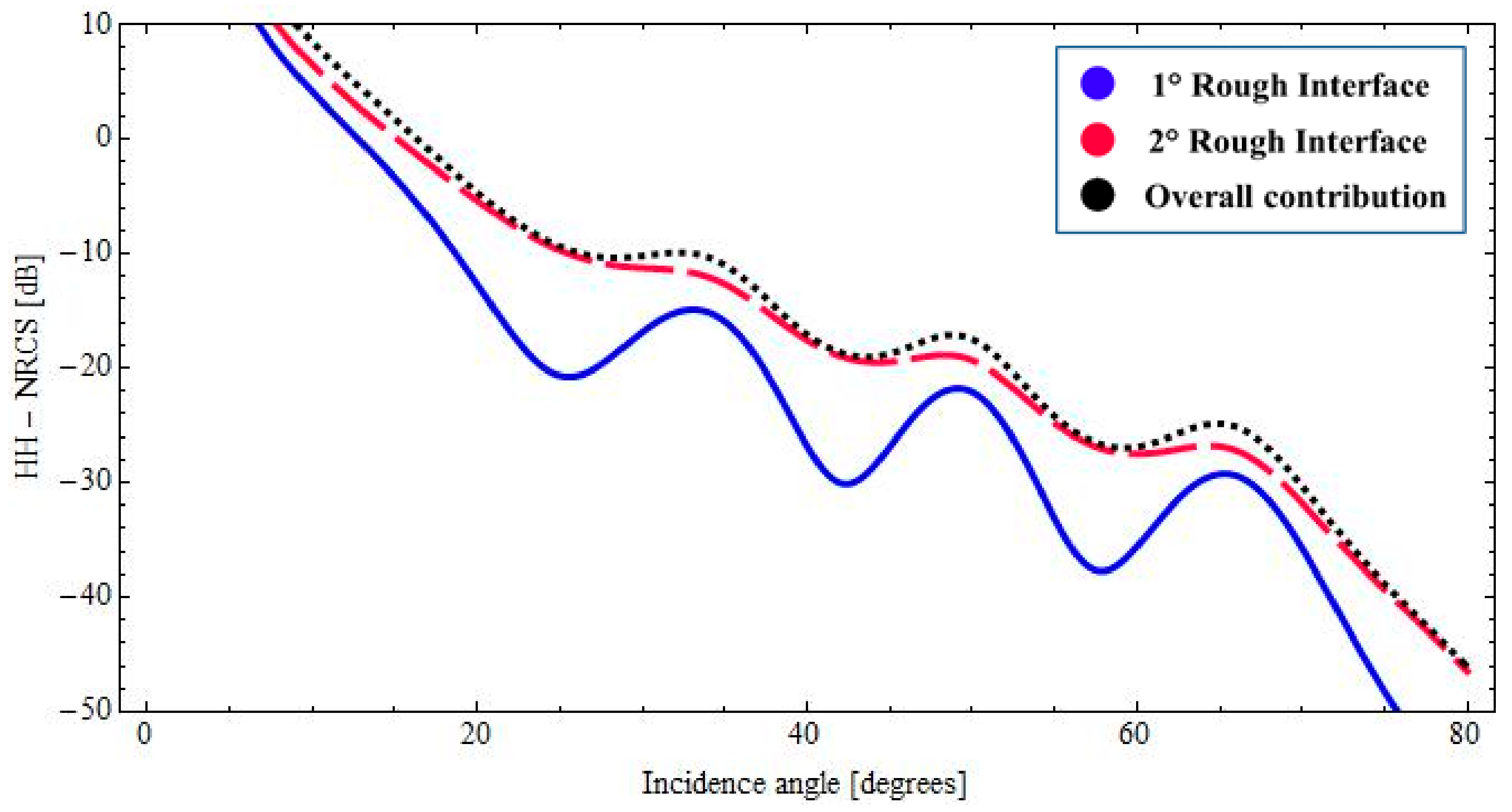
3.1. Sub-Surface Sensing of Wet Paleosoil Covered by a Low Loss Dry Sand Layer
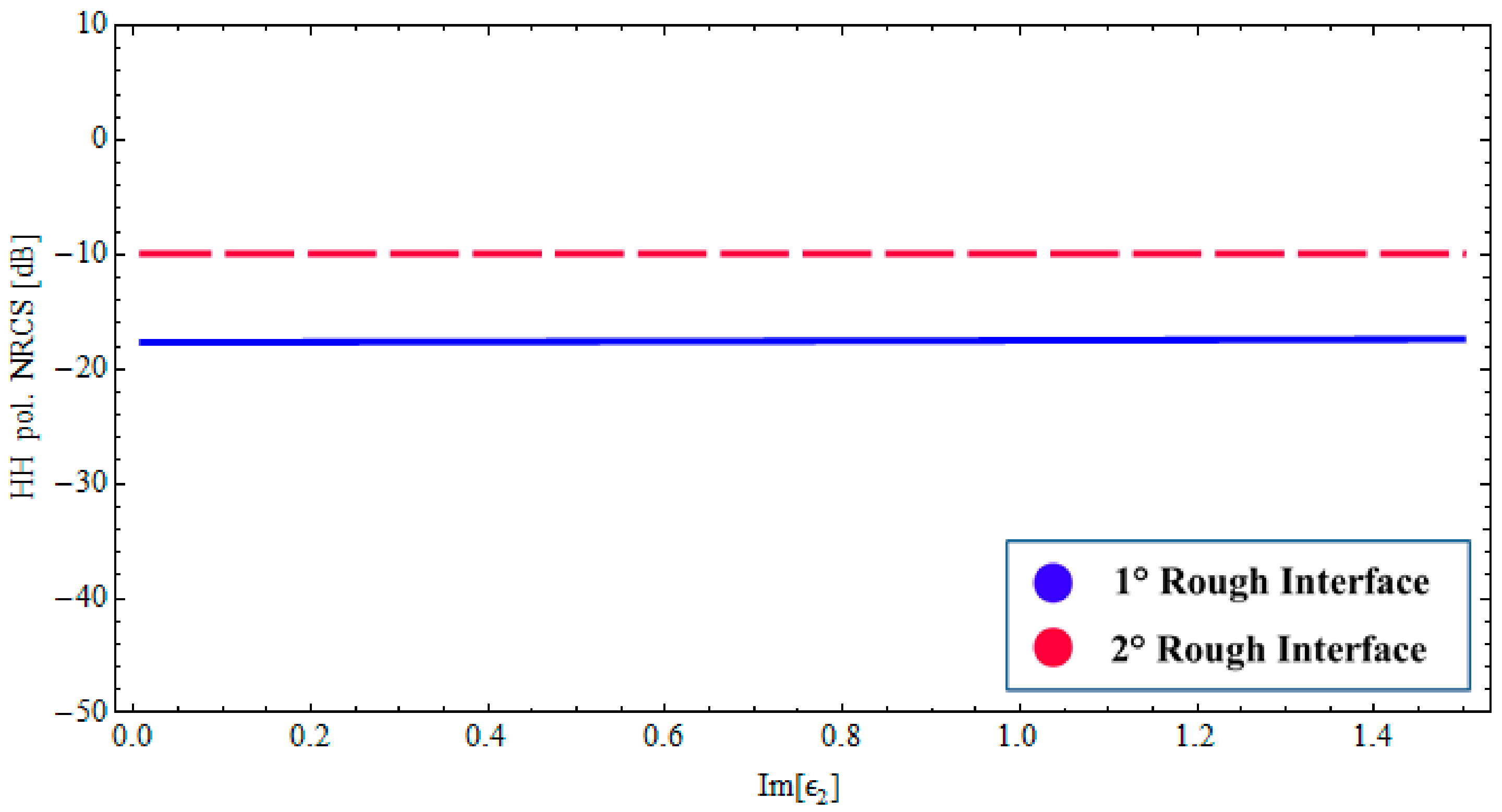
3.2. Wet Paleosoil Covered by a Low Loss Dry Sand Layer: Sensitivity of Radar Signature to the Model Parameters
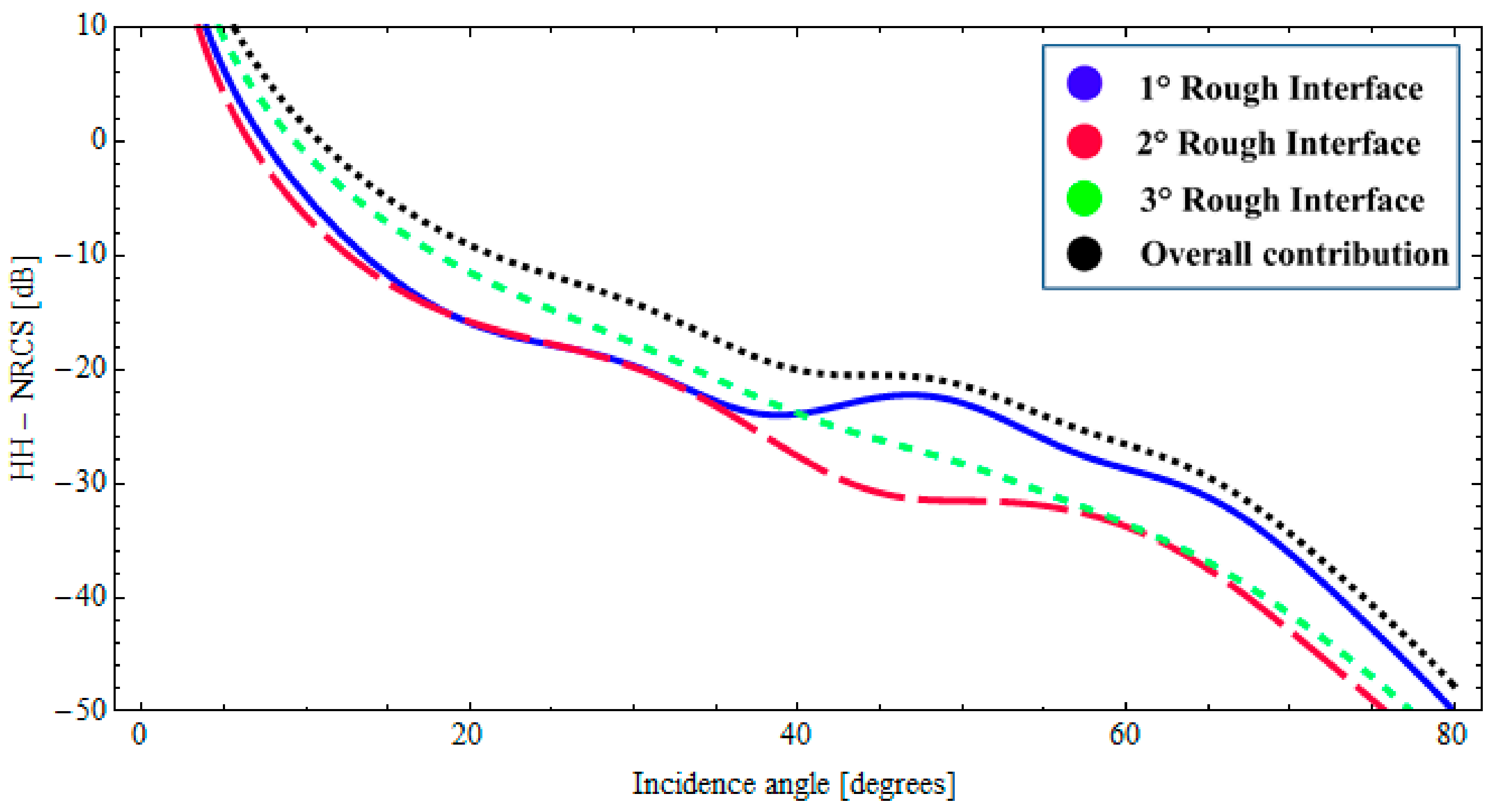
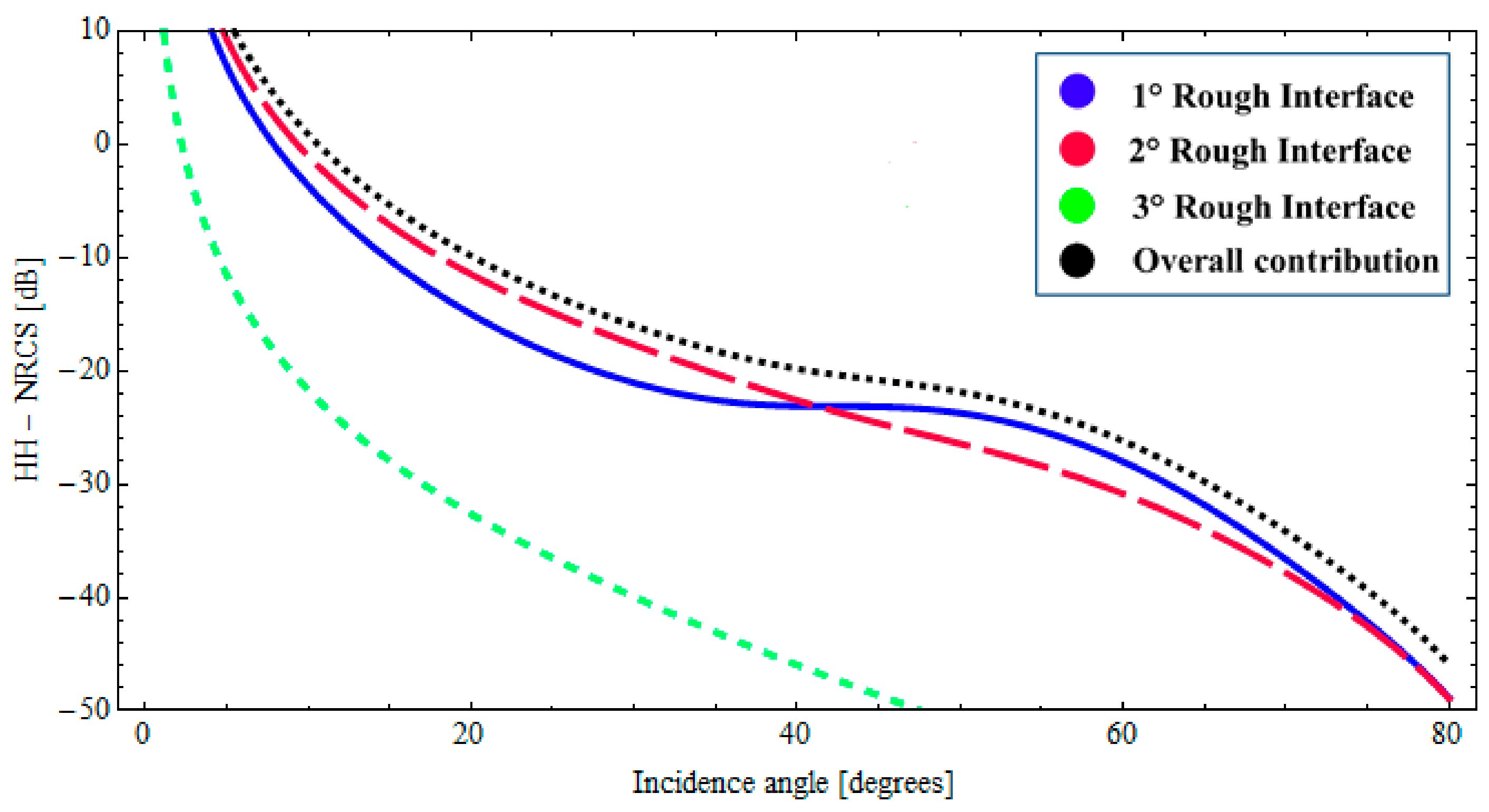
3.3. Remote Sensing of a Sea-Ice Layer above Water with Dry Snow Cover
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Elachi, C.; Roth, L.; Schaber, G. Spaceborne radar subsurface imaging in hyperarid regions. IEEE Trans. Geosci. Remote Sens. 1984, 22, 383–388. [Google Scholar] [CrossRef]
- Grandjean, G.; Paillou, P.; Dubois-Fernandez, P.; August-Bernex, T.; Baghdadi, N.; Achache, J. Subsurface structures detection by combining L-band polarimetric SAR and GPR data: Example of the Pyla Dune (France). IEEE Trans. Geosci. Remote Sens. 2001, 39, 1245–1258. [Google Scholar] [CrossRef]
- Kuo, C.-H.; Moghaddam, M. Electromagnetic scattering from multi-layer rough surfaces with arbitrary dielectric profiles for remote sensing of subsurface soil moisture. IEEE Trans. Geosci. Remote Sens. 2007, 45, 349–366. [Google Scholar] [CrossRef]
- Kuo, C.-H.; Moghaddam, M. Scattering from multilayer rough surfaces based on the extended boundary condition method and truncated singular value decomposition. IEEE Trans. Antennas. Propag. 2006, 54, 2917–2929. [Google Scholar] [CrossRef]
- Déchamps, N.; Bourlier, C. Electromagnetic scattering from a rough layer: Propagation-inside-layer expansion method combined to an updated BMIA/CAG approach. IEEE Trans. Antennas. Propag. 2007, 55, 2790–2802. [Google Scholar] [CrossRef]
- Déchamps, N.; Bourlier, C. Electromagnetic scattering from a rough layer: Propagation-inside-layer expansion method combined to the forward-backward novel spectral acceleration. IEEE Trans. Antennas. Propag. 2007, 55, 3576–3586. [Google Scholar] [CrossRef]
- Pinel, N.; Johnson, J.; Bourlier, C. A geometrical optics model of three-dimensional scattering from a rough surface over a planar surface. IEEE Trans. Antennas Propag. 2009, 57, 546–554. [Google Scholar] [CrossRef]
- Pinel, N.; Johnson, J.; Bourlier, C. A geometrical optics model of three-dimensional scattering from a rough layer with two rough surfaces. IEEE Trans. Antennas Propag. 2010, 58, 809–816. [Google Scholar] [CrossRef]
- Sarabandi, K.; Chiu, T. Electromagnetic scattering from slightly rough surface with inhomogeneous dielectric profiles. IEEE Trans. Antennas Propagat. 1997, 45, 1419–1430. [Google Scholar] [CrossRef]
- Yarovoy, A.G.; de Jongh, R.V.; Ligthard, L.P. Scattering properties of a statistically rough interface inside a multilayered medium. Radio Sci. 2000, 35, 455–462. [Google Scholar] [CrossRef]
- Fuks, I.M. Wave diffraction by a rough boundary of an arbitrary plane-layered medium. IEEE Trans. Antennas Propag. 2001, 49, 630–639. [Google Scholar] [CrossRef]
- Imperatore, P. Perturbation Theory for Electromagnetic Wave Scattering in Random Layered Structures. Ph.D. Thesis, Dipartimento di Ingegneria Biomedica, Elettronica e delle Telecomunicazioni, Università di Napoli Federico II, Naples, Italy, 2010. [Google Scholar]
- Imperatore, P.; Iodice, A.; Riccio, D. Boundary Perturbation Theory for Scattering in Layered Rough Structures. In Passive Microwave Components and Antennas; Zhurbenko, V., Ed.; InTech: Vukovar, Croatia, 2010; pp. 1–25. [Google Scholar]
- Imperatore, P.; Iodice, A.; Riccio, D. Electromagnetic Wave Scattering from Layered Structures with an Arbitrary Number of Rough Interfaces. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1056–1072. [Google Scholar] [CrossRef]
- Imperatore, P.; Iodice, A.; Riccio, D. Transmission through Layered Media with Rough Boundaries: First-Order Perturbative Solution. IEEE Trans. Antennas Propag. 2009, 57, 1481–1494. [Google Scholar] [CrossRef]
- Imperatore, P.; Iodice, A.; Riccio, D. Physical Meaning of Perturbative Solutions for Scattering from and Through Multilayered Structures with Rough Interfaces. IEEE Trans. Antennas Propag. 2010, 58, 2710–2724. [Google Scholar] [CrossRef]
- Imperatore, P.; Iodice, A.; Riccio, D. Reciprocity, Coupling and Scattering: A New Look at SPM for Rough Surface. In Proceedings of the European Microwave Conference (EuMC 2009), Rome, Italy, 29 September–1 October 2009; pp. 994–997. [Google Scholar]
- Imperatore, P.; Iodice, A.; Riccio, D. Volumetric-Perturbative Reciprocal Formulation for Scattering from Rough Multilayers. IEEE Trans. Antennas Propag. 2011, 59, 877–887. [Google Scholar] [CrossRef]
- Imperatore, P.; Iodice, A.; Riccio, D. Second-Order Volumetric-Perturbative Reciprocal Scattering Theory. IEEE Trans. Antennas Propag. 2012, 60, 1505–1520. [Google Scholar] [CrossRef]
- Imperatore, P.; Iodice, A.; Riccio, D. Electromagnetic Models for Remote Sensing of Layered Rough Media. In Geoscience and Remote Sensing New Achievements; Imperatore, P., Riccio, D., Eds.; InTech: Vukovar, Croatia, 2010; pp. 177–202. [Google Scholar]
- Imperatore, P.; Iodice, A.; Riccio, D. Consistency and Validity of Perturbative Formulations for Scattering from Rough Multilayers. IEEE Trans. Antennas Propag. 2012, 60, 2019–2027. [Google Scholar] [CrossRef]
- Demir, M.A.; Johnson, J.T.; Zajdel, T.J. A study of the fourth-order small perturbation method for scattering from two-layer rough surfaces. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3374–3382. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, X. Second-order perturbative solutions for 3-D electromagnetic radiation and propagation in a layered structure with multilayer rough interfaces. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 180–194. [Google Scholar] [CrossRef]
- Zamani, H.; Tavakoli, A.; Dehmollaian, M. Second-order perturbative solution of cross-polarized scattering from multilayered rough surfaces. IEEE Trans. Antennas Propag. 2016, 64, 1877–1890. [Google Scholar] [CrossRef]
- Tsang, L.; Kong, J.A.; Shin, R.T. Theory of Microwave Remote Sensing; Wiley: New York, NY, USA, 1985. [Google Scholar]
- Imperatore, P.; Riccio, D. (Eds.) Geoscience and Remote Sensing New Achievements; InTech: Vukovar, Croatia, 2010. [Google Scholar]
- Ulaby, F.T.; Moore, R.K.; Fung, A.K. Microwave Remote Sensing; Addison-Wesley: Reading, MA, USA, 1982. [Google Scholar]
- Falconer, K. Fractal Geometry; John Wiley & Sons: Chichester, UK, 1990. [Google Scholar]
- Franceschetti, G.; Riccio, D. Scattering, Natural Surfaces and Fractals; Academic: Burlington, MA, USA, 2007. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman & C.: New York, NY, USA, 1983. [Google Scholar]
- Feder, J.S. Fractals; Plenum: New York, NY, USA, 1988. [Google Scholar]
- Turcotte, D.L. Fractals and Chaos in Geology and Geophysics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Imperatore, P.; Iodice, A.; Riccio, D. Backscattering from fractal rough multilayer. In Proceedings of the 2012 IEEE International Geoscience and Remote Sensing Symposium, Munich, Germany, 22–27 July 2012; pp. 610–613. [Google Scholar]
- Lasne, Y.; Paillou, P.; August-Bernex, T.; Ruffié, G.; Grandjean, G. A Phase Signature for Detecting Wet Subsurface Structures Using Polarimetric L-Band SAR. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1683–1694. [Google Scholar] [CrossRef]
- Tjuatja, S.; Fung, A.K.; Bredow, J.; Hosseinmostafa, R.; Gogineni, S.; Lytle, V. Analysis of backscattering from snow covers on Arctic and Antarctic sea ice. In Proceedings of the IGARSS ’93 Geoscience and Remote Sensing Symposium, Tokyo, Japan, 18–21 August 1993; Volume 3, pp. 1035–1037. [Google Scholar]
- Kim, J.-W.; Kim, D.-J.; Hwang, B.J. Characterization of Arctic Sea Ice Thickness Using High-Resolution Spaceborne Polarimetric SAR Data. IEEE Trans. Geosci. Remote Sens. 2012, 50, 13–22. [Google Scholar] [CrossRef]
- Iodice, A.; Natale, A.; Riccio, D. Retrieval of Soil Surface Parameters via a Polarimetric Two-Scale Model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2531–2547. [Google Scholar] [CrossRef]





| Interface Height Variance | |
| Interface Slope Variance |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Imperatore, P.; Iodice, A.; Riccio, D. Perturbation Theory for Scattering from Multilayers with Randomly Rough Fractal Interfaces: Remote Sensing Applications. Sensors 2018, 18, 54. https://doi.org/10.3390/s18010054
Imperatore P, Iodice A, Riccio D. Perturbation Theory for Scattering from Multilayers with Randomly Rough Fractal Interfaces: Remote Sensing Applications. Sensors. 2018; 18(1):54. https://doi.org/10.3390/s18010054
Chicago/Turabian StyleImperatore, Pasquale, Antonio Iodice, and Daniele Riccio. 2018. "Perturbation Theory for Scattering from Multilayers with Randomly Rough Fractal Interfaces: Remote Sensing Applications" Sensors 18, no. 1: 54. https://doi.org/10.3390/s18010054






