Dynamic Reconstruction Algorithm of Three-Dimensional Temperature Field Measurement by Acoustic Tomography
Abstract
:1. Introduction
2. The Principle of Acoustic Pyrometry and the Static Model
3. Modeling and Solving of the Dynamic Reconstruction Model
3.1. The Establishment of the Dynamic Reconstruction Model
3.2. Extension of Objective Function by Using Robust Estimation
3.3. Solving of the Objective Function
4. Temperature Field Reconstruction with Noiseless Measurement Signals
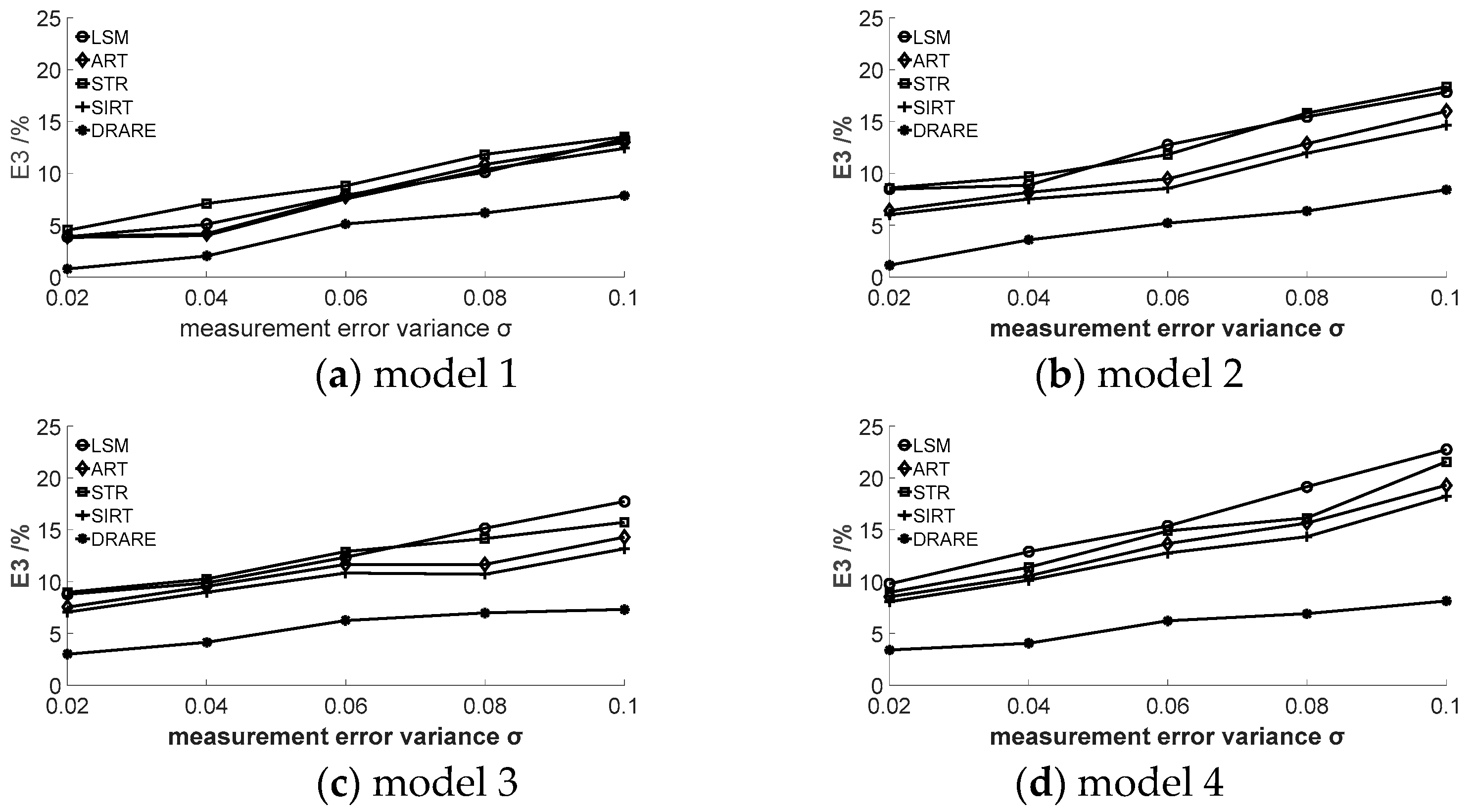
5. Temperature Field Reconstruction Using Measurement Signals with Noise
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Fumio, I.; Masayasu, S. Fundamental studies of acoustic measurement and reconstruction combustion temperature in large boilers. Trans. Jpn. Soc. Mech. Eng. 1985, 53, 1610–1614. [Google Scholar]
- Ebrahimkhanlou, A.; Salamone, S. Acoustic emission source localization in thin metallic plates: A single-sensor approach based on multimodal edge reflections. Ultrasonics 2017, 78, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimkhanlou, A.; Salamone, S. A probabilistic framework for single-sensor acoustic emission source localization in thin metallic plates. Smart Mater. Struct. 2017, 26, 95026. [Google Scholar] [CrossRef]
- Mao, J.; Wu, Y.; Fan, W.; Pan, H. Acoustic temperature field measurement in deep-sea hydrothermal vents and reconstruction algorithm. Chin. J. Sci. Instrum. 2010, 31, 2339–2344. [Google Scholar]
- Lu, J.; Wakai, K.; Takahashi, S. Acoustic computer tomographic pyrometry for two-dimensional measurement of gases taking into account the effect of refraction of sound wave paths. Sci. Technol. 2000, 11, 692–697. [Google Scholar] [CrossRef]
- Bramanti, M.; Salerno, E.A.; Tonazzini, A.; Pasini, S.; Gray, A. An Acoustic Pyrometer System for Tomographic Thermal Imaging in Power Plant Boilers. IEEE Trans. Instrum. Meas. 1996, 1, 159–167. [Google Scholar] [CrossRef]
- Tian, F.; Sun, X.; Deng, F.; Shao, F.; Wang, F. Research and Comparison on Reconstruction Algorithm of Temperature Field in Power Plant Boilers Based on Acoustic Method. Chen. J. Quantum Electron. 2003, 5, 607–612. [Google Scholar]
- Shao, F.; Wu, J. The Measurement of Complex Temperature Field by Using Acoustic Reconstruction. Control Decis. 1999, 2, 120–124. [Google Scholar]
- Tian, F.; Shao, F.; Wang, F. Complex Temperature Field Reconstruction Algorithm Based on Combination of Regularization Method and Iterative Technology. J. Northeast. Univ. 2003, 4, 307–310. [Google Scholar]
- Tian, F.; Sun, X.; Shao, F.; Wang, F.; Wang, L. A Study of Complex Temperature Field Reconstruction Algorithm based on Combination of Gaussian Functions with Regularization Method. Proc. CSEE 2004, 5, 212–220. [Google Scholar]
- Sun, X.; Tian, F.; Shao, F.; Xie, Z. Image Reconstruction Algorithm for Complex Temperature Field. J. Northeast. Univ. 2006, 7, 268–271. [Google Scholar]
- Shen, G.; An, L.; Jiang, G.; Zhang, B. Simulation of Two-dimensional Temperature Field in Furnace Based on Acoustic Computer Tomography. Proc. CSEE 2007, 2, 11–14. [Google Scholar]
- Wang, Y.; Zhao, G.; Huang, D.; Yuan, H. Study of Ultrasonic Pyrometer. Control Instrum. Chem. Ind. 2012, 5, 631–634. [Google Scholar]
- Li, Z.; Yan, H.; Chen, G. Acoustic temperature field reconstruction algorithm based on modified Landweber iterative method. J. Shenyang Univ. Technol. 2008, 30, 90–93. [Google Scholar]
- Shen, G.; Wu, Z.; An, L.; Li, K.; Jiang, G. Reconstruction of Temperature Fields of Furnace on the Basis of Few Acoustic Data. J. Power Eng. 2007, 27, 702–706. [Google Scholar]
- Yan, H.; Wang, S.; Zhou, Y. Acoustic CT temperature field reconstruction based on adaptive regularization parameter selection. Chin. J. Sci. Instrum. 2012, 33, 1301–1307. [Google Scholar]
- An, L.; Li, G.; Shen, G.; Zhang, S.; Feng, Q. Application of Acoustic Pyrometer in a 200 MW Power Plant Boiler. J. Chin. Soc. Power Eng. 2011, 31, 928–932. [Google Scholar]
- Zhang, S.; Shen, G.; An, L.; Niu, Y. Study of the Monitoring of the Local Ash Fouling on the Water Walls of a Utility Boiler Based on the Acoustic Pyrometry. J. Eng. Therm. Energy Power 2013, 28, 409–414. [Google Scholar]
- Yan, H.; Li, K.; Wang, S. A 3D acoustic temperature field reconstruction algorithm based on Tikhonov regularization. Adv. Intell. Soft Comput. 2012, 168, 365–370. [Google Scholar]
- Yan, H.; Cui, K.; Xu, Y. Temperature field reconstruction based on a few sound travel-time data. Chin. J. Sci. Instrum. 2010, 31, 470–475. [Google Scholar]
- Liu, D.; Shi, W.; Xiong, Q.; Shi, X. Temperature field reconstruction based on Gaussian radial basis function with subarea optimization. Appl. Res. Comput. 2015, 33, 2618–2621. (In Chinese) [Google Scholar] [CrossRef]
- Xie, L.; Liu, T.; Zhang, Z.; Shao, W. The 2-D Temperature Reconstruction Based on the Algorithm of Interpolation and Iterative. Proc. CSEE 2004, 24, 249–252. [Google Scholar]
- Tian, F.; Liu, Z.; Sun, X. Temperature field Reconstruction algorithm based on RBF neural network. Chin. J. Sci. Instrum. 2006, 27, 1460–1464. [Google Scholar]
- Shen, G.; An, L.; Zhang, B. Research on Reconstruction Algorithm of Temperature Field by Acoustic Measurement in Boiler. Boiler Technol. 2005, 36, 52–55. [Google Scholar]
- Sielschott, H.; Derichs, W. Tomography with Few Data: Use of Co1location Methods in Acoustic Pyrometry. Available online: https://www.uni-muenster.de/AMM/num/Preprints/1997/sielschott_2/paper.pdf (accessed on 6 September 2017).
- Yang, Q.; Chen, G.; Yan, H. Development of area partitioning in circle temperature field reconstruction by acoustic. China New Technol. Prod. 2010, 2, 9–10. [Google Scholar]
- Yan, H.; Li, Z.; Chen, G. Acoustic Temperature Reconstruction Algorithm Based on Regularized Eponential Approach. In Proceedings of the 7th International Conference on Measurement and Control of Granular Materials, Shanghai, China, 26–28 August 2006; pp. 308–312. [Google Scholar]
- Kan, Z.; Meng, G.; Wang, X. Research of boiler temperature field reconstruction algorithm based on genetic algorithm. J. Electron. Meas. Instrum. 2014, 28, 1149–1154. [Google Scholar]
- Yan, H.; Chen, G.; Yang, Q.; Liu, L. Research on complicated temperature field reconstruction base on acoustic CT. Acta Acoust. 2012, 37, 370–377. [Google Scholar]
- Yan, H.; Chen, G.; Zhou, Y.; Liu, L. Primary study of temperature distribution measurement in stored grain based on acoustic tomography. Exp. Therm. Fluid Sci. 2012, 42, 55–63. [Google Scholar] [CrossRef]
- Yan, H.; Chen, G.; Liu, J.; Zhou, Y. Temperature monitoring method for stored grain based on acoustic tomography. J. Shenyang Univ. Technol. 2013, 35, 541–547. [Google Scholar]
- Wang, M.; Wang, R.; Jiang, F. Acoustic reconstruction of three-dimensional temperature gradient field base on computer simulation. Mod. Electron. Tech. 2012, 35, 121–123. [Google Scholar]
- Wang, R.; An, L.; Shen, G.; Zhang, S. Research on simulation of furnace three-dimensional temperature field reconstruction by acoustics based on singular value decomposition. Proc. CSEE 2014, 34, 147–152. (In Chinese) [Google Scholar] [CrossRef]
- An, L.; Wang, R.; Shen, G.; Zhang, S. Research on reconstruction of three-dimensional temperature field in furnace by acoustics based on iterative algorithm. J. North China Electr. Power Univ. 2015, 42, 69–73. (In Chinese) [Google Scholar]
- Zhou, X.; Wang, Q.; Miao, Z.; Wu, W. Three-dimensional temperature field reconstruction algorithm based on RBF neural network. Instrum. Tech. Sens. 2013, 5, 99–102. [Google Scholar]
- An, L.; Wang, R.; Shen, G.; Zhang, S. Simulation study on reconstruction of 3D temperature field in boiler furnace by acoustic CT algorithm. J. Chin. Soc. Power Eng. 2015, 35, 13–18. (In Chinese) [Google Scholar]
- Wang, R.; An, L.; Shen, G. Three-dimensional temperature field reconstruction with acoustics based on regularized SVD algorithm. Chin. J. Comput. Phys. 2015, 32, 195–201. [Google Scholar]
- An, L.; Ru, Y.; Shen, G.; Wang, R. Applications of the GMRES Algorithm in Reconstructing a Three-dimensional Temperature Field by Using the Acoustic Method. J. Eng. Therm. Energy Power 2015, 30, 88–94. (In Chinese) [Google Scholar]
- Manuela, B.; Armin, R. Acoustic tomographic imaging of temperature and flow fields in air. Meas. Sci. Technol. 2011, 22, 1–13. [Google Scholar]
- Ma, P.; Liu, N.; Wang, Z.; Zhao, Q. Optimization of Tangential Boiler Furnace Temperature Field Balance. Electric. Power 2016, 49, 124–130. (In Chinese) [Google Scholar] [CrossRef]
- Li, D.; Xu, Q.; Shen, Y.; Deng, J.; Liu, Y.; Wen, Z. Numerical Simulation on Combustion Characteristics in a Tangentially-fired Boiler with Variable Volumes of SOFA. J. Chin. Soc. Power Eng. 2014, 34, 921–931. [Google Scholar]
- Leny, A.V.; Montalvo, A. The tunneling algorithm for the global minimization of functions. SIAM J. Sci. Stat. Comput. 1985, 6, 15–29. [Google Scholar]
- Butala, M.D.; Hewett, R.J.; Frazin, R.A.; Kamalabadi, F. Dynamic three-dimensional tomography of the solar corona. Sol. Phys. 2010, 2, 495–509. [Google Scholar] [CrossRef]
- Lin, H.; Hao, X.; Wang, L.; Yang, J. Weighing method for truck scale based on neural network with weight-smoothing constraint. Measurement 2017, 106, 128–136. [Google Scholar] [CrossRef]
- Li, J.; Zhang, Y.; Li, Z.; Fan, H.; Yin, G. 3D magnetic gradient tensor regularization inversion method based on smooth constrained. Chin. J. Nonferrous Met. 2016, 26, 2640–2646. (In Chinese) [Google Scholar]
- Tong, X.; Liu, J.; Guo, R.; Liu, H.; Gong, L. Three-dimensional magnetotelluric regularized inversion based on smoothness-constrained model. Trans. Nonferrous Met. Soc. China. 2014, 24, 509–513. [Google Scholar] [CrossRef]
- Huber, P.J. Robust Statistics; John Wiley and Sons: New York, NY, USA, 1981. [Google Scholar]
- Huber, P.J. Robust estimation of a location parameter. Ann. Math. Stat. 1964, 35, 73–101. [Google Scholar] [CrossRef]
- Hampel, F.R. The influence curve and its role in robust estimation. J. Am. Stat. Assoc. 1974, 69, 383–393. [Google Scholar] [CrossRef]
- Hampel, F.R.; Ronchetti, E.M.; Rousseeuw, P.J.; Stahel, W.A. Robust Statistics: The Approach Based on Influence Function; John Wiley and Sons: New York, NY, USA, 1986. [Google Scholar]
- Ronchetti, E.; Field, C.; Blanchard, W. Robust linear model selection by crossvalidation. J. Am. Stat. Assoc. 1997, 92, 1017–1023. [Google Scholar] [CrossRef]
- Wang, R.; Wu, Y.; Mu, Z.; Xu, Y. Application of Kalman Filtering Algorithm based M-Estimation in Deformation Monitoring of Concrete Gravity Dam. Water Resour. Power 2015, 33, 89–92. (In Chinese) [Google Scholar]
- Dümbgena, L.; Nordhausenb, K.; Schuhmachera, H. New algorithms for M-estimation of multivariate scatter and location. J. Multivar. Anal. 2016, 144, 200–217. [Google Scholar] [CrossRef]
- Belge, M.; Kilmer, M.E.; Miller, E.L. Simultaneous multiple regularization parameter selection by means of the L-hypersurface with applications to linear inverse problems posed in the wavelet domain. Proc. SPIE 1998, 3459, 328–336. [Google Scholar]
- Brlge, M.; Kilmer, M.E.; Miller, E.L. Efficient determination of multiple regularization parameters in a generalized L-curve framework. Inverse Probl. 2002, 18, 1161–1183. [Google Scholar]
- Wang, S.; Zhang, Y.; Xu, Y. The BP Neural Network Hydrological Forecasting Algorithm Based on Tunneling Function Method. Oper. Res. Trans. 2011, 15, 45–54. [Google Scholar]
- Li, J.; Shang, Y.; Han, P. New Tunnel-Filled Function Method for Discrete Global Optimization. J. Oper. Res. Soc. China 2017, 5, 291–300. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Y.; Wang, S. A modified tunneling function method for non-smooth global optimization and its application in artificial neural network. Appl. Math. Model. 2015, 39, 6438–6450. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, Y. Modified tunneling algorithm for global minimization. Commun. Appl. Math. Comput. 2016, 30, 181–190. [Google Scholar]
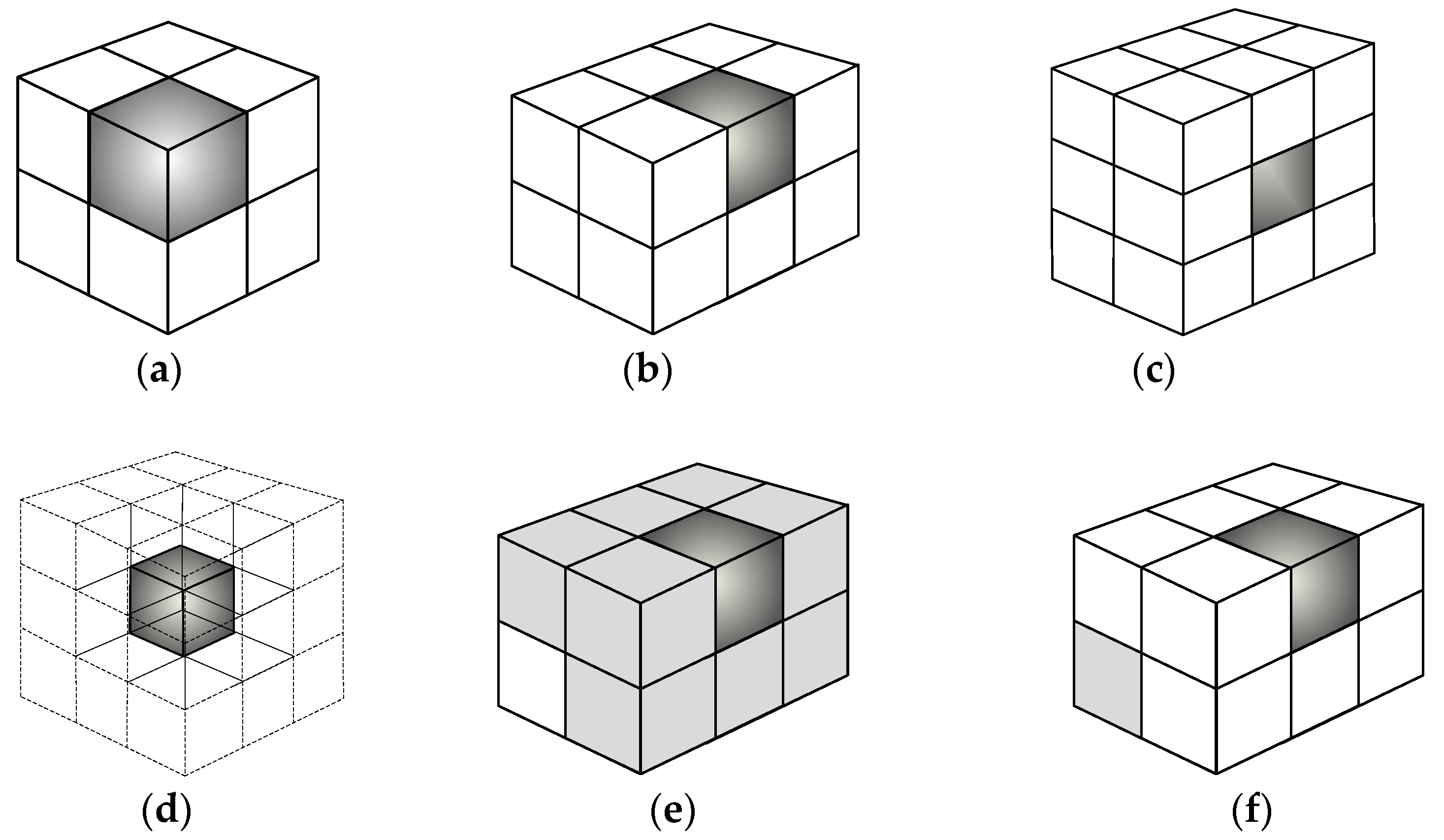
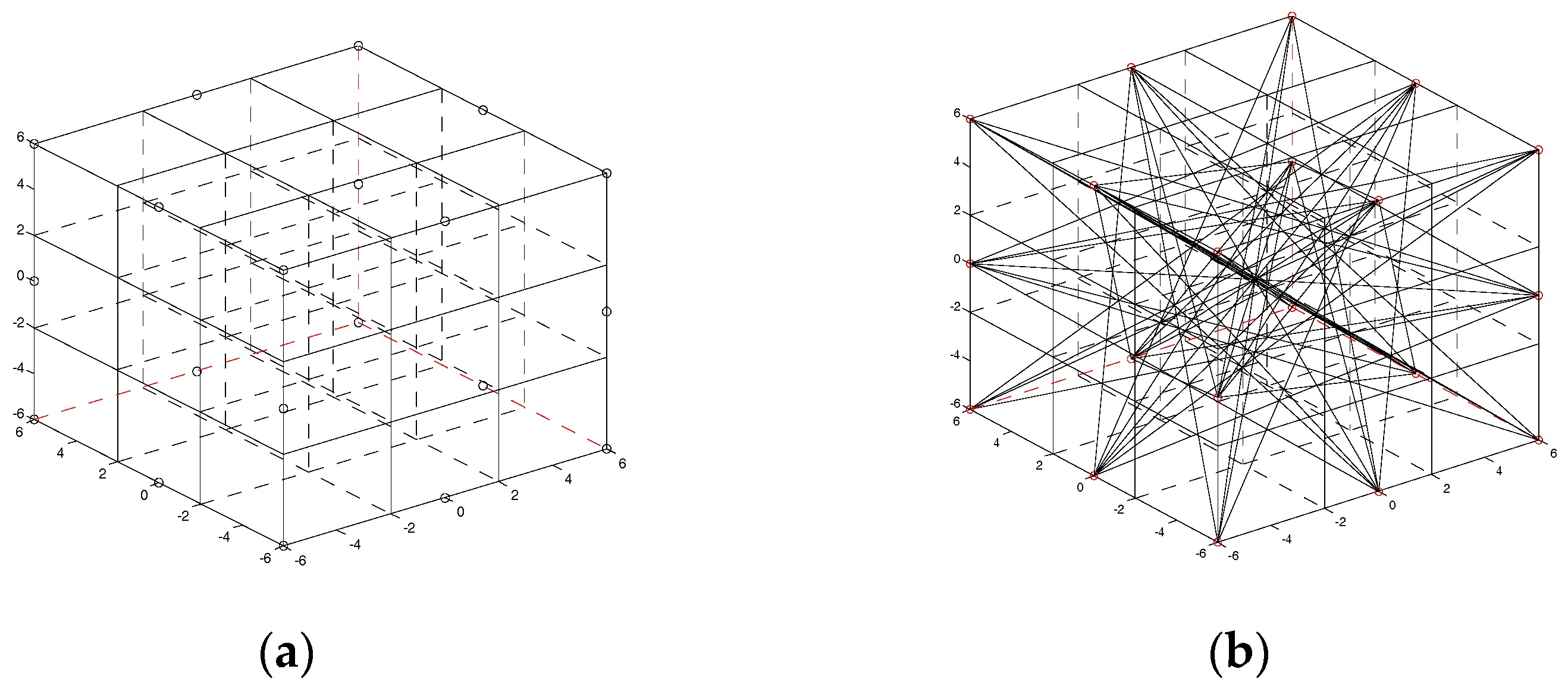
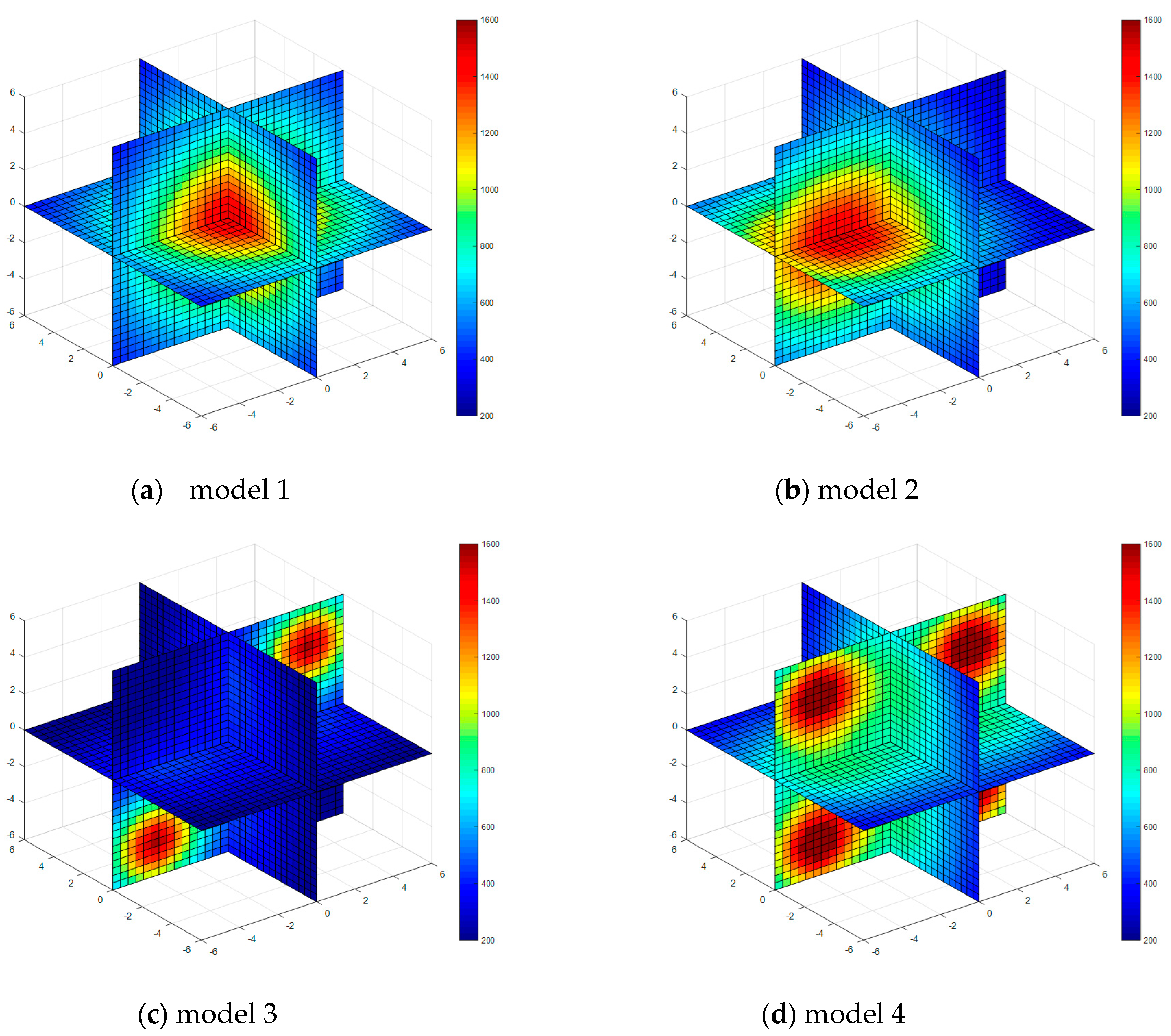
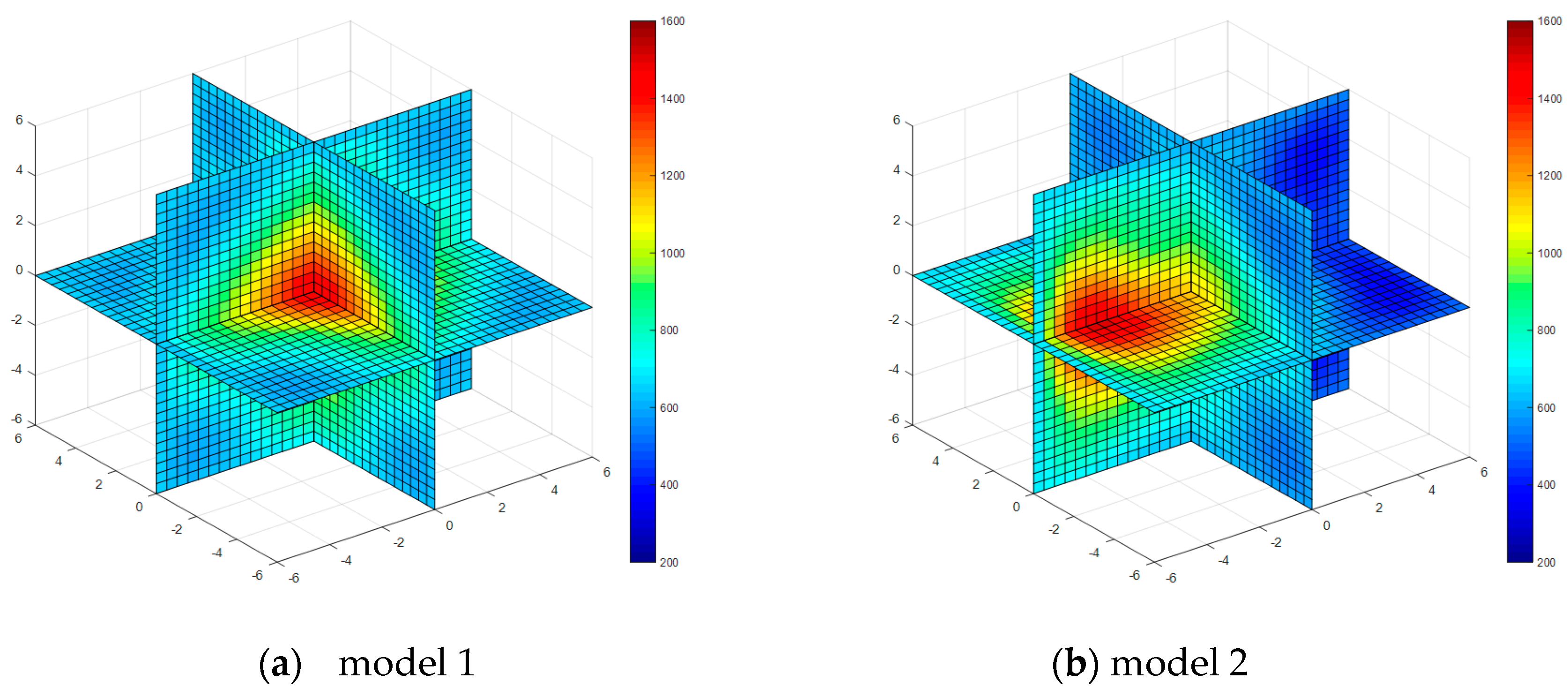
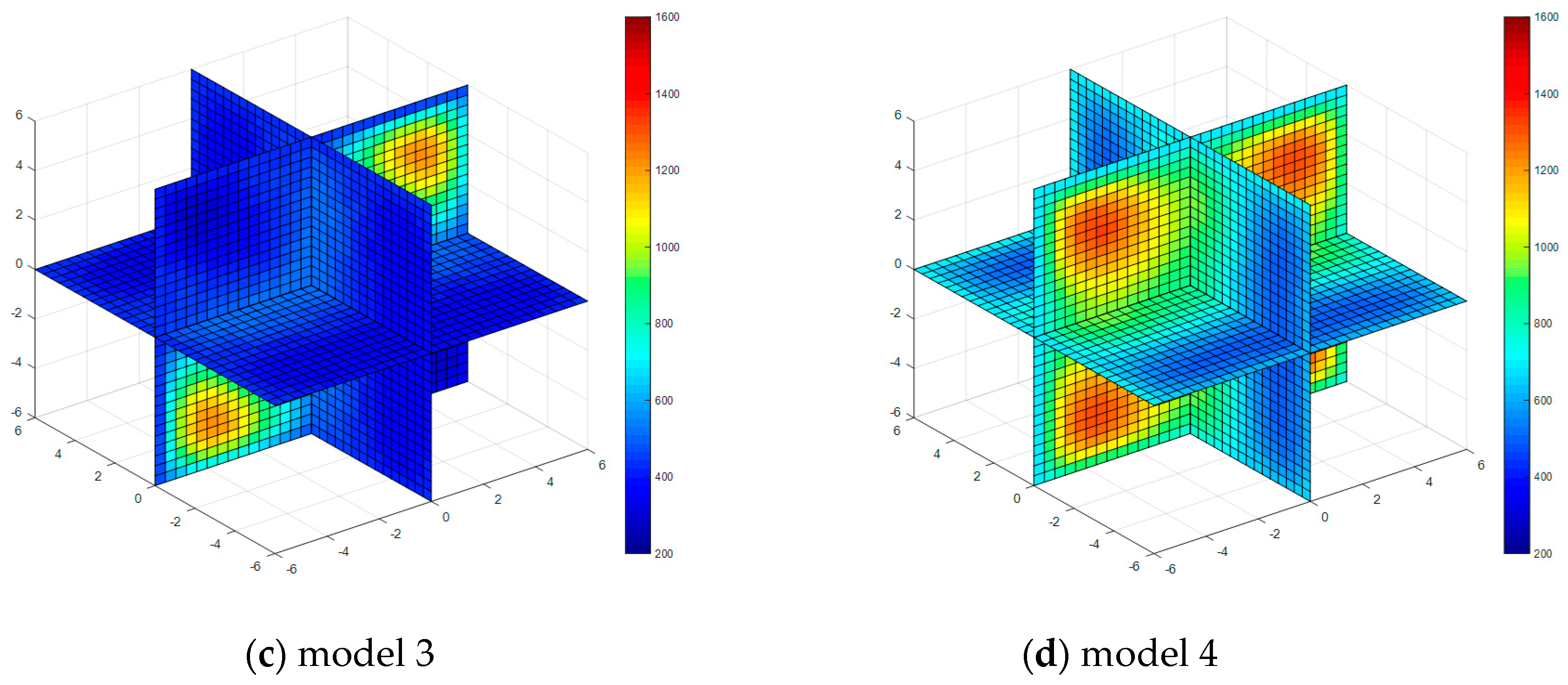
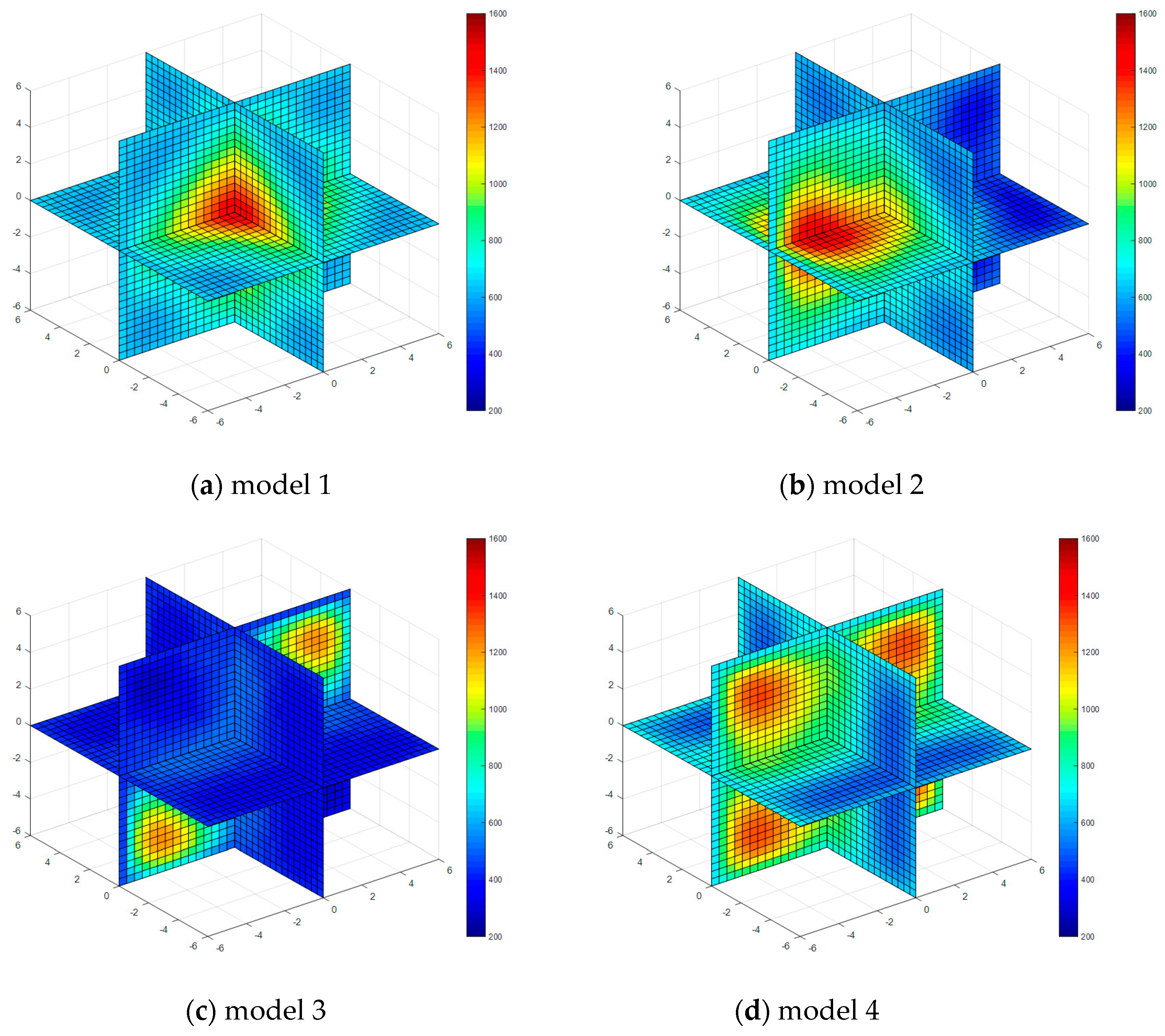
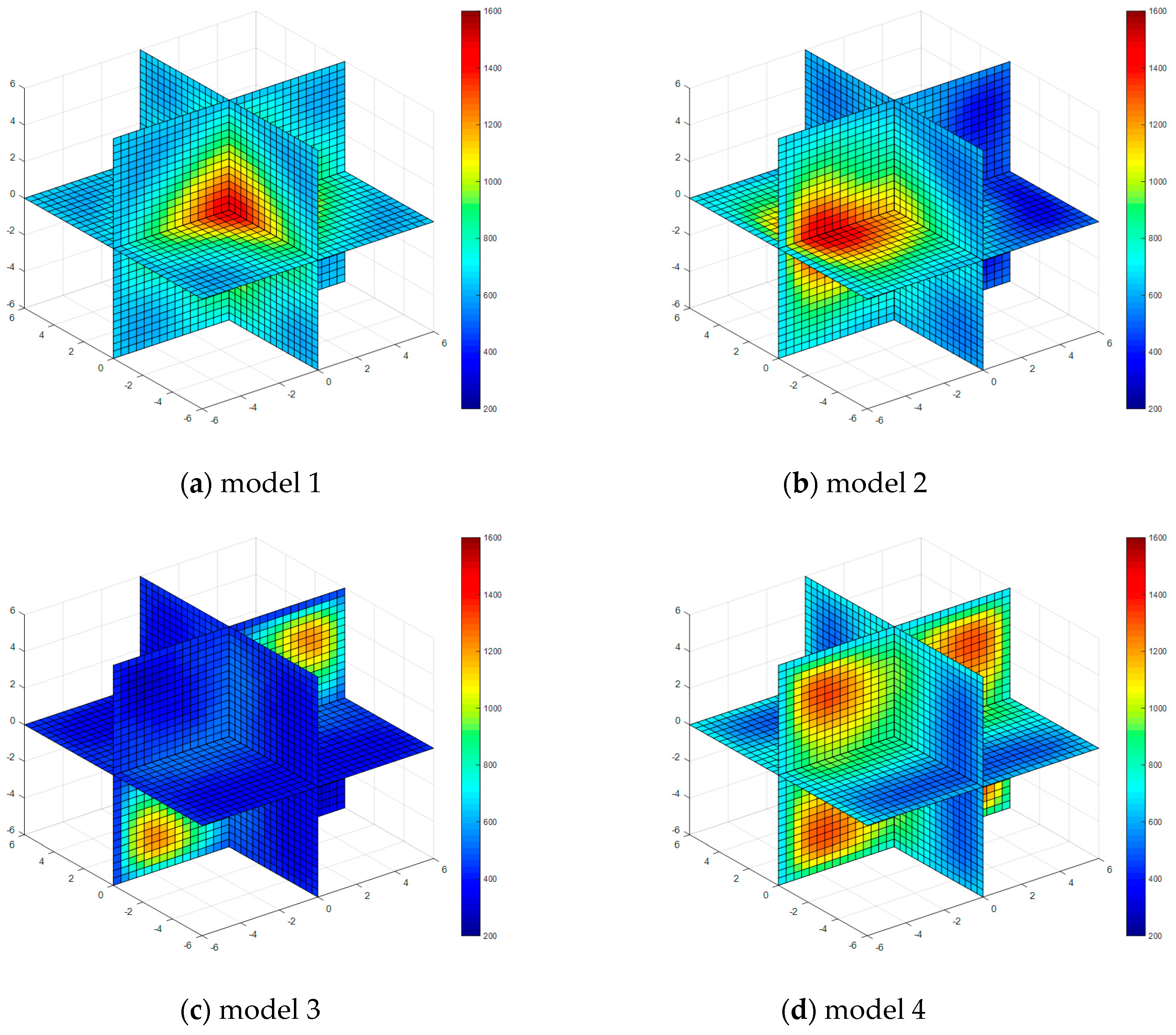
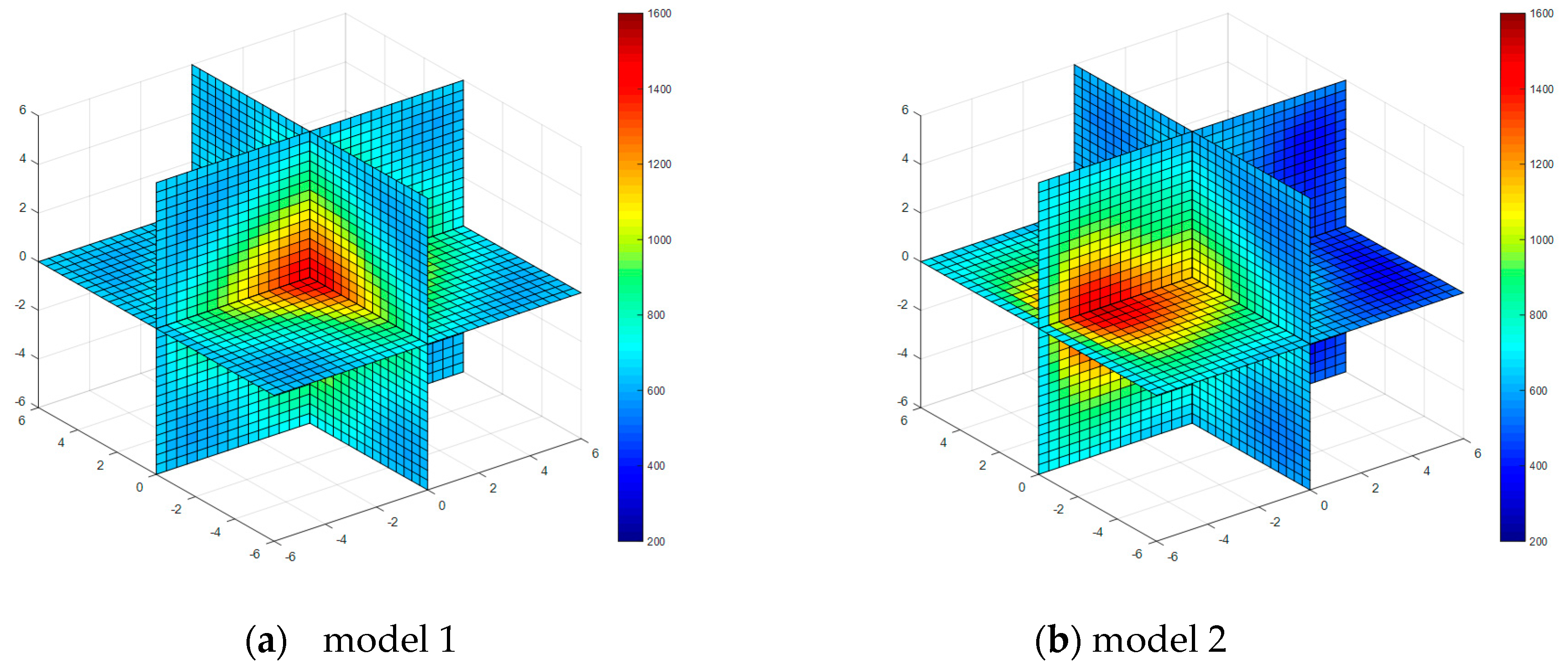
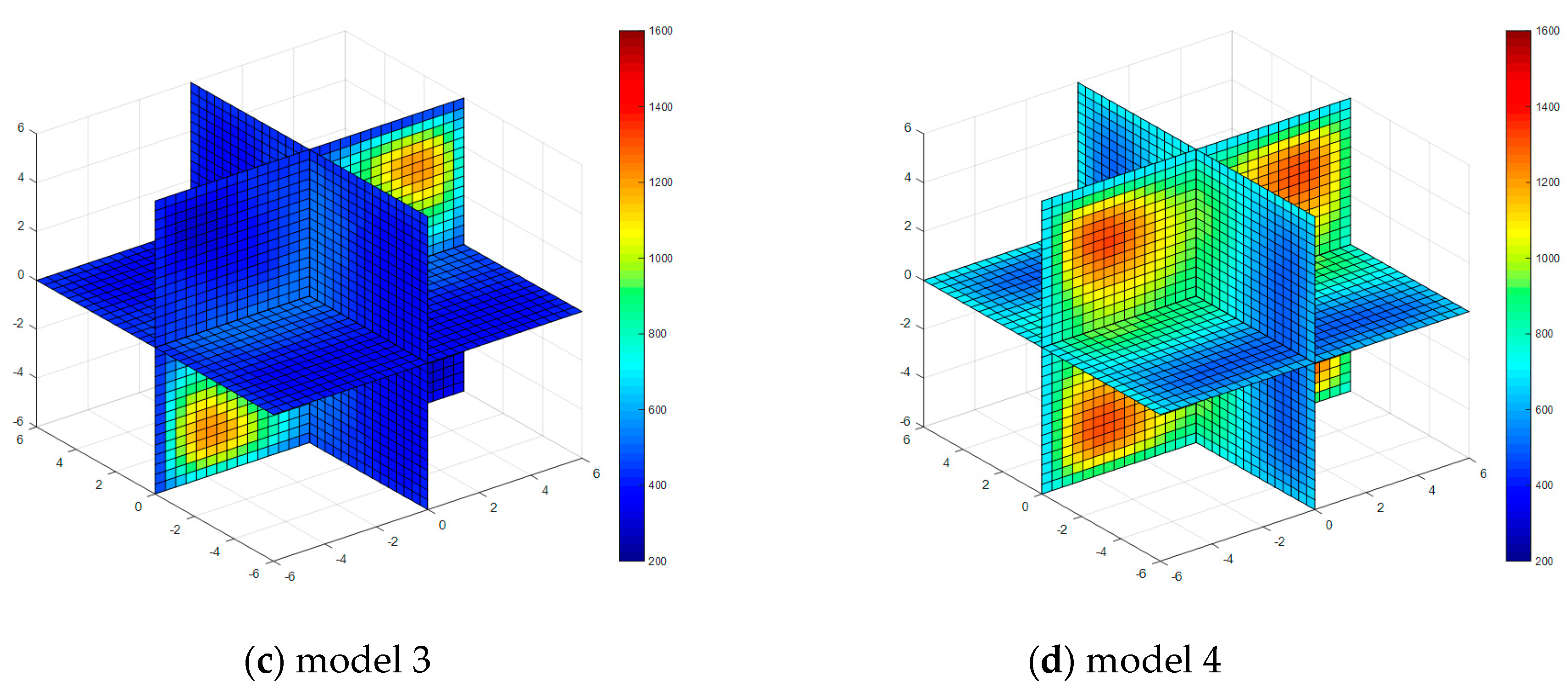
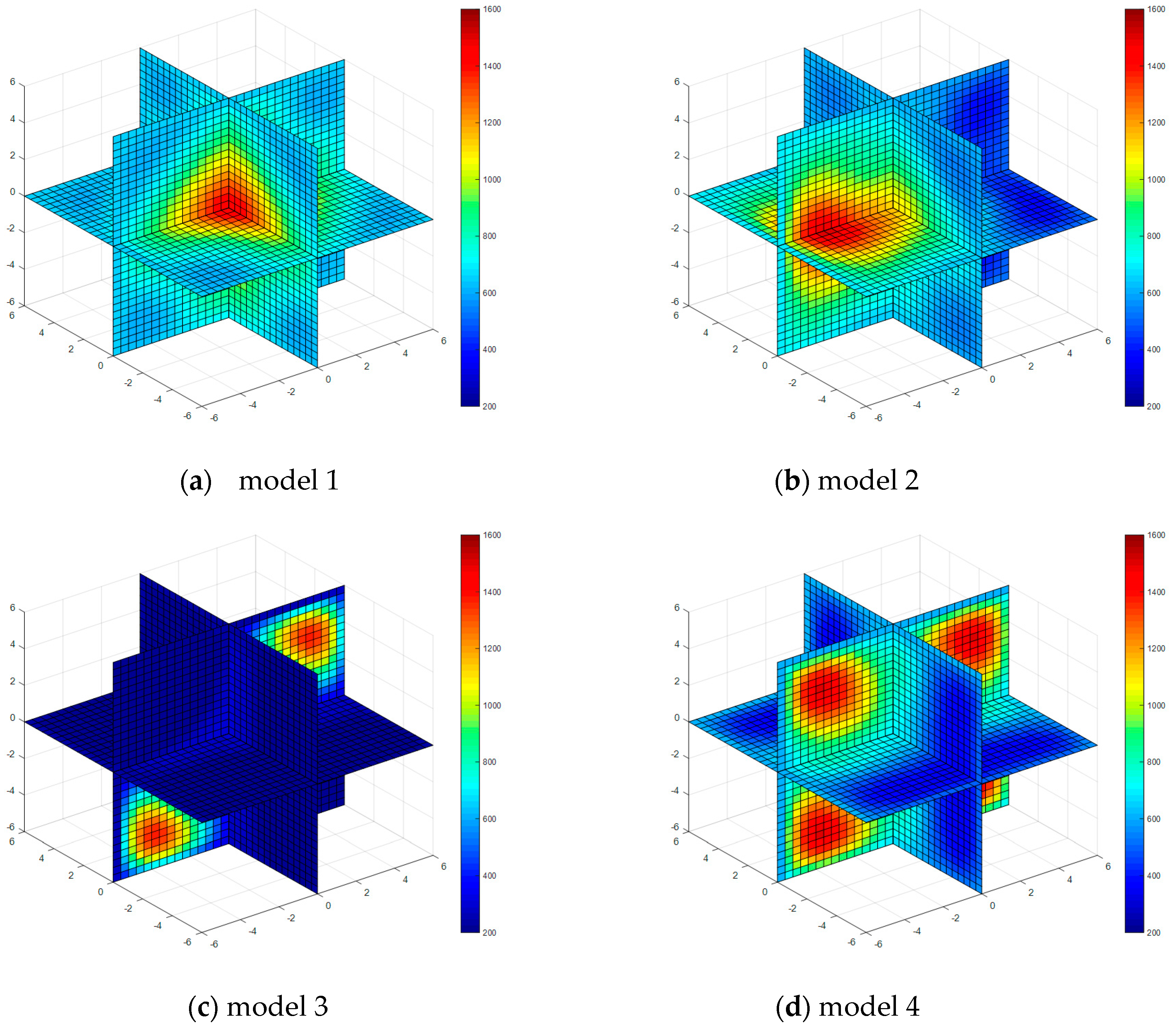
| Property | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| relaxation factor | 0.24 | 0.22 | 0.20 | 0.20 |
| iteration step | 120 | 120 | 120 | 120 |
| Algorithm | Model | E1 | E2 | E3 |
|---|---|---|---|---|
| LSM | model 1 | 1.02 | 3.30 | 1.88 |
| model 2 | 7.21 | 2.45 | 6.67 | |
| model 3 | 11.26 | 6.82 | 9.86 | |
| model 4 | 26.05 | 11.53 | 10.37 | |
| ART | model 1 | 1.02 | 3.30 | 1.88 |
| model 2 | 5.41 | 2.02 | 5.52 | |
| model 3 | 7.83 | 6.23 | 9.74 | |
| model 4 | 16.04 | 10.68 | 10.34 | |
| STR | model 1 | 1.02 | 3.30 | 1.88 |
| model 2 | 7.23 | 2.53 | 6.69 | |
| model 3 | 12.37 | 5.36 | 9.87 | |
| model 4 | 26.37 | 11.50 | 10.38 | |
| SIRT | model 1 | 1.01 | 3.30 | 1.88 |
| model 2 | 4.25 | 1.94 | 5.21 | |
| model 3 | 7.04 | 6.11 | 7.81 | |
| model 4 | 15.24 | 10.13 | 10.15 | |
| DRARE | model 1 | 0.43 | 0.89 | 0.33 |
| model 2 | 2.02 | 1.07 | 0.41 | |
| model 3 | 4.85 | 2.27 | 2.06 | |
| model 4 | 8.36 | 6.15 | 4.21 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, S.; Inaki, S.H. Dynamic Reconstruction Algorithm of Three-Dimensional Temperature Field Measurement by Acoustic Tomography. Sensors 2017, 17, 2084. https://doi.org/10.3390/s17092084
Li Y, Liu S, Inaki SH. Dynamic Reconstruction Algorithm of Three-Dimensional Temperature Field Measurement by Acoustic Tomography. Sensors. 2017; 17(9):2084. https://doi.org/10.3390/s17092084
Chicago/Turabian StyleLi, Yanqiu, Shi Liu, and Schlaberg H. Inaki. 2017. "Dynamic Reconstruction Algorithm of Three-Dimensional Temperature Field Measurement by Acoustic Tomography" Sensors 17, no. 9: 2084. https://doi.org/10.3390/s17092084




