Underdetermined Blind Source Separation of Synchronous Orthogonal Frequency Hopping Signals Based on Single Source Points Detection
Abstract
:1. Introduction
2. The Problem Formulation
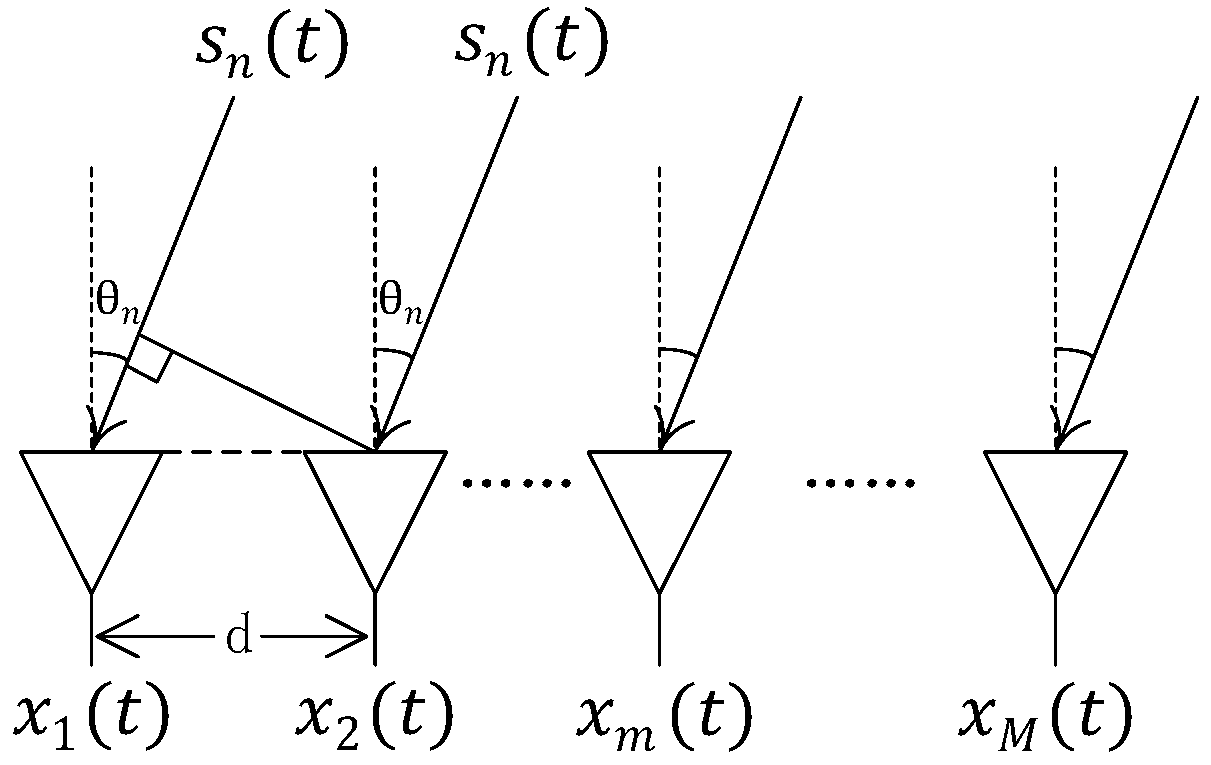
2.1. The Signal Model
2.2. The UBSS Assumptions
3. The Proposed Algorithms
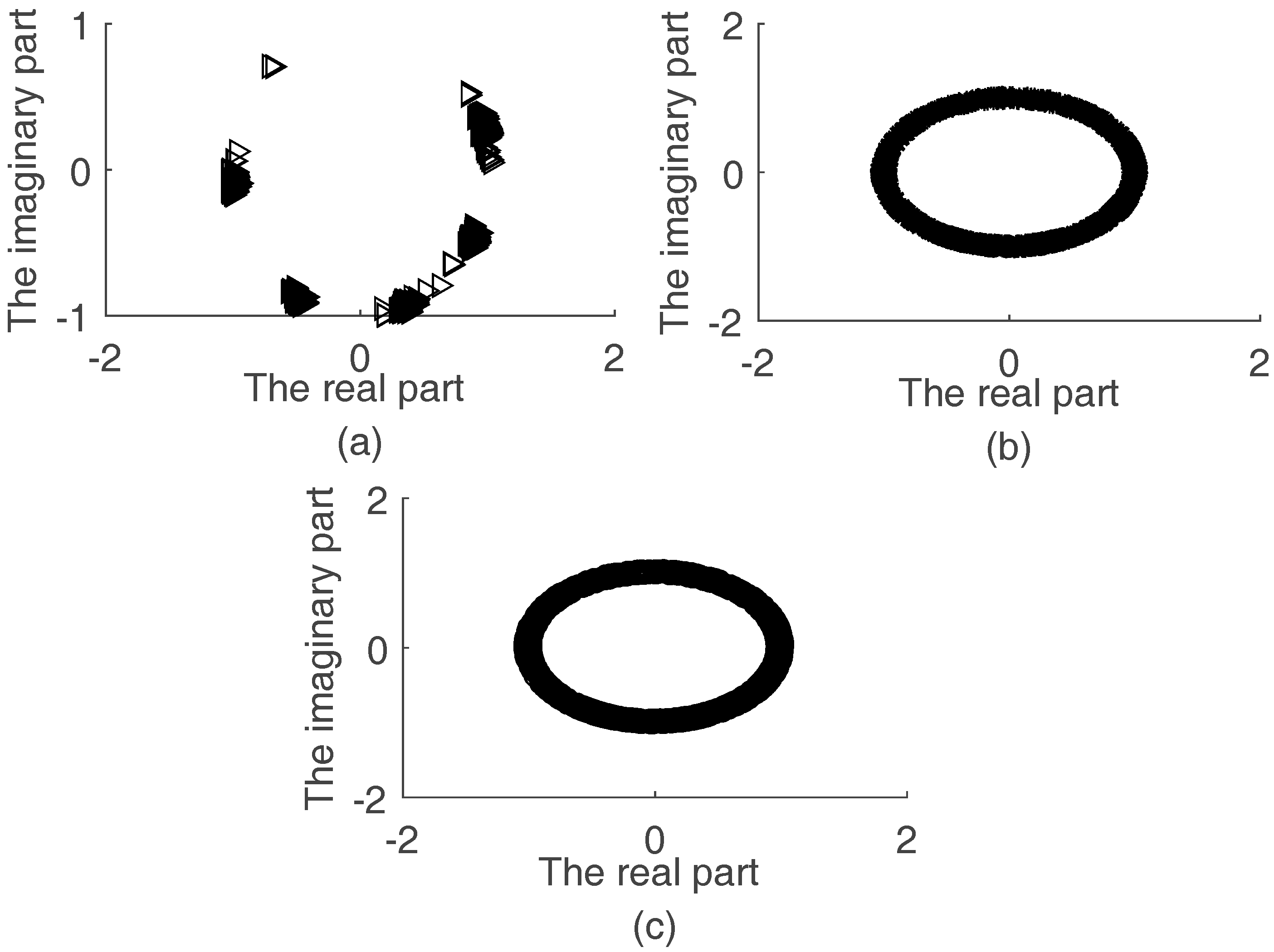
3.1. Single Source Detection
3.2. The Mixing Matrix Estimation
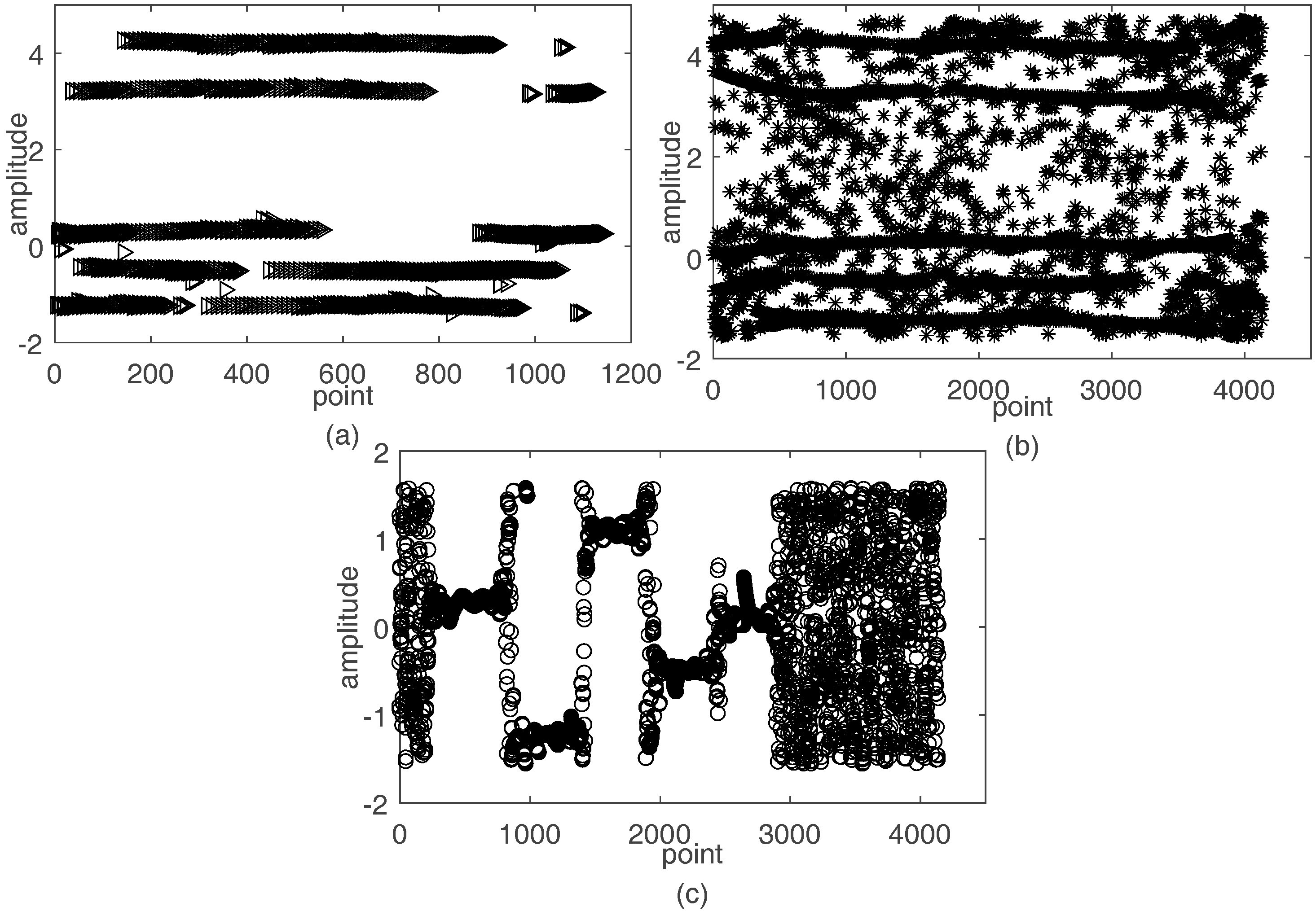
3.3. FH Signals Recovery
3.4. DOA Estimation and Splicing of FH Signals
| Algorithm 1 The proposed algorithm |
| Input: The received signals |
Step 1: Segment the received signals based on the known or estimated hop timings. Step 2: In one hop duration, calculate the STFT of the received signals. For each TF point , calculate and utilize Theorem (8) to detect signal-source-points. Step 3: Calculate for all SSPs. Based on (11), can be obtained and is calculated via clustering method. Step 4: Calculate the mixing matrix by (12). Step 5: Estimate by (13), and calculate the inverse STFT to obtain FH signals. The frequency can be calculated by FFT. Step 6: Calculate DOAs by (14). Step 7: In another hop duration, repeat Step 2 to Step 6. Step 8: Compare the DOAs in different hop durations. The recovered FH signals can be spliced according to (15). Output: , and recovered FH signals. |
4. Simulations
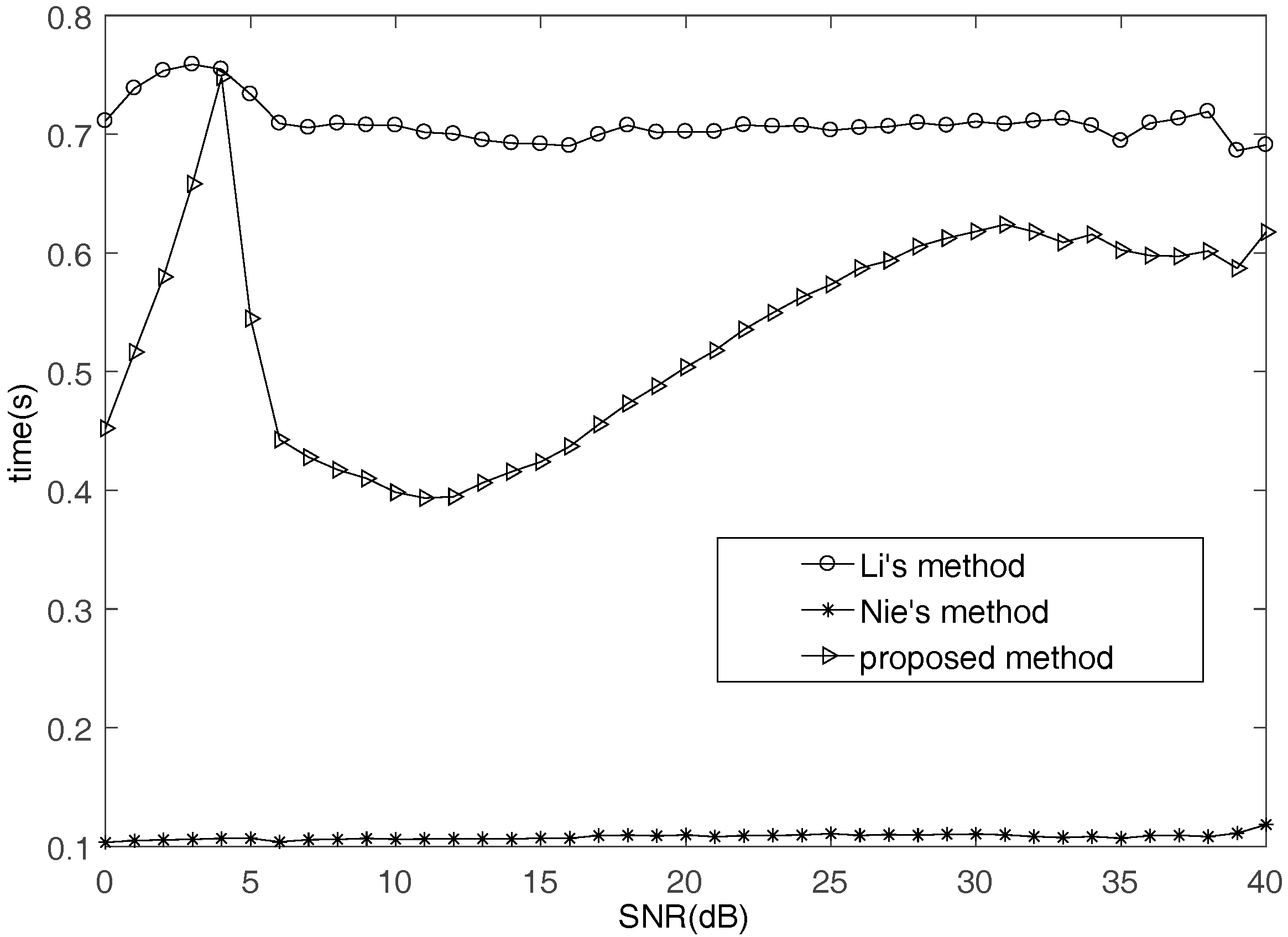
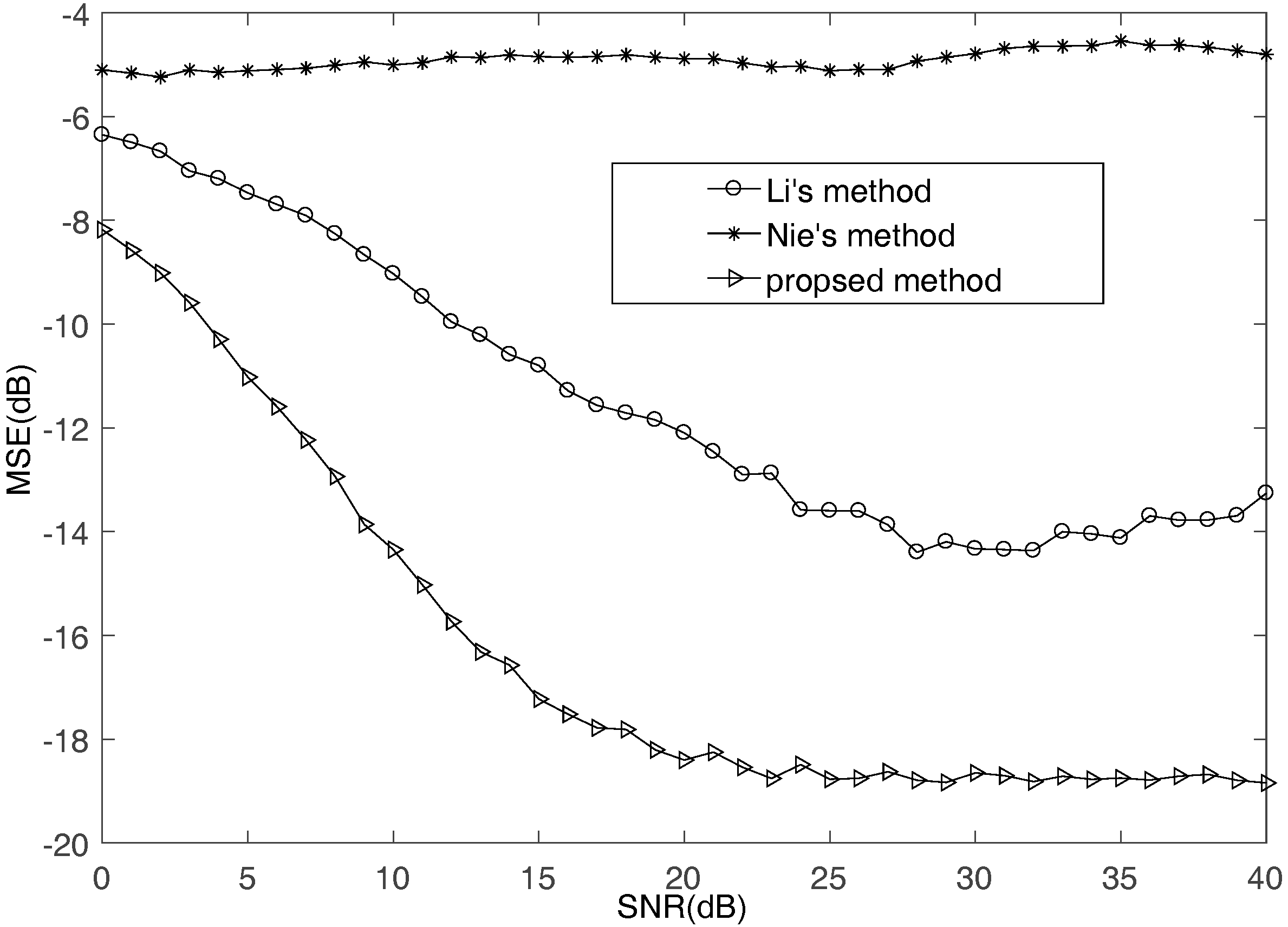
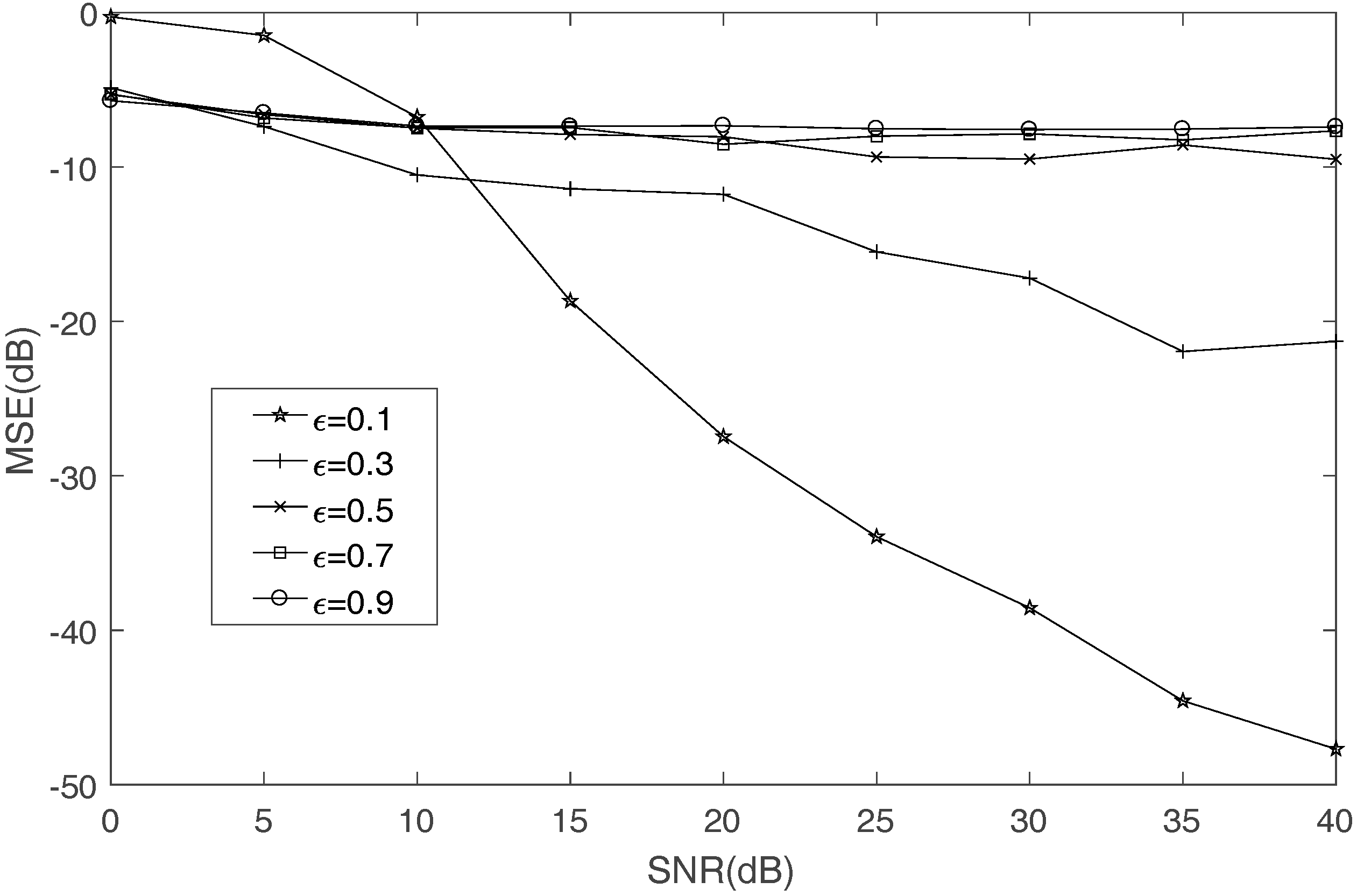
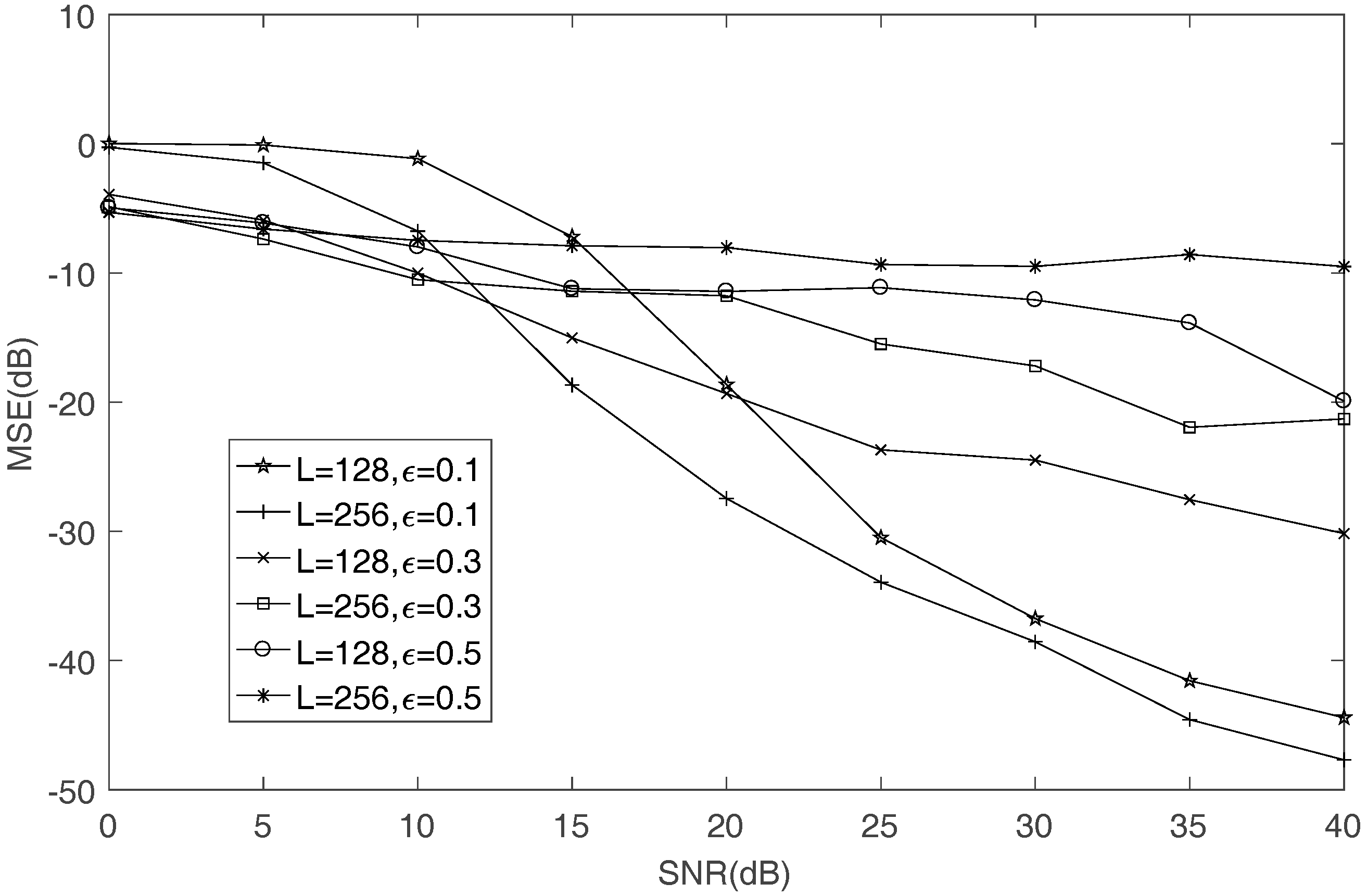
4.1. Mixing Matrix Estimation
4.2. FH Signals Recovery
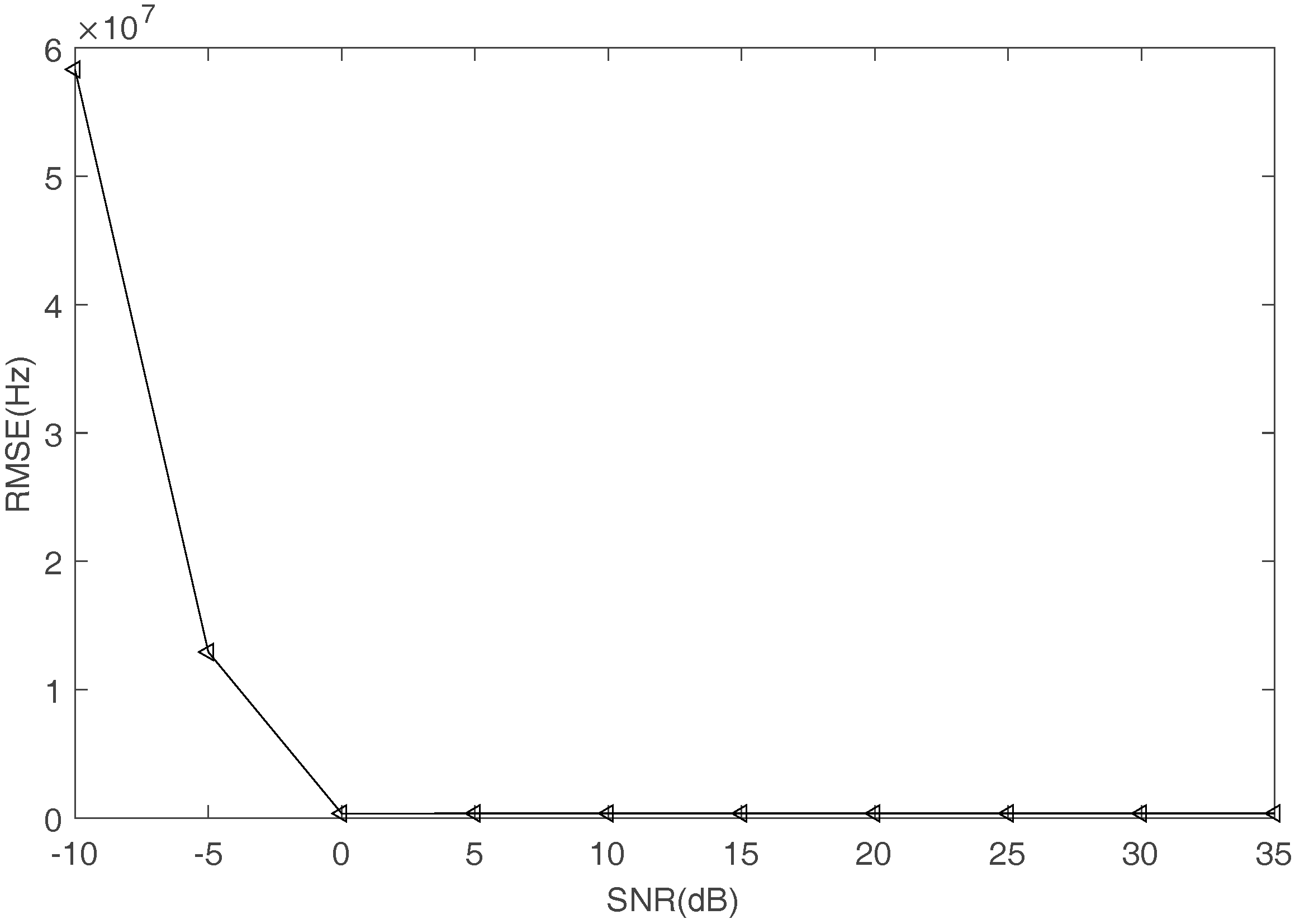
4.3. DOA Estimation and Splicing FH Signals
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Notation
| , , | the transpose, inverse and conjugate transpose of , respectively. |
| norm of matrix | |
| the absolute value of | |
| the real part of | |
| the imaginary part of |
Appendix A
References
- Torrieri, D.J. Mobile frequency-hopping cdma systems. IEEE Trans. Commun. 2000, 48, 1318–1327. [Google Scholar] [CrossRef]
- Barbarossa, S.; Scaglione, A. Parameter estimation of spread spectrum frequency-hopping signals using time-frequency distributions. In Proceedings of the 1997 First IEEE Signal Processing Workshop on Signal Processing Advances in Wireless Communications, Paris, France, 16–18 April 1997; pp. 213–216. [Google Scholar]
- Bae, S.; Kim, S.; Kim, J. Efficient frequency-hopping synchronization for satellite communications using dehop-rehop transponders. IEEE Trans. Aerosp. Electr. Syst. 2016, 52, 261–274. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, W.; Yan, J. Direction of arrival estimation for off-grid signals based on sparse bayesian learning. IEEE Sens. J. 2015, 16, 2004–2016. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Y. Frequency hopping radar signals blind separation using tensor analysis in time domain. In Proceedings of the IEEE/ACES International Conference on Wireless Information Technology and Systems, Honolulu, HI, USA, 13–18 March 2016. [Google Scholar]
- Gu, Y.; Leshem, A. Robust adaptive beamforming based on interference covariance matrix reconstruction and steering vector estimation. IEEE Trans. Signal Process. 2012, 60, 3881–3885. [Google Scholar]
- Zhou, C.; Gu, Y.; He, S.; Shi, Z. A robust and efficient algorithm for coprime array adaptive beamforming. IEEE Trans. Veh. Technol. 2017. [Google Scholar] [CrossRef]
- Shi, Z.; Zhou, C.; Gu, Y.; Goodman, N.A.; Qu, F. Source estimation using coprime array: A sparse reconstruction perspective. IEEE Sens. J. 2017, 17, 755–765. [Google Scholar] [CrossRef]
- Gu, Y.; Goodman, N.A. Information-theoretic compressive sensing kernel optimization and bayesian cramer-rao bound for time delay estimation. IEEE Trans. Signal Process. 2017, 65, 4525–4537. [Google Scholar] [CrossRef]
- Guo, M.; Tao, C.; Wang, B. An improved doa estimation approach using coarray interpolation and matrix denoising. Sensors 2017, 17, 1140. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhang, Y.D.; Wang, W. Robust DOA estimation in the presence of mis-calibrated sensors. IEEE Signal Process. Lett. 2017, 24, 1073–1077. [Google Scholar] [CrossRef]
- Zhou, C.W.; Zhang, Y.M.D.; Shi, Z.G.; Jin, T.; Wu, X.D. Compressive sensing based coprime arrey direction-of-arrival estimation. IET Commun. 2016. [Google Scholar] [CrossRef]
- Wan, L.; Han, G.; Shu, L.; Chan, S.; Zhu, T. The application of doa estimation approach in patient tracking systems with high patient density. IEEE Trans. Ind. Inform. 2016, 12, 2353–2364. [Google Scholar] [CrossRef]
- Wan, L.; Han, G.; Shu, L.; Chan, S.; Feng, N. Pd source diagnosis and localization in industrial high-voltage insulation system via multimodal joint sparse representation. IEEE Trans. Ind. Electron. 2016, 63, 2506–2516. [Google Scholar] [CrossRef]
- Liu, X.; Sidiropoulos, N.D.; Swami, A. Joint hop timing and frequency estimation for collision resolution in fh networks. IEEE Trans. Wirel. Commun. 2005, 4, 3063–3074. [Google Scholar]
- Liu, X.; Sidiropoulos, N.D.; Swami, A. Blind high-resolution localization and tracking of multiple frequency hopped signals. Signal Process. IEEE Trans. 2002, 50, 889–901. [Google Scholar]
- Liu, X.; Sidiropoulos, N.D.; Swami, A. Joint hop timing and doa estimation for multiple noncoherent frequency hopped signals. Sens. Array Multichannel Signal Process. Workshop Proc. 2002, 164–168. [Google Scholar] [CrossRef]
- Liu, X.; Li, J.; Ma, X. An em algorithm for blind hop timing estimation of multiple fh signals using an array system with bandwidth mismatch. IEEE Trans. Veh. Technol. 2007, 56, 2545–2554. [Google Scholar] [CrossRef]
- Fu, W.; Hei, Y.; Li, X. Ubss and blind parameters estimation algorithms for synchronous or thogonal fh signals. Syst. Eng. Electron. J. 2014, 25, 911–920. [Google Scholar] [CrossRef]
- Sha, Z.C.; Huang, Z.T.; Zhou, Y.Y.; Wang, F.H. Frequency-hopping signals sorting based on underdetermined blind source separation. IET Commun. 2013, 7, 1456–1464. [Google Scholar] [CrossRef]
- Bofill, P.; Zibulevsky, M. Underdetermined blind source separation using sparse representations. Signal Process. 2001, 81, 2353–2362. [Google Scholar] [CrossRef]
- Sadhu, A.; Hazra, B.; Narasimhan, S. Decentralized modal identification of structures using parallel factor decomposition and sparse blind source separation. Mech. Syst. Signal Process. 2013, 41, 396–419. [Google Scholar] [CrossRef]
- Georgiev, P.; Theis, F.; Cichocki, A. Sparse component analysis and blind source separation of underdetermined mixtures. IEEE Trans. Neural Netw. 2005, 16, 992–996. [Google Scholar] [CrossRef] [PubMed]
- Abrard, F.; Deville, Y. A time–frequency blind signal separation method applicable to underdetermined mixtures of dependent sources. Signal Process. 2005, 85, 1389–1403. [Google Scholar] [CrossRef]
- Esmaeilbeig, M.; Sheikhzadeh, H.; Razzazi, F. A novel and fast algorithm for solving permutation in convolutive bss, based on real and imaginary decomposition. Circuits Syst. Signal Process. 2016, 35, 4532–4549. [Google Scholar] [CrossRef]
- He, X.S.; He, F.; Cai, W.H. Underdetermined bss based on k -means and ap clustering. Circuits Syst. Signal Process. 2016, 35, 1–33. [Google Scholar] [CrossRef]
- Kim, S.G.; Yoo, C.D. Underdetermined blind source separation based on subspace representation. IEEE Trans. Signal Process. 2009, 57, 2604–2614. [Google Scholar]
- Reju, V.G.; Koh, S.N.; Soon, I.Y. An algorithm for mixing matrix estimation in instantaneous blind source separation. Signal Process. 2009, 89, 1762–1773. [Google Scholar] [CrossRef]
- Thiagarajan, J.J.; Karthikeyan, N.R.; Spanias, A. Mixing matrix estimation using discriminative clustering for blind source separation. Digit. Signal Process. 2013, 23, 9–18. [Google Scholar] [CrossRef]
- Xu, J.D.; Yu, X.C.; Hu, D.; Zhang, L.B. A fast mixing matrix estimation method in the wavelet domain. Signal Process. 2014, 95, 58–66. [Google Scholar] [CrossRef]
- Xie, S.; Yang, L.; Yang, J.M.; Zhou, G.; Xiang, Y. Time-frequency approach to underdetermined blind source separation. Neural Netw. Learn. Syst. IEEE Trans. 2012, 23, 306–316. [Google Scholar]
- Peng, D.; Xiang, Y. Underdetermined blind separation of non-sparse sources using spatial time-frequency distributions. Digit. Signal Process. 2010, 20, 581–596. [Google Scholar] [CrossRef]
- Yang, L.; Lv, J.; Xiang, Y. Underdetermined blind source separation by parallel factor analysis in time-frequency domain. Cogn. Comput. 2013, 5, 207–214. [Google Scholar] [CrossRef]
- Peng, T.L.; Chen, Y.; Liu, Z.L. A time-frequency domain blind source separation method for underdetermined instantaneous mixtures. Circuits Syst. Signal Process. 2015, 34, 3883–3895. [Google Scholar] [CrossRef]
- Li, H.; Shen, Y.H.; Wang, J.G.; Ren, X.S. Estimation of the complex-valued mixing matrix by single-source-points detection with less sensors than sources. Trans. Emerg. Telecommun. Technol. 2012, 23, 137–147. [Google Scholar] [CrossRef]
- Li, Y.; Nie, W.; Ye, F. A complex mixing matrix estimation algorithm based on single source points. Circuits Syst. Signal Process. 2015, 34, 3709–3723. [Google Scholar] [CrossRef]
- Lu, F.; Huang, Z.; Jiang, W. Underdetermined blind separation of non-disjoint signals in time-frequency domain based on matrix diagonalization. Signal Process. 2011, 91, 1568–1577. [Google Scholar] [CrossRef]
- Aissa-El-Bey, A.; Linh-Trung, N.; Abed-Meraim, K.; Belouchrani, A.; Grenier, Y. Underdetermined blind separation of nondisjoint sources in the time-frequency domain. IEEE Trans. Signal Process. 2007, 55, 897–907. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, J.; Lu, K.; Zhang, Q. Modified subspace method based on convex model for underdetermined blind speech separation. IEEE Trans. Consum. Electron. 2014, 60, 225–232. [Google Scholar] [CrossRef]
- Zhao, L.F.; Wang, L.; Bi, G.A.; Zhang, L.R.; Zhang, H.J. Robust frequency-hopping spectrum estimation based on sparse bayesian method. IEEE Trans. Wirel. Commun. 2015, 14, 781–793. [Google Scholar] [CrossRef]
- Angelosante, D.; Giannakis, G.B.; Sidiropoulos, N.D. Estimating multiple frequency-hopping signal parameters via sparse linear regression. IEEE Trans. Signal Process. 2010, 58, 5044–5056. [Google Scholar] [CrossRef]
- Yilmaz, O.; Rickard, S. Blind separation of speech mixtures via time-frequency masking. Signal Process. IEEE Trans. 2004, 52, 1830–1847. [Google Scholar] [CrossRef]
- Dong, T.; Lei, Y.; Yang, J. An algorithm for underdetermined mixing matrix estimation. Neurocomputing 2013, 104, 26–34. [Google Scholar] [CrossRef]
- Yang, J.; Liao, G.; Li, J. An efficient off-grid doa estimation approach for nested array signal processing by using sparse bayesian learning strategies. Signal Proc. 2016, 128, 110–122. [Google Scholar] [CrossRef]





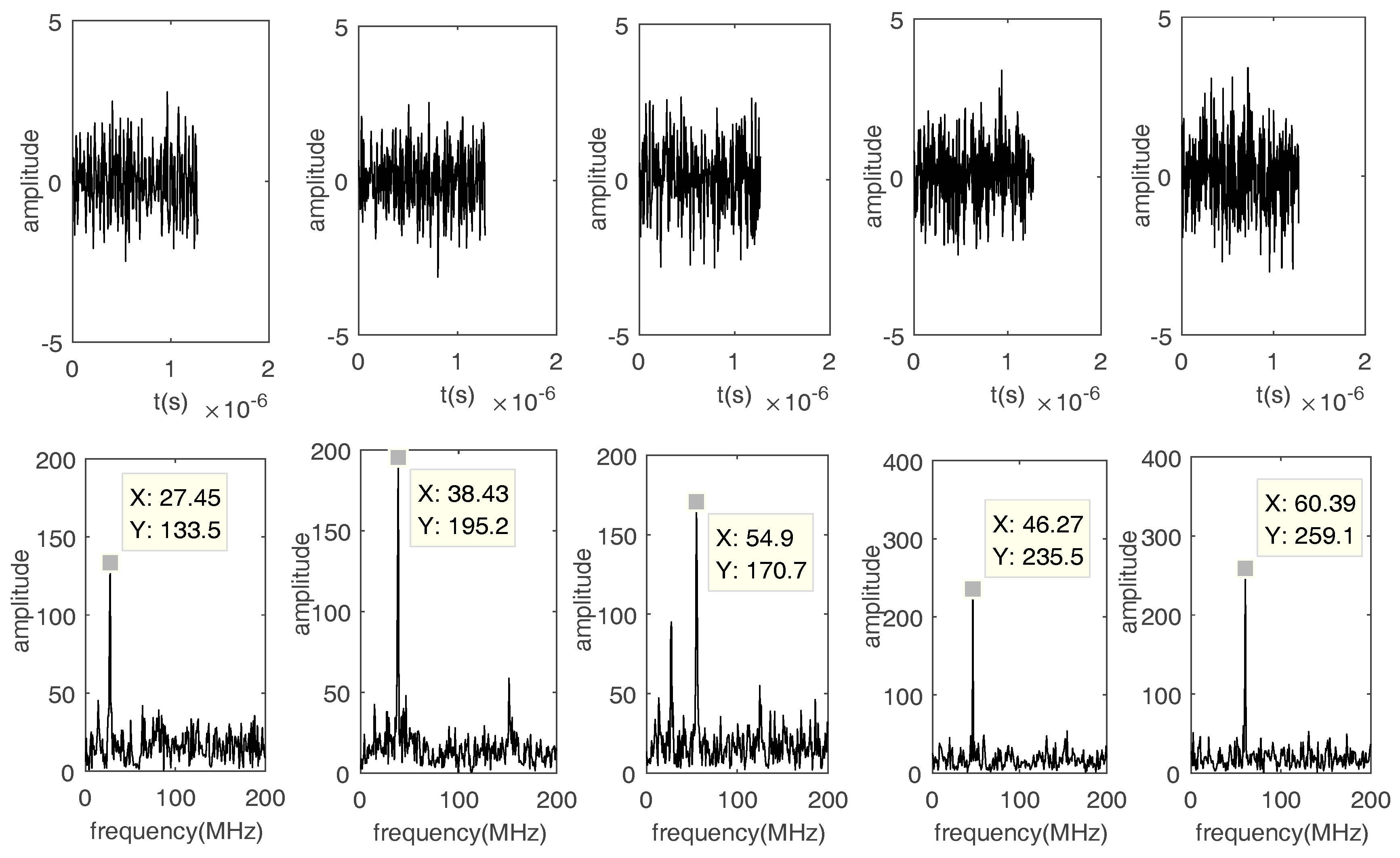
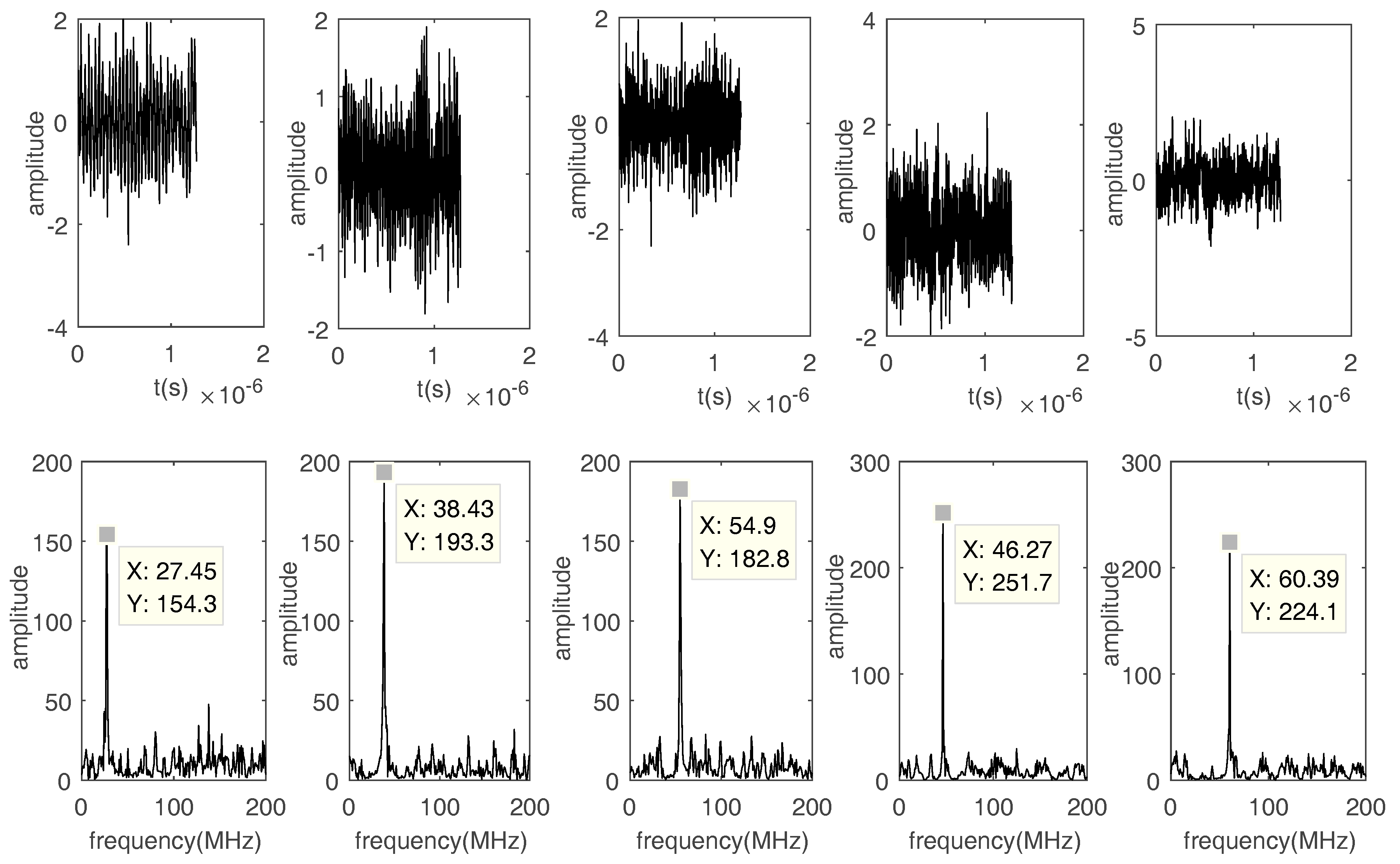


| Signals | Frequency (MHz) | DOA(°) |
|---|---|---|
| Signal 1 | 27, 33 | 100 |
| Signal 2 | 38, 44 | 50 |
| Signal 3 | 55, 61 | 80 |
| Signal 4 | 46, 52 | 30 |
| Signal 5 | 60, 66 | 10 |
| SNR = 15 dB | SNR = 25 dB | SNR = 30 dB | SNR = 40 dB | ||
|---|---|---|---|---|---|
| Hop duration 1 | Estimation DOAs (°) | 99.4272 | 99.7098 | 99.9485 | 99.8157 |
| 50.6795 | 50.4218 | 50.5310 | 50.5380 | ||
| 80.1626 | 80.0028 | 79.9600 | 79.9867 | ||
| 30.3958 | 30.5444 | 30.6250 | 30.5645 | ||
| 11.6847 | 12.0813 | 11.9910 | 11.8942 | ||
| RMSE | 0.8741 | 0.9890 | 0.9634 | 0.9197 | |
| Hop duration 2 | Estimation DOAs (°) | 99.9952 | 99.9788 | 100.0327 | 100.0226 |
| 49.8621 | 49.9086 | 49.8987 | 49.8865 | ||
| 79.6136 | 80.0633 | 49.8987 | 49.8865 | ||
| 31.7015 | 31.2438 | 30.9527 | 31.0309 | ||
| 10.3528 | 9.6034 | 9.1250 | 9.2847 | ||
| RMSE | 0.7985 | 0.5860 | 0.5805 | 0.5626 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Wang, Y.; Jing, F. Underdetermined Blind Source Separation of Synchronous Orthogonal Frequency Hopping Signals Based on Single Source Points Detection. Sensors 2017, 17, 2074. https://doi.org/10.3390/s17092074
Zhang C, Wang Y, Jing F. Underdetermined Blind Source Separation of Synchronous Orthogonal Frequency Hopping Signals Based on Single Source Points Detection. Sensors. 2017; 17(9):2074. https://doi.org/10.3390/s17092074
Chicago/Turabian StyleZhang, Chaozhu, Yu Wang, and Fulong Jing. 2017. "Underdetermined Blind Source Separation of Synchronous Orthogonal Frequency Hopping Signals Based on Single Source Points Detection" Sensors 17, no. 9: 2074. https://doi.org/10.3390/s17092074




