Secure Communications in CIoT Networks with a Wireless Energy Harvesting Untrusted Relay
Abstract
:1. Introduction
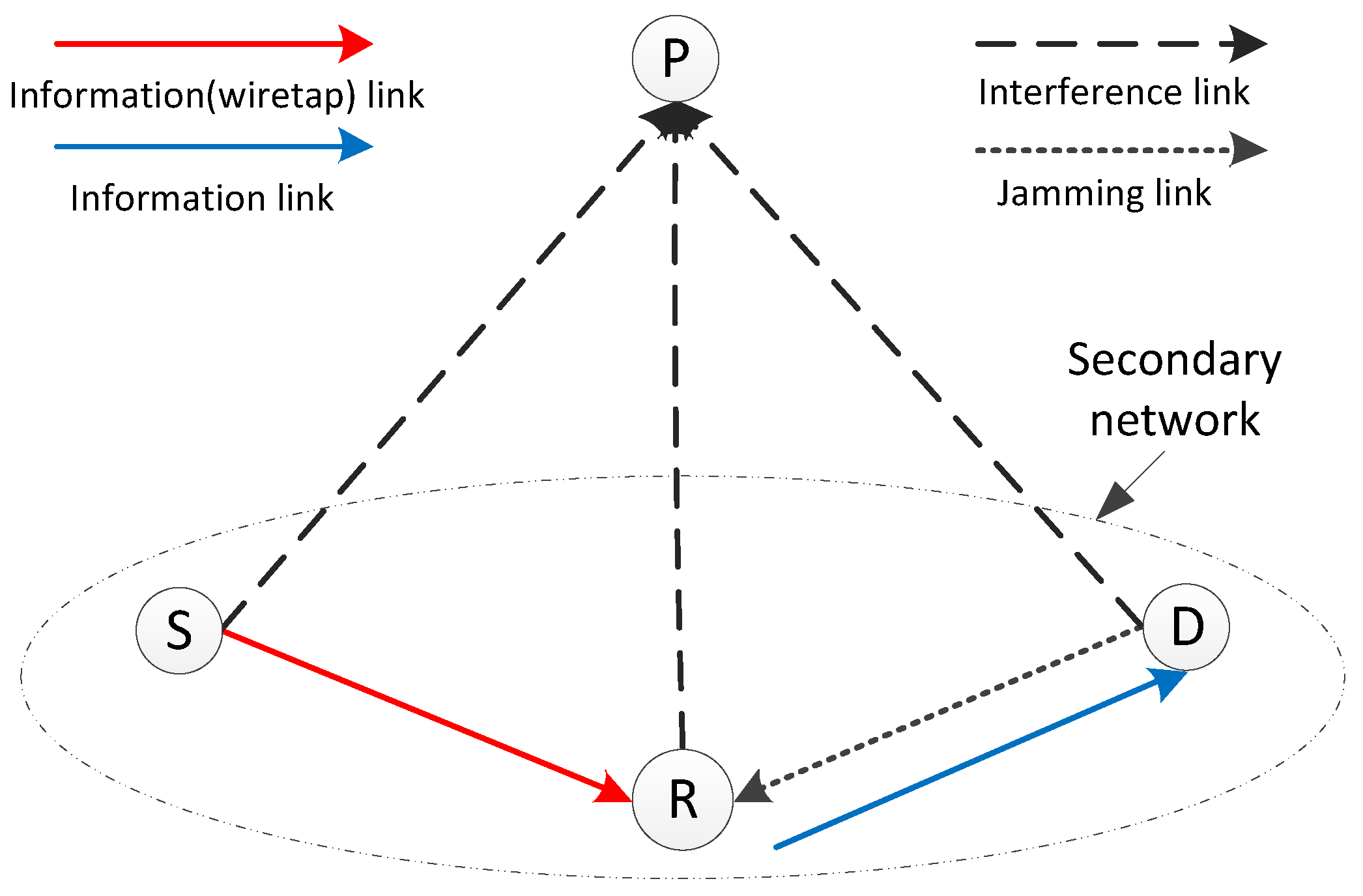
- We propose PLS transmission schemes for a CIoT network where an untrusted relay helps the secondary transmission. To the best of our knowledge, this is the first paper to consider the security issue in an underlay CIoT network with an untrusted relay from the PLS perspective. Since the transmissions of the IoT nodes may cause interference with the primary receiver, the existing secrecy criteria (e.g., secrecy outage or secrecy rate) can not describe the system performance properly. In this paper, we derived a new criterion to illustrate the secrecy performance of the CIoT network.
- To protect the information from being intercepted by the untrusted relay, amplify-and-forward relaying protocol is used and destination-aided jamming strategy is adopted. An intuitive secure scheme and a precoded secure scheme are proposed for the CIoT network based on PS and TS policies, respectively. The secrecy performances of these schemes are evaluated by the probability of successfully secure transmission (), which represents the probability that the interference threshold constraint is satisfied and the secrecy rate of the secondary transmission is positive. The closed forms of of the precoded secure schemes based on PS and TS policies are given and verified with the simulation results.
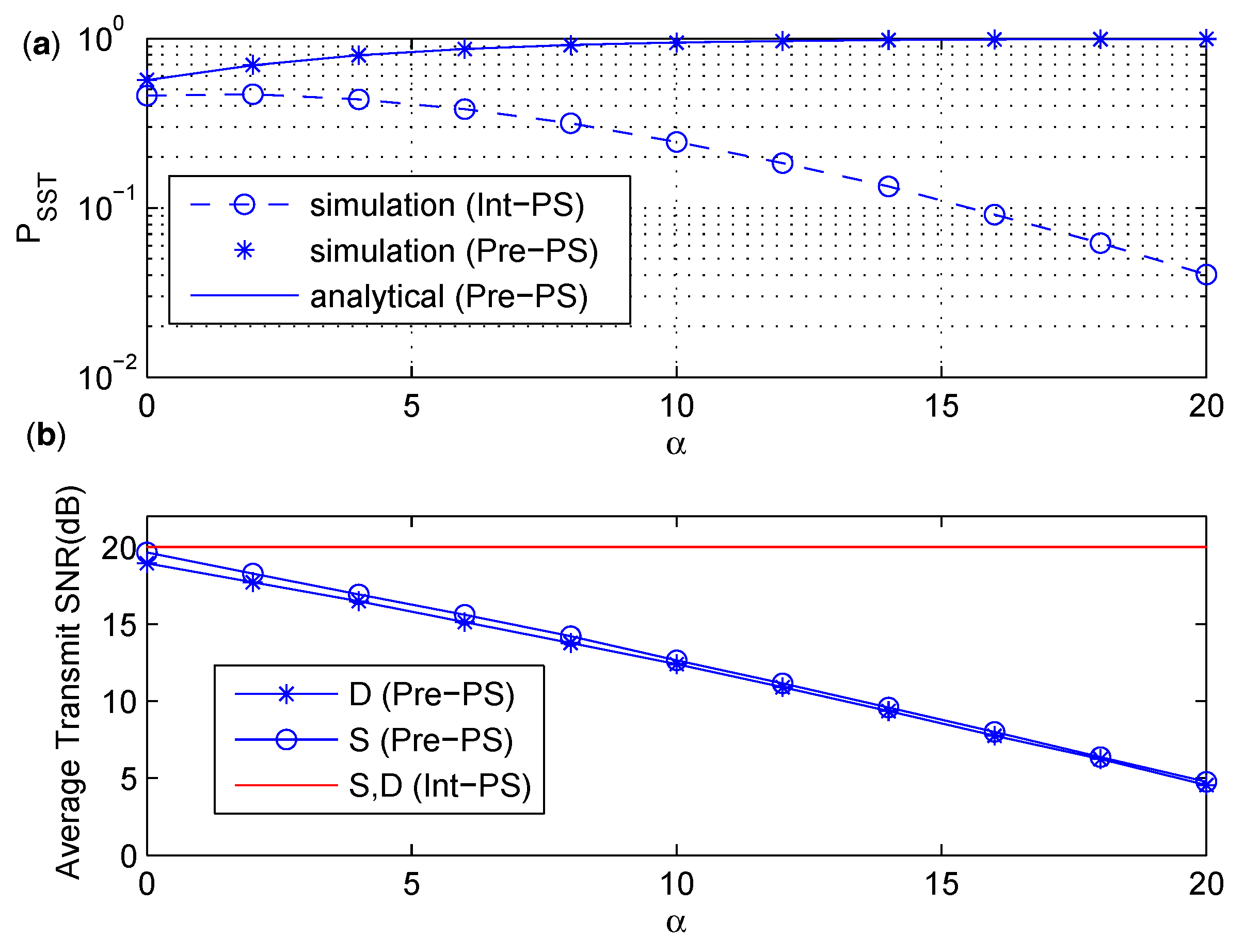
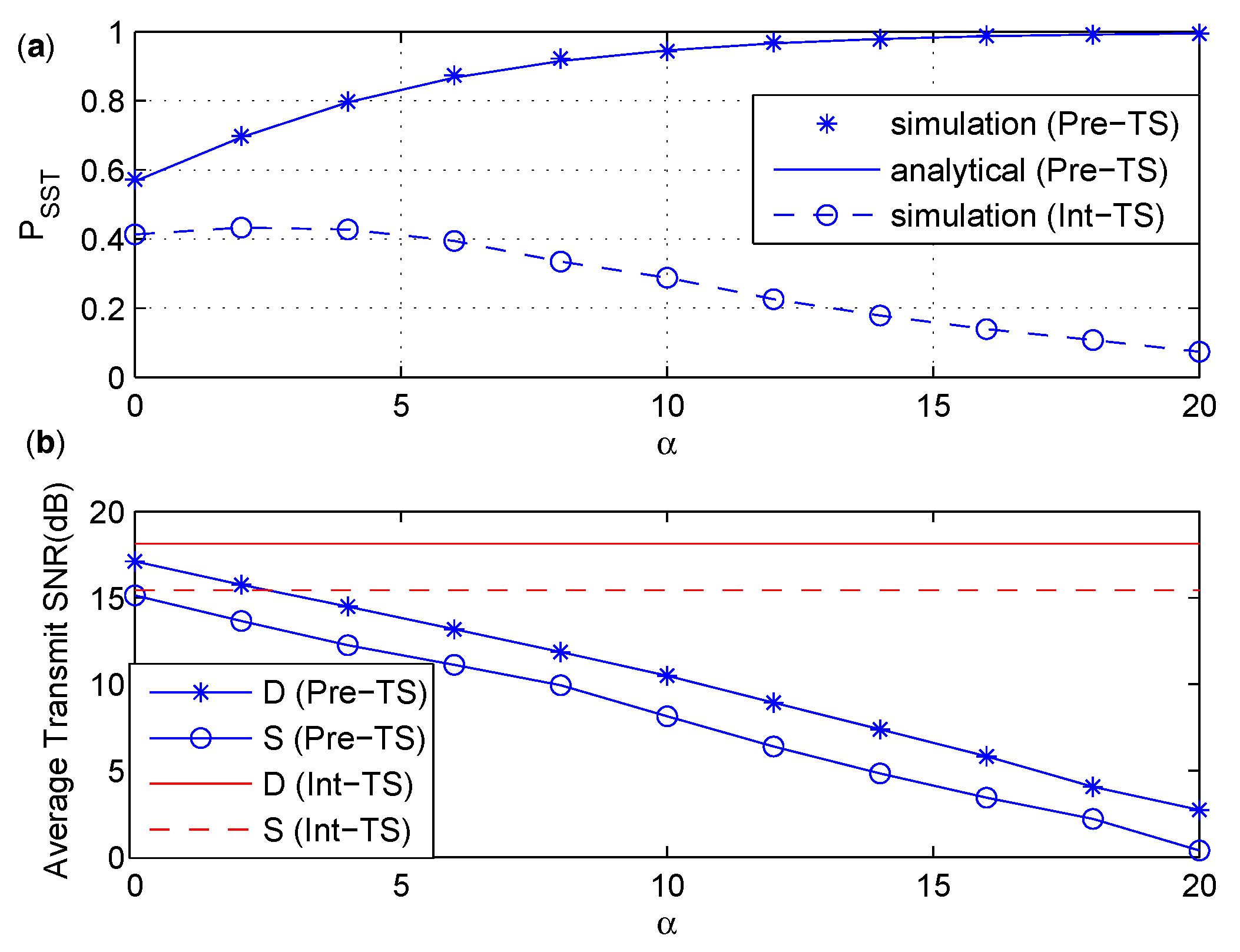
- We compare the intuitive secure scheme and the precoded secure scheme based on PS and TS policies, and find out that the precoded secure schemes have better than the intuitive secure schemes under similar power consumption. Moreover, the precoded secure scheme based on TS policy is more energy efficient than that based on PS policy.
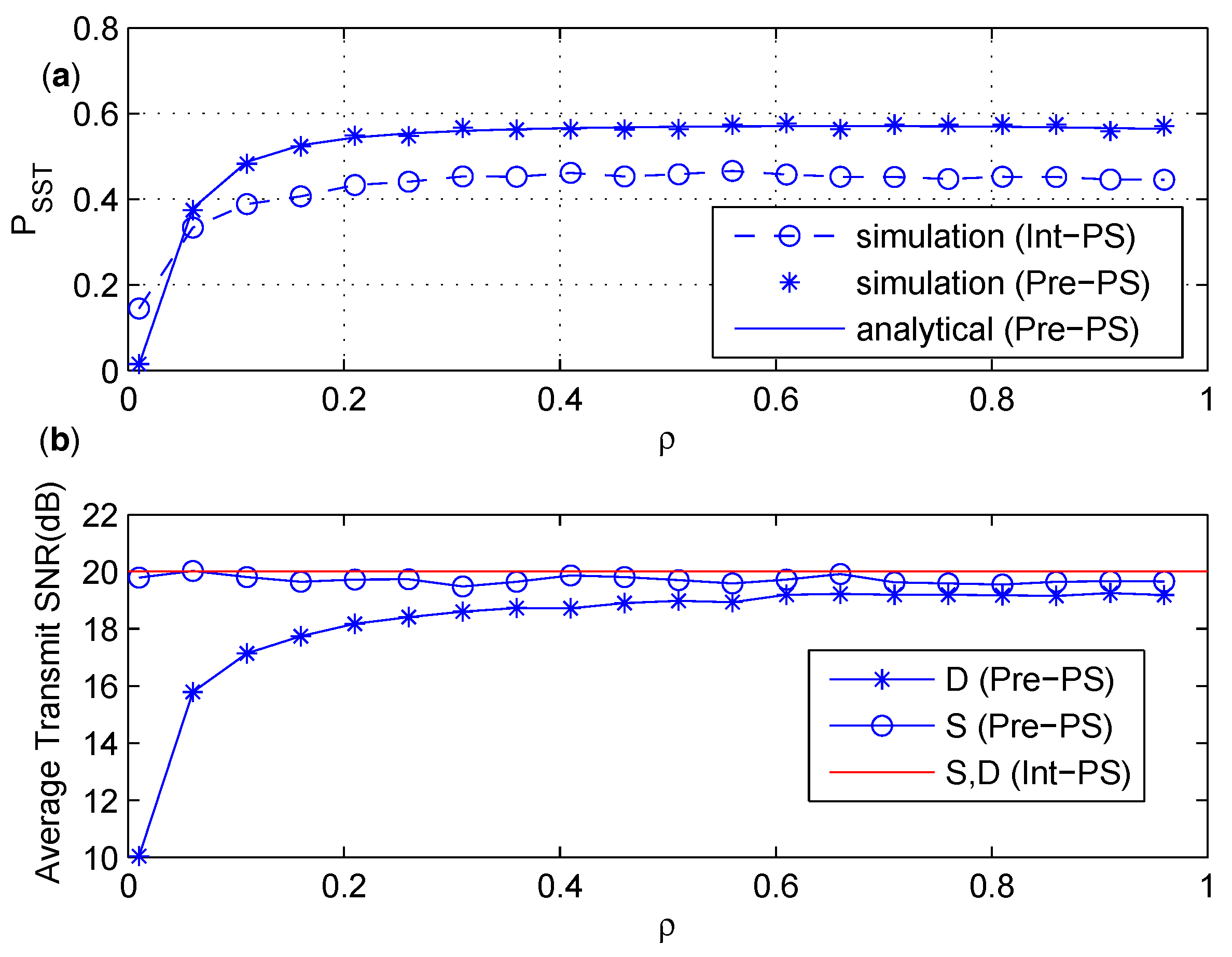
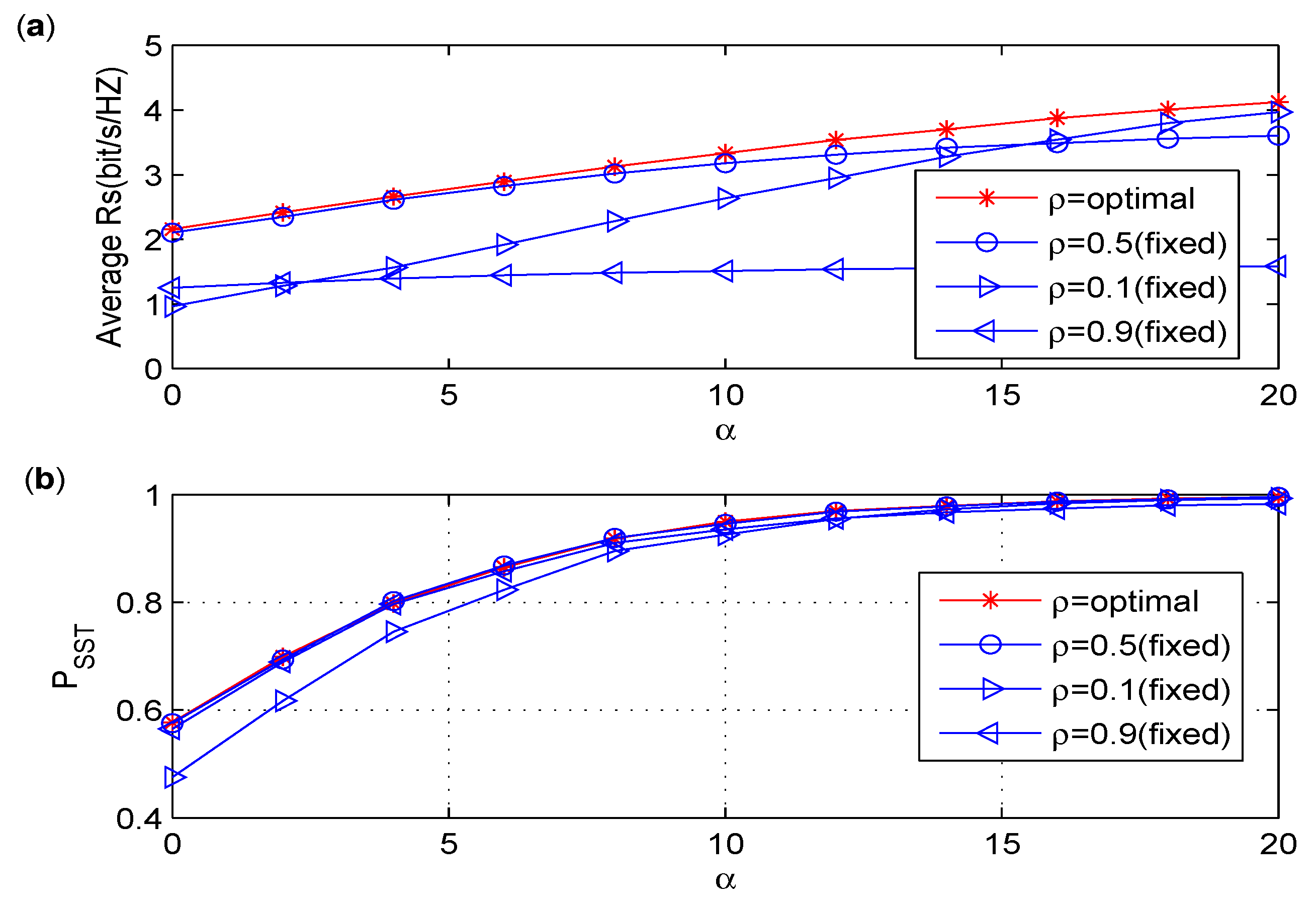
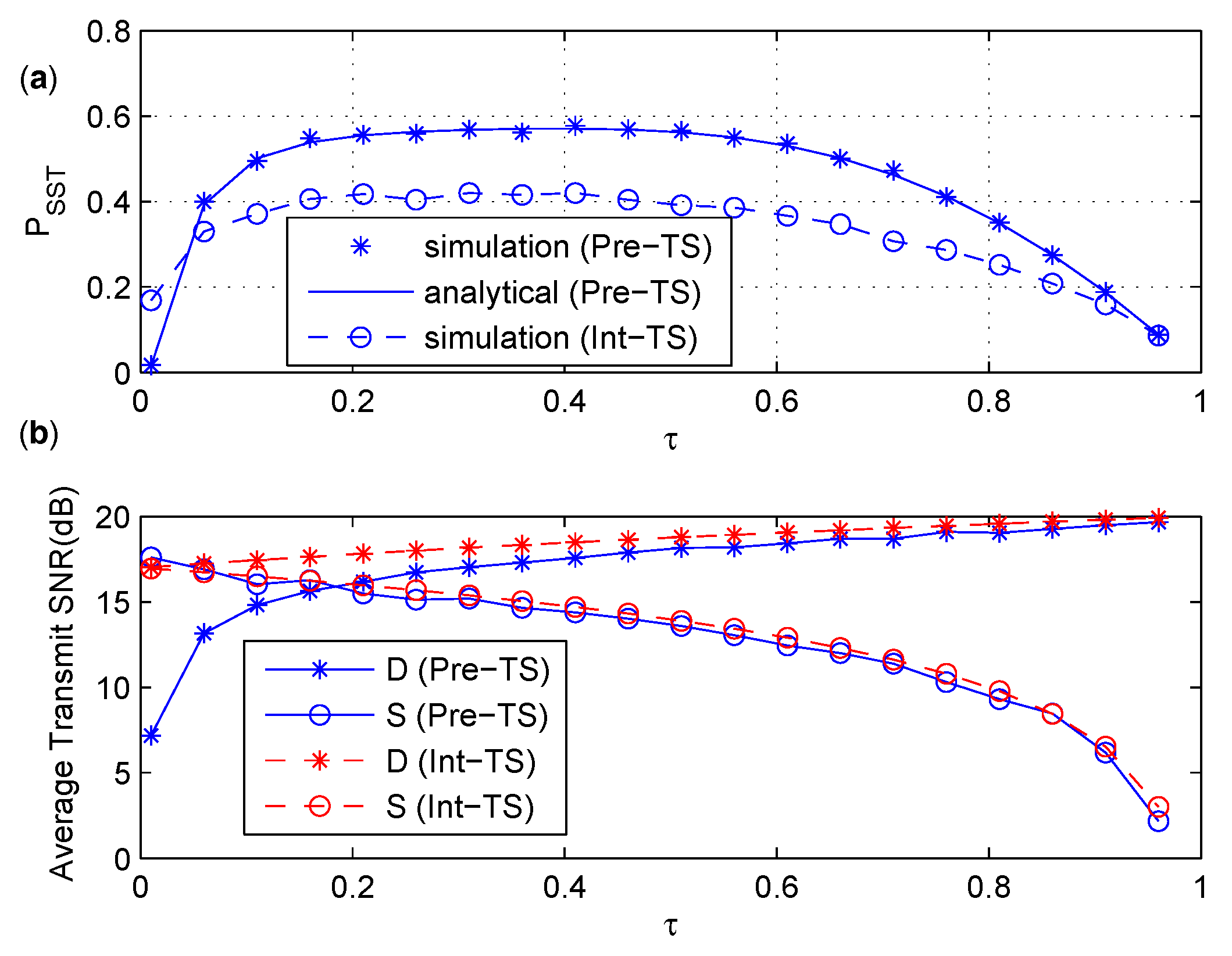
- The numerical results show that of the PS policy is not sensitive to the PS ratio when reaches a certain value, and an optimal PS ratio maximizing the achievable secrecy rate is considered under the constraint. In the TS policy, the time splitting ratio shows both constructive and destructive effects on the two-hop secondary transmission via the EH untrusted relay. Thus, there exists an optimal energy harvesting time in the TS policy that maximizes .
2. Related Work
3. System Model
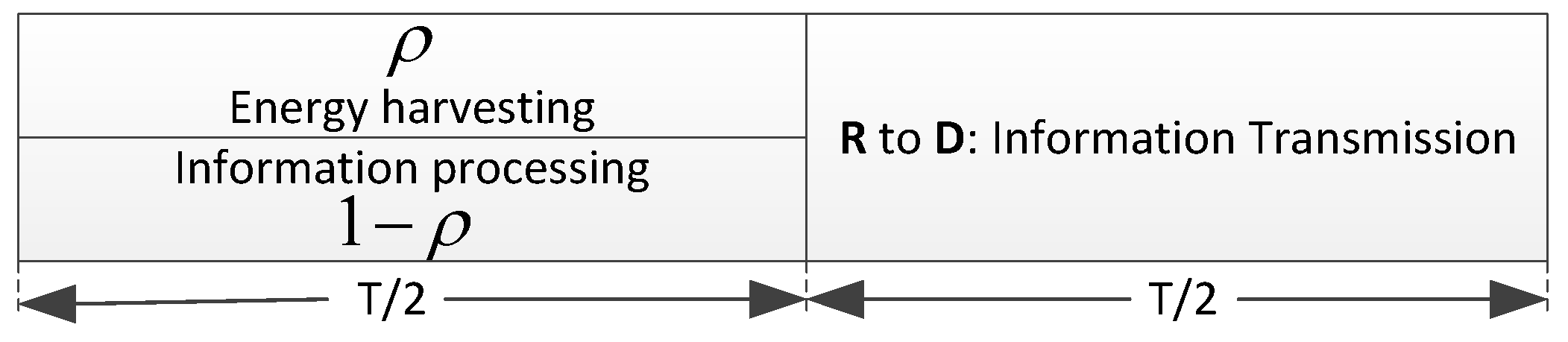
4. Secure Schemes Based on PS Policy
4.1. Intuitive Secure Scheme Based on PS Policy
4.1.1. Energy Harvesting and Information Processing of Int-PS
4.1.2. Probability of Successfully Secure Transmission of Int-PS
4.2. Precoded Secure Scheme Based on PS Policy
4.2.1. Energy Harvesting and Information Processing of Pre-PS
4.2.2. Probability of Successfully Secure Transmission of Pre-PS
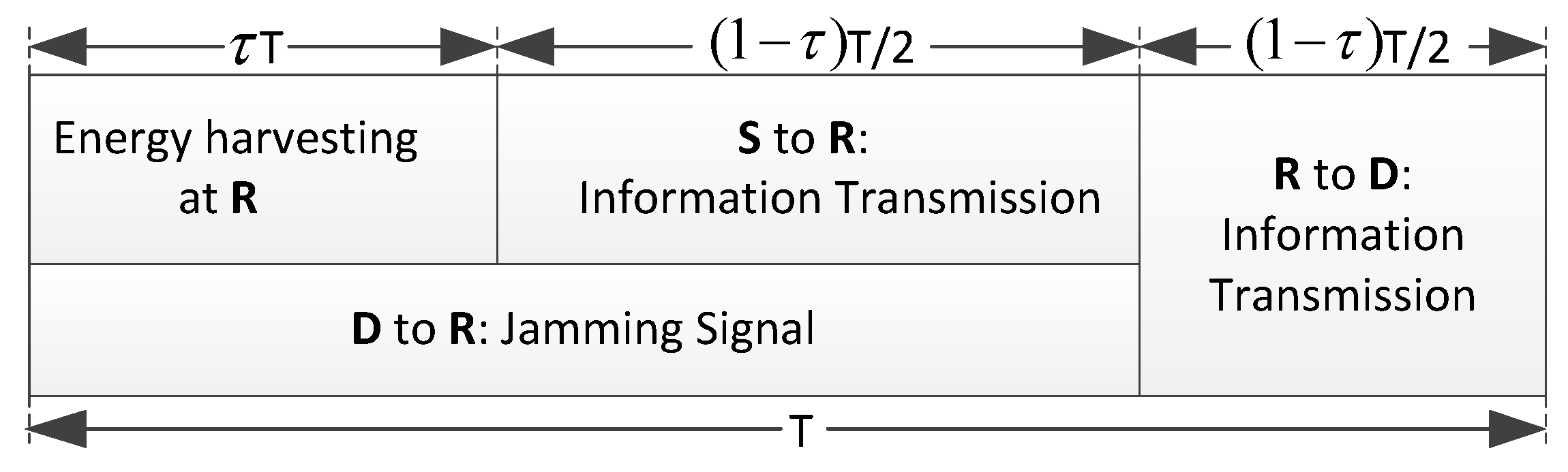
5. Secure Schemes Based on TS Policy
5.1. Intuitive Secure Scheme Based on TS Policy
5.1.1. Energy Harvesting and Information Processing of Int-TS
5.1.2. Probability of Successfully Secure Transmission of Int-TS
5.2. Precoded Secure Scheme Based on TS Policy
5.2.1. Energy Harvesting and Information Processing of Pre-TS
5.2.2. Probability of Successfully Secure Transmission of Pre-TS
6. Discussion and Simulations
6.1. Comparison between Int-PS and Pre-PS
6.2. Discussion on the Effect of Power Splitting Ratio
6.3. Comparison between Int-TS and Pre-TS
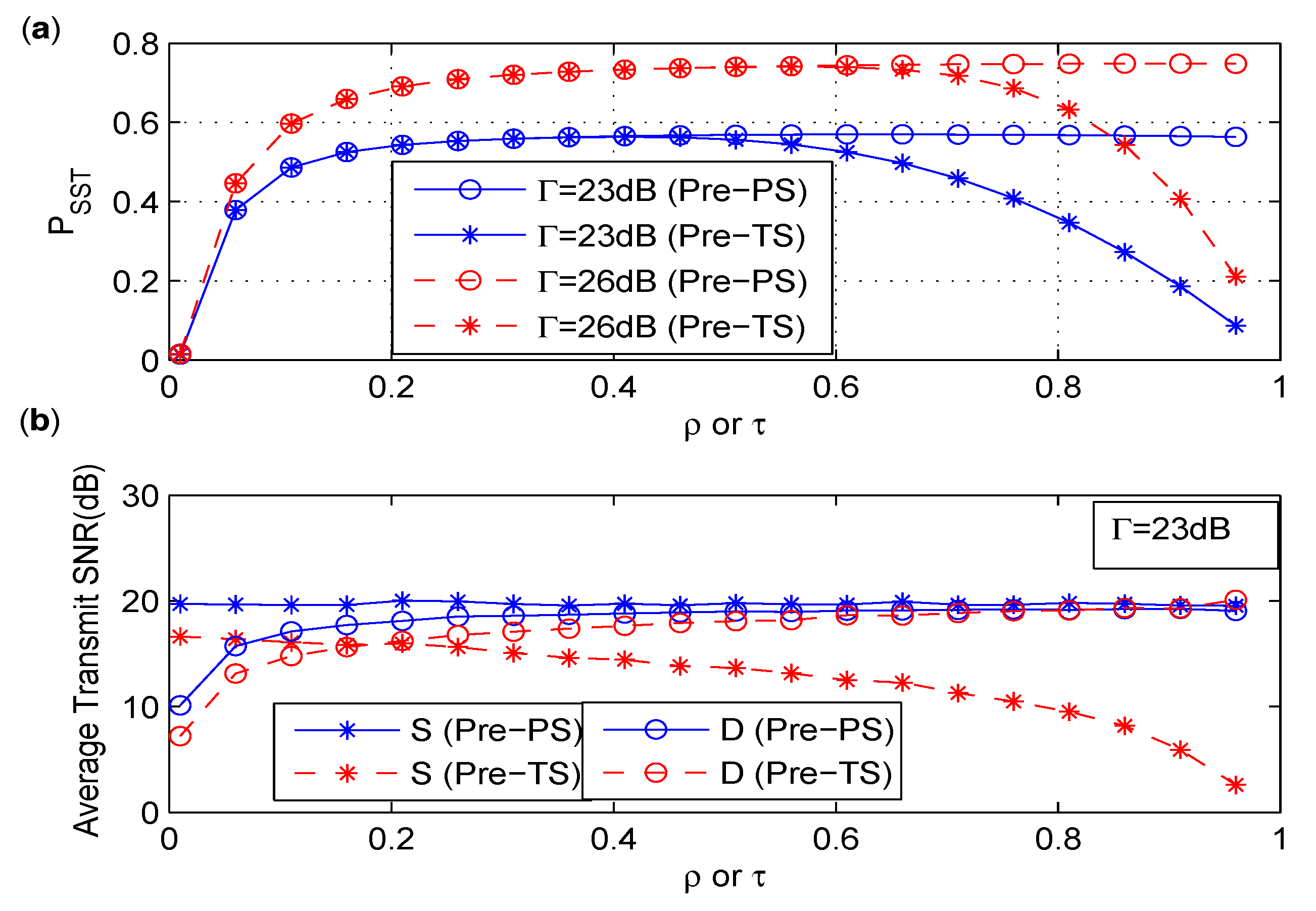
6.4. Comparison between Pre-PS and Pre-TS
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| IOT | The Internet of Things |
| CIOT | Cognitive IOT |
| EH | Energy harvesting |
| PS | Power splitting |
| TS | Time splitting |
| Int-PS/TS | The intuitive secure scheme based on PS/TS |
| Pre-PS/TS | The precoded secure scheme based on PS/TS |
| The probability of successfully secure transmission | |
| RATs | Radio access technologies |
| PLS | Physical layer security |
| CAE | Channel-aware encryption |
| CSRNs | Cognitive sensor radio networks |
| QoS | Quality-of-service |
| FD | Full-duplex |
| SPSC | Strictly positive secrecy capacity |
| AF | Amplify-and-forward |
| MF | Modulo-and-forward |
References
- Xu, L.D.; Wu, H.; Li, S. Internet of things in industries. IEEE Trans. Ind. Inf. 2014, 10, 2233–2243. [Google Scholar] [CrossRef]
- Zanella, A.; Bui, N.; Castellani, A.; Vangelista, L.; Zorzi, M. Internet of things for smart cities. IEEE Internet Things J. 2014, 1, 22–32. [Google Scholar] [CrossRef]
- Suciu, G.; Vulpe, A.; Halunga, S.; Fratu, O.; Todoran, G.; Suciu, V. Smart cities built on resilient cloud computing and secure internet of things. In Proceedings of the 19th IEEE International Conference on Control Systems and Computer Science (CSCS), Bucharest, Romania, 29–31 May 2013; pp. 513–518. [Google Scholar]
- Vlacheas, P.; Giaffreda, R.; Stavroulaki, V.; Kelaidonis, D.; Foteinos, V.; Poulios, G.; Demestichas, P.; Somov, A.; Biswas, A.R.; Moessner, K. Enabling smart cities through a cognitive management framework for the internet of things. IEEE Commun. Mag. 2013, 51, 102–111. [Google Scholar] [CrossRef]
- Ashton, K. Internet of things. RFID J. 2009. Available online: http://www.rfidjournal.com/articles/view?4986 (accessed on 18 June 2017).
- Wu, Q.H.; Ding, G.R.; Xu, Y.H.; Feng, S.; Du, Z.Y.; Wang, J.L.; Long, K.P. Cognitive internet of things: A new paradigm beyond connection. IEEE Internet Things J. 2014, 1, 129–143. [Google Scholar] [CrossRef]
- Shah, M.A.; Zhang, S.J.; Maple, C. Cognitive radio networks for internet of things: Applications, challenges and future. In Proceedings of the 19th International Conference on Automation and Computing, London, UK, 13–14 September 2013; pp. 1–6. [Google Scholar]
- Khan, A.A.; Rehmani, M.H.; Rachedi, A. Cognitive-Radio-Based Internet of Things: Applications, Architectures, Spectrum Related Functionalities, and Future Research Directions. IEEE Trans. Wirel. Commun. 2017, 24, 17–25. [Google Scholar] [CrossRef]
- Li, Z.; Jing, T.; Ma, L.; Huo, Y.; Qian, J. Worst-case cooperative jamming for secure communications in CIoT networks. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Sun, A.; Liang, T.; Li, B. Secrecy performance analysis of cognitive sensor radio networks with an EH-based eavesdropper. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Son, P.N.; Har, D.; Cho, N.I.; Kong, H.Y. Optimal power allocation of relay sensor node capable of energy harvesting in cooperative cognitive radio network. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Khoshkholgh, M.G.; Navaie, K.; Yanikomeroglu, H. Access strategies for spectrum sharing in fading environment: Overlay, underlay, and mixed. IEEE Trans. Mob. Comput. 2010, 9, 1780–1793. [Google Scholar] [CrossRef]
- “Spectrum Policy Taskforce Report”, Technical Report, Fed. Comm. Commission. November 2002. Available online: https://apps.fcc.gov/edocspublic/attachmatch/DOC-228542A1.pdf (accessed on 23 June 2017).
- Mukherjee, A. Physical-layer security in the internet of things: Sensing and communication confidentiality under resource constraints. Proc. IEEE 2015, 103, 1747–1761. [Google Scholar] [CrossRef]
- Granjal, J.; Monteiro, E.; Silva, J. Security for the internet of things: A survey of existing protocols and open research issues. IEEE Commun. Surv. Tutor. 2015, 17, 1294–1312. [Google Scholar] [CrossRef]
- Pirbhulal, S.; Zhang, H.; Alahi, M.E.A.; Ghayvat, H.; Mukhopadhyay, S.C.; Zhang, Y.-T.; Wu, W. A novel secure IoT-based smart home automation system using a wireless sensor Network. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Goel, S.; Negi, R. Guaranteeing secrecy using artificial noise. IEEE Trans. Wireless Commun. 2008, 7, 2180–2189. [Google Scholar] [CrossRef]
- Zou, Y.; Wang, X.; Shen, W. Optimal relay selection for physical-layer security in cooperative wireless networks. IEEE J. Sel. Areas Commun. 2013, 31, 2099–2111. [Google Scholar] [CrossRef]
- Liao, W.C.; Chang, T.H.; Ma, W.K.; Chi, C.Y. QoS-based transmit beamforming in the presence of eavesdroppers: An optimized artficialnoise-aided approach. IEEE Trans. Signal Process. 2011, 59, 1202–1216. [Google Scholar] [CrossRef]
- Sun, L.; Ren, P.; Du, Q.; Wang, Y. Fountain-coding aided strategy for secure cooperative transmission in industrial wireless sensor networks. IEEE Trans. Ind. Inf. 2016, 12, 291–300. [Google Scholar] [CrossRef]
- Krikidis, I.; Thompson, J.S.; Mclaughlin, S. Relay selection for secure cooperative networks with jamming. IEEE Trans. Wirel. Commun. 2009, 8, 5003–5011. [Google Scholar] [CrossRef]
- Xu, H.; Sun, L.; Ren, P.; Du, H.; Wang, Y. Cooperative privacy preserving scheme for downlink transmission in multiuser relay networks. IEEE Trans. Inf. Forensics Secur. 2017, 12, 825–839. [Google Scholar] [CrossRef]
- Zhang, S.; Fan, L.; Peng, M.; Poor, H.V. Near-optimal modulo-and-forward scheme for the untrusted relay channel. IEEE Trans. Inf. Theory 2016, 62, 2545–2556. [Google Scholar] [CrossRef]
- He, X.; Yener, A. End-to-end secure multi-hop communication with untrusted relays. IEEE Trans. Wirel. Comm. 2013, 12, 1–11. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless information and power transfer: Architecture design and rate-energy tradeoff. IEEE Trans. Commun. 2013, 61, 4754–4767. [Google Scholar] [CrossRef]
- Zhang, J.; Duong, T.Q.; Marshall, A.; Woods, R. Key generation from wireless channels: A review. IEEE Access. 2016, 4, 614–626. [Google Scholar] [CrossRef]
- Jeon, H.; Choi, J.; McLaughlin, S.; Ha, J. Channel aware encryption and decision fusion for wireless sensor networks. IEEE Trans. Inf. Forensics Secur. 2013, 8, 619–625. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, H. Secure distributed detection under energy constraint in IoT-oriented sensor networks. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.; Ren, P.; Song, H.; Du, Q. Security Enhancement for IoT Communications Exposed to Eavesdroppers with Uncertain Locations. IEEE Access. 2016, 4, 2840–2853. [Google Scholar] [CrossRef]
- Salameh, H.B.; Almajali, S.; Ayyash, M.; Elgala, H. Security-aware channel assignment in IoT-based cognitive radio networks for time-critical applications. In Proceedings of the Fourth International Conference on Software Defined Systems (SDS), Valencia, Spain, 8–11 May 2017; pp. 43–47. [Google Scholar]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying protocols for wireless energy harvesting and information processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Kalamkar, S.S.; Banerjee, A. Secure communication via a wireless energy harvesting untrusted relay. IEEE Trans. Veh. Technol. 2017, 66, 2199–2213. [Google Scholar] [CrossRef]
- Zhang, J.; Pan, G.; Wang, H. On physical-layer security in underlay cognitive radio networks with full-duplex wireless-powered secondary system. IEEE Access. 2016, 4, 3887–3893. [Google Scholar] [CrossRef]
- Wang, W.; Teh, K.C.; Li, K.H. Relay selection for secure successive AF relaying networks with untrusted nodes. IEEE Trans. Inf. Forensics Secur. 2016, 11, 2466–2476. [Google Scholar] [CrossRef]
- Xiong, J.; Cheng, L.; Ma, D.; Wei, J. Destination-aided cooperative jamming for dual-hop amplify-and-forward MIMO untrusted relay systems. IEEE Trans. Veh. Technol. 2016, 65, 7274–7284. [Google Scholar] [CrossRef]
- Yang, L.; Jiang, H.; Vorobyov, S.A. Secure communications in underlay cognitive radio networks: User scheduling and performance analysis. IEEE Commun. Lett. 2016, 20, 1191–1194. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Wireless-powered relays in cooperative communications: Time-switching relaying protocols and throughput analysis. IEEE Trans. Commun. 2015, 63, 1607–1622. [Google Scholar] [CrossRef]
- Bloch, M.; Barros, J.; Rodrigues, M.R.D.; McLaughlin, S.W. Wireless information-theoretic security. IEEE Trans. Inf. Theory 2008, 54, 2515–2534. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. The integral of special exponential function. In Table of Integrals, Series, and Products, 7th ed.; Jeffrey, A., Zwillinger, D., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 340–342. [Google Scholar]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, H.; Gao, Z.; Liao, X.; Leung, V.C.M. Secure Communications in CIoT Networks with a Wireless Energy Harvesting Untrusted Relay. Sensors 2017, 17, 2023. https://doi.org/10.3390/s17092023
Hu H, Gao Z, Liao X, Leung VCM. Secure Communications in CIoT Networks with a Wireless Energy Harvesting Untrusted Relay. Sensors. 2017; 17(9):2023. https://doi.org/10.3390/s17092023
Chicago/Turabian StyleHu, Hequn, Zhenzhen Gao, Xuewen Liao, and Victor C. M. Leung. 2017. "Secure Communications in CIoT Networks with a Wireless Energy Harvesting Untrusted Relay" Sensors 17, no. 9: 2023. https://doi.org/10.3390/s17092023





