Study on Finite Element Model Updating in Highway Bridge Static Loading Test Using Spatially-Distributed Optical Fiber Sensors
Abstract
:1. Introduction
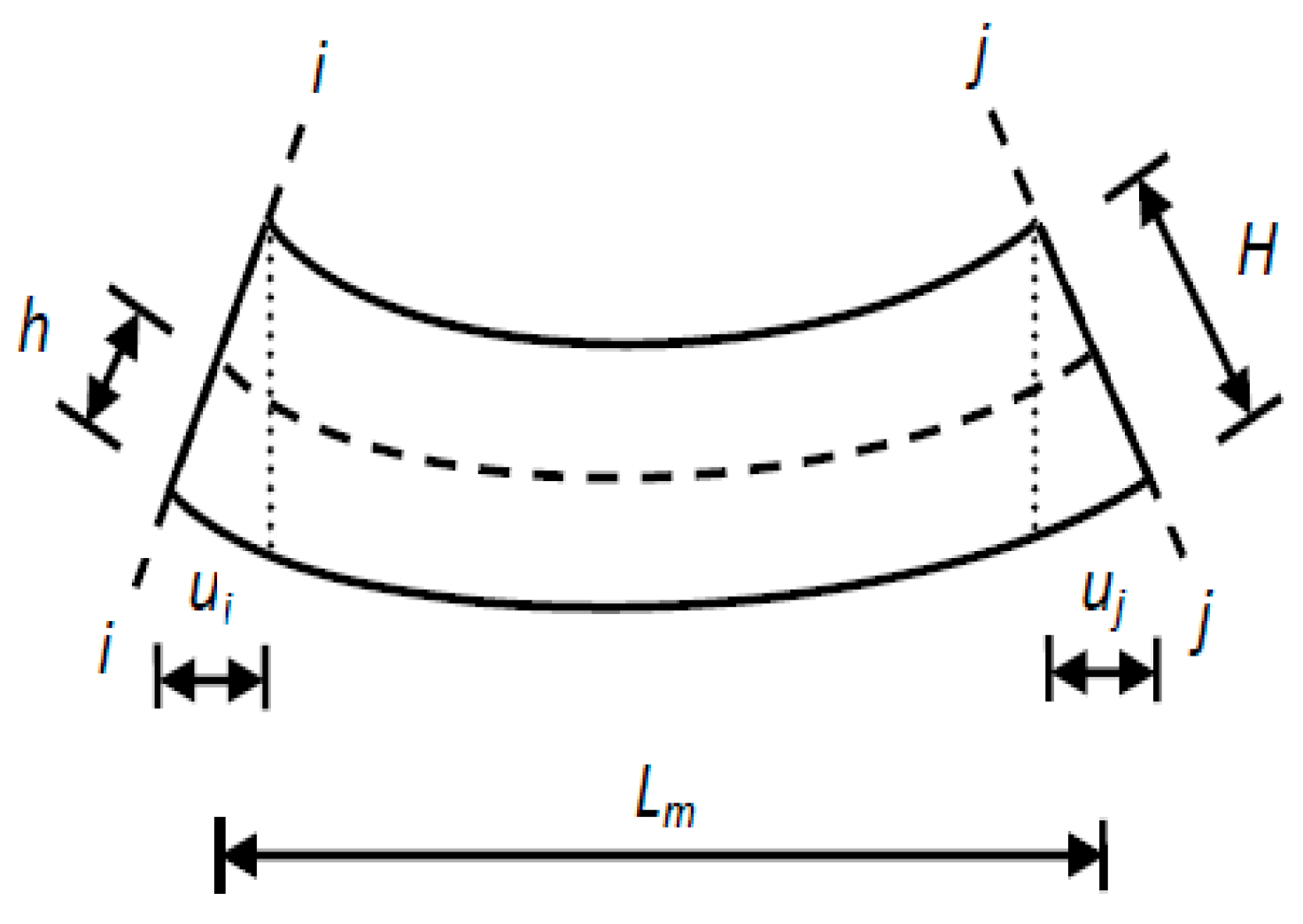
2. Objective Function Based on Element Macro-Strain
3. Numerical Simulation
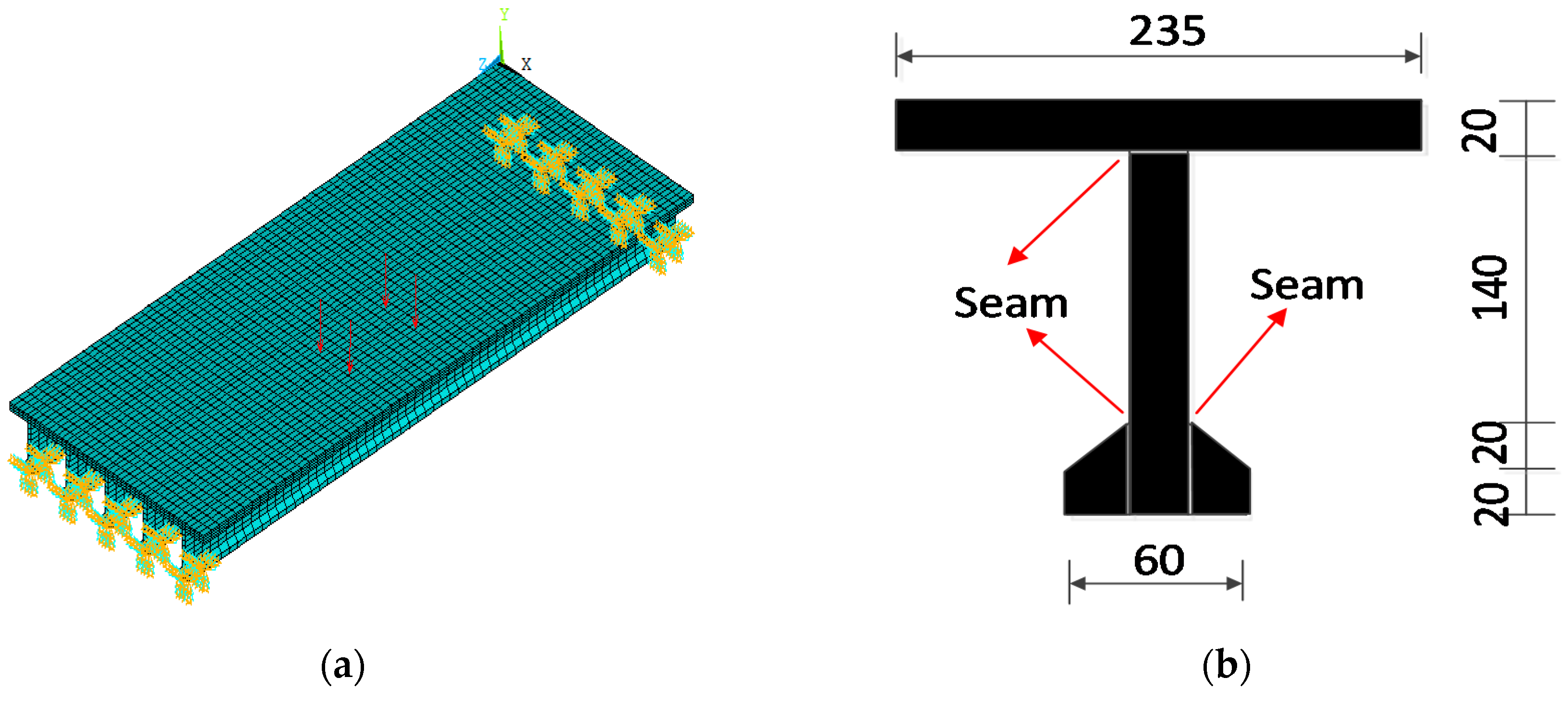
3.1. Numerical Analysis Case
3.2. Macro-Strain Modal of the Updated Beam
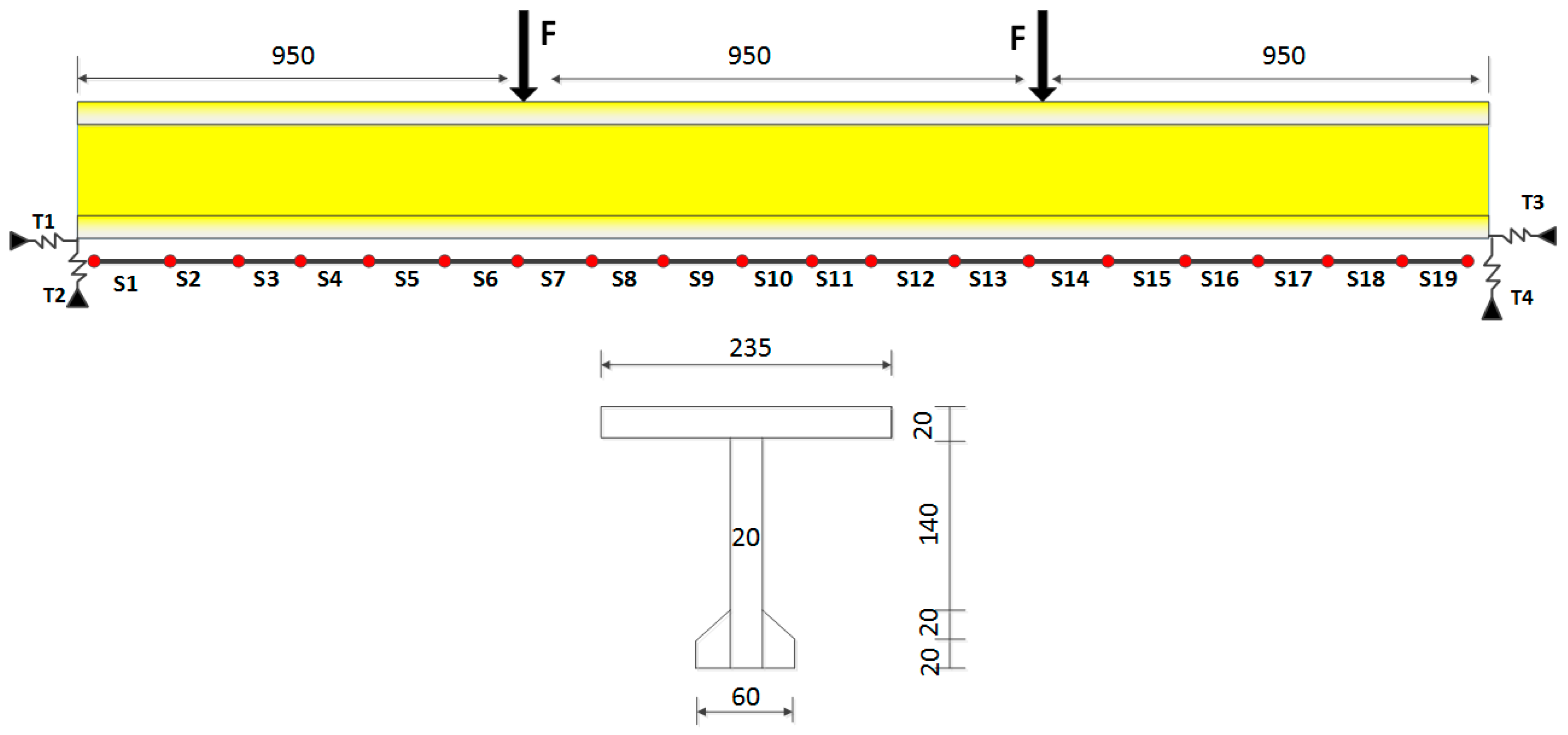
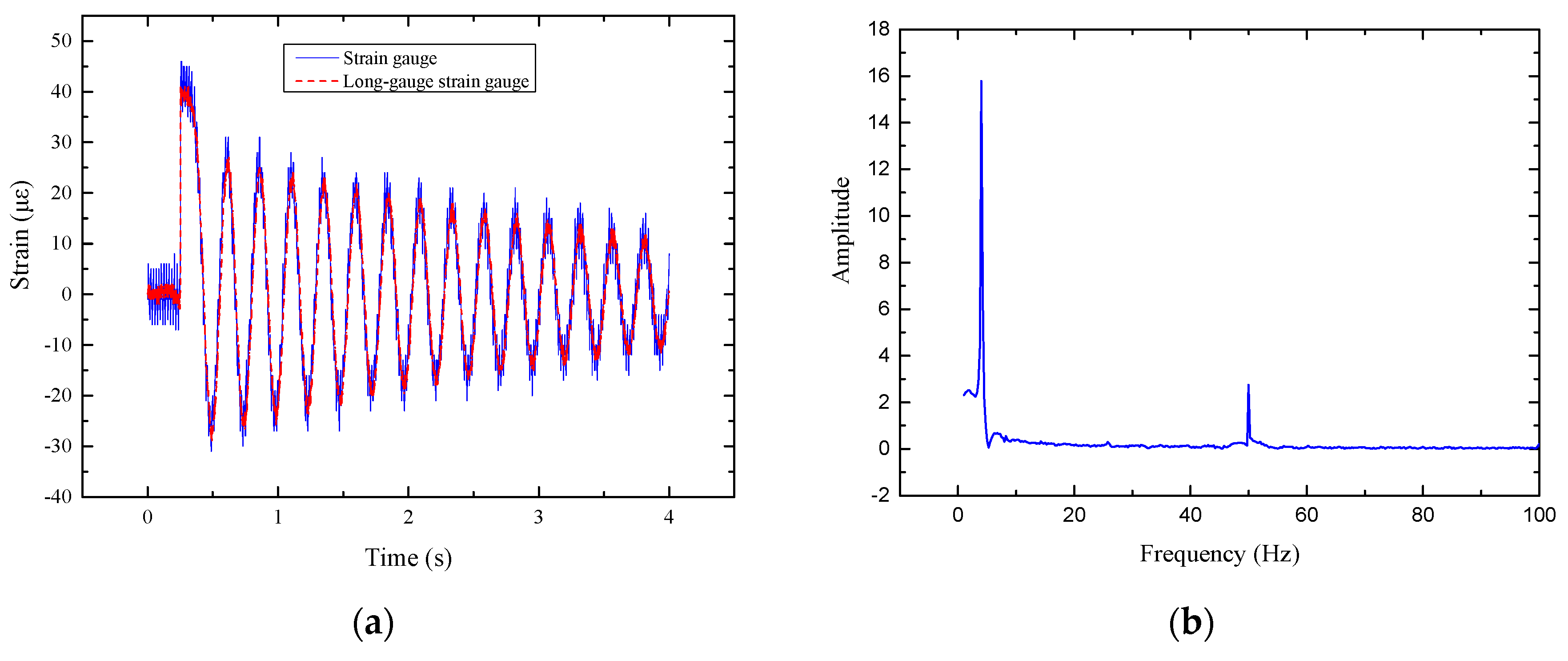
4. Experimental Verification
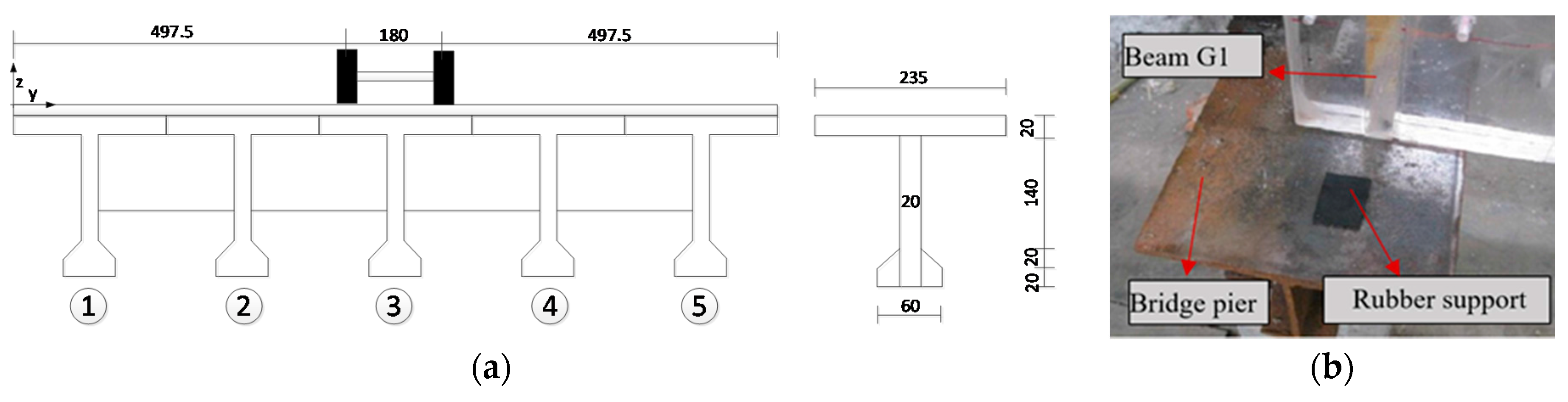
4.1. Experimental Details
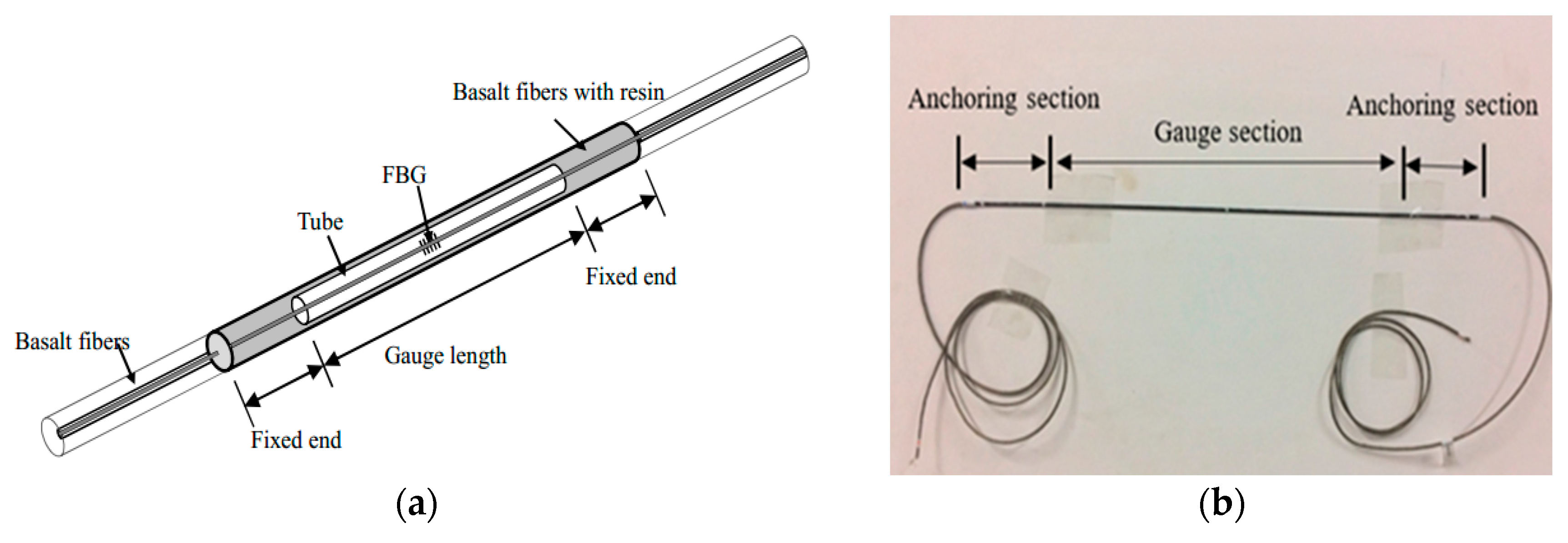
4.1.1. Fabrication of Long-Gauge Fiber Bragg Grating (FBG) Sensors and Specimen
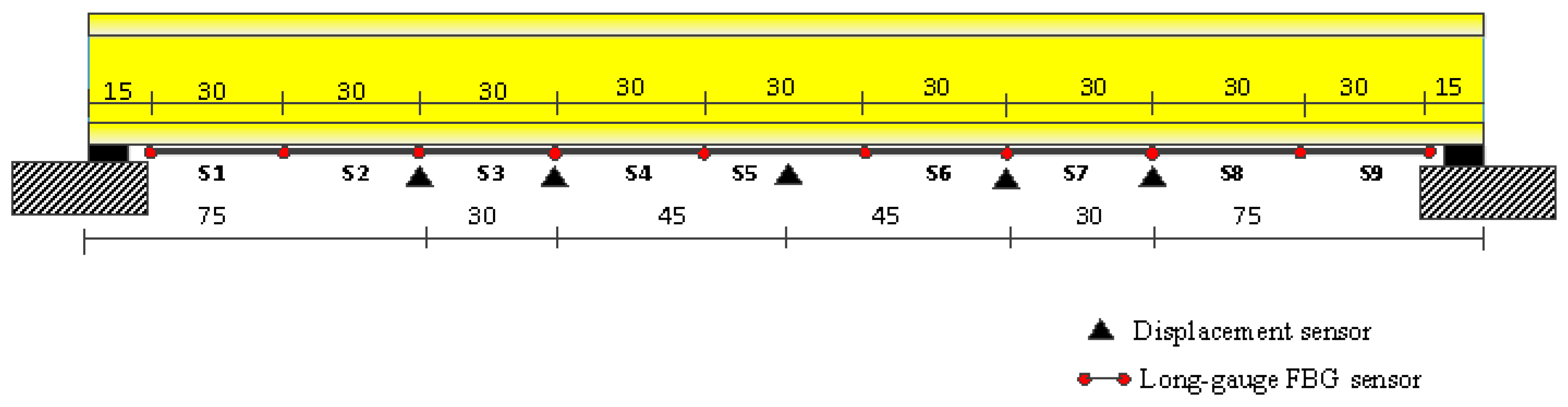
4.1.2. Experiment Setup
4.2. Model Updating Based on the Macro-Strain Response
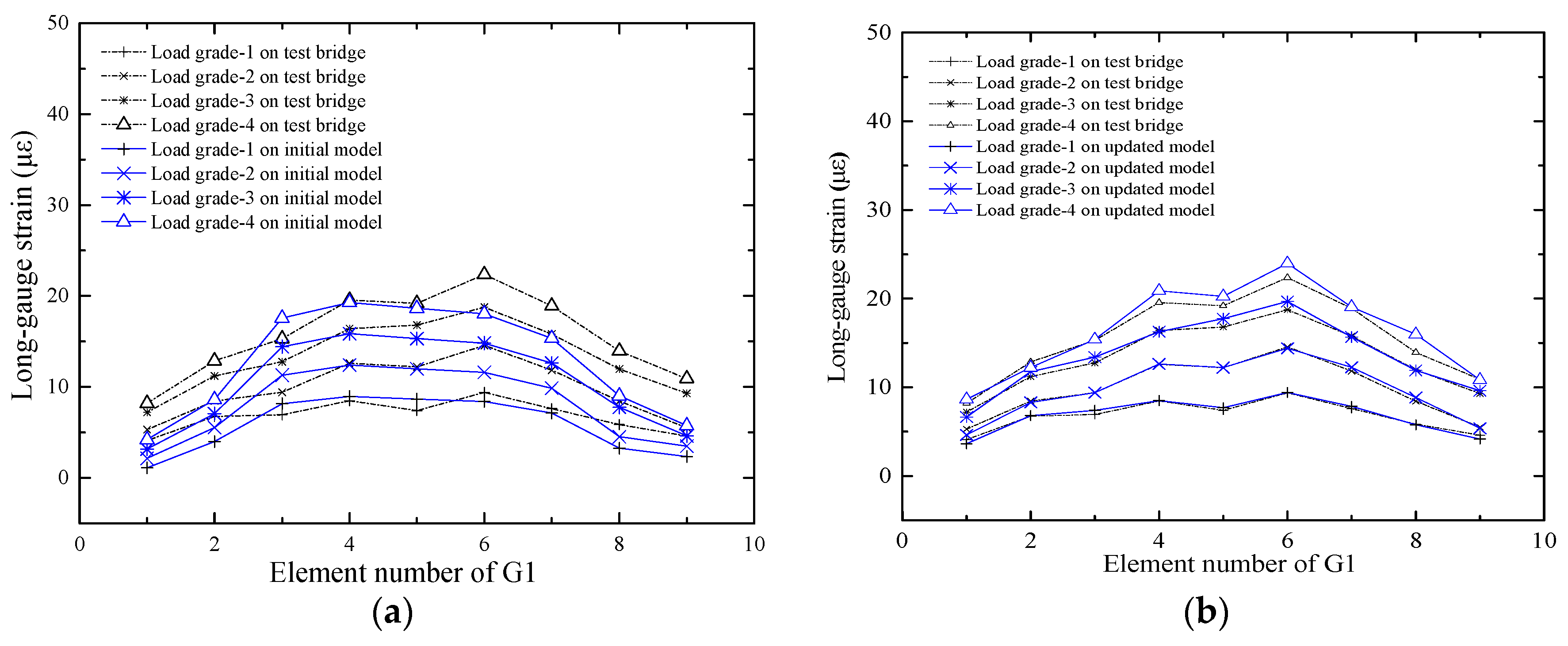
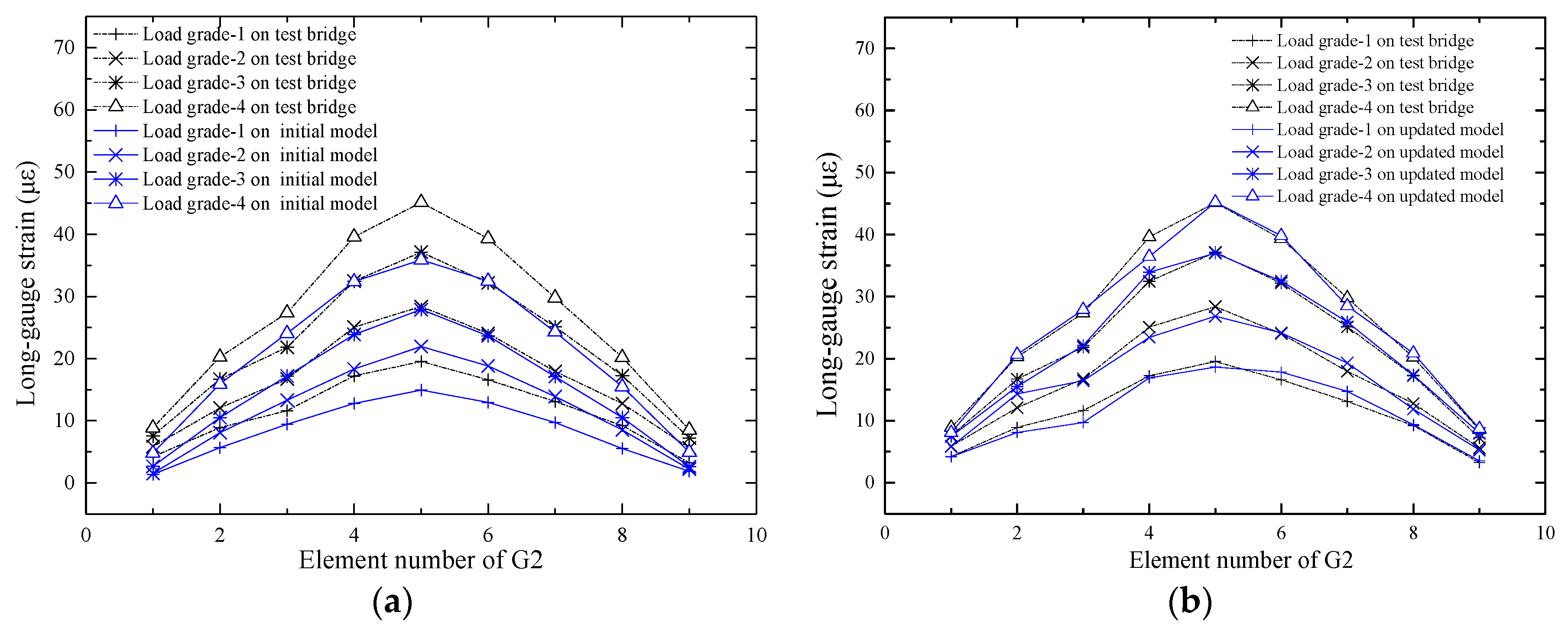
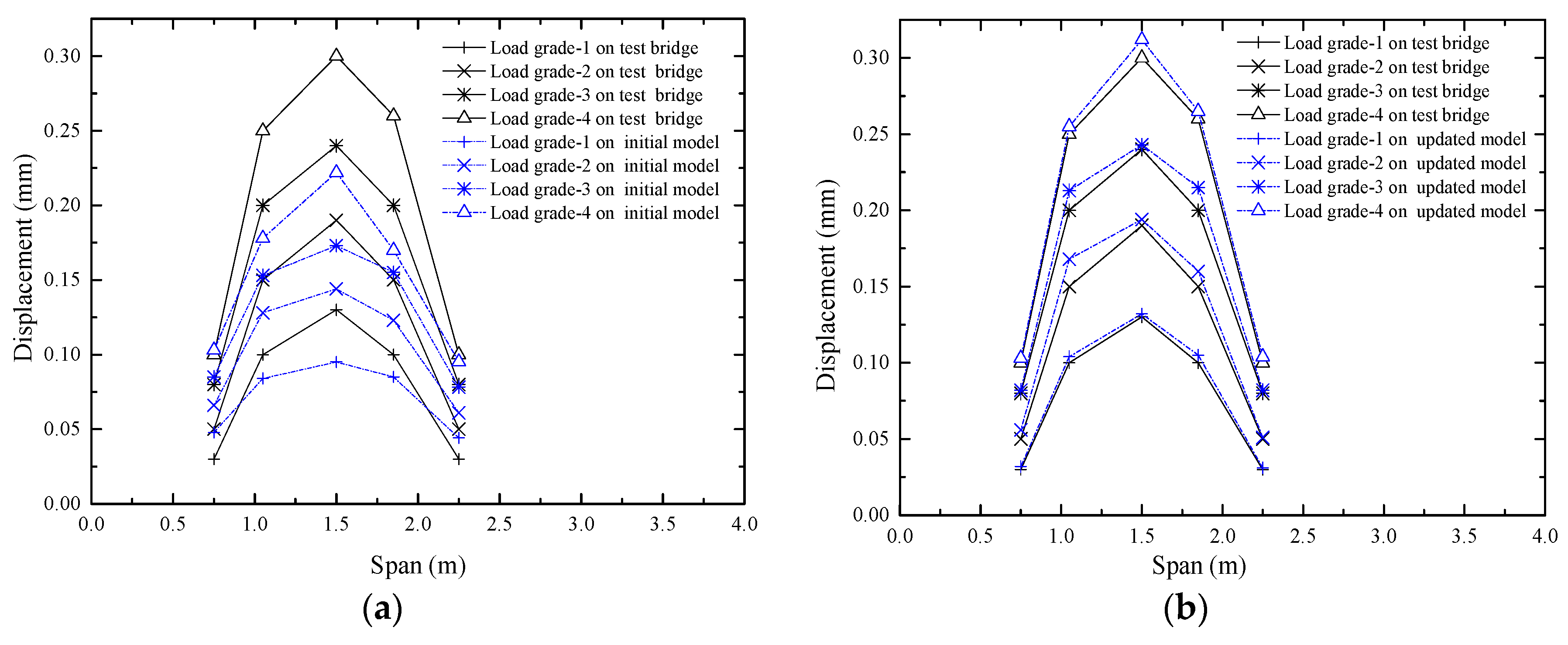
4.3. Prediction Response Based on the Updated Model
4.3.1. Prediction of the Macro-Stain Response
4.3.2. Prediction of the Displacement Deformation
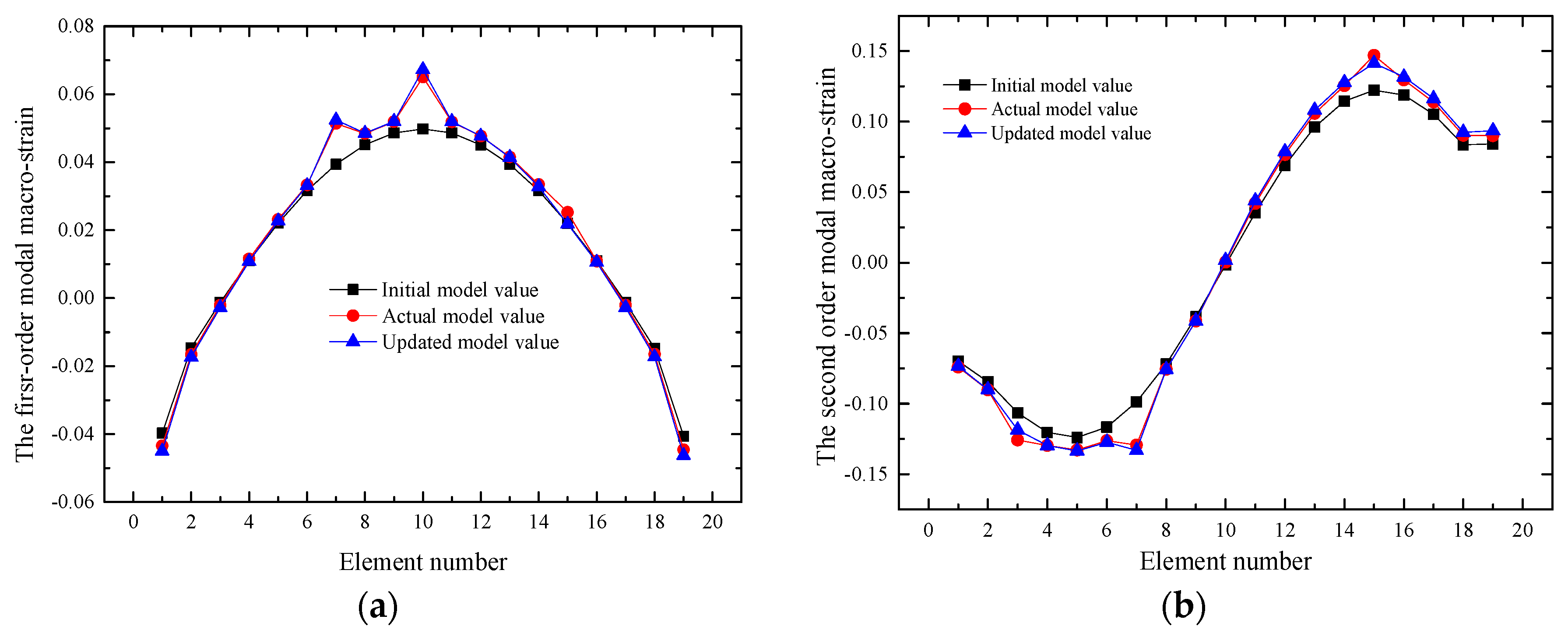
4.3.3. Prediction of the First Order Macro-Strain Modal
5. Conclusions
- The macro-strain is inversely proportional to the local average element stiffness that is covered by the gauge. The corresponding relation is important to verify the local stiffness based on the macro-strain. The objective function of the static macro-stains and frequency was established, and the local bending stiffness and boundary conditions of structures can be selected as the design variables.
- The macro-strain, displacement and first-order macro-strain modal of the updated model are compared with the measured response. The prediction response is notably close to the actual values, and the results show that the dynamic and static characteristics can be updated. The local and global parameters can be simultaneously modified and only one type of sensor is required in the proposed method.
- The proposed method is mainly useful for medium-small span beam-like bridges in highways. However, it is unrealistic to place long-gauge strain sensors all over the bridge. There is still some work to be done in the future to make the proposed method more useful and applicable. Different types of beam sections and actual bridge models should be investigated to further verify the proposed method, and the optimal sensor placement and number require further research.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chong, K.P.; Carino, N.J.; Washer, G.A. Health monitoring of civil infrastructures. Smart. Mater. Struct. 2003, 12, 483. [Google Scholar] [CrossRef]
- Kinet, D.; Mégret, P.; Goossen, K.W. Fiber Bragg Grating Sensors toward Structural Health Monitoring in Composite Materials: Challenges and Solutions. Sensors 2014, 14, 7394–7419. [Google Scholar] [CrossRef] [PubMed]
- Shimada, Y. Development of Optical Fiber Bragg Grating Sensors for Structural Health Monitoring. J. Laser Micro 2013, 8, 110–114. [Google Scholar] [CrossRef]
- Daniell, W.E.; Macdonald, J.H. Improved finite element modeling of a cable-stayed bridge through systematic manual tuning. Eng. Struct. 2007, 29, 358–371. [Google Scholar] [CrossRef]
- Benedettini, F.; Gentile, C. Operational modal testing and finite element model tuning of a cable-stayed bridge. Eng. Struct. 2011, 33, 2063–2073. [Google Scholar] [CrossRef]
- Liu, X.G.; Fan, J.S.; Nie, J.G. Behavior of composite rigid frame bridge under bi-directional seismic excitations. J. Traffic Trans. Eng. 2014, 1, 62–71. [Google Scholar] [CrossRef]
- Brownjohn, J.M.; Xia, P.Q.; Hao, H. Civil structure condition assessment by finite element model updating: Methodology and case studies. Finite Elem. Anal. Des. 2001, 37, 761–775. [Google Scholar] [CrossRef]
- Zapicoa, J.L.; Gonzaleza, M.P.; Friswellb, M.I. Finite element model updating of a small scale bridge. J. Sound Vib. 2003, 268, 993–1012. [Google Scholar] [CrossRef]
- Mottershead, J.E.; Friswell, M.I. Model updating in structural dynamics: A survey. J. Sound Vib. 1993, 167, 347–375. [Google Scholar] [CrossRef]
- Banan, M.R.; Hjelmstad, K.D. Parameter estimation of structures from static response 2 numerical simulation studies. J. Struct. Eng. 1994, 120, 3259–3283. [Google Scholar] [CrossRef]
- Stubbs, N.; Osegueda, R. Global Non-Destructive Damage Evaluation in Solids. Int. J. Anal. Exp. Modal Anal. 1990, 5, 67–79. [Google Scholar]
- Hearn, G.; Testa, R.B. Modal analysis for damage detection in structures. J. Struct. Eng. 1991, 117, 3042–3063. [Google Scholar] [CrossRef]
- Hassiotis, S.; Jeong, G.D. Identification of stiffness reductions using natural frequencies. J. Eng. Mech. 1995, 121, 1106–1113. [Google Scholar] [CrossRef]
- Link, M. Updating of analytical models-review of numerical procedures and application aspects. In Structural Dynamic Forum SD2000; Research Studies Press: Baldock, UK, 1999. [Google Scholar]
- Kim, J.T.; Ryu, Y.S.; Cho, H.M.; Stubbs, N. Damage identification in beam type structures: Frequency-based method vs. mode-shape-based method. Eng. Struct. 2003, 25, 57–67. [Google Scholar] [CrossRef]
- Lin, R.M.; Ewins, D.J. Model updating using FRF data. In Proceedings of the 15th International Seminar on Modal Analysis, Heverlee, Belgium, 19–21 September 1990. [Google Scholar]
- Imregun, M.; Visser, W.J. A review of model updating techniques. Shock Vib. Dig. 1991, 23, 9–20. [Google Scholar] [CrossRef]
- Imregun, M.; Sanliturk, K.Y.; Ewins, D.J. Finite element model updating using frequency response function data: II. Case study on a medium-size finite element model. Mech. Syst. Signal Proc. 1995, 9, 203–213. [Google Scholar] [CrossRef]
- Imregun, M.; Visser, W.J.; Ewins, D.J. Finite element model updating using frequency response function data: I. Theory and initial investigation. Mech. Syst. Signal Proc. 1995, 9, 187–202. [Google Scholar] [CrossRef]
- Rahmatalla, S.; Eun, H.C.; Lee, E.T. Damage detection from the variation of parameter matrices estimated by incomplete FRF data. Smart Struct. Syst. 2012, 9, 55–70. [Google Scholar] [CrossRef]
- Ren, W.X.; Chen, H.B. Finite element model updating in structural dynamics by using the response surface method. Eng. Struct. 2010, 32, 2455–2465. [Google Scholar] [CrossRef]
- Ren, W.X.; Fang, S.E.; Deng, Y.M. Response surface based finite element model updating by using structure static response. J. Eng. Mech. 2011, 137, 248–257. [Google Scholar] [CrossRef]
- Deng, L.; Cai, C.S. Bridge Model Updating Using Response Surface Method and Genetic Algorithm. J. Bridge Eng. 2010, 15, 553–564. [Google Scholar] [CrossRef]
- Feng, D.; Feng, M.Q. Vision-based multipoint displacement measurement for structural health monitoring. Struct. Control Health Monit. 2016, 23, 876–890. [Google Scholar] [CrossRef]
- Moreno-Gomez, A.; Perez-Ramirez, C.A. Sensors Used in Structural Health Monitoring. Arch. Comput. Method Eng. 2017, 1–18. [Google Scholar] [CrossRef]
- Feng, X.; Sun, C.; Zhang, X. Determination of the coefficient of thermal expansion with embedded long-gauge fiber optic sensors. Meas. Sci. Technol. 2010, 6, 065302. [Google Scholar] [CrossRef]
- Abdeljaber, H.; Glisic, B. A method for the on-site determination of prestressing forces using long-gauge fiber optic strain sensors. Smart. Mater. Struct. 2014, 23, 075004. [Google Scholar] [CrossRef]
- Rodrigues, C.; Inaudi, D. Laboratory and Field Comparison of Long-Gauge Strain Sensing Technologies. In Proceedings of the 5th European Workshop on Structural Health Monitoring, Naples, Italy, 28 June–4 July 2010; pp. 1289–1294. [Google Scholar]
- Li, S.Z.; Wu, Z.S. Development of distributed long-gage fiber optic sensing system for structural health monitoring. Struct. Health Monit. 2007, 6, 133–143. [Google Scholar] [CrossRef]
- Wu, B.; Wu, G.; Yang, C. Damage identification and bearing capacity evaluation of bridges based on distributed long-gauge strain envelope line under moving vehicle loads. J. Intell. Mater. Syst. Struct. 2016, 27, 2344–2358. [Google Scholar] [CrossRef]
- Calderón, P.A.; Glisic, B. Influence of mechanical and geometrical properties of embedded long-gauge strain sensors on the accuracy of strain measurement. Meas. Sci. Technol. 2012, 23, 65604–65618. [Google Scholar] [CrossRef]
- Glisic, B. Influence of the gauge length on the accuracy of long-gauge sensors employed in monitoring of prismatic beams. Meas. Sci. Technol. 2011, 22, 035206. [Google Scholar] [CrossRef]
- Hong, W.; Wu, Z.; Yang, C.; Wu, G.; Zhang, Y. Finite element model updating of flexural structures based on modal parameters extracted from dynamic distributed macro-strain responses. J. Intell. Mater. Syst. Struct. 2015, 26, 201–218. [Google Scholar] [CrossRef]





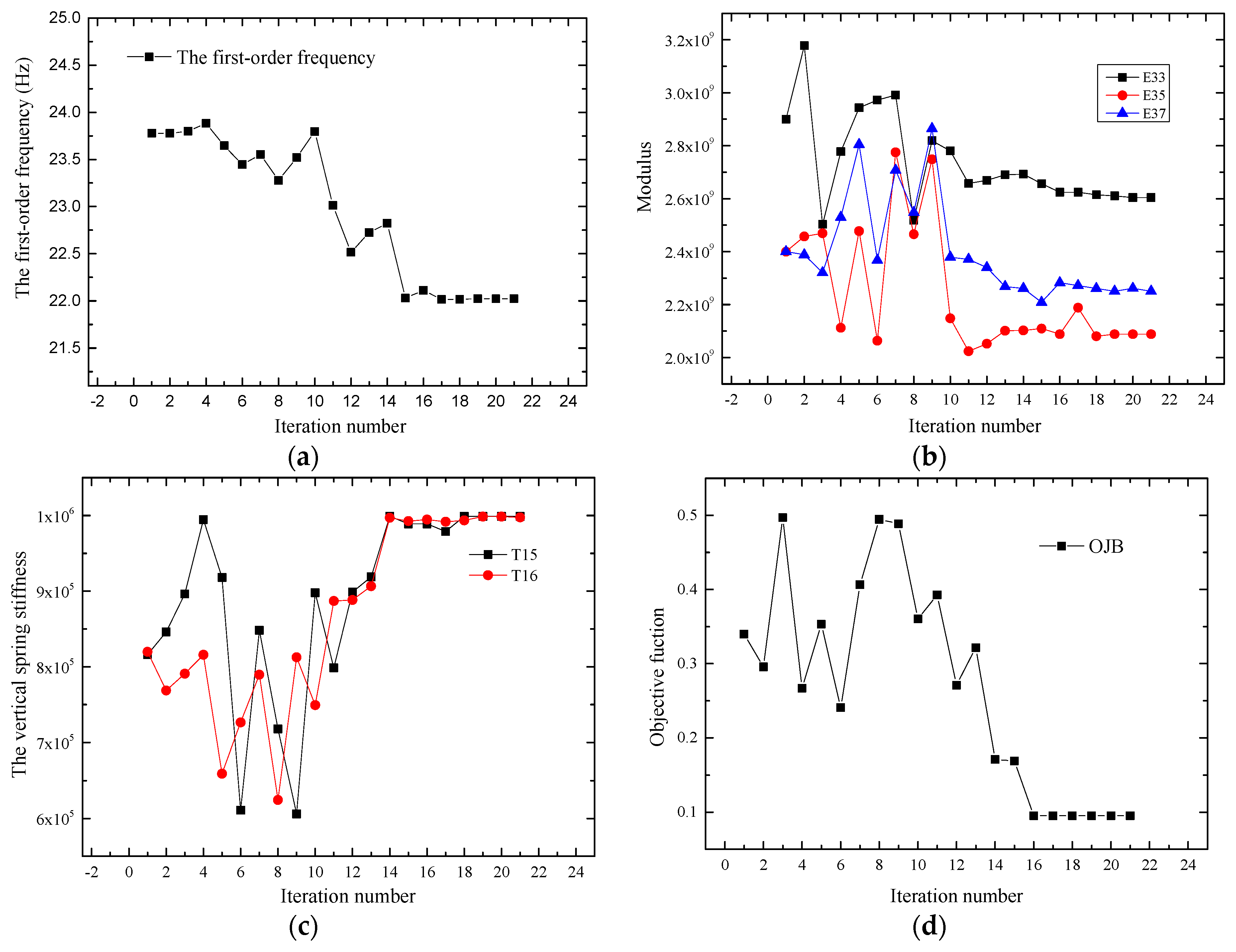



| Initial Value | Updated Value (Pa) | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| E1–E9 | E1 | E2 | E3 | E4 | E5 | E6 | E7 | E8 | E9 | |
| G1 | 3.12 × 109 | 2.5 × 109 | 2.6 × 109 | 2.5 × 109 | 2.5 × 109 | 2.4 × 109 | 2.5 × 109 | 2. 5 × 109 | 2. 5 × 109 | 2.5 × 109 |
| G2 | 3.12 × 109 | 2.5 × 109 | 2.5 × 109 | 2.4 × 109 | 2.5 × 109 | 2.3 × 109 | 2.3 × 109 | 2. 3 × 109 | 2. 3 × 109 | 2.5 × 109 |
| G3 | 3.12 × 109 | 2.4 × 109 | 2.7 × 109 | 2.6 × 109 | 2.5 × 109 | 2.3 × 109 | 2.3 × 109 | 2.3 × 109 | 2.4 × 109 | 2.4 × 109 |
| G4 | 3.12 × 109 | 2.4 × 109 | 2.4 × 109 | 2.4 × 109 | 2.4 × 109 | 2.3 × 109 | 2.4 × 109 | 2. 4 × 109 | 2. 4 × 109 | 2.4 × 109 |
| G5 | 3.12 × 109 | 2.5 × 109 | 2.5 × 109 | 2.5 × 109 | 2.4 × 109 | 2.4 × 109 | 2.4 × 109 | 2. 4 × 109 | 2. 4 × 109 | 2.4 × 109 |
| Initial Value | Updated Value | Measured Value | |
|---|---|---|---|
| F (Hz) | 23.85 | 22.21 | 22.82 |
| T15 (N/m) | 8.19 × 105 | 9.98 × 105 | / |
| T16 (N/m) | 8.19 × 105 | 9.97 × 105 | / |
| T17 (N/m) | 2.75 × 102 | 1.58 × 102 | / |
| T18 (N/m) | 2.75 × 102 | 1.37 × 102 | / |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, B.; Lu, H.; Chen, B.; Gao, Z. Study on Finite Element Model Updating in Highway Bridge Static Loading Test Using Spatially-Distributed Optical Fiber Sensors. Sensors 2017, 17, 1657. https://doi.org/10.3390/s17071657
Wu B, Lu H, Chen B, Gao Z. Study on Finite Element Model Updating in Highway Bridge Static Loading Test Using Spatially-Distributed Optical Fiber Sensors. Sensors. 2017; 17(7):1657. https://doi.org/10.3390/s17071657
Chicago/Turabian StyleWu, Bitao, Huaxi Lu, Bo Chen, and Zhicheng Gao. 2017. "Study on Finite Element Model Updating in Highway Bridge Static Loading Test Using Spatially-Distributed Optical Fiber Sensors" Sensors 17, no. 7: 1657. https://doi.org/10.3390/s17071657




