Calibration of Magnetometers with GNSS Receivers and Magnetometer-Aided GNSS Ambiguity Fixing
Abstract
:1. Introduction
2. Measurement Models
Measurement Model for Magnetic Field Sensor
- transformation from local geomagnetic frame into local geographic navigation-frame, depending on the magnetic declination ,
- transformation from local geographic navigation-frame into body-fixed frame, depending on the attitude of sensor’s platform (roll , pitch and heading ),
- transformation from body-fixed frame into sensor-fixed frame, depending on misalignment errors of sensors (roll offset , pitch offset and heading offset ).
3. Calibration of Magnetic Flux Sensors
3.1. Estimation of Magnetometer Biases
3.2. Attitude Determination with Three GNSS Receivers
- Carrier phase measurement ,⊕ carrier phase can be tracked with millimeter accuracy,⊖ carrier phase is period with cm and requires ambiguity resolution,
- Pseudorange measurement ,⊕ pseudorange is an unambiguous range measurement,⊖ pseudorange measurement is more sensitive to multipath,⊖ pseudorange measurement can only be tracked with meter-level accuracy.
3.2.1. Modeling of Differential GNSS Measurements
3.2.2. Joint Estimation of Baselines, Pseudorange Multipaths and Ambiguities
3.2.3. Integer Ambiguity Fixing Using Prior Information on Baseline Coordinates
| baseline estimate for partially fixed integer ambiguities, | |
| variance of length of baseline estimate assuming correct partial ambiguity fixing, | |
| variance of prior information on baseline length, | |
| upper bound on the squared normalized baseline length error, | |
| upper bound on the sum of squared baseline residuals. |
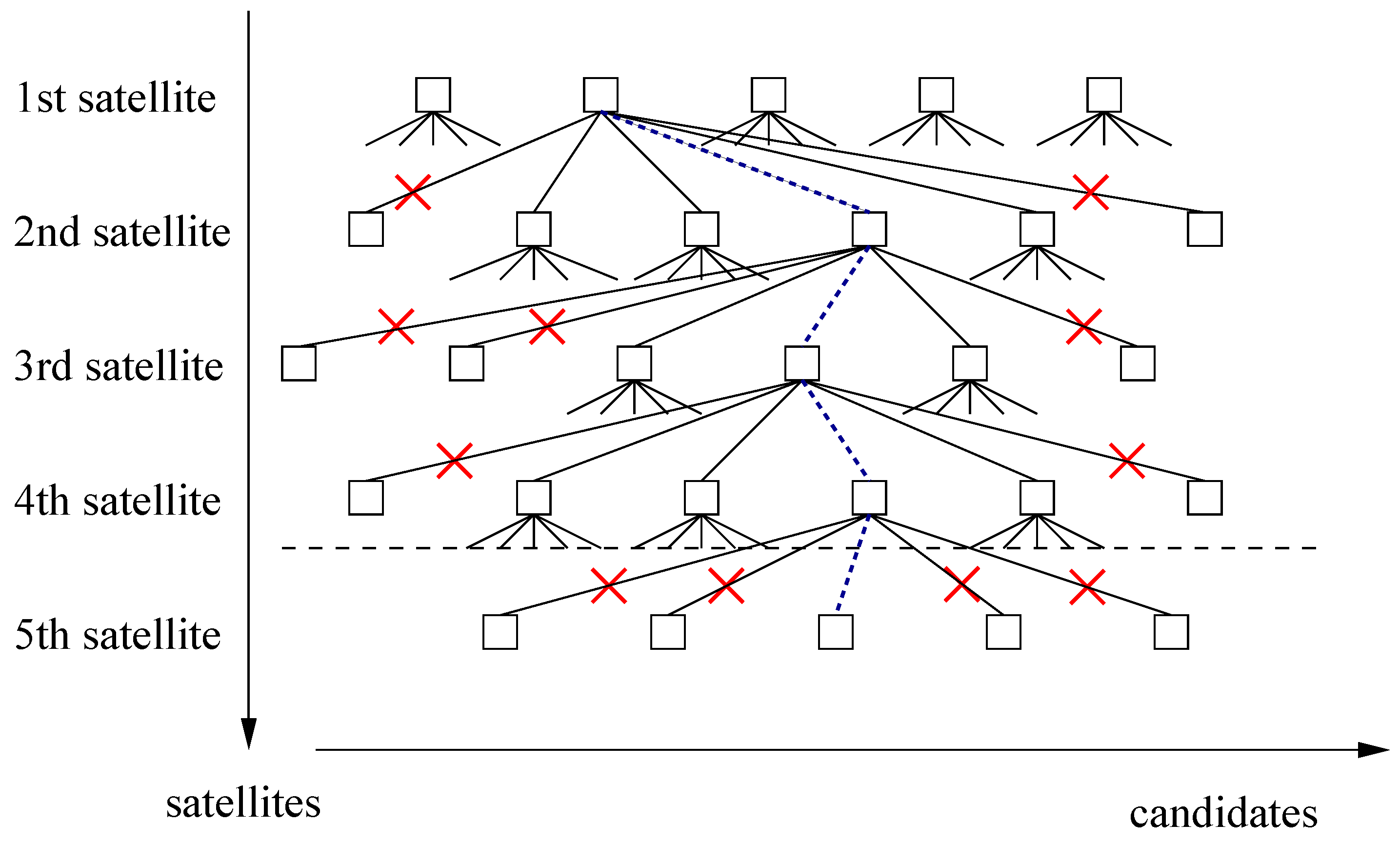
4. Fast Initialization of GNSS Attitude Ambiguity Fixing with Calibrated Magnetometers
Analysis of Benefit of Magnetometer-Based Attitude Information for GNSS Integer Ambiguity Fixing
- Estimation of float solution of baselines and ambiguities by least-squares estimation using single epoch measurements,
- Normalization of baseline estimates with prior information on baseline length and respective adjustment of float ambiguities,
- Integer ambiguity fixing with sequential tree search and integer decorrelation using magnetometer-based attitude information and baseline length prior information.
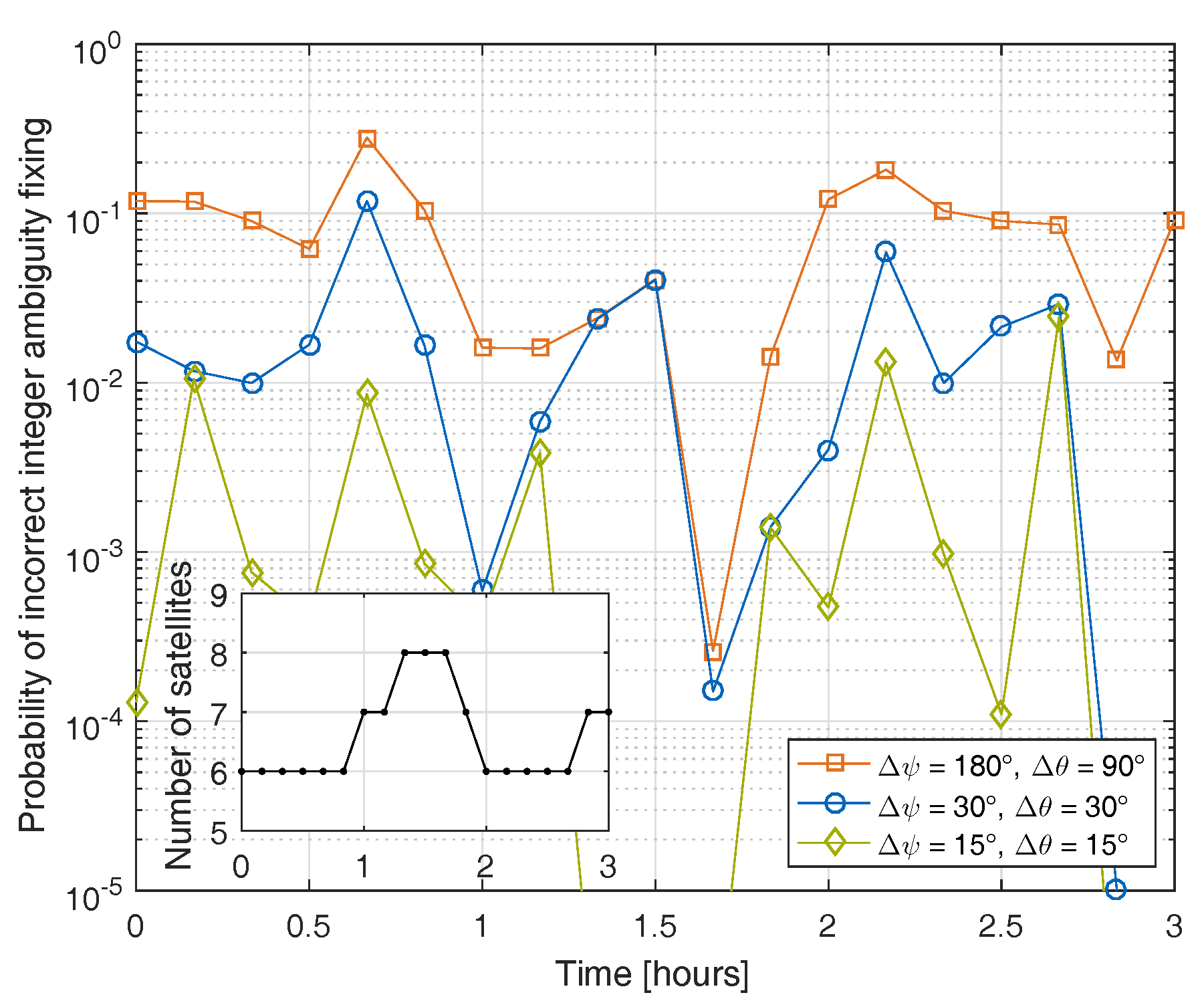
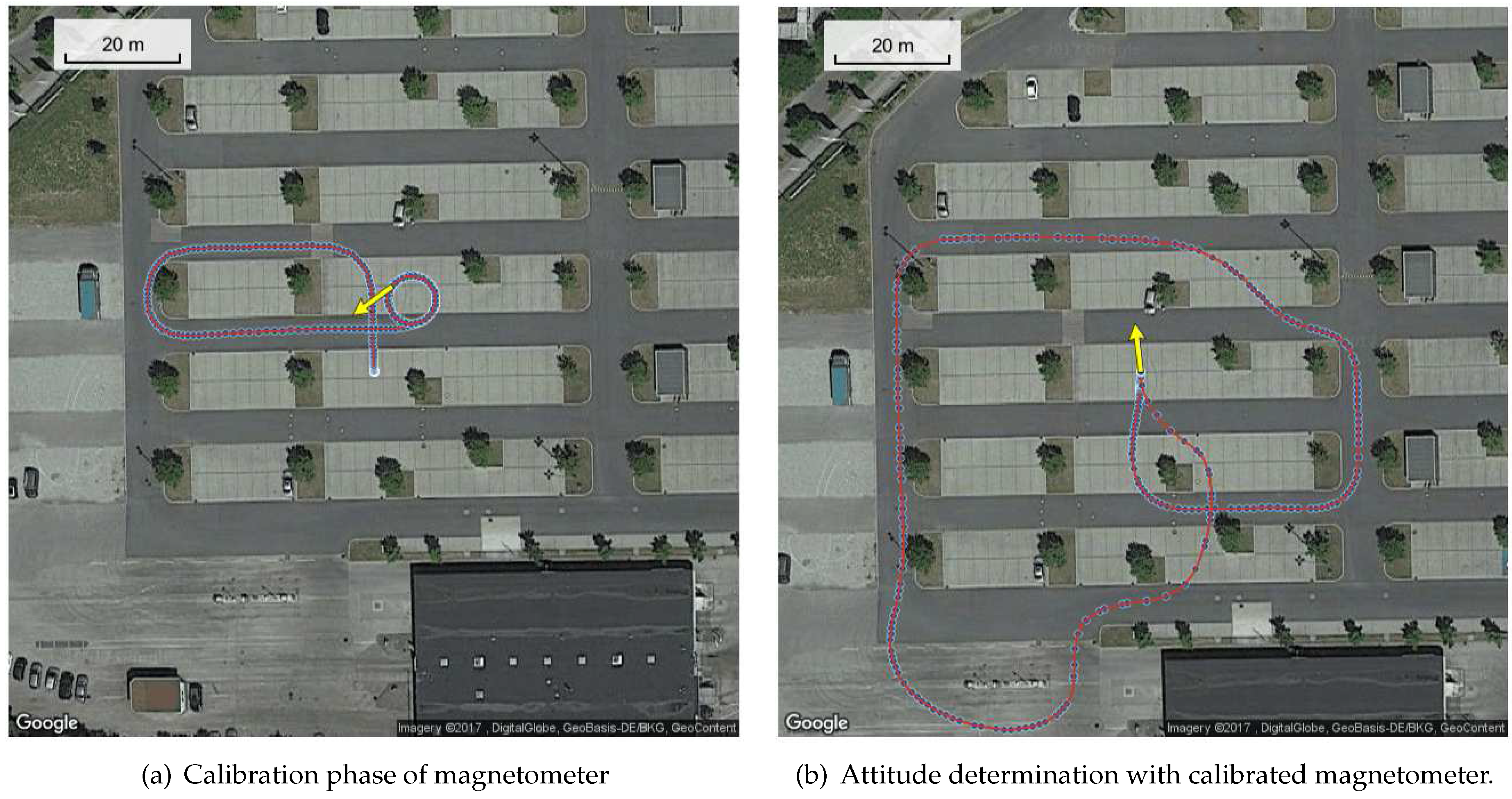
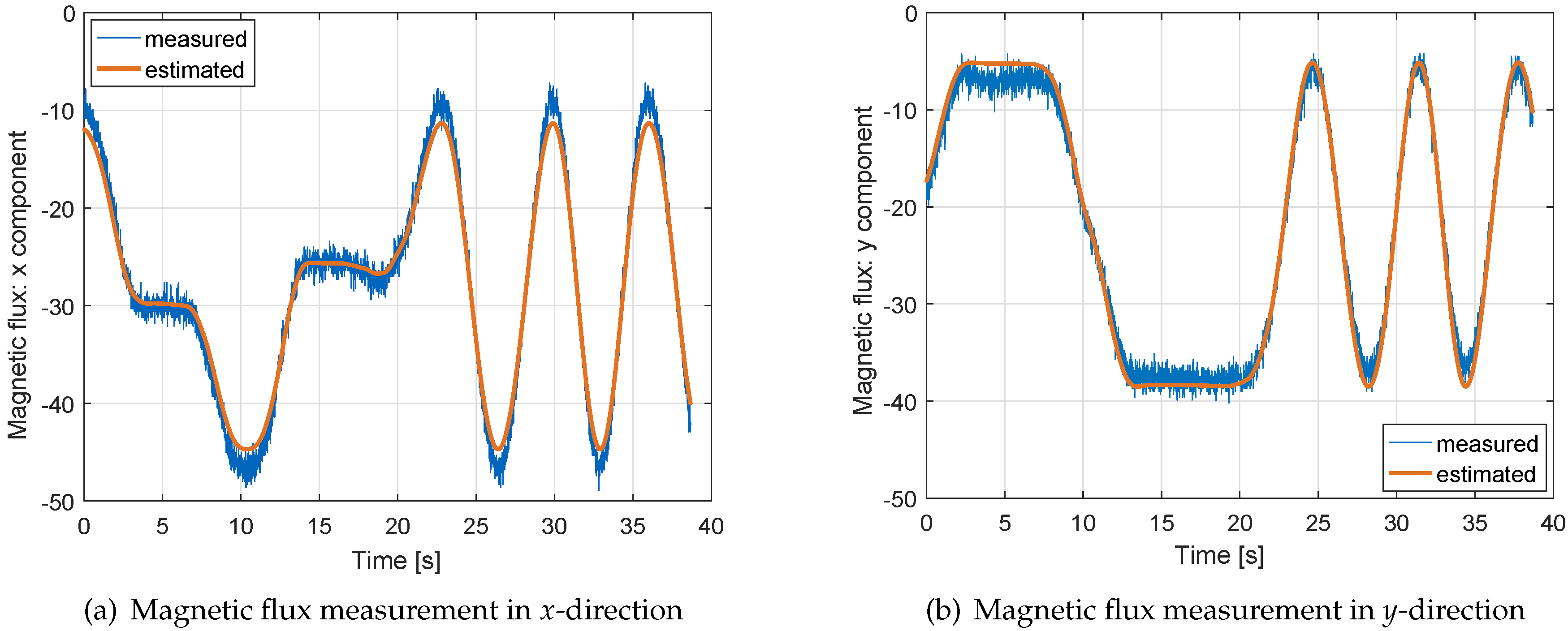
5. Measurement Results
- Calibration with Multi-GNSS (GPS + GLONASS)/INS tightly coupled attitude information instead of GPS-only attitude estimate, enabling higher reliability due to inertial sensors and faster calibration due to higher update rate,
- Use of three instead of two GNSS receivers for full 3D attitude information,
- Estimation of 3D magnetic flux in North-East-Down frame instead of 1D magnetic flux in the North-only direction, enabling use also in areas with systematic distortions of magnetic field and/or close to magnetic poles,
- Use of the newest sensor generation: LEA M8T Multi-GNSS receiver of u-blox (Thalwil, Switzerland), Taoglas AGGP.35F dual-band GNSS antenna (Enniscorthy, Ireland), and MPU 9250 inertial sensor (San Jose, CA, USA).
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Teunissen, P. The least-squares ambiguity decorrelation adjustment: A method for fast GPS ambiguity estimation. J. Geod. 1995, 70, 65–82. [Google Scholar] [CrossRef]
- Teunissen, P. The LAMBDA method for the GNSS compass. Artif. Satell. 2006, 41, 89–103. [Google Scholar] [CrossRef]
- Teunissen, P. Integer least-squares theory for the GNSS compass. J. Geod. 2010, 84, 433–447. [Google Scholar] [CrossRef]
- Henkel, P.; Günther, C. Reliable Integer Ambiguity Resolution: Multi-Frequency Code Carrier Linear Combinations and Statistical A Priori Knowledge of Attitude. Navigation 2012, 59, 61–75. [Google Scholar] [CrossRef]
- Henkel, P.; Berthold, P.; Kiam, J. Calibration of Magnetic Field Sensors with Two Mass-Market GNSS Receivers. In Proceedings of the IEEE Workshop on Positioning, Navigation and Communication (WPNC), Dresden, Germany, 12–13 March 2014; p. 5. [Google Scholar]
- Crassidis, J.; Lai, K.-L.; Harman, R. Real-time attitude-independent three-axis magnetometer calibration. J. Guid. Control Dyn. 2005, 28, 115–120. [Google Scholar] [CrossRef]
- Psiaki, M.; Martel, F.; Pal, P. Three-axis attitude determination via Kalman filtering of magnetometer data. J. Guid. Control Dyn. 1990, 13, 506–514. [Google Scholar] [CrossRef]
- Brown, R.G.; Hwang, P.Y.C. Random Signals and Applied Kalman Filtering, 4th ed.; John Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Jonge, P.; Tiberius, C. The LAMBDA Method for Integer Ambiguity Estimation: Implementation Aspects; LGR Series; Publications of the Delft Geodetic Computing Centre: Delft, The Netherlands, 1996; Volume 12, pp. 1–59. [Google Scholar]
- Blewitt, G. Carrier phase ambiguity resolution for the Global Positioning System applied to geodetic baselines up to 2000 km. J. Geophy. Res. 1989, 94, 10187–10203. [Google Scholar] [CrossRef]
- Wahba, G. A Least Squares Estimate of Satellite Attitude. SIAM Rev. 1965, 7, 409. [Google Scholar] [CrossRef]
- Zandbergen, R.; Dinwiddy, S.; Hahn, J.; Breeuwer, E.; Blonski, D. Galileo Orbit Selection. In Proceedings of the 17th International Technology Meeting of the Satellite Division of the Institute of Navigation (ION GNSS), Long Beach, CA, USA, 8–12 September 2004; pp. 616–623. [Google Scholar]
- Specification of Inertial Sensor MPU 9250. Invensense. Available online: https://www.invensense.com/wp-content/uploads/2015/02/PS-MPU-9250A-01-v1.1.pdf (accessed on 28 May 2017).
- Henkel, P.; Oku, N. Cycle slip detection and correction for heading determination with low-cost GPS/INS receivers. In Proceedings of the IAG Proceedings of VIII Hotine Marussi Symposium on Mathematical Geodesy, Rome, Italy, 17–21 June 2013. [Google Scholar]
- Henkel, P.; Günther, C. Attitude determination with low-cost GPS/INS. In Proceedings of the 26th International Technology Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+), Nashville, TN, USA, 16–20 September 2013; pp. 2015–2023. [Google Scholar]
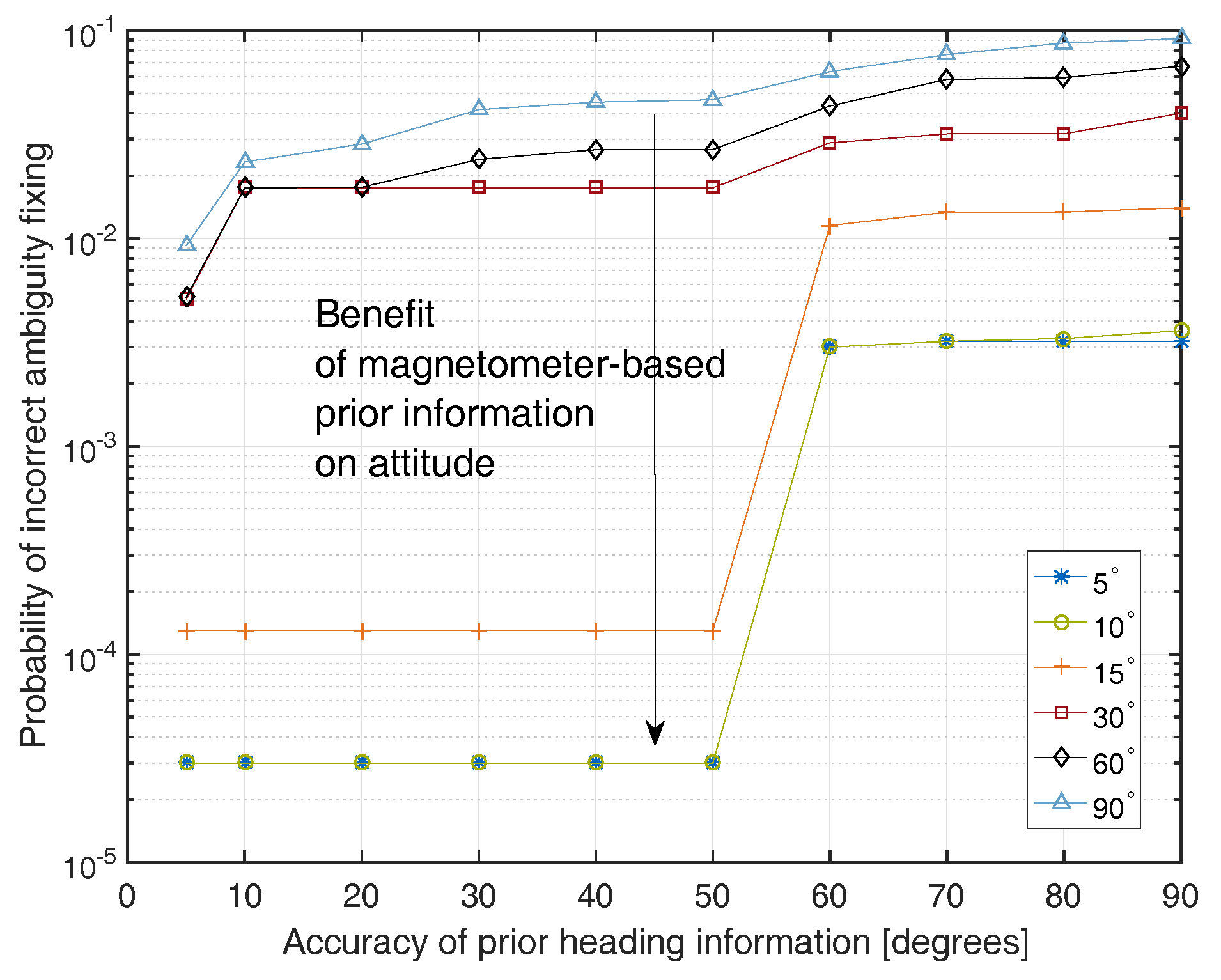


| simulated measurements | single frequency double difference |
| pseudoranges and carrier phase measurements | |
| on L1 ( MHz) of 27 Galileo satellites | |
| using nominal Walker constellation [12] | |
| (satellite altitude: km, orbital inclination: ) | |
| receiver position | longitude E, latitude N |
| baseline vector | length of 1 m, random attitude angles |
| noise statistics | phase noise: mm |
| code noise: m including multipath | |
| accuracy of prior information on baseline length | cm |
| accuracy of magnetometer based attitude information | variable accuracies for both heading and pitch angles |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Henkel, P. Calibration of Magnetometers with GNSS Receivers and Magnetometer-Aided GNSS Ambiguity Fixing. Sensors 2017, 17, 1324. https://doi.org/10.3390/s17061324
Henkel P. Calibration of Magnetometers with GNSS Receivers and Magnetometer-Aided GNSS Ambiguity Fixing. Sensors. 2017; 17(6):1324. https://doi.org/10.3390/s17061324
Chicago/Turabian StyleHenkel, Patrick. 2017. "Calibration of Magnetometers with GNSS Receivers and Magnetometer-Aided GNSS Ambiguity Fixing" Sensors 17, no. 6: 1324. https://doi.org/10.3390/s17061324





