A Hybrid Generalized Hidden Markov Model-Based Condition Monitoring Approach for Rolling Bearings
Abstract
:1. Introduction
- Rolling bearing feature extraction from noise-contaminated sensor signals based on VMD and GHMM is proposed firstly to improve the reliability of recognition with more information provided by the interval probability values;
- Selection of balancing parameter is set in the form of the generalized intervals to quantify the epistemic uncertainty;
- System errors that are inherent during data collection for the learning and feature recognition stage are incorporated.
2. Background
2.1. Variational Mode Decomposition
2.2. Multi-Scale Permutation Entropy
2.3. Principal Component Analysis
2.4. Generalized Hidden Markov Model
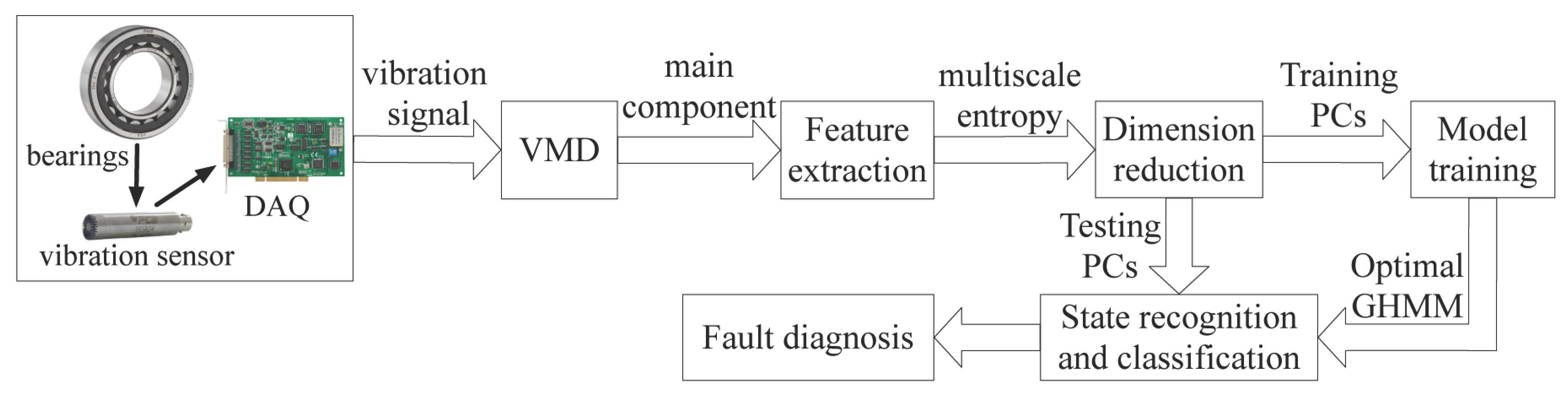
3. Methodology
4. Experimental Verification
4.1. Experimental Setup
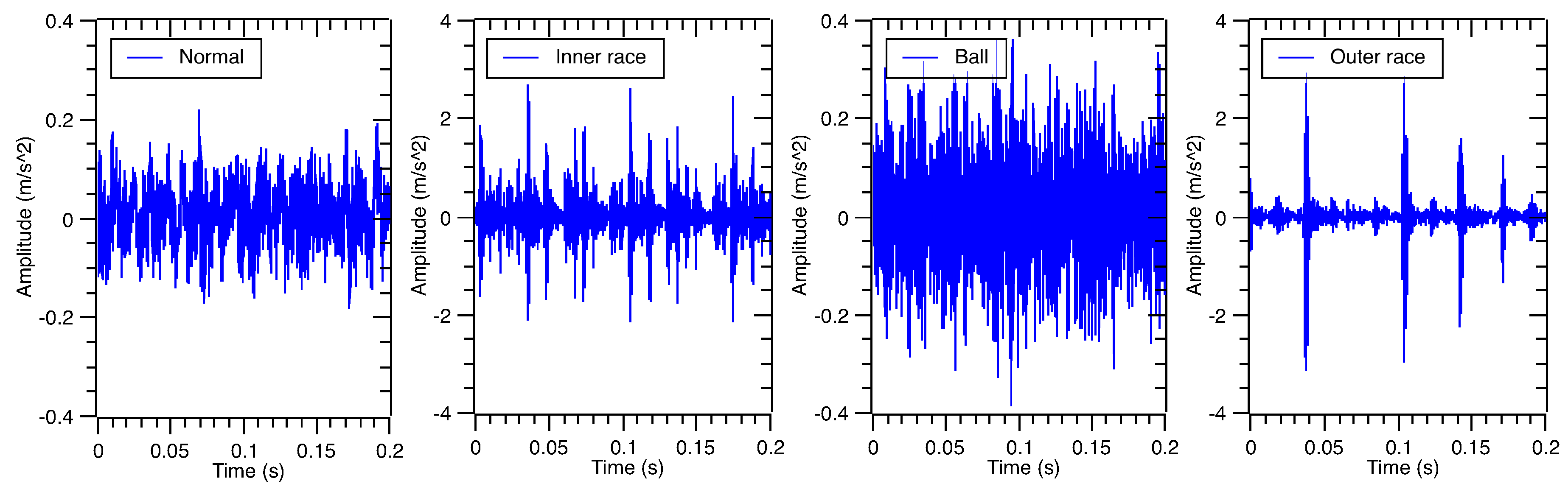
4.2. Signal Analysis
4.3. Signal Decomposition
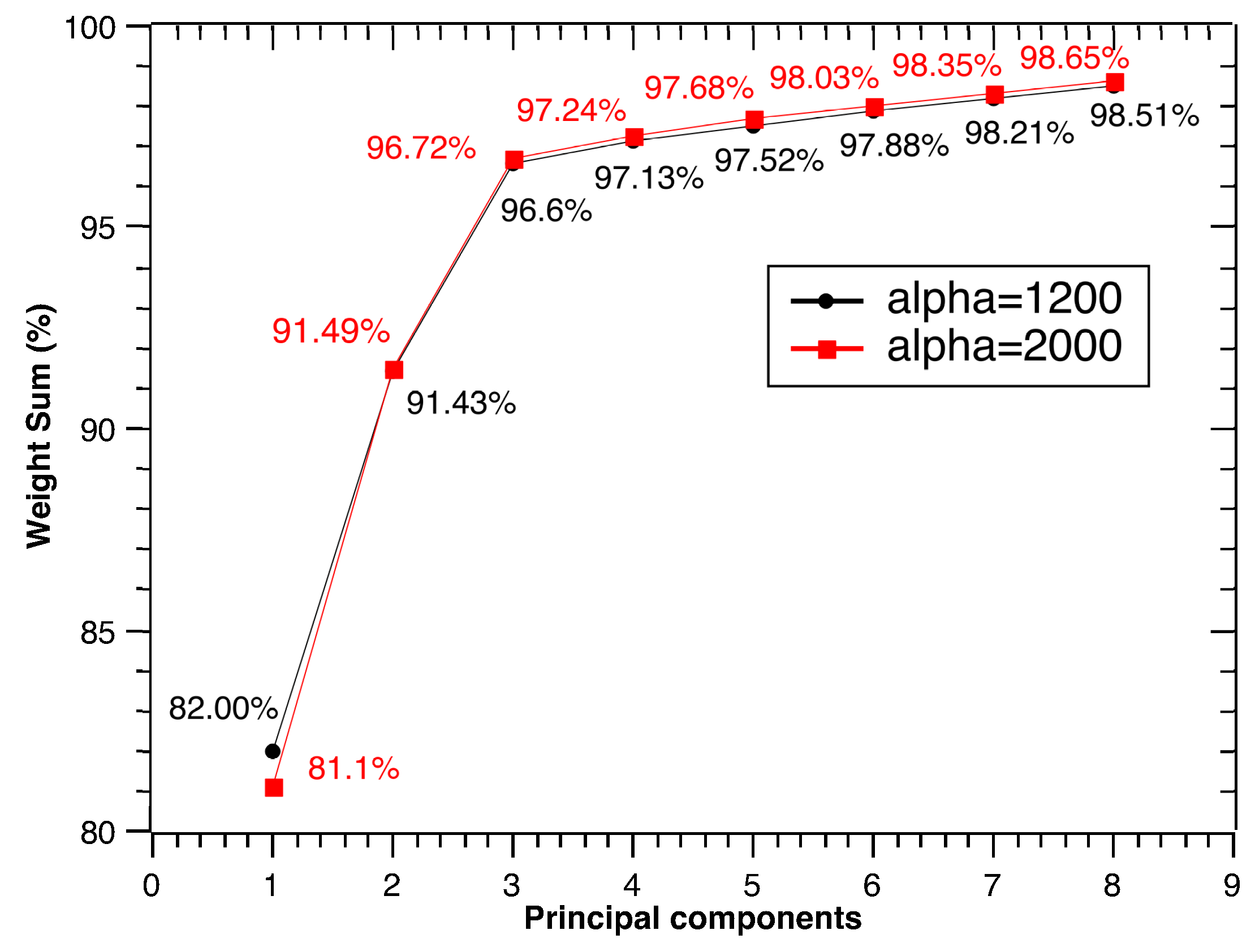
4.4. Reduced Features Extraction
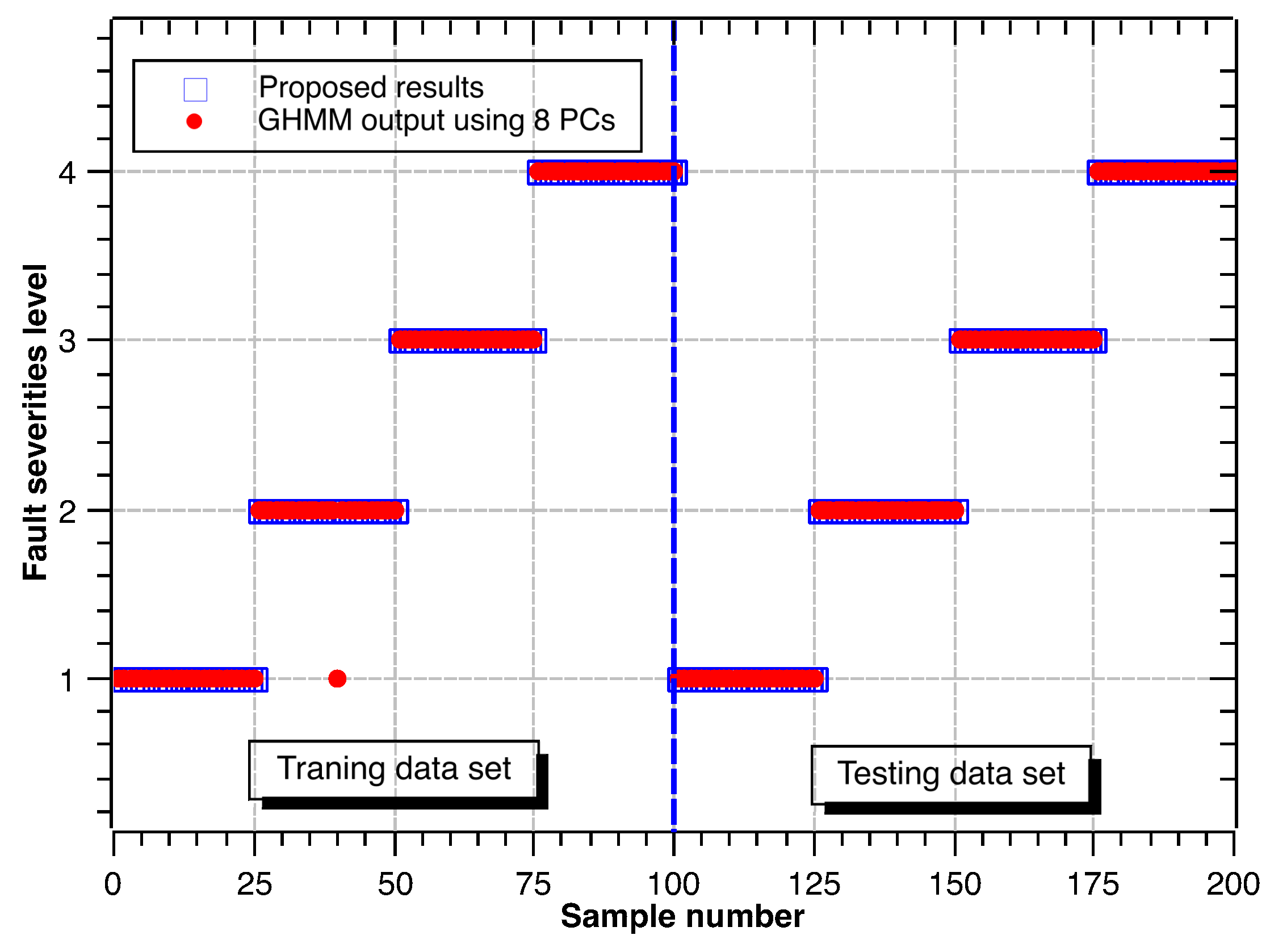
4.5. Fault Diagnosis
4.6. Discussion
4.6.1. Improvement in Signal Decomposition
4.6.2. Improvement in Features Extraction
- MPE-based extraction: The MPE with time scale factor 20 is used to extract features from the third decomposed sub-signal, and then, the PCA reduces the feature dimension into three PCs.
- PE-based extraction: The PE is used to calculate the third decomposed sub-signal.
4.6.3. Improvement in Pattern Recognition
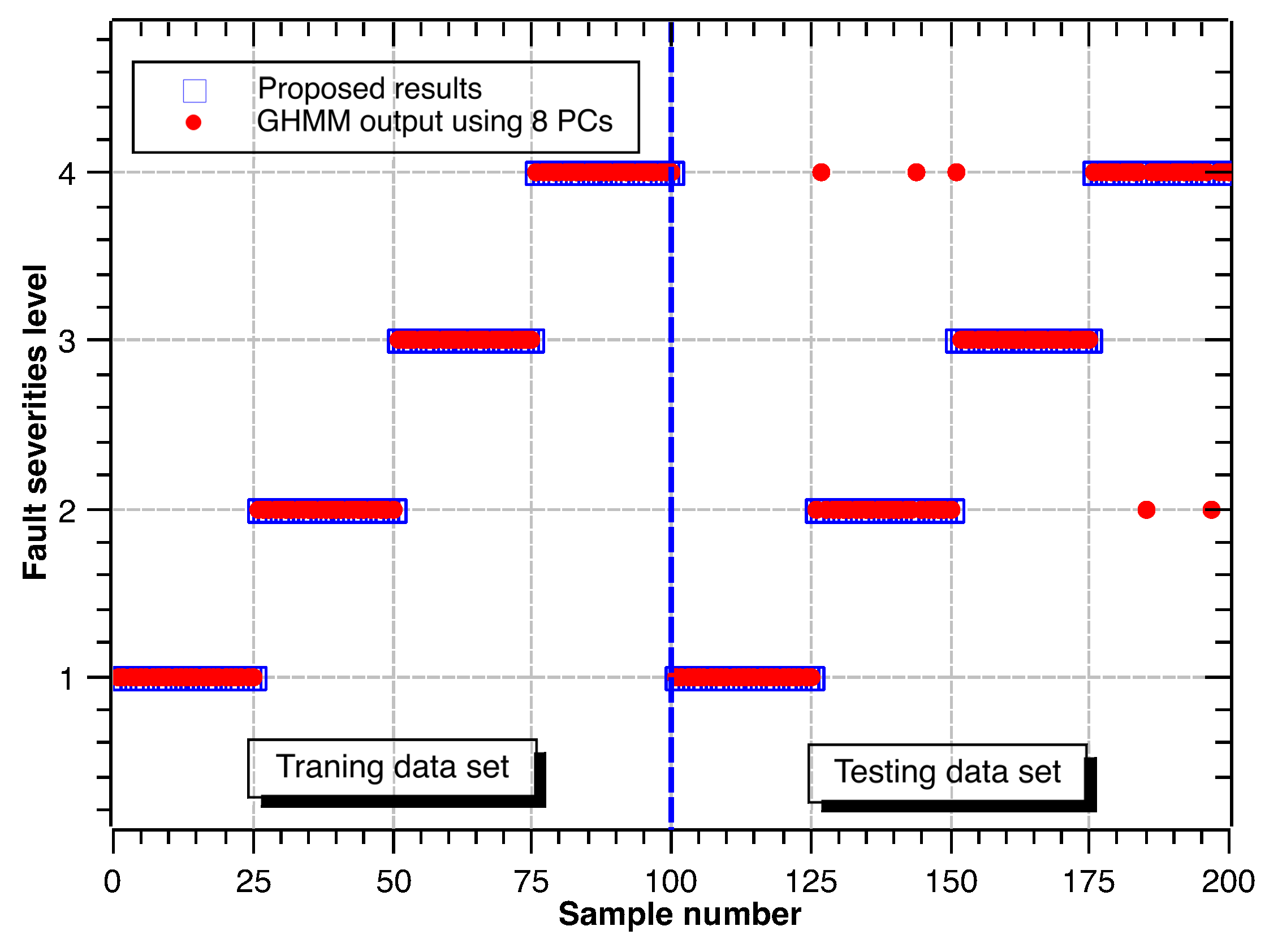
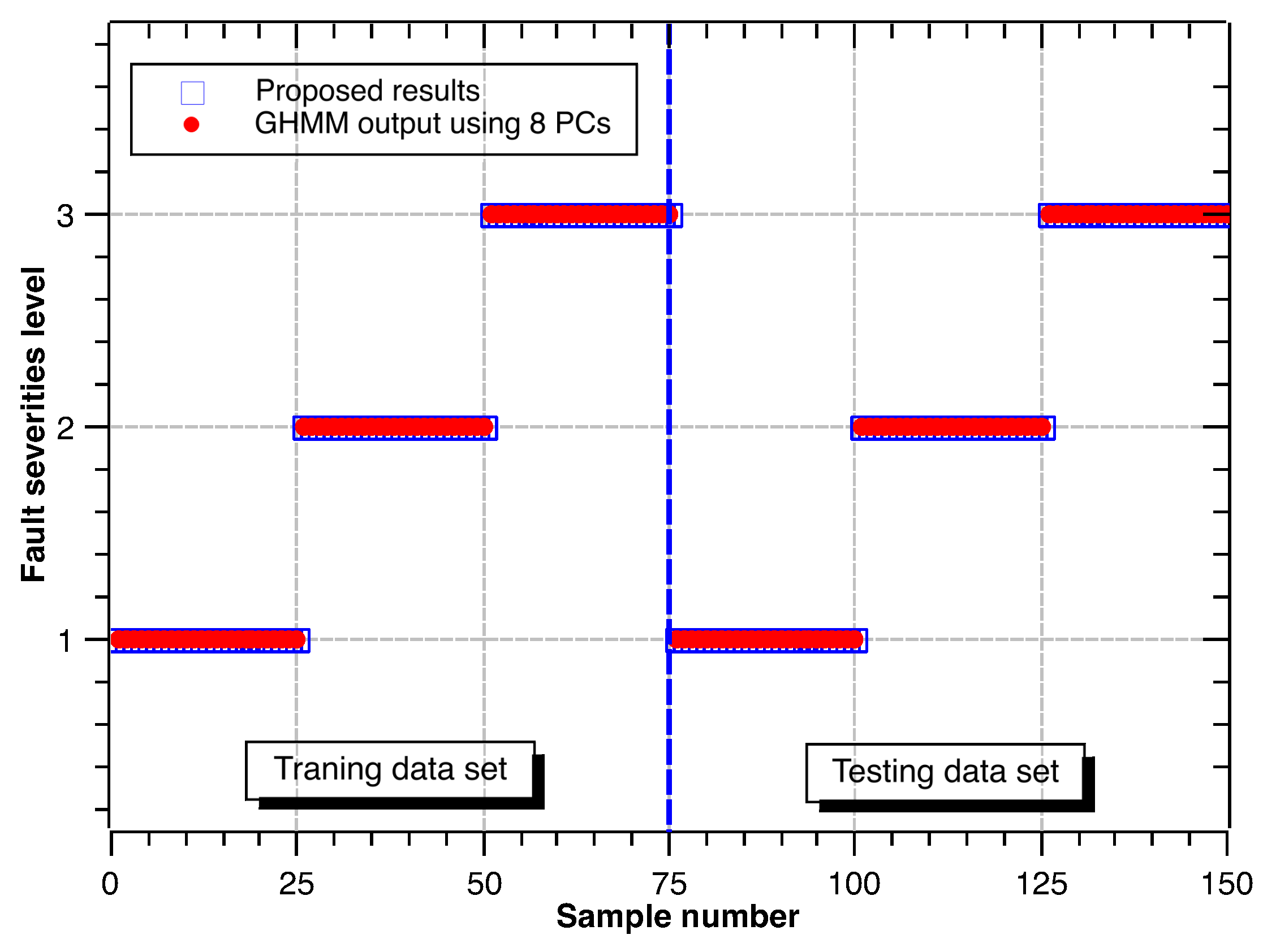
4.7. Fault Severity Levels’ Classification
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Antoni, J. Cyclic spectral analysis of rolling-element bearing signals: Facts and fictions. J. Sound Vib. 2007, 304, 497–529. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R. Vibration response of spalled rolling element bearings: Observations, simulations and signal processing techniques to track the spall size. Mech. Syst. Signal Process. 2011, 25, 846–870. [Google Scholar] [CrossRef]
- Lei, Y.; Lin, J.; He, Z.; Zuo, M.J. A review on empirical mode decomposition in fault diagnosis of rotating machinery. Mech. Syst. Signal Process. 2013, 35, 108–126. [Google Scholar] [CrossRef]
- Borghesani, P.; Pennacchi, P.; Randall, R.; Sawalhi, N.; Ricci, R. Application of cepstrum pre-whitening for the diagnosis of bearing faults under variable speed conditions. Mech. Syst. Signal Process. 2013, 36, 370–384. [Google Scholar] [CrossRef]
- Sawalhi, N.; Randall, R.B. Gear parameter identification in a wind turbine gearbox using vibration signals. Mech. Syst. Signal Process. 2014, 42, 368–376. [Google Scholar] [CrossRef]
- Tabaszewski, M. Optimization of a nearest neighbors classifier for diagnosis of condition of rolling bearings. Diagnostyka 2014, 15, 37–42. [Google Scholar]
- Abboud, D.; Antoni, J.; Eltabach, M.; Sieg-Zieba, S. Angle/time cyclostationarity for the analysis of rolling element bearing vibrations. Measurement 2015, 75, 29–39. [Google Scholar] [CrossRef]
- Figlus, T.; Stańczyk, M. A method for detecting damage to rolling bearings in toothed gears of processing lines. Metalurgija 2016, 55, 75–78. [Google Scholar]
- Strączkiewicz, M.; Czop, P.; Barszcz, T. Supervised and unsupervised learning process in damage classification of rolling element bearings. Diagnostyka 2016, 17, 71–80. [Google Scholar]
- Daubechies, I. The wavelet transform, time-frequency localization and signal analysis. IEEE Trans. Inf. Theory 1990, 36, 961–1005. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. R. Soc. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, C.; Hu, Z.; Kong, F.; Liu, X. Adaptive variational mode decomposition based on artificial fish swarm algorithm for fault diagnosis of rolling bearings. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 231, 635–654. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z. A Fault Diagnosis Scheme for Rolling Bearing Based on Particle Swarm Optimization in Variational Mode Decomposition. Shock Vib. 2016. [Google Scholar] [CrossRef]
- Zhang, M.; Jiang, Z.; Feng, K. Research on variational mode decomposition in rolling bearings fault diagnosis of the multistage centrifugal pump. Mech. Syst. Signal Process. 2017, 93, 460–493. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, Y.; He, S.; Jiang, Z. Bearing fault diagnosis based on variational mode decomposition and total variation denoising. Meas. Sci. Technol. 2016, 27, 075101. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Wu, B.; Jin, C. A hybrid health condition monitoring method in milling operations. Int. J. Adv. Manuf. Technol. 2017. [Google Scholar] [CrossRef]
- Ge, M.F.; Guan, Z.H.; Hu, B.; He, D.X.; Liao, R.Q. Distributed controller–estimator for target tracking of networked robotic systems under sampled interaction. Automatica 2016, 69, 410–417. [Google Scholar] [CrossRef]
- Eldred, M.S.; Swiler, L.P.; Tang, G. Mixed aleatory-epistemic uncertainty quantification with stochastic expansions and optimization-based interval estimation. Reliab. Eng. Syst. Saf. 2011, 96, 1092–1113. [Google Scholar] [CrossRef]
- Wang, Y. Imprecise probabilities based on generalised intervals for system reliability assessment. Int. J. Reliab. Saf. 2010, 4, 319–342. [Google Scholar] [CrossRef]
- Xie, F.; Wu, B.; Hu, Y.; Wang, Y.; Jia, G.; Cheng, Y. A generalized interval probability-based optimization method for training generalized hidden Markov model. Signal Process. 2014, 94, 319–329. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef] [PubMed]
- Aziz, W.; Arif, M. Multiscale permutation entropy of physiological time series. In Proceedings of the 9th International Multitopic Conference, IEEE INMIC 2005, Karachi, Pakistan, 24–25 December 2005; pp. 1–6. [Google Scholar]
- Wu, S.D.; Wu, P.H.; Wu, C.W.; Ding, J.J.; Wang, C.C. Bearing fault diagnosis based on multiscale permutation entropy and support vector machine. Entropy 2012, 14, 1343–1356. [Google Scholar] [CrossRef]
- Costa, M.; Goldberger, A.L.; Peng, C.K. Multiscale entropy analysis of complex physiologic time series. Phys. Rev. Lett. 2002, 89, 068102. [Google Scholar] [CrossRef] [PubMed]
- Jolliffe, I. Principal Component Analysis; John Wiley and Sons, Ltd.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Wang, Y. Multiscale uncertainty quantification based on a generalized hidden Markov model. J. Mech. Des. 2011, 133, 031004. [Google Scholar] [CrossRef]
- Wang, Y. Training Generalized Hidden Markov Model with Interval Probability Parameters. In Vulnerability, Uncertainty, and Risk: Quantification, Mitigation, and Management; CDRM 9: Liverpool, UK, 2014; pp. 876–886. [Google Scholar] [CrossRef]
- Xie, F.Y.; Hu, Y.M.; Wu, B.; Wang, Y. A generalized hidden Markov model and its applications in recognition of cutting states. Int. J. Precis. Eng. Manuf. 2016, 17, 1471–1482. [Google Scholar] [CrossRef]
- Loparo, K. Case Western Reserve University Bearing Data Center. Available online: http://csegroups.case.edu/bearingdatacenter/home (accessed on 11 May 2017).
- Daszykowski, M.; Walczak, B.; Massart, D. Representative subset selection. Anal. Chim. Acta 2002, 468, 91–103. [Google Scholar] [CrossRef]
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. An analytical model for the prediction of the vibration response of rolling element bearings due to a localized defect. J. Sound Vib. 1997, 205, 275–292. [Google Scholar] [CrossRef]
- Ho, D.; Randall, R. Optimisation of bearing diagnostic techniques using simulated and actual bearing fault signals. Mech. Syst. Signal Process. 2000, 14, 763–788. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Signal Process. 2015, 60, 243–251. [Google Scholar] [CrossRef]
- Li, Z.; Chen, J.; Zi, Y.; Pan, J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive. Mech. Syst. Signal Process. 2017, 85, 512–529. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, G.; Li, M.; Yin, H. Variational mode decomposition denoising combined the detrended fluctuation analysis. Signal Process. 2016, 125, 349–364. [Google Scholar] [CrossRef]
- Matilla-García, M. A non-parametric test for independence based on symbolic dynamics. J. Econ. Dyn. Control 2007, 31, 3889–3903. [Google Scholar] [CrossRef]
- Sabin, M.; Gray, R. Global convergence and empirical consistency of the generalized Lloyd algorithm. IEEE Trans. Inf. Theory 1986, 32, 148–155. [Google Scholar] [CrossRef]
- Cabulea, L.; Aldea, M. Making a decision when dealing with uncertain conditions. Acta Univ. Apulensis Math.-Inform. 2004, 7, 85–92. [Google Scholar]
- Liu, J.; Wu, B.; Wang, Y.; Hu, Y. An integrated condition monitoring method for milling process using reduced decomposition features. Meas. Sci. Technol. 2017. [Google Scholar] [CrossRef]
- Rabiner, L.R. A tutorial on hidden Markov models and selected applications in speech recognition. Proc. IEEE 1989, 77, 257–286. [Google Scholar] [CrossRef]
- Liu, H.; Han, M. A fault diagnosis method based on local mean decomposition and multi-scale entropy for roller bearings. Mech. Mach. Theory 2014, 75, 67–78. [Google Scholar] [CrossRef]
- Liu, Z.; Cao, H.; Chen, X.; He, Z.; Shen, Z. Multi-fault classification based on wavelet SVM with PSO algorithm to analyze vibration signals from rolling element bearings. Neurocomputing 2013, 99, 399–410. [Google Scholar] [CrossRef]
- Vakharia, V.; Gupta, V.; Kankar, P. A multiscale permutation entropy based approach to select wavelet for fault diagnosis of ball bearings. J. Vib. Control 2015, 21, 3123–3131. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Wei, Y.; Huang, W. A new rolling bearing fault diagnosis method based on multiscale permutation entropy and improved support vector machine based binary tree. Measurement 2016, 77, 80–94. [Google Scholar] [CrossRef]
- Ao, H.; Cheng, J.; Li, K.; Truong, T.K. A roller bearing fault diagnosis method based on LCD energy entropy and ACROA-SVM. Shock Vib. 2014. [Google Scholar] [CrossRef]
- Wu, S.D.; Wu, C.W.; Wu, T.Y.; Wang, C.C. Multi-scale analysis based ball bearing defect diagnostics using Mahalanobis distance and support vector machine. Entropy 2013, 15, 416–433. [Google Scholar] [CrossRef]
- Yu, Y.; Junsheng, C. A roller bearing fault diagnosis method based on EMD energy entropy and ANN. J. Sound Vib. 2006, 294, 269–277. [Google Scholar] [CrossRef]
- Han, T.; Jiang, D. Rolling Bearing Fault Diagnostic Method Based on VMD-AR Model and Random Forest Classifier. Shock Vib. 2016. [Google Scholar] [CrossRef]





| Types | Values |
|---|---|
| Fault types | inner race defect, ball defect, outer race defect |
| Fault severity levels | 7 mil, 14 mil, 21 mil, 28 mil |
| Rotation speed | 1730 rpm, 1750 rpm, 1772 rpm, 1797 rpm |
| Sampling frequency | 12 kHz |
| Types | Values |
|---|---|
| Rolling element number (N) | 9 |
| Ball diameter (d) | 312.6 mil |
| Pitch diameter (D) | 1537 mil |
| Contact angle () | 0 |
| Types | Values |
|---|---|
| Shaft rotation frequency () | 29.17 Hz |
| Inner defect frequency () | 157.95 Hz |
| Ball defect frequency () | 137.48 Hz |
| Outer defect frequency () | 104.56 Hz |
| Sample No. | Optimal GHMM for NC | Optimal GHMM for IRDC | Optimal GHMM for BDC | Optimal GHMM for ORDC |
|---|---|---|---|---|
| 1 | [−0.0842, −0.0412] | [−Inf, −1617.4] | [−172.79, −582.69] | [−Inf, −1949.5] |
| 2 | [−Inf, −Inf] | [−2.248, −51.994] | [−94.4, −110.13] | [−Inf, −97.352] |
| 3 | [−Inf, −Inf] | [−Inf, −623] | [−108.19, −4.997] | [−Inf, −639.01] |
| 4 | [−921.2, −Inf] | [−424.76, −165.2] | [−11.965, −54.34] | [−9.16, −12.445] |
| Number of PCs | Training | Testing | Total |
|---|---|---|---|
| 8 | 100.0% | 98.0% | 99.0% |
| 7 | 100.0% | 98.0% | 99.0% |
| 6 | 100.0% | 98.0% | 99.0% |
| 5 | 100.0% | 99.0% | 99.5% |
| 4 | 100.0% | 100.0% | 100.0% |
| 3 | 100.0% | 94.0% | 97.0% |
| Signal Decomposition | 3 PCs | 4 PCs | 5 PCs | 6 PCs | 7 PCs | 8 PCs | |
|---|---|---|---|---|---|---|---|
| Training | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | 100.0% | |
| VMD | Testing | 96.0% | 100.0% | 100.0% | 99.0% | 100.0% | 100.0% |
| Total | 98.0% | 100.0% | 100.0% | 99.5% | 100.0% | 100.0% | |
| Training | 91.0% | 96.0% | 97.0% | 97.0% | 95.0% | 95.0% | |
| EMD | Testing | 89.0% | 94.0% | 95.0% | 94.0% | 92.0% | 93.0% |
| Total | 90.0% | 95.0% | 96.0% | 95.5% | 93.5% | 94.0% | |
| Training | 100.0% | 100.0% | 100.0% | 100.0% | 99.0% | 100.0% | |
| Without signal decomposition | Testing | 95.0% | 93.0% | 91.0% | 91.0% | 95.0% | 98.0% |
| Total | 97.5% | 96.5% | 95.5% | 95.5% | 97.0% | 99.0% |
| Feature Extractions | Training | Testing | Total |
|---|---|---|---|
| MPE-based extraction | 100.0% | 94.0% | 97.0% |
| PE-based extraction | 90.0% | 84.0% | 87.0% |
| PE ratio-based extraction | 94.0% | 93.0% | 93.5% |
| SE ratio-based extraction | 100.0% | 94.0% | 97.0% |
| Samples No. | Optimal HMM for NC | Optimal HMM for IRDC | Optimal HMM for BDC | Optimal HMM for ORDC |
|---|---|---|---|---|
| 1 | −0.67167 | −1482.5 | −649.79 | −Inf |
| 2 | −Inf | −5.7906 | −75.438 | −Inf |
| 3 | −Inf | −497.99 | −657.96 | −Inf |
| 4 | −Inf | −115.62 | −83.03 | −2.1655 |
| Fault Type | Preprocess | Feature Technique | Feature Selection | Classifier and Model | Maximum Classification | References |
|---|---|---|---|---|---|---|
| ORD, IRD, BD | LMD | MSE | N/A | SVM | 100.0% | Liu and Han [45] |
| ORD, IRD, BD | EMD | Statistics | N/A | PSO-SVM | 97.5% | Liu et al. [46] |
| ORD, IRD, BD | N/A | MPE | N/A | SVM | 100.0% | Wu et al. [26] |
| ORD, IRD, BD | Wavelet | Different attribute filters | N/A | SVM and ANN | 97.5% | Vakharia et al. [47] |
| ORD, IRD, BD | LMD | MPE | LS | SVM-BT | 100.0% | Li et al. [48] |
| ORD, IRD | LCD | Energy entropy | N/A | ACROA-SVM | 100.0% | Ao et al. [49] |
| ORD, IRD, BD | NA | Multi-scale analysis | MD | SVM | 99.79% | Wu et al. [50] |
| ORD, IRD | EMD | Energy entropy | N/A | ANN | 93.0% | Yu et al. [51] |
| ORD, IRD, BD | VMD | AR | N/A | RF | 100.0% | Han et al. [52] |
| ORD, IRD, BD | VMD | MPE | PCA | GHMM | 100.0% | present work |
| Fault Types | Fault Diameters | Training | Testing | Total |
|---|---|---|---|---|
| IRD | 7 mil | 100.0% | 100.0% | 100.0% |
| 14 mil | 96.0% | 100.0% | 98.0% | |
| 21 mil | 100.0% | 100.0% | 100.0% | |
| 28 mil | 100.0% | 100.0% | 100.0% | |
| BD | 7 mil | 100.0% | 100.0% | 100.0% |
| 14 mil | 100.0% | 92.0% | 96.0% | |
| 21 mil | 100.0% | 96.0% | 98.0% | |
| 28 mil | 100.0% | 92.0% | 96.0% | |
| ORD | 7 mil | 100.0% | 100.0% | 100.0% |
| 14 mil | 100.0% | 100.0% | 100.0% | |
| 21 mil | 100.0% | 100.0% | 100.0% |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Hu, Y.; Wu, B.; Wang, Y.; Xie, F. A Hybrid Generalized Hidden Markov Model-Based Condition Monitoring Approach for Rolling Bearings. Sensors 2017, 17, 1143. https://doi.org/10.3390/s17051143
Liu J, Hu Y, Wu B, Wang Y, Xie F. A Hybrid Generalized Hidden Markov Model-Based Condition Monitoring Approach for Rolling Bearings. Sensors. 2017; 17(5):1143. https://doi.org/10.3390/s17051143
Chicago/Turabian StyleLiu, Jie, Youmin Hu, Bo Wu, Yan Wang, and Fengyun Xie. 2017. "A Hybrid Generalized Hidden Markov Model-Based Condition Monitoring Approach for Rolling Bearings" Sensors 17, no. 5: 1143. https://doi.org/10.3390/s17051143





