Social Welfare Control in Mobile Crowdsensing Using Zero-Determinant Strategy
Abstract
:1. Introduction
- We make use of two types of iterated games to formulate the interactions between the requestor and the worker in mobile crowdsensing when they adopt discrete strategies and continuous strategies.
- Based on the original zero-determinant strategy derived under the discrete model, we extend it with sufficient theoretic derivation to make it applicable for the continuous model. Note that this extension not only provides theoretical foundation for our proposed mechanism but also expands the application range of zero-determinant strategy.
- We propose two social welfare control mechanisms for the requestor under two different situations, which helps the requestor establish an overall control over the quality of the whole crowdsensing system so as to solve the low-quality data problem from the perspective of the ultimate goal.
2. Game Formulation
3. Game Analysis and Mechanism Design
3.1. Zero-Determinant Strategy Based Scheme in the Discrete Model
3.2. Zero-Determinant Strategy Based Scheme in the Continuous Model
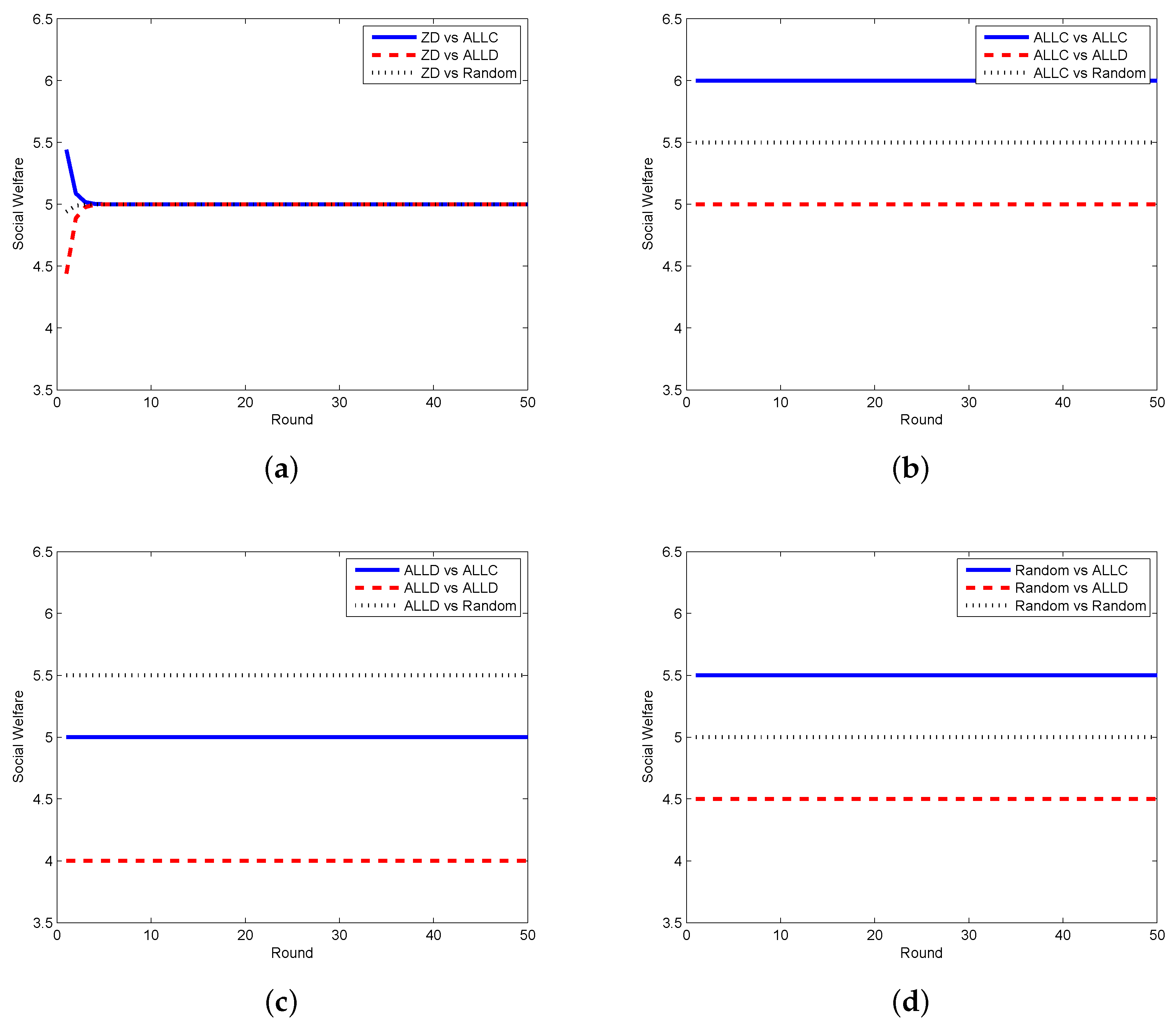
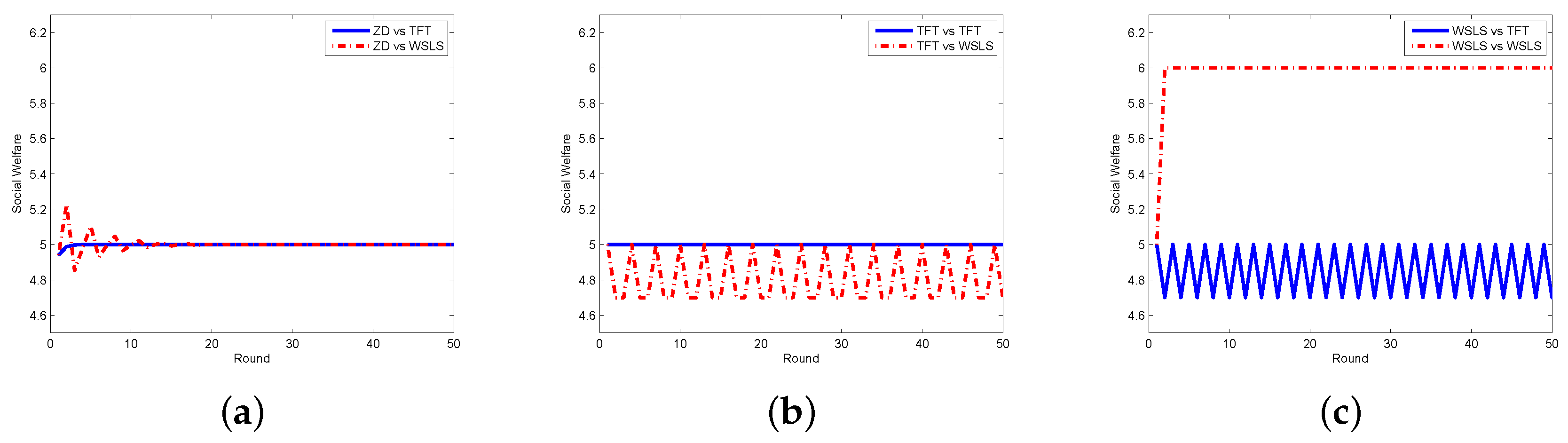
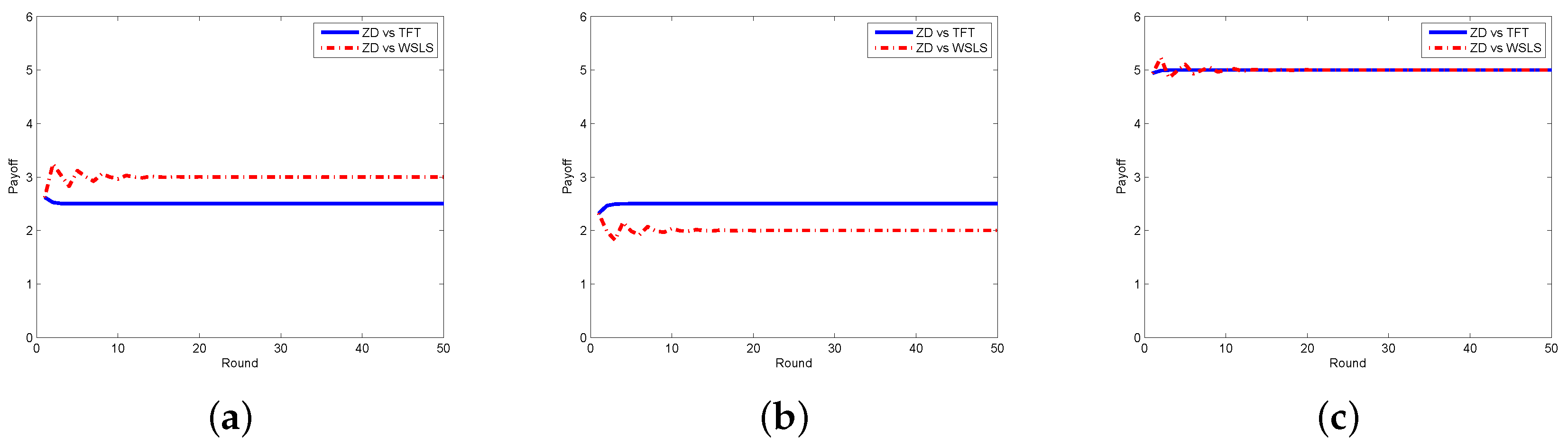
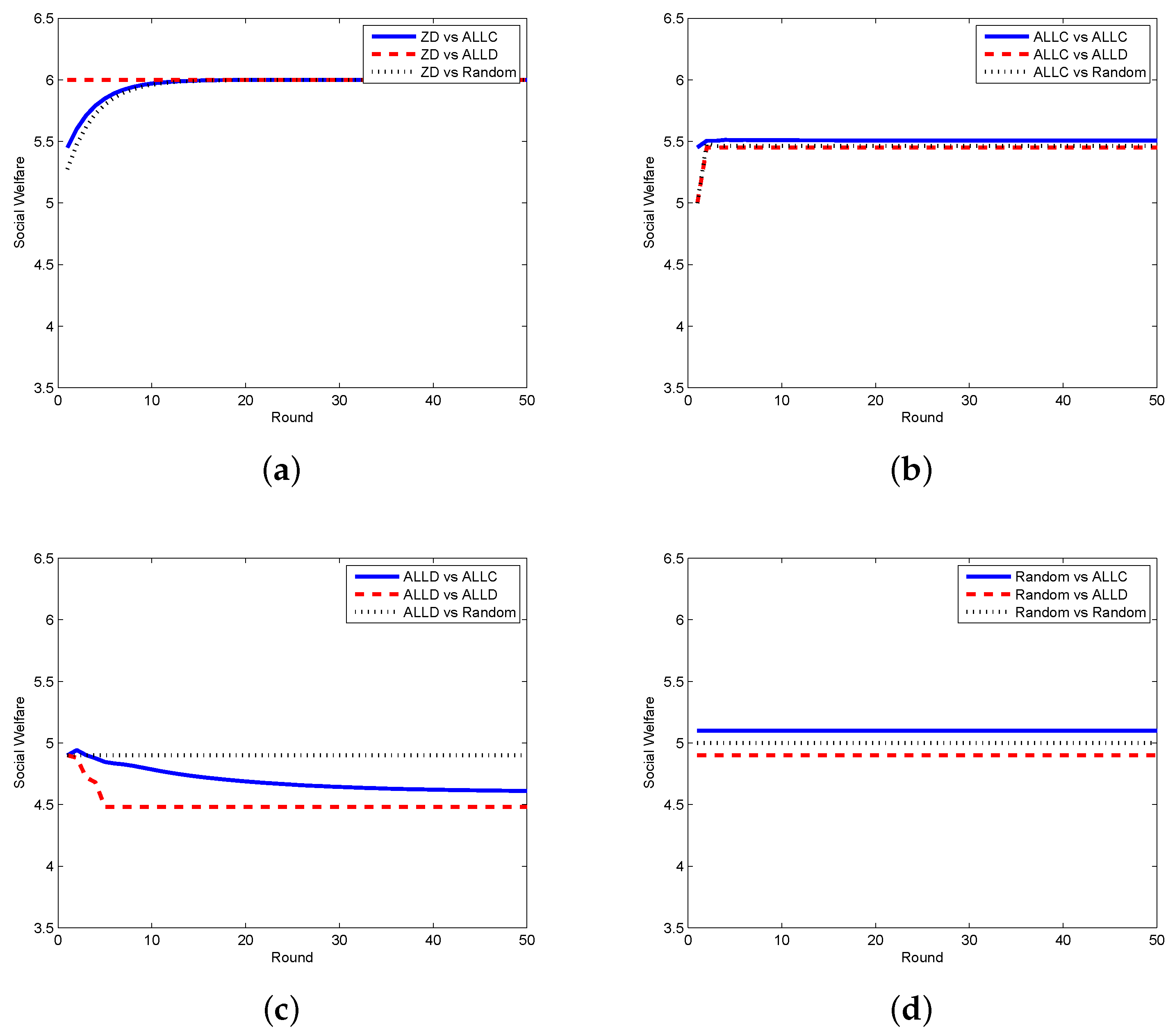
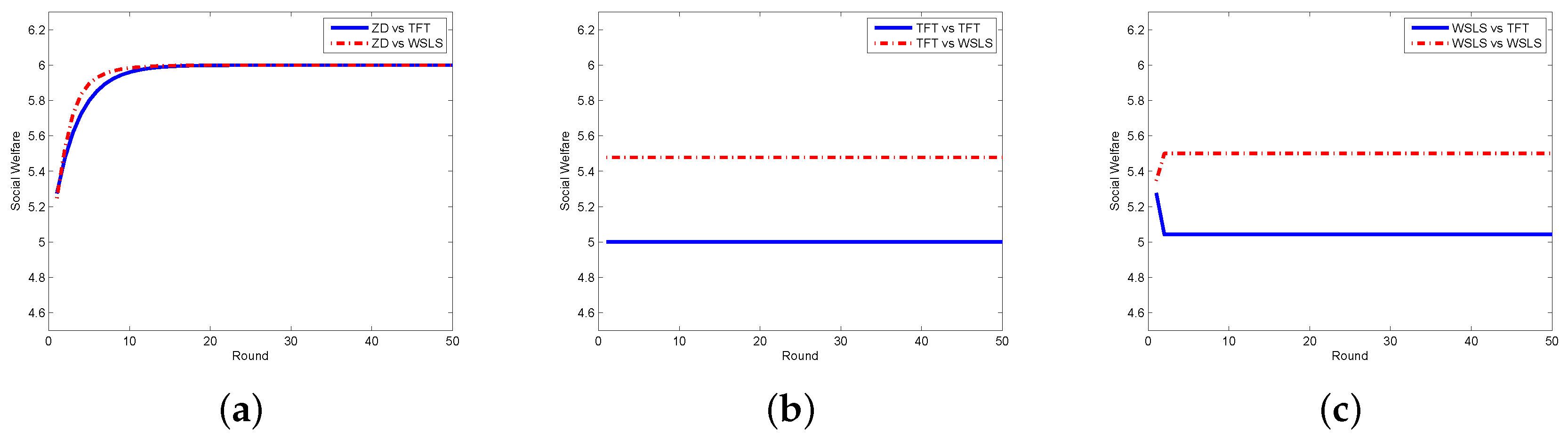
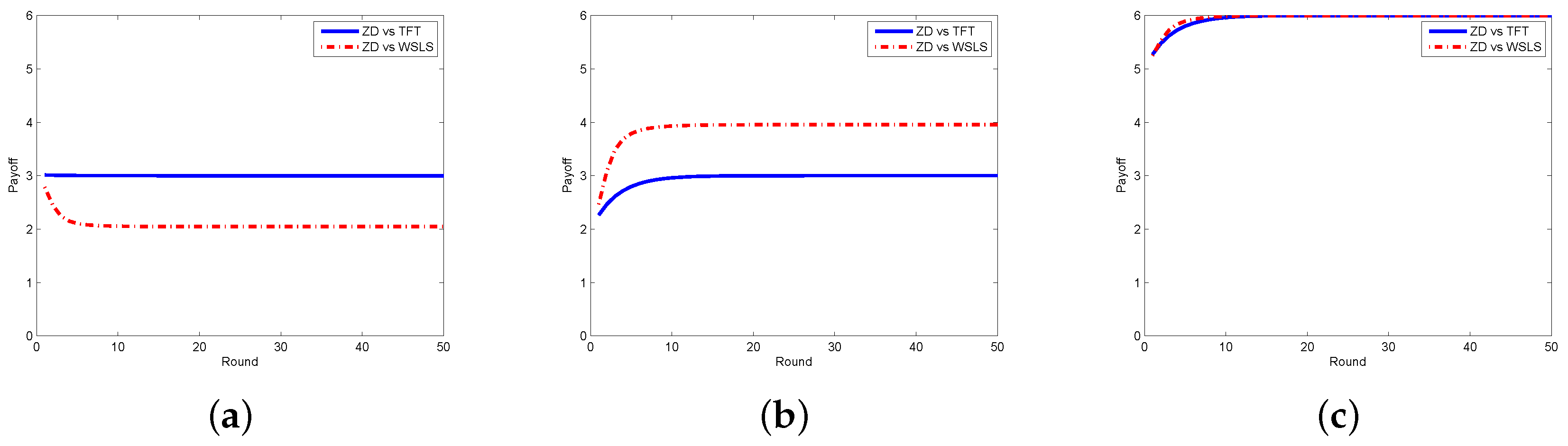
4. Evaluation of the Proposed Schemes
5. Related Work
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ganti, R.K.; Ye, F.; Lei, H. Mobile crowdsensing: Current state and future challenges. IEEE Commun. Mag. 2011, 49. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, D.; Yuan, P. Opportunities in mobile crowd sensing. IEEE Commun. Mag. 2014, 52, 29–35. [Google Scholar] [CrossRef]
- Guo, B.; Wang, Z.; Yu, Z.; Wang, Y.; Yen, N.Y.; Huang, R.; Zhou, X. Mobile crowd sensing and computing: The review of an emerging human-powered sensing paradigm. ACM Comput. Surv. CSUR 2015, 48, 7. [Google Scholar] [CrossRef]
- Intanagonwiwat, C.; Govindan, R.; Estrin, D. Directed Diffusion: A Scalable and Robust Communication Paradigm for Sensor Networks. In Proceedings of the 6th Annual International Conference on Mobile Computing and Networking, Boston, MA, USA, 6–11 August 2000; pp. 56–67. [Google Scholar]
- Yu, J.; Wang, N.; Wang, G.; Yu, D. Connected dominating sets in wireless ad hoc and sensor networks—A comprehensive survey. Comput. Commun. 2013, 36, 121–134. [Google Scholar] [CrossRef]
- Sun, J.; Ma, H. A Behavior-Based Incentive Mechanism for Crowd Sensing with Budget Constraints. In Proceedings of the 2014 IEEE International Conference on Communications (ICC), Sydney, Australia, 10–14 June 2014; pp. 1314–1319. [Google Scholar]
- Jin, H.; Su, L.; Chen, D.; Nahrstedt, K.; Xu, J. Quality of Information Aware Incentive Mechanisms for Mobile Crowd Sensing Systems. In Proceedings of the 16th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Hangzhou, China, 22–25 June 2015; pp. 167–176. [Google Scholar]
- Wen, Y.; Shi, J.; Zhang, Q.; Tian, X.; Huang, Z.; Yu, H.; Cheng, Y.; Shen, X. Quality-driven auction-based incentive mechanism for mobile crowd sensing. IEEE Trans. Veh. Technol. 2015, 64, 4203–4214. [Google Scholar] [CrossRef]
- Amintoosi, H.; Kanhere, S.S. A reputation framework for social participatory sensing systems. Mob. Netw. Appl. 2014, 19, 88–100. [Google Scholar] [CrossRef]
- Kawajiri, R.; Shimosaka, M.; Kashima, H. Steered Crowdsensing: Incentive Design towards Quality-Oriented Place-Centric Crowdsensing. In Proceedings of the 2014 ACM International Joint Conference on Pervasive and Ubiquitous Computing, Seattle, WA, USA, 13–17 September 2014; pp. 691–701. [Google Scholar]
- Press, W.H.; Dyson, F.J. Iterated Prisoner’s Dilemma contains strategies that dominate any evolutionary opponent. Proc. Natl. Acad. Sci. USA 2012, 109, 10409–10413. [Google Scholar] [CrossRef] [PubMed]
- Jordan, K.; Sheptykin, I.; Grüter, B.; Vatterrott, H.R. Identification of Structural Landmarks in a Park Using Movement Data Collected in a Location-Based Game. In Proceedings of the First ACM SIGSPATIAL International Workshop on Computational Models of Place, Orlando, FL, USA, 5–8 November 2013; pp. 1–8. [Google Scholar]
- Hoh, B.; Yan, T.; Ganesan, D.; Tracton, K.; Iwuchukwu, T.; Lee, J.S. Trucentive: A Game-Theoretic Incentive Platform for Trustworthy Mobile Crowdsourcing Parking Services. In Proceedings of the 2012 15th International IEEE Conference on Intelligent Transportation Systems (ITSC), Anchorage, AK, USA, 16–19 September 2012; pp. 160–166. [Google Scholar]
- Lan, K.c.; Chou, C.M.; Wang, H.Y. An incentive-based framework for vehicle-based mobile sensing. Procedia Comput. Sci. 2012, 10, 1152–1157. [Google Scholar] [CrossRef]
- Chou, C.M.; Lan, K.c.; Yang, C.F. Using Virtual Credits to Provide Incentives for Vehicle Communication. In Proceedings of the 2012 12th International Conference on ITS Telecommunications (ITST), Taipei, Taiwan, 5–8 November 2012; pp. 579–583. [Google Scholar]
- Zhang, X.; Yang, Z.; Zhou, Z.; Cai, H.; Chen, L.; Li, X. Free market of crowdsourcing: Incentive mechanism design for mobile sensing. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 3190–3200. [Google Scholar] [CrossRef]
- Chen, X.; Liu, M.; Zhou, Y.; Li, Z.; Chen, S.; He, X. A Truthful Incentive Mechanism for Online Recruitment in Mobile Crowd Sensing System. Sensors 2017, 17, 79. [Google Scholar] [CrossRef] [PubMed]
- Xiao, L.; Liu, J.; Li, Q.; Poor, H.V. Secure Mobile Crowdsensing Game. In Proceedings of the 2015 IEEE International Conference on Communications (ICC), London, UK, 8–12 June 2015; pp. 7157–7162. [Google Scholar]
- Peng, D.; Wu, F.; Chen, G. Pay as How Well You Do: A Quality Based Incentive Mechanism for Crowdsensing. In Proceedings of the 16th ACM International Symposium on Mobile Ad Hoc Networking and Computing, Hangzhou, China, 22–25 June 2015; pp. 177–186. [Google Scholar]
- Alsheikh, M.A.; Jiao, Y.; Niyato, D.; Wang, P.; Leong, D.; Han, Z. The Accuracy-Privacy Tradeoff of Mobile Crowdsensing. arXiv, 2017; arXiv:1702.04565. [Google Scholar]
- Gisdakis, S.; Giannetsos, T.; Papadimitratos, P. Sppear: Security & Privacy-Preserving Architecture for Participatory-Sensing Applications. In Proceedings of the 2014 ACM Conference on Security and Privacy in Wireless & Mobile Networks, Oxford, UK, 23–25 July 2014; pp. 39–50. [Google Scholar]
- Gisdakis, S.; Giannetsos, T.; Papadimitratos, P. Security, Privacy, and Incentive Provision for Mobile Crowd Sensing Systems. IEEE Internet Things J. 2016, 3, 839–853. [Google Scholar] [CrossRef]
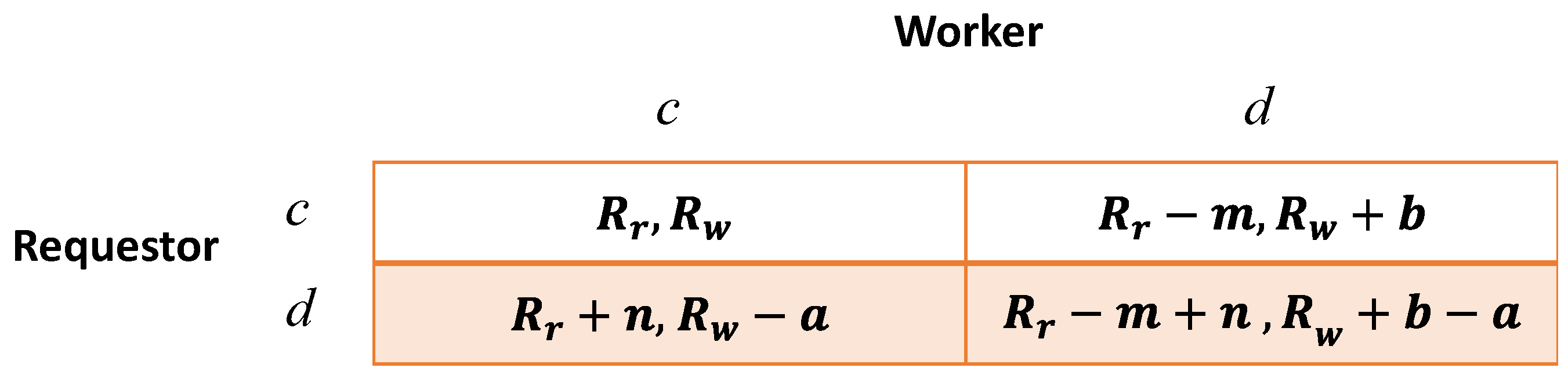


© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Q.; Wang, S.; Bie, R.; Cheng, X. Social Welfare Control in Mobile Crowdsensing Using Zero-Determinant Strategy. Sensors 2017, 17, 1012. https://doi.org/10.3390/s17051012
Hu Q, Wang S, Bie R, Cheng X. Social Welfare Control in Mobile Crowdsensing Using Zero-Determinant Strategy. Sensors. 2017; 17(5):1012. https://doi.org/10.3390/s17051012
Chicago/Turabian StyleHu, Qin, Shengling Wang, Rongfang Bie, and Xiuzhen Cheng. 2017. "Social Welfare Control in Mobile Crowdsensing Using Zero-Determinant Strategy" Sensors 17, no. 5: 1012. https://doi.org/10.3390/s17051012




