Computationally Efficient 2D DOA Estimation with Uniform Rectangular Array in Low-Grazing Angle
Abstract
:1. Introduction
- The method in [22] can only use the auto-correlations of different subarrays, while the proposed method can use more information including auto-correlations and cross-correlations.
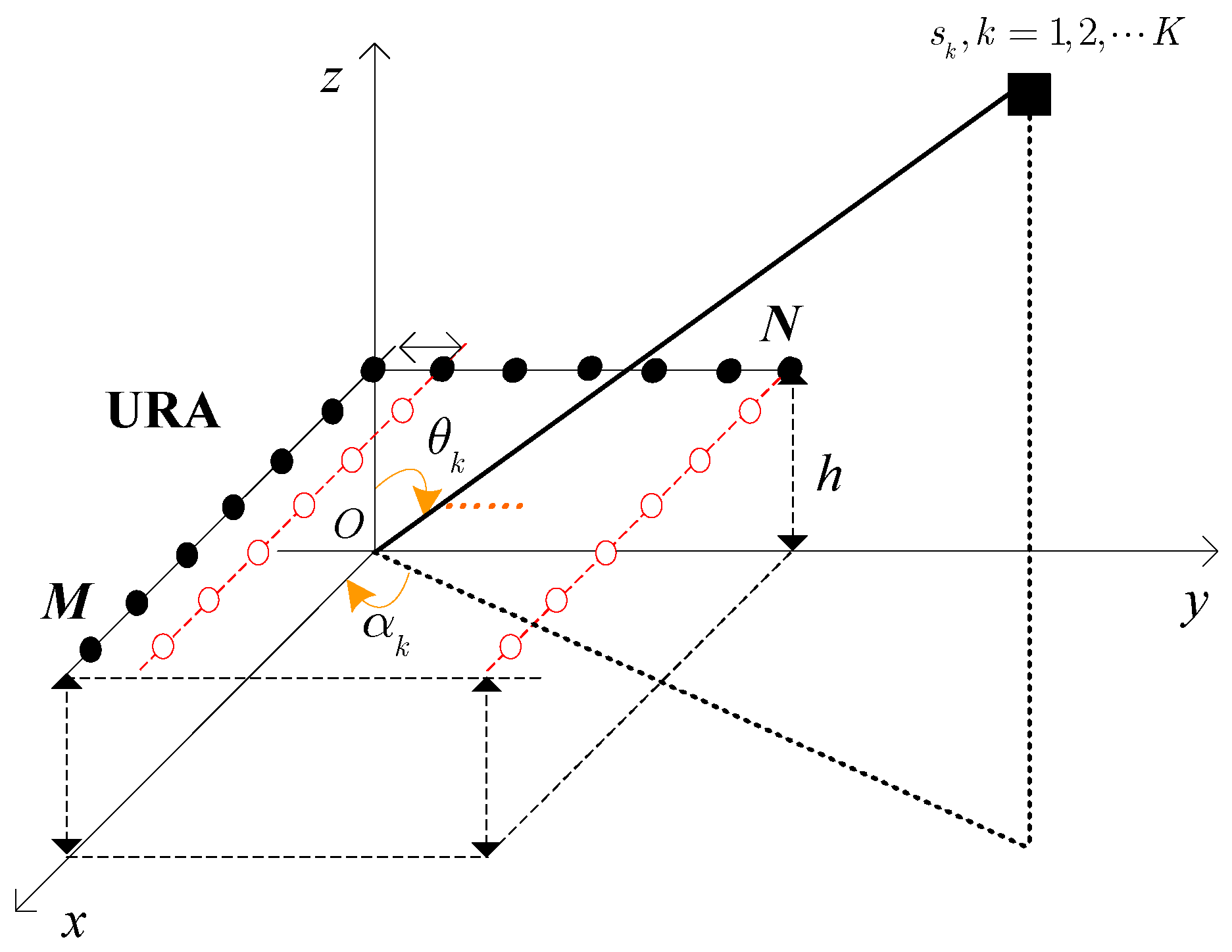
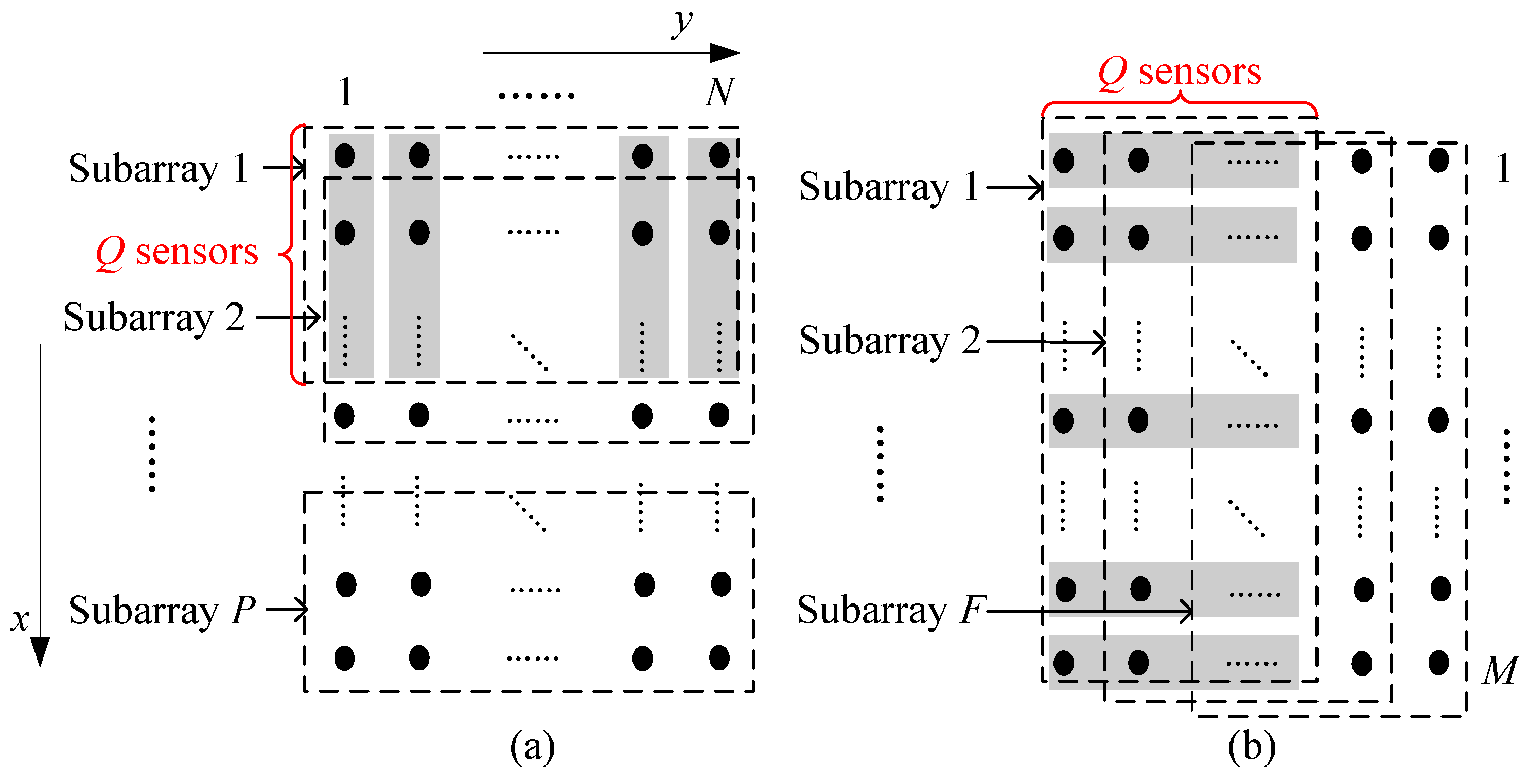
2. System Model
3. 2D DOA Estimation in LGA
3.1. 1D Estimation of Parameter
3.2. 1D Estimation of Parameter
3.3. Pair-Matching of Parameters and
3.4. Implementation of the Proposed Method
- Calculate the estimated sample covariance matrix in (4) asflops.
- Form the FB SDMS-x in (8) and the FB SDMS-y in (12) aswhere and can be calculated by using the covariance matrixflops.
- Estimate the orthogonal projectors in Section 3.1 and in Section 3.2.flops.
- Estimate the parameters and by finding the phases of the p zeros of the polynomial and using (11) and (17), where and , orflops.
- Perform the pair-matching of the parameters and by using (18)–(21) and estimate the azimuth and elevation angles by (22)flops.
3.5. Cramér–Rao Bounds (CRB)
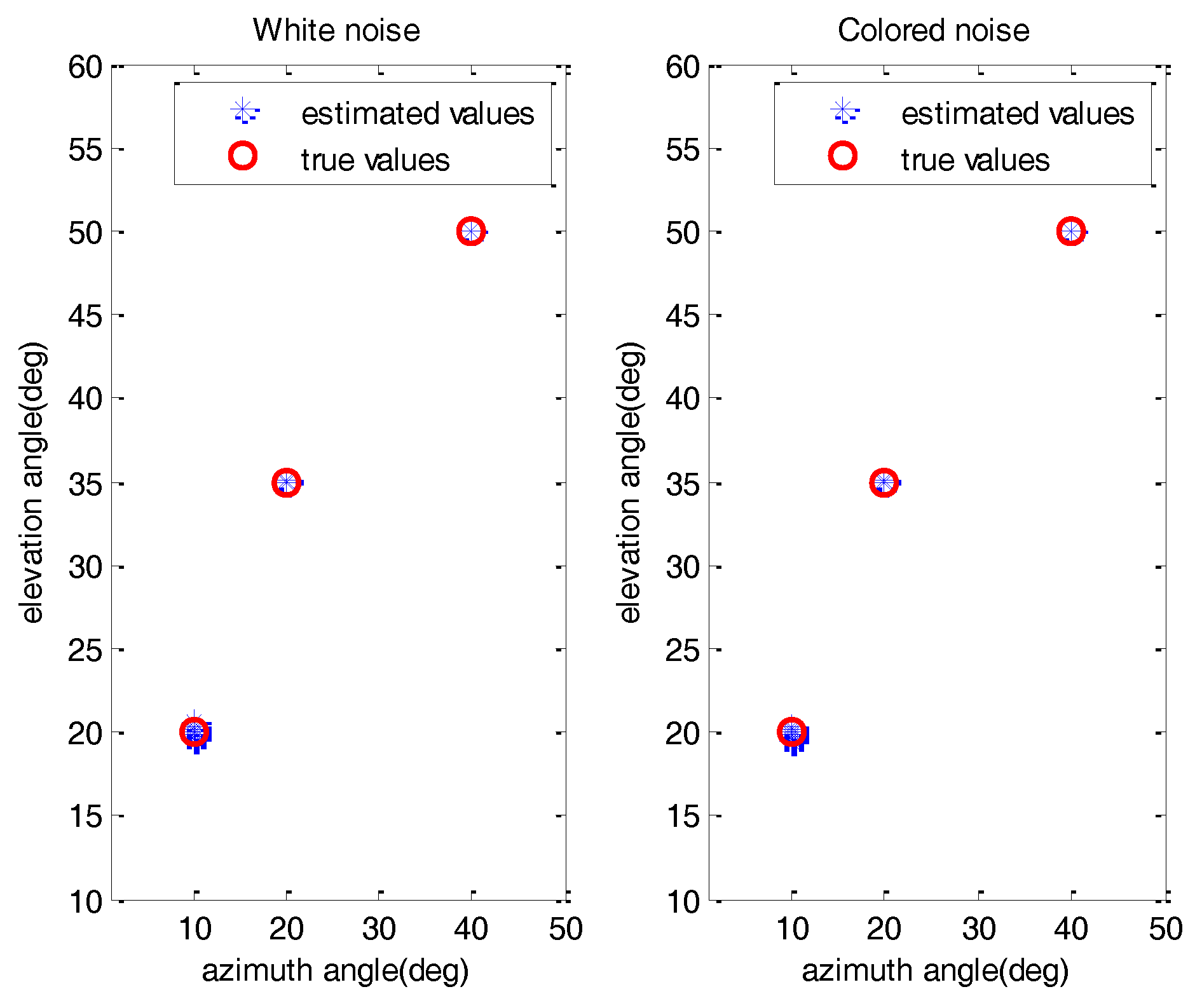
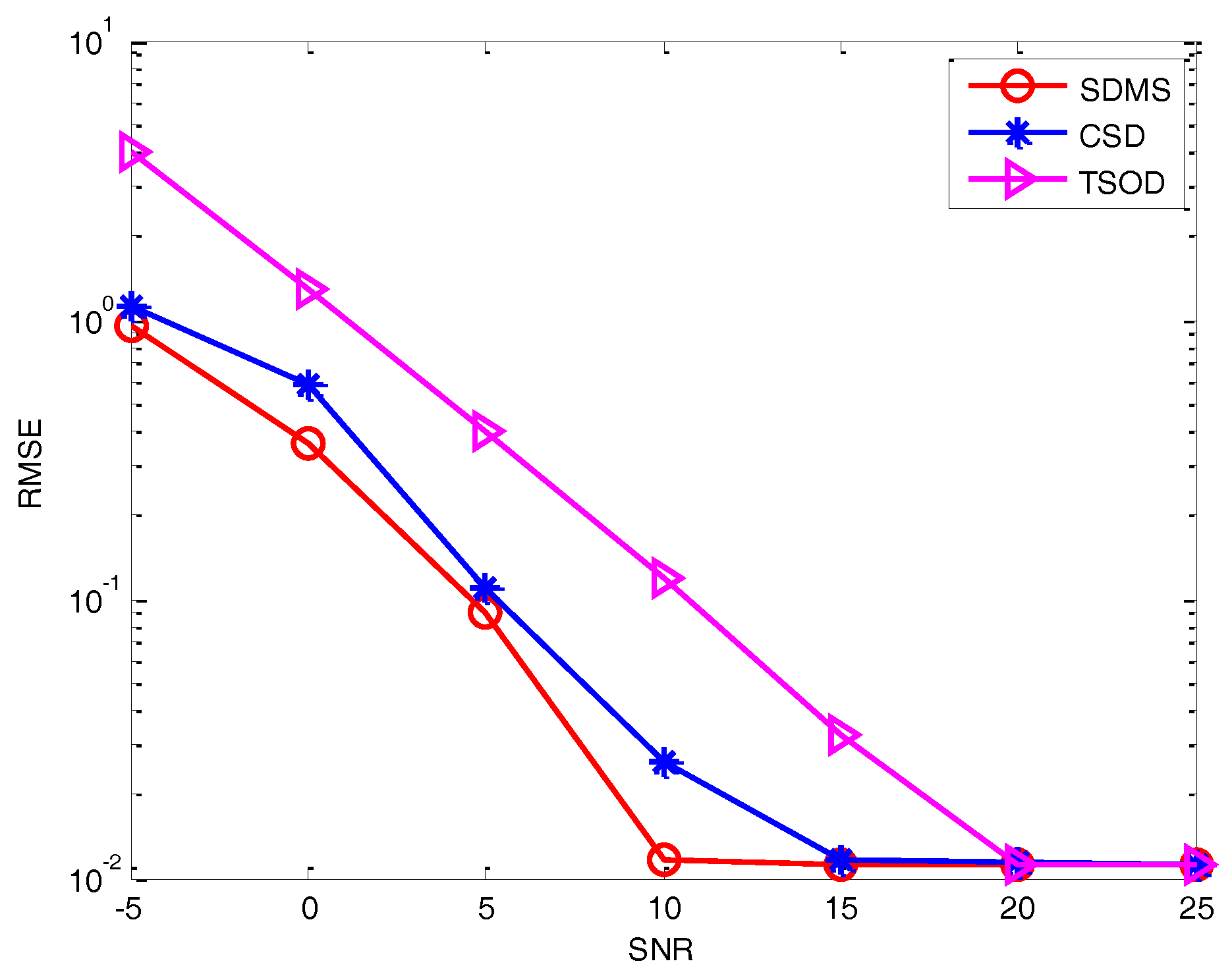
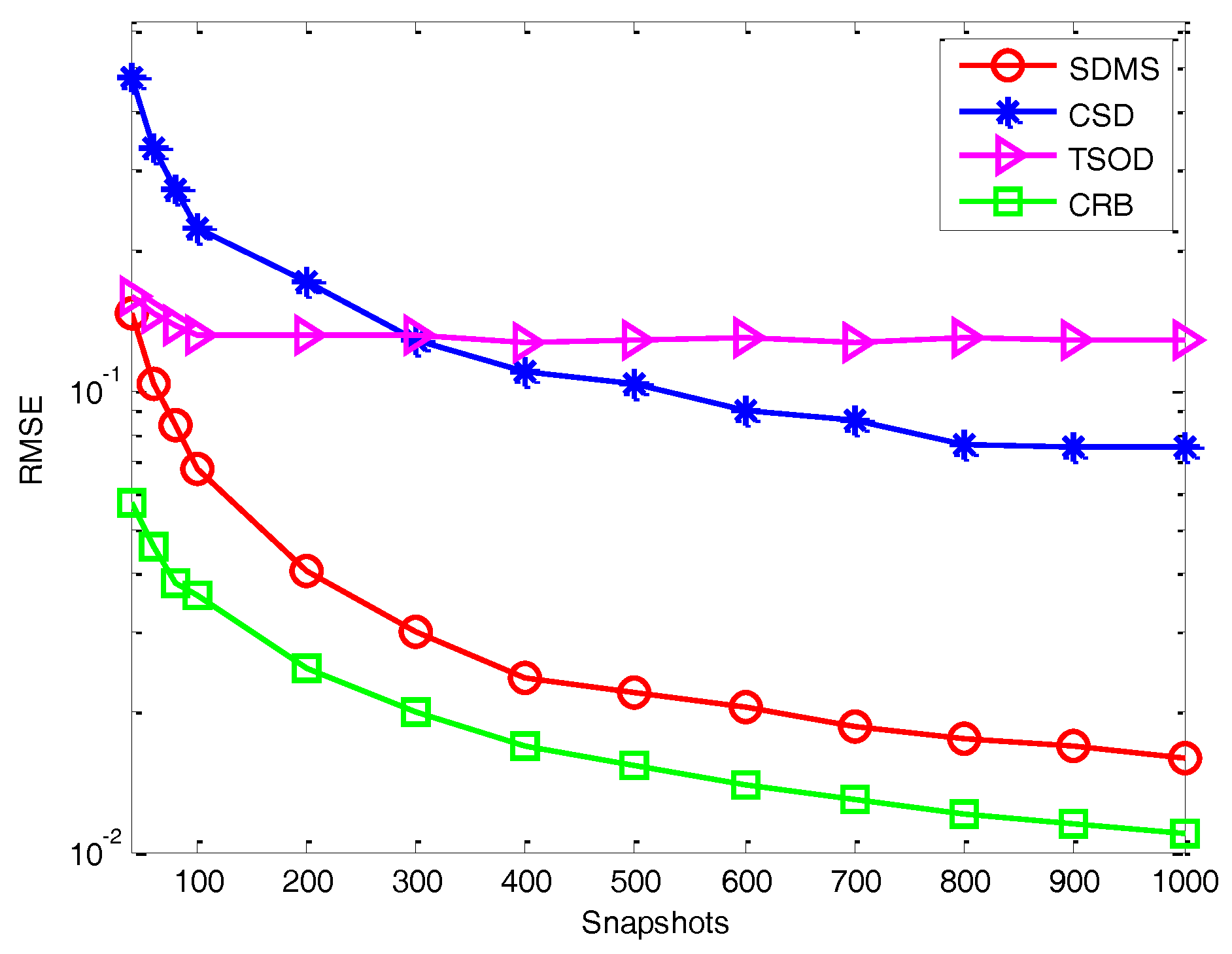
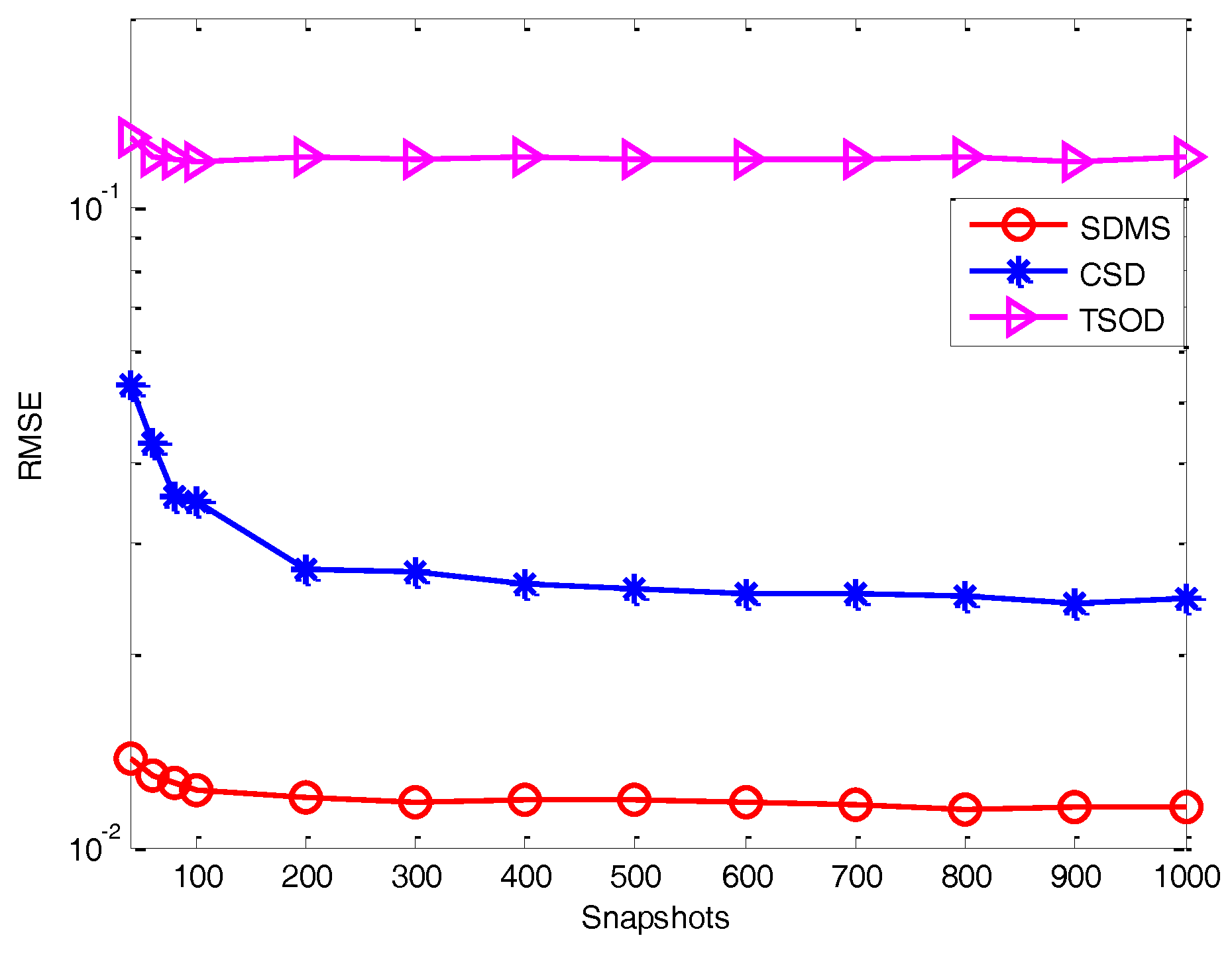
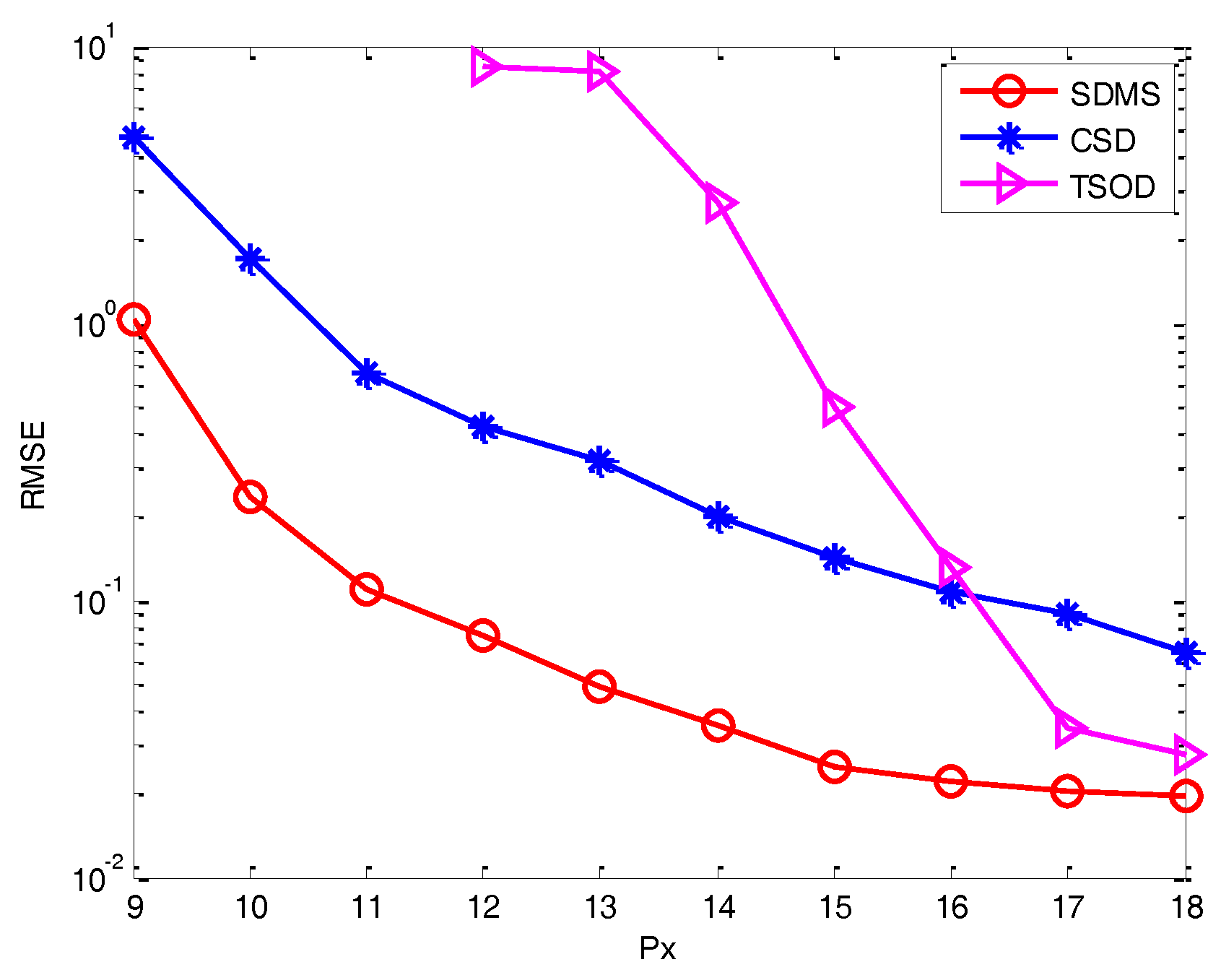
4. Simulation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Godara, L. Applications of antenna arrays to mobile communications-Part I: Performance improvement, feasibility, and system considerations. Proc. IEEE 1997, 85, 1031–1060. [Google Scholar] [CrossRef]
- Heidenreich, P.; Zoubir, A.; Rubsamen, M. Joint 2D DOA estimation and phase calibration for uniform rectangular arrays. IEEE Trans. Signal Process. 2012, 60, 4683–4693. [Google Scholar] [CrossRef]
- Lin, J.; Ma, X.; Hao, C.; Jiang, L. Direction of Arrival Estimation of Sparse Rectangular Array via Two-Dimensional Continuous Compressive Sensing. In Proceedings of the Sixth international Conference on Information Science and Technology, Dalian, China, 6–8 May 2016; Volume 5, pp. 539–543.
- Zhang, W.; Liu, W.; Wang, J.; Wu, S. Computationally efficient 2D DOA estimation for uniform rectangular arrays. Multidimens. Syst. Signal Process. 2014, 25, 847–857. [Google Scholar] [CrossRef]
- Swindlehurst, A.; Kailath, T. Azimuth/elevation direction finding using regular array geometries. IEEE Trans. Aerosp. Electron. Syst. 1993, 29, 145–155. [Google Scholar] [CrossRef]
- Schmidt, R.O. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Yilmazer, N.; Fernandez-Recio, R.; Sarkar, T.K. Matrix pencil method for simultaneously estimating azimuth and elevation angles of arrival along with the frequency of the incoming signals. Digit. Signal Process. 2006, 16, 796–816. [Google Scholar] [CrossRef]
- Sen, S.; Nehorai, A. OFDM MIMO radar with mutual-Information waveform design for low-grazing angle tracking. IEEE Trans. Signal Process. 2010, 58, 3152–3162. [Google Scholar] [CrossRef]
- Sen, S.; Nehorai, A. OFDM MIMO radar for low-grazing angle tracking. In Proceedings of the 2009 Conference Record of the Forty-Third Asilomar Conference on Signals, Systems and Computers, Pacific Grove, CA, USA, 1–4 November 2009; Volume 11, pp. 125–129.
- Liu, J.; Liu, Z.; Xie, R. Low angle estimation in MIMO radar. Electron. Lett. 2010, 46, 1565–1566. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Lei, T. DOA estimation algorithms for low-angle targets with MIMO radar. Electron. Lett. 2016, 52, 652–654. [Google Scholar] [CrossRef]
- Shi, J.; Hu, G.; Zong, B.; Chen, M. DOA estimation using multipath echo power for MIMO radar in low-grazing angle. IEEE Sens. J. 2016, 16, 6087–6094. [Google Scholar] [CrossRef]
- Pillai, S.U.; Kwon, B.H. Forward/backward spatial smoothing techniques for coherent signal identification. IEEE Trans. Acoust Speech Signal Process. 1989, 37, 8–15. [Google Scholar] [CrossRef]
- Yeh, C.; Lee, J.; Chen, Y. Estimating two-dimensional angles of arrival in coherent source environment. IEEE Trans. Acoust Speech Signal Process. 1989, 37, 153–155. [Google Scholar] [CrossRef]
- Shan, T. J.; Wax, M.; Kailath, T. On spatial smoothing for direction-of-arrival estimation of coherent signals. IEEE Trans. Acoust Speech Signal Process. 1997, 33, 806–811. [Google Scholar] [CrossRef]
- Xu, L.; Ye, Z. Two-dimensional direction of arrival estimation by exploiting the symmetric configuration of uniform rectangular array. IET Radar Sonar Navig. 2012, 6, 307–313. [Google Scholar] [CrossRef]
- Liu, F.; Wang, J.; Sun, C.; Du, R. Spatial differencing method for DOA estimation under the coexistence of both uncorrelated and coherent signals. IEEE Trans. Antennas Propag. 2012, 60, 2052–2062. [Google Scholar] [CrossRef]
- Ma, X.; Dong, X.; Xie, Y. An improved spatial differencing method for DOA estimation with the coexistence of uncorrelated and coherent signals. IEEE Sens. J. 2016, 16, 3719–3723. [Google Scholar] [CrossRef]
- Hong, S.; Wan, X.; Ke, H. An improved spatial differencing method for DOA estimation with the coexistence of uncorrelated and coherent signals. Signal Process. 2015, 109, 69–73. [Google Scholar] [CrossRef]
- Wu, Q.; Sun, F.; Lan, P.; Ding, G. Two-dimensional direction-of-arrival estimation for co-prime planar arrays: A partial spectral search approach. IEEE Sens. J. 2016, 16, 5660–5670. [Google Scholar] [CrossRef]
- Wang, Y.; Lee, L.; Yang, S.; Chen, J. A tree structure one-dimensional based algorithm for estimating the two-dimensional direction of arrivals and its performance analysis. IEEE Trans. Antennas Propag. 2008, 56, 178–188. [Google Scholar] [CrossRef]
- Wang, H.; Liu, K. 2D spatial smoothing for multipath coherent signal separation. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 391–405. [Google Scholar] [CrossRef]
- Vu, D.; Renaux, A.; Boyer, R.; Marcos, S. A Cramér-Rao bounds based analysis of 3D antenna array geometries made from ULA branches. IEEE Trans. Aerosp. Electron. Syst. 2013, 24, 121–155. [Google Scholar] [CrossRef] [Green Version]
- Jiang, H.; Zhang, J.K.; Wong, K.M. Joint DOD and DOA Estimation for Bistatic MIMO Radar in Unknown Correlated Noise. IEEE Trans. Veh. Technol. 2015, 64, 5113–5125. [Google Scholar] [CrossRef]

| FBSS-MUSIC | FBSS-DOAM | CSD | TSOD | Proposed Method | |
|---|---|---|---|---|---|
| EVD | one, | two, | one, | , | w/o |
| 1D searching | w/o | two | w/o | two | w/o |
| 2D searching | one | w/o | one | w/o | w/o |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, J.; Hu, G.; Zhang, X.; Sun, F.; Xiao, Y. Computationally Efficient 2D DOA Estimation with Uniform Rectangular Array in Low-Grazing Angle. Sensors 2017, 17, 470. https://doi.org/10.3390/s17030470
Shi J, Hu G, Zhang X, Sun F, Xiao Y. Computationally Efficient 2D DOA Estimation with Uniform Rectangular Array in Low-Grazing Angle. Sensors. 2017; 17(3):470. https://doi.org/10.3390/s17030470
Chicago/Turabian StyleShi, Junpeng, Guoping Hu, Xiaofei Zhang, Fenggang Sun, and Yu Xiao. 2017. "Computationally Efficient 2D DOA Estimation with Uniform Rectangular Array in Low-Grazing Angle" Sensors 17, no. 3: 470. https://doi.org/10.3390/s17030470






