An Efficient Estimator for Moving Target Localization Using Multi-Station Dual-Frequency Radars
Abstract
:1. Introduction
- (1)
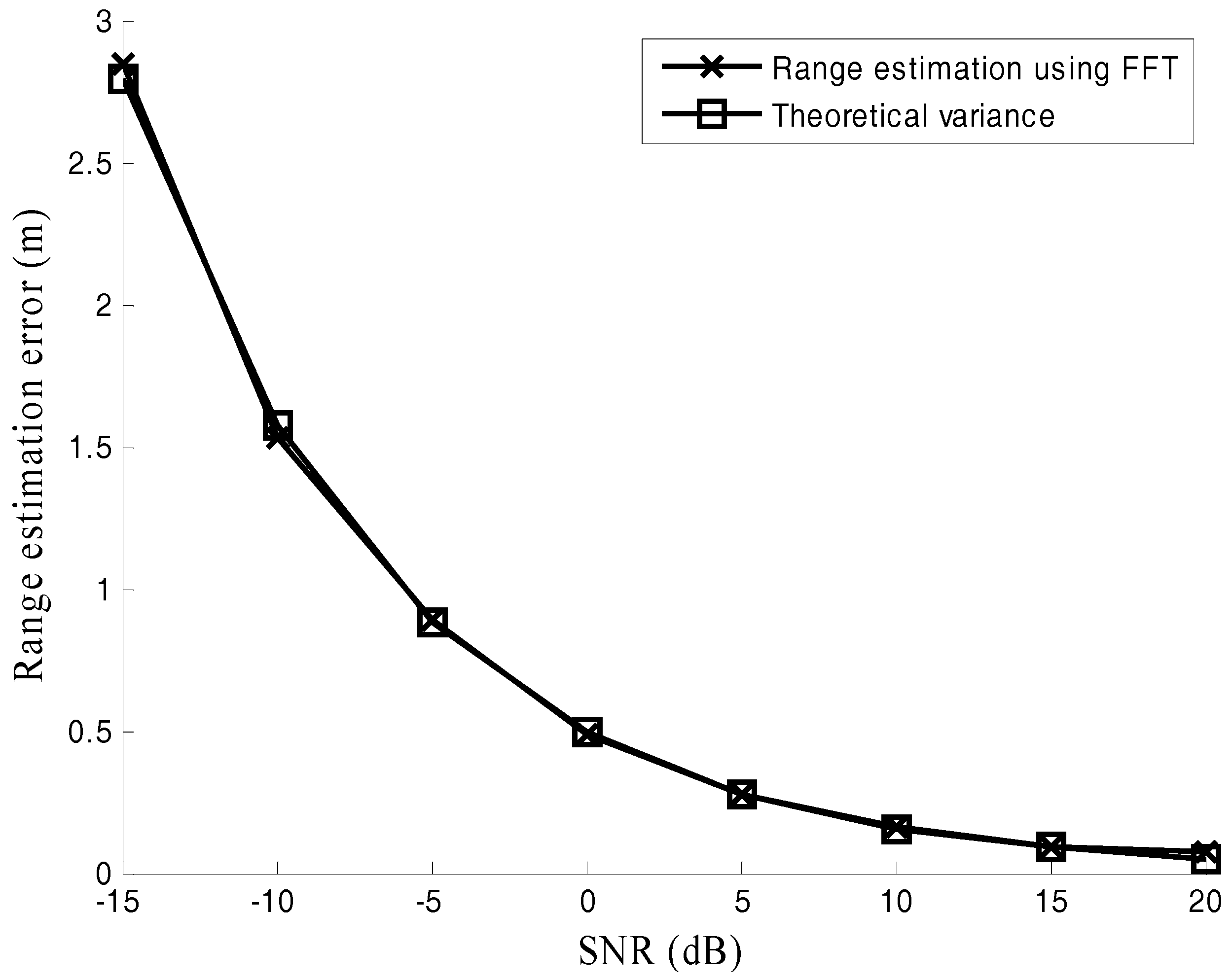
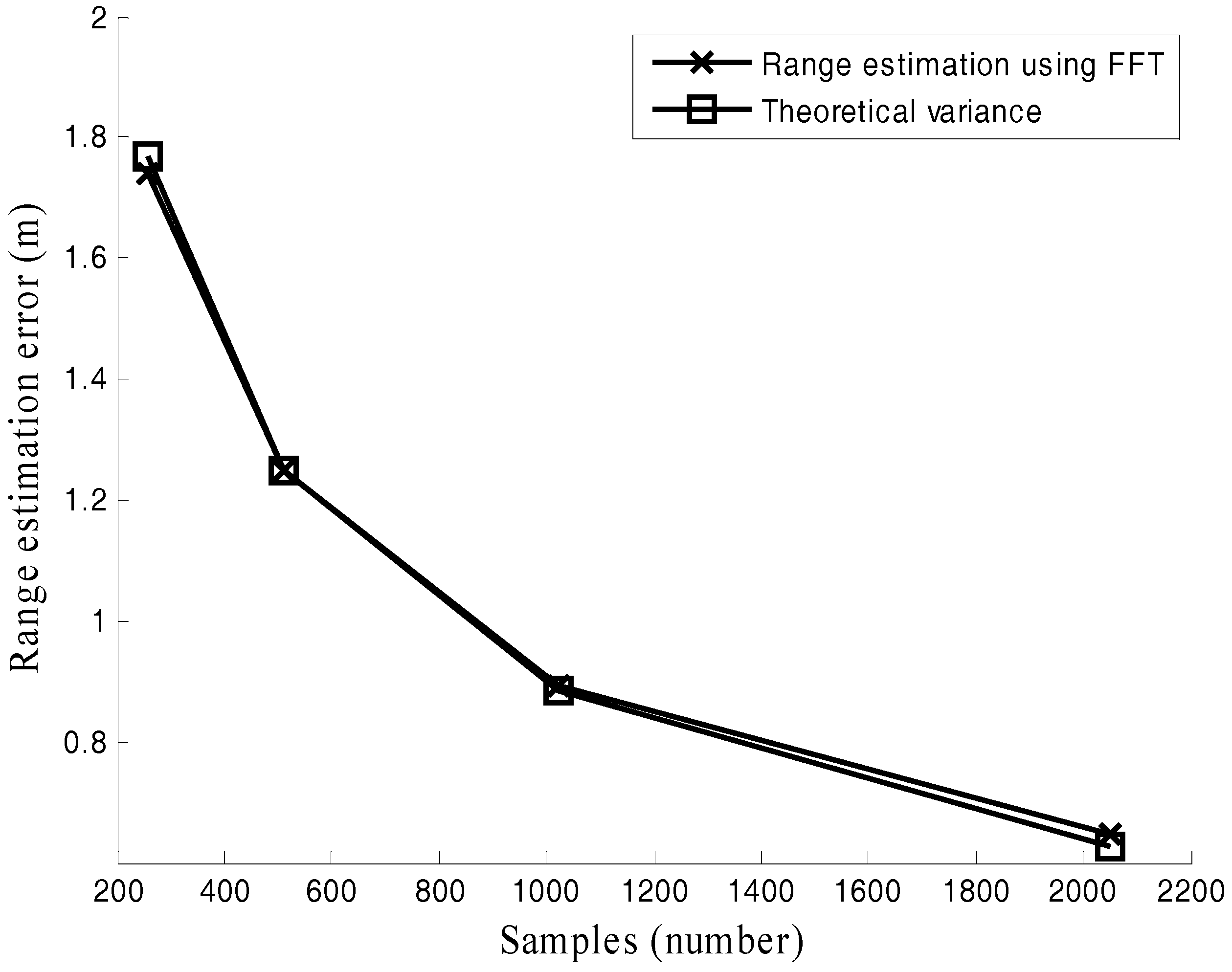
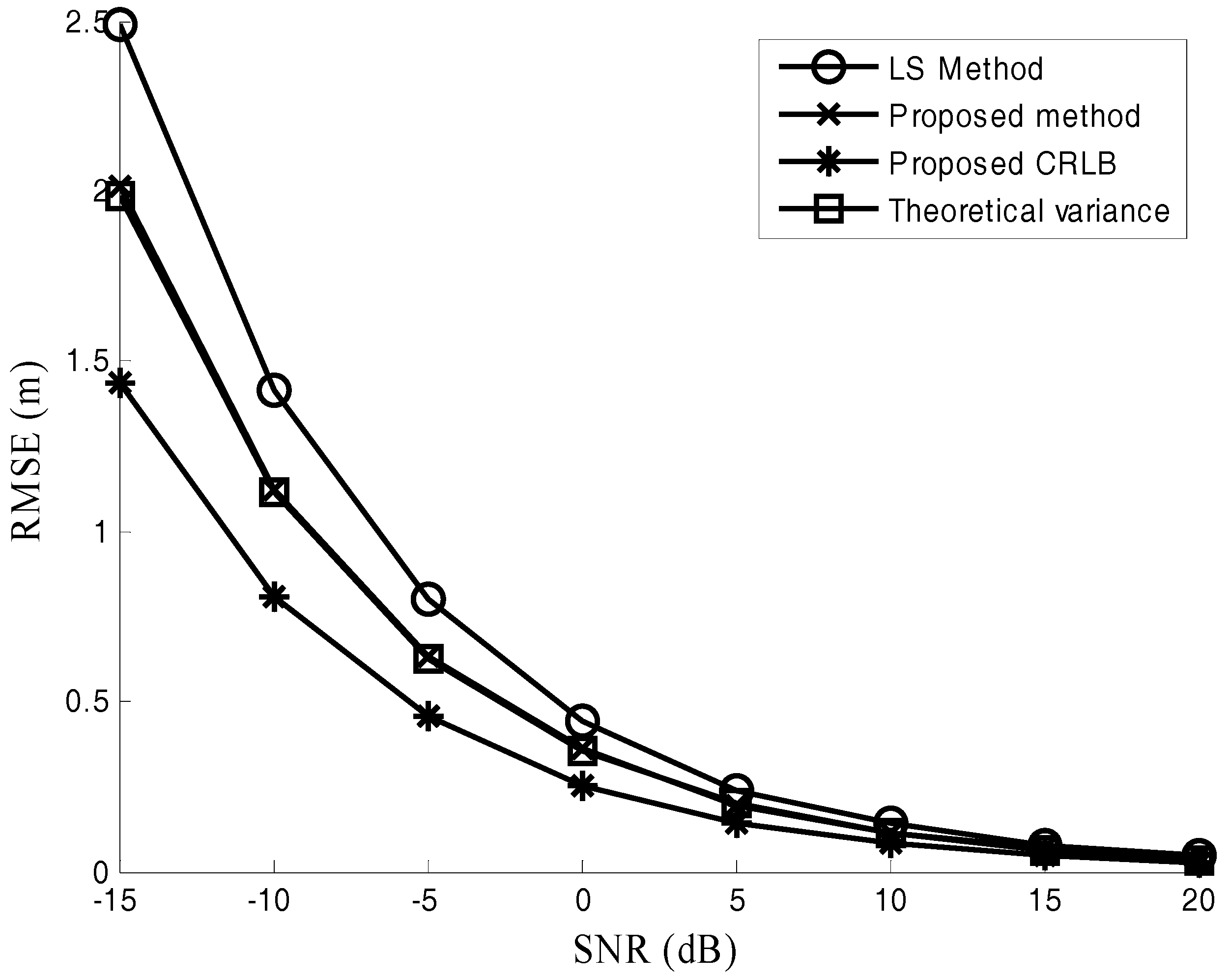
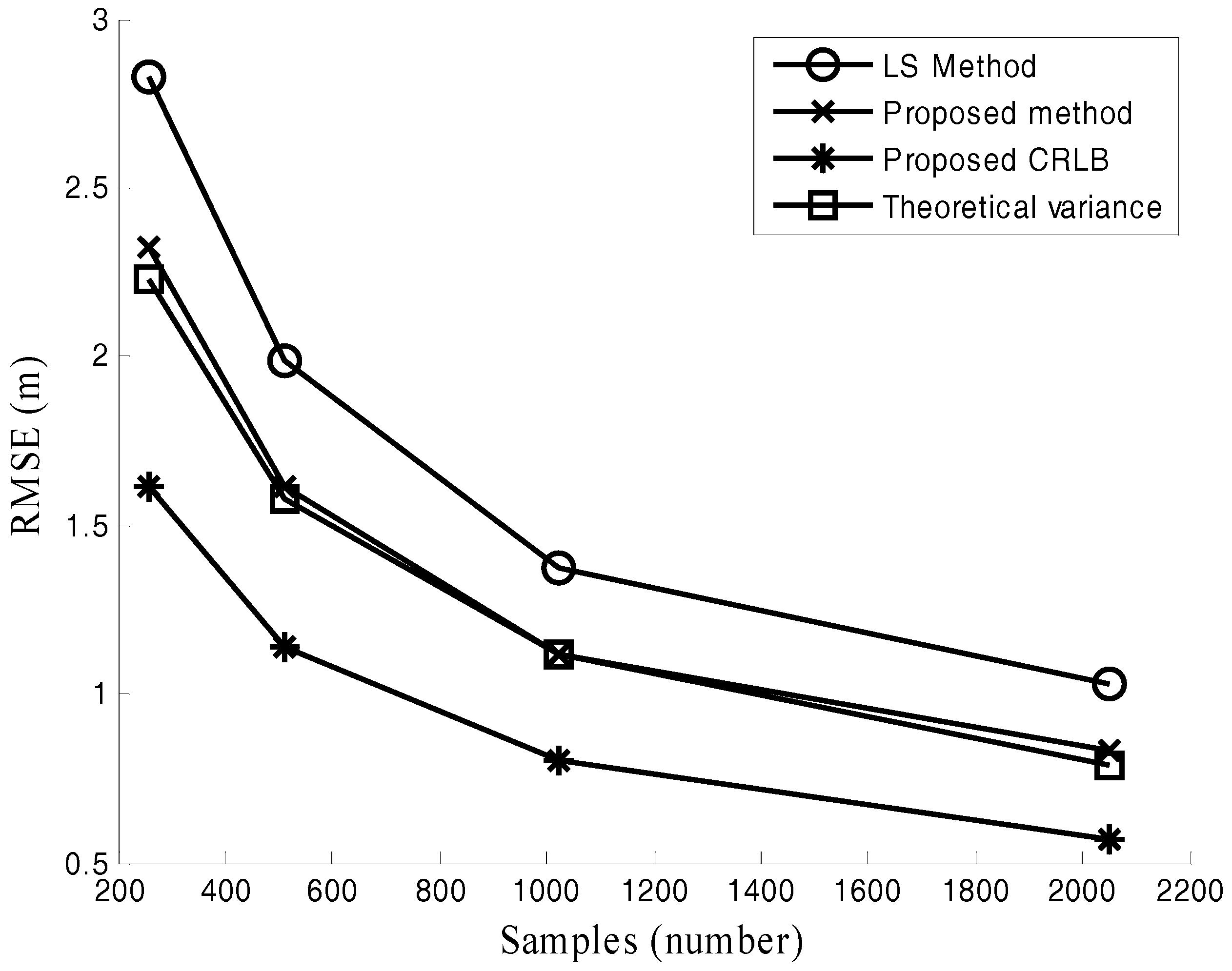
- The effects of signal noise ratio (SNR) and the number of samples on the performance of range estimation are analyzed in the paper. The fundamental work has been done for performance analysis of dual-frequency radars in [10] where the influences of drift in frequency and I/Q mismatch were studied. SNR and the number of samples are another two important factors which will greatly affect the performance of range estimation.
- (2)
- A novel localization method with closed-form solution and high positioning accuracy is proposed for a multi-station dual-frequency radars system. The proposed method first derives the variances of the phase measurements. Based on the derived variances, the two weighted matrices can be calculated for two-step solutions. Due to the weighted information, the proposed method can provide the better performance than the LS estimator.
- (3)
- Performance analysis for the proposed method is presented in this paper. Both the theoretical variance and Cramer–Rao lower bound (CRLB) for the proposed method are derived in the paper. The derived CRLB can provide a benchmark for MT localization in the dual-frequency radars system to evaluate the performance of any unbiased estimator. They have not been addressed in the literature.
2. System Model
3. Closed-Form Solution for Dual-Frequency Radars
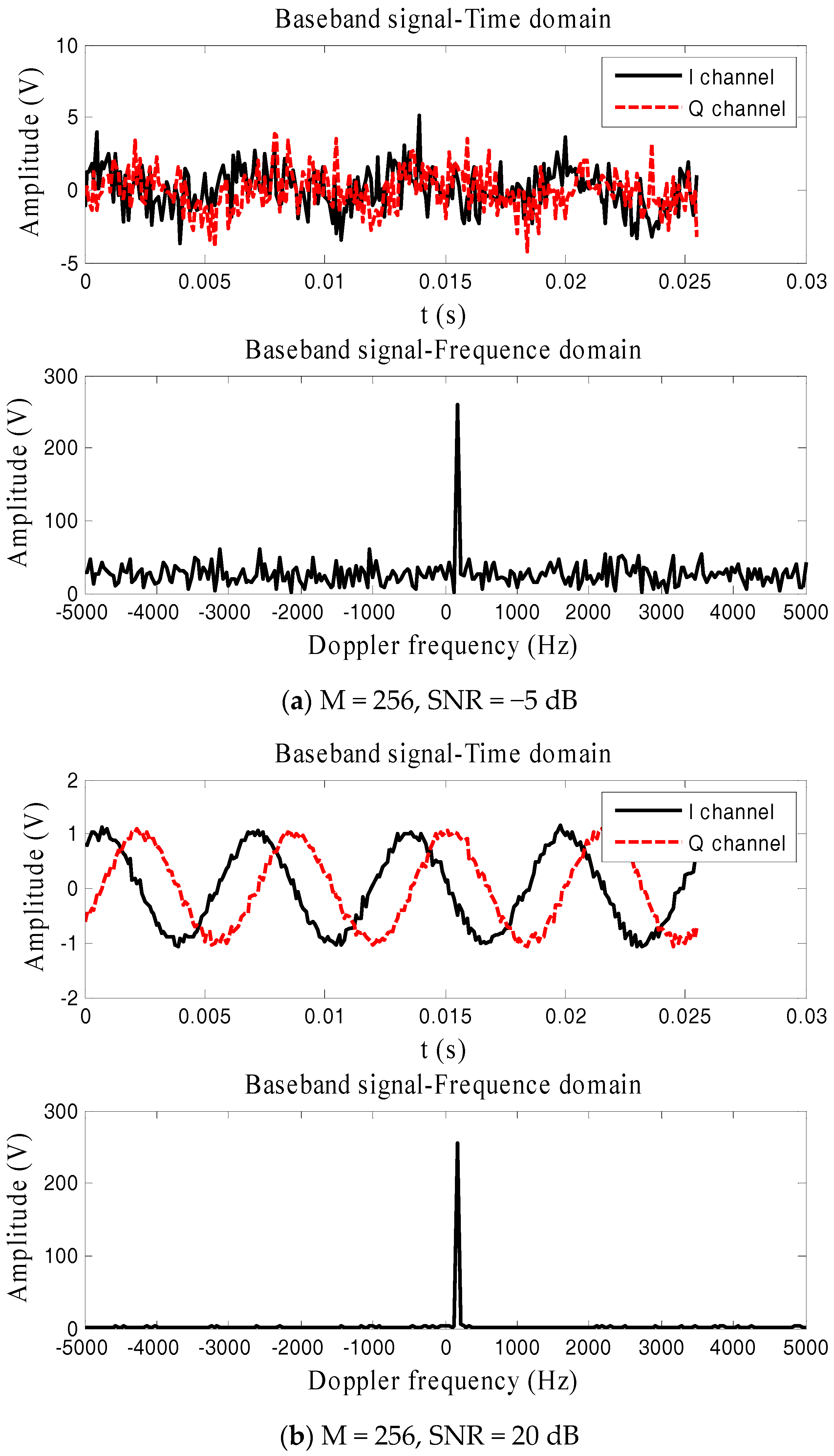
3.1. Performance Analysis of Range Estimation Using FFT
3.2. Closed-Form Solution for Multi-Station Dual-Frequency Radars System
4. Cramer–Rao Lower Bound
- ,
- , where the starting index of 1 in is .
- , where the starting index of 1 in is .
- is the noise vector and
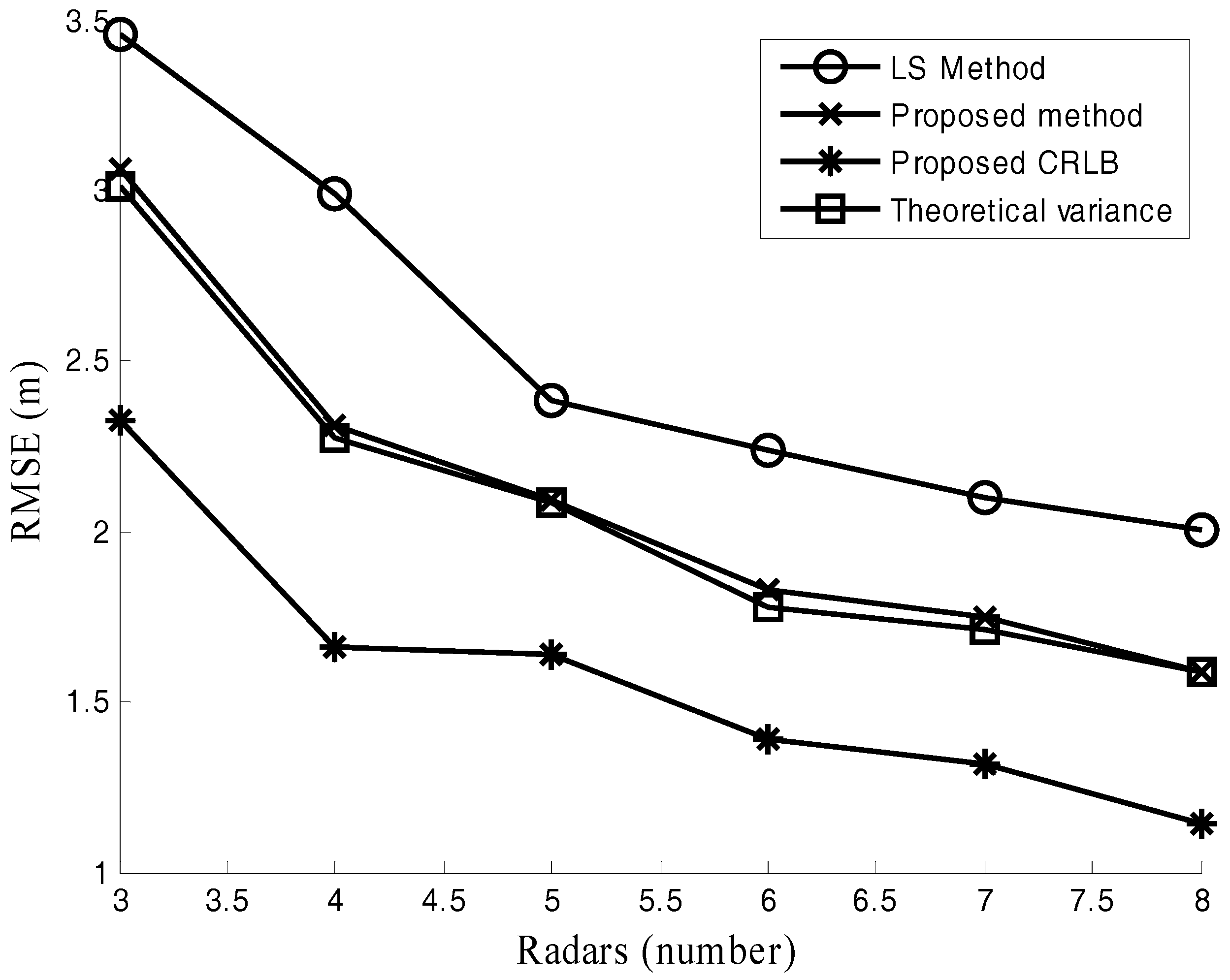
5. Simulation Results
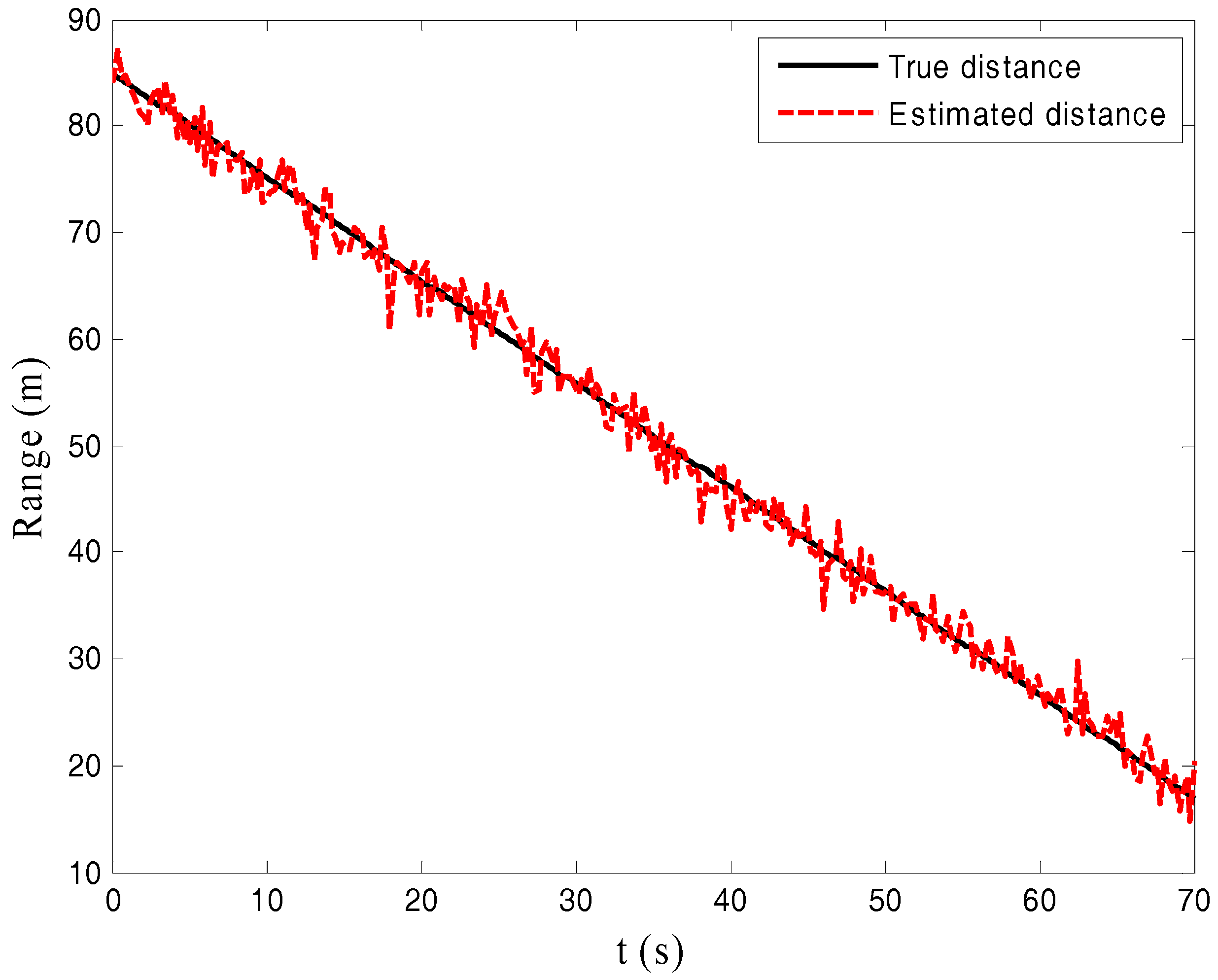
5.1. Range Estimation
5.2. Target Localization
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, C.Z.; Peng, Z.Y.; Huang, T.Y.; Fan, T.L.; Wang, F.K.; Horng, T.S.; Muñoz-Ferreras, J.; Gómez-García, R.; Ran, L.X.; Lin, J.S. A Review on Recent Progress of Portable Short-Range Noncontact Microwave Radar Systems. IEEE Trans. Microw. Theory Tech. 2017, 65, 1692–1706. [Google Scholar] [CrossRef]
- Alimenti, F.; Palazzi, V.; Mariotti, C.; Virili, M.; Orecchini, G.; Bonafoni, S.; Roselli, L.; Mezzanotte, P. A 24-GHz Front-End Integrated on a Multilayer Cellulose-Based Substrate for Doppler Radar Sensors. Sensors 2017, 17, 2090. [Google Scholar] [CrossRef] [PubMed]
- Etinger, A.; Litvak, B.; Pinhasi, Y. Multi Ray Model for Near-Ground Millimeter Wave Radar. Sensors 2017, 17, 1983. [Google Scholar] [CrossRef] [PubMed]
- Pohl, N.; Jaeschke, T.; Aufinger, K. An ultra-wideband 80 GHz FMCW radar system using a SiGe bipolar transceiver chip stabilized by a fractional-N PLL synthesizer. IEEE Trans. Microw. Theory Tech. 2012, 60, 757–765. [Google Scholar] [CrossRef]
- Khan, F.; Leem, S.K.; Cho, S.H. Hand-Based Gesture Recognition for Vehicular Applications Using IR-UWB Radar. Sensors 2017, 17, 833. [Google Scholar] [CrossRef] [PubMed]
- Gu, C.Z.; Lien, J. A Two-Tone Radar Sensor for Concurrent Detection of Absolute Distance and Relative Movement for Gesture Sensing. IEEE Sens. Lett. 2017, 1. [Google Scholar] [CrossRef]
- Amin, M.; Zemany, P.; Setlur, P.; Ahmad, F. Moving Target Localization for Indoor Imaging using Dual-Frequency CW Radars. In Proceedings of the Fourth IEEE Workshop on Sensor Array and Multichannel Processing, Waltham, UK, 12–14 July 2006; pp. 367–371. [Google Scholar]
- Lin, A.; Ling, H. Three-dimensional tracking of humans using very low-complexity radar. Electron. Lett. 2006, 42, 1062–1063. [Google Scholar] [CrossRef]
- Lin, A.; Ling, H. Location Tracking of Indoor Movers Using a Two-Frequency Doppler and Direction-of-Arrival (DDOA) Radar. In Proceedings of the 2006 IEEE Antennas and Propagation Society International Symposium, Albuquerque, NM, USA, 9–14 July 2006; pp. 1125–1128. [Google Scholar]
- Ahmad, F.; Amin, M.G.; Zemany, P.D. Dual-Frequency Radars for Target Localization in Urban Sensing. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 1598–1609. [Google Scholar] [CrossRef]
- Chan, Y.T.; Ho, K.C. A simple and efficient estimator for hyperbolic location. IEEE Trans. Signal Process. 1994, 42, 1905–1915. [Google Scholar] [CrossRef]
- Peng, Z.Y.; Ran, L.X.; Li, C.Z. K-Band Portable FMCW Radar with Beamforming Array for Short-Range Localization and Vital-Doppler Targets Discrimination. IEEE Trans. Microw. Theory Tech. 2017, 65, 3443–3452. [Google Scholar] [CrossRef]
- Huang, X.J.; Guo, Y.J.; Zhang, J.A. Transceiver I/Q Imbalance Self-Calibration With Phase-Shifted Local Loopback for Multichannel Microwave Backhaul. IEEE Trans. Wirel. Commun. 2016, 15, 7657–7669. [Google Scholar] [CrossRef]
- Amin, M. Radar for Indoor Monitoring: Detection, Classification, and Assessment; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Gennarelli, G.; Al Khatib, O.; Soldovieri, F. Inverse Source Data-Processing Strategies for Radio-Frequency Localization in Indoor Environments. Sensors 2017, 17, 2469. [Google Scholar] [CrossRef] [PubMed]
- Kay, S.M. Fundamentals of Statistical Signal Processing: Estimation Theory; Prentice-Hall: Englewood Cliffs, NJ, USA, 1993. [Google Scholar]
- Gennarelli, G.; Vivone, G.; Braca, P.; Soldovieri, F.; Amin, M.G. Multiple Extended Target Tracking for Through-Wall Radars. IEEE Trans. Geosci. Remote Sens. 2015, 53, 6482–6494. [Google Scholar] [CrossRef]
- Chen, X.; Leung, H.; Tian, M. Multitarget detection and tracking for through-the-wall radars. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 1403–1415. [Google Scholar] [CrossRef]
- Gennarelli, G.; Amin, M.G.; Soldovieri, F.; Solimene, R. Passive multiarray image fusion for RF tomography by opportunistic sources. IEEE Geosci. Remote Sens. Lett. 2015, 12, 641–645. [Google Scholar] [CrossRef]
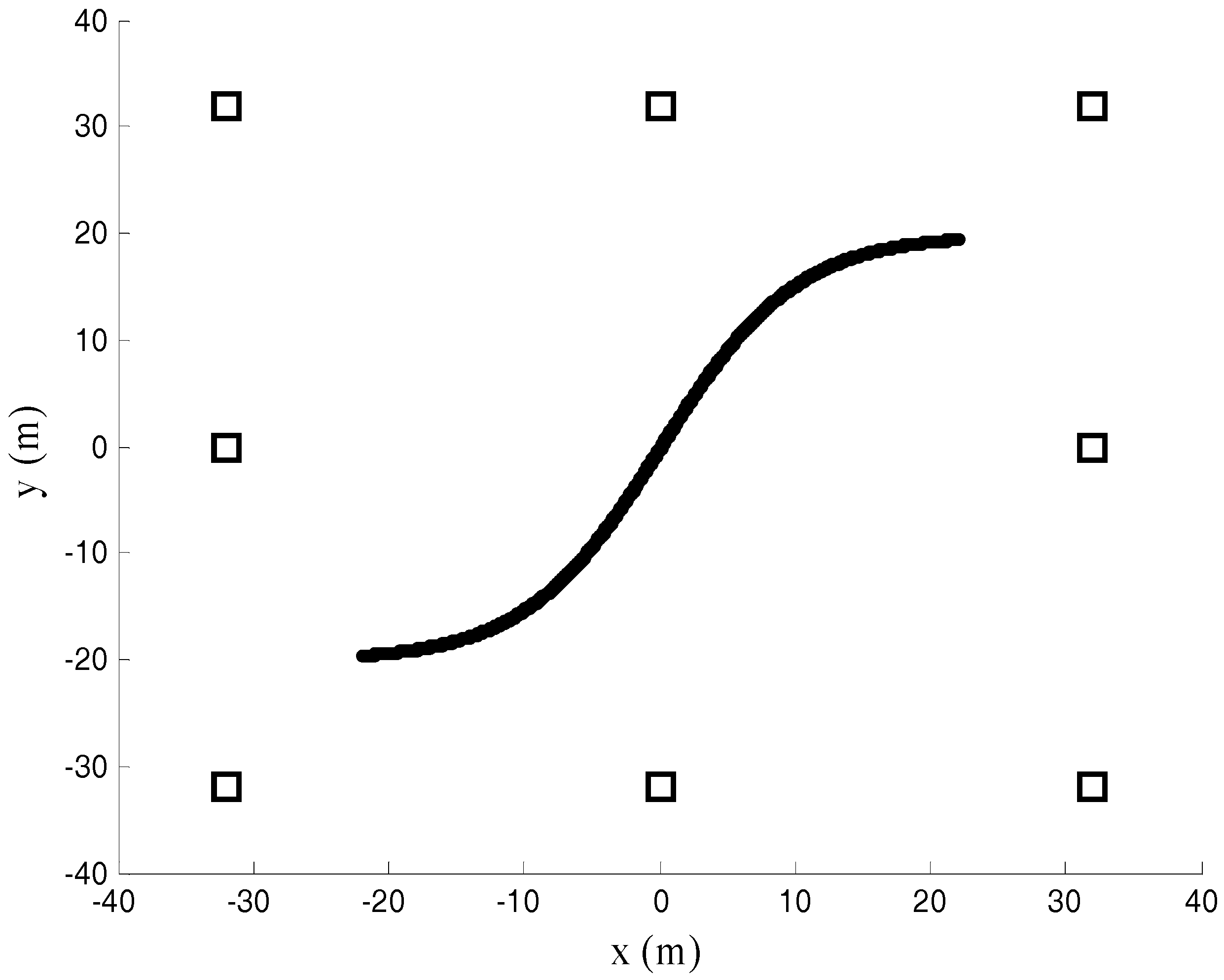
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, J.; Zhang, Y.; Luo, S. An Efficient Estimator for Moving Target Localization Using Multi-Station Dual-Frequency Radars. Sensors 2017, 17, 2914. https://doi.org/10.3390/s17122914
Huang J, Zhang Y, Luo S. An Efficient Estimator for Moving Target Localization Using Multi-Station Dual-Frequency Radars. Sensors. 2017; 17(12):2914. https://doi.org/10.3390/s17122914
Chicago/Turabian StyleHuang, Jiyan, Ying Zhang, and Shan Luo. 2017. "An Efficient Estimator for Moving Target Localization Using Multi-Station Dual-Frequency Radars" Sensors 17, no. 12: 2914. https://doi.org/10.3390/s17122914




