1. Introduction
Due to the inherent broadcast nature of the wireless medium, eavesdropping is one of major threats in wireless network security. Especially, wireless sensor networks, where tiny sensing devices are transmitting information data through radio links, are vulnerable to eavesdroppers (Eves). Physical layer security emerges as an effective means of securing wireless communications against eavesdropping by exploiting the physical characteristics of wireless channels. In the presence of an Eve, a so-called secrecy capacity is given in [
1,
2] as the difference between the channel capacity from a source (referred to as Alice) to destination (referred to as Bob) and that from the source to Eve.
In tremendous research efforts in enhancing physical layer security (for example, listed in [
3]), jamming has been widely accepted as an attractive way, which prevents Eves from snooping legitimate communications by generating friendly interference or noise. In [
4], the coverage of friendly jamming is evaluated, and the secrecy outage probability (SOP) is characterized for various levels of channel state information. In [
5], optimal power allocation between multiple friendly jammers that cooperatively jam multiple Eves is investigated in order to maximize the secrecy capacity, and SOP is also analyzed. Jamming signals are sometimes transmitted by intermediate relay nodes to secure the source signals, which is so-called cooperative jamming [
6,
7]. In [
8], multiple intermediate nodes are designated as either relays or jammers, for which optimal relay and jammer selection is investigated. In [
9], the cooperative jammers harvest energy transmitted by a source and use it to generate artificial noise to jam the Eves cognitive Internet-of-Things networks, in which an auction framework that formulates the jammer selection and the power allocation together is also provided. In an amplify-and-forward relay network, the destination can work as a friendly jammer by generating artificial noise in the first phase to prevent the possibly untrusted relay from decoding the signal [
10].
Though there have been plenty of works on investigating the secrecy performance of friendly or cooperative jamming, to the best of our knowledge, why and how much the jammers waste their valuable power or time for Alice is not well modeled in the literature. In [
11], a game-theoretic model is established for this purpose, where Alice pays the jammer for the jamming power to interfere with Eve, therefore achieving more secrecy capacity, and the relationship between the jamming power and the price is investigated.
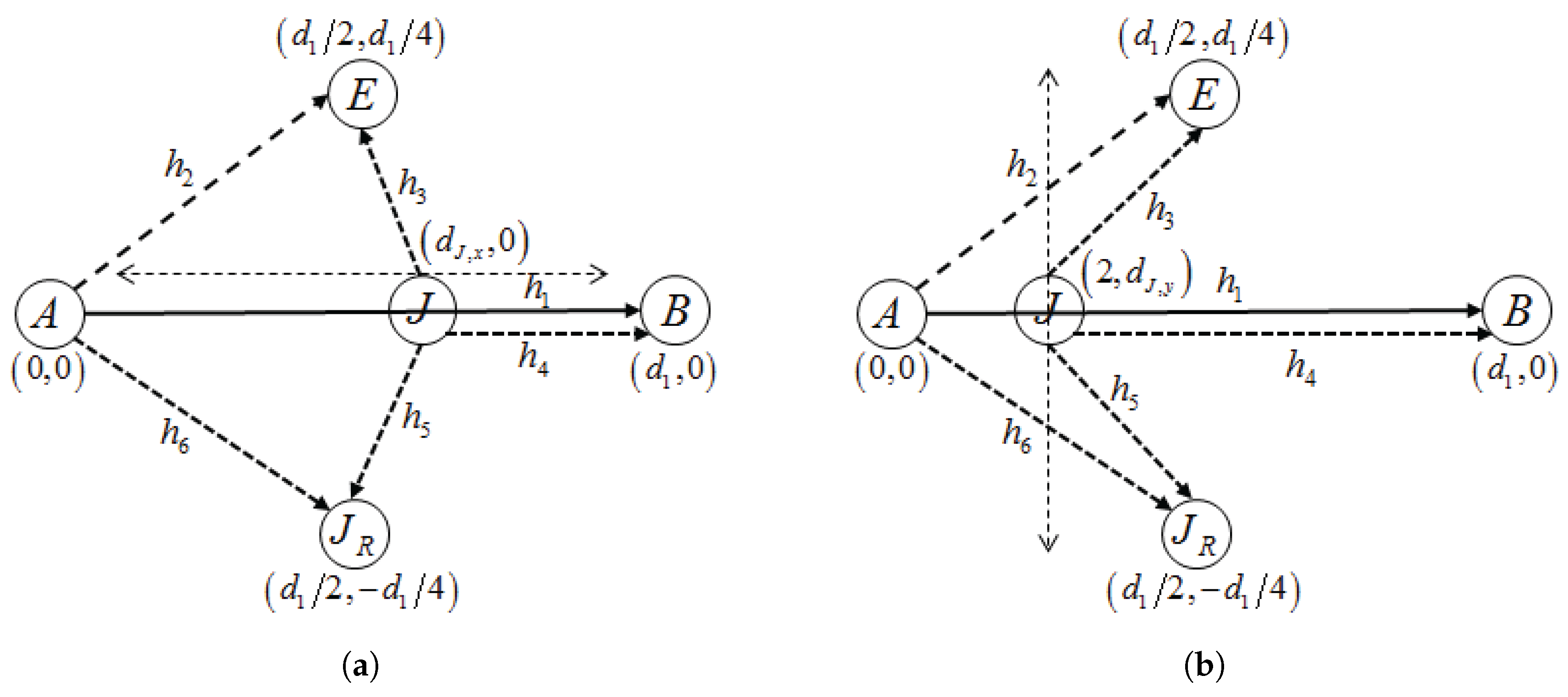
In this paper, we pay attention to the great burden that Alice should suffer in the previous model, though it is a legitimate user having a valuable right to access certain bandwidth. Our model relieves its burden by allowing the jammer to send its own data as a secondary legitimate user and letting Alice charge for the power used to deliver the jammer’s signal, which is referred to as collaborative jamming in this paper. The proposed collaborative jamming is more efficient than the previous jamming techniques in the sense that the jamming power is not just wasted, but used to send information data. To maintain the communication quality of Alice, the collaboration is allowed only if it does not degrade a predetermined level of secrecy capacity.
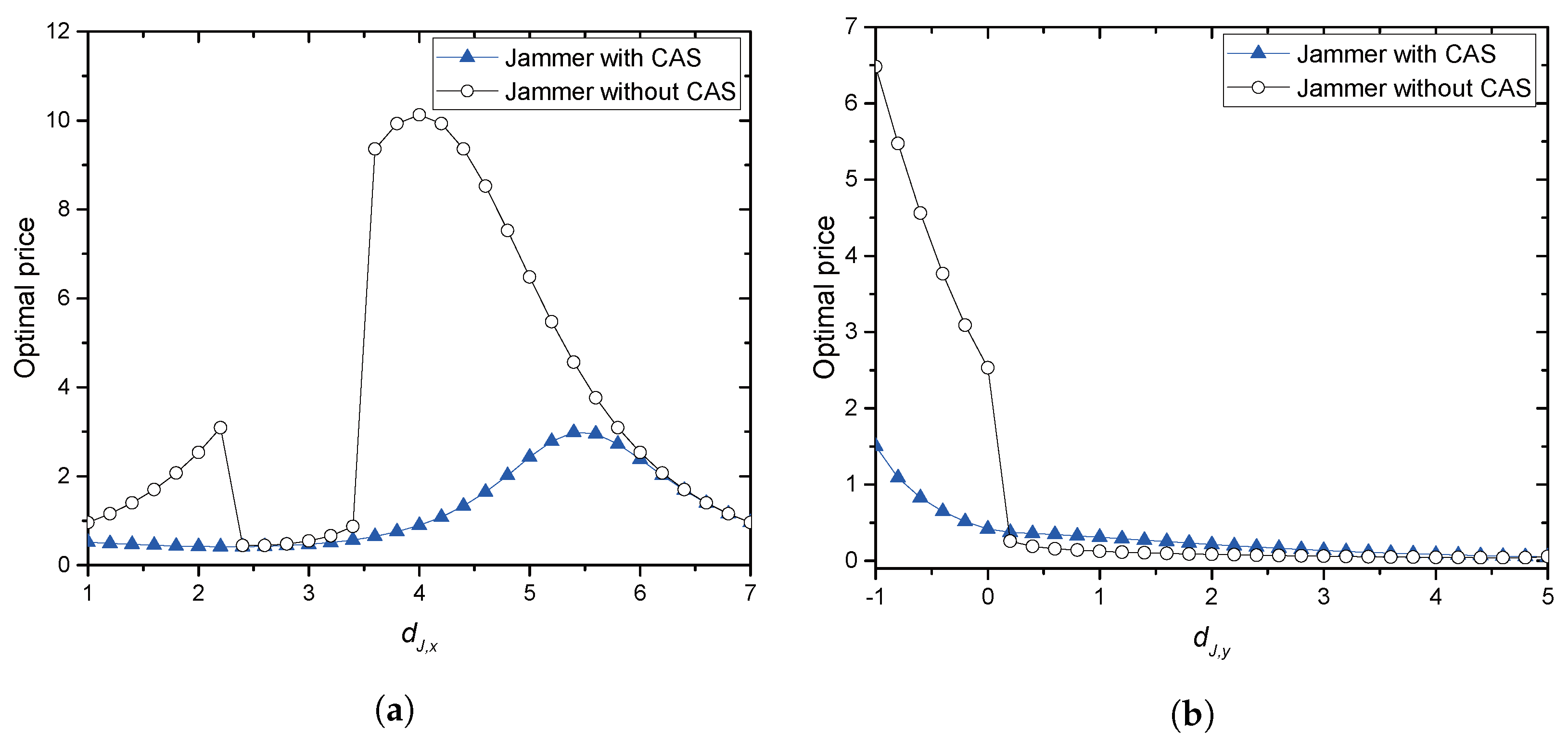
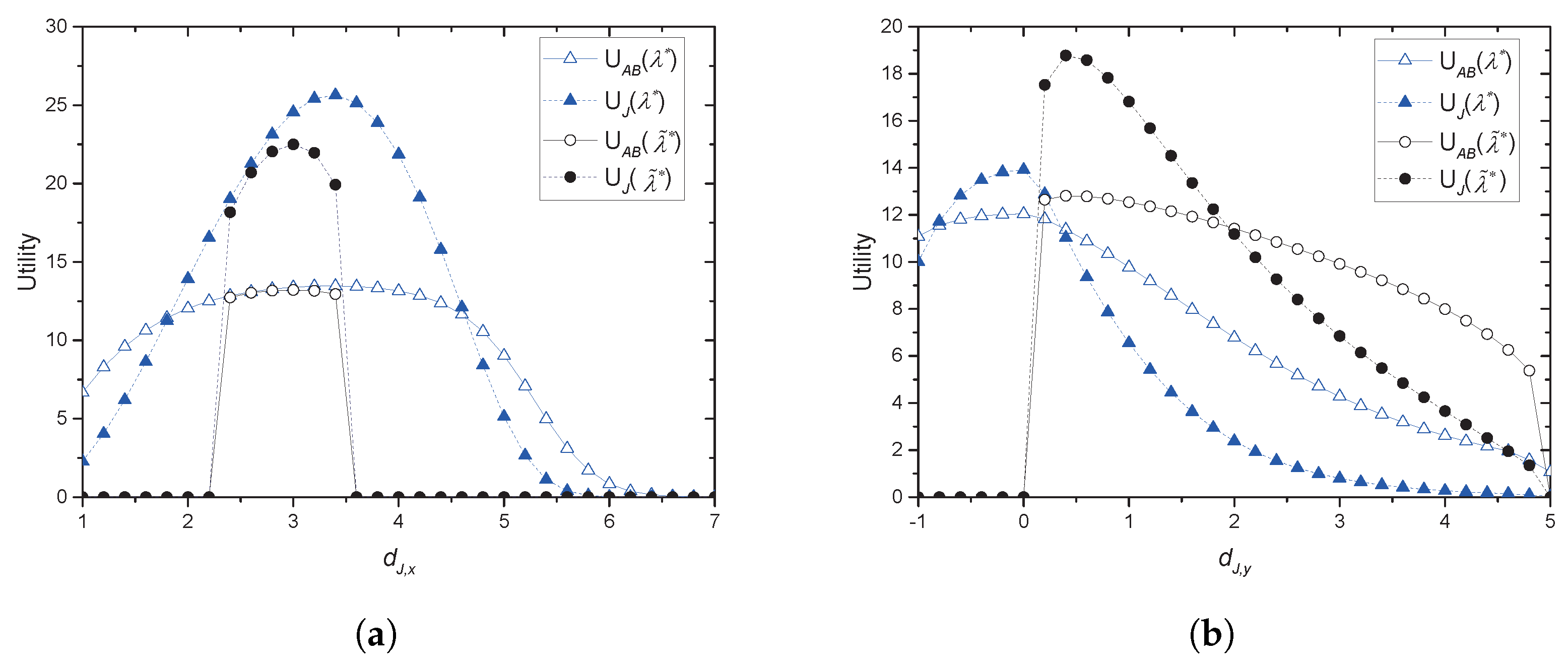
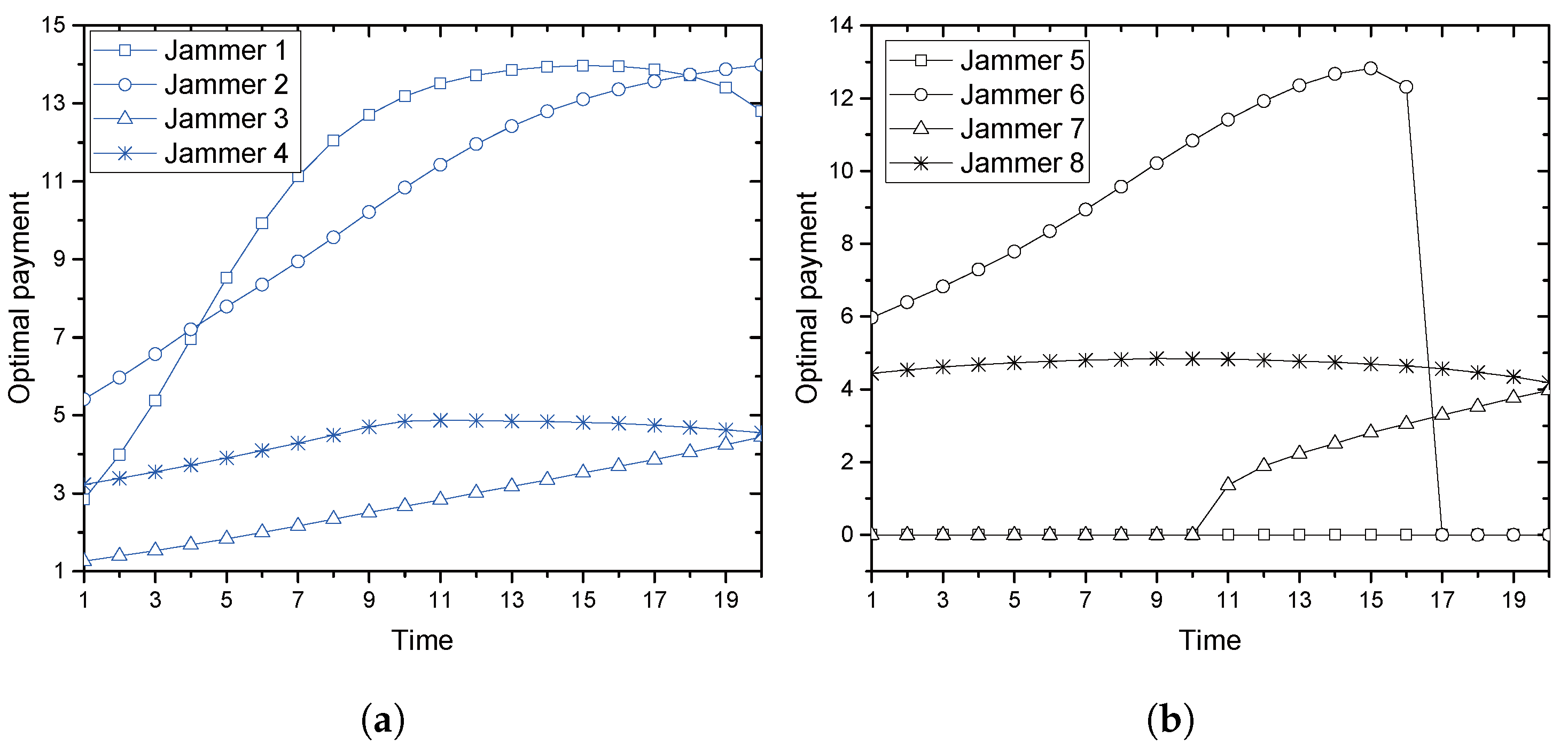
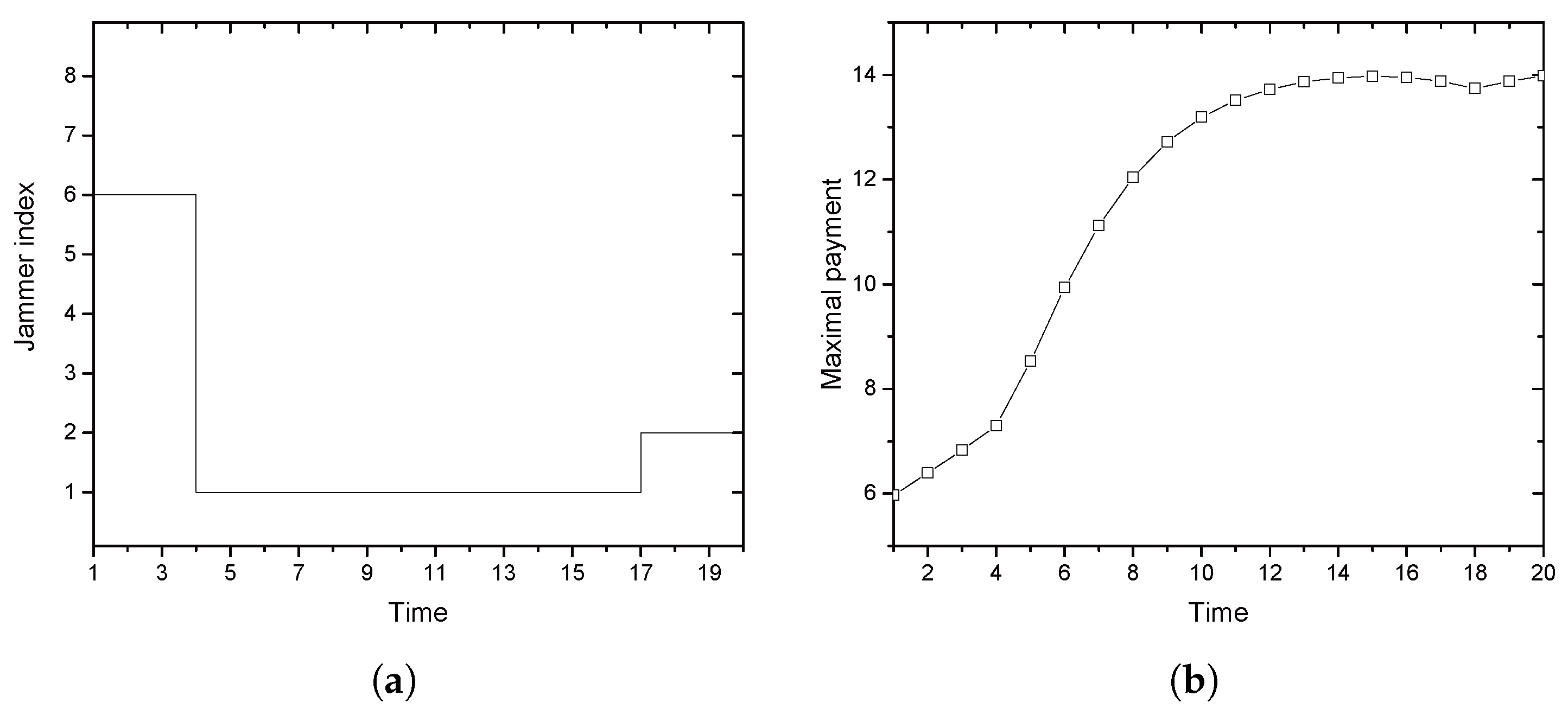
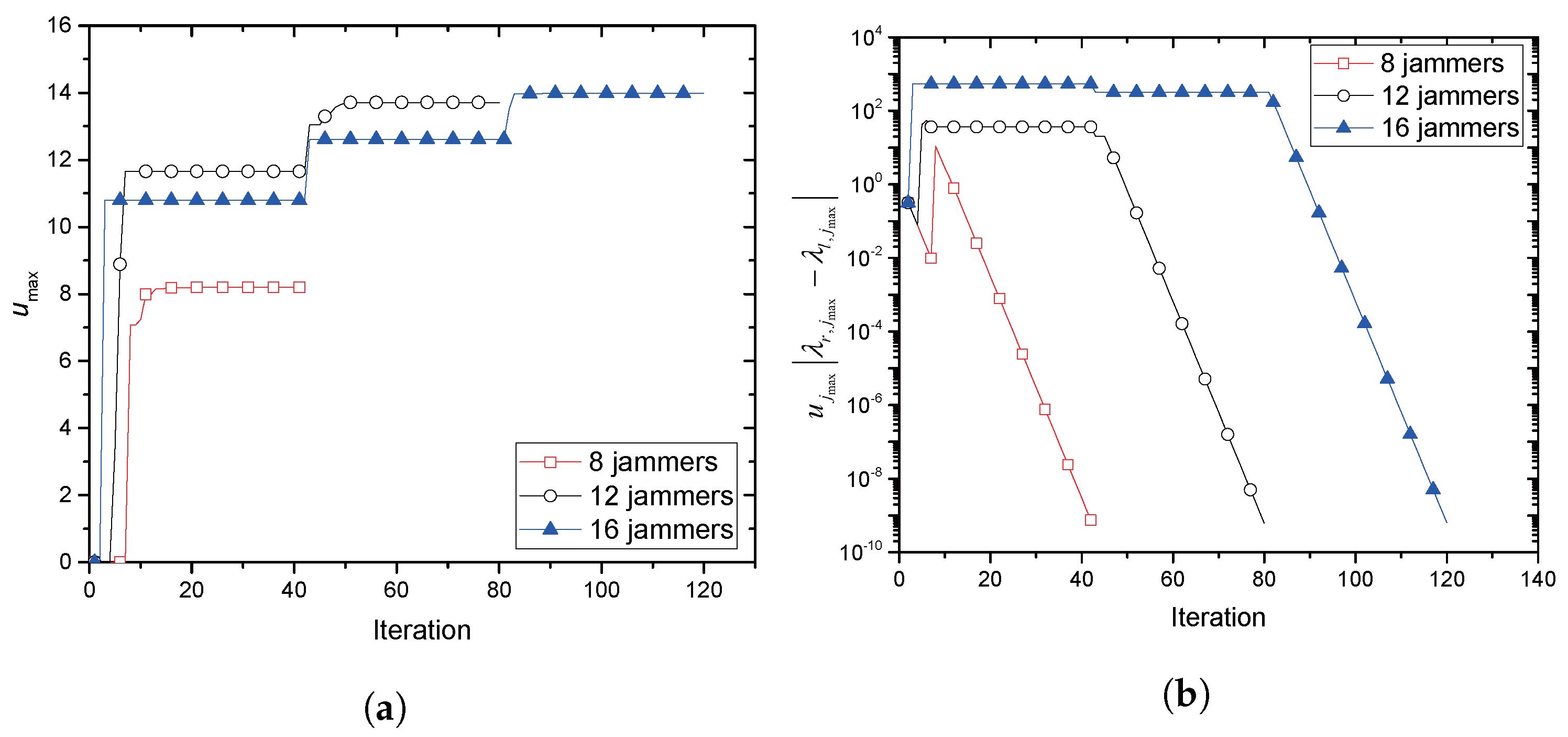
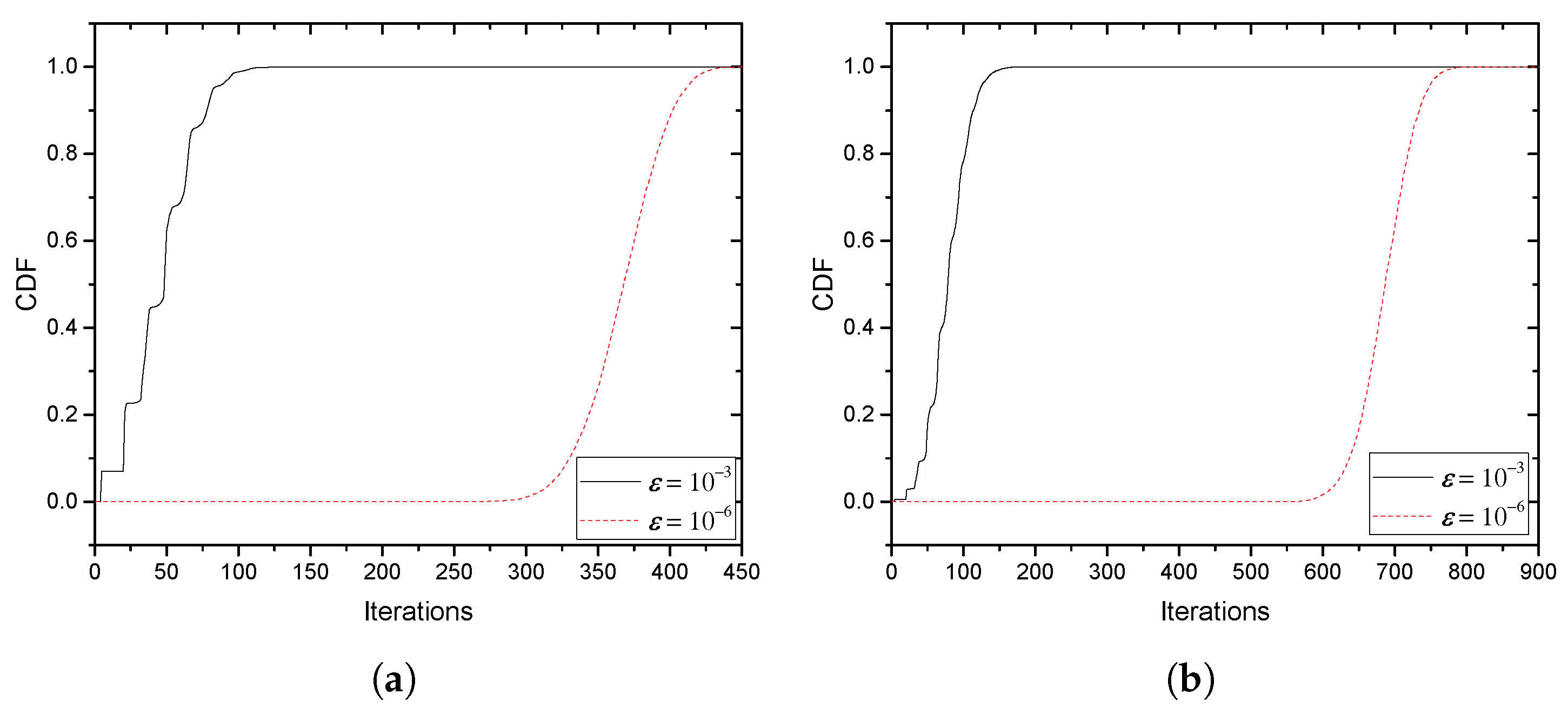
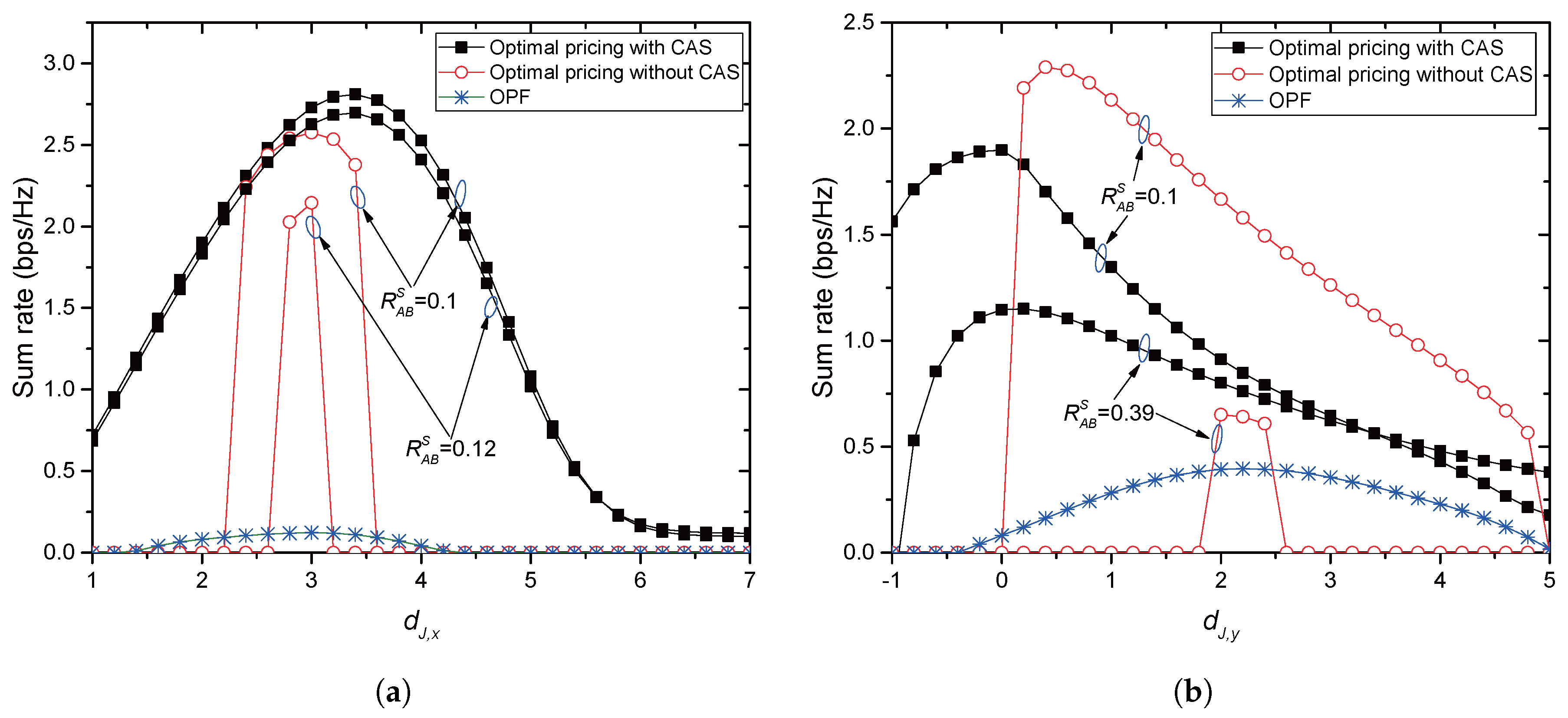
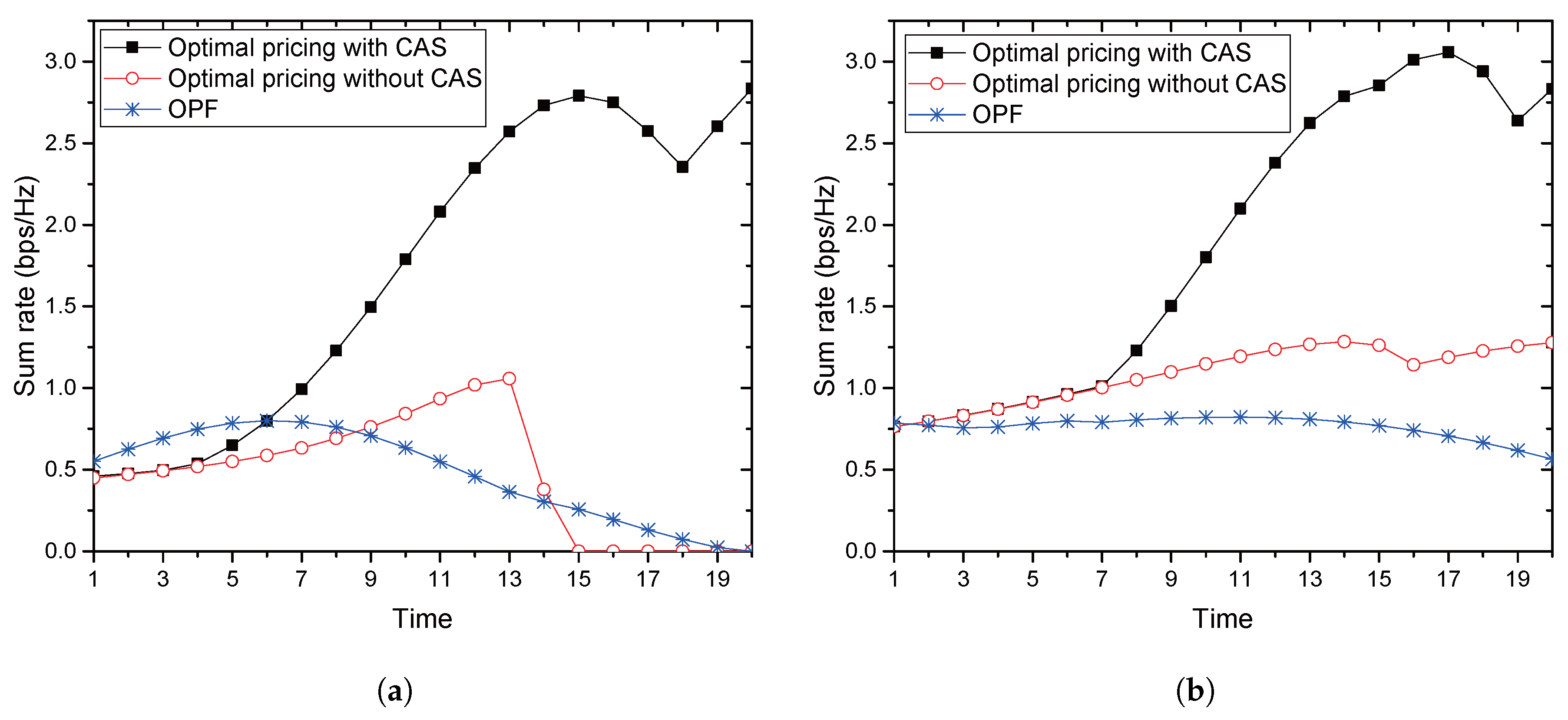
With the collaboration, we provide an optimal price issued by Alice and an optimal power allocation by the jammer corresponding to the price, where Alice is often called a price-leader and Jack is a price-follower in Stackelberg games. In order to provide the optimal solutions, we assume that legitimate sensors have perfect and full knowledge of Eve’s channel in their vicinity. We further investigate two scenarios for the collaboration: Bob and the jammer share common artificial signals (CASs) that are used for jamming signals so that Bob could (partly) cancel the jamming interference from the received signals; Additionally, Bob and the jammer have no CASs, and thus, the whole power from the jammer is treated as interference by Bob. We further extend the model with multiple jammers, in which Alice selects the most beneficial jammer that would provide the greatest payment. With such a greedy-selection policy, it is shown that the benefit taken by Alice increases as the number of potential jammers increases. Moreover, the probability (in asymptotic environments) that Alice’s benefit drops below a certain predefined threshold is shown to decrease geometrically as the number of jammers grows. If multiple jammers exist, it is hard for Alice to know the network-wide channel information for jammers and/or for Eves. By assuming that only the jammers, but Alice, know the relevant channel information, an interactive and iterative price-searching procedure is provided. The procedure converges geometrically to an optimal price. With numerical investigation, we show that the convergence speed is sufficiently fast with the moderate number of jammers. Numerical examples are also provided for illustrating the proposed optimal pricing and power allocation for a single jammer and multiple jammers, respectively. The result especially show that about a 6–28% increase in Alice’s benefit is achieved by allowing eight jammers to participate in the price-searching procedure.
The contributions of this paper can be summarized as follows:
provides a new price-searching model that explains an adequate price level of the transmitting power used to deliver secondary traffic by friendly jammers; who also contribute to protecting the secure transmission of Alice,
presents, in closed-form, an optimal price that maximizes Alice’s benefit and the corresponding optimal power allocation from a jammers’ perspective;
provides a distributed and interactive price-searching procedure that can be applied for multiple-jammer scenarios and geometrically converges to an optimal price; and
shows that Alice by a greedy selection policy achieves a certain diversity gain, which increases log-linearly as the number of (potential) jammers grows.
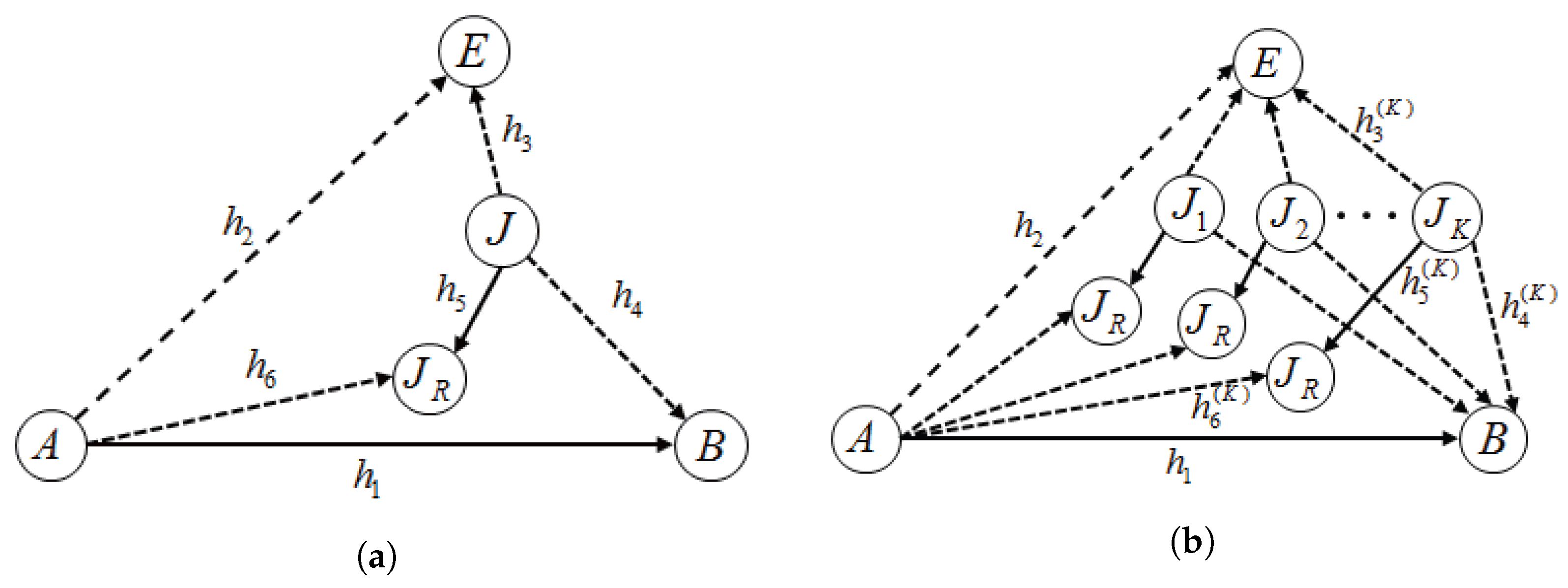
The remainder of the paper is organized as follows. The system model that includes the collaboration condition and signal representations in the collaboration is provided in
Section 1, In
Section 2, optimal pricing and power allocation are provided for a single-jammer case. An optimal price is presented in closed-form for both scenarios: with and without CAS, respectively.
Section 3 extends the result with a single jammer to a case of multiple jammers. When Alice selects the best jammer among potential jammers, it is shown that it enjoys a certain diversity gain that log-linearly increases as the number of jammers grows. In order to cope with a more practical problem in which Alice cannot gather the whole channel information in the network, a distributed and interactive collaboration search procedure (ICSP) is also provided in
Section 3. The convergence of ICSP is numerically investigated in
Section 4, in which a variety of other numerical examples is also discussed. Finally, conclusions are presented in
Section 5. The main notations used in this paper are listed in
Table 1.
4. Extension to Multiple Jammers
4.1. Greedy Jammer Selection
Let
and
denote sets of jammers who have CASs or not, respectively, and let us assume
. For jammer
, we assume that each of them transmits at a maximum power level
. Hereafter, superscript
is used to denote the respective jammers. For
, we assume that each jammer has real roots for (
20), and the greater one is denoted by
; further assume that
without loss of generality.
When
is given by Alice, jammers compute
and
according to (
13) and (
23), respectively. Let the payment by each of the jammers be denoted by
. Then:
Thus, optimal price
for multiple jammers is given by:
In (
27), it can be seen that there exists at least one
such that
for given
. Let us denote by
k a jammer that provides
. Thus, jammer
k offers a maximum payment to Alice. Alice maximizes its utility by choosing jammer
k, which is referred to as a greedy selection in this paper. Ties, if any, could be broken arbitrarily. Selected jammer
k determines its optimal power allocation according to either (
13) or (
23).
4.2. Asymptotic Analysis
When there are
K jammers, Alice can select one of them as a friendly jammer, which may provide a maximum payment. Let
be the maximum payment by jammer
j, which is determined when an optimal price is offered by Alice. Then, Alice’s maximum utility with
K cooperative jammers
can be:
obviously increases as
K increases, which means that Alice enjoys the benefit from the diversity of potential jammers with the greedy selection principle. To quantify this benefit, let us assume that Alice has a utility target
and suffers from a utility outage when
. The probability of utility outage is then defined by:
We assume that for brevity. It is easy to show that the following observation is analogously valid for .
As
goes to infinity,
decreases and converges to:
where
. Additionally,
also converges to:
When
further goes to infinity,
where
. An asymptotic expression of
is given by:
where
. Let:
Then, the asymptotic outage probability becomes (if we assume that every jammer has the same
for brevity):
where
and
represent the PDF of
and the CDF of
, respectively.
We assume that
and
(
) have the exponential distribution with mean
and mean
, respectively, and that all the channels are mutually independent. Then, the PDF of
is given by
, and the PDF of
is given by
. The CDF of
is then given by:
where
and
.
Lemma 4. achieves full diversity gain in the sense that the log of utility outage probability decreases as an order of K when every and the channel gain is known and fixed.
Proof. Let us denote the fixed
by
, and we assume independent and identical
’s (
), so that
for all j. By using approximation
in (
36), when
,
with given
becomes:
When Alice wants to keep its utility from dropping below a threshold , the increasing number of cooperative jammers probabilistically helps to reduce the probability of utility outage. Lemma 4 tells us how the number of jammers contributes to diminishing the outage probability. It tells us that when the channel between Jack and its receiver becomes relatively very good compared to the interfering links: Alice to and Jack to Bob, both of which are unwanted signal paths, the outage probability decreases log-linearly. This property also holds for jammers in even without assuming fixed . For the utility provided in Lemma 3, it is seen that only the ratio / matters in achieving the full diversity gain for jammers in .
4.3. Distributed Collaboration Protocol for Multiple Jammers
For a single jammer, Alice and Jack can share the whole channel knowledge by adequate feedback channels. However, if there are multiple (potential) jammers, it is hard for Alice and the jammers to have the wide-range channel information over the whole network. In this subsection, we assume that Alice has only the channel information on and , and each jammer has its own channel information on , , and .
Looking for the collaboration, Alice initially broadcasts
with channel information
,
and secrecy rate target
(and also
if it is not known to the jammers in advance). Each jammer
j that has some message to send and also seeks the collaboration opportunity then computes either
or
according to (
13) and (
23), respectively. Of course, each jammer has prior knowledge of
and
. Each jammer sends either
or
with
, if needed, which could be already known to Alice by previous communications. Jammers send the power allocation as an agreement of the collaboration when the power allocation is positive. Alice receives the response from the jammers and tries to determine whether it will send a new price or stop sending the price and choose the best jammer with the feedbacks so far.
According to (
13),
is not dependent on
if
. However, it decreases if
. Let us denote by
the
i-th price successively sent by Alice looking for the collaboration. By using two successive designated prices
and
(
), Alice can have partial information on power allocation by jammer
from the responses such that if
, then
and
. Getting
and a lower bound on
by the above reasoning, Alice can also have an upper bound on
by a response
, which means
.
For jammer , its response on power allocation will be one of , , and . When Alice increases , the response finally reaches either or : If , it eventually becomes ; Otherwise, . When Alice increases , regarding the sequence of responses, jammer falls into one of three classes: the first type that responds with either fixed power or , the second type that increases its power from to and the third type that increases its power from to . Since Alice knows from the feedback, it finally understands whether the jammer allocates or .
Motivated by the above findings, an interactive and iterative collaboration search procedure (ICSP) is provided in
Table 2. It is primarily based on the bisectional search that guides Alice’s pricing trials to find
or
. In this procedure,
and
represent a lower and an upper limit of the price in practice, respectively, which are set by Alice. ICSP tries to find the collaboration starting with the smallest possible price
, by which Alice can attract as many as friendly jammers possible. In ICSP, if
for a predefined threshold
, it is regarded that the price is sufficiently exploited for jammer
j. If every potential jammer satisfies the condition, ICSP terminates with an individual pricing range of the jammers, and then, the most plausible jammer is selected for the collaboration. Otherwise, further improvement in the payment by jammer
j is expected by
and the biggest jammer is selected for the next price-searching. Since
replaces either
or
for some
j, ICSP converges geometrically and terminates within
, where
N represents the total number of potential jammers in
.