Automated As-Built Model Generation of Subway Tunnels from Mobile LiDAR Data
Abstract
:1. Introduction
2. Literature Review
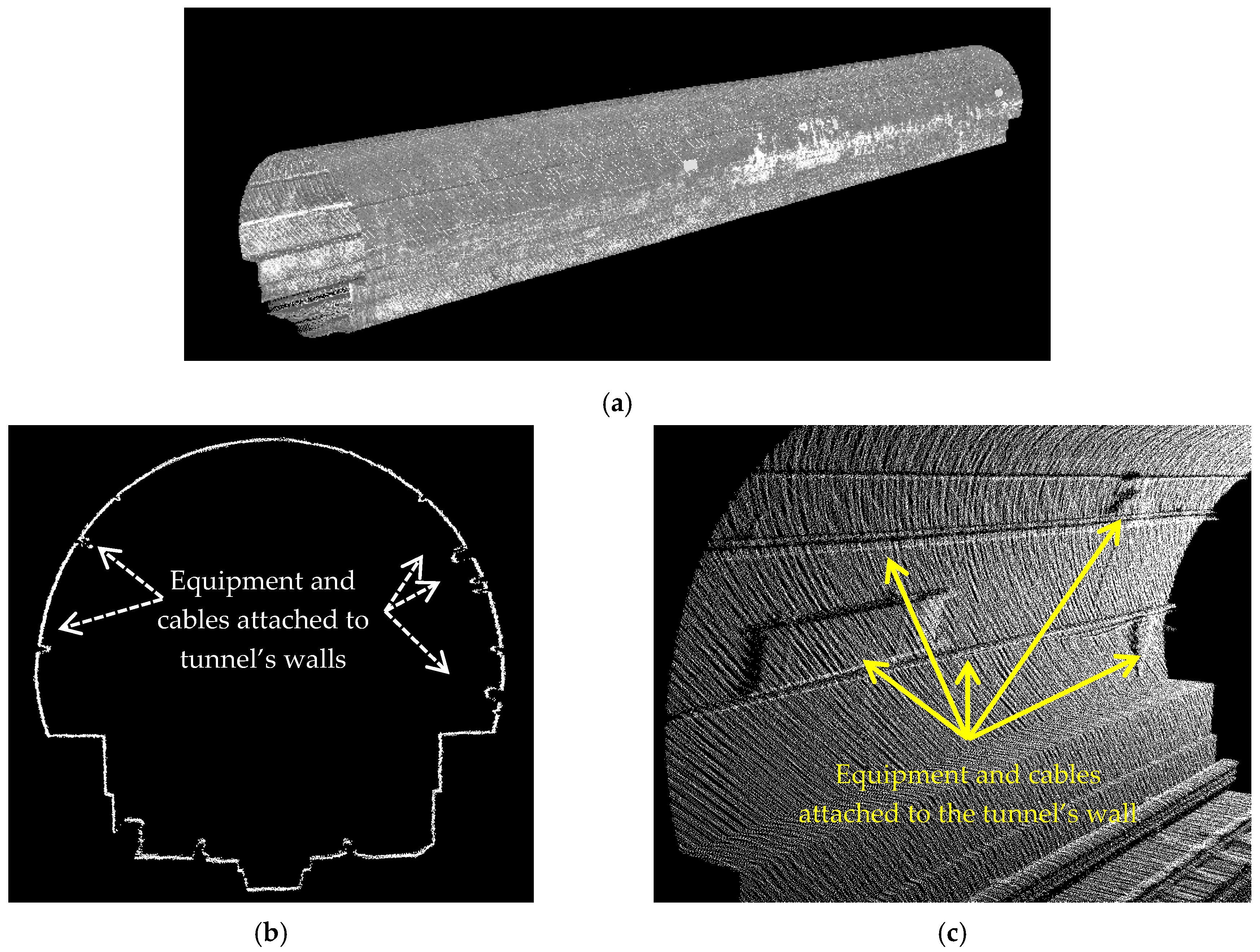
3. Dataset
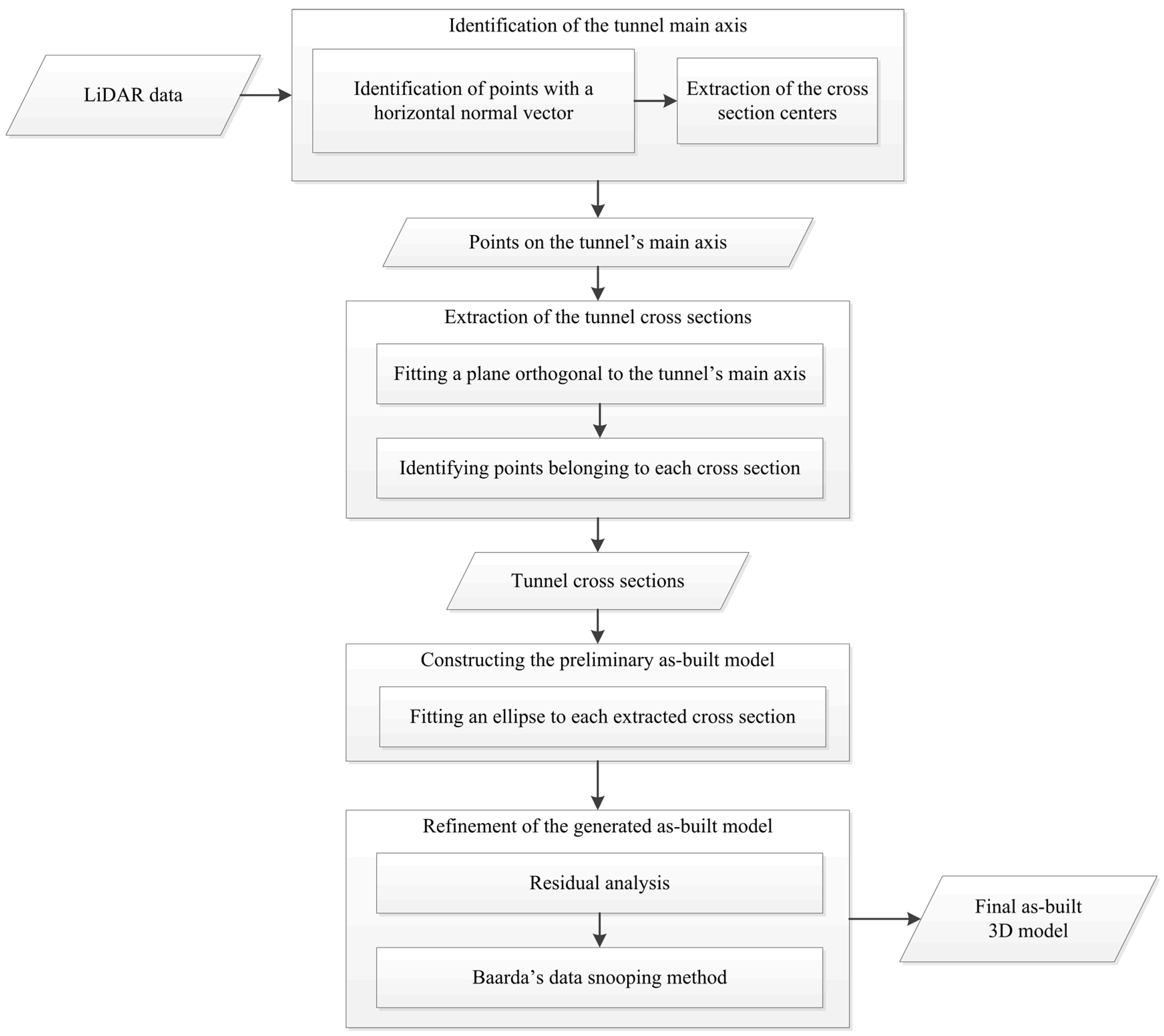
4. Methodology
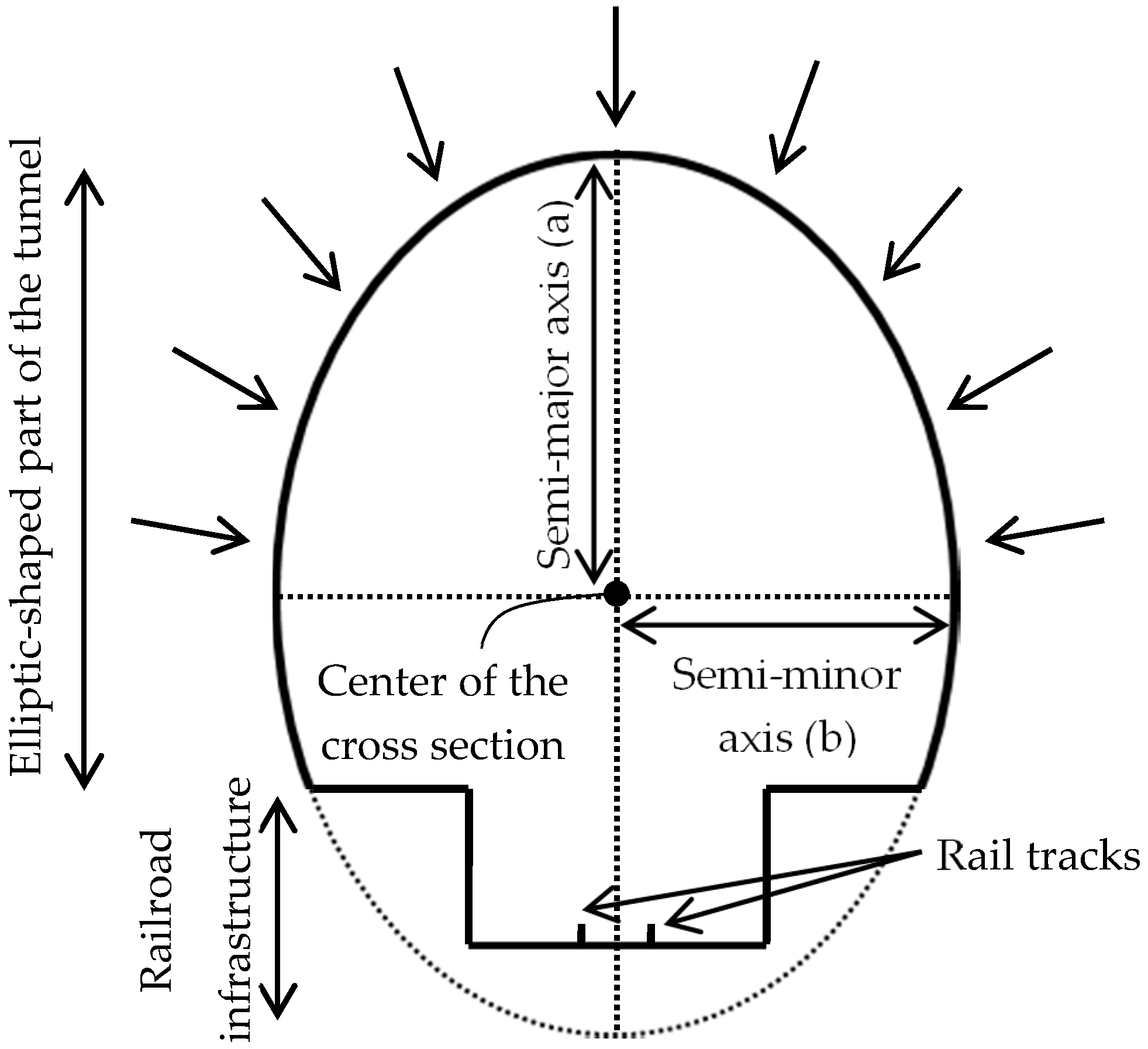
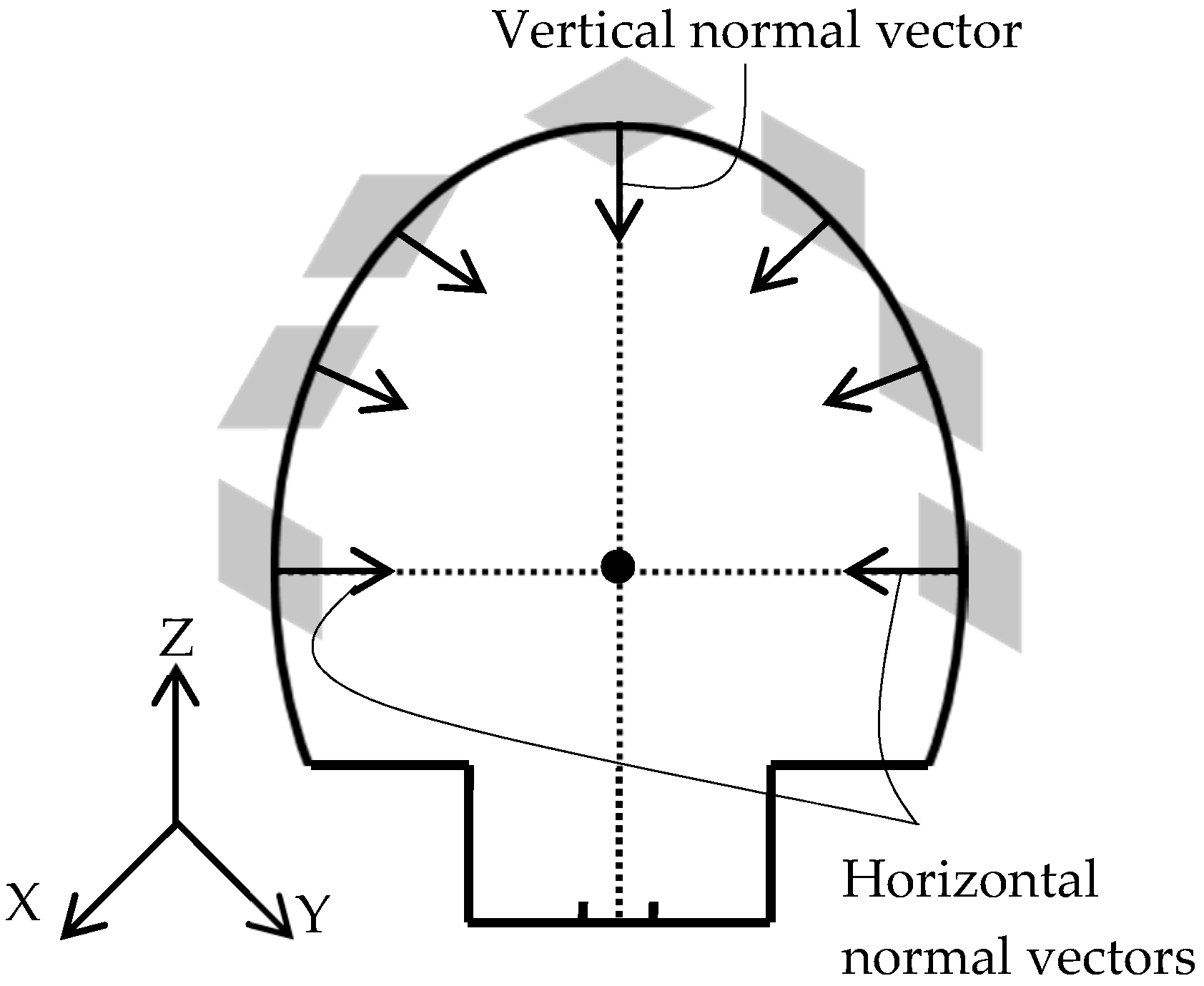
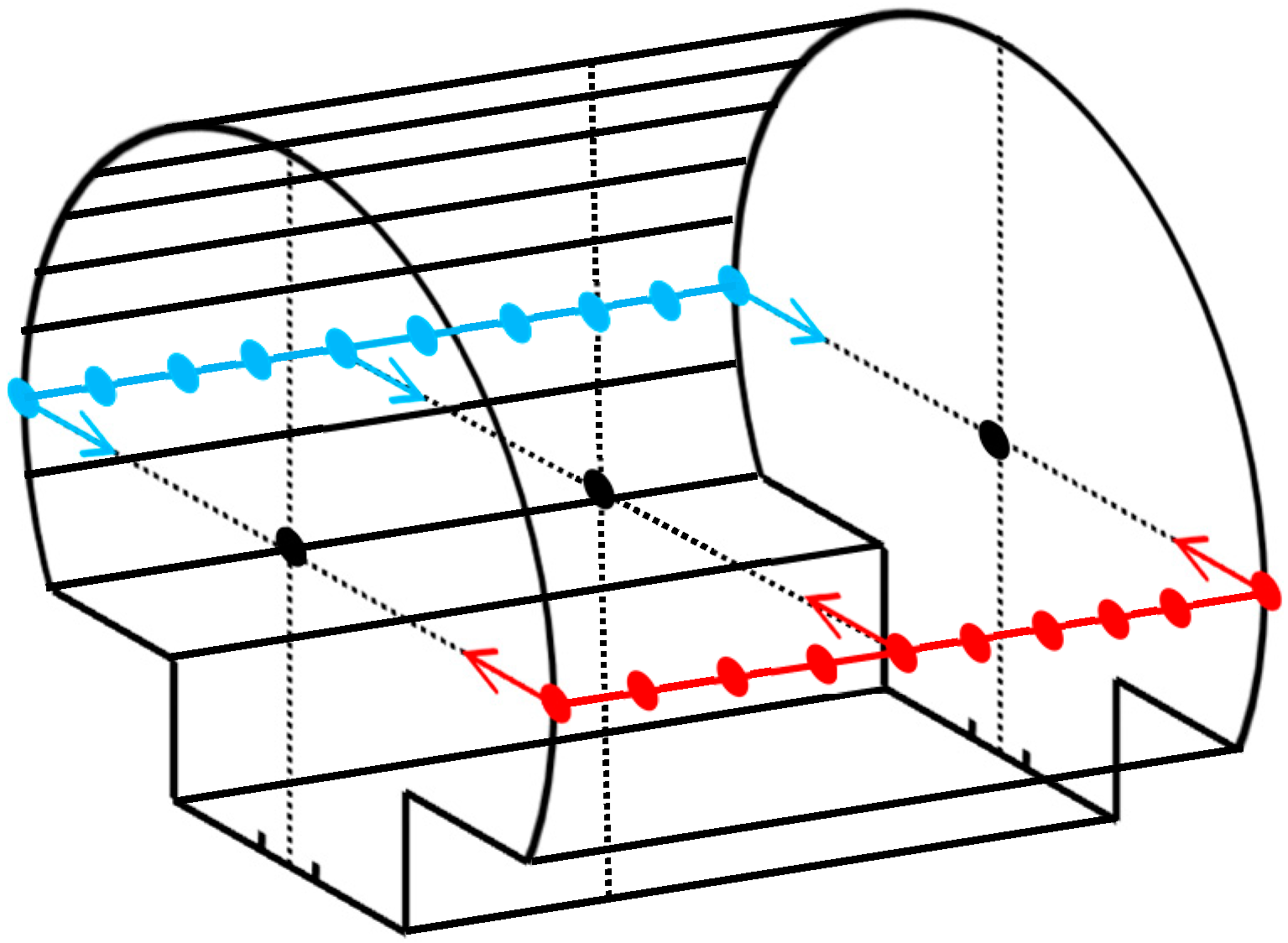
4.1. Identification of the Tunnel’s Main Axis
4.2. Extraction of the Tunnel Cross Sections
4.3. As-Built Model Generation
4.3.1. Modeling by Least Squares Adjustment
4.3.2. Model Refinement
4.4. Evaluation of the Generated Model
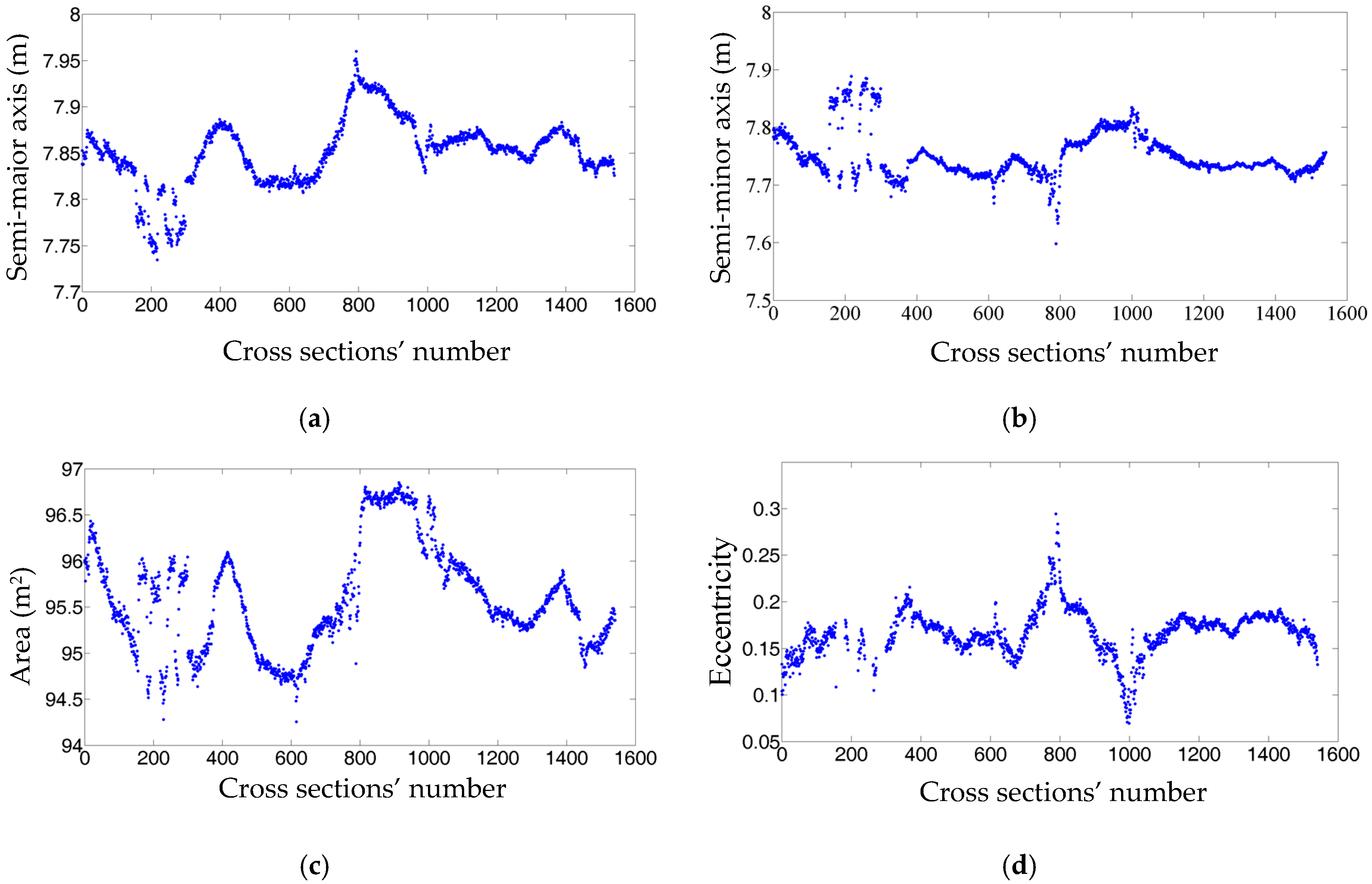
4.4.1. Dimensions of the Extracted Cross Sections
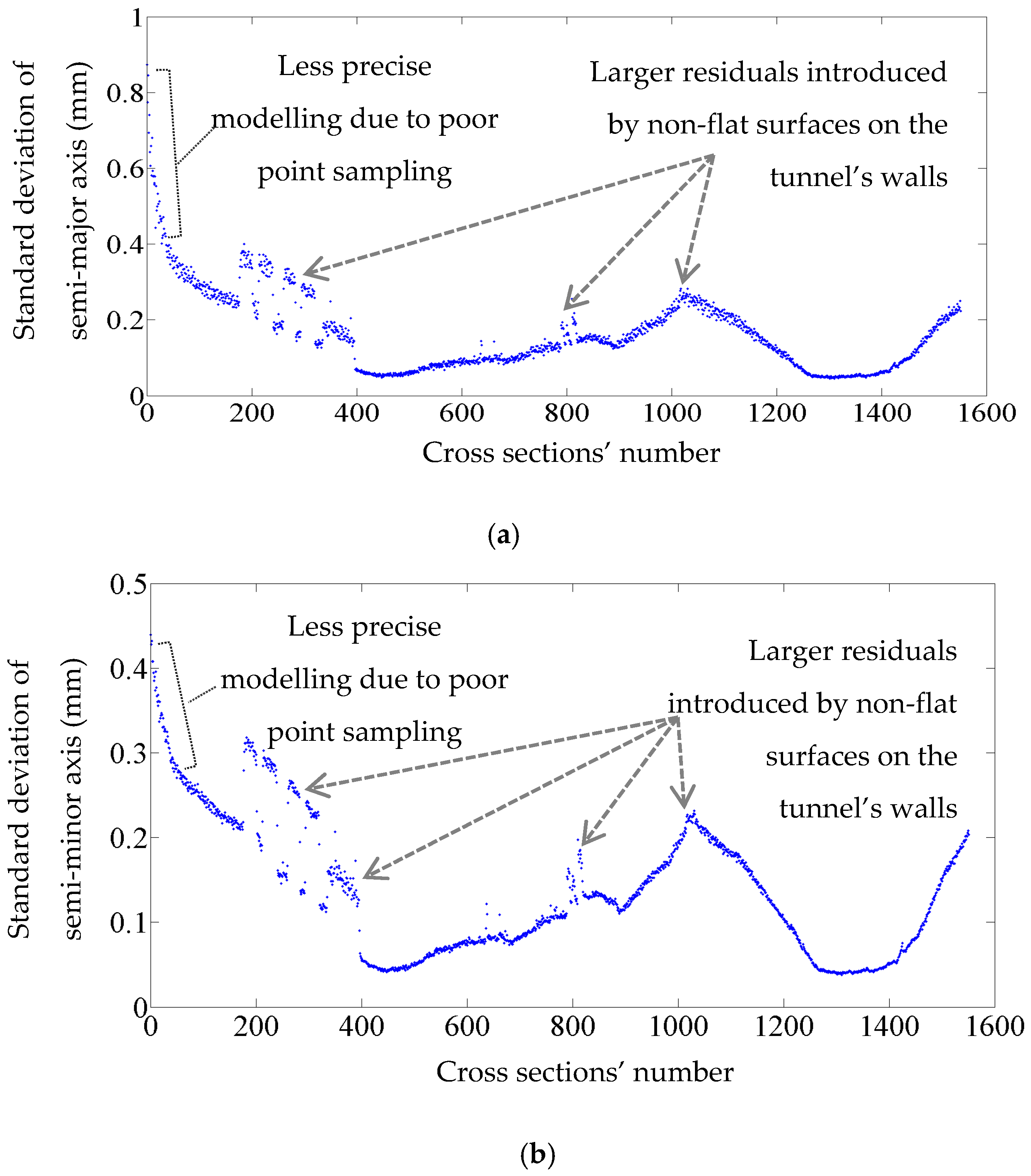
4.4.2. Precision of the Estimated Parameters
5. Results and Discussion
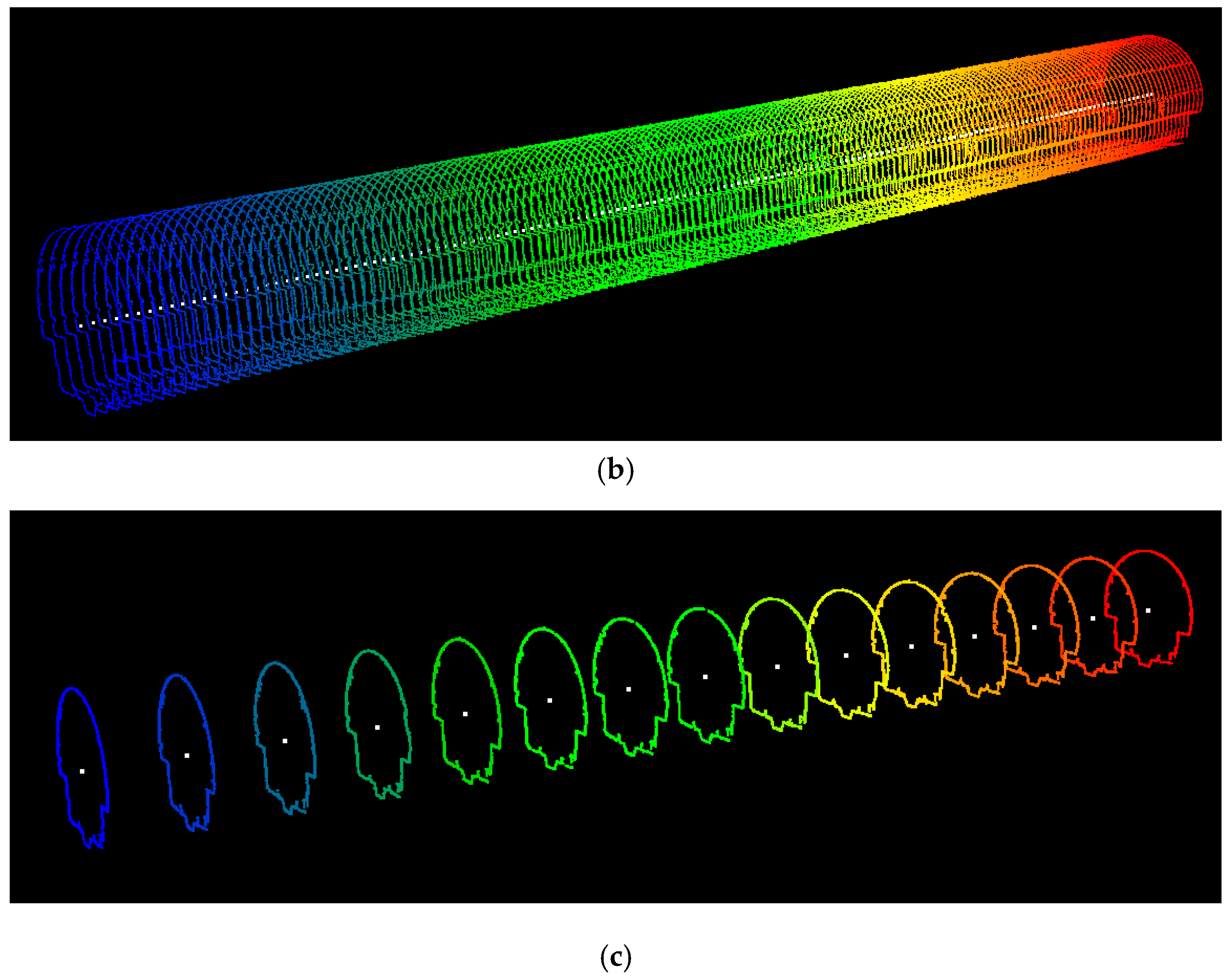
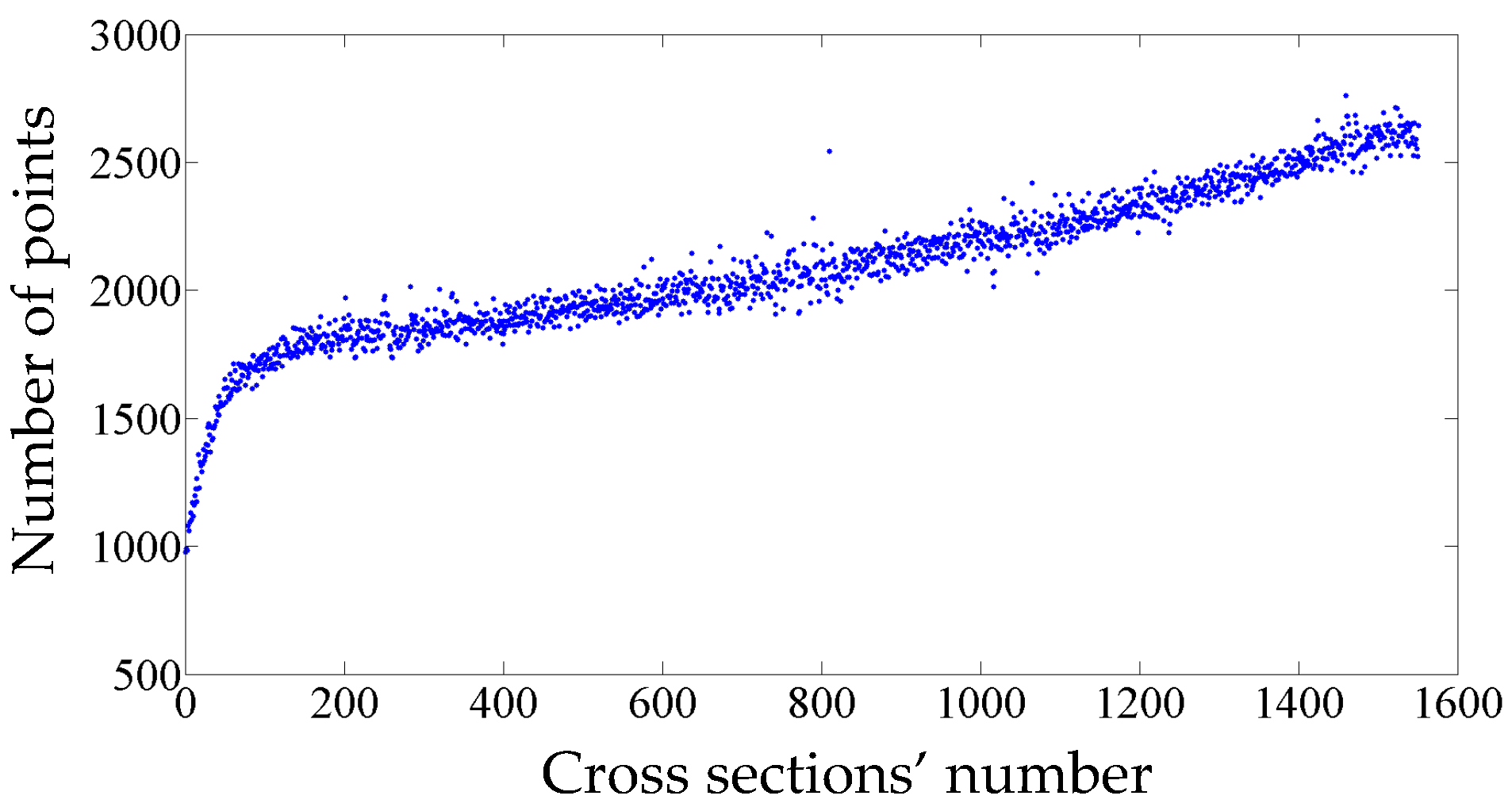
5.1. Results of Cross Section Extraction
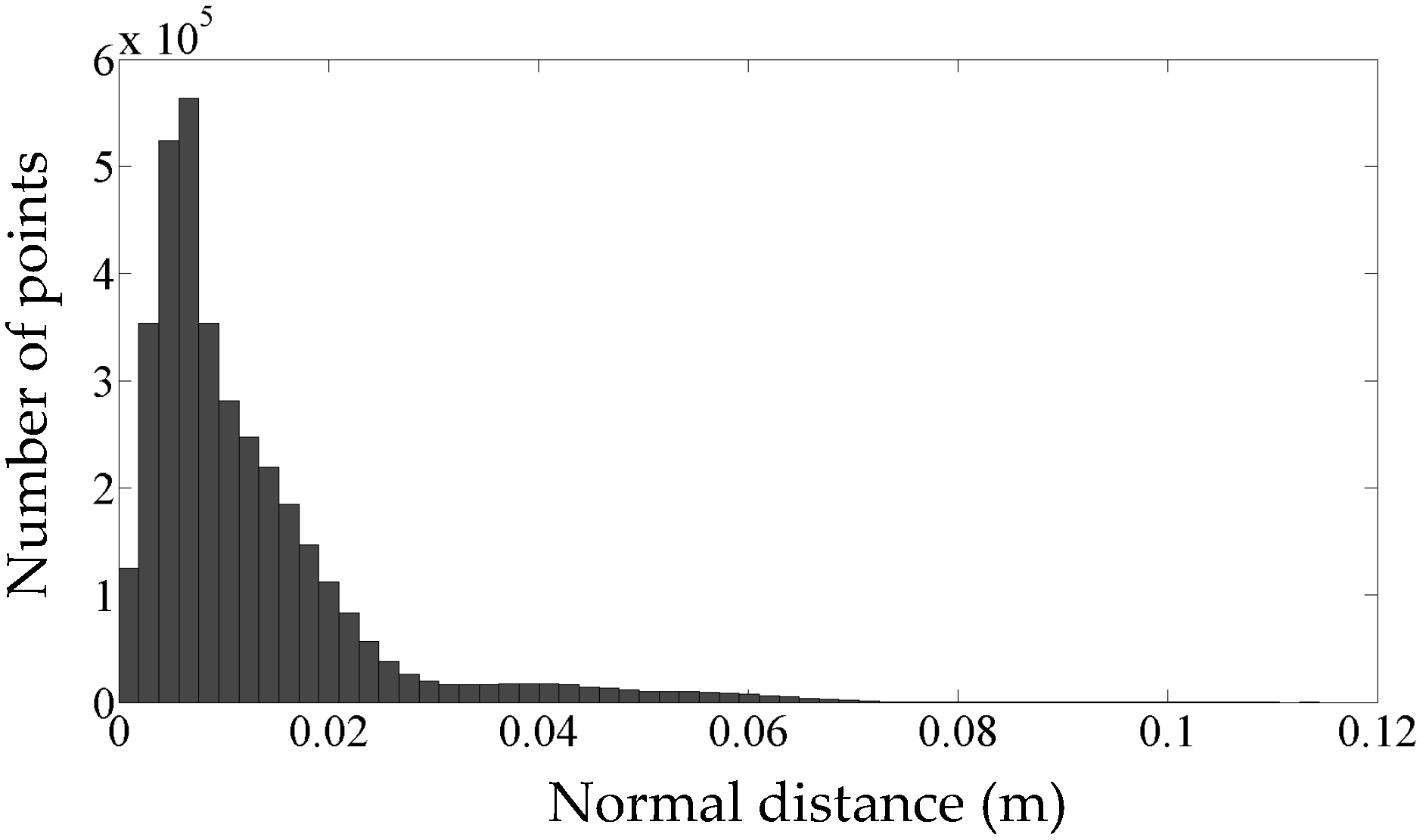
5.2. The Generated As-Built Model
- Speed reduction of the train carrying the LiDAR sensor
- Change in the setting of the employed LiDAR sensor during data collection
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Qiu, D.W.; Wu, J.G. Terrestrial Laser Scanning for Deformation Monitoring of the Thermal Pipeline Traverses Subway Tunnel Engineering. In Proceedings of the IXX ISPRS Congress, commission V, Beijing, China, 3–11 July 2008; pp. 491–494.
- Dorninger, P.; Pfeifer, N. A comprehensive automated 3D approach for building extraction, reconstruction, and regularization from airborne laser scanning point clouds. Sensors 2008, 8, 7323–7343. [Google Scholar] [CrossRef]
- Pu, S.; Vosselman, G. Building facade reconstruction by fusing terrestrial laser points and images. Sensors 2009, 9, 4525–4542. [Google Scholar] [PubMed]
- Kim, C.; Habib, A.F. Object-based integration of photogrammetric and LiDAR data for automated generation of complex polyhedral building models. Sensors 2009, 9, 5679–5701. [Google Scholar] [CrossRef] [PubMed]
- Jaakkola, A.; Hyyppä, J.; Hyyppä, H.; Kukko, A. Retrieval algorithms for road surface modelling using laser-based mobile mapping. Sensors 2008, 8, 5238–5249. [Google Scholar] [CrossRef]
- Yan, L.; Liu, H.; Tan, J.; Li, Z.; Xie, H.; Chen, C. Scan line based road marking extraction from mobile LiDAR point clouds. Sensors 2016, 16, 903. [Google Scholar] [CrossRef] [PubMed]
- Arastounia, M.; Lichti, D.D. Automatic object extraction from electrical substation point clouds. Remote Sens. 2015, 7, 15605–15629. [Google Scholar] [CrossRef]
- Leslar, M.; Gordon, P.; Keith, M.N. Using Mobile LiDAR to Survey a Railway Line for Asset Inventory. In Proceedings of the ASPRS 2010 Annual Conference, San Diego, CA, USA, 26–30 April 2010.
- Oude Elberink, S.; Khoshelham, K. Automatic extraction of railroad centerlines from mobile laser scanning data. Remote Sens. 2015, 7, 5565–5583. [Google Scholar] [CrossRef]
- Arastounia, M. Automated recognition of railroad infrastructure in rural areas from LiDAR data. Remote Sens. 2015, 7, 14916–14938. [Google Scholar] [CrossRef]
- Tsakiri, M.; Lichti, D.D.; Pfeifer, N. Terrestrial Laser Scanning for Deformation Monitoring. In Proceedings of the 12th FIG symposium on deformation monitoring, Baden, Germany, 22–24 May 2006.
- Wang, W.; Zhao, W.; Huang, L.; Vimarlund, V.; Wang, Z. Applications of terrestrial laser scanning for tunnels: A review. J. Traff. Trans. Eng. 2014, 1, 325–337. [Google Scholar] [CrossRef]
- Gosliga, R.V.; Lindenbergh, R.; Pfeifer, N. Deformation Analysis of a Bored Tunnel by Means of Terrestrial Laser. In Proceedings of the ISPRS Technical Commission V Symposium, Dresden, Germany, 25–27 September 2006; pp. 1–6.
- Vezočnik, R.; Ambrožič, T.; Sterle, O.; Bilban, G.; Pfeifer, N.; Stopar, B. Use of terrestrial laser scanning technology for long term high precision deformation monitoring. Sensors 2009, 9, 9873–9895. [Google Scholar] [CrossRef] [PubMed]
- Delaloye, D.; Hutchinson, J.; Diederichs, M.S. Using Terrestrial LiDAR for Tunnel Deformation Monitoring in Circular Tunnels and Shafts. In Proceedings of the Eurock 2012–the 2012 ISRM International Symposium, Stockholm, Sweden, 28–30 May 2012.
- Goncalves, J.A.; Mendes, R.; Araujo, E.; Oliviera, A.; Boavida, J. Planar Projection of Mobile Laser Scanning Data in Tunnels. In Proceedings of the ISPRS Technical Commission III Symposium, Melbourne, Australia, 25 August–1 September 2012; pp. 109–113.
- Han, J.; Guo, J.; Jiang, Y. Monitoring tunnel profile by means of multi-epoch dispersed 3-D LiDAR point clouds. Tunnel. Undergr. Space Technol. 2013, 33, 186–192. [Google Scholar] [CrossRef]
- Han, J.; Guo, J.; Jiang, Y. Monitoring tunnel profile by means of multi-epoch dispersed 3-D LiDAR point clouds: An improved approach. Tunnel Undergr. Space Technol. 2013, 38, 385–389. [Google Scholar] [CrossRef]
- Kang, A.; Zhang, L.; Tuo, L.; Wang, B.; Chen, J. Continuous extraction of subway tunnel cross sections based on terrestrial point clouds. Remote Sens. 2014, 6, 857–879. [Google Scholar] [CrossRef]
- Zai, D.; Li, J.; Yu, Y.; Guan, H.; Wang, C. Road Tunnel Deformation Monitoring Using Terrestrial LiDAR Data. In Proceedings of the ISPRS Technical Commission I Symposium, Denver, CO, USA, 17–20 November 2014; pp. 17–20.
- Walton, G.; Delaloye, D.; Diederichs, M.S. Development of an elliptical fitting algorithm to improve change detection capabilities with applications for deformation monitoring in circular tunnels and shafts. Tunnel Undergr. Space Technol. 2014, 43, 336–349. [Google Scholar] [CrossRef]
- Ray, A.; Srivastava, D.C. Non-linear least squares ellipse fitting using the genetic algorithm with applications to strain analysis. J. Struct. Geol. 2008, 30, 1593–1602. [Google Scholar] [CrossRef]
- Nuttens, T.; Stal, C.; Backer, H.D.; Schotte, K.; Bogaert, P.V.; Wulf, A.D. Methodology for the ovalization monitoring of newly built circular train tunnels based on laser scanning: Liefkenshoek rail link (Belgium). Autom. Constr. 2014, 43, 1–9. [Google Scholar] [CrossRef]
- Nuttens, T.; Stal, C.; Backer, H.D.; Schotte, K.; Bogaert, P.V.; Detry, P.; Wulf, A.D. Terrestrial laser scanning as a key element in the integrated monitoring of tidal influences on a twin-tube concrete tunnel. Photogramm. Rec. 2014, 29, 402–416. [Google Scholar] [CrossRef] [Green Version]
- Nuttens, T.; Stal, C.; Backer, H.D.; Deruyter, G.; Schotte, K.; Bogaert, P.V.; Wulf, A.D. Laser Scanning for Precise Ovalization Measurements: Standard Deviations and Smoothing Levels. Available online: http://dx.doi.org/10.1061/(ASCE)SU.1943-5428.0000165 (accessed on 2 September 2016).
- Velodyne LiDAR. Available online: http://velodynelidar.com/lidar/hdlproducts/97-0038d%20HDL-32E_datasheet.pdf (accessed on 12 December 2015).
- Mikhail, E.M.; Ackermann, F.E. Introduction to Least Squares Adjustment. In Observations and Least Squares, 1st ed.; Brinker, R.C., Ed.; University Press of America: New York, NY, USA, 1982; pp. 101–110. [Google Scholar]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks, 1st ed.; Netherlands Geodetic Commission: Delft, The Netherlands, 1968; pp. 53–56. [Google Scholar]
- Bookstein, F.L. Fitting conic sections to scattered data. Comput. Graph. Image Process. 1979, 9, 56–71. [Google Scholar] [CrossRef]
- Sampson, P.D. Fitting conic sections to very scattered data: An iterative refinement of the Bookstein algorithm. Comput. Graph. Image Process. 1982, 18, 97–108. [Google Scholar] [CrossRef]
- Taubin, G. Estimation of planar curves, surfaces and non-planar space curves defined by implicit equations, with applications to edge and range image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 1991, 13, 1115–1138. [Google Scholar] [CrossRef]
- Fitzgibbon, A.W.; Pilu, M.; Fisher, R.B. Direct least squares fitting of ellipses. IEEE Trans. Pattern Anal. Mach. Intell. 1999, 21, 476–480. [Google Scholar] [CrossRef]






| Parameters | Value |
|---|---|
| Dimensions | 0.145 m × 0.086 m |
| Measurement rate | 700,000 (points/s) |
| Measurement range | 100 m |
| Positional accuracy | 0.02 m |
| Angular resolution | 1.33° |
| Object | Sampling (Points per/m2) |
|---|---|
| Side wall | 1426 |
| Ceiling | 509 |
| Floor (around rail tracks) | 652 |
| Statistics | Mean | Standard Deviation |
|---|---|---|
| Semi-major axis (m) | 7.8508 | 0.0002 |
| Semi-minor axis (m) | 7.7509 | 0.0001 |
| Area (m2) | 95.5838 | 0.0003 |
| Eccentricity | 0.17606 | 0.00002 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arastounia, M. Automated As-Built Model Generation of Subway Tunnels from Mobile LiDAR Data. Sensors 2016, 16, 1486. https://doi.org/10.3390/s16091486
Arastounia M. Automated As-Built Model Generation of Subway Tunnels from Mobile LiDAR Data. Sensors. 2016; 16(9):1486. https://doi.org/10.3390/s16091486
Chicago/Turabian StyleArastounia, Mostafa. 2016. "Automated As-Built Model Generation of Subway Tunnels from Mobile LiDAR Data" Sensors 16, no. 9: 1486. https://doi.org/10.3390/s16091486







