Modeling and Analysis of a 2-DOF Spherical Parallel Manipulator
Abstract
:1. Introduction
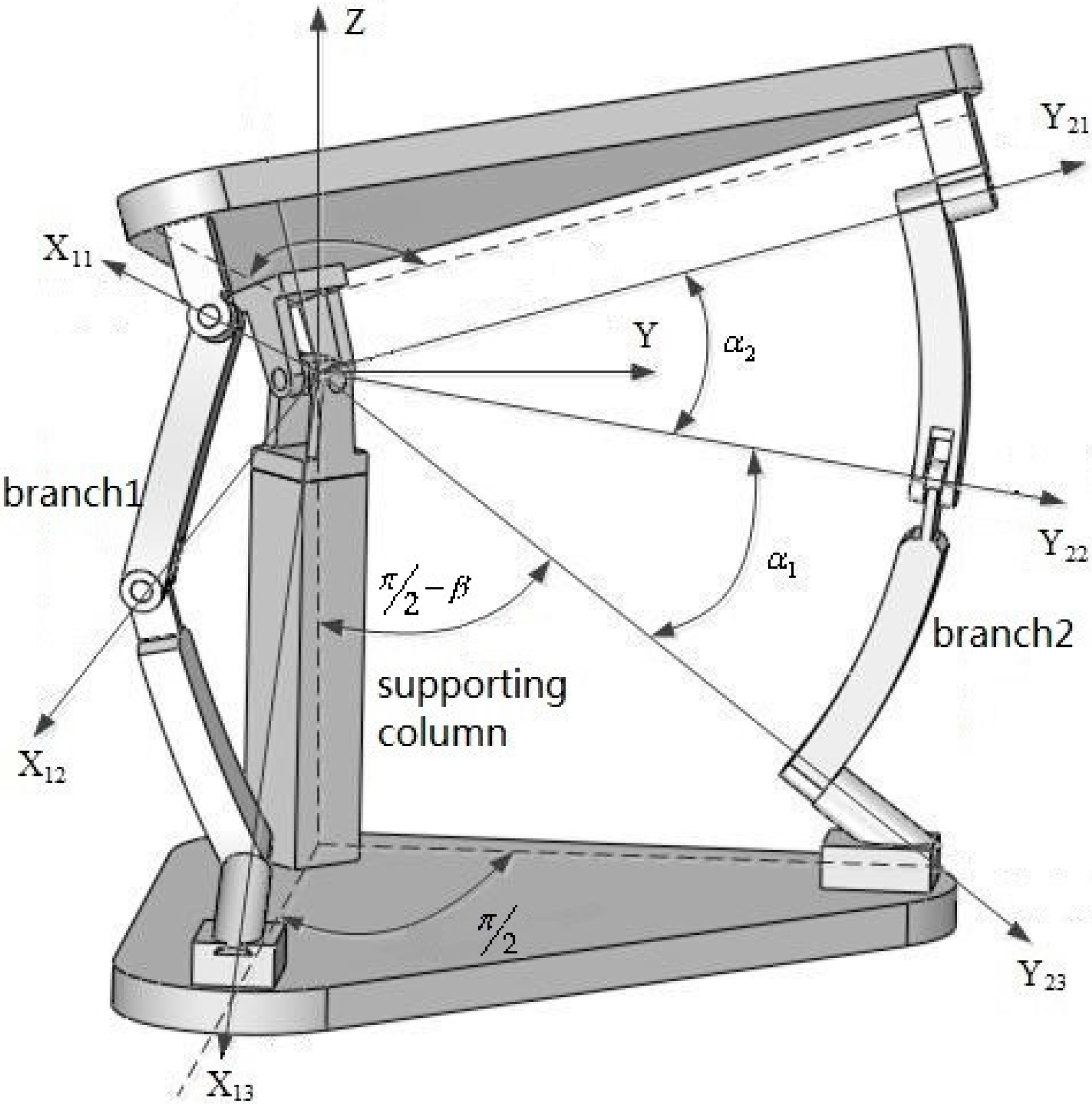
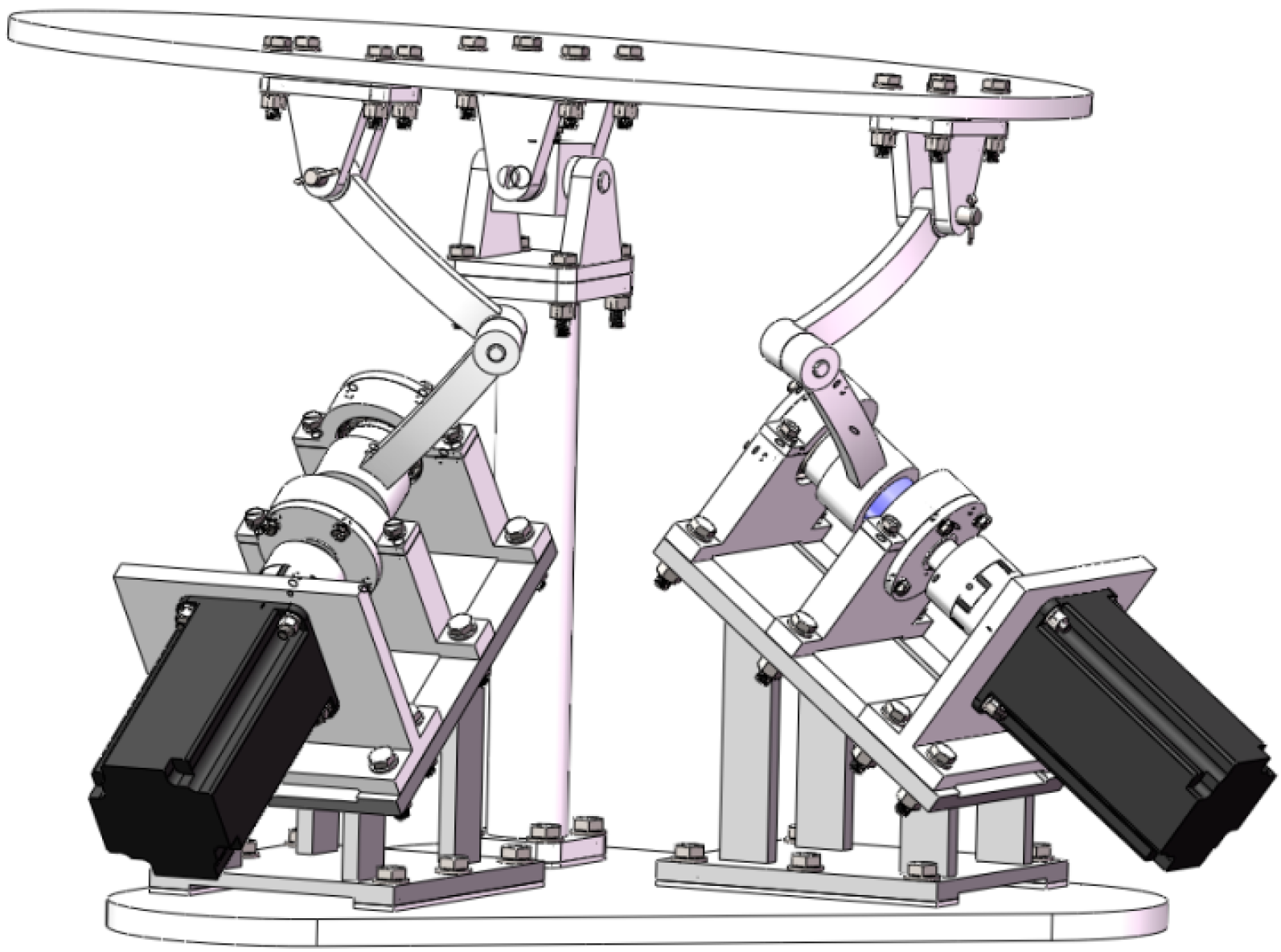
2. Description of the Spherical Parallel Manipulator
3. Kinematics
3.1. Representation of the Joints
3.2. Inverse Kinematics
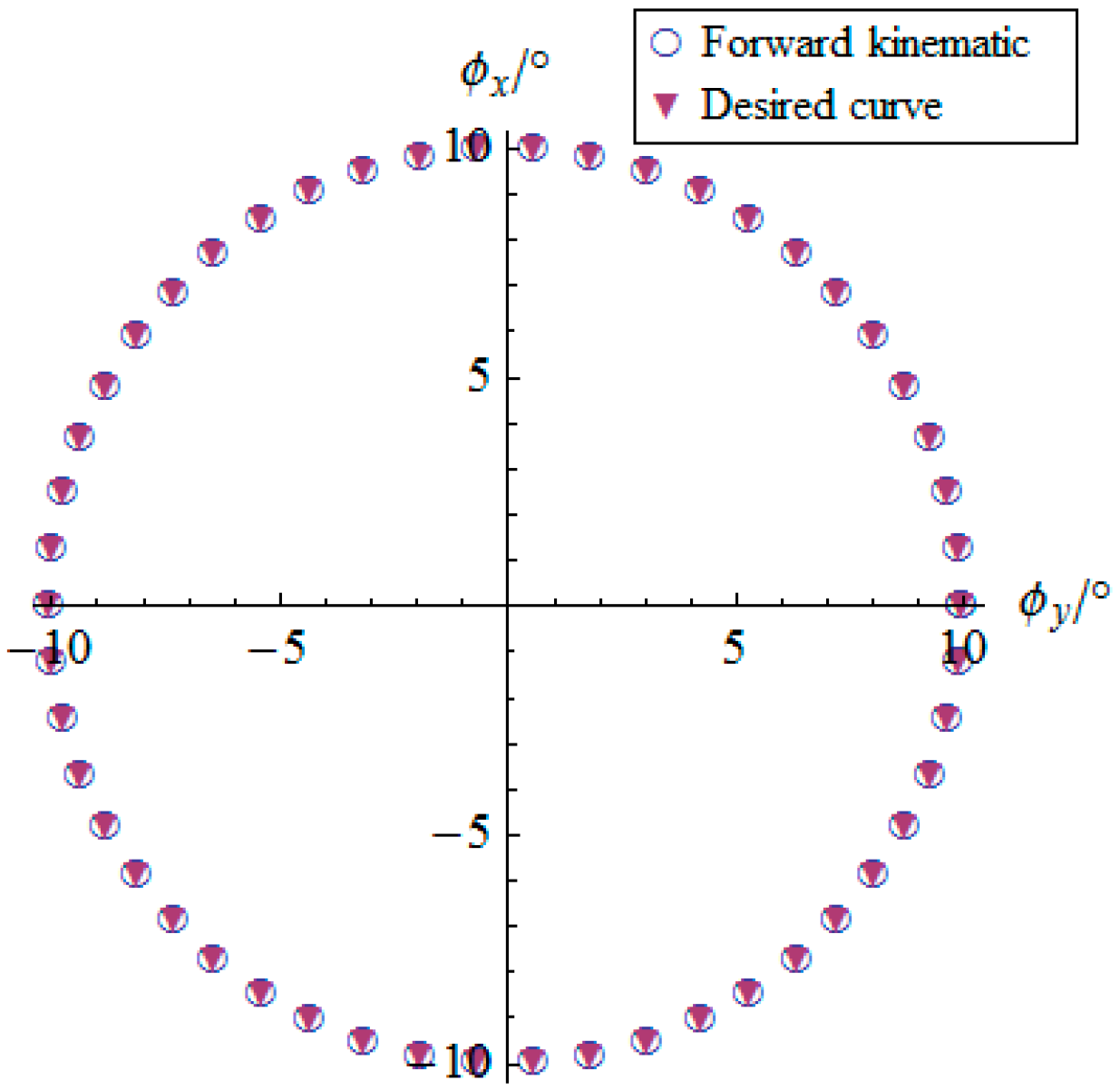
3.3. Forward Kinematics
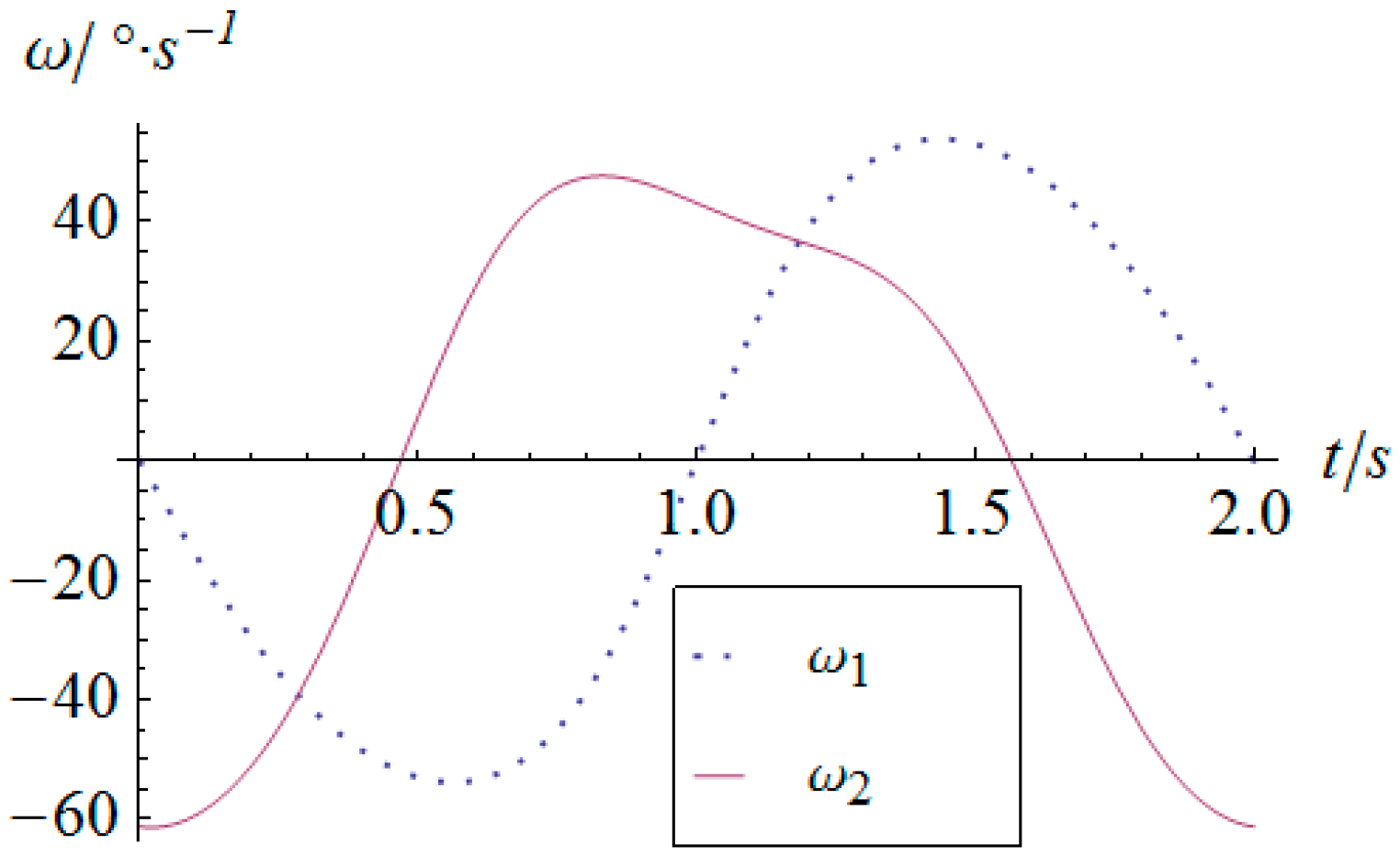
3.4. Analysis of Velocity and Acceleration
4. The Dynamics Model Based on the Virtual Work Principle
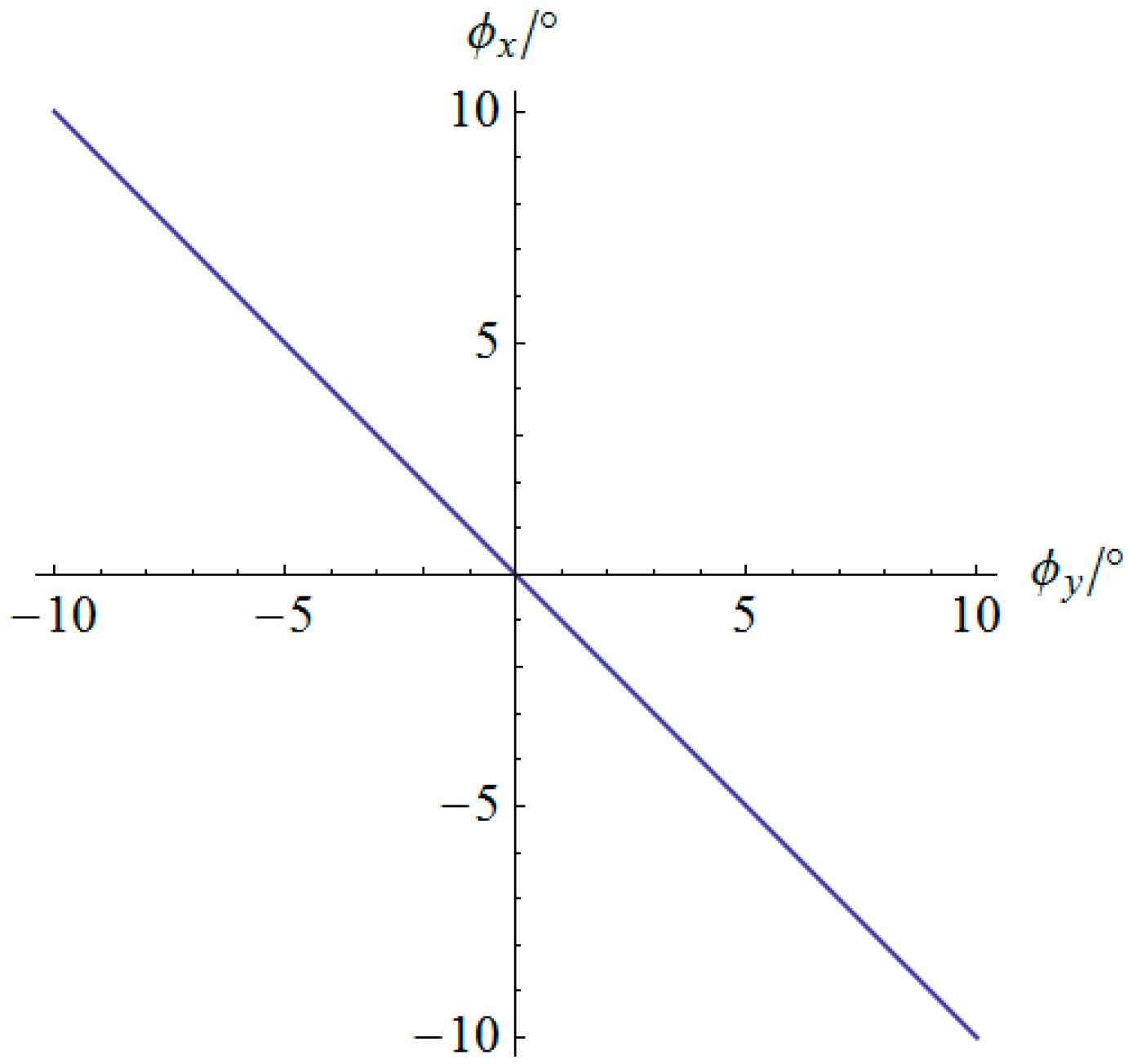
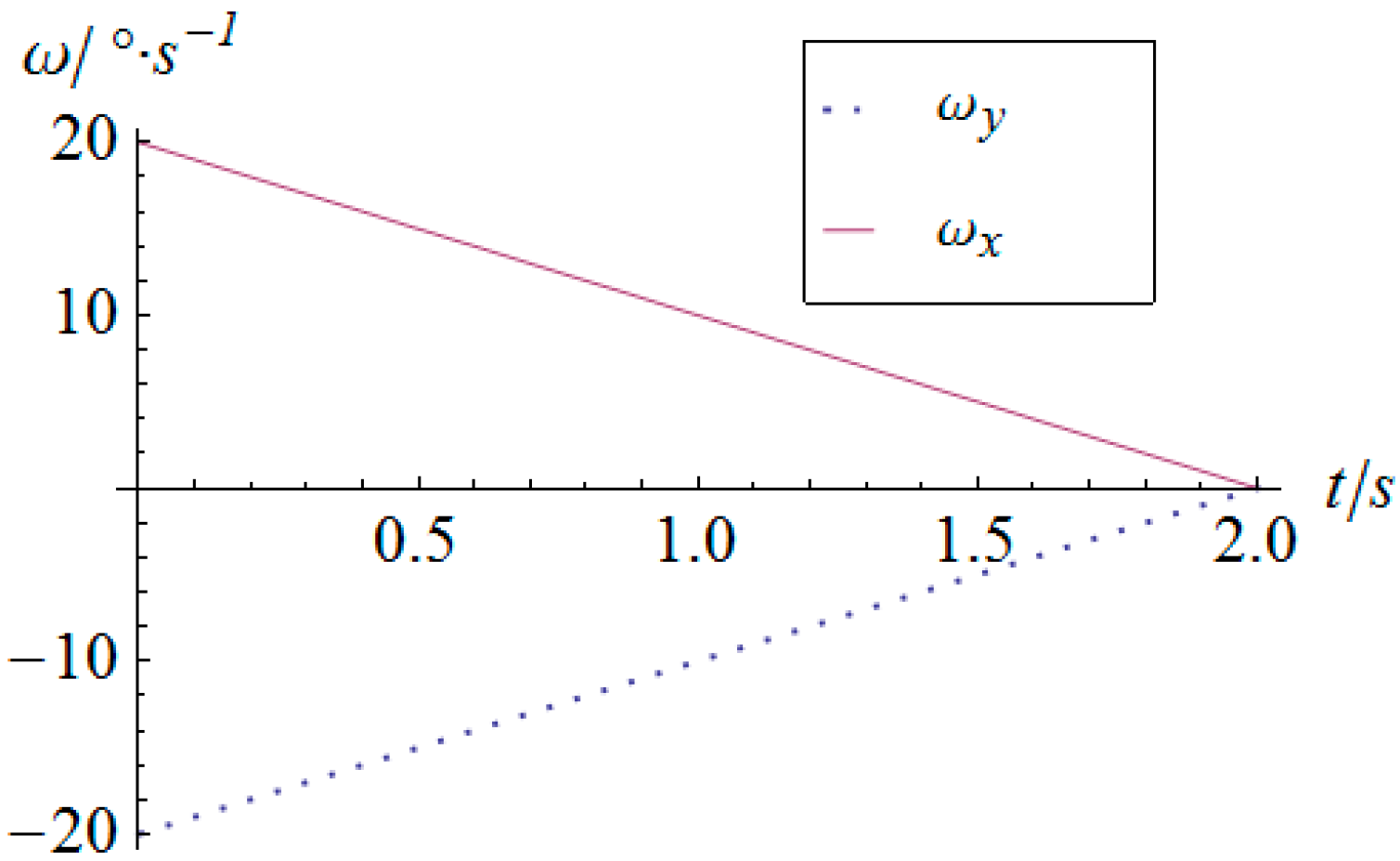
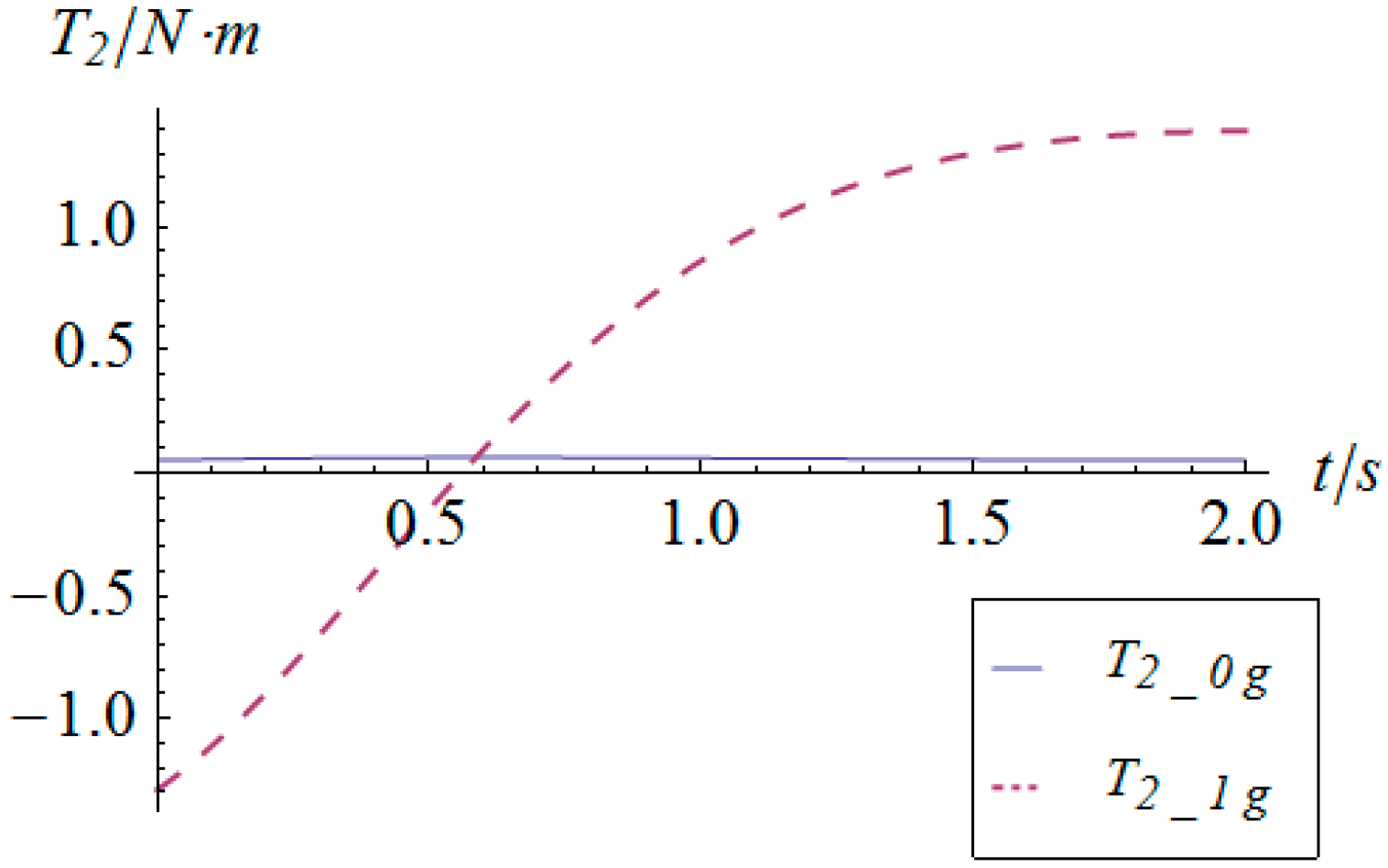
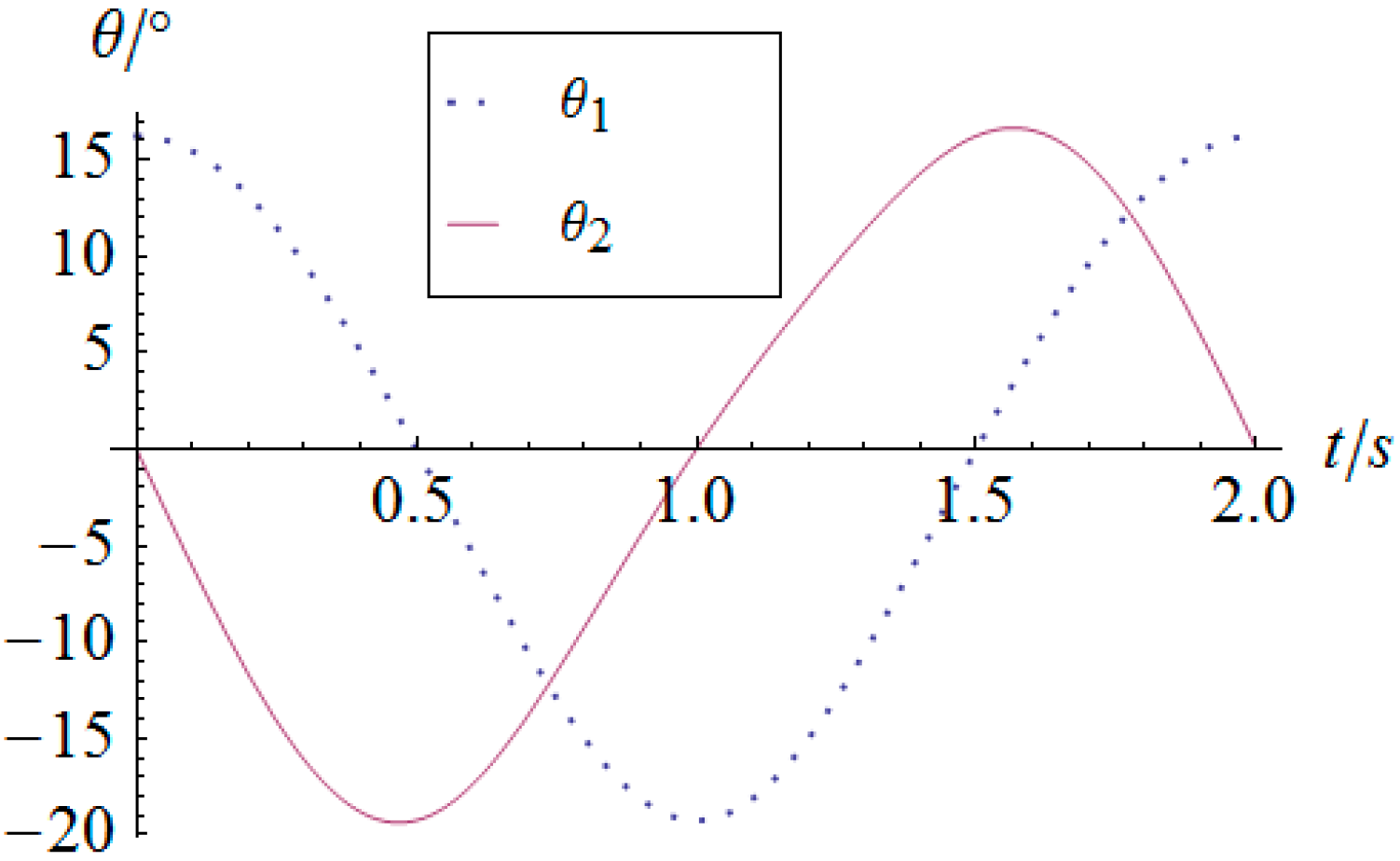
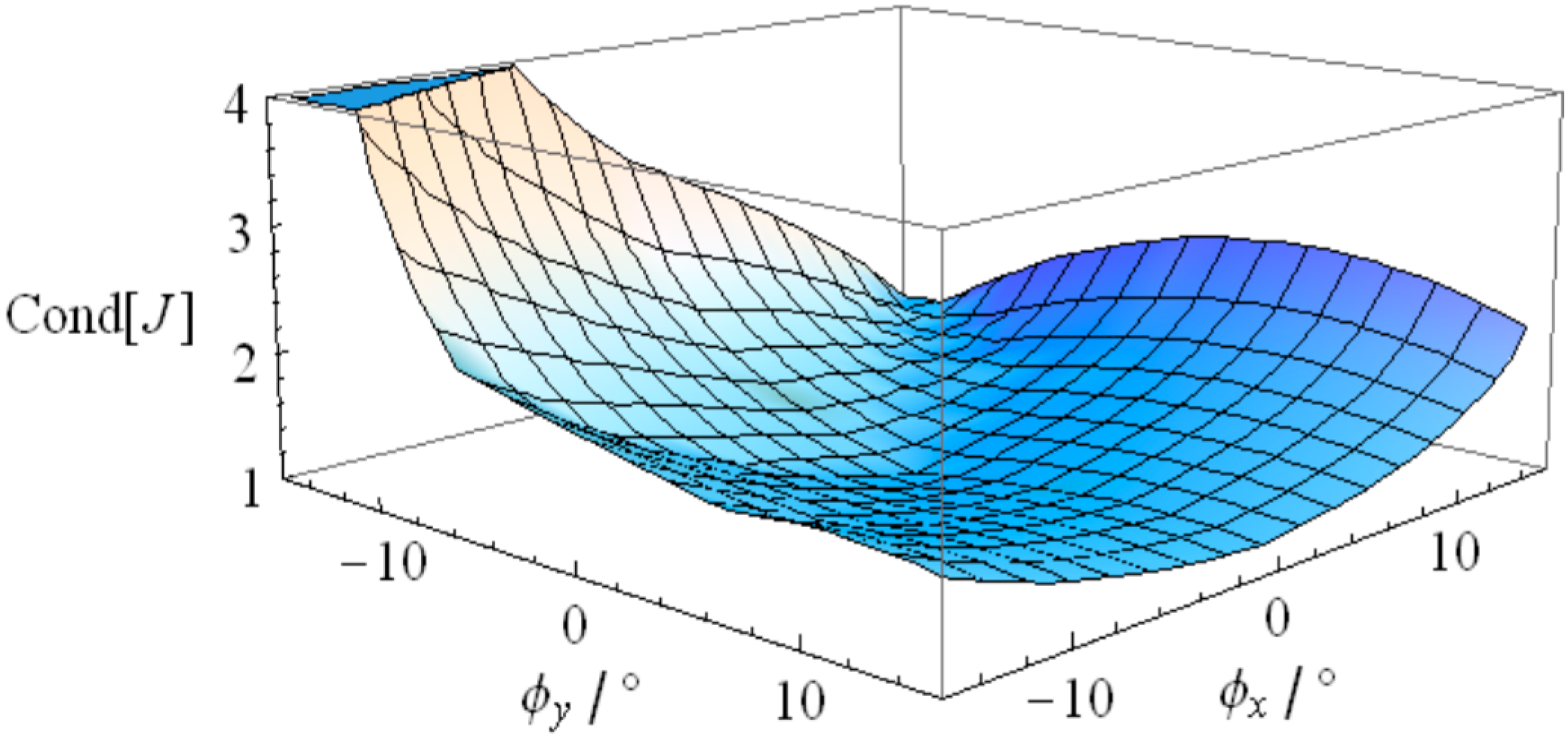
5. Numerical Simulation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Dasgupta, B.; Mruthyunjaya, T.S. The Stewart platform manipulator: A review. Mech. Mach. Theory 2000, 35, 15–40. [Google Scholar] [CrossRef]
- Merlet, J.P. Parallel Robots; Springer: Dordrecht, The Netherlands, 2006. [Google Scholar]
- Zhang, D. Parallel Robotic Machine Tools; Springer: New York, NY, USA, 2010; pp. 127–138. [Google Scholar]
- Coppola, G.; Zhang, D.; Liu, K. A 6-DOF reconfigurable hybrid parallel manipulator. Robot. Comput. Int. Manuf. 2014, 30, 99–106. [Google Scholar] [CrossRef]
- Gwinnett, J.E. Amusement Devices. U.S. Patent No. 1,789,680, 20 January 1931. [Google Scholar]
- Cox, D.J. The Dynamic Modeling and Command Signal Formulation for Parallel Multi-Parameter Robotic Device. Ph.D. Thesis, University of Florda, Gainesville, FL, USA, 1981. [Google Scholar]
- Cox, D.J.; Tesar, D. The Dynamic Model of a 3-DOF Parallel Robotic Shoulder Module. In Proceedings of the 4th International Conference on Advanced Robotics, Columbus, OH, USA, 13–15 June 1989.
- Asada, H.; Granito, J.A. Kinematic and Static Characterization of Wrist Joint and Their Optimal Design. In Proceedings of the IEEE International Conference on Robots and Automation, St. Louis, MO, USA, 25–28 March 1985.
- Gosselin, C.; Angeles, J. The optimum kinematic design of a spherical 3-DOF parallel manipulator. ASME J. Mech. Transm. Autom. Des. 1989, 111, 202–207. [Google Scholar] [CrossRef]
- Kim, W.K.; Tesar, D. Study On Structural Design of Force Reflecting Manual Controllers. In Proceedings of the ASME 21th Biennial Mechanisms Conference, Chicago, IL, USA, 16–19 September 1990.
- Gosselin, C.M.; Humel, J.F. The Agile Eye: A High-Performance Three-Degree-of-Freedom Camera-Orienting Device. In Proceedings of the IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994.
- Gosselin, C.M.; St-Pierre, E. Development and experimentation of a fast 3-DOF camera-orienting device. Int. J. Robot. Res. 1997, 16, 619–630. [Google Scholar] [CrossRef]
- Gosselin, C.M.; St-Pierre, E.; Gagne, M. On the development of the agile eye. IEEE Robot. Autom. Mag. 1996, 3, 29–37. [Google Scholar] [CrossRef]
- Birglen, L.; Gosselin, C.; Pouliot, N.; Monsarrat, B.; Laliberté, T. SHaDe, a new 3-DOF haptic device. IEEE Trans. Robot. Autom. 2002, 18, 166–175. [Google Scholar] [CrossRef]
- Gallardo, J; Rico, J.M.; Frisoli, A.; Checcacci, D.; Bergamasco, M. Dynamics of parallel manipulators by means of screw theory. Mech. Mach. Theory 2003, 38, 1113–1131. [Google Scholar] [CrossRef]
- Zhang, L.J.; Li, Y.Q.; Huang, Z. On the kinematics analysis of a 2-DOF spherical 5R parallel manipulator. China Mech. Eng. 2006, 17, 343–346. [Google Scholar]
- Jame-Bozorgi, E.R.; Yahyapour, I.; Karimi, A.; Masouleh, M.T. Design, Development, Dynamic Analysis and Control of a 2-DOF Spherical Parallel Mechanism. In Proceedings of the Second RSI/ISM International Conference, Tehran, Iran, 15–17 October 2014.
- Kong, X. Reconfiguration analysis of a 2-DOF 3-4R parallel manipulator with orthogonal base and platform. Adv. Reconfigurable Mech. Robot. II 2016, 36, 235–245. [Google Scholar]
- Xu, Y.; Chen, L.; Yan, W.; Yao, J.; Zhao, Y. Motion decoupling analysis of a kind of 2R parallel mechanism with two continuous rotational axes. Mech. Mach. Sci. 2016, 36, 307–313. [Google Scholar]
- Hu, B.; Huang, Z. A family of 2R1T parallel manipulators with intersecting rotational axes. Mech. Mach. Sci. 2016, 36, 287–295. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004; pp. 154–196. [Google Scholar]


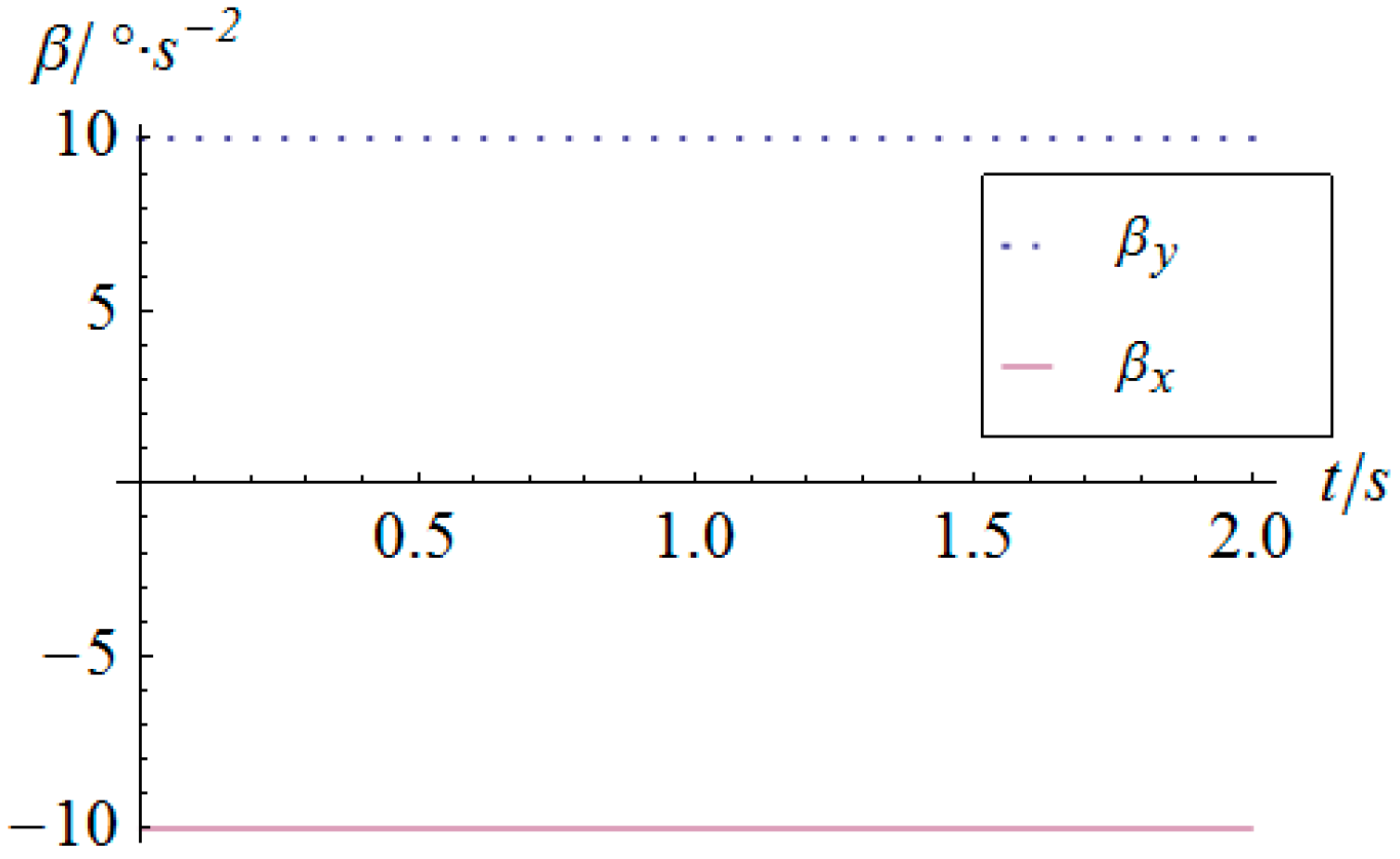
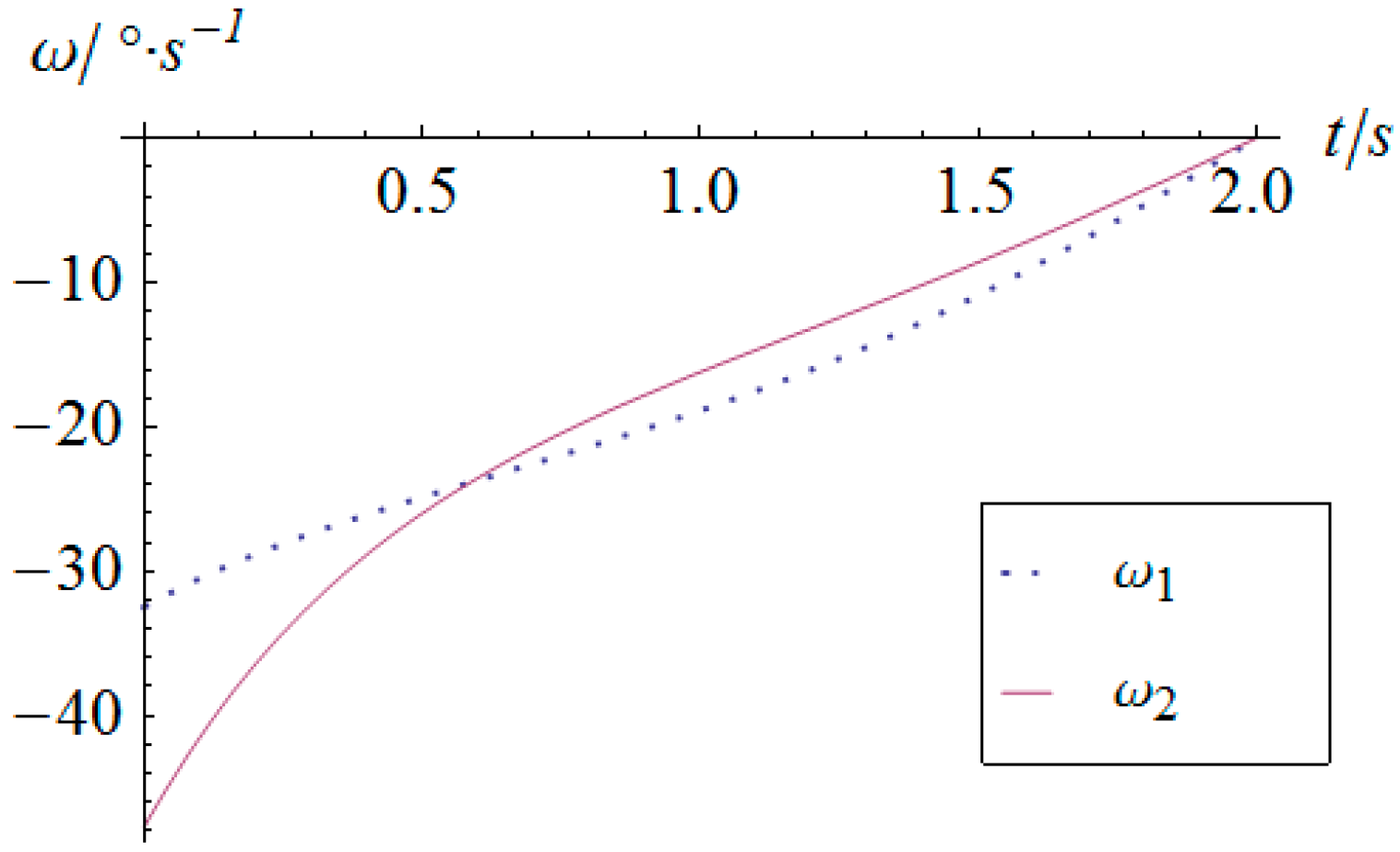
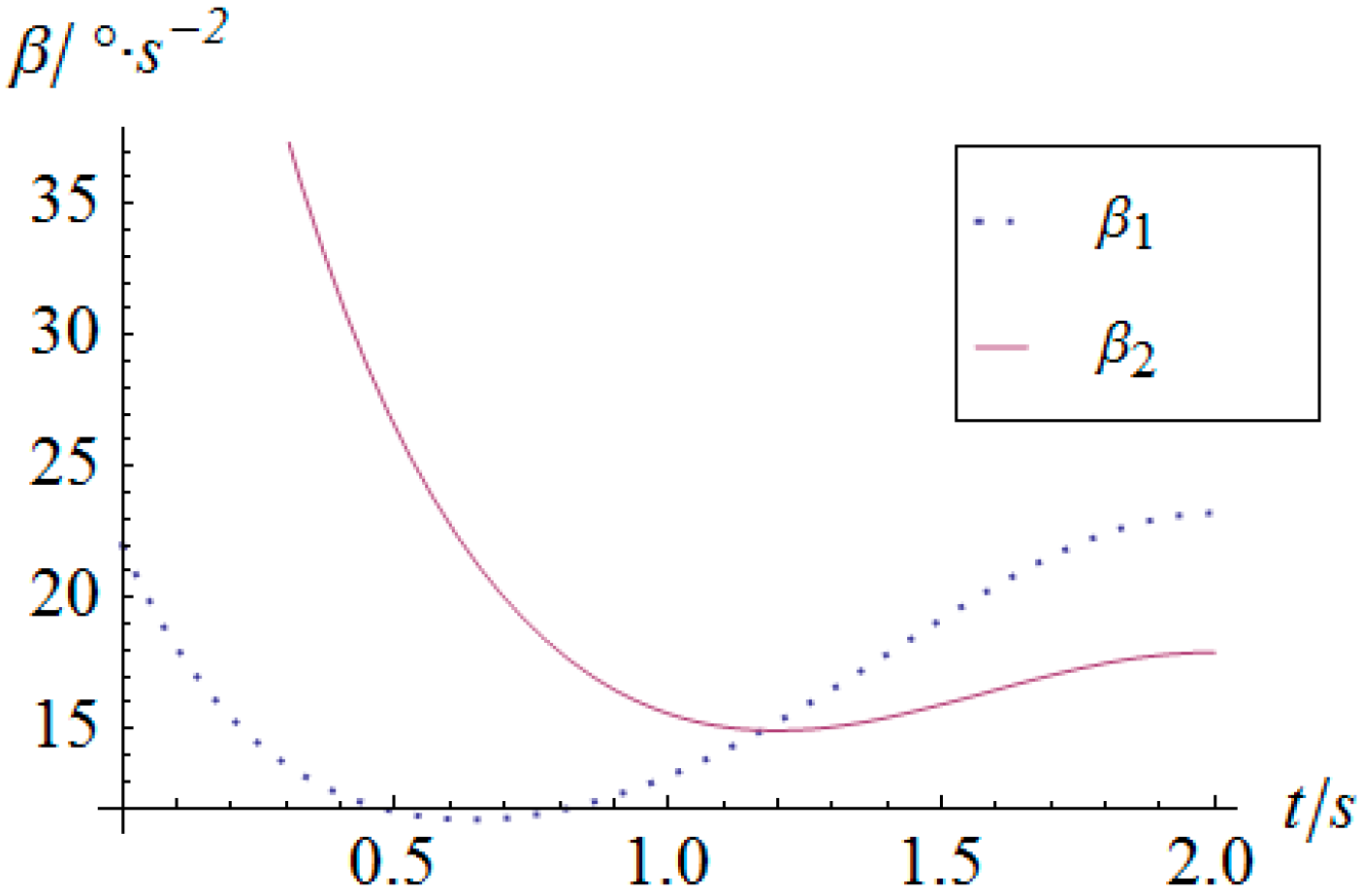
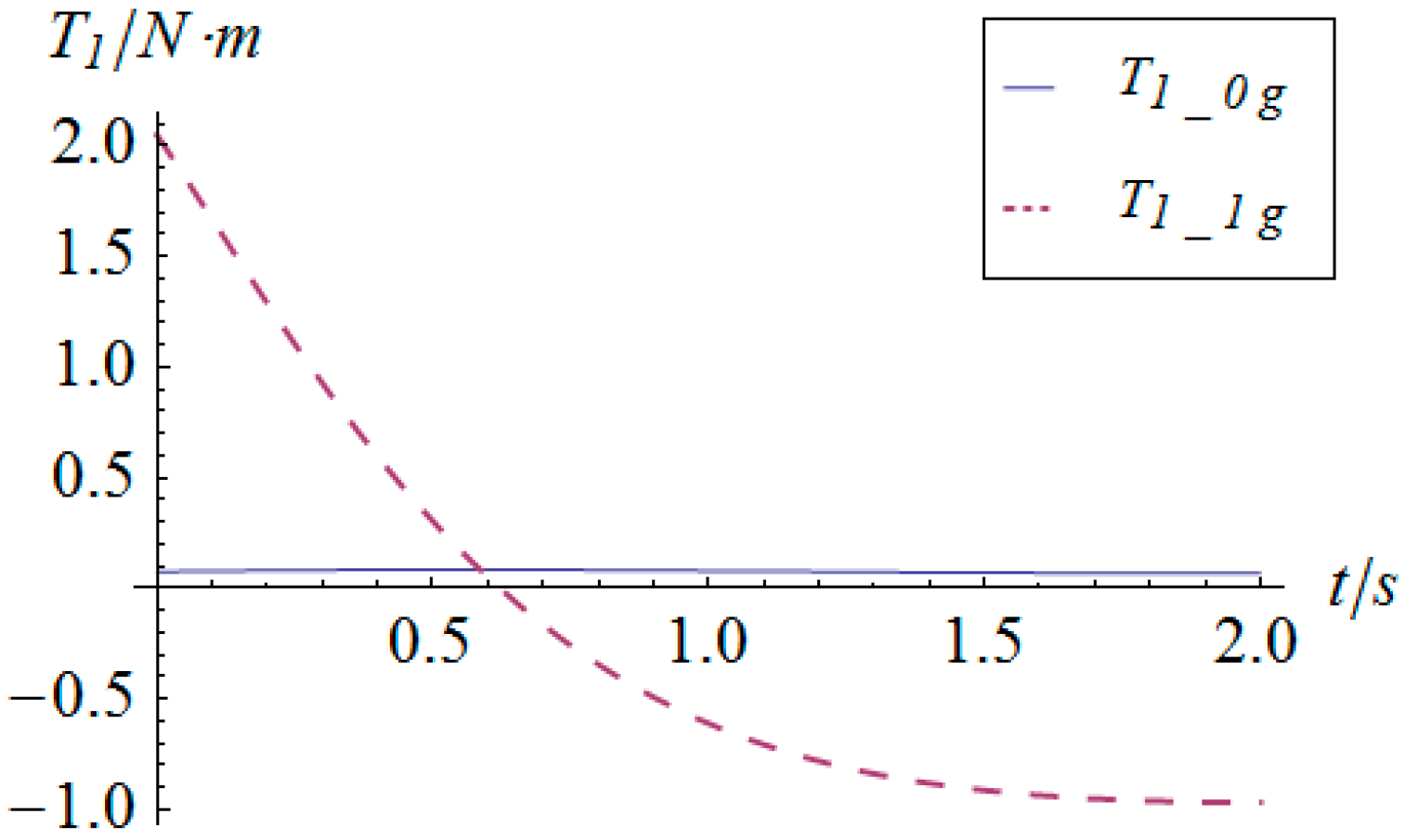




| α1/° | α2/° | β/° | m/kg | g0/N·kg−1 | r/m | h/m | |
|---|---|---|---|---|---|---|---|
| 25 | 30 | 36.87 | 27 | 9.8 | 0.3 | 0.026 | |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, X.; Yang, Y.; Cheng, B. Modeling and Analysis of a 2-DOF Spherical Parallel Manipulator. Sensors 2016, 16, 1485. https://doi.org/10.3390/s16091485
Duan X, Yang Y, Cheng B. Modeling and Analysis of a 2-DOF Spherical Parallel Manipulator. Sensors. 2016; 16(9):1485. https://doi.org/10.3390/s16091485
Chicago/Turabian StyleDuan, Xuechao, Yongzhi Yang, and Bi Cheng. 2016. "Modeling and Analysis of a 2-DOF Spherical Parallel Manipulator" Sensors 16, no. 9: 1485. https://doi.org/10.3390/s16091485






