Dynamic Mode Decomposition of Fast Pressure Sensitive Paint Data
Abstract
:1. Introduction
2. Background
2.1. Dynamic Mode Decomposition
2.2. Acoustic Theory
3. Experimental Framework
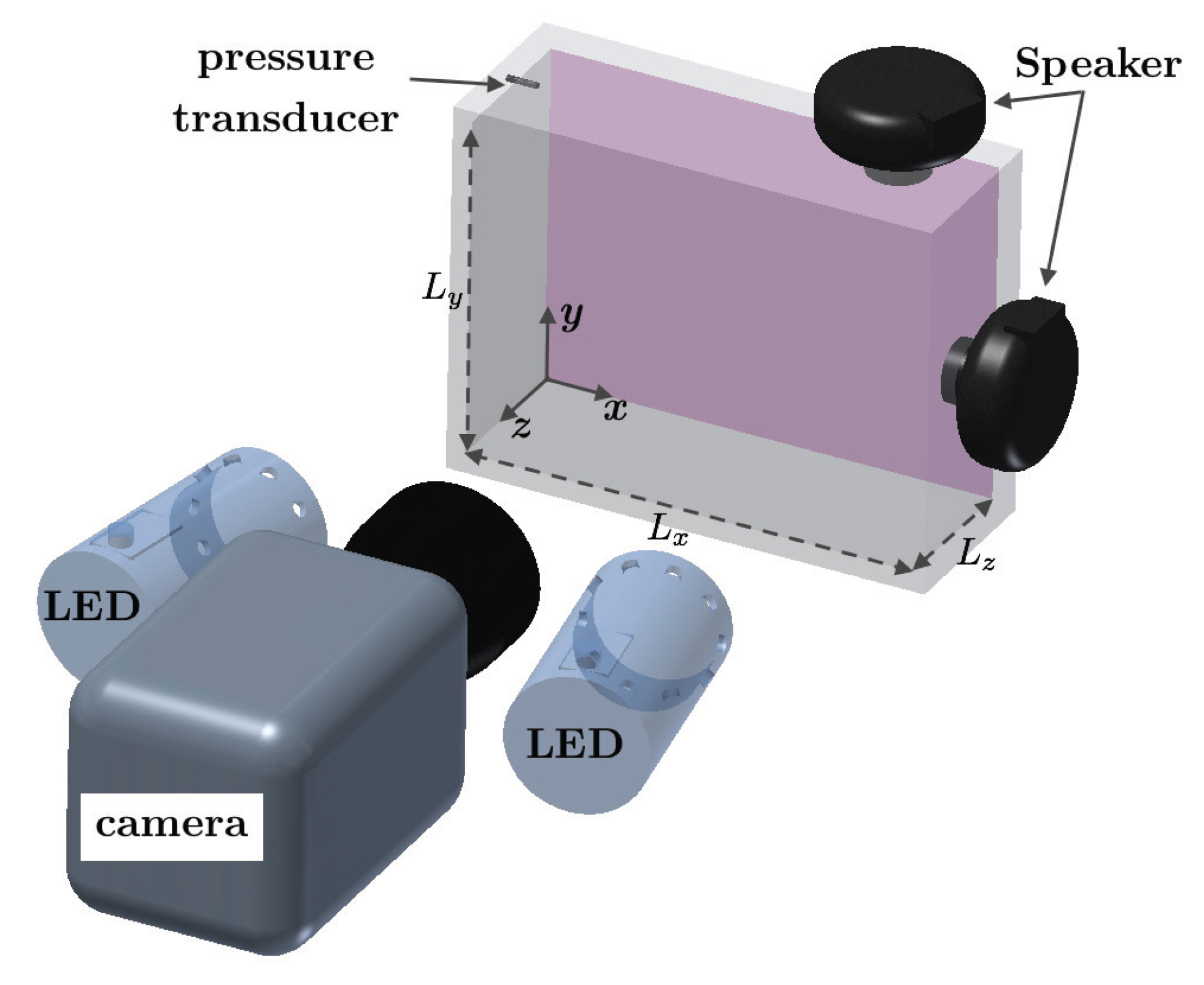
3.1. Apparatus and Instrumentation
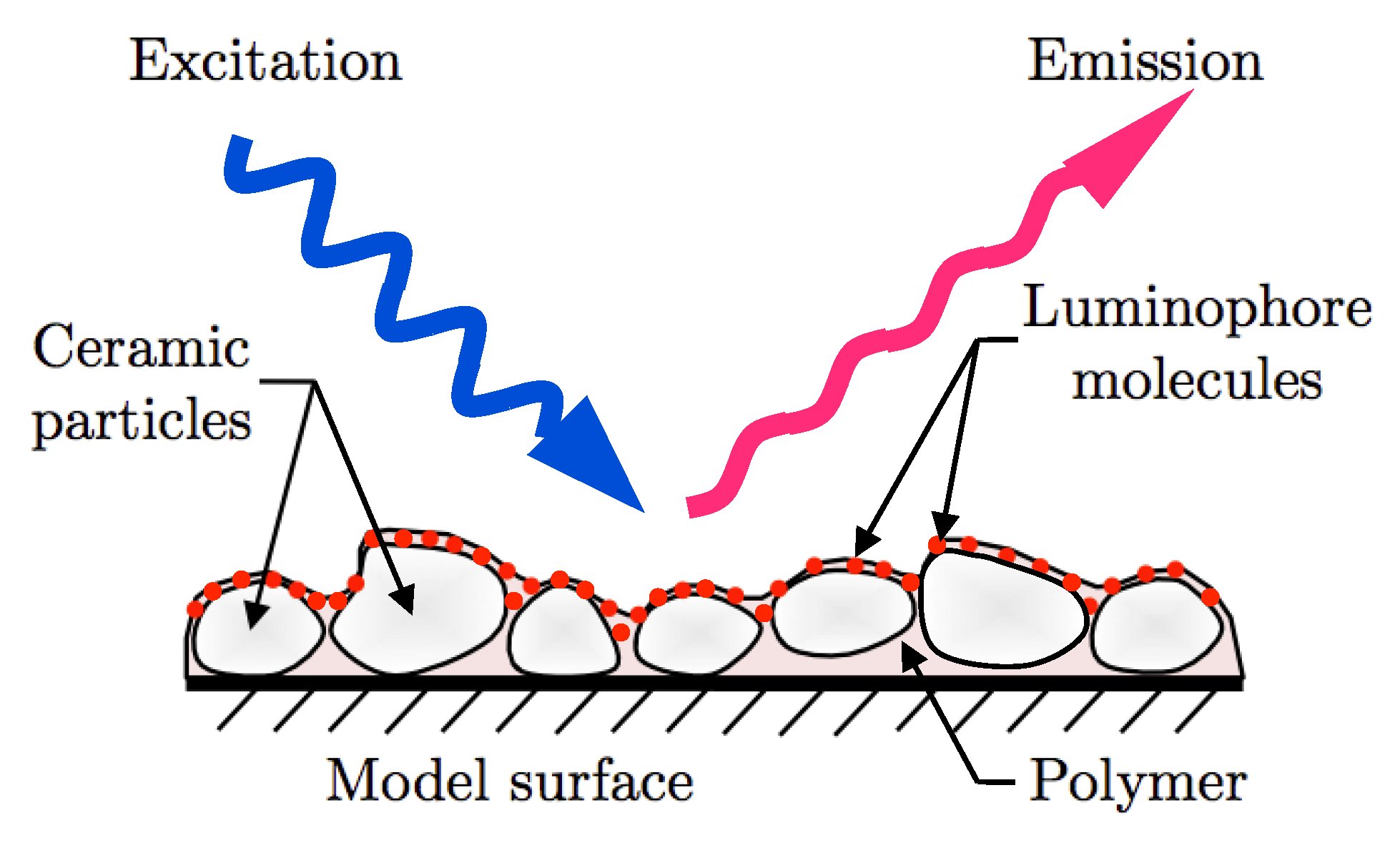
3.2. Pressure Sensitive Paint
3.3. Data Acquisition and Processing
4. Results and Discussion
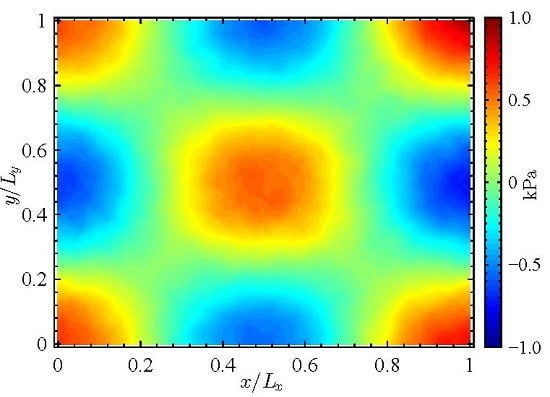
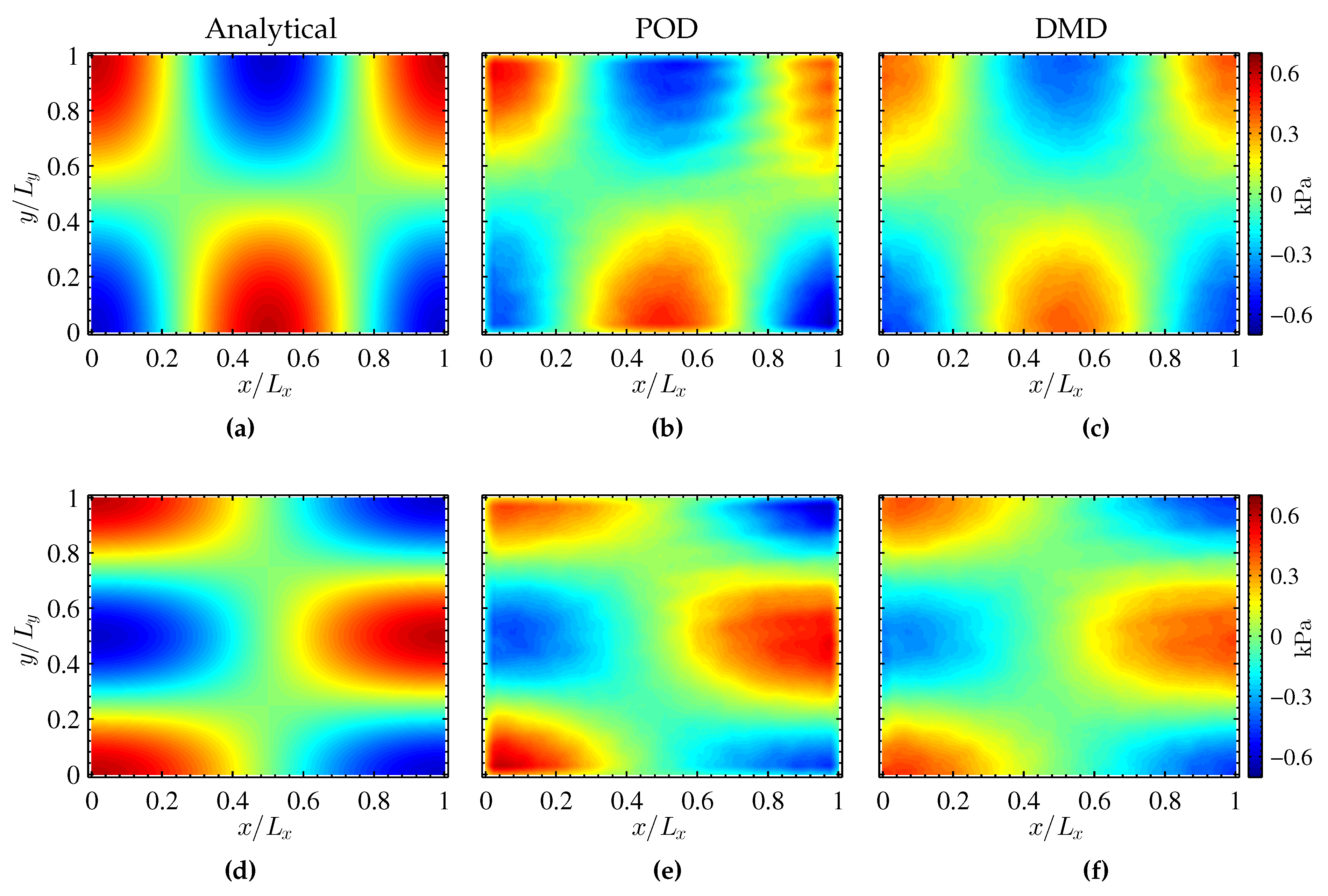
4.1. Mode Shape
4.2. Mode Shape
4.3. Combined Mode Shapes and
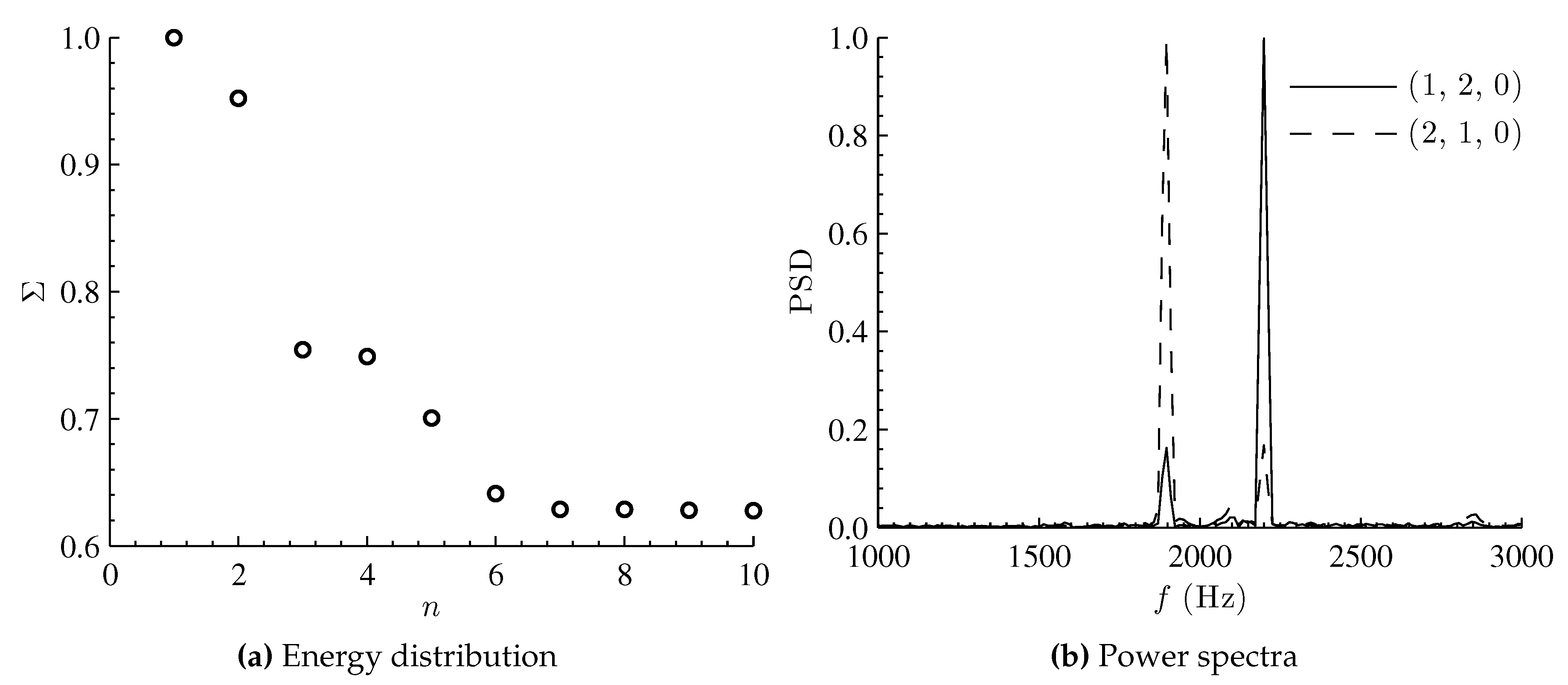
4.3.1. POD Analysis
4.3.2. DMD Analysis
4.3.3. Comparison of POD and DMD
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PSP | Pressure Sensitive Paint |
| PC-PSP | Polymer Ceramic-Pressure Sensitive Paint |
| DMD | Dynamic Mode Decomposition |
| POD | Proper Orthogonal Decomposition |
| SVD | Single Value Decomposition |
| FFT | Fast Fourier Transform |
| LED | Light Emitting Diode |
| CCD | Charge-Coupled Device |
| CMOS | Complementary Metal-Oxide Semiconductor |
References
- Bell, J.H.; Schairer, E.T.; Hand, L.A.; Mehta, R.D. Surface pressure measurements using luminescent coatings. Annu. Rev. Fluid Mech. 2001, 33, 155–206. [Google Scholar] [CrossRef]
- Liu, T.; Sullivan, J.P. Pressure and Temperature Sensitive Paints; Springer: New York, NY, USA, 2005. [Google Scholar]
- Gregory, J.W.; Asai, K.; Kameda, M.; Liu, T.; Sullivan, J.P. A review of pressure-sensitive paint for high-speed and unsteady aerodynamics. J. Aerosp. Eng. 2007, 222, 249–290. [Google Scholar] [CrossRef]
- Gregory, J.W.; Sakaue, H.; Liu, T.; Sullivan, J.P. Fast pressure-sensitive paint for flow and acoustic diagnostics. Annu. Rev. Fluid Mech. 2014, 46, 303–330. [Google Scholar] [CrossRef]
- Pastuhoff, M.; Tillmark, N.; Alfredsson, P.H. Measuring Surface Pressure on Rotating Compressor Blades Using Pressure Sensitive Paint. Sensors 2016, 16, 344. [Google Scholar] [CrossRef] [PubMed]
- Liu, T. Pressure-correction method for low-speed pressure-sensitive paint measurements. AIAA J. 2003, 41, 906–911. [Google Scholar] [CrossRef]
- Gregory, J.W.; Sullivan, J.P.; Wanis, S.; Komerath, N.M. Pressure-sensitive paint as a distributed optical microphone array. J. Acoutical Soc. Am. 2006, 119, 251–261. [Google Scholar] [CrossRef]
- Yorita, D.; Nagai, H.; Asai, K.; Narumi, T. Unsteady PSP technique for measuring naturally-disturbed periodic phenomena. AIAA Paper 2010, 2010, 0307. [Google Scholar]
- Asai, K.; Yorita, D. Unsteady PSP measurement in low-speed flow—Overview of recent advancement at Tohoku University. AIAA Paper 2011, 2011, 0847. [Google Scholar]
- Nakakita, K. Unsteady pressure distribution measurement around 2D-cylinders using pressure-sensitive paint. AIAA Paper 2007, 2007, 3819. [Google Scholar]
- Pastuhoff, M.; Yorita, D.; Asai, K.; Alfredsson, P.H. Enhancing the signal-to-noise ratio of pressure sensitive paint data by singular value decomposition. Meas. Sci. Technol. 2013, 24, 075301. [Google Scholar] [CrossRef]
- Gordeyev, S.; De Lucca, N.; Jumper, E.J.; Hird, K.; Juliano, T.J.; Gregory, J.W.; Thordahl, J.; Wittich, D.J. Comparison of unsteady pressure fields on turrets with different surface features using pressure-sensitive paint. Exp. Fluids 2014, 55, 1–20. [Google Scholar] [CrossRef]
- Peng, D.; Wang, S.; Liu, Y. Fast PSP measurements of wall-pressure fluctuation in low-speed flows: Improvements using proper orthogonal decomposition. Exp. Fluids 2016, 57, 1–17. [Google Scholar] [CrossRef]
- Rowley, C.W.; Mezić, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Ruhe, A. Rational Krylov sequence methods for eigenvalue computation. Linear Algebra Appl. 1984, 58, 391–405. [Google Scholar] [CrossRef]
- Pierce, A.D. Acoustics-–An Introduction to Its Physical Principles and Applications; Acoustical Society of America: Melville, NY, USA, 1989. [Google Scholar]
- Pandey, A.; Gregory, J.W. Step Response Characteristics of Polymer/Ceramic Pressure-Sensitive Paint. Sensors 2015, 15, 22304–22324. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.; Gregory, J.W. Frequency response characteristics of polymer/ceramic pressure-sensitive paint. AIAA J. 2016, 54, 174–185. [Google Scholar] [CrossRef]
- Disotell, K.J.; Gregory, J.W. Measurement of transient acoustic fields using a single-shot pressure-sensitive paint system. Rev. Sci. Instrum. 2011, 82, 075112:1–075112:8. [Google Scholar] [CrossRef] [PubMed]




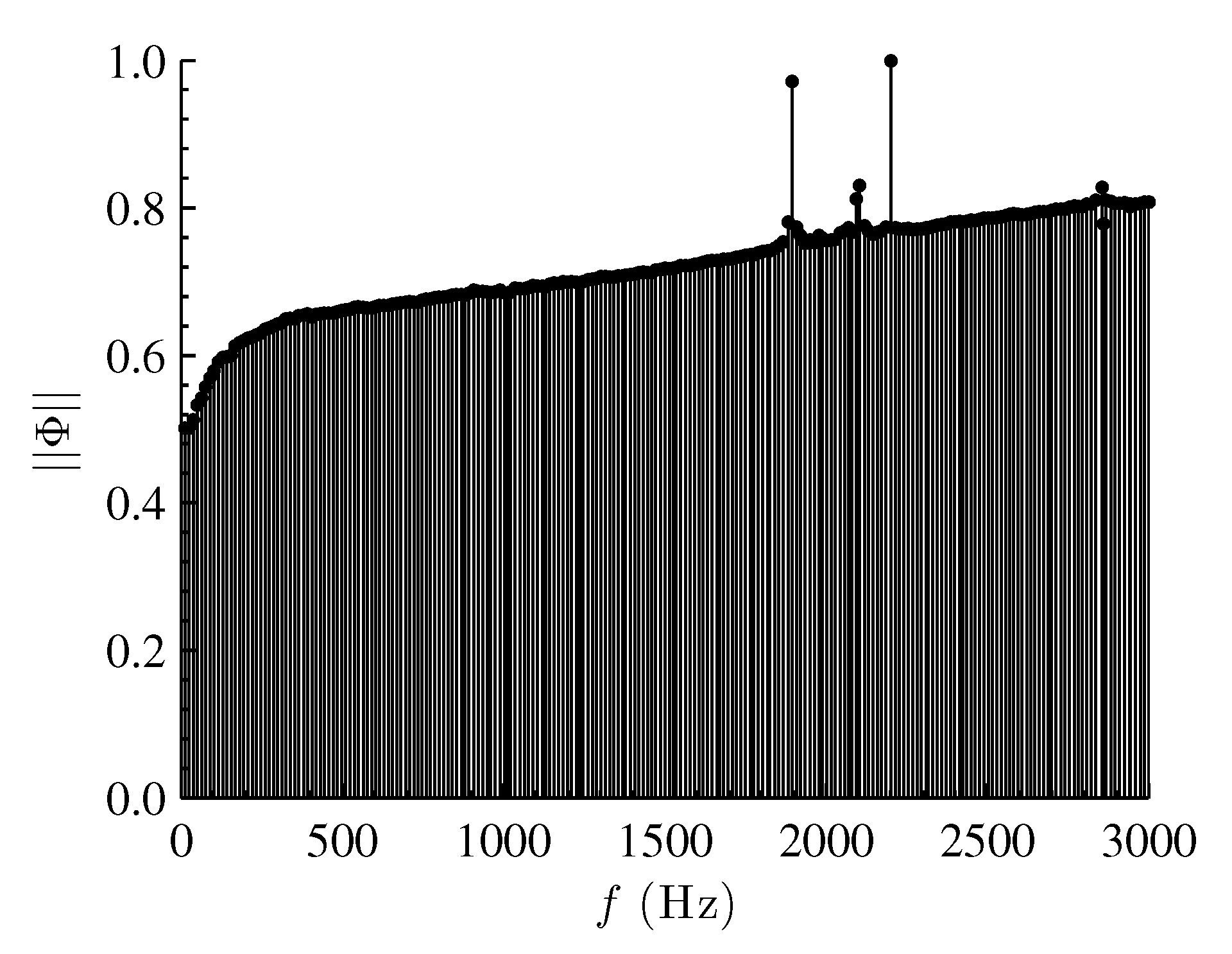
| Speaker | Mode | (Hz) | (Hz) | Cycles/Record | SPL (dB) |
|---|---|---|---|---|---|
| Top | 1300 | 5100 | 127 | 151 | |
| Side | 2594 | 8000 | 162 | 148 | |
| Top & Side | & | 1897 & 2202 | 6600 | 144 & 167 | 147 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, M.Y.; Pandey, A.; Gregory, J.W. Dynamic Mode Decomposition of Fast Pressure Sensitive Paint Data. Sensors 2016, 16, 862. https://doi.org/10.3390/s16060862
Ali MY, Pandey A, Gregory JW. Dynamic Mode Decomposition of Fast Pressure Sensitive Paint Data. Sensors. 2016; 16(6):862. https://doi.org/10.3390/s16060862
Chicago/Turabian StyleAli, Mohd Y., Anshuman Pandey, and James W. Gregory. 2016. "Dynamic Mode Decomposition of Fast Pressure Sensitive Paint Data" Sensors 16, no. 6: 862. https://doi.org/10.3390/s16060862