Online Kinematic and Dynamic-State Estimation for Constrained Multibody Systems Based on IMUs
Abstract
:1. Introduction
- Accelerometers are suitable for the analysis of vibrations. However, precise measurements of the position and velocity of a body exclusively from their signals is not practical because of the large errors that result from integrating accelerations.
- Encoders ensure noise-free measurements of the angular position of an axle in a given rotatory motion. It is relatively easy to determine angular velocity by differentiating such signals with respect to time. The main disadvantage of these sensors involves their physical placement. It is not always possible to gain access to the part of a machine where the sensor should be positioned. This is especially important in biomechanics. Furthermore, encoders are typically rather expensive and bulky devices.
- Computer vision systems: Motion capture based on computer vision is increasing becoming widespread in recent years due to its suitability for remote, non-contact sensing. However, the systems invariably require an accurate calibration process [20], and expensive imaging sensors may be needed if the system under study moves at high speed. A major drawback of computer vision is the line-of-sight restriction.
- Inertial Measurement Units (IMUs): These sensors arise as useful alternative. Typically the combination of gyroscopes together with accelerometers and magnetometers provides high-rate, accurate information on three-dimensional motion. IMUs can offer greater placement flexibility than encoders can, and also provide more precise measurement of angular accelerations because the gyroscope output needs to be differentiated only once.
2. Theoretical Background
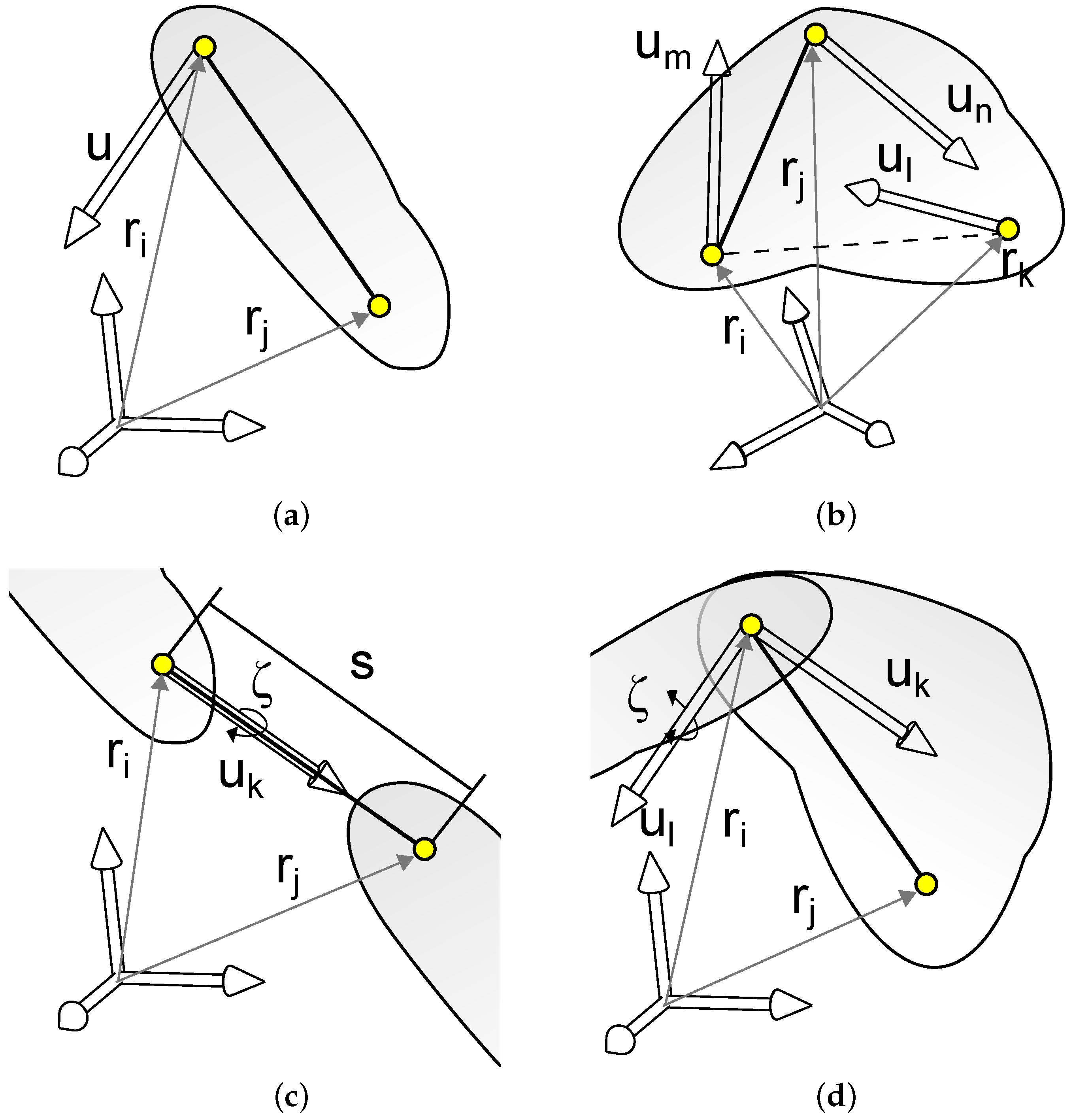
- Each solid must contain, at least, one point and one vector, or two points. If this condition is not met, it is not possible to determine the orientation of such body.
- For the revolute joints to be considered implicitly, it is strongly recommended that a point be placed at each joint.
- In the case of prismatic joints, at least three aligned points are necessary: two for defining the axis of the displacement and one more for the slider. Alternatively, these kinds of joints can be also defined by using two points and a vector.
- As many additional points can be used as desired.
3. Methodology
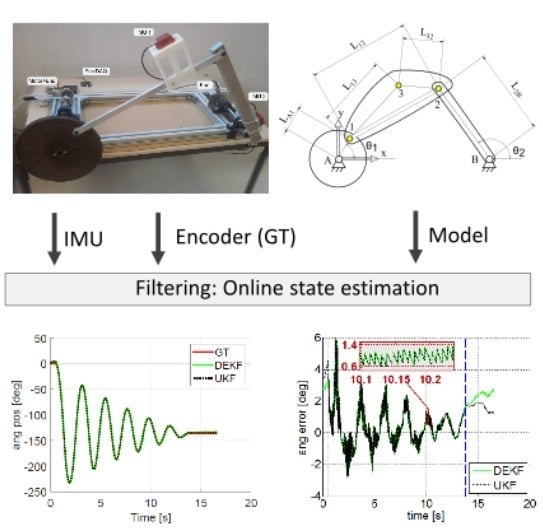
3.1. Kinematic Modeling of the Experimental Testbed

3.2. Modelization of Virtual Sensors
3.3. Dynamical Modeling and State Estimation
3.3.1. Discrete Extended Kalman Filter (DEKF)
3.3.2. Unscented Kalman Filter (UKF)
4. Experimental Setup
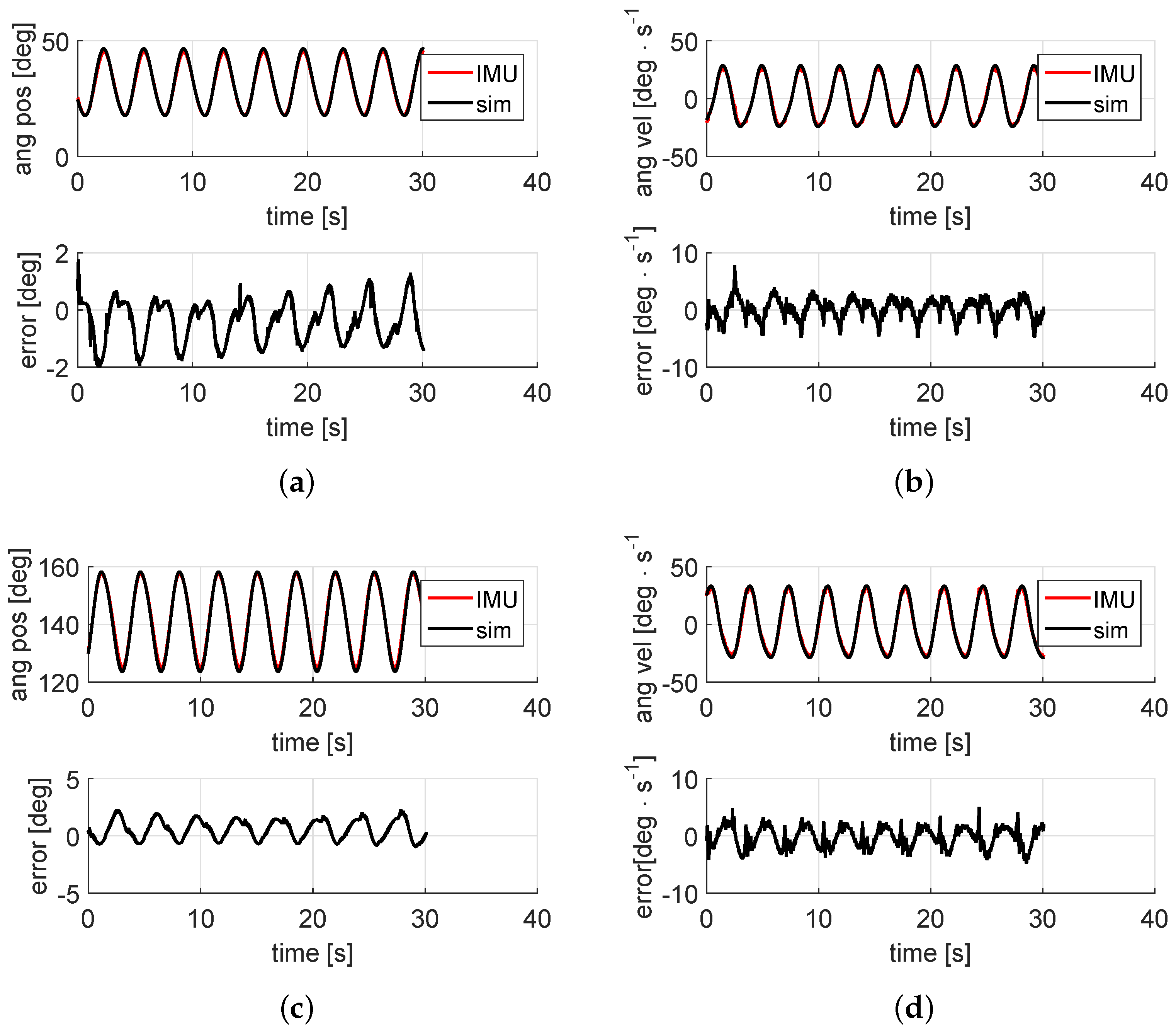
5. Results and Discussion
5.1. KinematicS-Based Estimation
5.2. Dynamics-Based Estimation
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ceccarelli, M. Renaissance of machines in Italy: From Brunelleschi to Galilei through Francesco di Giorgio and Leonardo. Mech. Mach. Theory 2008, 43, 1530–1542. [Google Scholar] [CrossRef]
- Ceccarelli, M.; Koetsier, T. Burmester and Allievi: A Theory and Its Application for Mechanism Design at the End of 19th Century. J. Mech. Design 2008, 130, 072301. [Google Scholar] [CrossRef]
- García de Jalón, J.; Bayo, E. Kinematic and Dynamic Simulation of Multibody Systems: The Real Time Challenge; Springer-Verlag: New York, NY, USA, 1994. [Google Scholar]
- Cuadrado, J.; Cardenal, J.; Bayo, E. Modeling and Solution Methods for Efficient Real-Time Simulation of Multibody Dynamics. Multibody Syst. Dyn. 1997, 1, 259–280. [Google Scholar] [CrossRef]
- Schiehlen, W. Multibody system dynamics: Roots and perspectives. Multibody Syst. Dyn. 1997, 1, 149–188. [Google Scholar] [CrossRef]
- Shabana, A.A. Flexible multibody dynamics: Review of past and recent developments. Multibody Syst. Dyn. 1997, 1, 189–222. [Google Scholar] [CrossRef]
- Ulrich, S.; Sasiadek, J.Z. Extended Kalman filtering for flexible joint space robot control. In Proceedings of the 2011 American Control Conference, San Francisco, CA, USA, 29 June–1 July 2011; pp. 1021–1026.
- Bauchau, O.A.; Laulusa, A. Review of contemporary approaches for constraint enforcement in multibody systems. J. Comput. Nonlinear Dyn. 2008, 3, 011005. [Google Scholar] [CrossRef]
- Machado, M.; Moreira, P.; Flores, P.; Lankarani, H.M. Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mech. Mach. Theory 2012, 53, 99–121. [Google Scholar] [CrossRef] [Green Version]
- González, M.; González, F.; Dopico, D.; Luaces, A. On the effect of linear algebra implementations in real-time multibody system dynamics. Comput. Mech. 2008, 41, 607–615. [Google Scholar] [CrossRef]
- Torres-Moreno, J.L.; Blanco-Claraco, J.L.; Giménez, A.; López-Martínez, J. A comparison of Algorithms for Sparse Matrix Factoring and Variable Reordering aimed at Real-time Multibody Dynamic Simulation. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Catalonia, Spain, 29 June–2 July 2013.
- Uchida, T.; Callejo, A.; García de Jalón, J.; McPhee, J. On the Gröbner basis triangularization of constraint equations in natural coordinates. Multibody Syst. Dyn. 2014, 31, 371–392. [Google Scholar] [CrossRef]
- Cuadrado, J.; Gutiérrez, R.; Naya, M.; González, M. Experimental Validation of a Flexible MBS Dynamic Formulation through Comparison between Measured and Calculated Stresses on a Prototype Car. Multibody Syst. Dyn. 2004, 11, 147–166. [Google Scholar] [CrossRef]
- Cuadrado, J.; Dopico, D.; Perez, J.; Pastorino, R. Automotive observers based on multibody models and the extended Kalman filter. Multibody Syst. Dyn. 2012, 27, 3–19. [Google Scholar] [CrossRef]
- Uchida, T.; McPhee, J. Driving simulator with double-wishbone suspension using efficient block-triangularized kinematic equations. Multibody Syst. Dyn. 2012, 28, 331–347. [Google Scholar] [CrossRef]
- Jain, A. Unified formulation of dynamics for serial rigid multibody systems. J. Guid. Control Dyn. 1991, 14, 531–542. [Google Scholar] [CrossRef]
- López-Martínez, J.; García-Vallejo, D.; Giménez-Fernández, A.; Torres-Moreno, J.L. A Flexible Multibody Model of a Safety Robot Arm for Experimental Validation and Analysis of Design Parameters. J. Comput. Nonlinear Dyn. 2013, 9, 11003-1–11003-10. [Google Scholar] [CrossRef]
- Sherman, M.A.; Seth, A.; Delp, S.L. Simbody: Multibody dynamics for biomedical research. Procedia IUTAM 2011, 2, 241–261. [Google Scholar] [CrossRef] [PubMed]
- Lugrís, U.; Carlín, J.; Pàmies-Vilà, R.; Font-Llagunes, J.; Cuadrado, J. Solution methods for the double-support indeterminacy in human gait. Multibody Syst. Dyn. 2013, 30, 247–263. [Google Scholar] [CrossRef]
- Zhang, Z. A flexible new technique for camera calibration. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 1330–1334. [Google Scholar] [CrossRef]
- Palomba, I.; Richiedei, D.; Trevisani, A. Simultaneous estimation of kinematic state and unknown input forces in rigid-link multibody systems. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Lisbon, Portugal, 25–27 June 2015; pp. 229–238.
- Bouvier, B.; Duprey, S.; Claudon, L.; Dumas, R.; Savescu, A. Upper Limb Kinematics Using Inertial and Magnetic Sensors: Comparison of Sensor-to-Segment Calibrations. Sensors 2015, 15, 18813–18833. [Google Scholar] [CrossRef] [PubMed]
- Seel, T.; Raisch, J.; Schauer, T. IMU-Based Joint Angle Measurement for Gait Analysis. Sensors 2014, 14, 6891–6909. [Google Scholar] [CrossRef] [PubMed]
- Young, A. Comparison of Orientation Filter Algorithms for Realtime Wireless Inertial Posture Tracking. In Proceedings of the 2009 Sixth International Workshop on Wearable and Implantable Body Sensor Networks, Berkeley, CA, USA, 3–5 June 2009; pp. 59–64.
- Cooper, G.; Sheret, I.; McMillian, L.; Siliverdis, K.; Sha, N.; Hodgins, D.; Kenney, L.; Howard, D. Inertial sensor-based knee flexion/extension angle estimation. J. Biomech. 2009, 42, 2678–2685. [Google Scholar] [CrossRef] [PubMed]
- Wittmann, R.; Hildebrandt, A.C.; Wahrmann, D.; Rixen, D.; Buschmann, T. State Estimation for Biped Robots Using Multibody Dynamics. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015.
- Pastorino, R.; Richiedei, D.; Cuadrado, J.; Trevisani, A. State estimation using multibody models and non-linear Kalman filters. Int. J. Non-Linear Mech. 2013, 53, 83–90. [Google Scholar] [CrossRef]
- Serna, M.; Avilés, R.; García de Jalón, J. Dynamic analysis of plane mechanisms with lower pairs in basic coordinates. Mech. Mach. Theory 1982, 17, 397–403. [Google Scholar] [CrossRef]
- Wheeler, J.A.; Taylor, E.F. Spacetime Physics; WH Freeman: San Francisco, CA, USA, 1966. [Google Scholar]
- Raven, F. Velocity and acceleration analysis of plane and space mechanisms by independent-position equations. J. Appl. Mech. Trans. ASME 1958, 80, 1–6. [Google Scholar]
- Sanjurjo, E.; Blanco, J.L.; Torres, J.L.; Naya, M.Á. Testing the efficiency and accuracy of multibody-based state observers. In Proceedings of the ECCOMAS Thematic Conference on Multibody Dynamics, Lisbon, Portugal, 25–27 June 2015.
- Wan, E.; van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. In Proceedings of the IEEE Adaptive Systems for Signal Processing, Communications, and Control Symposium, Lake Louise, AB, Canada, 1–4 October 2000; pp. 153–158.
- MAPIR Lab (University of Málaga), ARM Group (University of Almería). Open Mobile Robot Arquitecture (OpenMORA). Available online: http://sourceforge.net/projects/openmora (accessed on 3 March 2016).
- Gonzalez-Monroy, J.; Blanco, J.L.; González-Jiménez, J. An Open Source Framework for Simulating Mobile Robotics Olfaction. In Proceedings of the 15th International Symposium on Olfaction and Electronic Nose (ISOEN) ISOCS (International Society for Olfaction and Chemical Sensing), Daegu, Korea, 2–5 July 2013.
- Torres-Moreno, J.L.; Blanco, J.L.; Bellone, M.; Rodriguez, F.; Giménez-Fernández, A.; Reina, G. A proposed software framework aimed at energy-efficient autonomous driving of electric vehicles. In Proceedings of the International Conference on Simulation, Modelling, and Programming for Autonomous Robots (SIMPAR 2014), Bergamo, Italy, 20–23 October 2014.





| Variable | IMU 1 | IMU 2 | Enc 1 | Model Coord. |
|---|---|---|---|---|
| Acceleration () | accx,accz | - | - | , |
| Pitch angle () | φ | ψ | - | - |
| Pitch velocity () | - | - | ||
| Angular position () | - | - | , | |
| Angular velocity () | - | - | , |
| Symbol | Description |
|---|---|
| Vector of independent coordinates | |
| Vector of dependent coordinates | |
| Constraint equations | |
| Jacobian of Φ with respect to q | |
| Mass matrix | |
| Vector of generalized forces | |
| Real value and estimation of the filter state vector | |
| Estimation mean at time step k, before and after the update stage | |
| Estimation covariance at time step k, before and after the update stage | |
| Transition model and its Jacobian w.r.t. | |
| Observation (sensor) model and its Jacobian w.r.t. | |
| Sensor measurements at time step k | |
| Covariance matrix of system transition ("plant") noise | |
| Covariance matrix of sensors noise | |
| Kalman gain matrix | |
| The unit matrix |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torres-Moreno, J.L.; Blanco-Claraco, J.L.; Giménez-Fernández, A.; Sanjurjo, E.; Naya, M.Á. Online Kinematic and Dynamic-State Estimation for Constrained Multibody Systems Based on IMUs. Sensors 2016, 16, 333. https://doi.org/10.3390/s16030333
Torres-Moreno JL, Blanco-Claraco JL, Giménez-Fernández A, Sanjurjo E, Naya MÁ. Online Kinematic and Dynamic-State Estimation for Constrained Multibody Systems Based on IMUs. Sensors. 2016; 16(3):333. https://doi.org/10.3390/s16030333
Chicago/Turabian StyleTorres-Moreno, José Luis, José Luis Blanco-Claraco, Antonio Giménez-Fernández, Emilio Sanjurjo, and Miguel Ángel Naya. 2016. "Online Kinematic and Dynamic-State Estimation for Constrained Multibody Systems Based on IMUs" Sensors 16, no. 3: 333. https://doi.org/10.3390/s16030333