Analysis of Abnormal Intra-QRS Potentials in Signal-Averaged Electrocardiograms Using a Radial Basis Function Neural Network
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Acquisition
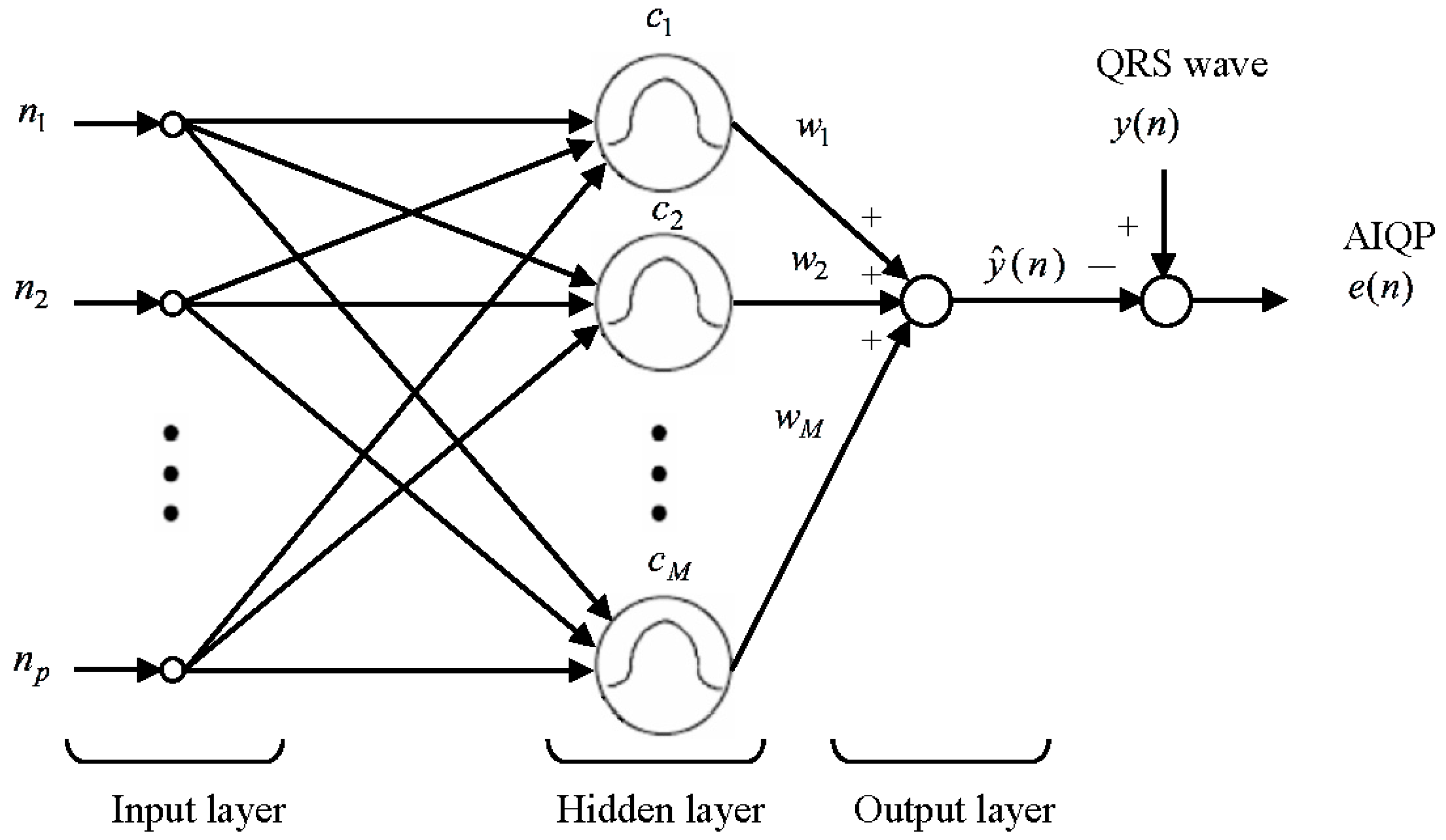
2.2. RBF Neural Network for the AIQP Analysis
2.3. RBF Center Locations Determined through an Orthogonal Least Squares Algorithm
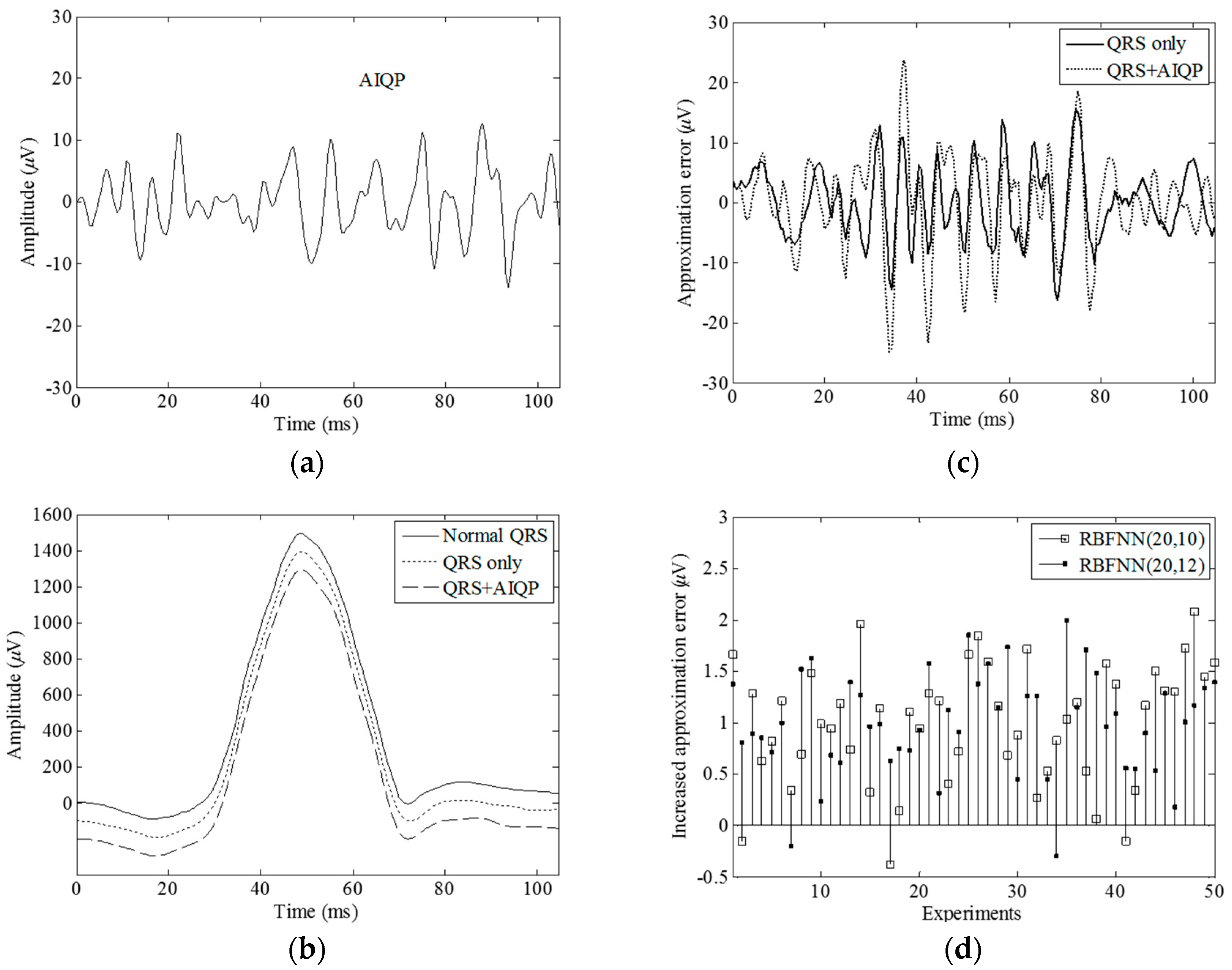
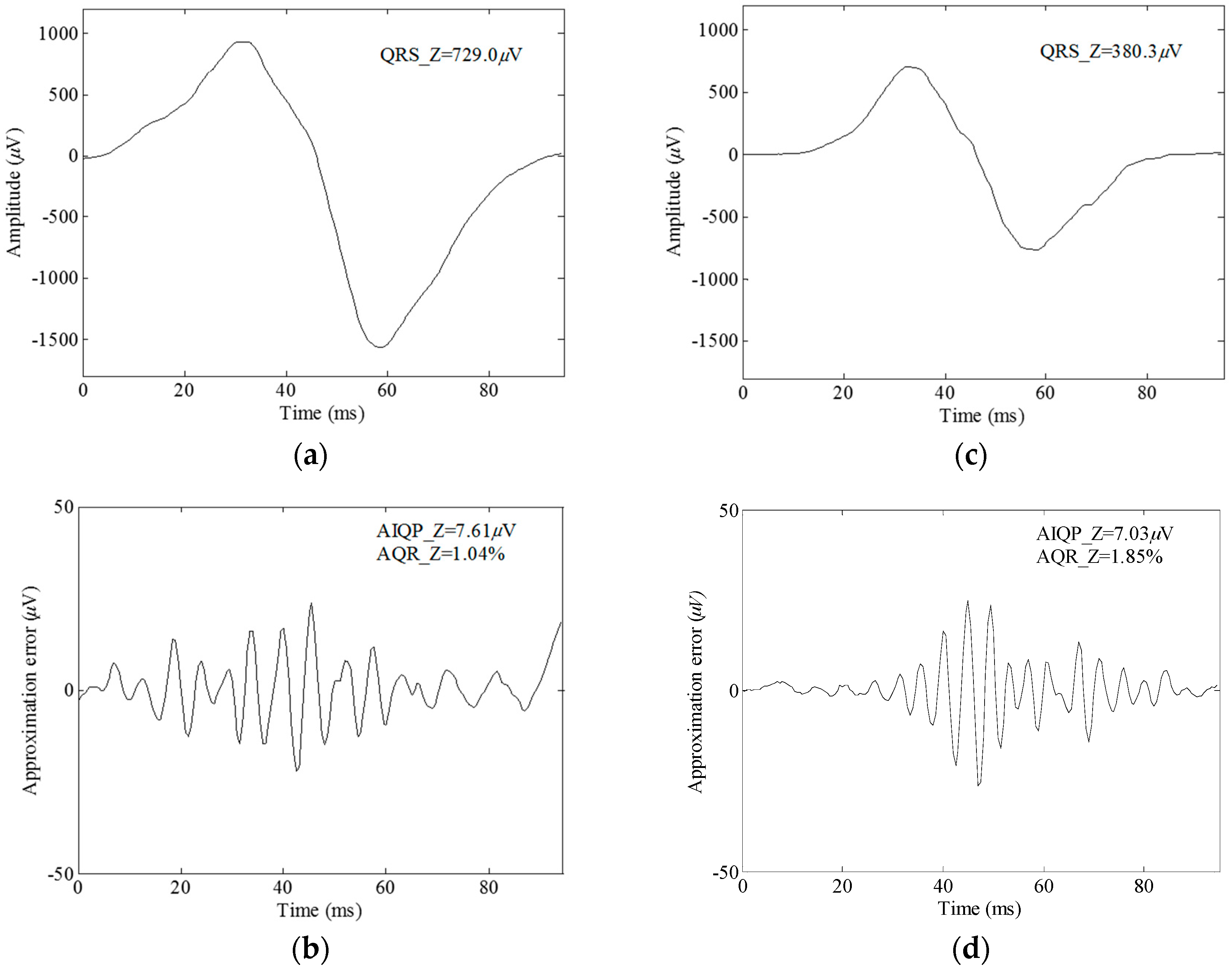
2.4. Definition of AIQP
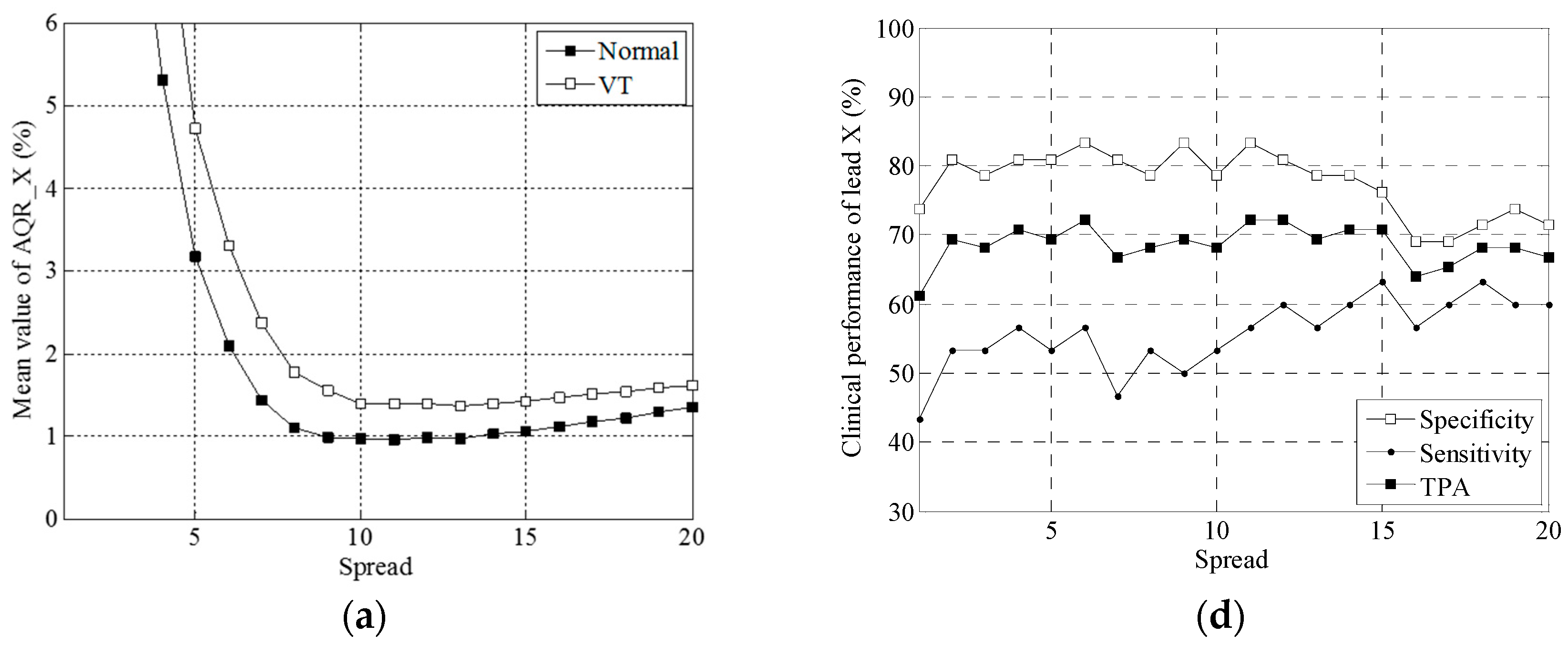
2.5. Statistical Approaches
3. Results
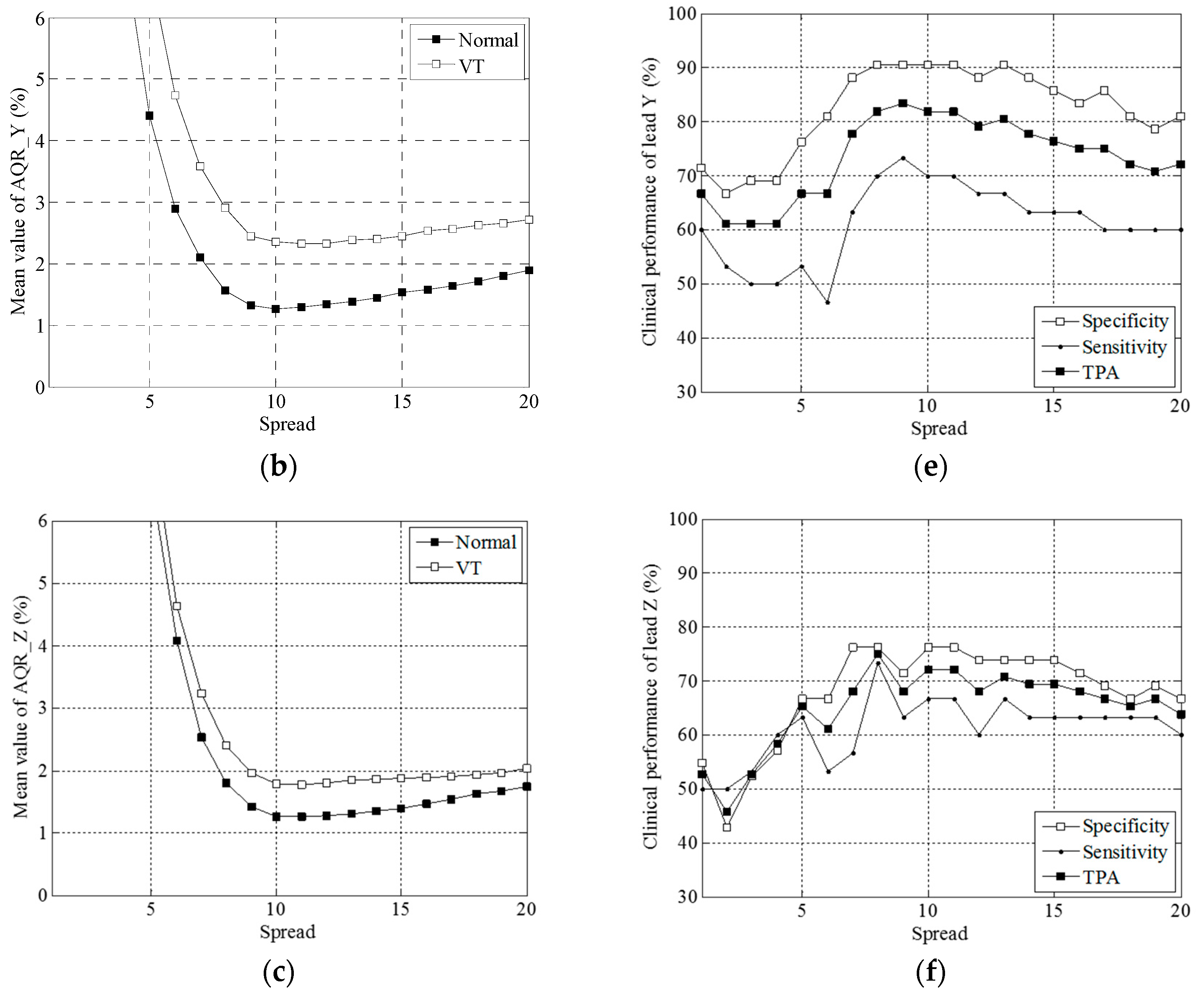
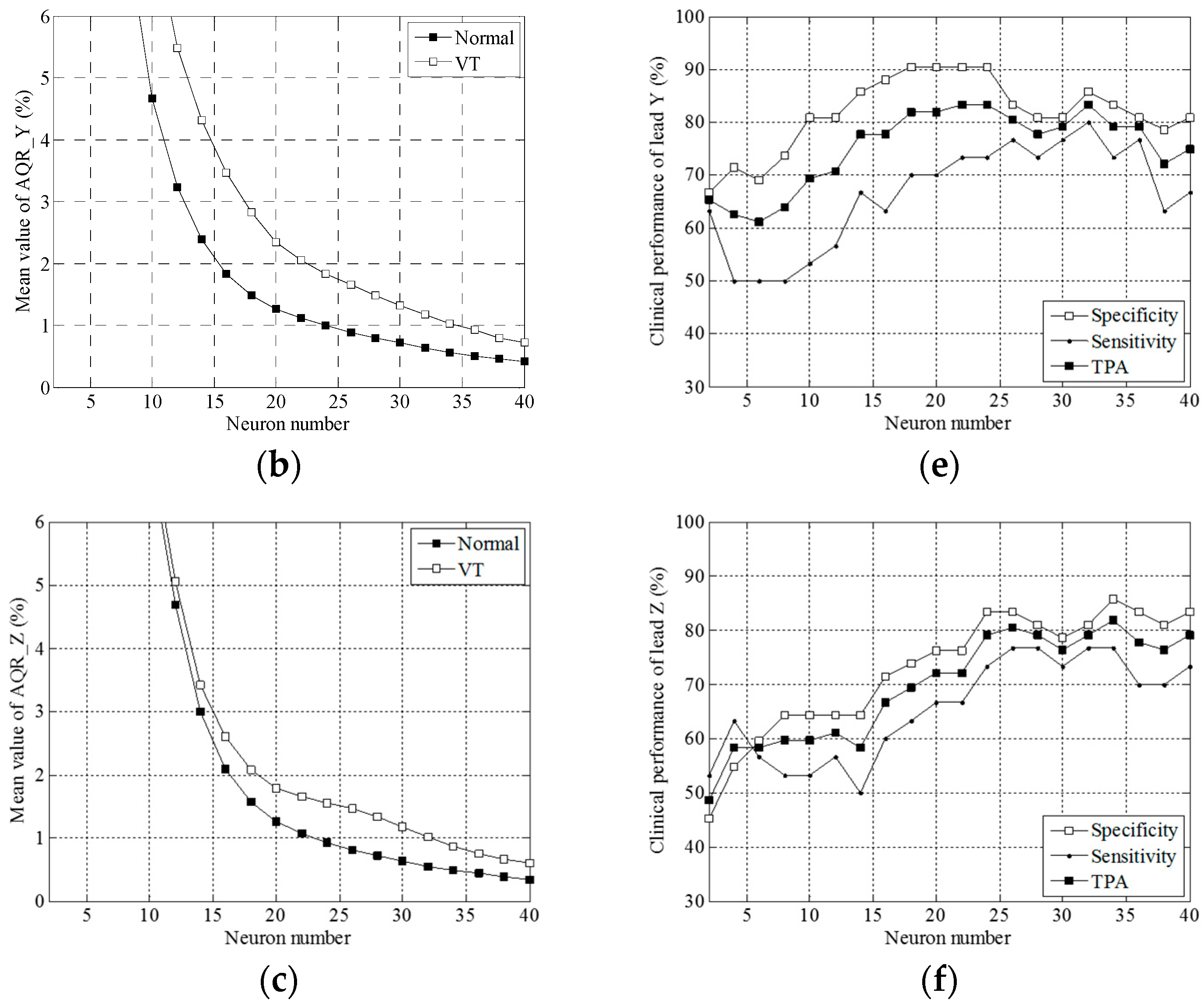
3.1. Simulation Results
3.2. Clinical Trial Results
4. Discussion
4.1. The Proposed RBF Neural Network for Extracting Abnormal Intra-QRS Potentials
4.2. Comparisons with Previous Studies
4.3. Limitations of the Study
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Cain, M.E.; Anderson, J.L.; Arnsdorf, M.F.; Mason, J.W.; Scheinman, M.M.; Waldo, A.L. Signal-averaged electrocardiography. J. Am. Coll. Cardiol. 1996, 27, 238–249. [Google Scholar]
- Ismàeel, H.; Shamseddeen, W.; Taher, A.; Gharzuddine, W.; Dimassi, A.; Alam, S.; Masri, L.; Khoury, M. Ventricular late potentials among thalassemia patients. Int. J. Cardiol. 2009, 132, 453–455. [Google Scholar] [CrossRef] [PubMed]
- Rejdak, K.; Rubaj, A.; Głowniak, A.; Furmanek, K.; Kutarski, A.; Wysokiński, A.; Stelmasiak, Z. Analysis of ventricular late potentials in signal-averaged ECG of people with epilepsy. Epilepsia 2011, 52, 2118–2124. [Google Scholar] [CrossRef] [PubMed]
- Schuller, J.L.; Lowery, C.M.; Zipse, M.; Aleong, R.G.; Varosy, P.D.; Weinberger, H.D.; Sauer, W.H. Diagnostic utility of signal-averaged electrocardiography for detection of cardiac sarcoidosis. Ann. Noninvasive Electrocardiol. 2011, 16, 70–76. [Google Scholar] [CrossRef] [PubMed]
- Bae, M.H.; Kim, J.H.; Jang, S.Y.; Park, S.H.; Lee, J.H.; Yang, D.H.; Park, H.S.; Cho, Y.; Chae, S.C. Changes in follow-up ECG and signal-averaged ECG in patients with arrhythmogenic right ventricular cardiomyopathy. Pacing Clin. Electrophysiol. 2014, 37, 430–438. [Google Scholar] [CrossRef] [PubMed]
- Benchimol-Barbosa, P.R.; Nasario-Junior, O.; Nadal, J. The effect of configuration parameters of time-frequency maps in the detection of intra-QRS electrical transients of the signal-averaged electrocardiogram: Impact in clinical diagnostic performance. Int. J. Cardiol. 2010, 145, 59–61. [Google Scholar] [CrossRef] [PubMed]
- Gadaleta, M.; Giorgio, A. A method for ventricular late potentials detection using time-frequency representation and wavelet denoising. ISRN Cardiol. 2012, 2012, 258769. [Google Scholar] [CrossRef] [PubMed]
- Olivassé, N.J.; Paulo, R.B.B.; Jurandir, N. Principal component analysis in high resolution electrocardiogram for risk stratification of sustained monomorphic ventricular tachycardia. Biomed. Signal Process. Control 2014, 10, 275–280. [Google Scholar]
- Schwarzmaier, H.J.; Karbenn, U.; Borggrefe, M.; Ostermeyer, J.; Breithardt, G. Relation between ventricular late endocardial activity during intraoperative endocardial mapping and low amplitude signals within the terminal QRS complex on the signal-averaged surface electrocardiogram. Am. J. Cardiol. 1990, 66, 308–314. [Google Scholar] [CrossRef]
- Vaitkus, P.T.; Kindwall, K.E.; Marchlinski, F.E.; Miller, J.M.; Buxton, A.E.; Josephson, M.E. Differences in electrophysiological substrate in patients with coronary artery disease and cardiac arrest or ventricular tachycardia Insights from endocardial mapping and signal-averaged electrocardiography. Circulation 1991, 84, 672–678. [Google Scholar] [CrossRef] [PubMed]
- Gomis, P.; Jones, D.L.; Caminal, P.; Berbari, E.J.; Lander, P. Analysis of abnormal signals within the QRS complex of the high-resolution electrocardiogram. IEEE Trans. Biomed. Eng. 1997, 44, 681–693. [Google Scholar] [CrossRef] [PubMed]
- Lander, P.; Gomis, P.; Goyal, R.; Berbari, E.J.; Caminal, P.; Lazzara, R.; Steinberg, J.S. Analysis of abnormal intra-QRS potentials Improved predictive value for arrhythmic events with the signal-averaged electrocardiogram. Circulation 1997, 95, 1386–1393. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.C. Analysis of unpredictable intra-QRS Potentials in signal-averaged electrocardiograms using an autoregressive moving average prediction model. Med. Eng. Phys. 2010, 32, 136–144. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.C. Analysis of unpredictable components within QRS Complex using a finite-impulse-response prediction model for the diagnosis of patients with ventricular tachycardia. Comput. Biol. Med. 2010, 40, 643–649. [Google Scholar] [CrossRef] [PubMed]
- Tsutsumi, T.; Takano, N.; Matsuyama, N.; Higashi, Y.; Iwasawa, K.; Nakajima, T. High-frequency powers hidden within QRS complex as an additional predictor of lethal ventricular arrhythmias to ventricular late potential in post-myocardial infarction patients. Heart Rhythm 2011, 8, 1509–1515. [Google Scholar] [CrossRef] [PubMed]
- Yodogawa, K.; Ohara, T.; Takayama, H.; Seino, Y.; Katoh, T.; Mizuno, K. Detection of prior myocardial infarction patients prone to malignant ventricular arrhythmias using wavelet transform analysis. Int. Heart J. 2011, 52, 286–289. [Google Scholar] [CrossRef] [PubMed]
- Lin, C.C.; Hu, W.C. A radial basis function neural network for the detection of abnormal intra-QRS potentials. Comput. Cardiol. 2011, 38, 781–784. [Google Scholar]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1999. [Google Scholar]
- Oyang, Y.J.; Hwang, S.C.; Ou, Y.Y.; Chen, C.Y.; Chen, Z.W. Data classification with radial basis function networks based on a novel kernel density estimation algorithm. IEEE Trans. Neural Netw. 2005, 16, 225–236. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Cowan, C.N.; Grant, P.M. Orthogonal least squares learning algorithm for radial basis function networks. IEEE Trans. Neural Netw. 1991, 2, 302–309. [Google Scholar] [CrossRef] [PubMed]
- Griner, P.F.; Mayewski, R.J.; Mushlin, A.I.; Greenland, P. Selection and interpretation of diagnostic tests and procedures. Principles and applications. Ann. Intern. Med. 1981, 94, 557–592. [Google Scholar] [PubMed]
- Metz, C.E. Basic principles of ROC analysis. Semin. Nucl. Med. 1978, 8, 283–298. [Google Scholar] [CrossRef]
- Zweig, M.H.; Campbell, G. Receiver-operating characteristic (ROC) plots: A fundamental evaluation tool in clinical medicine. Clin. Chem. 1993, 39, 561–577. [Google Scholar] [PubMed]
- Lin, C.C. Enhancement of accuracy and reproducibility of parametric modeling for estimating abnormal intra-QRS potentials in signal-averaged electrocardiograms. Med. Eng. Phys. 2008, 30, 834–842. [Google Scholar] [CrossRef] [PubMed]


| Parameters | Number of Parameters | SP (%) | SE (%) | TPA (%) | AUC (%) |
|---|---|---|---|---|---|
| Time-domain VLP parameters | |||||
| fQRSD | 1 | 64.3 | 73.3 | 68.1 | 71.4 |
| RMS40 | 1 | 64.3 | 90.0 | 75.0 | 86.7 |
| LAS40 | 1 | 71.4 | 70.0 | 70.8 | 81.1 |
| Linear combination of VLP parameters | |||||
| fQRSD + RMS40 + LAS40 | 3 | 73.8 | 73.3 | 73.6 | 83.8 |
| Individual AQR parameters | |||||
| AQR_X(20, 12) | 1 | 81.0 | 60.0 | 72.2 | 75.3 |
| AQR_Y(20, 9) | 1 | 90.5 | 73.3 | 83.3 | 84.6 |
| AQR_Z(20, 8) | 1 | 76.2 | 73.3 | 75.0 | 77.3 |
| AQR_X(26, 10) | 1 | 78.6 | 70.0 | 75.0 | 74.4 |
| AQR_Y(32, 10) | 1 | 85.7 | 80.0 | 83.3 | 81.1 |
| AQR_Z(34, 10) | 1 | 85.7 | 76.7 | 81.9 | 81.3 |
| Linear combination of AQR parameters | |||||
| AQR_X(20, 1:20) | 20 | 85.7 | 80.0 | 83.3 | 88.6 |
| AQR_Y(20, 1:20) | 20 | 92.9 | 80.0 | 87.5 | 93.6 |
| AQR_Z(20, 1:20) | 20 | 88.1 | 80.0 | 84.7 | 93.3 |
| AQR_X(20, 1:20) + AQR_Y(20, 1:20) + AQR_Z(20, 1:20) | 60 | 97.6 | 86.7 | 93.1 | 99.1 |
| AQR_X(2:40, 10) | 20 | 85.7 | 86.7 | 86.1 | 92.5 |
| AQR_Y(2:40, 10) | 20 | 83.3 | 80.0 | 81.9 | 89.4 |
| AQR_Z(2:40, 10) | 20 | 88.1 | 80.0 | 84.7 | 92.4 |
| AQR_X(2:40, 10) + AQR_Y(2:40, 10) + AQR_X(2:40, 10) | 60 | 100 | 90 | 95.8 | 99.4 |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, C.-C. Analysis of Abnormal Intra-QRS Potentials in Signal-Averaged Electrocardiograms Using a Radial Basis Function Neural Network. Sensors 2016, 16, 1580. https://doi.org/10.3390/s16101580
Lin C-C. Analysis of Abnormal Intra-QRS Potentials in Signal-Averaged Electrocardiograms Using a Radial Basis Function Neural Network. Sensors. 2016; 16(10):1580. https://doi.org/10.3390/s16101580
Chicago/Turabian StyleLin, Chun-Cheng. 2016. "Analysis of Abnormal Intra-QRS Potentials in Signal-Averaged Electrocardiograms Using a Radial Basis Function Neural Network" Sensors 16, no. 10: 1580. https://doi.org/10.3390/s16101580





