An Online Gravity Modeling Method Applied for High Precision Free-INS
Abstract
:1. Introduction
2. Gravity Model in High Precision INS
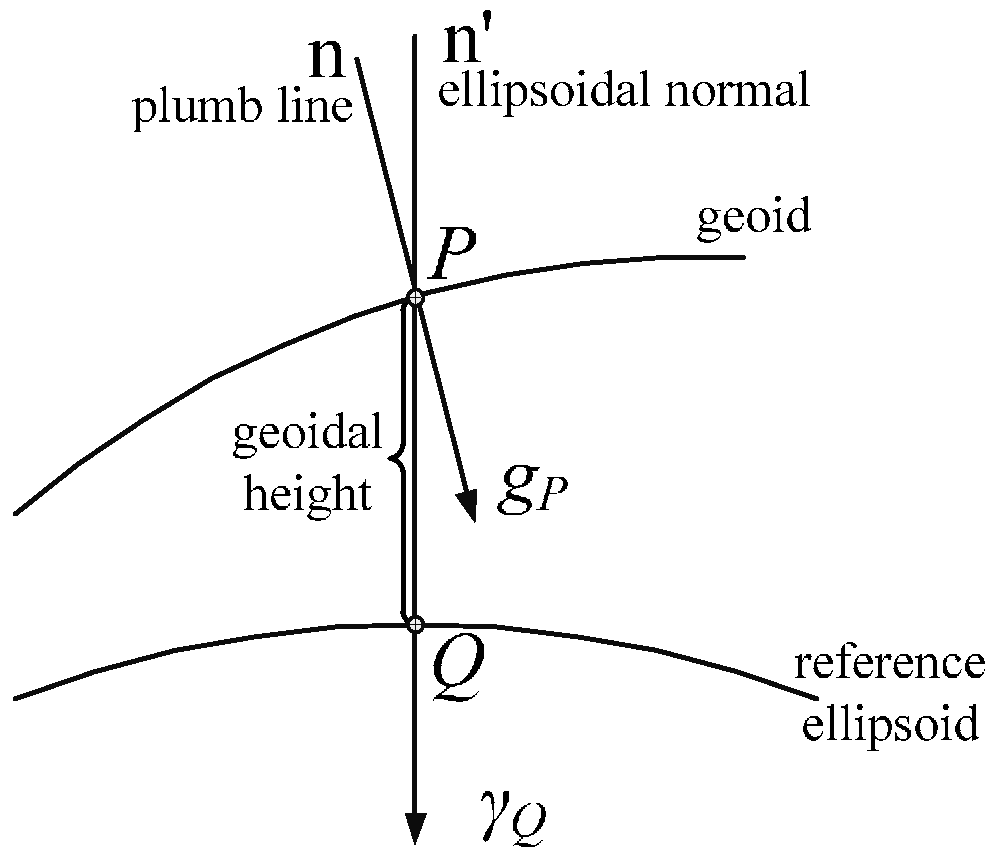
2.1. Definition of Gravity Disturbance Vector
2.2. Spherical Harmonic Model
3. Mathematic Analysis of Spherical Harmonic Model
3.1. Gravity Disturbing Potential in Small Area
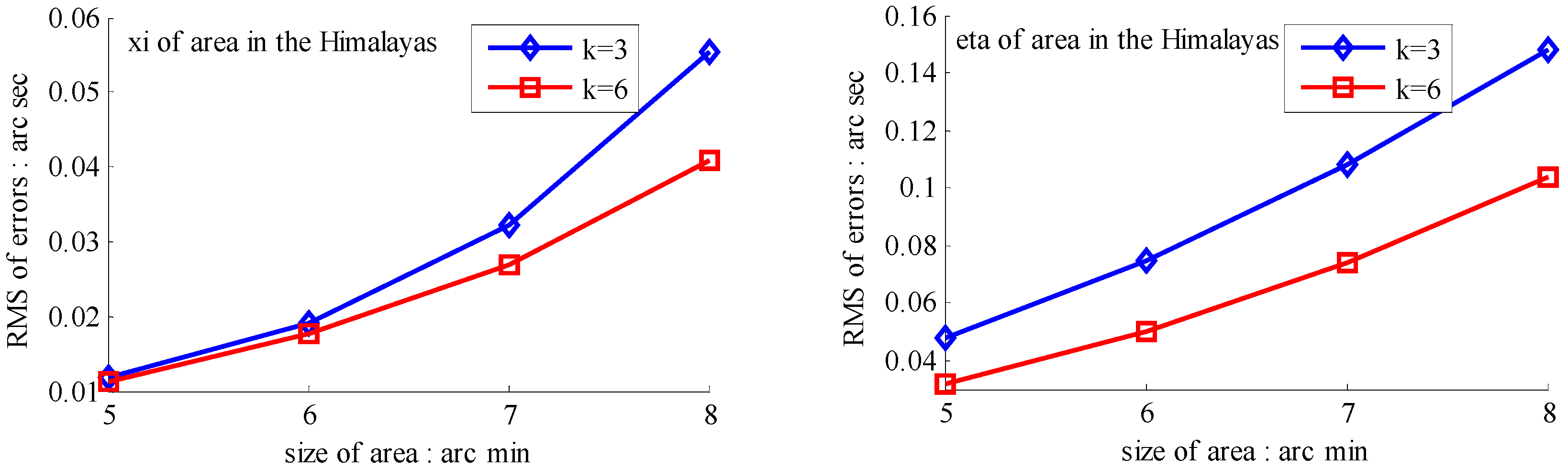
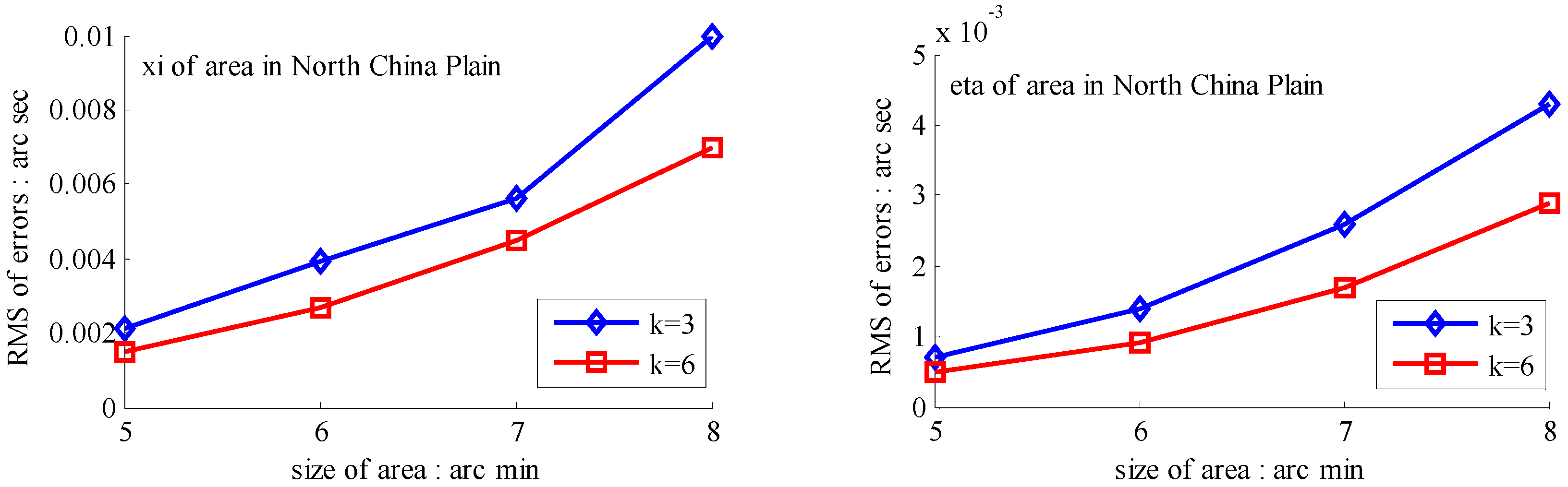
3.2. Numerical Tests
3.2.1. Test Design
3.2.2. Test Results
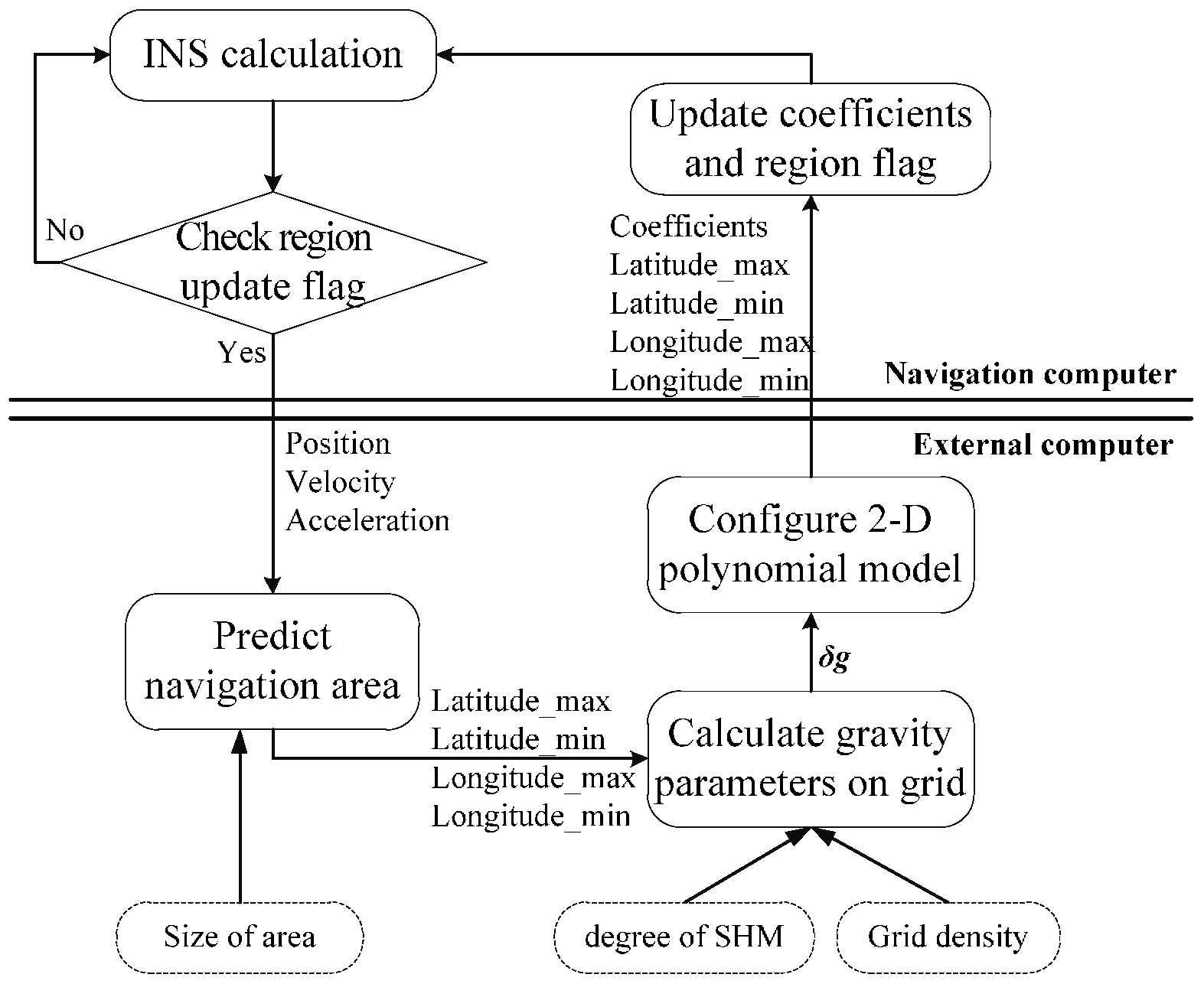
4. Online Gravity Modeling in INS
- Step 1:
- INS gives the motion information of vehicle to the external computer, consisting of position, velocity and acceleration.
- Step 2:
- The prediction module calculates the applicative area of the updated model, concluding maximum latitude, longitude and minimum latitude, longitude.
- Step 3:
- Program of SHM computes DOVs on grid points in batches.
- Step 4:
- The configuration of the 2-D PM gives coefficients of updated models by fitting low order PM to the DOVs in step 3. This parameters combined with the position range of applicative area are transferred to the INS. The applicative area updates once the vehicle travels close to the boundary.
4.1. Model Configuration
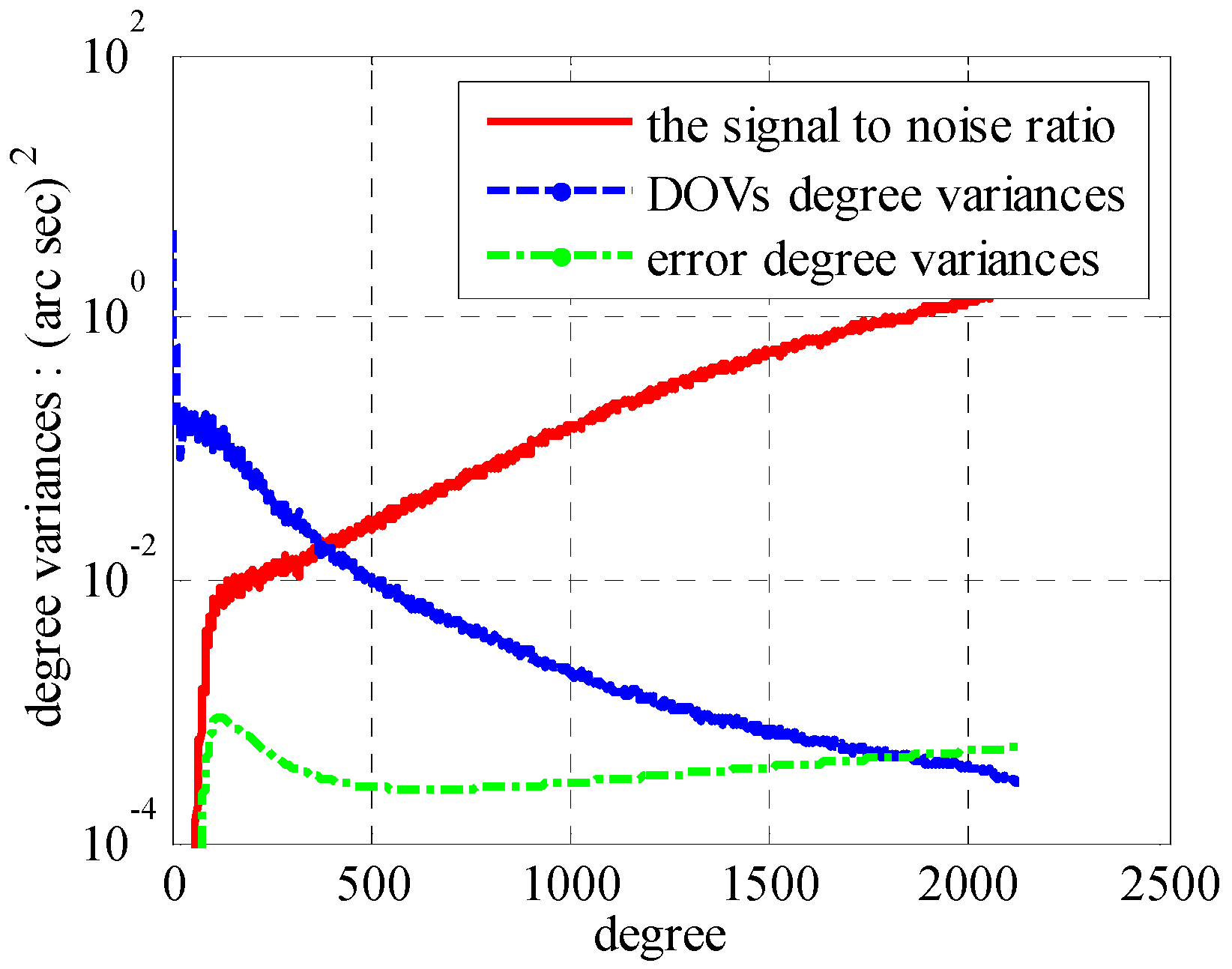
4.1.1. Degree Selection of Base Model
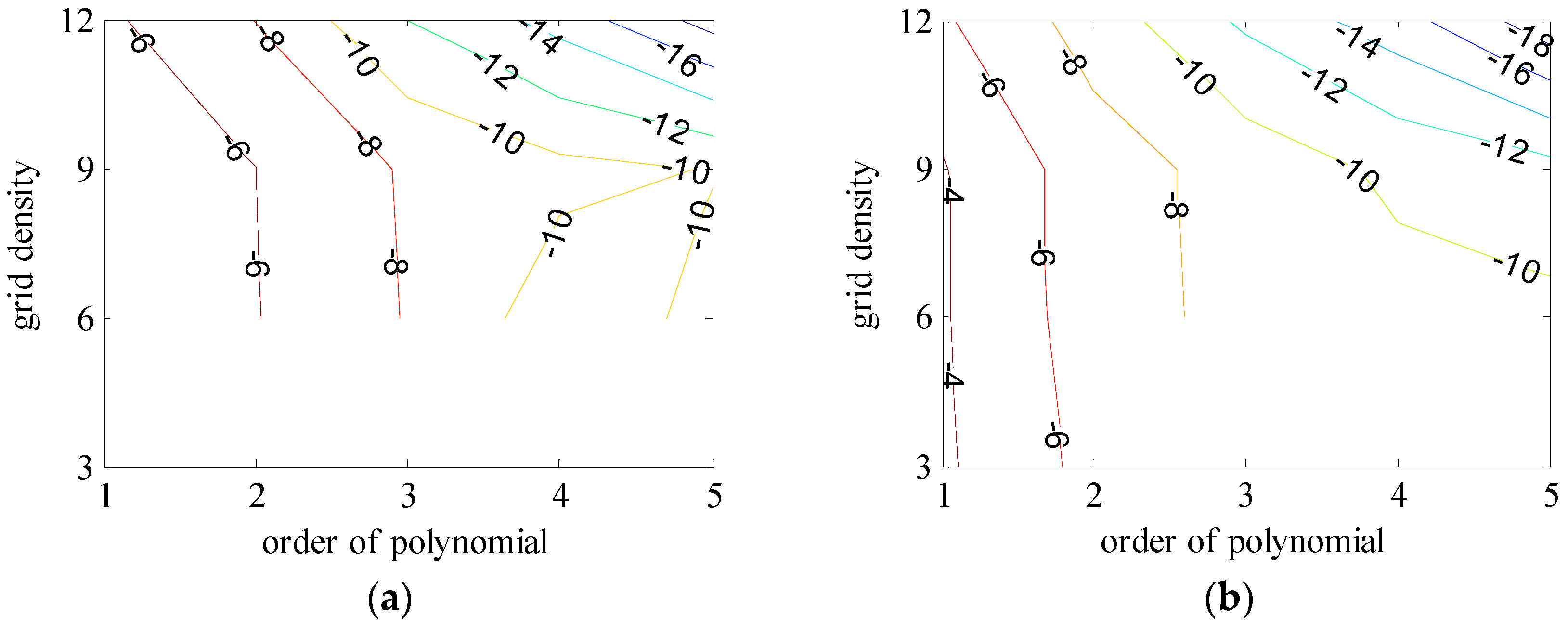
4.1.2. Configuration of Polynomial Model
4.2. Computational Complexity
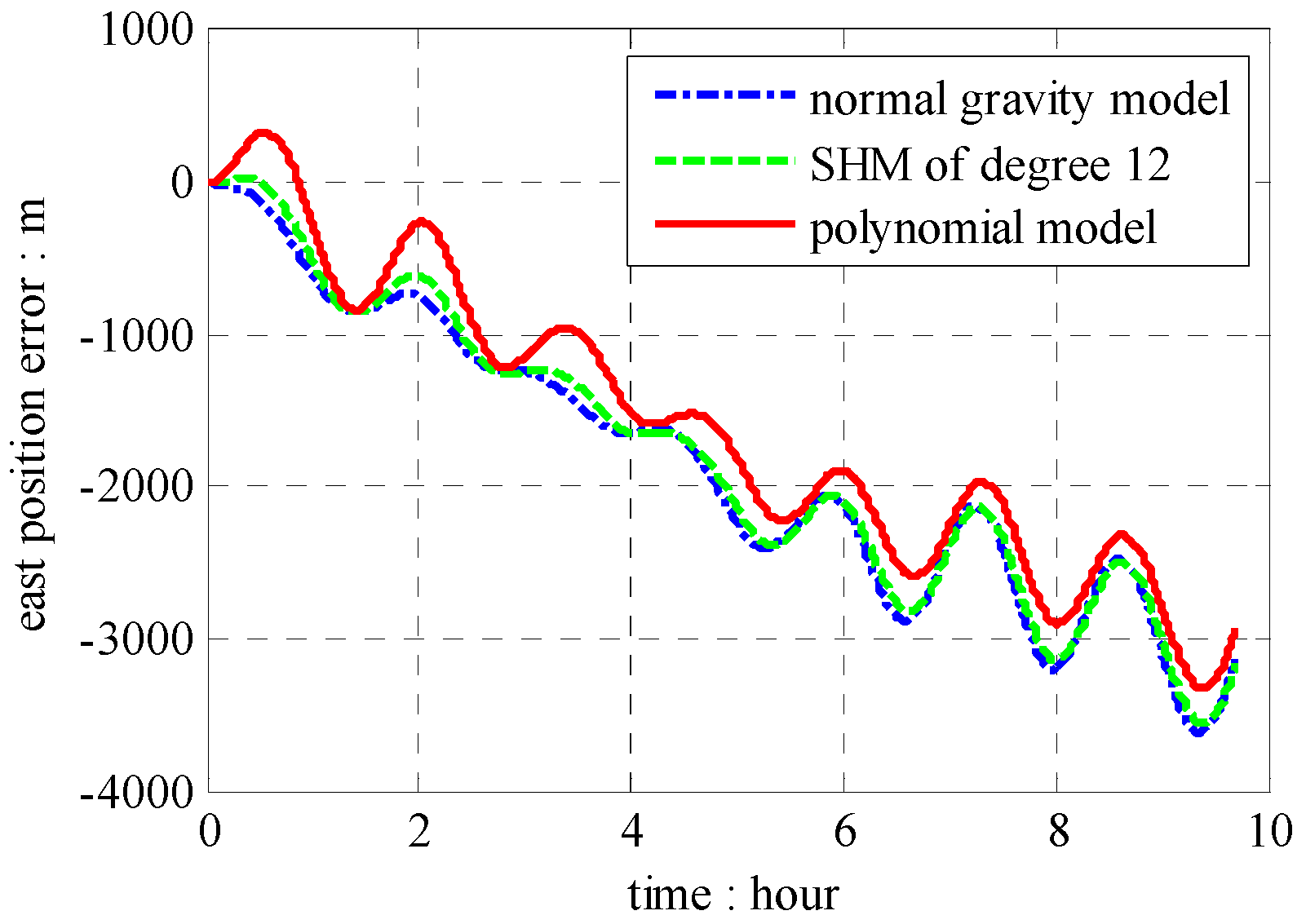
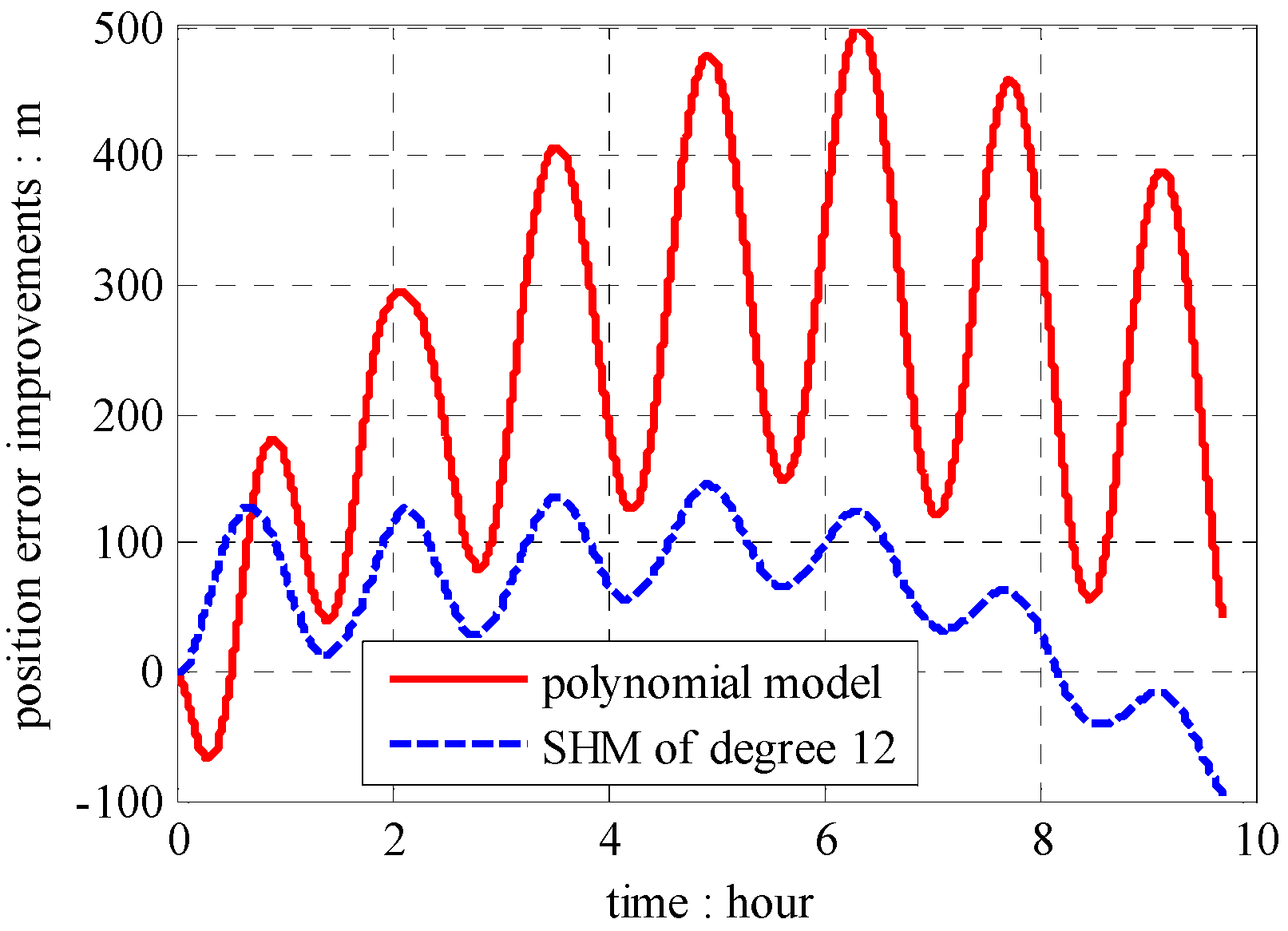
5. Experimental Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Petritoli, E.; Leccese, F. Improvement of Altitude Precision in Indoor and Urban Canyon Navigation for Small Flying Vehicles. In Proceedings of the Metrology for Aerospace, Benevento, Italy, 4–5 June 2015; pp. 56–60.
- Petritoli, E.; Giagnacovo, T.; Leccese, F. Lightweight GPS/IRS AIME Integrated Navigation System for UAV Vehicles. In Proceedings of the Metrology for Aerospace, Benevento, Italy, 29–30 May 2014; pp. 56–61.
- Kwon, J.H.; Jekeli, C. Gravity requirements for compensation of ultra-precise inertial navigation. J. Navig. 2005, 58, 479–492. [Google Scholar] [CrossRef]
- Jekeli, C. Precision free-inertial navigation with gravity compensation by an onboard gradiometer. J. Guid. Control Dyn. 2006, 29, 704–713. [Google Scholar] [CrossRef]
- Siouris, G.M. Gravity modeling in aerospace applications. Aerosp. Sci. Technol. 2009, 13, 301–315. [Google Scholar] [CrossRef]
- Dai, D.K.; Wang, X.S.; Zhan, D.J.; Huang, Z.S. An improved method for dynamic measurement of deflections of the vertical based on the maintenance of attitude reference. Sensors 2014, 14, 16322–16342. [Google Scholar] [CrossRef] [PubMed]
- Wellenhof, B.H.; Moritz, H. Physical Geodesy, 2nd ed.; Springer: Graz, Austria, 2005. [Google Scholar]
- Hsu, D.Y. An Accurate and Efficient Approximation to the Normal Gravity. In Proceedings of the IEEE Position Location and Navigation Symposium, Palm Springs, CO, USA, 20–23 April 1998; pp. 38–44.
- Hsu, D.Y.; Hills, A. Method for Determining Gravity in an Inertial Navigation System. U.S. Patent 6073077, 6 June 2000. [Google Scholar]
- Kopcha, P.D. 2004 NGA Gravity Support for Inertial Navigation. In Proceedings of the ION GNSS, Dayton, CA, USA, 7–9 June 2004; pp. 497–504.
- Wang, J.; Yang, G.L.; Li, X.Y.; Zhou, X. Application of spherical harmonic gravity model in high precision. INS Meas. Sci. Technol. 2016, 27, 095103. [Google Scholar] [CrossRef]
- Arora, N.; Russell, R.P. Fast efficient and adaptive interpolation of the geopotential. J. Guid. Control Dyn. 2014, 38, 1345–1355. [Google Scholar] [CrossRef]
- Junkins, J.L. Investigation of finite-element representations of the geopotential. AIAA J. 1976, 14, 803–808. [Google Scholar] [CrossRef]
- Hujsak, R.S. Gravity acceleration approximation functions. Adv. Astronaut. Sci. 1996, 93, 335–349. [Google Scholar]
- Jones, B.A.; Born, G.H.; Beylkin, G. Comparisons of the Cubed-Sphere gravity model with the spherical harmonics. J. Guid. Control Dyn. 2010, 33, 415–425. [Google Scholar] [CrossRef]
- Pavlis, N.K. An earth gravitational model to degree 2160: EGM2008. Geophys. Res. Abstr. 2008, 10, 1981. [Google Scholar]
- Hirt, C. Prediction of vertical deflections from high-degree spherical harmonic synthesis and residual terrain model data. J. Geod. 2010, 84, 179–190. [Google Scholar] [CrossRef]
- Hirt, C. Efficient and accurate high-degree spherical harmonic synthesis of gravity field functionals at the Earth’s surface using the gradient approach. J. Geod. 2012, 86, 729–744. [Google Scholar] [CrossRef]
- Hwang, C.; Kao, Y.C. Spherical harmonic analysis and synthesis using FFT application to temporal gravity variation. Comput. Geosci. 2006, 32, 442–451. [Google Scholar]
- Cheong, H.B.; Park, J.R.; Kang, H.G. Fourier-series representation and projection of spherical harmonic functions. J. Geod. 2012, 86, 975. [Google Scholar] [CrossRef]
- Grejner-Brzezinska, D.A.; Yi, Y.; Toth, C. Enhanced Gravity Compensation for Improved Inertial Navigation Accuracy. In Proceedings of the ION GPS/GNSS, Portland, OR, USA, 9–12 September 2003; pp. 2897–2909.
- Wang, J.; Yang, G.L.; Li, X.Y.; Zhou, X. Error indicator analysis for gravity disturbance vector’s influence on inertial navigation system. J. Chin. Inert. Technol. 2016, 24, 285–290. [Google Scholar]
- Eling, C.; Klingbeil, L.; Kuhlmann, H. Real-time single-frequency GPS/MEMS-IMU attitude determination of lightweight UAVs. Sensors 2015, 15, 26212–26235. [Google Scholar] [CrossRef] [PubMed]
- Moritz, H. Advanced Physical Geodesy; Abacus Press: Kent, UK, 1980. [Google Scholar]









| Size of Area | DOVs | 2160 | 900 | 360 |
|---|---|---|---|---|
| 15′ × 15′ | ξ |  |  |  |
| η |  |  |  | |
| 6′ × 6′ | ξ |  |  |  |
| η |  |  |  | |
| 2.5′ × 2.5′ | ξ |  |  |  |
| η |  |  |  |
| Size of Area | DOVs | 2160 | 900 | 360 |
|---|---|---|---|---|
| 15′×15′ | ξ |  |  |  |
| η |  |  |  | |
| 6′×6′ | ξ |  |  |  |
| η |  |  |  | |
| 2.5′×2.5′ | ξ |  |  |  |
| η |  |  |  |
| Size of Area | Degree of Polynomials | DOVs | 2160 | 900 | 360 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMS | Max | Min | RMS | Max | Min | RMS | Max | Min | |||
| 15′ × 15′ | 2 | ξ | 0.0270 | 0.0534 | −1.259 | 0.0231 | 0.0516 | −0.1051 | 0.0035 | 0.0121 | −0.0130 |
| η | 0.0263 | 0.0864 | −0.1458 | 0.0192 | 0.0750 | −0.1058 | 0.0043 | 0.0128 | −0.0234 | ||
| 3 | ξ | 0.0179 | 0.0406 | −0.0660 | 0.0087 | 0.0140 | −0.0300 | 6.84 × 10−4 | 0.0056 | −0.0013 | |
| η | 0.0106 | 0.0387 | −0.0385 | 0.0032 | 0.0074 | −0.0190 | 8.64 × 10−4 | 0.0016 | −0.0067 | ||
| 6′ × 6′ | 2 | ξ | 0.0043 | 0.0159 | −0.0182 | 0.0036 | 0.0123 | −0.0134 | 3.06 × 10−4 | 8.75 × 10−4 | −8.60 × 10−4 |
| η | 0.0050 | 0.0190 | −0.0269 | 0.0018 | 0.0080 | −0.0073 | 2.98 × 10−4 | 0.0011 | −0.0014 | ||
| 3 | ξ | 0.0014 | 0.0054 | −0.0060 | 1.39 × 10−4 | 4.55 × 10−4 | −6.68 × 10−4 | 1.49 × 10−5 | 1.16 × 10−4 | −2.71 × 10−5 | |
| η | 7.64 × 10−4 | 0.0017 | −0.0045 | 7.26 × 10−5 | 5.18 × 10−4 | −2.92 × 10−4 | 2.0 × 10−5 | 3.67 × 10−5 | −1.44 × 10−4 | ||
| 2.5′ × 2.5′ | 2 | ξ | 4.10 × 10−4 | 0.0022 | −0.0023 | 2.67 × 10−4 | 0.0011 | −0.0011 | 2.37 × 10−5 | 6.84 × 10−5 | −6.82 × 10−5 |
| η | 4.37 × 10−4 | 0.0024 | −0.0022 | 1.19 × 10−4 | 5.79 × 10−4 | −5.87 × 10−4 | 2.16 × 10−5 | 8.72 × 10−5 | −9.52 × 10−5 | ||
| 3 | ξ | 4.67 × 10−5 | 2.47 × 10−4 | −9.65 × 10−5 | 4.66 × 10−6 | 3.09 × 10−5 | −1.08 × 10−5 | 4.04 × 10−7 | 3.13 × 10−6 | −7.0 × 10−7 | |
| η | 2.50 × 10−5 | 9.93 × 10−5 | −6.13 × 10−5 | 3.44 × 10−6 | 2.63 × 10−5 | −6.81 × 10−6 | 5.64 × 10−7 | 8.95 × 10−7 | −4.14 × 10−6 | ||
| Size of Area | Degree of Polynomials | DOVs | 2160 | 900 | 360 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| RMS | Max | Min | RMS | Max | Min | RMS | Max | Min | |||
| 15′ × 15′ | 2 | ξ | 3.8582 | 16.1806 | −12.2163 | 0.4304 | 2.6393 | −1.8167 | 0.0718 | 0.2832 | −0.3048 |
| η | 3.3621 | 9.4731 | −9.1792 | 1.0048 | 4.9811 | −2.4415 | 0.0666 | 0.3633 | −0.3771 | ||
| 3 | ξ | 2.6084 | 15.6082 | −5.6079 | 0.1389 | 1.0797 | −0.4653 | 0.0030 | 0.0113 | −0.0133 | |
| η | 1.9458 | 7.4299 | −5.2106 | 0.2373 | 1.5610 | −0.4497 | 0.0046 | 0.0070 | −0.0346 | ||
| 6′ × 6′ | 2 | ξ | 0.5512 | 1.7377 | −2.6511 | 0.0405 | 0.1836 | −0.1771 | 0.0044 | 0.0202 | −0.0200 |
| η | 0.2777 | 1.3142 | −1.0185 | 0.0823 | 0.4472 | −0.4400 | 0.0048 | 0.0259 | −0.0260 | ||
| 3 | ξ | 0.1143 | 0.1969 | −0.9933 | 0.0024 | 0.0171 | −0.0071 | 9.82 × 10−5 | 3.99 × 10−4 | −3.1 × 10−4 | |
| η | 0.1453 | 0.3523 | −1.0071 | 0.0050 | 0.0385 | −0.0083 | 1.02 × 10−4 | 2.13 × 10−4 | −7.57 × 10−5 | ||
| 2.5′ × 2.5′ | 2 | ξ | 0.0334 | 0.1172 | −0.1594 | 0.0033 | 0.0139 | −0.0135 | 3.08 × 10−4 | 0.0014 | −0.0014 |
| η | 0.0504 | 0.2311 | −0.2644 | 0.0069 | 0.0350 | −0.0354 | 3.59 × 10−4 | 0.0019 | −0.0019 | ||
| 3 | ξ | 0.0035 | 0.0064 | −0.0265 | 5.16 × 10−5 | 2.49 × 10−4 | −1.82 × 10−4 | 3.23 × 10−6 | 1.31 × 10−5 | −9.38 × 10−6 | |
| η | 0.0027 | 0.0093 | −0.0202 | 9.39 × 10−5 | 5.6 × 10−4 | −2.98 × 10−4 | 2.71 × 10−6 | 6.41 × 10−6 | −1.9 × 10−5 | ||
| Model | Time Complexity | Space Complexity | Execution Time (s) | Speed-up Factor | Largest l2 Error (m/s2) | Real-Time Navigation |
|---|---|---|---|---|---|---|
| PM | 10ADD+18MUL | 12 float | 3.9868 × 10−6 | 7.5381 × 105 | 3.2368 × 10−6 | Available |
| NGM | 9ADD+11MUL | 3 float | 2.9605 × 10−6 | 1.0151 × 105 | 0.0130 | Available |
| Modified NGM | 9ADD+10MUL | 3 float | 2.2697 × 10−6 | 1.3243 × 106 | 0.0130 | Available |
| 12 degree SHM | O(122) | 352 float | 0.0028 | 1.0733 × 103 | 1.9897 × 10−4 | Available |
| Cubed-sphere model (m = 11 and N = 2048) | O(123) | 1,226,492,416 float | 0.0181 | 1.6604 × 102 | 2.3785 × 10−6 | Unavailable |
| 820 degree SHM | O(8202) | 572,137,984 float | 3.0053 | 1 | 0 | Unavailable |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Yang, G.; Li, J.; Zhou, X. An Online Gravity Modeling Method Applied for High Precision Free-INS. Sensors 2016, 16, 1541. https://doi.org/10.3390/s16101541
Wang J, Yang G, Li J, Zhou X. An Online Gravity Modeling Method Applied for High Precision Free-INS. Sensors. 2016; 16(10):1541. https://doi.org/10.3390/s16101541
Chicago/Turabian StyleWang, Jing, Gongliu Yang, Jing Li, and Xiao Zhou. 2016. "An Online Gravity Modeling Method Applied for High Precision Free-INS" Sensors 16, no. 10: 1541. https://doi.org/10.3390/s16101541





