Statistical Analysis of the Performance of MDL Enumeration for Multiple-Missed Detection in Array Processing
Abstract
:1. Introduction
2. Problem Formulation
2.1. Array Signal Model
2.2. Source Enumeration of MDL
3. Performance Analysis of Multiple-Missed Detection
| Multivariate Statistics | Random Matrix | Lawley | |
|---|---|---|---|
| E(li) *1 | *3 | ||
| Var(li) *1 | *2,*3 | *2 | |
| E(Aq) | |||
| Var(Aq) | *2 | / |
4. Simulation Setup and Numerical Results
4.1. Evaluation of the Proposed Method for Underestimation Analysis
| Haddadi et al. | Huang et al. | Lu &Zoubir | Ours | |
|---|---|---|---|---|
| E(lq) | Lawley | Lawley | Lawley | Lawley |
| Var(lq) | Multivariate Statistics | Random Matrix | Random Matrix | Lawley |
| E(Aq) | Lawley | Lawley | Lawley | Lawley |
| Var(Aq) | - * | - | Random Matrix | Random Matrix |
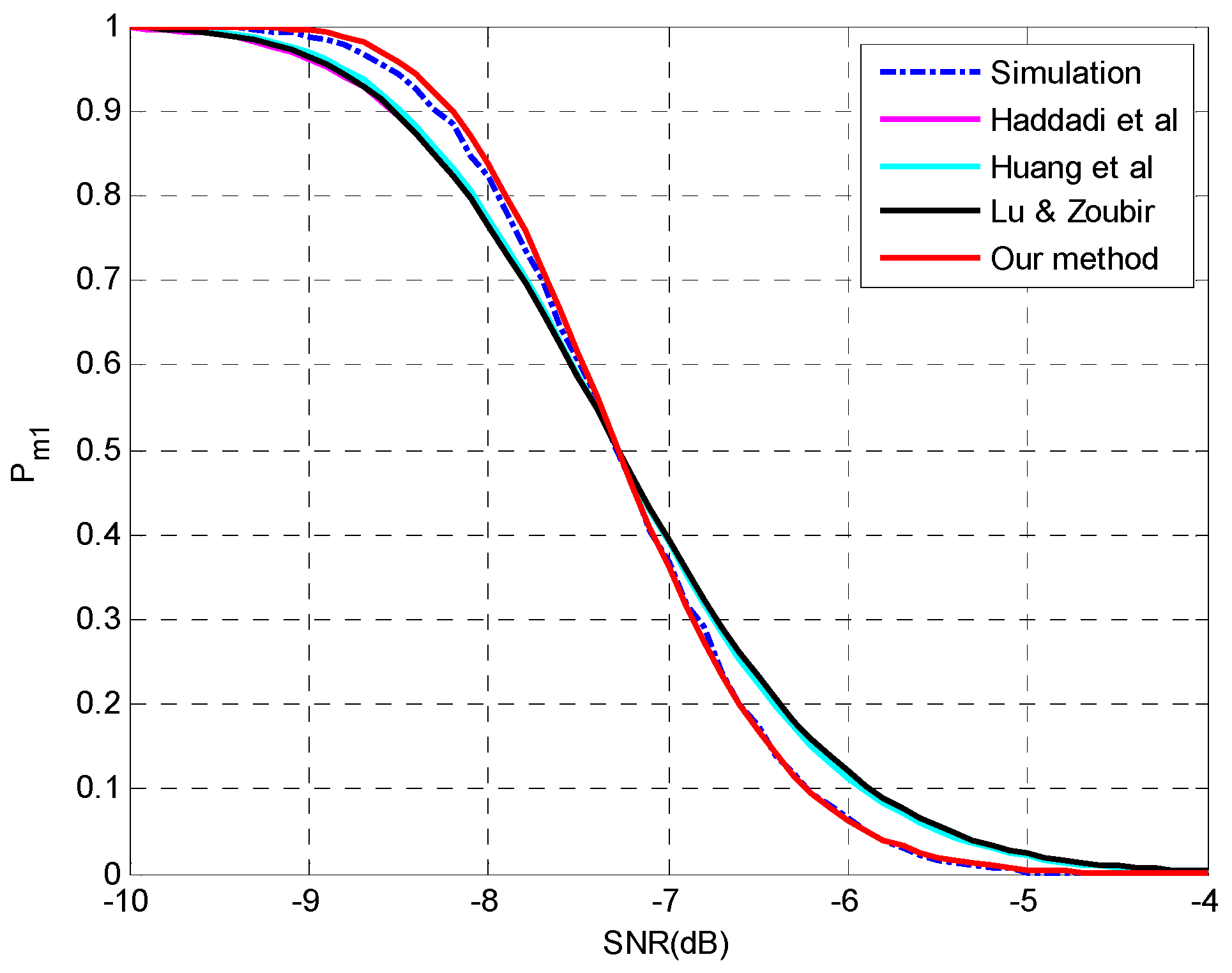
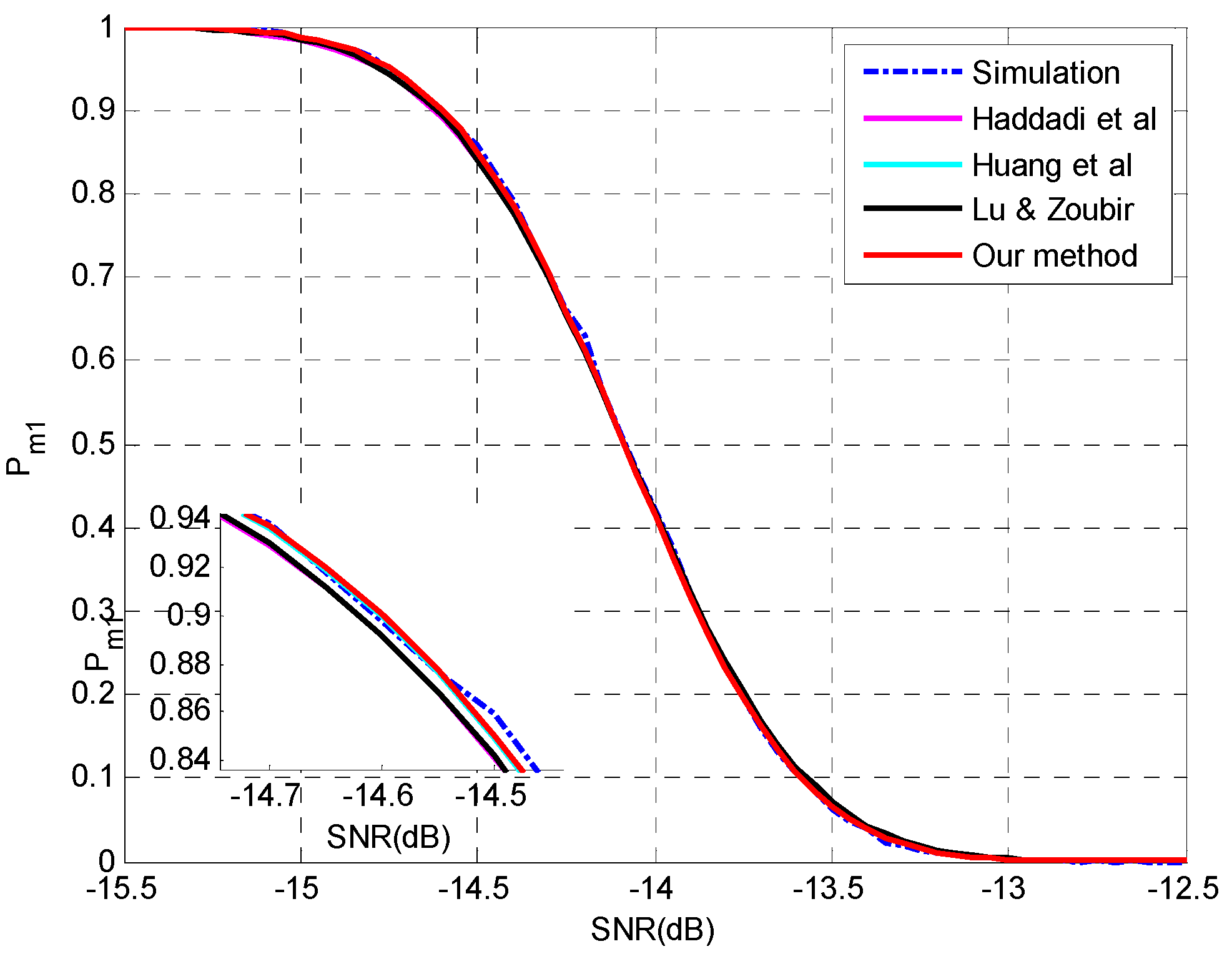
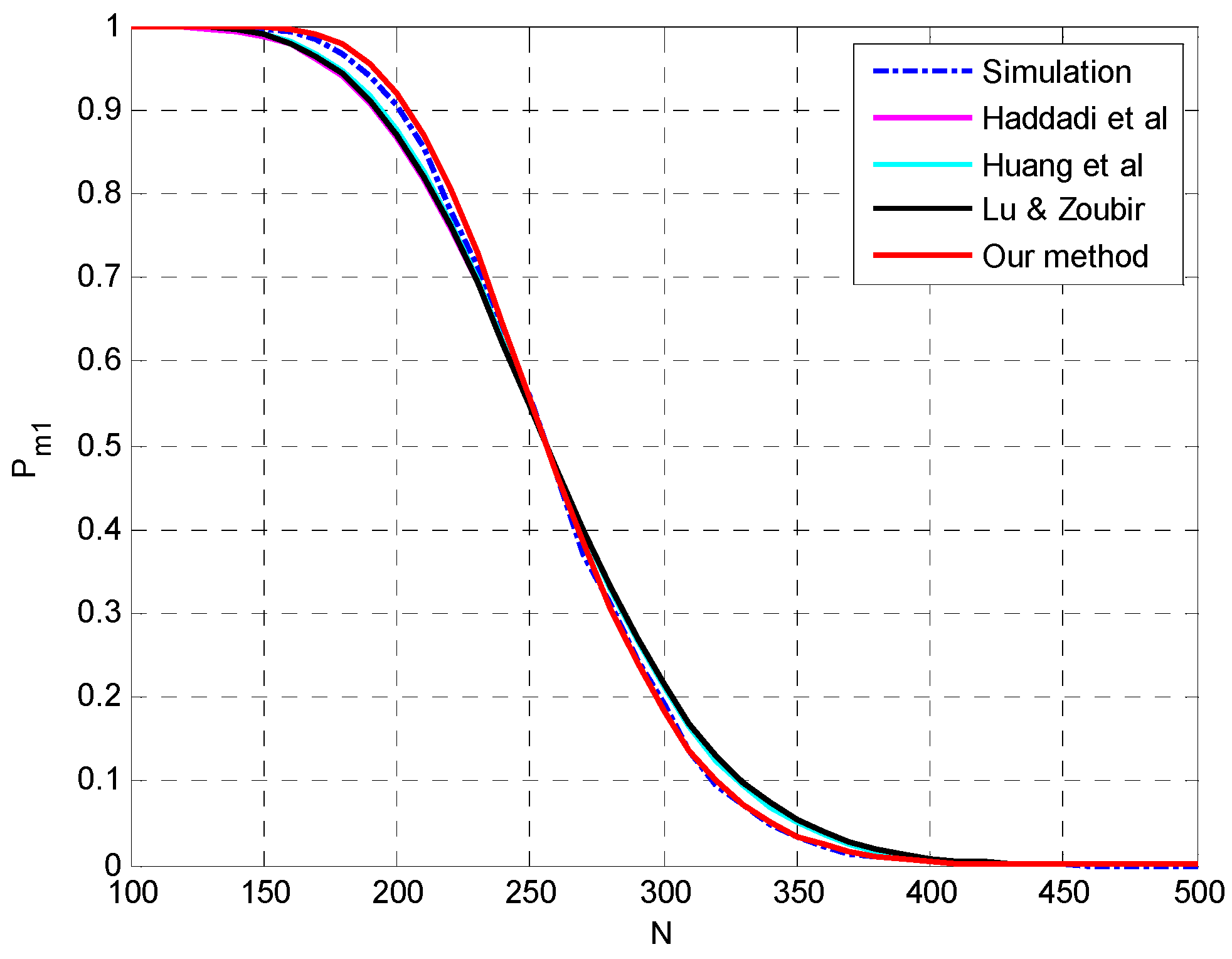

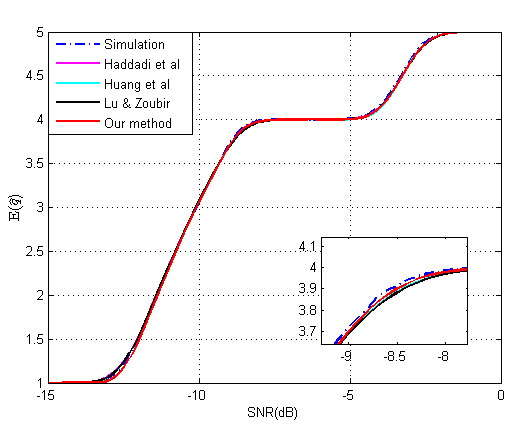
4.2. Evaluation of the Analysis on Multiple-Missed Detection
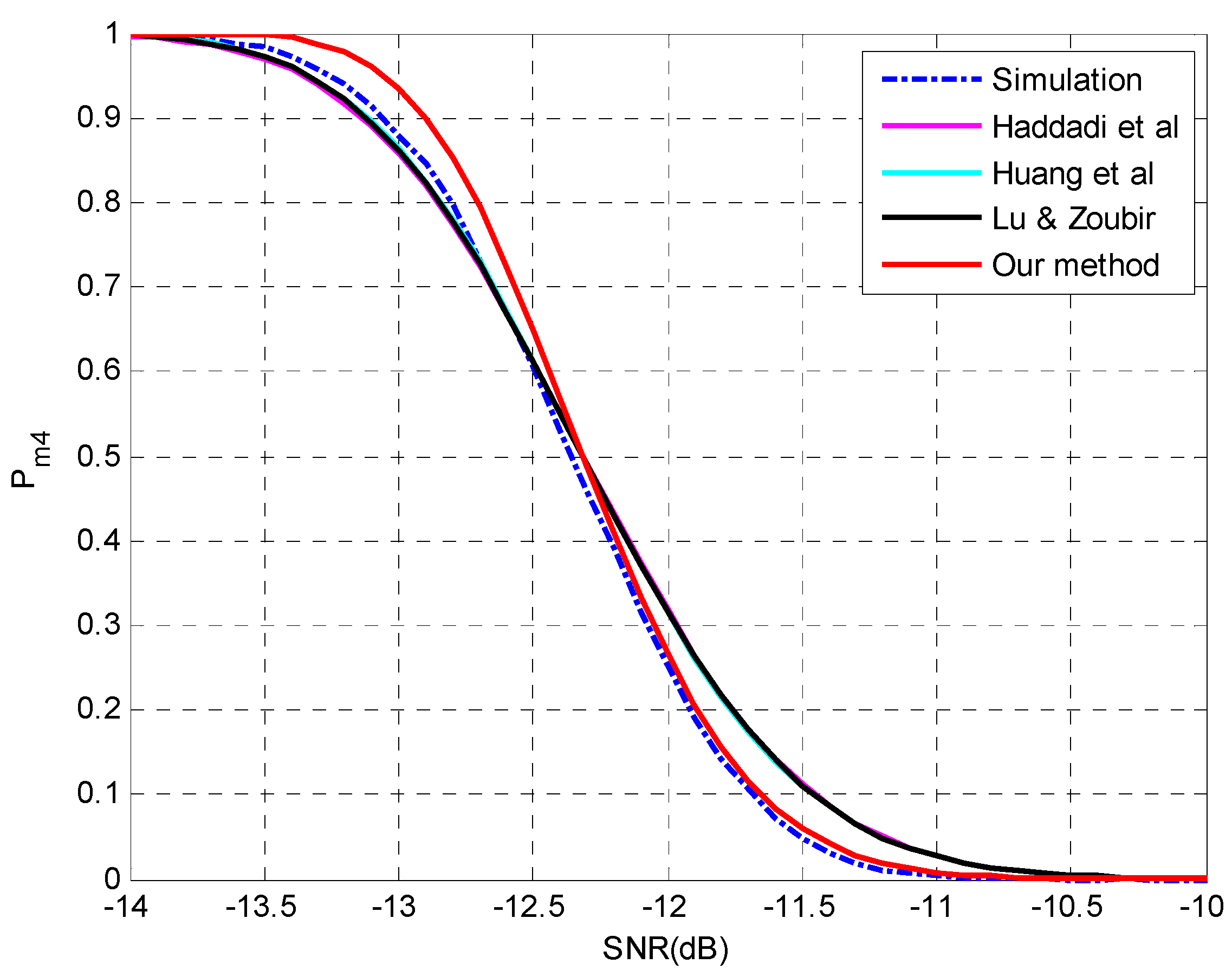
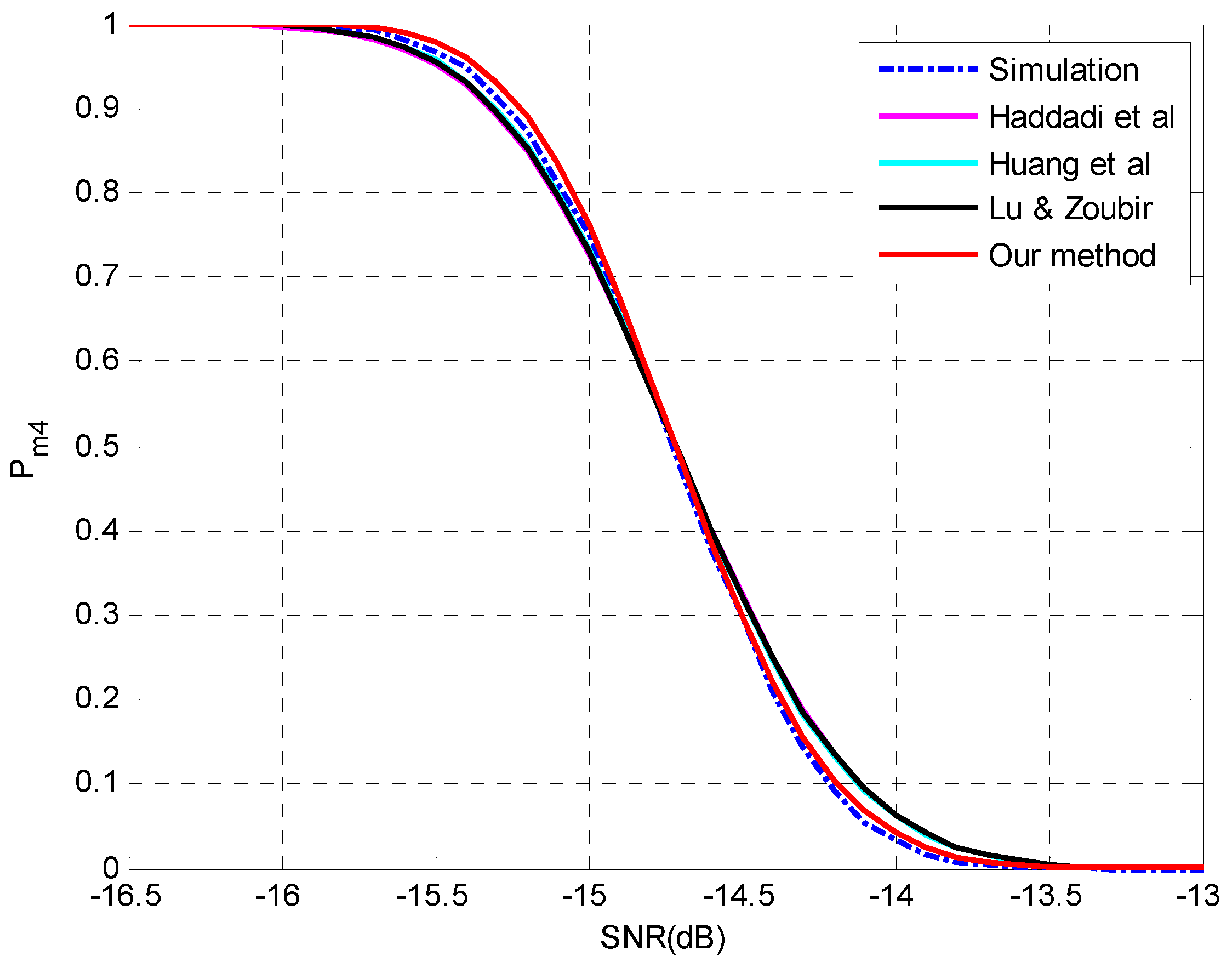
| MAE | Haddadi et al. | Huang et al. | Lu & Zoubir | Our Method |
|---|---|---|---|---|
| Setting 7 | 0.0143 | 0.0123 | 0.0140 | 0.0110 |
| Setting 8 | 0.0054 | 0.0047 | 0.0055 | 0.0043 |

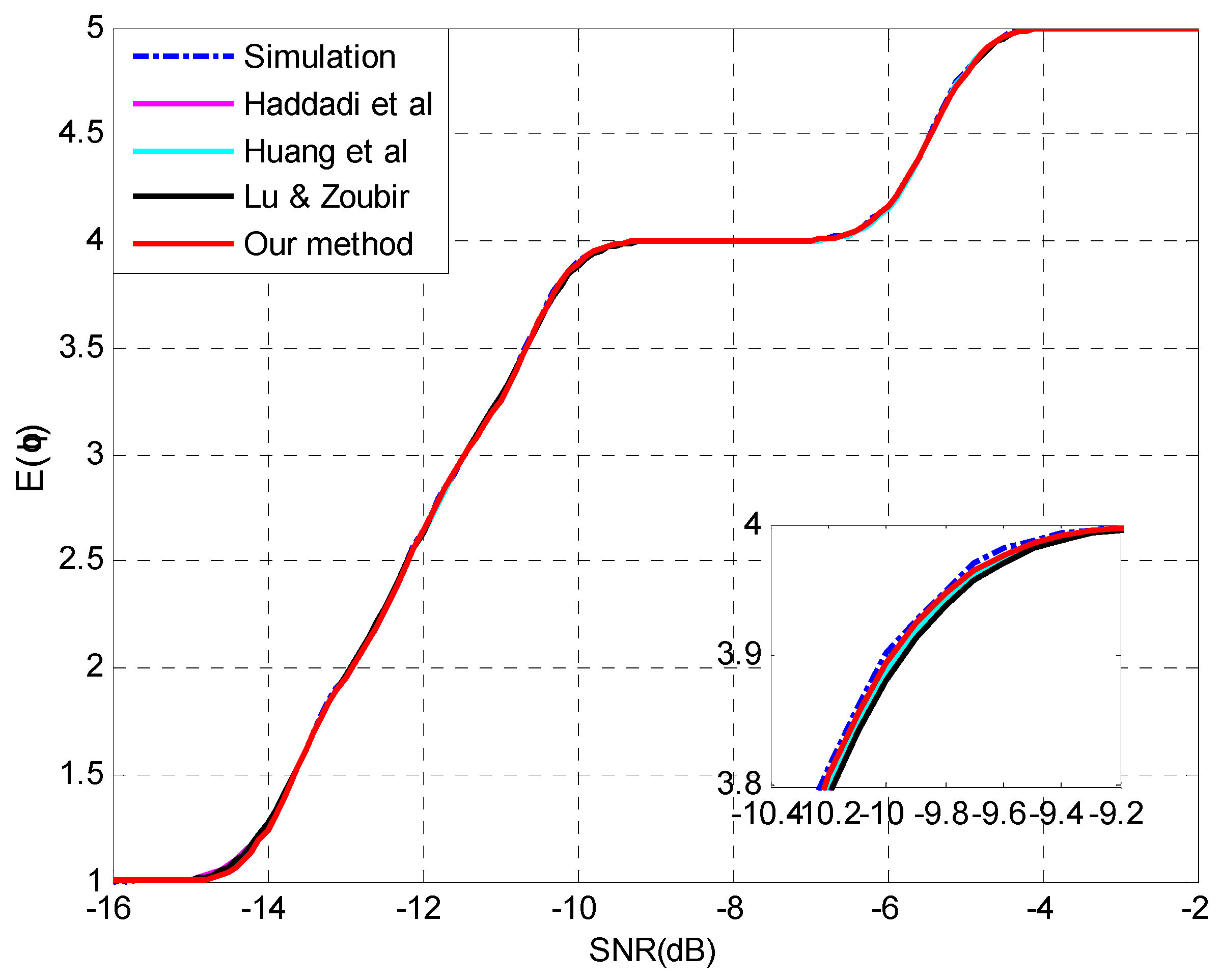
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: The parametric approach. IEEE Signal Process. Mag 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Atashbar, M.; Kahaei, M. Direction-of-arrival estimation using AMLSS method. IEEE Lat. Am. Trans 2012, 10, 2053–2058. [Google Scholar] [CrossRef]
- Naik, G.R.; Kumar, D.K. Dimensional reduction using blind source separation for identifying sources. Int. J. Innov. Comput. Inf. Control 2011, 7, 989–1000. [Google Scholar]
- Rissanen, J. Modeling by shortest data description. Automatica 1978, 14, 465–471. [Google Scholar] [CrossRef]
- Schwarz, G. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Wax, M.; Kailath, T. Detection of signals by information theoretic criteria. IEEE Trans. Acoust. Speech Signal Process 1985, 33, 387–392. [Google Scholar] [CrossRef]
- Dayan, A.G.; Rausley, A.A.S. Simple and efficient algorithm for improving the MDL estimator of the number of sources. Sensors 2014, 14, 19477–19492. [Google Scholar]
- Huang, L.; Long, T.; Mao, E.; So, H.C. MMSE-based MDL method for accurate source number estimation. IEEE Signal Process. Lett. 2009, 16, 98–801. [Google Scholar] [CrossRef]
- Huang, L.; So, H.C. Source enumeration via MDL criterion based on linear shrinkage estimation of noise subspace covariance matrix. IEEE Trans. Signal Process 2013, 61, 4806–4821. [Google Scholar] [CrossRef]
- Lu, Z.; Zoubir, A.M. Source enumeration using the pdf of sample eigenvalues via information theoretic criteria. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 3361–3364. [Google Scholar]
- Fishler, E.; Messer, H. On the use of order statistics for improved detection of signals by the MDL criterion. IEEE Trans. Signal Process 2000, 48, 2242–2247. [Google Scholar] [CrossRef]
- Zhen, J.; Si, X. A method for determining number of coherent signals with arbitrary plane array. In Proceedings of the IEEE International Conference on Information and Automation, Harbin, China, 20–23 June 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 240–244. [Google Scholar]
- Fishler, E.; Poor, H.V. Estimation of the number of sources in unbalanced arrays via information theoretic criteria. IEEE Trans. Signal Process 2005, 53, 3543–3553. [Google Scholar] [CrossRef]
- Huang, L.; Wu, S.; Li, X. Reduced-rank MDL method for source enumeration in high-resolution array processing. IEEE Trans. Signal Process 2007, 55, 5658–5667. [Google Scholar] [CrossRef]
- Huang, L.; Long, T.; Mao, E.; So, H.C. MMSE-based MDL method for robust estimation of number of sources without eigendecomposition. IEEE Trans. Signal Process 2009, 57, 4135–4142. [Google Scholar] [CrossRef]
- Wang, H.; Kaveh, M. On the performance of signal-subspace processing—Part I: Narrow-band systems. IEEE Trans. Acoust. Speech Signal Process 1986, 34, 1201–1209. [Google Scholar] [CrossRef]
- Kaveh, M.; Wang, H.; Hung, H. On the theoretical performance of a class of estimators of the number of narrow-band sources. IEEE Trans. Acoust. Speech Signal Process 1987, 35, 1350–1352. [Google Scholar] [CrossRef]
- Zhang, Q.T.; Wong, K.M.; Yip, P.C.; Reilly, J.P. Statistical analysis of the performance of information theoretic criteria in the detection of the number of signals in array processing. IEEE Trans. Acoust. Speech Signal Process 1989, 37, 1557–1567. [Google Scholar] [CrossRef]
- Xu, W.; Kaveh, M. Analysis of the performance and sensitivity of eigendecomposition-based detectors. IEEE Trans. Signal Process 1995, 43, 1413–1426. [Google Scholar]
- Liavas, A.P.; Regalia, P.A. On the behavior of information theoretic criteria for model order selection. IEEE Trans. Signal Process 2001, 49, 1689–1695. [Google Scholar] [CrossRef]
- Fishler, E.; Grosmann, M.; Messer, H. Detection of signals by information theoretic criteria: General asymptotic performance analysis. IEEE Trans. Signal Process 2002, 50, 1027–1036. [Google Scholar] [CrossRef]
- Delmas, J.P.; Meurisse, Y. Performance analysis of MDL criterion for the detection of noncircular or/and non-Gaussian components. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4188–4191. [Google Scholar]
- Delmas, J.P.; Meurisse, Y. On the second-order statistics of the EVD of sample covariance matrices—Application to the detection of noncircular or/and nonGaussian components. IEEE Trans. Signal Process 2011, 59, 4017–4023. [Google Scholar] [CrossRef]
- Nadler, B. Nonparametric detection of signals by information theoretic criteria: Performance analysis and an improved estimator. IEEE Trans. Signal Process 2010, 58, 2746–2756. [Google Scholar] [CrossRef]
- Haddadi, F.; Malek-Mohammadi, M.; Nayebi, M.M.; Aref, M.R. Statistical performance analysis of MDL source enumeration in array processing. IEEE Trans. Signal Process 2010, 58, 452–457. [Google Scholar] [CrossRef]
- Huang, L.; Xiao, Y.; Liu, K.; So, H.C.; Zhang, J. Bayesian information criterion for source enumeration in large-scale adaptive antenna array. IEEE Trans. Veh. Technol 2015. [Google Scholar] [CrossRef]
- Lu, Z.; Zoubir, A.M. Flexible detection criterion for source enumeration in array processing. IEEE Trans. Signal Process 2013, 61, 1303–1314. [Google Scholar] [CrossRef]
- Muirhead, R.J. Aspects of Multivariate Statistical Theory; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Bai, Z.D.; Silverstein, J.W. Spectral Analysis of Large Dimensional Random Matrices, 2nd ed.; Springer-Verlag: New York, NY, USA, 2010. [Google Scholar]
- Yi, H. Local Signal Search Enhanced RMT Estimator for Estimating the Number of Signals based on Random Matrix Theory. Available online: http://arxiv.org/abs/1405.4713 (accessed on 14 October 2014).
- Kritchman, S.; Nadler, B. Non-parametric detection of the number of signals: Hypothesis testing and random matrix theory. IEEE Trans. Signal Process 2009, 57, 3930–3941. [Google Scholar] [CrossRef]
- Nadakuditi, R.R.; Edelman, A. Sample eigenvalue based detection of high-dimensional signals in white noise using relatively few samples. IEEE Trans. Signal Process 2008, 56, 2625–2638. [Google Scholar] [CrossRef]
- Nadakuditi, R.R.; Edelman, A. Fundamental limit of sample generalized eigenvalue based detection of signals in noise using relatively few signal-bearing and noise-only samples. IEEE J. Sel. Top. Sign. Process 2010, 4, 468–480. [Google Scholar] [CrossRef]
- Lawley, D.N. Tests of significance for the latent roots of covariance and correlation matrices. Biometrika 1956, 43, 128–136. [Google Scholar] [CrossRef]
- Ding, Q.; Kay, S. Inconsistency of the MDL: On the performance of model order selection criteria with increasing signal-to-noise ratio. IEEE Trans. Signal Process 2011, 59, 1959–1969. [Google Scholar] [CrossRef]
- Hinkley, D.V. On the ratio of two correlated normal random variables. Biometrika 1969, 56, 635–639. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, F.; Li, Y.; Jin, S. Statistical Analysis of the Performance of MDL Enumeration for Multiple-Missed Detection in Array Processing. Sensors 2015, 15, 20250-20266. https://doi.org/10.3390/s150820250
Du F, Li Y, Jin S. Statistical Analysis of the Performance of MDL Enumeration for Multiple-Missed Detection in Array Processing. Sensors. 2015; 15(8):20250-20266. https://doi.org/10.3390/s150820250
Chicago/Turabian StyleDu, Fei, Yibo Li, and Shijiu Jin. 2015. "Statistical Analysis of the Performance of MDL Enumeration for Multiple-Missed Detection in Array Processing" Sensors 15, no. 8: 20250-20266. https://doi.org/10.3390/s150820250