Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding
Abstract
:1. Introduction
2. Statistical Locally Linear Embedding Algorithm
2.1. Locally Linear Embedding Algorithm
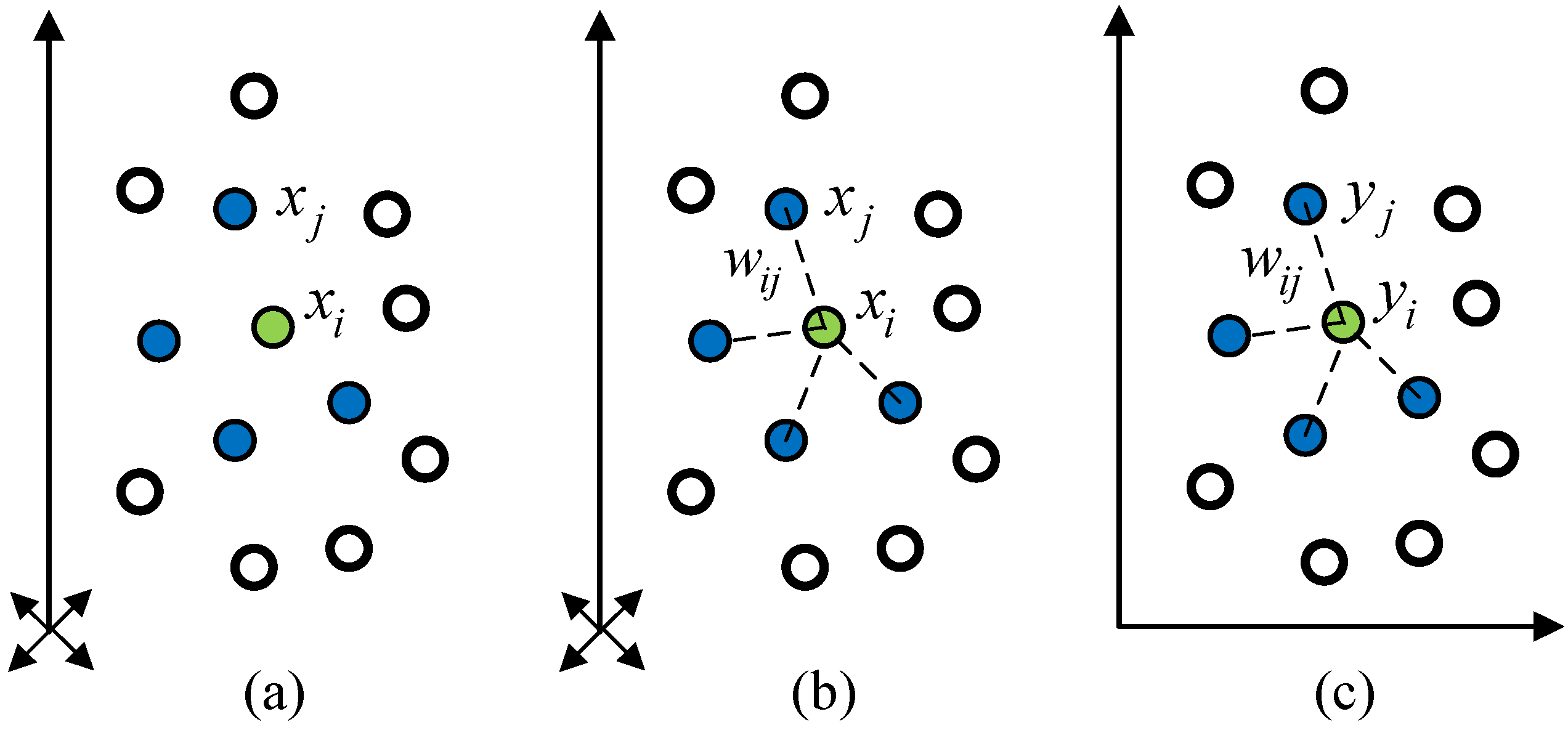
2.2. Statistical Locally Linear Embedding Algorithm
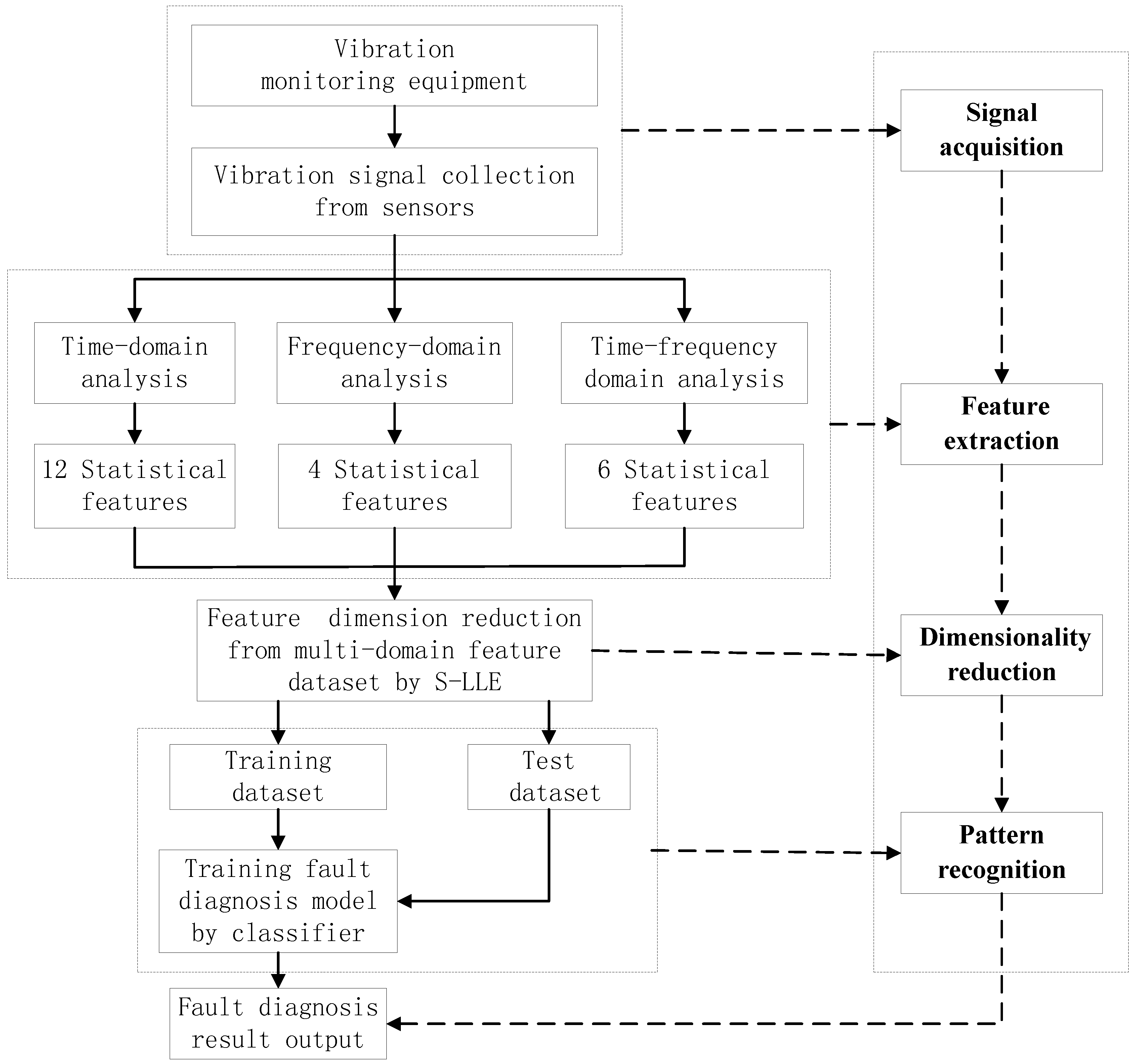
3. Statistical Locally Linear Embedding Algorithm for Bearing Fault Diagnosis
- (1)
- Signal acquisition: The acquisition of the original vibration signals is the first step in the rolling bearing fault diagnosis process.
- (2)
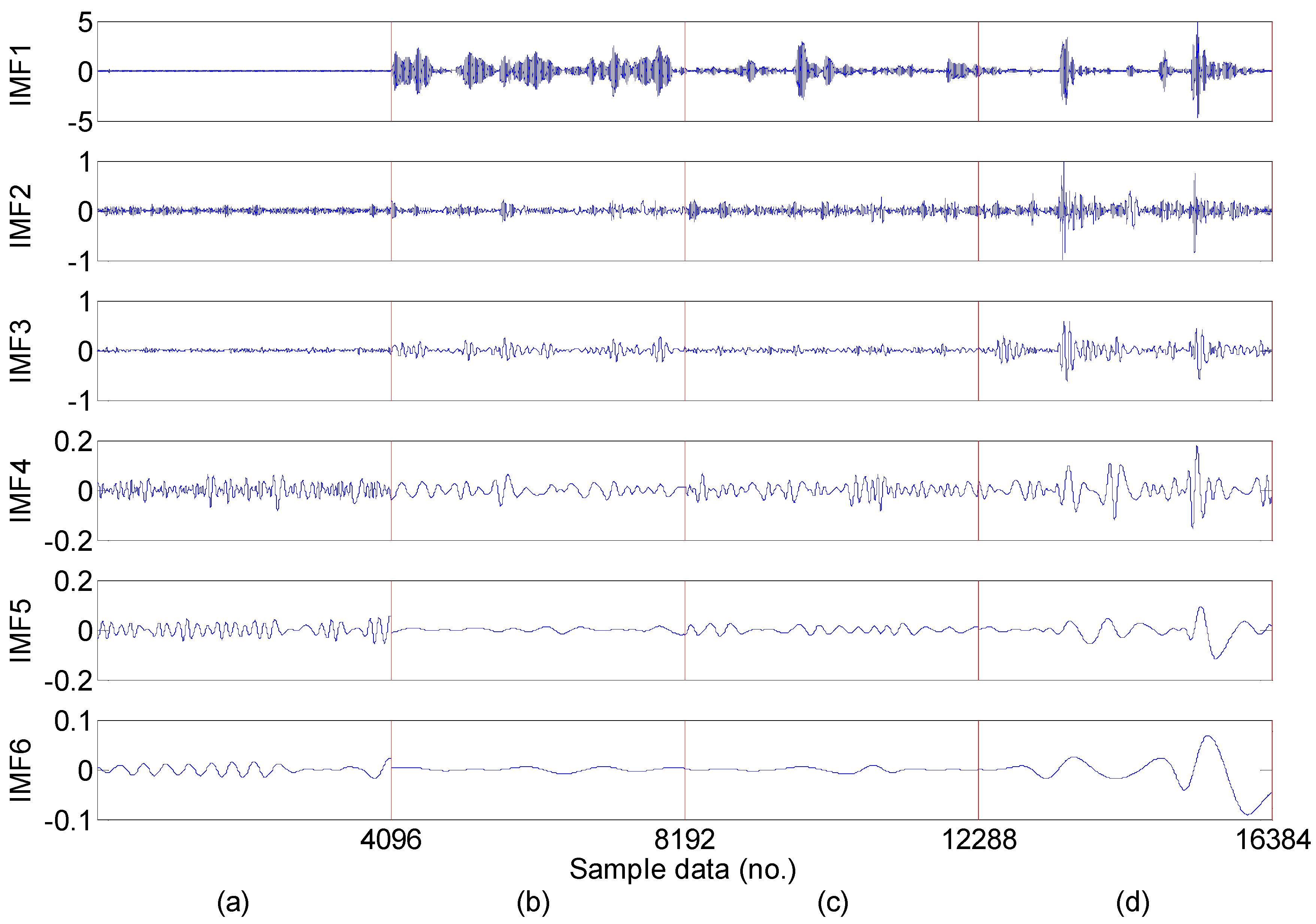
- Feature extraction: Feature extraction directly characterizes the information relevant to the bearing conditions and greatly affects the final diagnosis results. The time-domain, frequency-domain and time–frequency domain features extracted from the original vibration signal by the empirical mode decomposition method are utilized to construct the multi-domain fault feature dataset.
- (3)
- Dimensionality reduction: The multi-domain feature set can fully represent the bearing faults. However, all of these high-dimensional feature vectors are not independent of each other and there is much redundant information embedded in the high-dimensional feature space. In addition, different features have different importance in the different fault states. In order to reduce the computation time for the diagnosis model, the supervised manifold learning method S-LLE is used to select the salient features from the raw statistical feature dataset.
- (4)
- Pattern recognition: Implementing fault classification of the training samples in the low-dimensional embedded space according to class label information and learning geometric structure feature by optimized classifiers. To test the dataset, we also map it onto the same feature space according to the mapping matrix of the training dataset, and evaluate the classification capability. Finally, pattern recognition is carried out in the embedded spaces. In order to reliably diagnose complex roller bearing faults, the proposed fault diagnosis approach is applied for the roller bearings fault diagnosis.
- (1)
- The method is based on nonlinear dimensionality reduction and can treat high-dimensional nonlinear data, which avoids the “curse of dimensionality”.
- (2)
- The method can capture more accurately the intrinsic geometric distribution properties of samples by the sample label information, and utilize the obtained distribution feature to classify the fault category.
- (3)
- The feature extraction method based on time-domain, frequency-domain and time-frequency domain is simple and the implementation speed is high, which greatly reduces the fault diagnosis difficulties.
4. High-Dimensional Fault Features Extracted from Accelerometer Sensor Vibration Signals
| No. | Dimensional Features | Feature Definition | No. | Dimensionless Features | Feature Definition |
|---|---|---|---|---|---|
| 1 | Mean | 7 | Shape factor | ||
| 2 | Root mean square | 8 | Crest factor | ||
| 3 | Root | 9 | Impulse factor | ||
| 4 | Standard deviation | 10 | Clearance factor | ||
| 5 | Skewness | 11 | Skewness factor | ||
| 6 | Kurtosis | 12 | Kurtosis factor |
| No. | Features | Feature Definition | No. | Features | Feature Definition |
|---|---|---|---|---|---|
| 1 | Mean frequency | 3 | Frequency center | ||
| 2 | Root mean square frequency | 4 | Root variance frequency |
- (1)
- In the whole dataset, the number of extrema and the number of zero crossings must either equal or differ by at most one;
- (2)
- At any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero.
5. Roller Bearing Fault Diagnosis Experiments and Analysis
5.1. Experiment Setup and Signal Acquisition

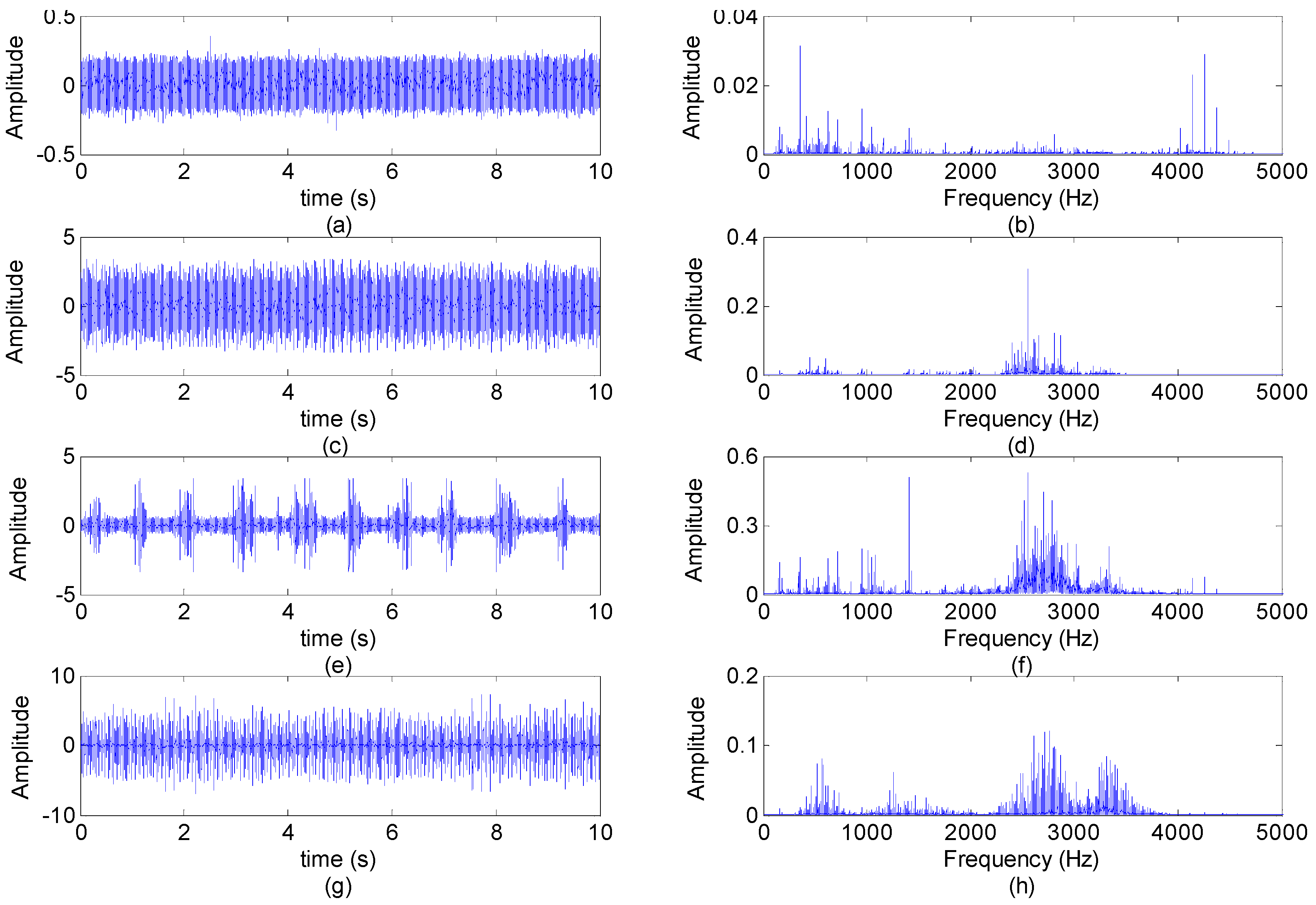
5.2. Feature Extraction
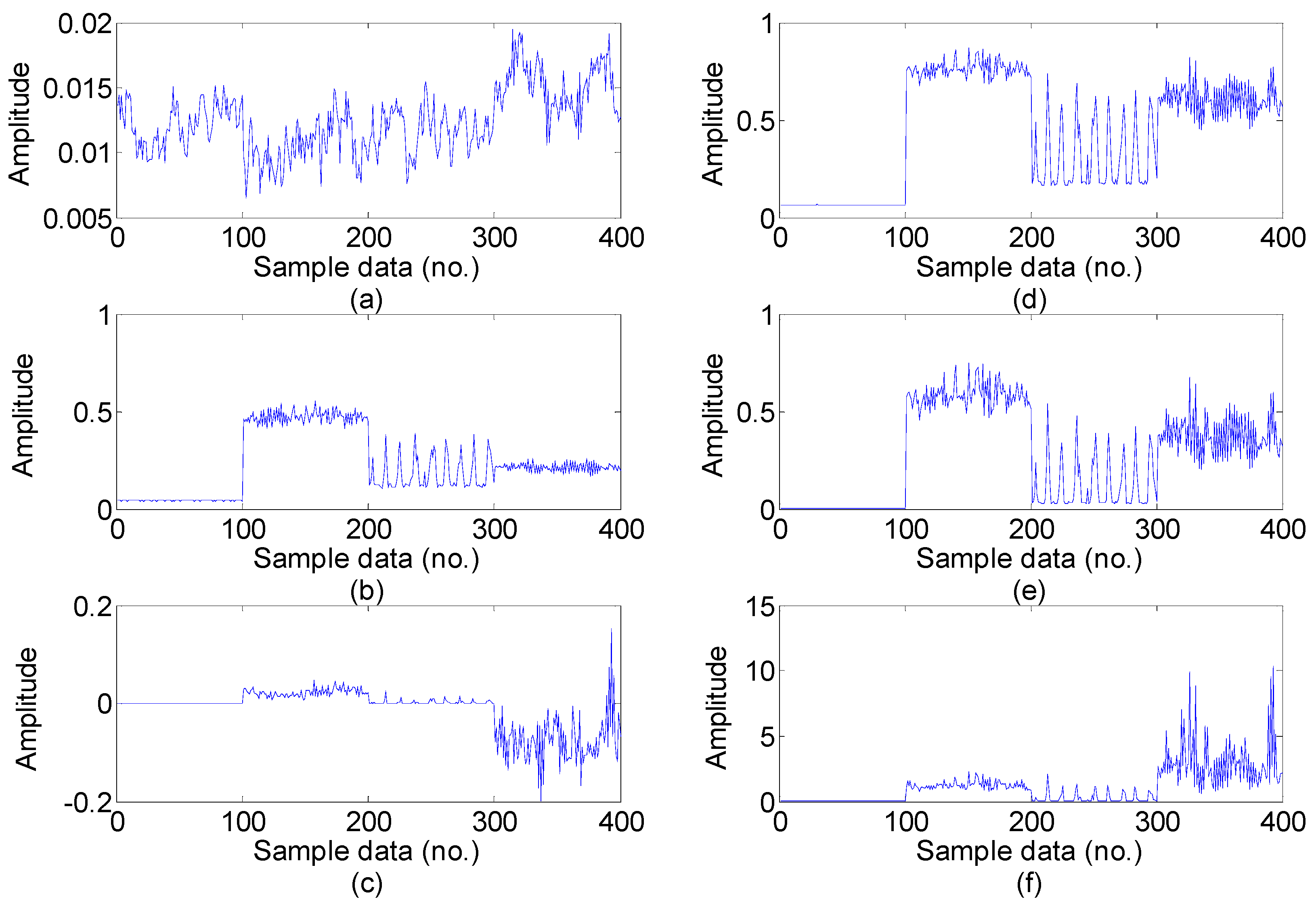
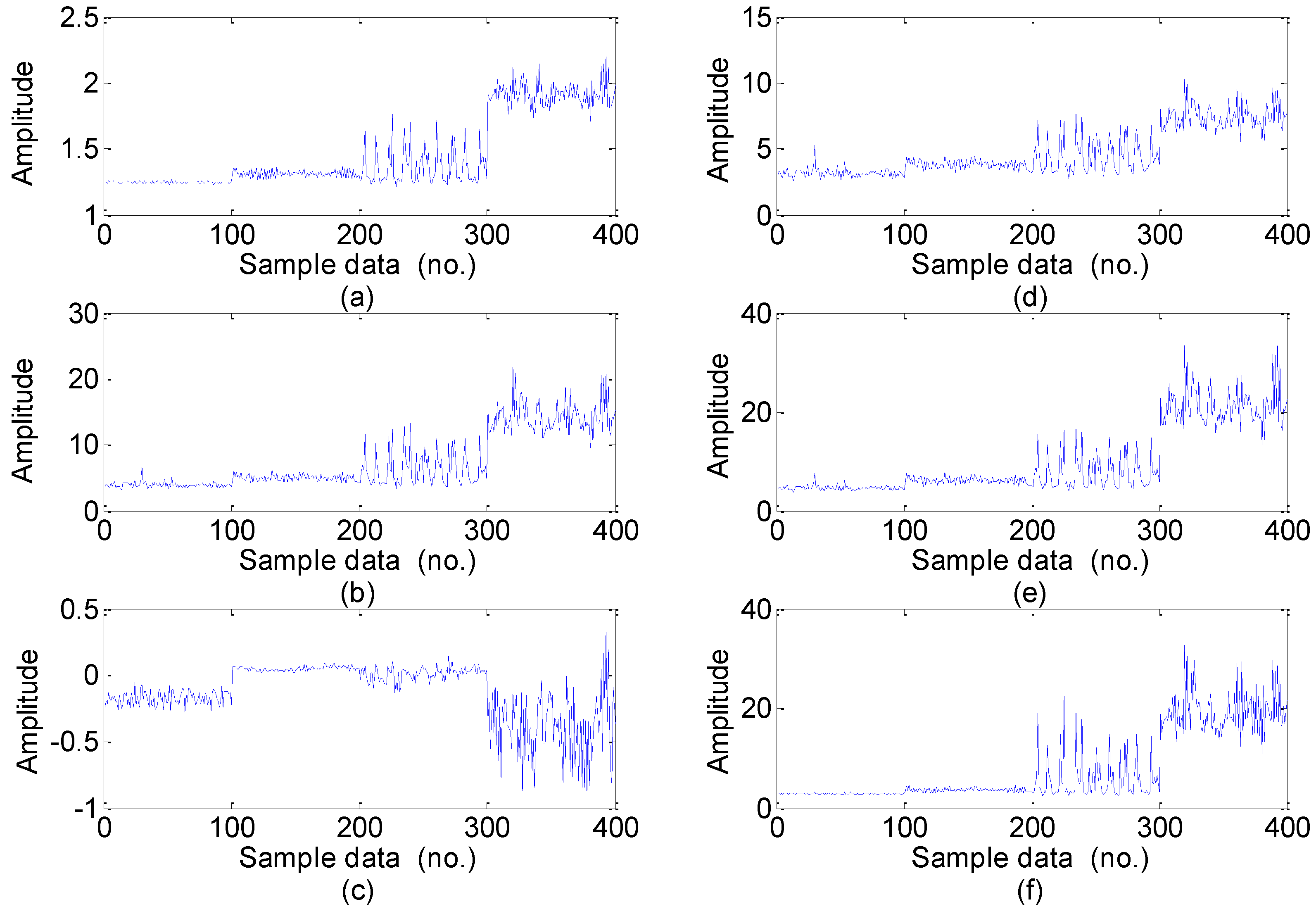
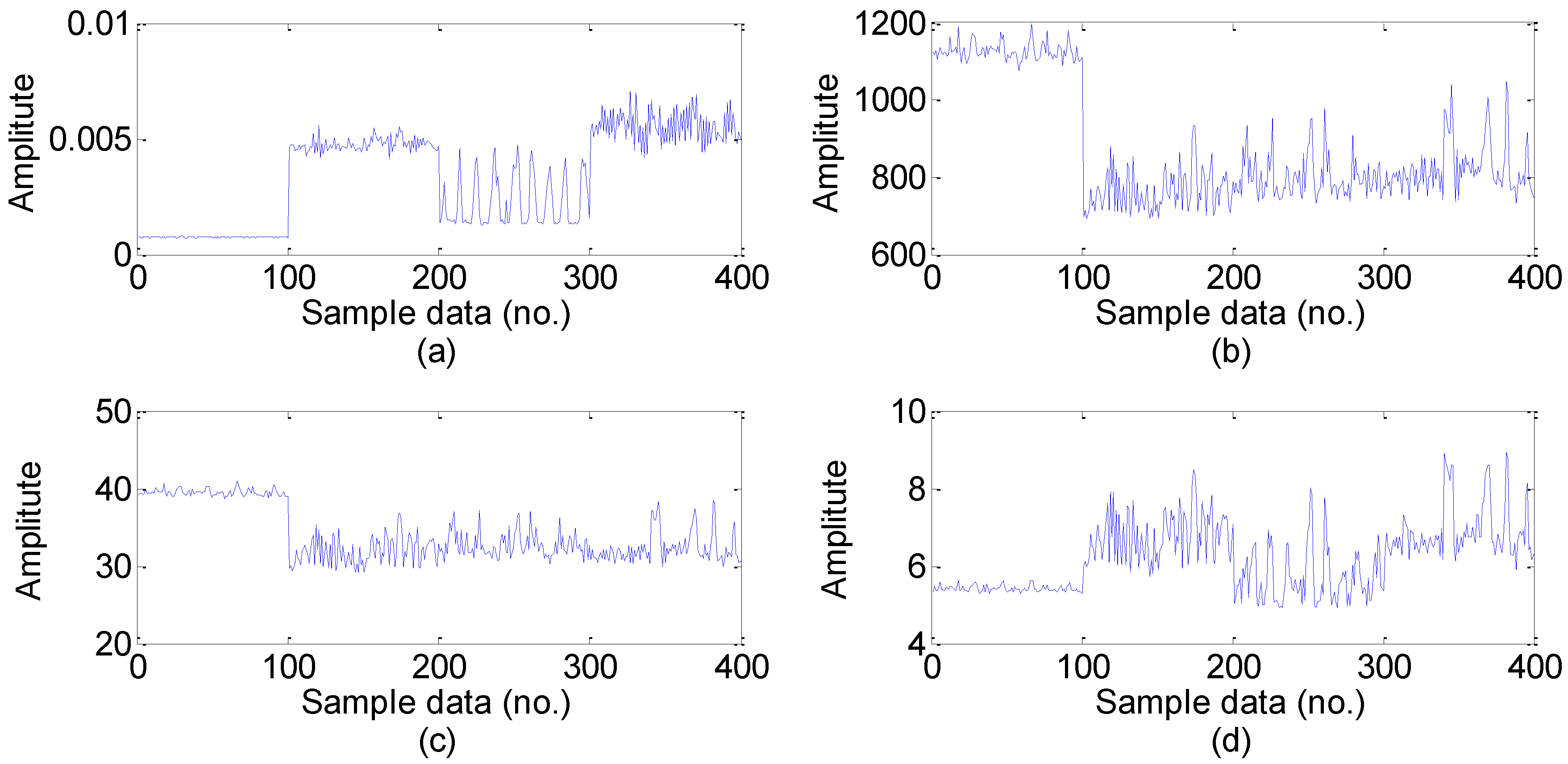
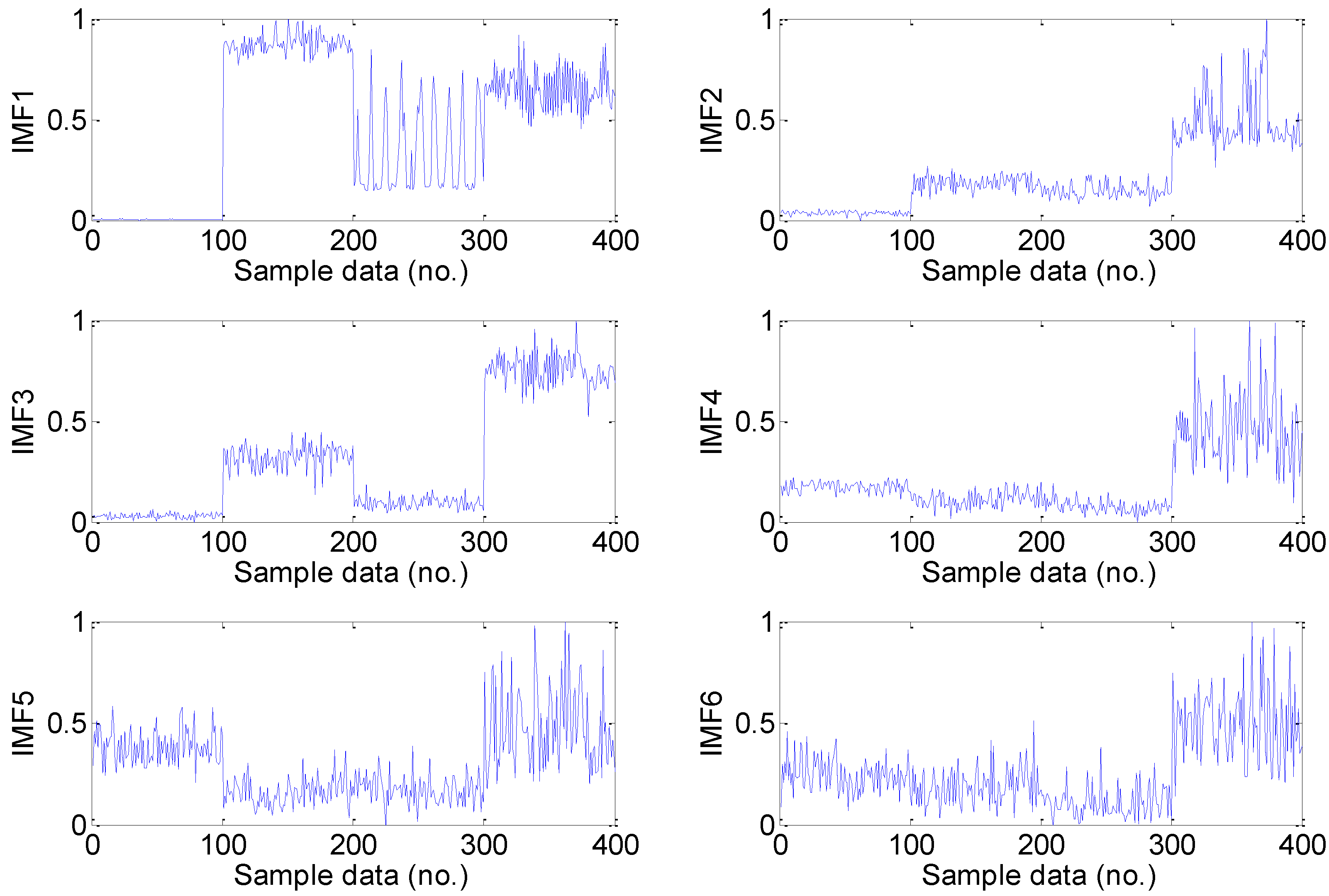
5.3. Feature Dimension Reduction
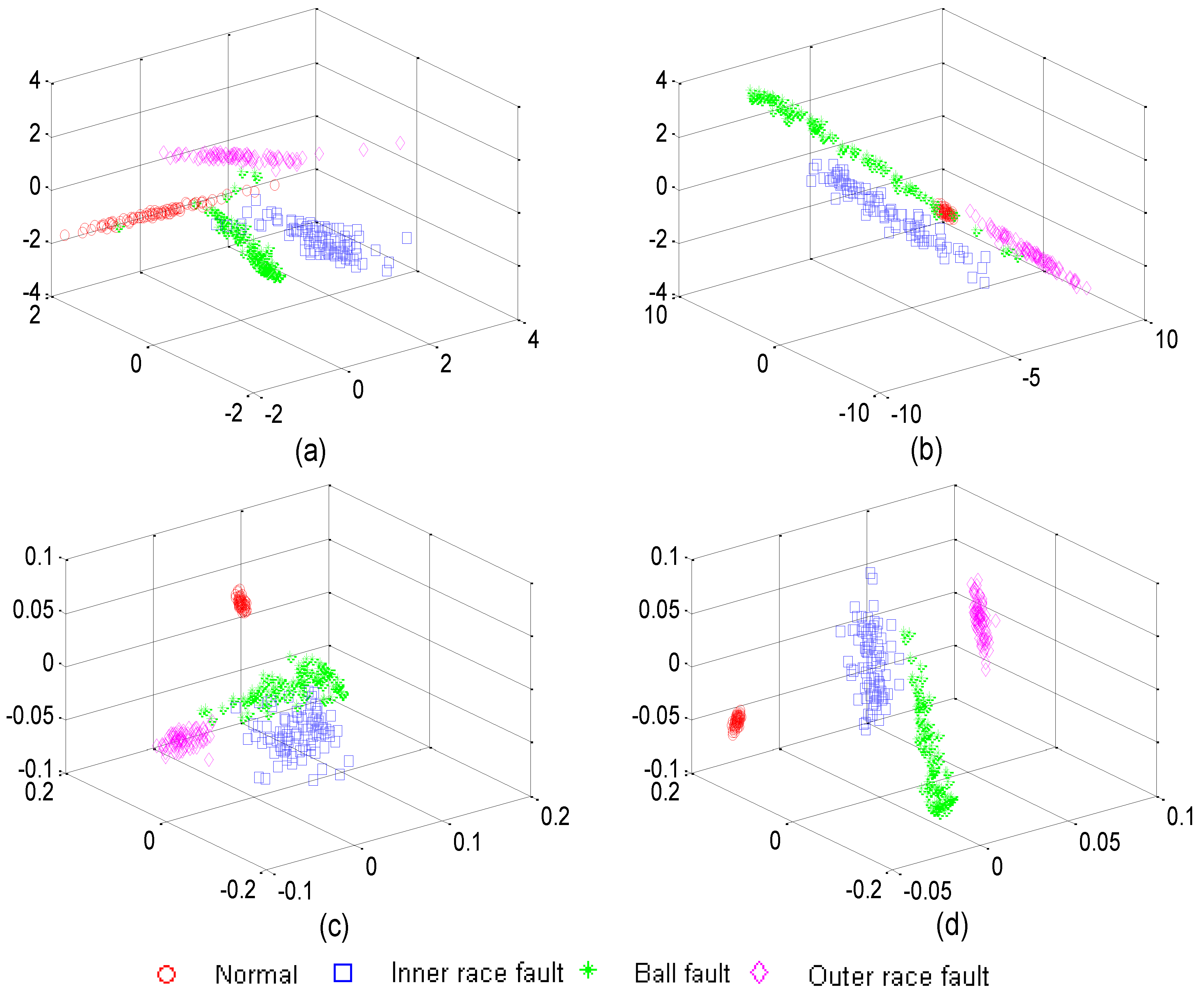
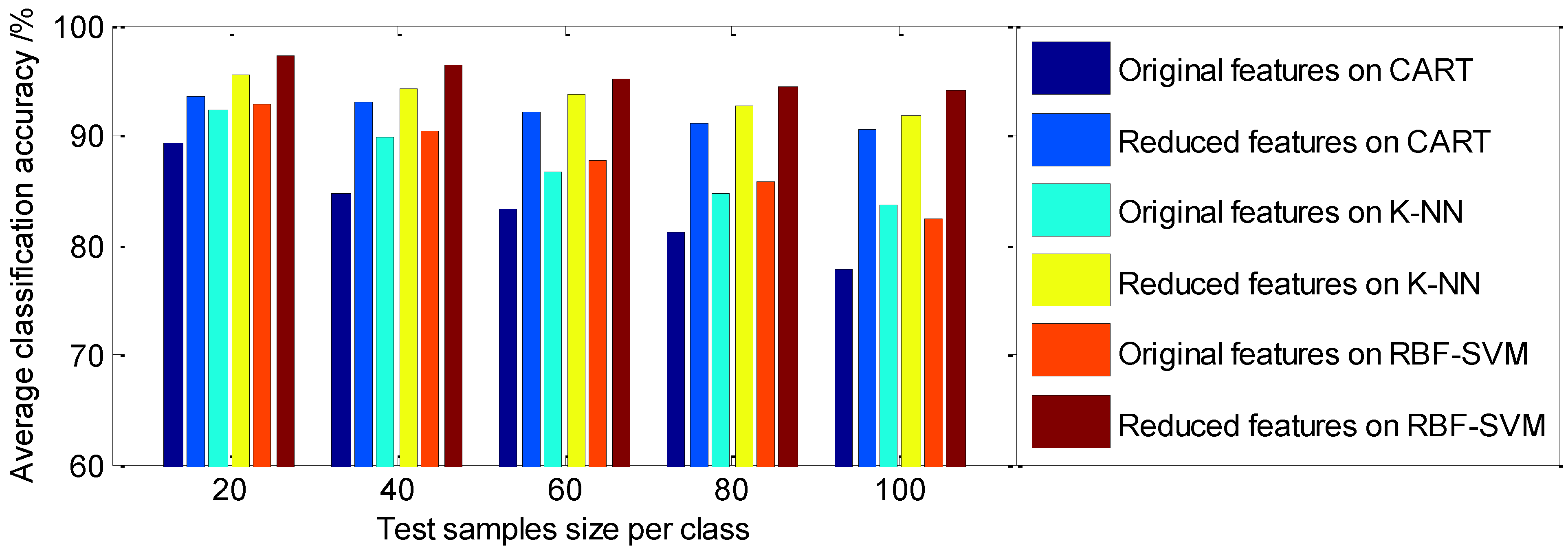
5.4. Classification Performance Analysis
| Test Samples Size per Class | CART | K-NN | RBF-SVM | |||
|---|---|---|---|---|---|---|
| Original Feature | Reduced Feature | Original Feature | Reduced Feature | Original Feature | Reduced Feature | |
| 20 | 89.24 | 93.56 | 92.35 | 95.43 | 92.79 | 97.26 |
| 40 | 84.63 | 93.05 | 89.87 | 94.25 | 90.35 | 96.34 |
| 60 | 83.35 | 92.17 | 86.61 | 93.78 | 87.63 | 95.22 |
| 80 | 81.14 | 91.10 | 84.75 | 92.63 | 85.81 | 94.35 |
| 100 | 77.76 | 90.54 | 83.56 | 91.84 | 82.32 | 94.07 |
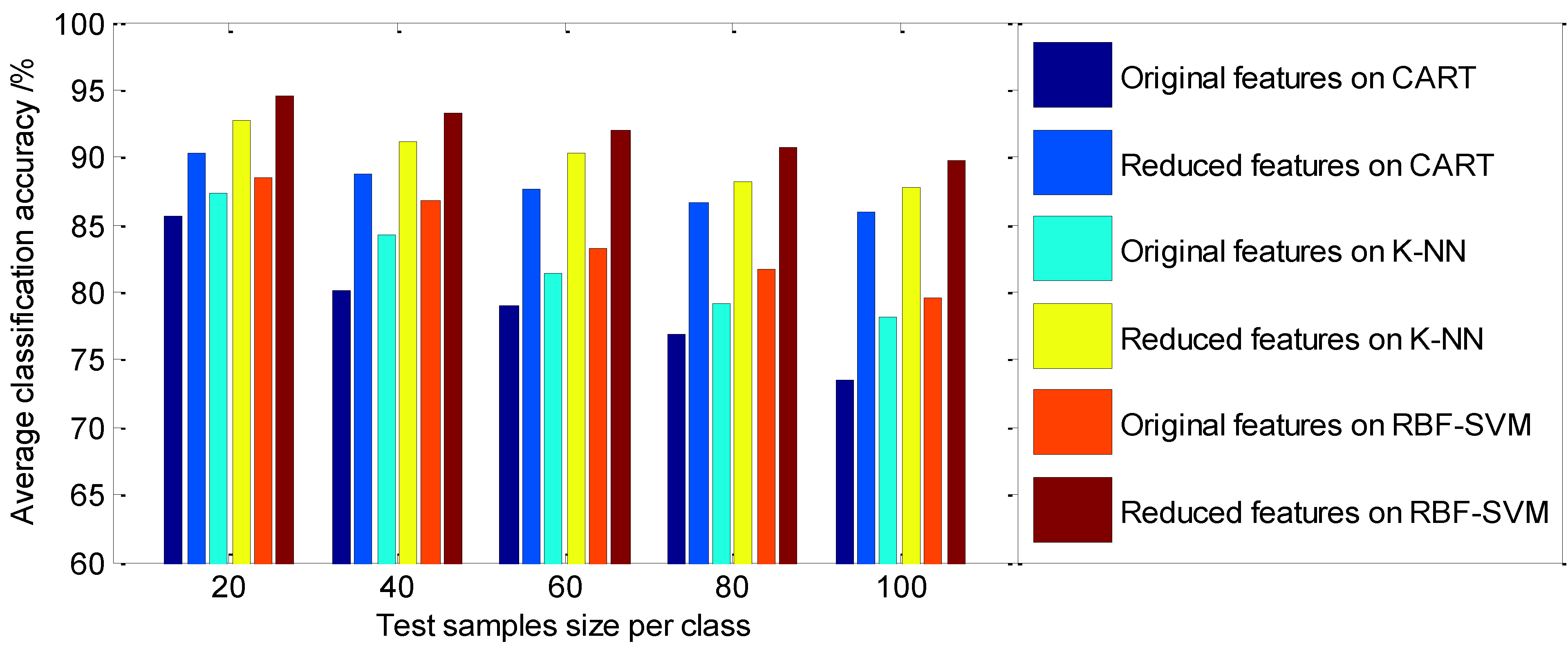
| Test Samples Size per Class | CART | K-NN | RBF-SVM | |||
|---|---|---|---|---|---|---|
| Original Feature | Reduced Feature | Original Feature | Reduced Feature | Original Feature | Reduced Feature | |
| 20 | 85.72 | 90.34 | 87.38 | 92.67 | 88.45 | 94.53 |
| 40 | 80.12 | 88.75 | 84.26 | 91.19 | 86.73 | 93.34 |
| 60 | 78.95 | 87.63 | 81.47 | 90.26 | 83.24 | 92.06 |
| 80 | 76.84 | 86.58 | 79.15 | 88.23 | 81.76 | 90.69 |
| 100 | 73.45 | 85.93 | 78.22 | 87.84 | 79.57 | 89.78 |
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, F.F.; Tang, B.P.; Song, T.; Li, L. Multi-fault diagnosis study on roller bearing based on multi-kernel support vector machine with chaotic particle swarm optimization. Measurement 2014, 47, 576–590. [Google Scholar] [CrossRef]
- Jiang, L.; Xuan, J.P.; Shi, T.L. Feature extraction based on semi-supervised kernel Marginal Fisher analysis and its application in bearing fault diagnosis. Mech. Syst. Sign. Process. 2013, 41, 113–126. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Principal Component Analysis, Series: Springer Series in Statistics, 2nd ed.; Springer: New York, NY, USA, 2010. [Google Scholar]
- Borg, I.; Groenen, P. Modern Multidimensional Scaling: Theory and Applications, 2nd ed.; Springer: New York, NY, USA, 2005; pp. 207–212. [Google Scholar]
- Martinez, A.M.; Kak, A.C. PCA versus LDA. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 228–233. [Google Scholar] [CrossRef]
- Lerner, B.; Guterman, H.; Aladjem, M.; Dinstein, I. On the Initialisation of Sammon’s Nonlinear Mapping. Pattern Anal. Appl. 2000, 3, 61–68. [Google Scholar] [CrossRef]
- Dong, D.; McAvoy, T.J. Nonlinear principal component analysis based on principal curves and neural networks. Comput. Chem. Eng. 1996, 20, 65–78. [Google Scholar] [CrossRef]
- Seung, H.S.; Daniel, D.L. The manifold ways of perception. Science 2000, 290, 2268–2269. [Google Scholar] [CrossRef] [PubMed]
- Roweis, S.T.; Saul, L.K. Nonlinear dimensionality reduction by locally linear embedding. Science 2000, 290, 2323–2326. [Google Scholar] [CrossRef] [PubMed]
- Tenenbaum, J.B.; Silva, V.D.; Langford, J.C. A global geometric framework for nonlinear dimensionality reduction. Science 2000, 290, 2319–2323. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.Y.; Zha, H.Y. Principal Manifolds and Nonlinear Dimension Reduction via Local Tangent Space Alignment. SIAM J. Sci. Comput. 2004, 26, 313–338. [Google Scholar] [CrossRef]
- Liu, X.; Tosun, D.; Weiner, M.W.; Schuff, N. Locally linear embedding (LLE) for MRI based Alzheimer’s disease classification. Neuroimage 2013, 83, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Kadoury, S.; Levine, M.D. Face detection in gray scale images using locally linear embeddings. Comput. Vis. Image Underst. 2007, 105, 1–20. [Google Scholar] [CrossRef]
- Hadid, A.; Koouropteva, O.; Pietikainen, M. Unsupervised learning using locally linear embedding: Experiments with face pose analysis. In Proceedings of the 16th International Conference on Pattern Recognition (ICPR 2002), Quebec, QC, Canada, 11–15 August 2002; pp. 111–114.
- Kima, K.; Lee, J. Sentiment visualization and classification via semi-supervised nonlinear dimensionality reduction. Pattern Recognit. 2014, 47, 758–768. [Google Scholar] [CrossRef]
- Yang, J.H.; Xu, J.W.; Yang, D.B. Noise reduction method for nonlinear time series based on principal manifold learning and its application to fault diagnosis. Chin. J. Mech. Eng. 2006, 42, 154–158. [Google Scholar] [CrossRef]
- Ridder, D.D.; Kouropteva, O.; Okun, O.; Pietikäinen, M.; Duin, R.P.W. Supervised locally linear embedding. In Proceedings of the Artificial Neural Networks and Neural Information Processing (ICANN/ICONIP2003), Istanbul, Turkey, 26–29 June 2003; pp. 333–341.
- Genaro, D.S.; German, C.D.; Jose, C.P. Locally linear embedding based on correntropy measure for visualization and classification. Neurocomputing 2012, 80, 19–30. [Google Scholar]
- Zhao, L.X.; Zhang, Z.Y. Supervised locally linear embedding with probability-based distance for classification. Comput. Math. Appl. 2009, 57, 919–926. [Google Scholar] [CrossRef]
- Raducanu, B.; Dornaika, F. A supervised non-linear dimensionality reduction approach for manifold learning. Pattern Recognit. 2012, 45, 2432–2444. [Google Scholar] [CrossRef]
- Zhao, H.T.; Sun, S.Y.; Jing, Z.L. Local structure based supervised feature extraction. Pattern Recognit. 2006, 39, 1546–1550. [Google Scholar] [CrossRef]
- Jiang, Q.S.; Jia, M.P.; Hua, J.Z.; Xu, F.Y. Machinery fault diagnosis using supervised manifold learning. Mech. Syst. Sign. Process. 2009, 23, 2301–2311. [Google Scholar] [CrossRef]
- Su, Z.Q.; Tang, B.P.; Deng, L.; Liu, Z. Fault diagnosis method using supervised extended local tangent space alignment for dimension reduction. Measurement 2015, 62, 1–14. [Google Scholar] [CrossRef]
- Yang, M.H. Class-Conditional Locally Linear Embedding for Classification. Master Thesis, National Cheng Kung University, Tainan, Taiwan, 28 June 2007. [Google Scholar]
- Kanungo, T.; Mount, D.M.; Netanyahu, N.S.; Piatko, C.D.; Silverman, R.; Wu, A.Y. An efficient k-means clustering algorithm: Analysis and implementation. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 881–892. [Google Scholar] [CrossRef]
- Peters, C.A.; Valafar, F. Comparison of three nonparametric density estimation techniques using Bayes’classifier applied to microarray data analysis. In Proceedings of the International Conference on Mathematics and Engineering Techniques in Medicine and Biological Sciences 2003 (METMBS’03), Las Vegas, NV, USA, 23–26 June 2003; pp. 119–125.
- Rafiee, J.; Rafiee, M.A.; Tse, P.W. Application of mother wavelet functions for automatic gear and bearing fault diagnosis. Expert Syst. Appl. 2010, 37, 4568–4579. [Google Scholar] [CrossRef]
- Wang, H.; Chen, P. A feature extraction method based on information theory for fault diagnosis of reciprocating machinery. Sensors 2009, 9, 2415–2436. [Google Scholar] [CrossRef] [PubMed]
- Peng, Z.; Zhang, W.; Lang, Z.; Meng, G.; Chu, F. Time–frequency data fusion technique with application to vibration signal analysis. Mech. Syst. Sign. Process. 2011, 29, 164–173. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. Roy. Soc. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Lei, Y.G.; He, Z.J.; Zi, Y.Y. A new approach to intelligent fault diagnosis of rotating machinery. Expert Syst. Appl. 2008, 35, 1593–1600. [Google Scholar] [CrossRef]
- Yang, Z.; Cai, L.; Gao, L.; Wang, H. Adaptive redundant lifting wavelet transform based on fitting for fault feature extraction of roller bearings. Sensors 2012, 12, 4381–4398. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Chen, J.; Li, X. Bearing performance degradation assessment based on lifting wavelet packet decomposition and fuzzy c-means. Mech. Syst. Sign. Process. 2010, 24, 559–566. [Google Scholar] [CrossRef]
- Lei, Y.G.; Li, N.P.; Lin, J.; Wang, S.Z. Fault diagnosis of rotating machinery based on an adaptive ensemble empirical mode decomposition. Sensors 2013, 13, 16950–16964. [Google Scholar] [CrossRef] [PubMed]
- Shen, Z.J.; Chen, X.F.; Zhang, X.L.; He, Z.J. A novel intelligent gear fault diagnosis model based on EMD and multi-class TSVM. Measurement 2012, 45, 30–40. [Google Scholar] [CrossRef]
- Loparo, K. Bearings Vibration Data Set, Case Western Reserve University. Available online: http://www.eecs.case.edu/laboratory/bearing/welcome_overview.htm (accessed on 20 July 2012).
- Yaqub, M.; Gondal, I.; Kamruzzaman, J. Inchoate fault detection framework: Adaptive selection of wavelet nodes and cumulant orders. IEEE Trans. Instrum. Measur. 2012, 61, 685–695. [Google Scholar] [CrossRef]
- Li, B.; Zhang, P.; Liu, D.; Mi, S.; Ren, G.; Tian, H. Feature extraction for rolling element bearing fault diagnosis utilizing generalized S transform and two-dimensional non-negative matrix factorization. J. Sound Vibr. 2011, 330, 2388–2399. [Google Scholar] [CrossRef]
- Duin, R.P.W.; Juszczak, P.; Paclik, P.; Pekalska, E.; Ridder, D.D.; Tax, D.M.J.; Verzakov, S. PRTools4.1, A Matlab Toolbox for Pattern Recognition; Delft University of Technology: Delft, South Holland, The Netherlands, 2007. [Google Scholar]
- Chang, C.C.; Lin, C.J. LIBSVM: A library for support vector machines. ACM Trans. Intell. Syst. Technol. 2011, 2, 1–27. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Zheng, Y.; Zhao, Z.; Wang, J. Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding. Sensors 2015, 15, 16225-16247. https://doi.org/10.3390/s150716225
Wang X, Zheng Y, Zhao Z, Wang J. Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding. Sensors. 2015; 15(7):16225-16247. https://doi.org/10.3390/s150716225
Chicago/Turabian StyleWang, Xiang, Yuan Zheng, Zhenzhou Zhao, and Jinping Wang. 2015. "Bearing Fault Diagnosis Based on Statistical Locally Linear Embedding" Sensors 15, no. 7: 16225-16247. https://doi.org/10.3390/s150716225





