A Trajectory and Orientation Reconstruction Method for Moving Objects Based on a Moving Monocular Camera
Abstract
:1. Introduction
- (1)
- When the point moves along a straight line, at least five images at different times and positions are required.
- (2)
- A conic trajectory needs at least nine similar images and an initial plane of motion. Furthermore, there is no definite solution when the trajectory of the optical center of the camera and the trajectory of the object are at the same quadric.
- (1)
- To expand the traditional “point intersection” to “trajectory intersection” for object points;
- (2)
- To deduce the conditions of a unique “trajectory intersection” solution;
- (3)
- To extend the method to get the orientations of a rigid body with poor a priori knowledge.
2. Problem Description and Methods
2.1. Problem Description
2.2. Point Models
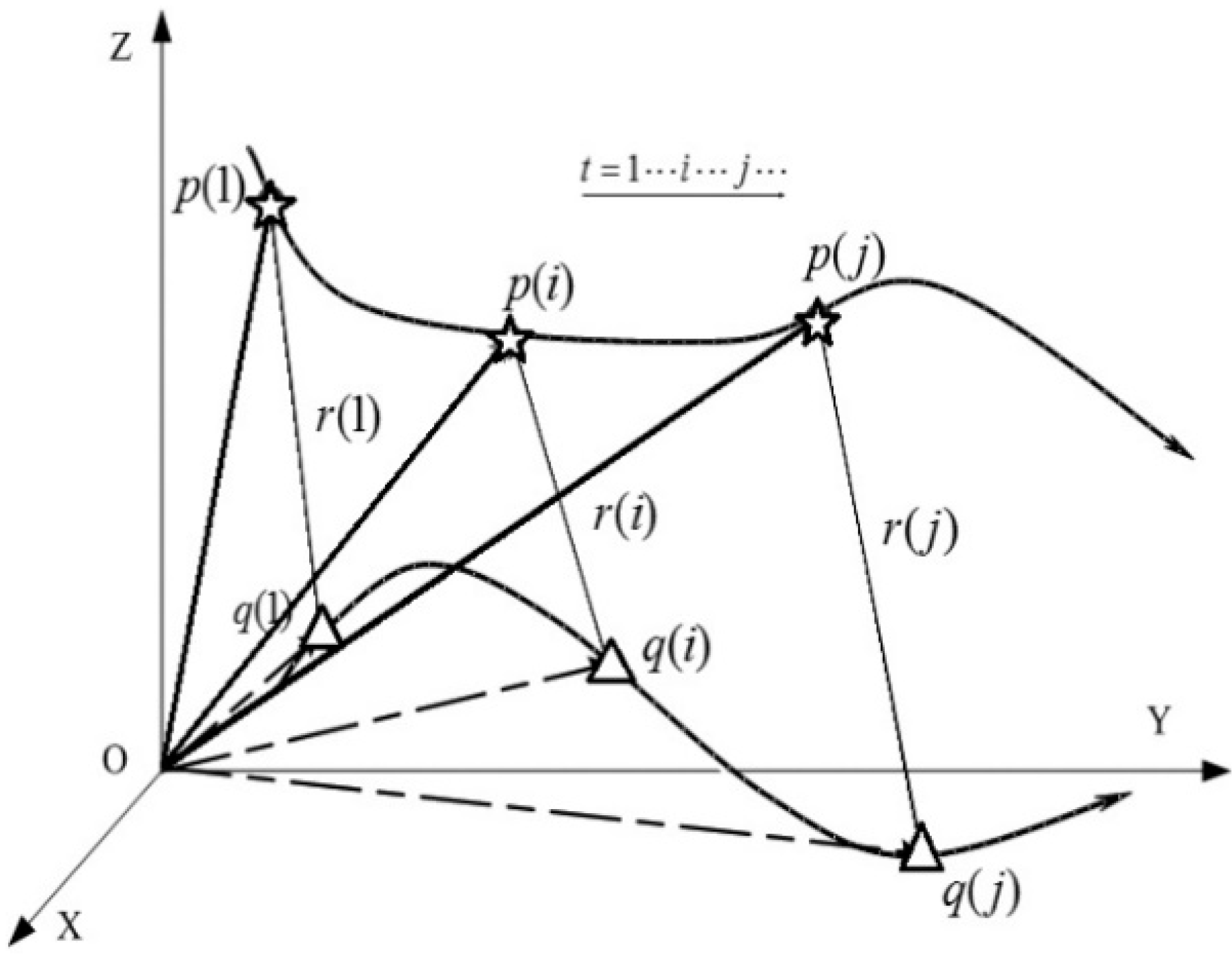
- (1)
- When the moving point can be completely described by a three-dimensional vector function of time with finite order, and if the trajectory of the camera’s optical center can be completely described by a three-dimensional vector function with an order below that of the point, the definite solution can’t be determined.
- (2)
- When all the lines of sight intersect at one point, the definite solution can’t be determined, as shown in Figure 2.
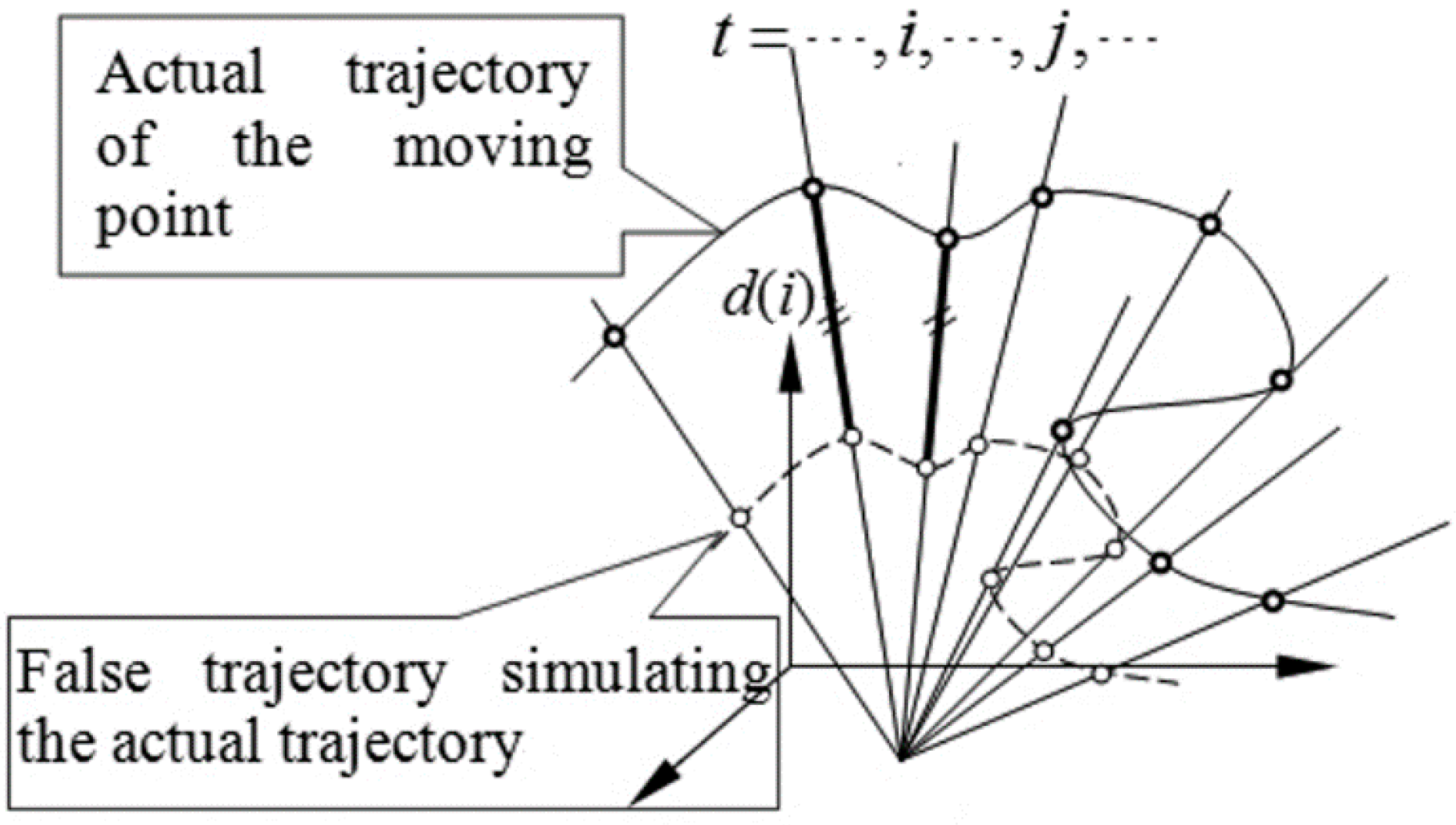
2.3. Required Conditions for Definite Solution of Point Motion
2.4. Solving Method for Position and Orientation of Rigid Body in Motion
- (1)
- How to determine the orientation partially or totally with less than three known points on rigid body?
- (2)
- How to determine the orientation with less than eight unknown points on rigid body?
- (1)
- Solve the initial trajectories value of the points.Assuming the number of points on the moving rigid body is M, the three-dimensional vector qi(t) denote the position of the i-th point at time t. Each initial value of qi(t) can be solved by Equation (3). Technically, the orientations can be estimated now.
- (2)
- Optimize the results with distances invariability to update the value of the trajectory.Based on the nature of rigid body motion, the distance between each point on the rigid body remains unchanged, namely:where, 1< i< M, 1< j< M, I ≠ j. dij is the distance between the i-th point and the j-th point, which is a constant and does not change over time. These constants are taken as constraints to improve the solution accuracy of the position and orientation. The two cases are discussed below, respectively:
- (A)
- Known relationship between pointsIn this situation, dij is known, and Equation (32) is taken as a conditional equation. The correct equation can be established based on the initial value and the known observations, for the solution of qi(t) by Levenberg-Marquard method.
- (B)
- Unknown relationship between pointsFor this case, dij is a constant but unknown. The adjustment process is as follows:
- The initial values of dij at different time are calculated by , then the mean value mdij and standard deviation sdij of over the time can be obtained. The values of dij are set to the mean value of , i.e., mdij.
- Now, dij is as known, Refer to case (A), the optimization of orientation can be obtained.
3. Experiments
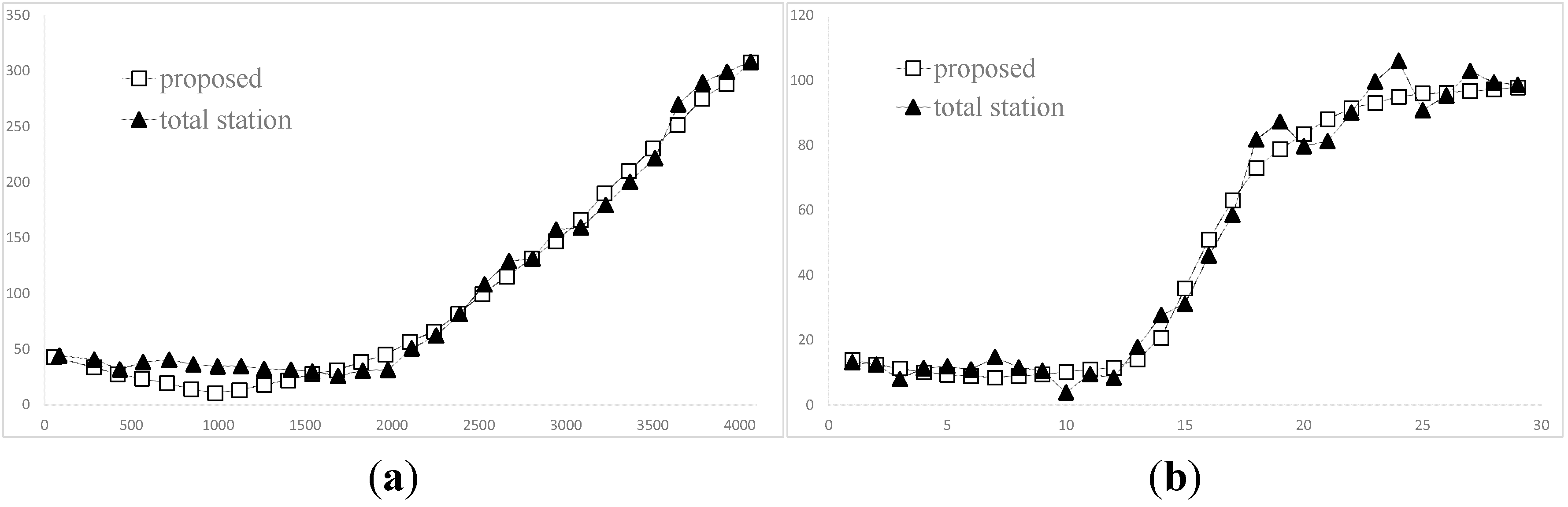
3.1. Reconstruction of 2D Trajectory


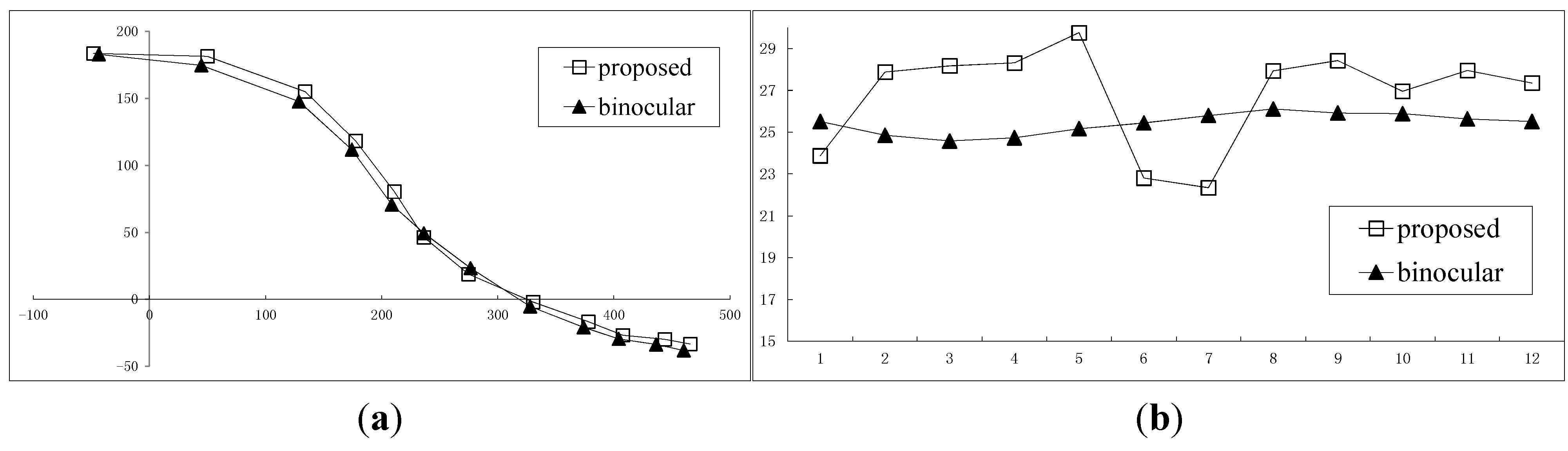
3.2. Reconstruction by Segmentation or by Reduced Order
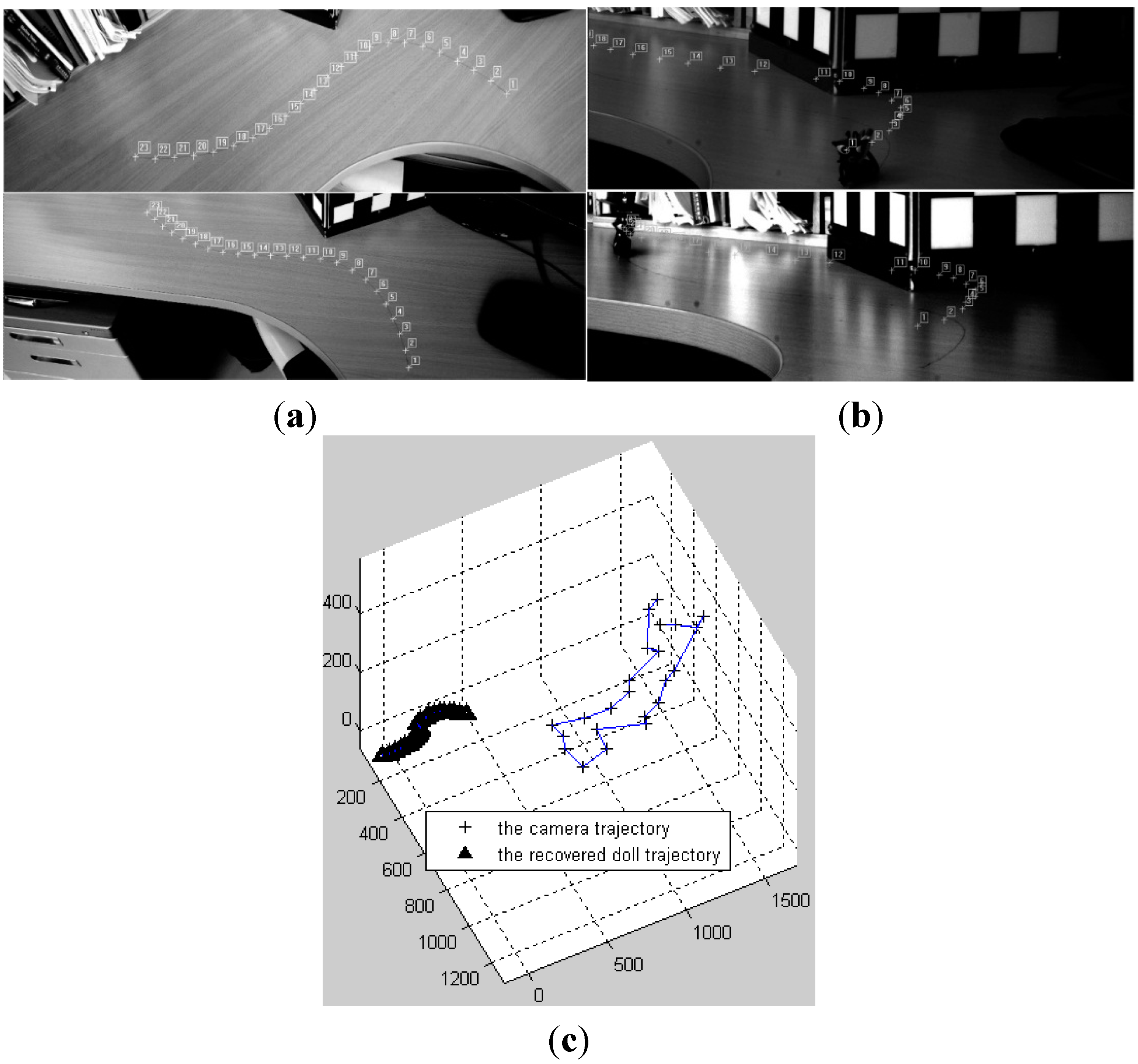
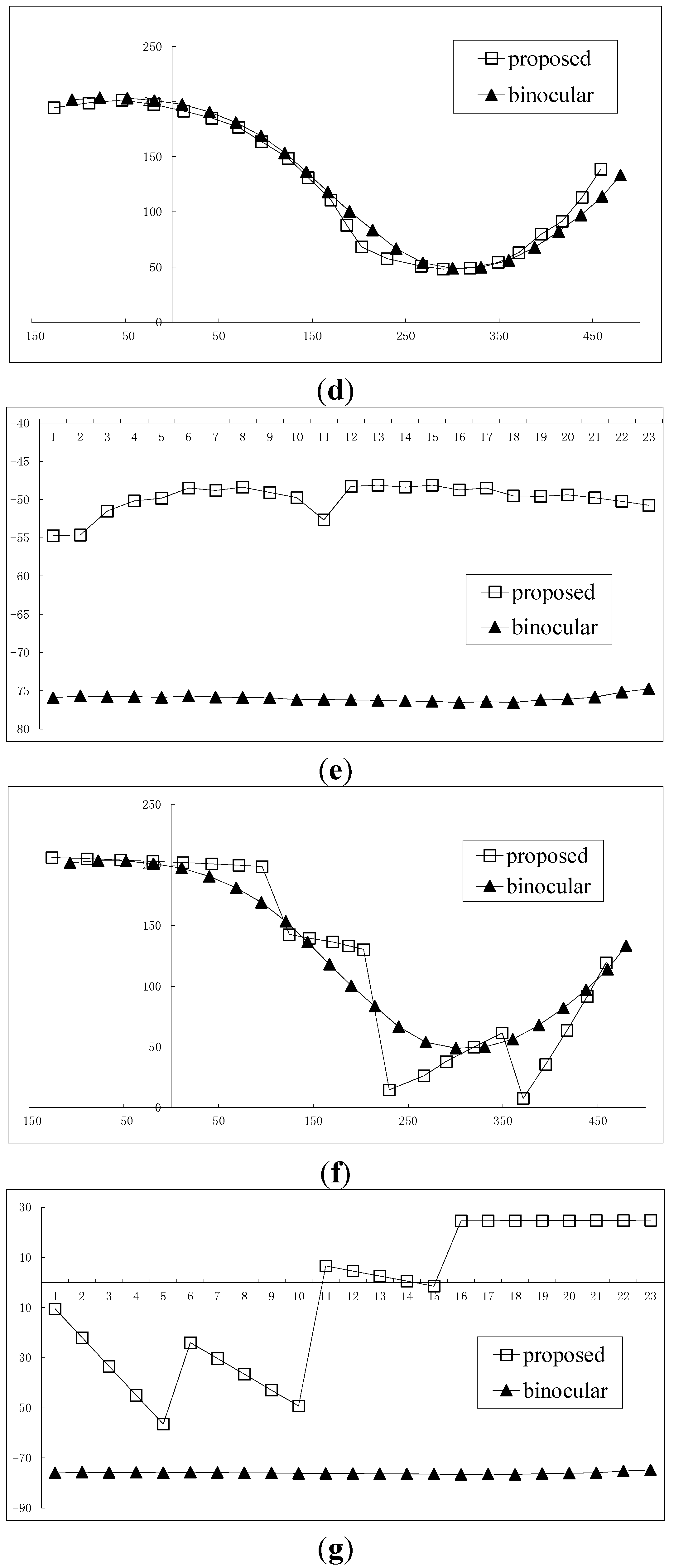

3.3. 3D Trajectory Reconstruction


3.4. Reconstruction of Orientations
3.4.1. Two Points Reconstruction Experiment with Known Distance

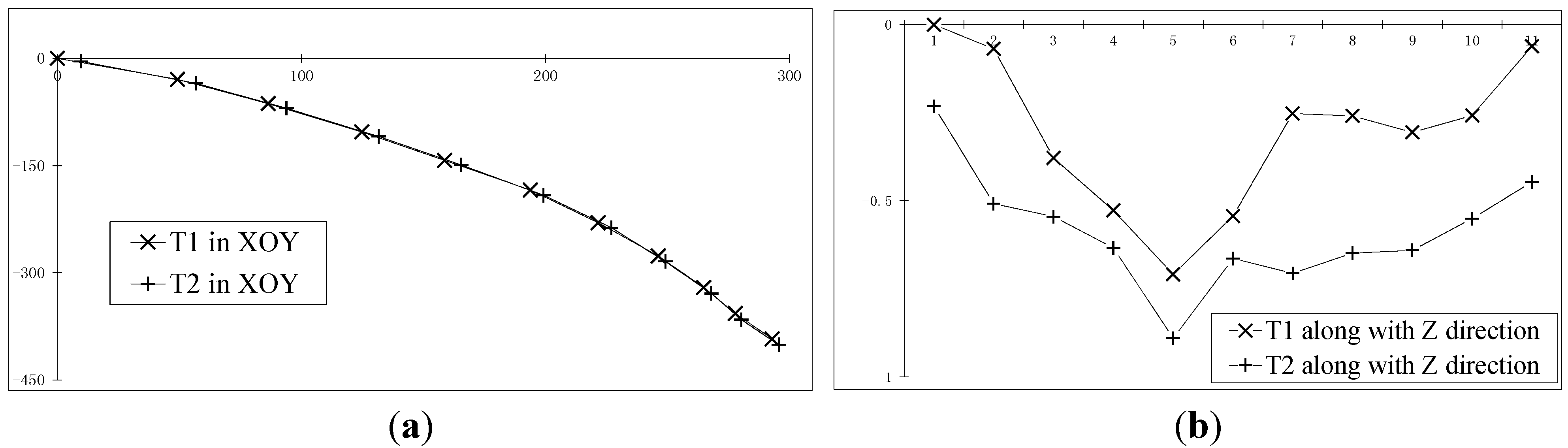

3.4.2. Two Points Reconstruction Experiment for Unknown Distance

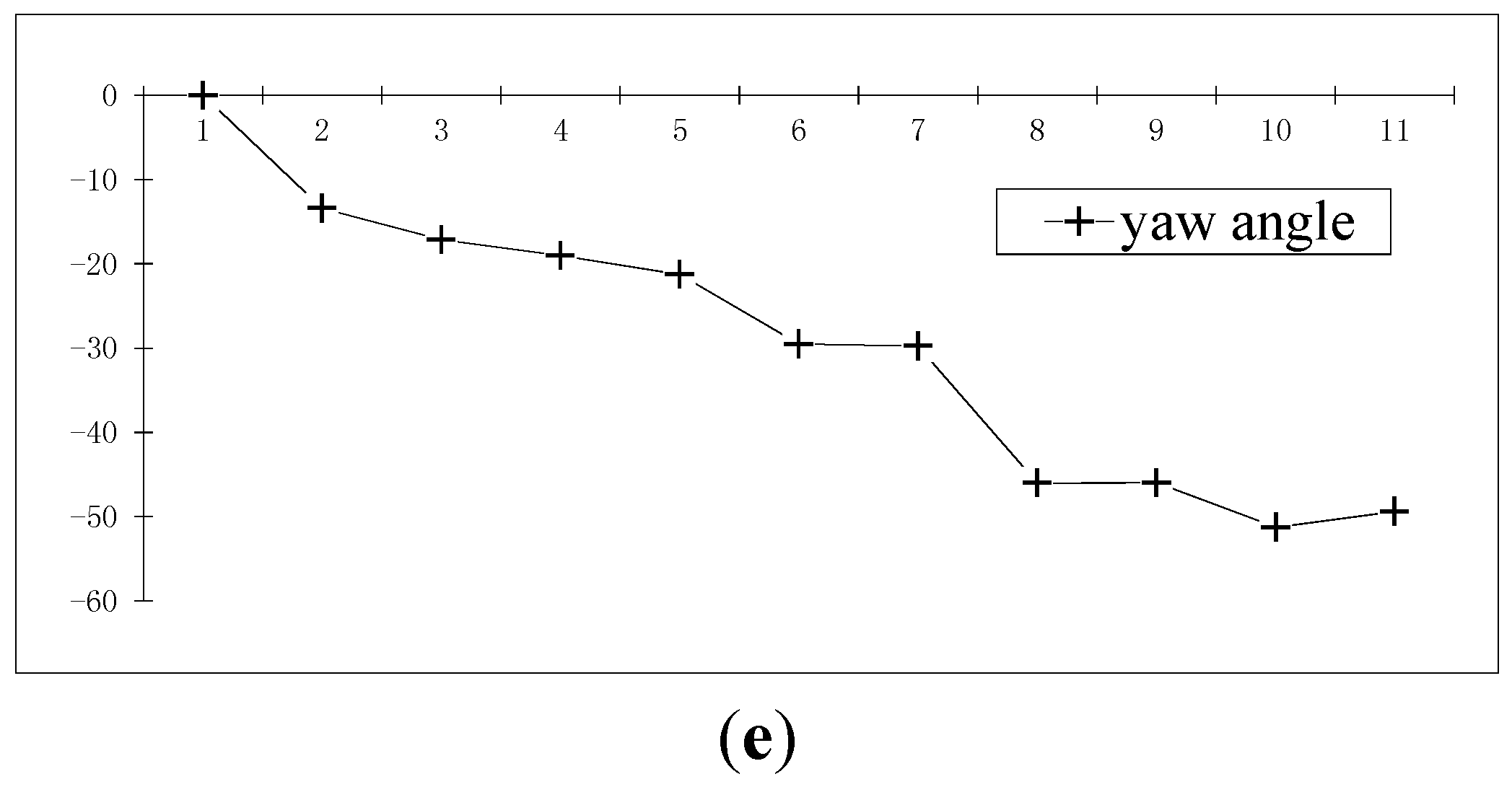
3.4.3. Multi-Points Reconstruction Experiment of Unknown Point Distances

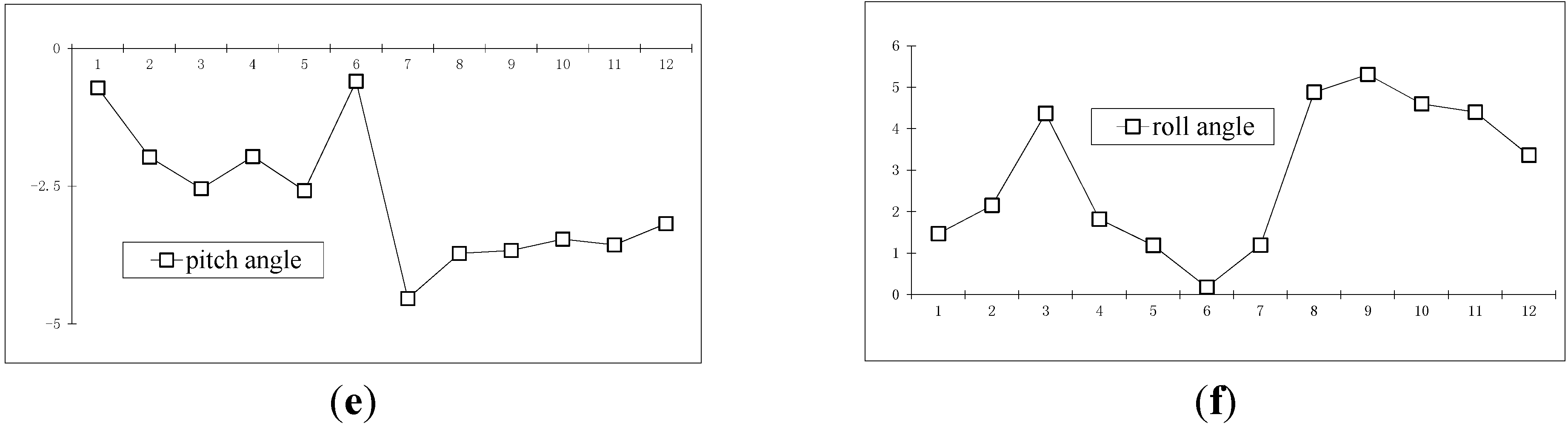
4. Conclusions
- (1)
- How to determine the optimal order of the object motion adaptively?
- (2)
- How to find the optimal time period to calculate as a whole trajectory?
- (3)
- How to get the optimal solution?
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Torr, P.H.S.; Zisserman, A.; Murray, D. Motion Clustering Using the Trilinear Constraint over Three Views. In Europe-China Workshop on Geometrical Modeling and Invariants for Computer Vision; Springer: Heidelberg, Germany, 1995. [Google Scholar]
- Triggs, B. Factorization Methods for Projective Structure and Motion. In Proceedings of the 1996 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’96), San Francisco, CA, USA, 18–20 June 1996; pp. 845–851.
- Leedan, Y.; Meer, P. Estimation with Bilinear Constraints in Computer Vision. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 733–738.
- Pollefeys, M.; Koch, R.; VanGool, L. Self-Calibration and Metric Reconstruction Inspite of Varying and Unknown Intrinsic Camera Parameters. Int. J. Comput. Vis. 1999, 32, 7–25. [Google Scholar]
- Fitzgibbon, A.W.; Zisserman, A. Multibody Structure and Motion: 3-D Reconstruction of Independently Moving Objects. In Computer Vision—ECCV 2000; LNCS 1842; Springer: Berlin/Heidelberg, Germany, 2000; pp. 891–906. [Google Scholar]
- Avidan, S.; Shashua, A. Trajectory Triangulation: 3D Reconstruction of Moving Points from a Monocular Image Sequence. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 348–357. [Google Scholar]
- Avidan, S.; Shashua, A. Triangulation of lines: Reconstruction of a 3D Point Moving along a Line from a Monocular Image Sequence. In Proceedings of the IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Fort Collins, CO, USA, 23–25 June 1999.
- Shashua, A.; Avidan, S.; Werman, M. Trajectory Triangulation over Conic Sections. In Proceedings of the Seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 330–337.
- Han, M.; Kanade, T. Multiple Motion Scene Reconstruction with Uncalibrated Cameras. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 884–894. [Google Scholar]
- Xu, F.; Lam, K.-M.; Dai, Q. Video-object segmentation and 3D-trajectory estimation for monocular video sequences. Image Vis. Comput. 2010, 29, 190–205. [Google Scholar]
- Escobal, P.R. Methods of Orbit Determination; Krieger Publishing: Malabar, FL, USA, 1976. [Google Scholar]
- Hartley, R.; Zisserman, A. Multiple View Geometry in Computer Vision; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Yu, Q.F.; Shang, Y.; Zhou, J.; Zhang, X.H.; Li, L.C. Monocular trajectory intersection method for 3D motion measurement of a point target. Sci. China Ser. E-Technol. Sci. 2009, 52, 3454–3463. [Google Scholar]
- Lu, C.; Hager, G.; Mjolsness, E. Fast and globally convergent pose estimation from video images. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 610–622. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, J.; Shang, Y.; Zhang, X.; Yu, W. A Trajectory and Orientation Reconstruction Method for Moving Objects Based on a Moving Monocular Camera. Sensors 2015, 15, 5666-5686. https://doi.org/10.3390/s150305666
Zhou J, Shang Y, Zhang X, Yu W. A Trajectory and Orientation Reconstruction Method for Moving Objects Based on a Moving Monocular Camera. Sensors. 2015; 15(3):5666-5686. https://doi.org/10.3390/s150305666
Chicago/Turabian StyleZhou, Jian, Yang Shang, Xiaohu Zhang, and Wenxian Yu. 2015. "A Trajectory and Orientation Reconstruction Method for Moving Objects Based on a Moving Monocular Camera" Sensors 15, no. 3: 5666-5686. https://doi.org/10.3390/s150305666




