A Modified Rife Algorithm for Off-Grid DOA Estimation Based on Sparse Representations
Abstract
:1. Introduction
2. Signal Model of DOA Estimation Based on Sparse Representations
2.1. Input Signal Model
2.2. Sparse Representations
2.3. The Proposed SRBWEV Algorithm
- (1)
- EVD for array covariance matrix ;
- (2)
- Determine the number of the larger eigenvalues () and eigenvectors corresponding to larger eigenvalues such as ,,,,,;
- (3)
- Make a single measurement vector combined by linear combination of eigenvectors ,,,,,,where () is the larger eigenvalues of array covariance matrix and ;
- (4)
- Search the index atoms in atomic dictionary by using OMP algorithm;
- (5)
- Output: DOA.
3. Refining the DOA Estimation Using the Rife Algorithm
3.1. Correlation of Two Distinct Dictionary Atoms in Atomic Dictionary
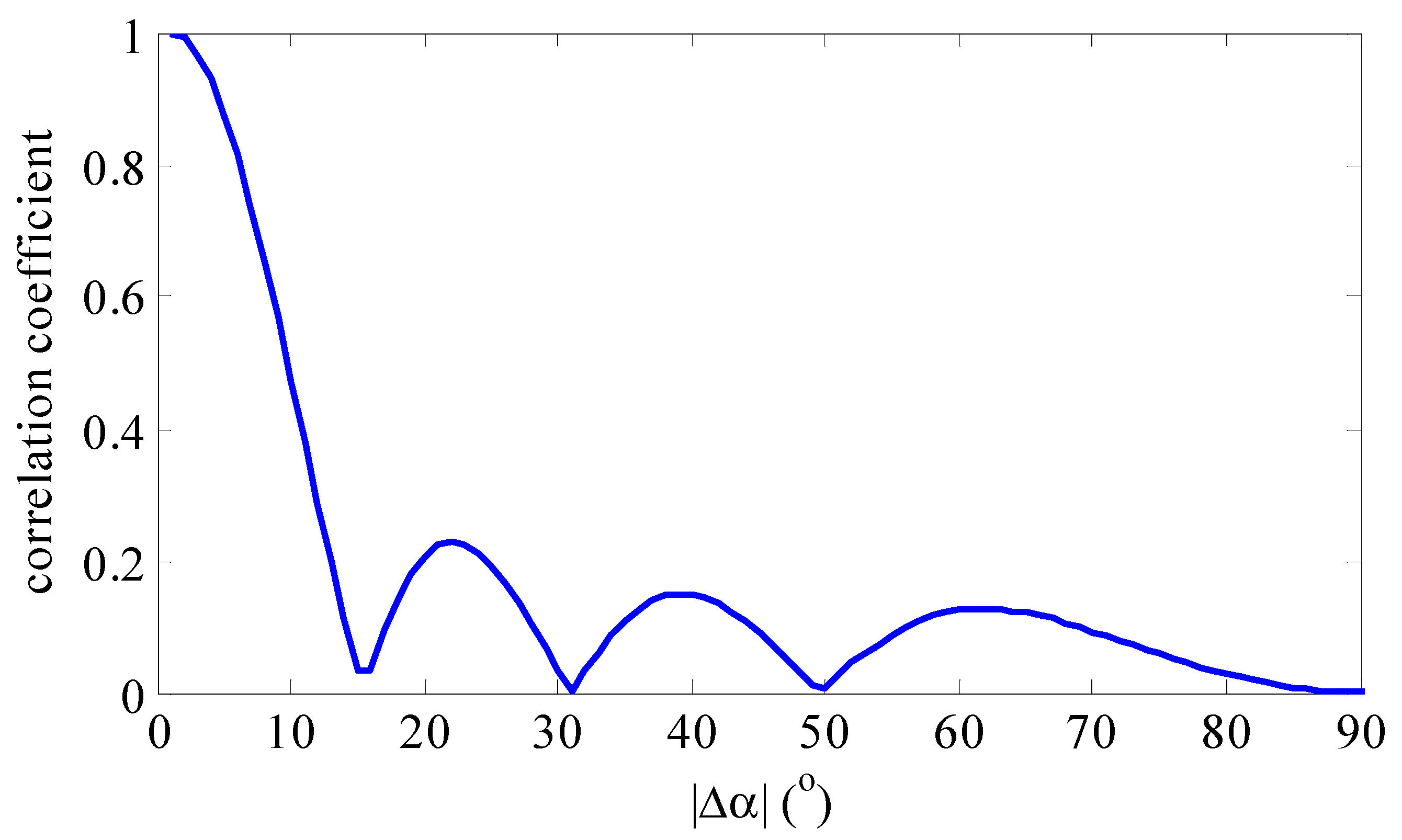
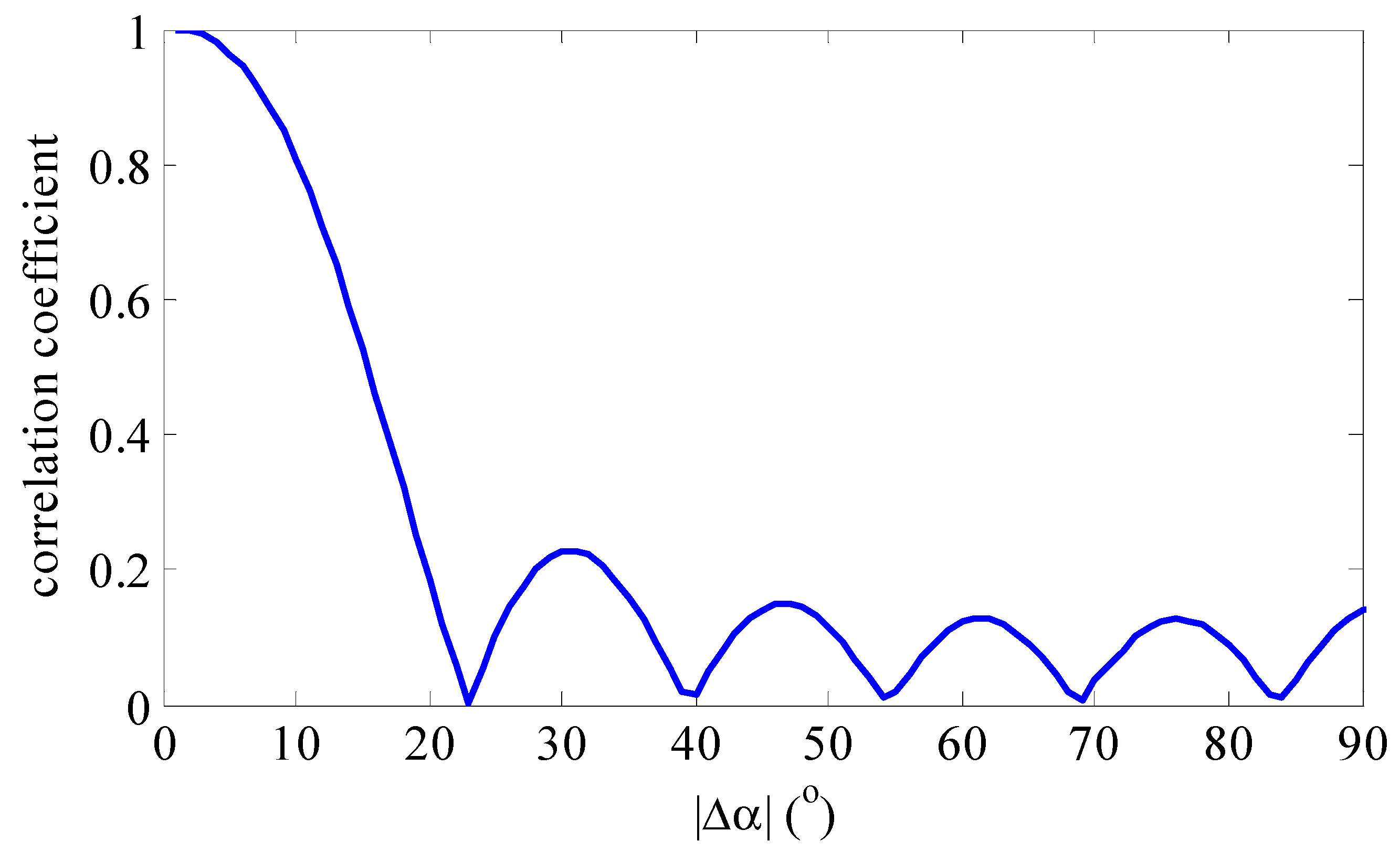
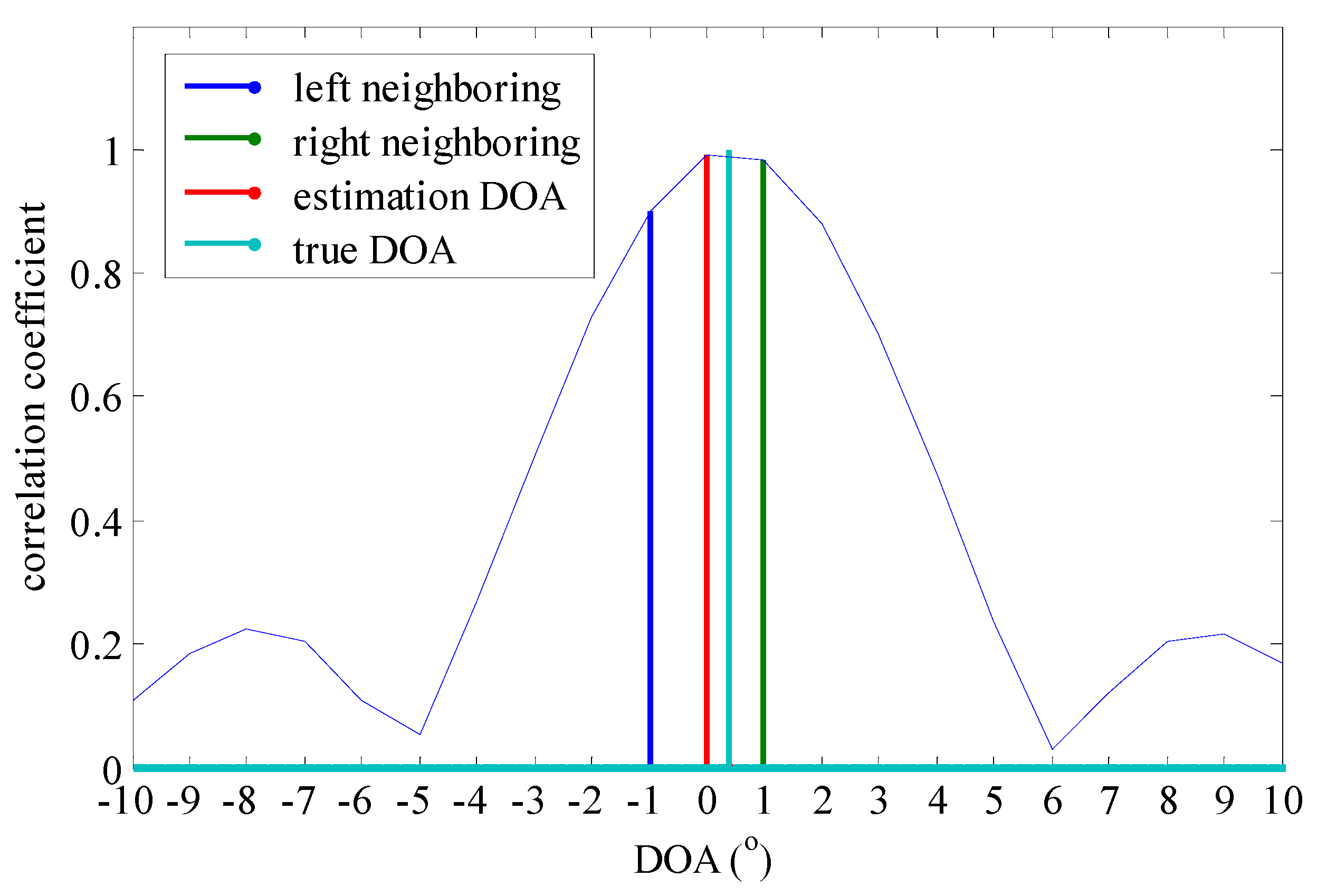
3.2. The Principle for the Rife Algorithm
- (1)
- Use the SRBWEV algorithm we obtain the on-grid DOA estimation and two neighboring on-grid DOAs and ;
- (2)
- Use the Rife algorithm we obtain the off-grid coarse DOA estimation ;
- (3)
- The Rife algorithm is modified:If , use the Rife algorithm secondly.(a) Compute two new inner products:(b) Obtain the off -grid fine DOA estimation:If :else:else:
- (4)
- Output: DOA= .
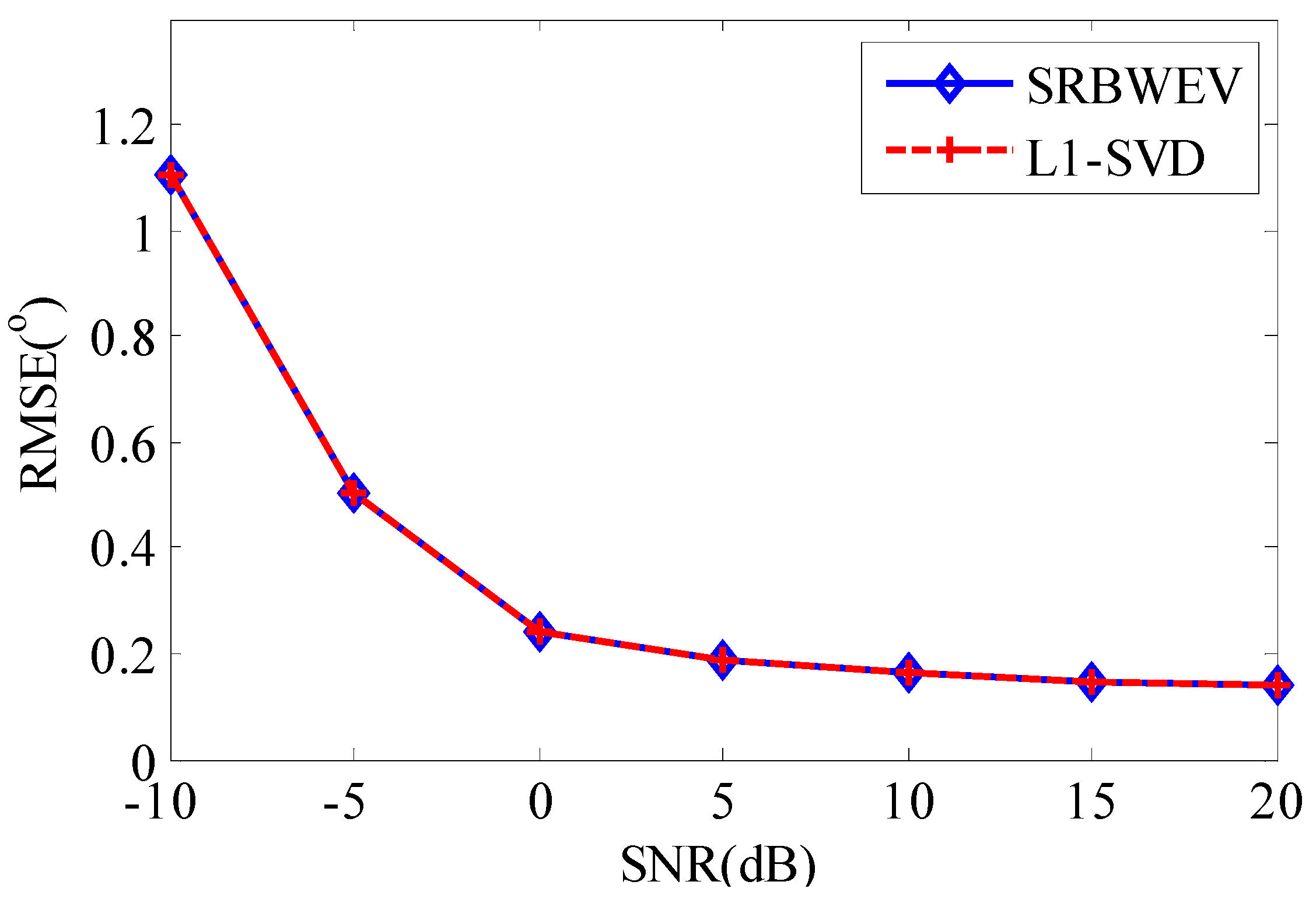
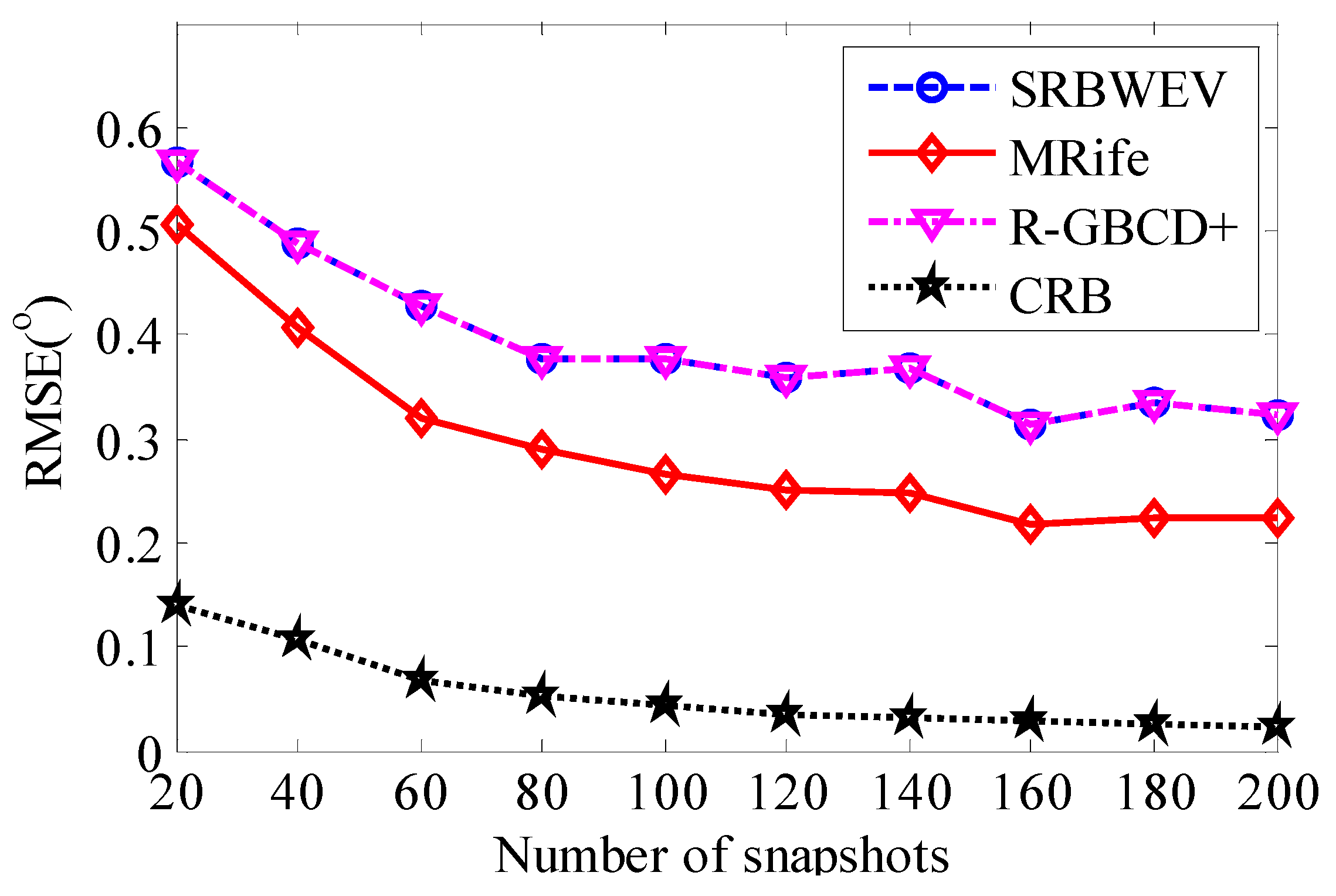
4. Simulation Experiments

| Number of Snapshots | MRife | SRBWEV | R-GBCD+ | L1-SVD |
|---|---|---|---|---|
| 50 | 0.0017 s | 0.0015 s | 0.0145 s | 4.9925 s |
| 100 | 0.0014 s | 0.0012 s | 0.015 s | 4.9916 s |
| 150 | 0.0016 s | 0.0014 s | 0.0136 s | 4.9594 s |
| 200 | 0.002 s | 0.0018 s | 0.0159 s | 5.0757 s |
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Krim, H.; Viberg, M. Two decades of array signal processing research: the parametric approach. IEEE Signal Process. Mag. 1996, 13, 67–94. [Google Scholar] [CrossRef]
- Wan, L.T.; Liu, L.T.; Si, W.J.; Tian, Z.X. Joint estimation of 2D-DOA and frequency based on space-time matrix and conformal array. Sci. World J. 2013, 12, 173–180. [Google Scholar] [CrossRef] [PubMed]
- Yan, F.G.; Shen, Y.; Jin, M. Fast DOA estimation based on a split subspace decomposition on the array covariance matrix. Signal Process. 2015, 115, 1–8. [Google Scholar] [CrossRef]
- Donelli, M.; Viani, F.; Rocca, P.; Massa, A. An innovative multiresolution approach for DOA estimation based on a support vector classification. IEEE Trans. Antennas Propag. 2009, 57, 2279–2292. [Google Scholar] [CrossRef]
- Wang, W.; Ren, S.; Ding, Y.; Wang, H. An efficient algorithm for direction finding against unknown mutual coupling. Sensors 2014, 14, 20064–20077. [Google Scholar] [CrossRef] [PubMed]
- Inghelbrecht, V.; Verhaevert, J.; Van Hecke, T.; Rogier, H. The influence of random element displacement on DOA estimates obtained with (Khatri–Rao-) root-MUSIC. Sensors 2014, 14, 21258–21280. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carlin, M.; Rocca, P.; Oliveri, G.; Viani, F.; Massa, A. Directions-of-arrival estimation through Bayesian compressive sensing strategies. IEEE Trans. Antennas Propag. 2013, 61, 3828–3838. [Google Scholar] [CrossRef]
- Carlin, M.; Rocca, P.; Oliveri, G.; Massa, A. Bayesian compressive sensing as applied to directions-of-arrival estimation in planar arrays. J. Electr. Comput. Eng. 2013, 2013. [Google Scholar] [CrossRef]
- He, Z.Q.; Shi, Z.P.; Huang, L.; So, H.C. Underdetermined DOA estimation for wideband signals using robust sparse covariance fitting. IEEE Signal Process. Lett. 2015, 22, 435–439. [Google Scholar] [CrossRef]
- Zhang, Y.; Ye, Z.; Xu, X.; Hu, N. Off-grid DOA estimation using array covariance matrix and block-sparse Bayesian learning. Signal Process. 2014, 98, 197–201. [Google Scholar] [CrossRef]
- Liu, J.; Han, C.Z.; Hu, Y. A novel coherent column replacement method in compressed sensing for DOA estimation. In Proceedings of the 32nd Chinese Control Conference (CCC), Xi’an, China, 26–28 July 2013; pp. 4832–4837.
- Tan, Z.; Nehorai, A. Sparse direction of arrival estimation using co-prime arrays with off-grid targets. IEEE Signal Process. Lett. 2014, 21, 26–29. [Google Scholar] [CrossRef]
- Liang, Y.; Ying, R.; Lu, Z.; Liu, P. Off-grid direction of arrival estimation based on joint spatial sparsity for distributed sparse linear arrays. Sensors 2014, 14, 21981–22000. [Google Scholar] [CrossRef] [PubMed]
- Rao, B.D.; Engan, K.; Cotter, S. Diversity measure minimization based method for computing sparse solutions to linear inverse problems with multiple measurement vectors. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP’04), Montreal, QC, Canada, 17–21 May 2004; p. 369.
- Wang, Y.; Leus, G.; Pandharipande, A. Direction estimation using compressive sampling array processing. In Proceedings of the IEEE/SP 15th Workshop on Statistical Signal Processing (SSP’09), Cardiff, UK, 31 August–3 September 2009; pp. 626–629.
- Malioutov, D.; Çetin, M.; Willsky, A.S. A sparse signal reconstruction perspective for source localization with sensor arrays. IEEE Trans. Signal Process. 2005, 53, 3010–3022. [Google Scholar] [CrossRef]
- Wei, X.; Yuan, Y.; Ling, Q. DOA estimation using a greedy block coordinate descent algorithm. IEEE Trans. Signal Process. 2012, 60, 6382–6394. [Google Scholar] [CrossRef]
- Xu, D.; Hu, N.; Ye, Z.; Bao, M. The estimate for DOAs of signals using sparse recovery method. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2573–2576.
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse Bayesian inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef]
- Li, B.; Zou, Y.X. Improved DOA estimation with acoustic vector sensor arrays using spatial sparsity and subarray manifold. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 2557–2560.
- Gretsistas, A.; Plumbley, M.D. An alternating descent algorithm for the off-grid DOA estimation problem with sparsity constraints. In Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 874–878.
- Song, J.; Liu, Y.F.; Liu, Y. An interpolation-based frequency estimator synthetic approach for sinusoid wave. In Proceedings of the 2011 7th International Conference on Wireless Communications, Networking and Mobile Computing (WiCOM), Wuhan, China, 23–25 September 2011; pp. 1–4.
- Cadzow, J.A.; Kim, Y.S.; Shiue, D.C. General direction-of-arrival estimation: a signal subspace approach. IEEE Trans. Aerosp. Electron. Syst. 1989, 25, 31–47. [Google Scholar] [CrossRef]
- Duarte, M.F. Localization and bearing estimation via structured sparsity models. In Proceedings of the 2012 IEEE Statistical Signal Processing Workshop (SSP), Ann Arbor, MI, USA, 5–8 August 2012; pp. 333–336.
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, T.; Wu, H.; Guo, L.; Liu, L. A Modified Rife Algorithm for Off-Grid DOA Estimation Based on Sparse Representations. Sensors 2015, 15, 29721-29733. https://doi.org/10.3390/s151129721
Chen T, Wu H, Guo L, Liu L. A Modified Rife Algorithm for Off-Grid DOA Estimation Based on Sparse Representations. Sensors. 2015; 15(11):29721-29733. https://doi.org/10.3390/s151129721
Chicago/Turabian StyleChen, Tao, Huanxin Wu, Limin Guo, and Lutao Liu. 2015. "A Modified Rife Algorithm for Off-Grid DOA Estimation Based on Sparse Representations" Sensors 15, no. 11: 29721-29733. https://doi.org/10.3390/s151129721






