Hybrid Molecular and Spin Dynamics Simulations for Ensembles of Magnetic Nanoparticles for Magnetoresistive Systems
Abstract
:1. Introduction
2. General Approach
2.1. Molecular Dynamics Equations of Motion
2.1.1. Integration of the Equations of Motion
2.1.2. Force Calculation
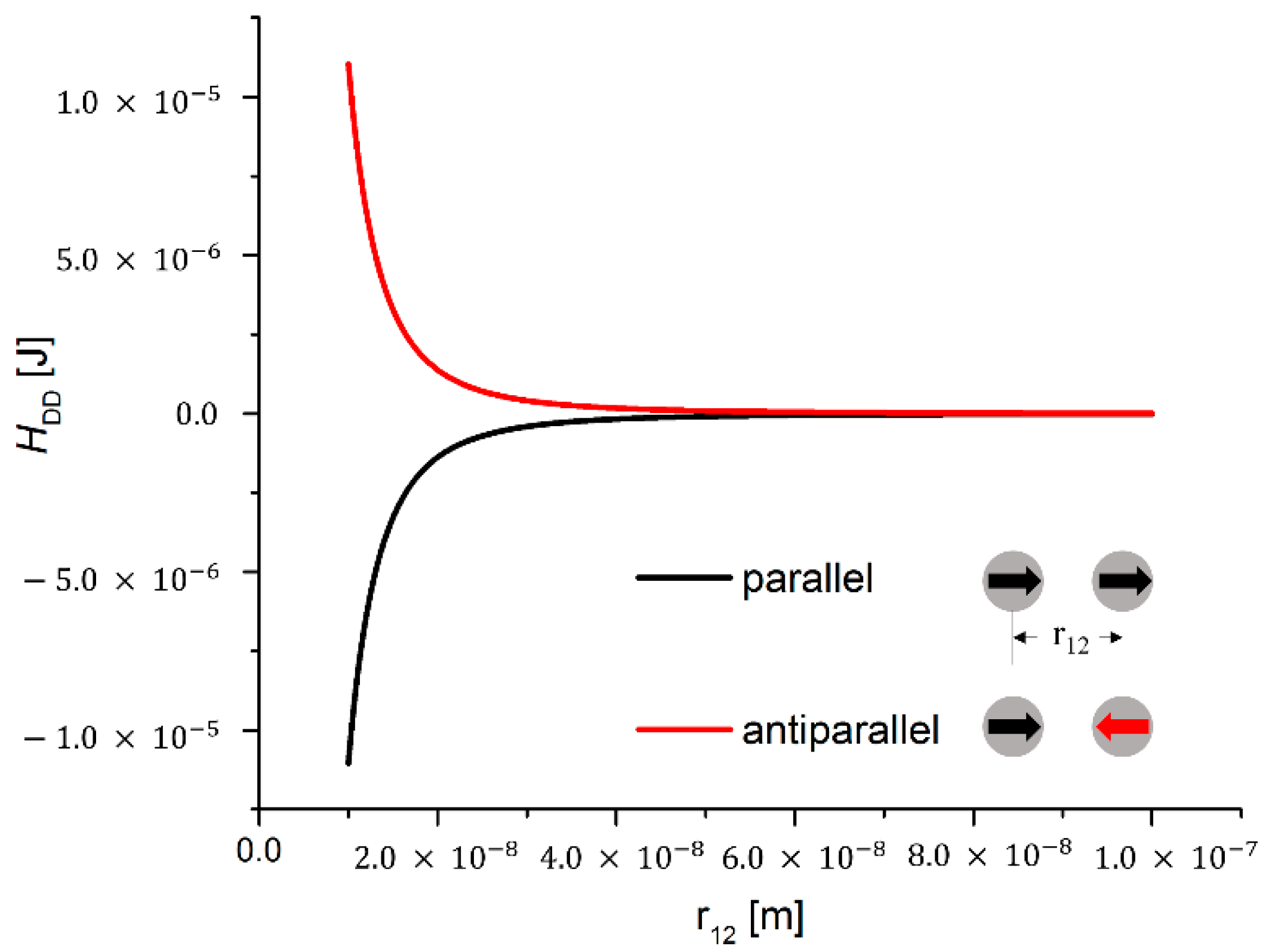
Magnetic Dipole-Dipole Interaction
Hard Particle Approach
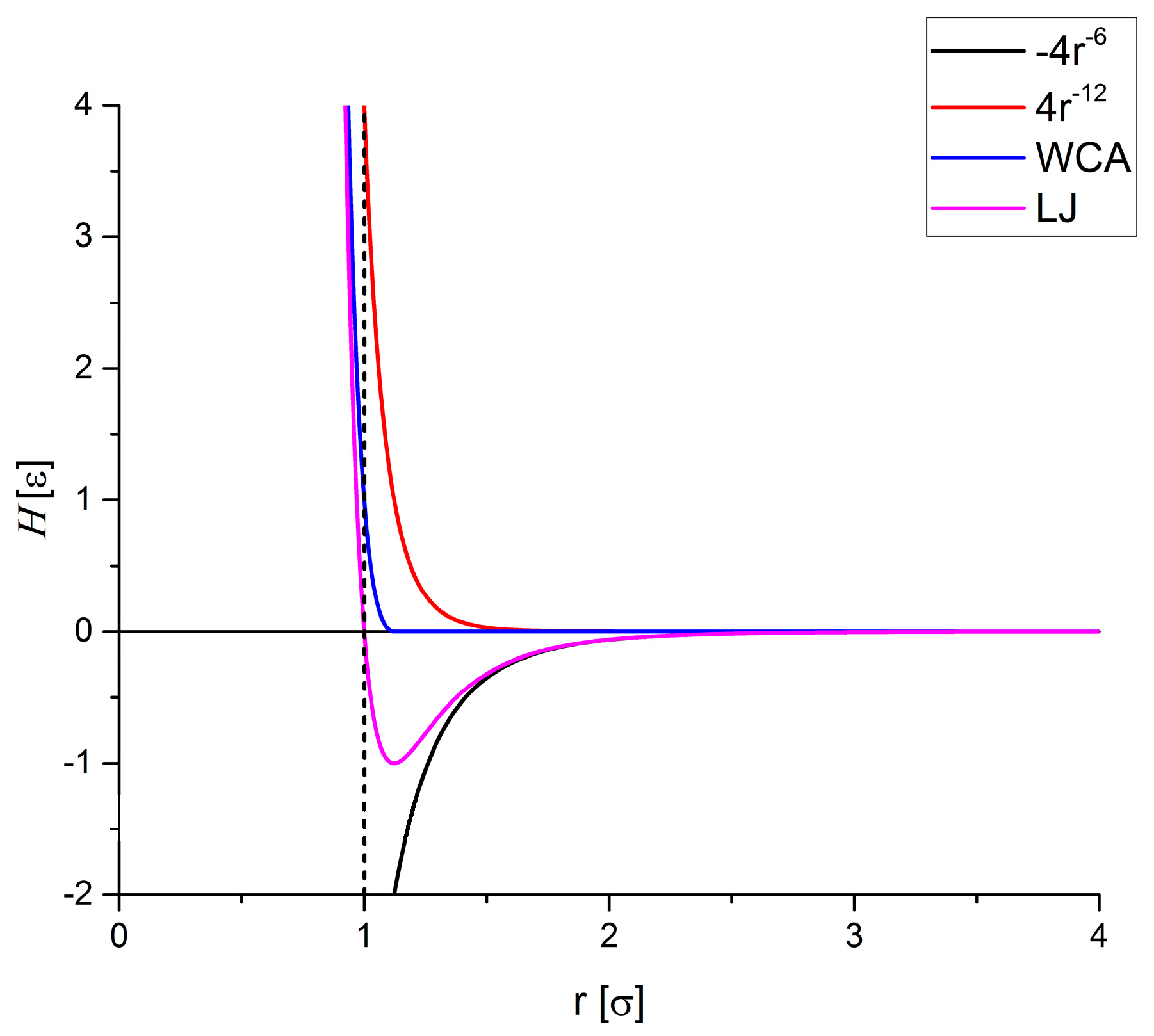
Stokes Drag
2.2. Classical Spin Dynamics Simulations
3. Hybrid Molecular and Spin Dynamics Simulations
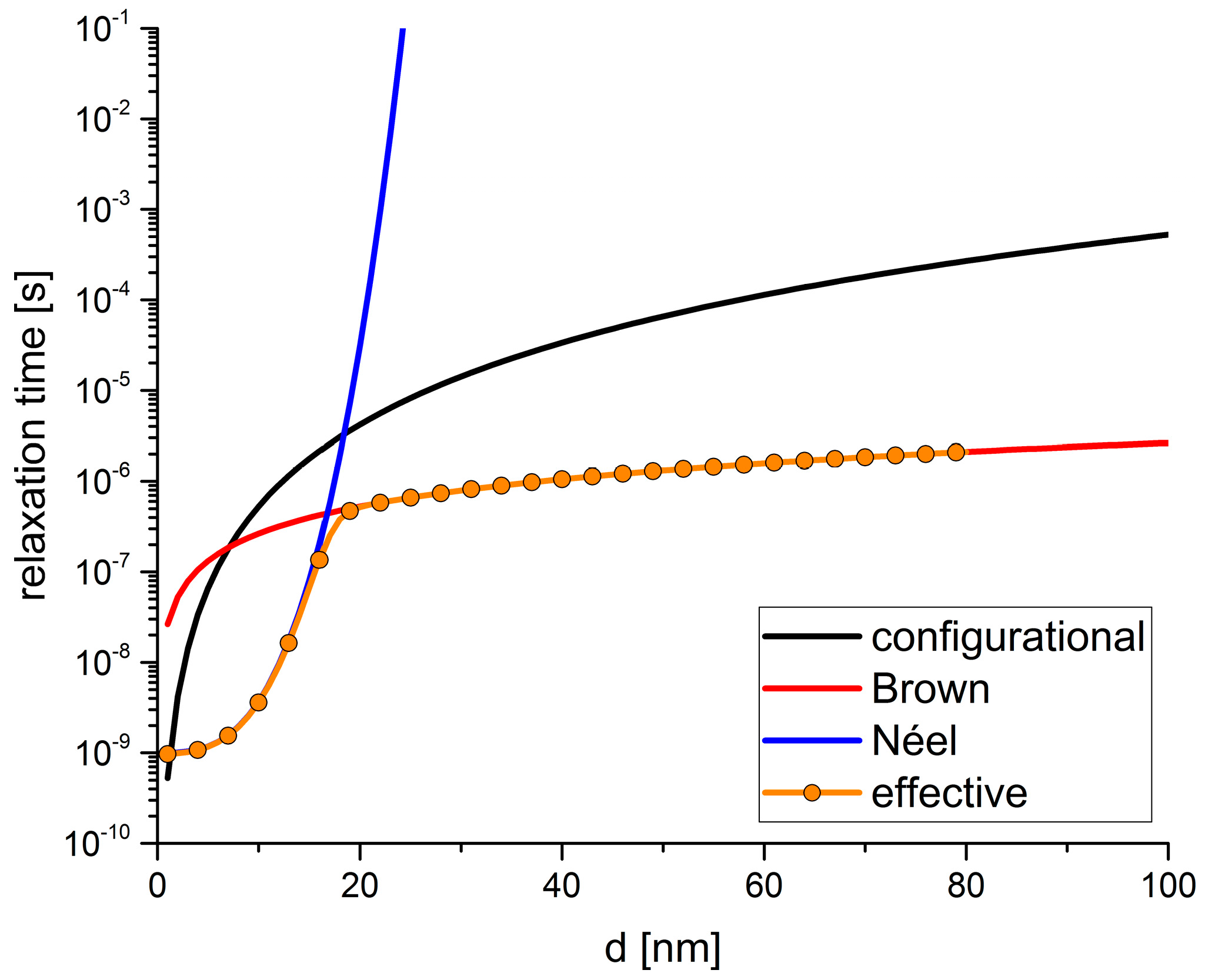
3.1. Translational Relaxation Time
3.2. Magnetic Relaxation Time
3.3. Comparison of Translational and Magnetic Relaxation Times
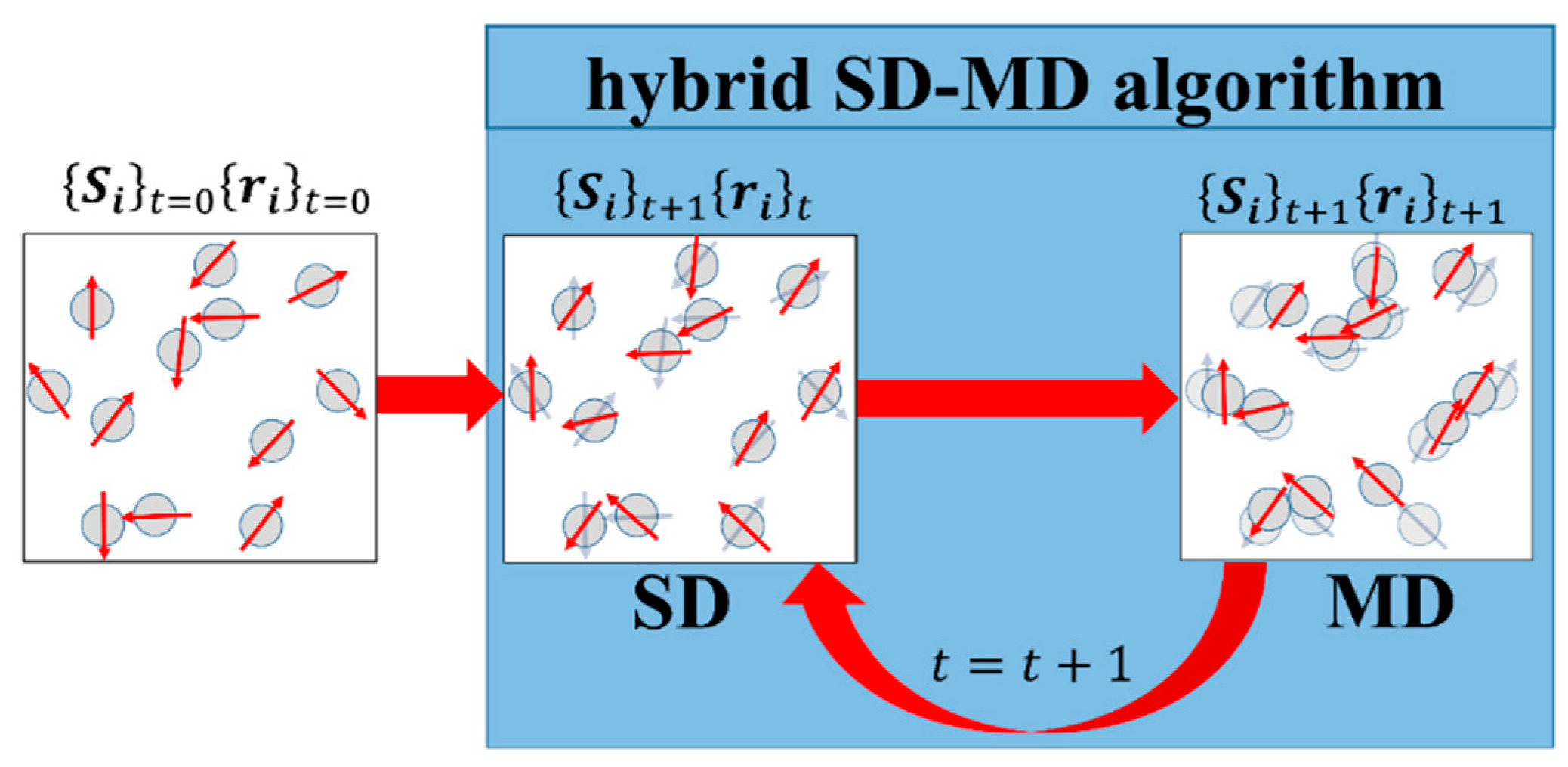
3.4. Hybrid Molecular and Spin Dynamics Coupling Scheme
3.5. The Role of Temperature
3.6. Calculation of Qualitative GMR Curves
4. Application: Magneto-Dynamics of Interacting Magnetic Nanoparticles in Gel Matrices for the Efficient Design of Magnetoresistive Systems
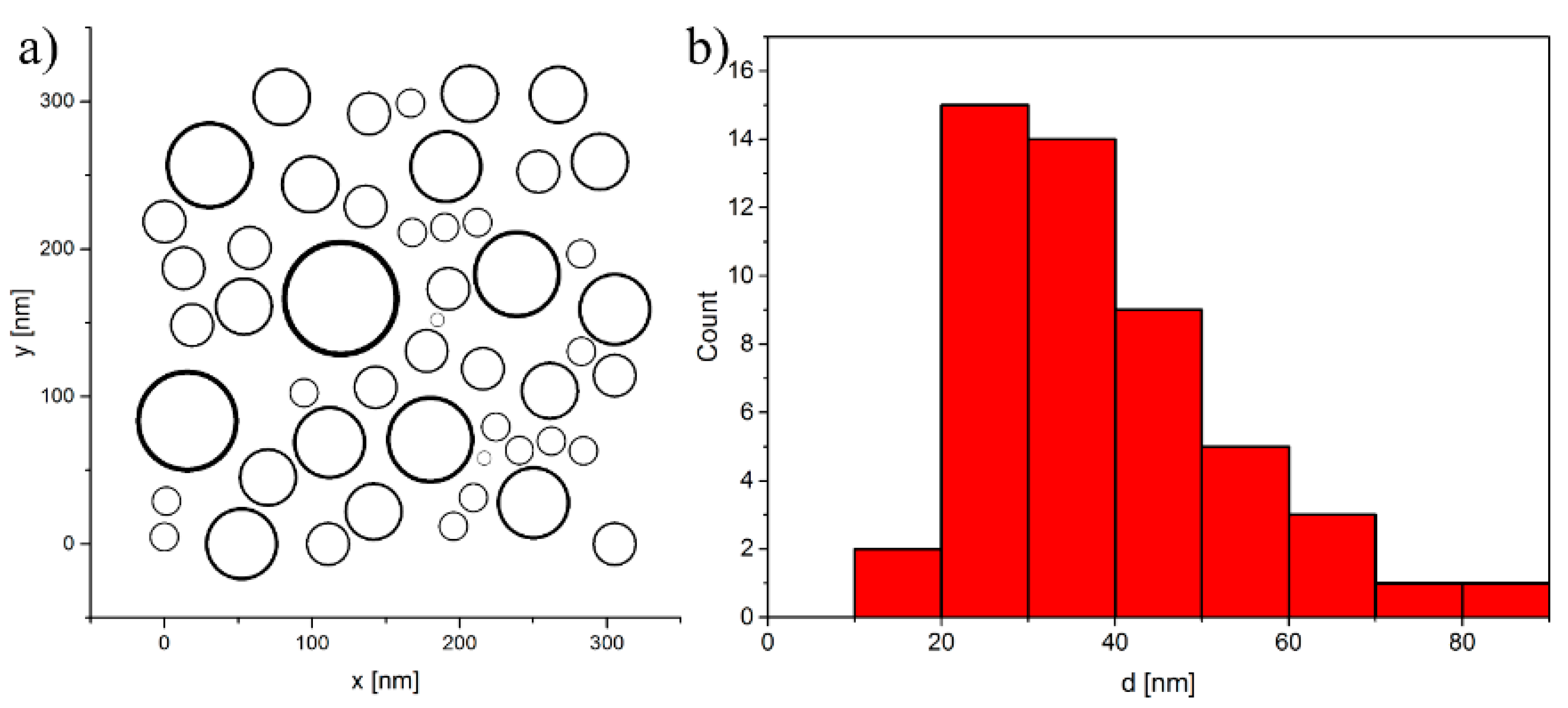
4.1. Model System
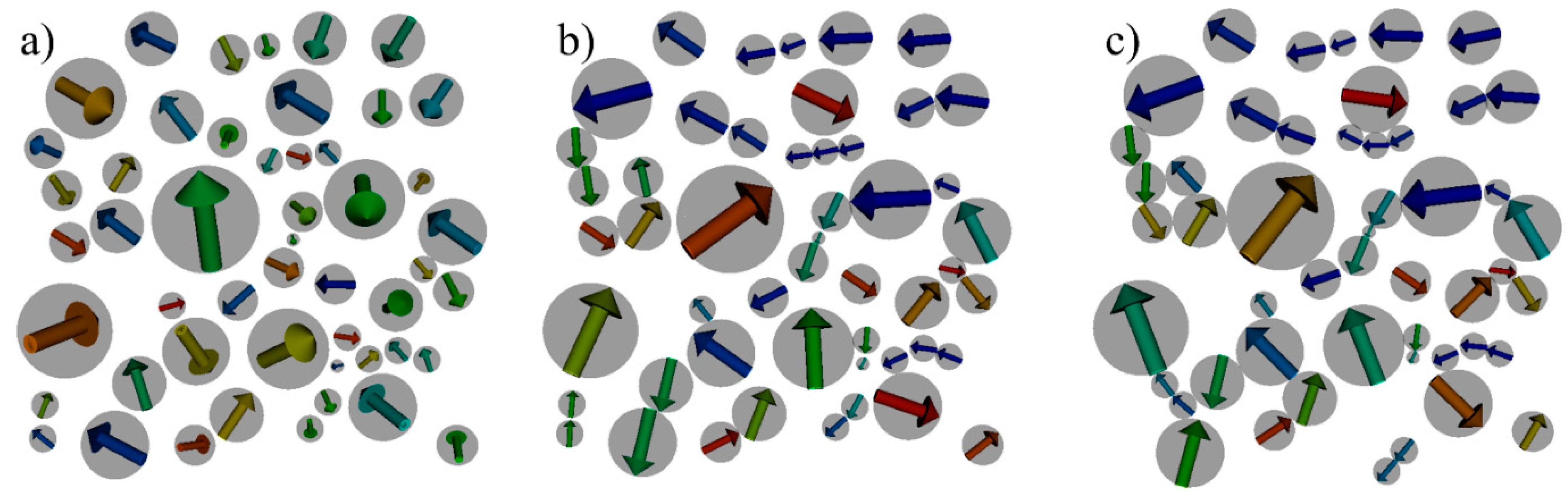
4.2. Structuring Process
4.3. Estimation of GMR Properties
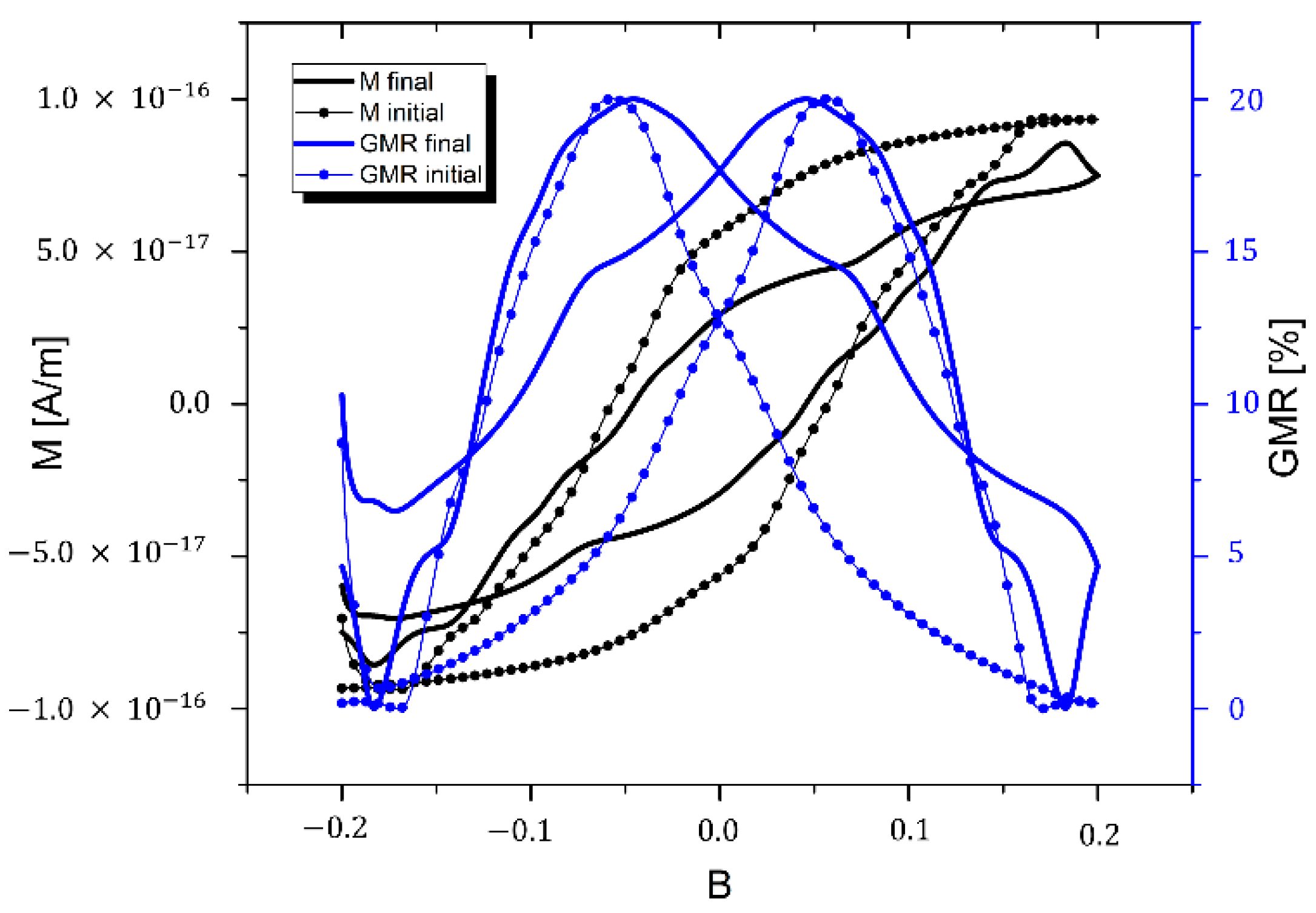
5. Conclusions/Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Binasch, G.; Grünberg, P.; Saurenbach, F.; Zinn, W. Enhanced magnetoresistance in layered magnetic structures with antiferromagnetic interlayer exchange. Phys. Rev. B 1989, 39. [Google Scholar] [CrossRef]
- Baibich, M.N.; Broto, J.M.; Fert, A.; van Dau, F.N.; Petroff, F.; Etienne, P.; Crouzet, G.; Friederich, A.; Chazelas, J. Giant Magnetoresistance of (001)Fe/(001)Cr Magnetic Superlattices. Phys. Rev. Lett. 1988, 61. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.Q.; Jiang, J.S.; Chien, C.L. Giant magnetoresistance in nonmultilayer systems. Phys. Rev. Lett. 1992, 68. [Google Scholar] [CrossRef] [PubMed]
- Berkowitz, A.E.; Mitchell, J.R.; Carey, M.J.; Young, A.P.; Zhang, S.; Spada, F.E.; Parker, F.T.; Hutten, A.; Thomas, G. Giant magnetoresistance in heterogeneous Cu-Co alloys. Phys. Rev. Lett. 1992, 68. [Google Scholar] [CrossRef] [PubMed]
- Meyer, J.; Rempel, T.; Schäfers, M.; Wittbracht, F.; Müller, C.; Patel, A.V.; Hütten, A. Giant magnetoresistance effects in gel-like matrices. Smart Mater. Struct. 2013, 22. [Google Scholar] [CrossRef]
- Teich, L.; Kappe, D.; Rempel, T.; Meyer, J.; Schröder, C.; Hütten, A. Modeling of Nanoparticular Magnetoresistive Systems and the Impact on Molecular Recognition. Sensors 2015, 15, 9251–9264. [Google Scholar] [CrossRef] [PubMed]
- Rempel, T.; Meyer, J.; Teich, L.; Gottschalk, M.; Rott, K.; Kappe, D.; Schröder, C.; Hütten, A. Giant magnetoresistance effects in gel-like matrices: Comparing experimental and theoretical data. Submitted for publication.
- Antropov, V.P.; Katsnelson, M.I.; van Schilfgaarde, M.; Harmon, B.N. Ab Initio spin dynamics in magnets. Phys. Rev. Lett. 1995, 75, 729–732. [Google Scholar] [CrossRef] [PubMed]
- Antropov, V.P.; Katsnelson, M.I.; Harmon, B.N.; van Schilfgaarde, M.; Kusnezov, D. Spin dynamics in magnets: Equation of motion and finite temperature effects. Phys. Rev. B 1996, 54, 1019–1035. [Google Scholar] [CrossRef]
- Omelyan, I.P.; Mryglod, I.M.; Folk, R. Algorithm of molecular dynamics simulations of spin liquids. Phys. Rev. Lett. 2001, 86, 898–901. [Google Scholar] [CrossRef] [PubMed]
- Omelyan, I.P.; Mryglod, I.M.; Folk, R. Molecular dynamics simulations of spin and pure liquids with preservation of all the conservation laws. Phys Rev. E 2001, 64. [Google Scholar] [CrossRef]
- Omelyan, I.P.; Mryglod, I.M.; Folk, R. Construction of high-order force-gradient algorithms for integration of motion in classical and quantum systems. Phys. Rev. E 2002, 66. [Google Scholar] [CrossRef] [PubMed]
- Ma, P.-W.; Woo, C.H. Large-scale simulation of the spin lattice dynamics in ferromagnetic iron. Phys. Rev. B 2008, 78. [Google Scholar] [CrossRef]
- Thibaudeau, P.; Beaujouan, D. Thermostatting the atomic spin dynamics from controlled demons. Phys. A 2012, 391, 1963–1971. [Google Scholar] [CrossRef]
- Anderson, J.A.; Lorenz, C.D.; Travesset, A. General purpose molecular dynamics simulations fully implemented on graphics processing units. J. Comp. Phys. 2008, 227, 5342–5359. [Google Scholar] [CrossRef]
- Glaser, J.; Nguyen, T.D.; Anderson, J.A.; Liu, P.; Spiga, F.; Millan, J.A.; Morse, D.C.; Glotzer, S.C. Strong scaling of general-purpose molecular dynamics on GPUs. Comput. Phys. Commun. 2015, 192, 97–107. [Google Scholar] [CrossRef]
- HOOMD—Blue Web Page. Available online: http://codeblue.umich.edu/hoomd-blue (accessed on 20 October 2015).
- Frenkel, D.; Smit, B. Understanding Molecular Simulation, 2nd ed.; Academic Press, Inc.: Orlando, FL, USA, 2001. [Google Scholar]
- Tuckerman, M.E. Statistical Mechanics: Theory and Molecular Simulation; Oxford University Press: Oxford, UK, 2010. [Google Scholar]
- Weeks, J.D.; Chandler, D.; Andersen, H.C. Role of repulsive forces in determining he equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237–5347. [Google Scholar] [CrossRef]
- Engelhardt, L.; Schröder, C. Simulating Computationally Complex Magnetic Molecules. In Molecular Cluster Magnets; Winpenny, R.E.P., Ed.; World Scientific Publishers: Singapore, 2011; pp. 241–291. [Google Scholar]
- Milstein, G.N.; Tretyakov, M.V. Stochastic Numerics for Mathematical Physics; Springer-Verlag: Berlin, Germany, 2004. [Google Scholar]
- Dünweg, B.; Ladd, A.J.C. Lattice Boltzmann simulations of soft matter systems. Adv. Polym. Sci. 2009, 221, 89–166. [Google Scholar]
- Batchelor, G.K. Brownian diffusion of particles with hydrodynamic interaction. J. Fluid. Mech. 1976, 74, 1–29. [Google Scholar] [CrossRef]
- Rosensweig, R.E. Ferrohydrodynamics; Dover Publications, Inc.: Mineola, NY, USA, 2014. [Google Scholar]
- Thomas, S.; Kalarikkal, N.; Stephan, A.M.; Raneesh, B. Advanced Nanomaterials: Synthesis, Properties and Application; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Teich, L.; Schröder, C.; Müller, C.; Patel, A.; Meyer, J.; Hütten, A. Efficient calculation of low energy configurations of nanoparticle ensembles for magnetoresistive sensor devices by means of stochastic spin dynamics and Monte Carlo methods. Acta. Phys. Pol. A 2015, 127, 374–376. [Google Scholar] [CrossRef]
- Lingenheil, M.; Denschlag, R.; Reichold, R.; Tavan, P. The “hot-solvent/cold-solute” problem revisited. J. Chem. Theory Comput. 2008, 4, 1293–1306. [Google Scholar] [CrossRef]
- Car, R.; Parrinello, M. Unified approach for molecular dynamics and density-functional theory. Phys. Rev. Lett. 1985, 55, 2471–2474. [Google Scholar] [CrossRef] [PubMed]
- Marx, D.; Hutter, J. Ab initio Molecular Dynamics: Basic Theory and Advanced Methods; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Wiser, N. Phenomenological theory of the giant magnetoresistance of superparamagnetic particles. J. Magn. Magn. Mater. 1996, 159, 119–124. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Teich, L.; Schröder, C. Hybrid Molecular and Spin Dynamics Simulations for Ensembles of Magnetic Nanoparticles for Magnetoresistive Systems. Sensors 2015, 15, 28826-28841. https://doi.org/10.3390/s151128826
Teich L, Schröder C. Hybrid Molecular and Spin Dynamics Simulations for Ensembles of Magnetic Nanoparticles for Magnetoresistive Systems. Sensors. 2015; 15(11):28826-28841. https://doi.org/10.3390/s151128826
Chicago/Turabian StyleTeich, Lisa, and Christian Schröder. 2015. "Hybrid Molecular and Spin Dynamics Simulations for Ensembles of Magnetic Nanoparticles for Magnetoresistive Systems" Sensors 15, no. 11: 28826-28841. https://doi.org/10.3390/s151128826