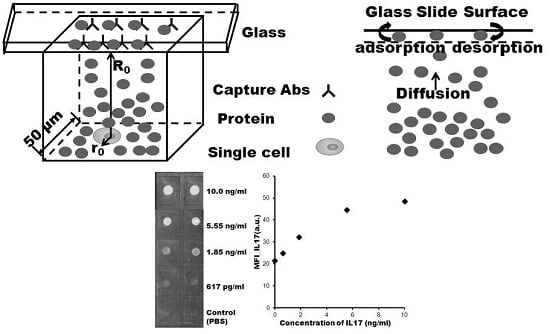
Protein Adsorption in Microengraving Immunoassays
Abstract
:1. Introduction
1.1. Scaling Arguments of Protein Adsorption Dynamics in Microengraving Immunoassay
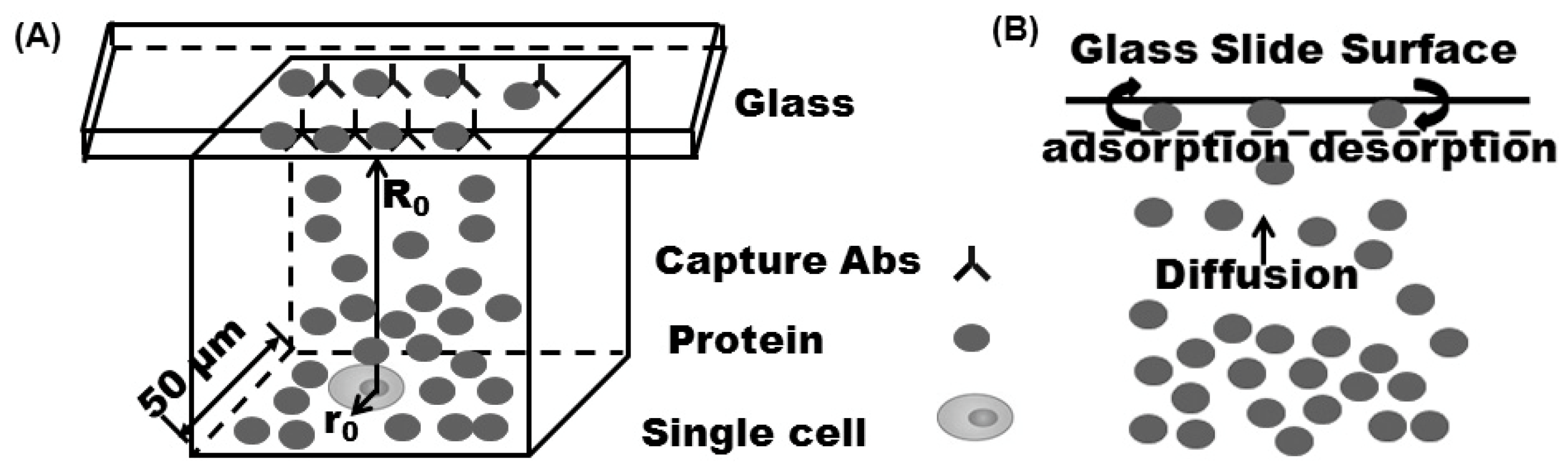
1.2. Protein Adsorption Mechanisms in Microengraving Immunoassay
1.3. Theoretical Model Method
2. Experimental Section
2.1. Recombinant Protein, Antibody and Antibody Conjugations
2.2. Preparing Poly-Lysine Glass Slides
2.3. Immobilization of Capture Antibody on Poly-Lysine Glass Slides
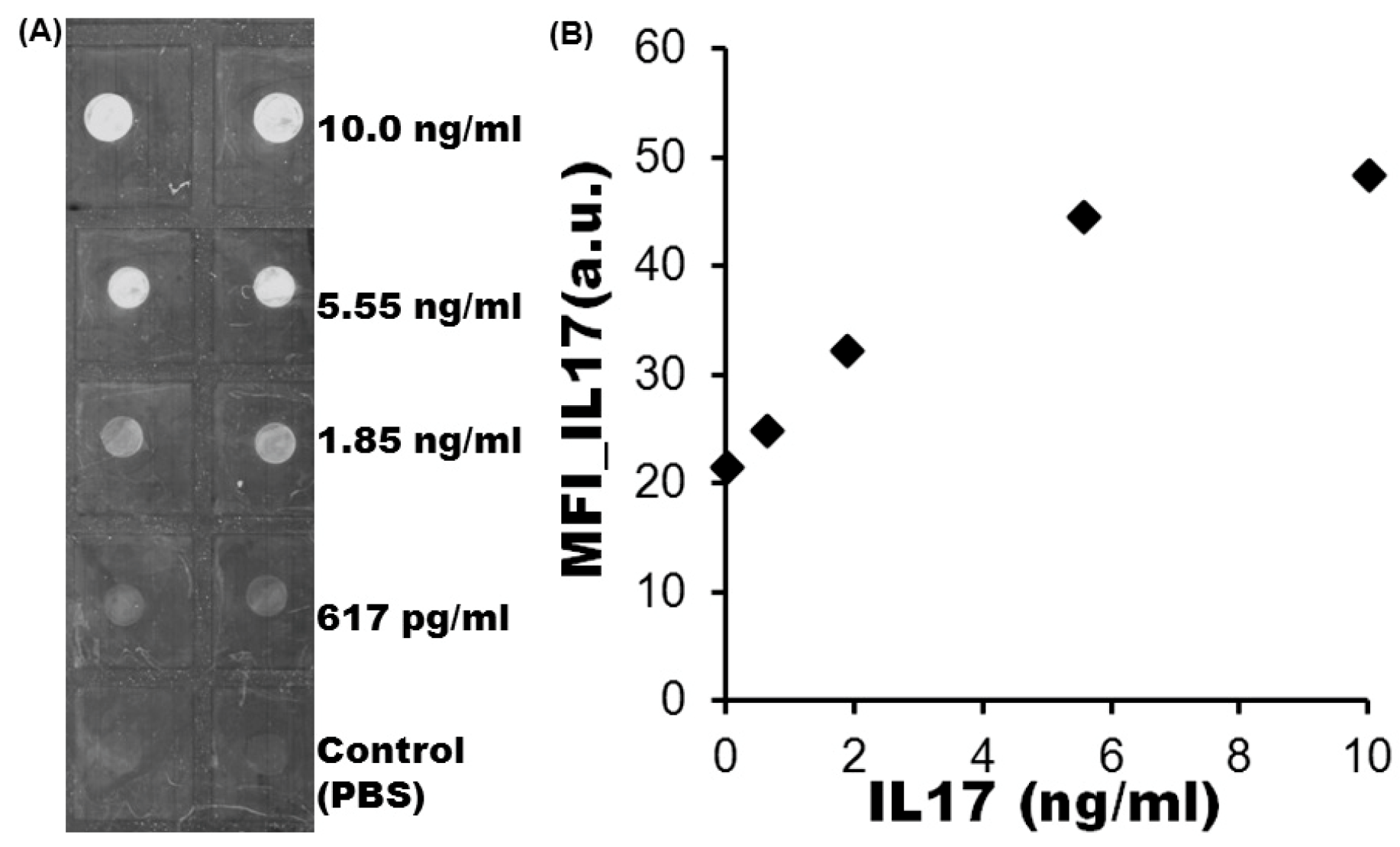
2.4. Staining Captured Proteins on Reference Slides
3. Results and Discussions
3.1. Characteristic Diffusion Time Scale and Kinetic Time Scale
| kon (M−1·s−1) | koff (s−1) | KD (M) | (molecule/s) | (s) | (s) | ||
|---|---|---|---|---|---|---|---|
| C*0 = 0.313 | 1.15 × 104 | 0.0001 | 8.7 × 10−9 | 1 | 14.5 | 7620 | 1.45 × 10−3 |
| 1.15 × 104 | 0.001 | 8.7 × 10−8 | 10 | 14.5 | 762.0 | 1.45 × 10−2 | |
| 1.15 × 104 | 0.01 | 8.7 × 10−7 | 100 | 14.5 | 76.2 | 0.145 | |
| 1.15 × 104 | 0.1 | 8.7 × 10−6 | 1000 | 14.5 | 7.62 | 1.45 | |
| C*0 = 3.13 | 1.15 × 105 | 0.0001 | 8.7 × 10−1° | 1 | 14.5 | 2420 | 1.45 × 10−3 |
| 1.15 × 105 | 0.001 | 8.7 × 10−9 | 10 | 14.5 | 242.0 | 1.45 × 10−2 | |
| 1.15 × 105 | 0.01 | 8.7 × 10−8 | 100 | 14.5 | 24.2 | 0.145 | |
| 1.15 × 105 | 0.1 | 8.7 × 10−7 | 1000 | 14.5 | 2.42 | 1.45 | |
| C*0 = 31.3 | 1.15 × 106 | 0.0001 | 8.7 × 10−11 | 1 | 14.5 | 310 | 1.45 × 10−3 |
| 1.15 × 106 | 0.001 | 8.7 × 10−1° | 10 | 14.5 | 31.0 | 1.45 × 10−2 | |
| 1.15 × 106 | 0.01 | 8.7 × 10−9 | 100 | 14.5 | 3.1 | 0.145 | |
| 1.15 × 106 | 0.1 | 8.7 × 10−8 | 1000 | 14.5 | 0.31 | 1.45 |
3.2. Concentration of Protein Captured on Glass Slide Surface as a Function of Time

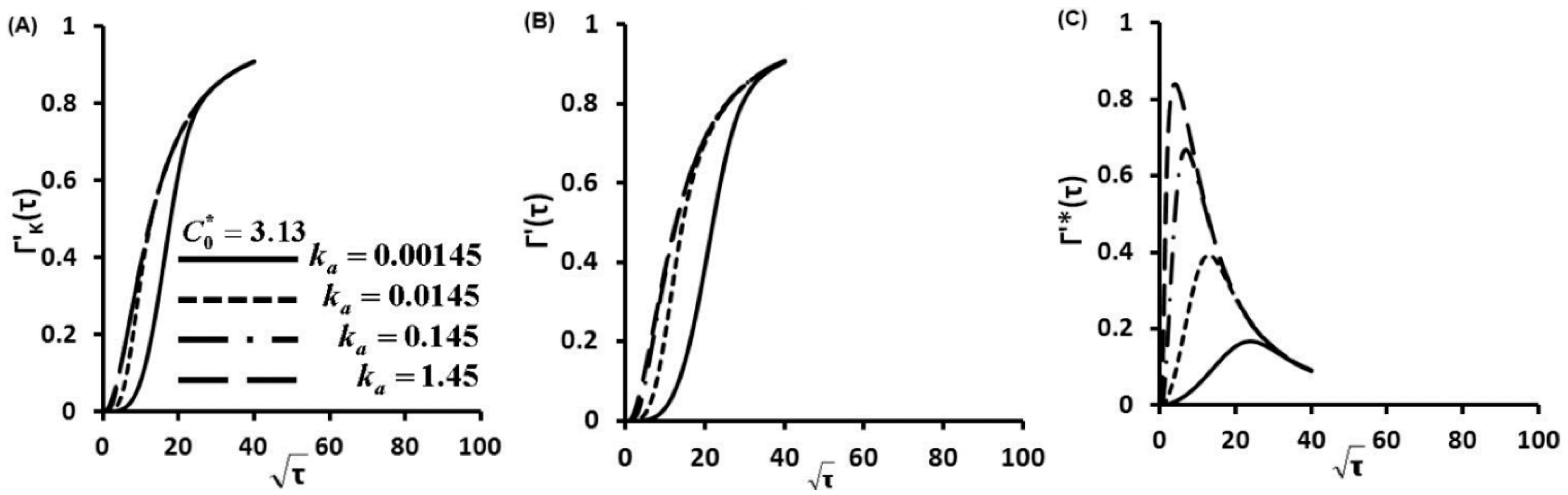
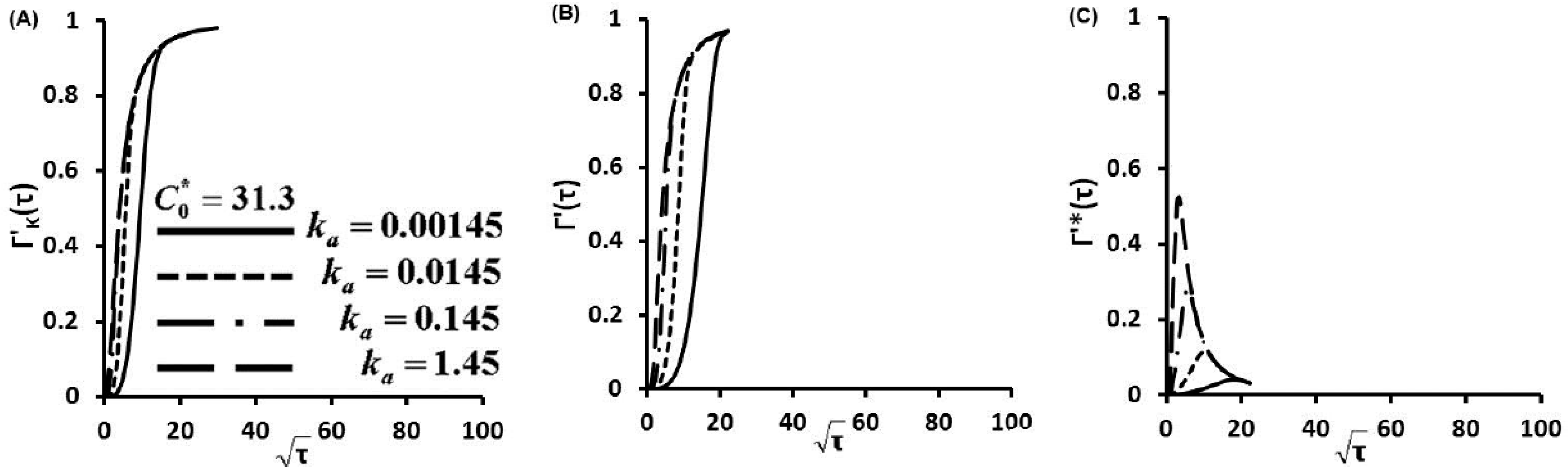
3.3. Protein Adsorption Rate as a Function of Time



3.4. Concentration of Protein in the Solution and at Sublayer as a Function of Time C(r,t) and
3.5. Protein Adsorption Isotherms
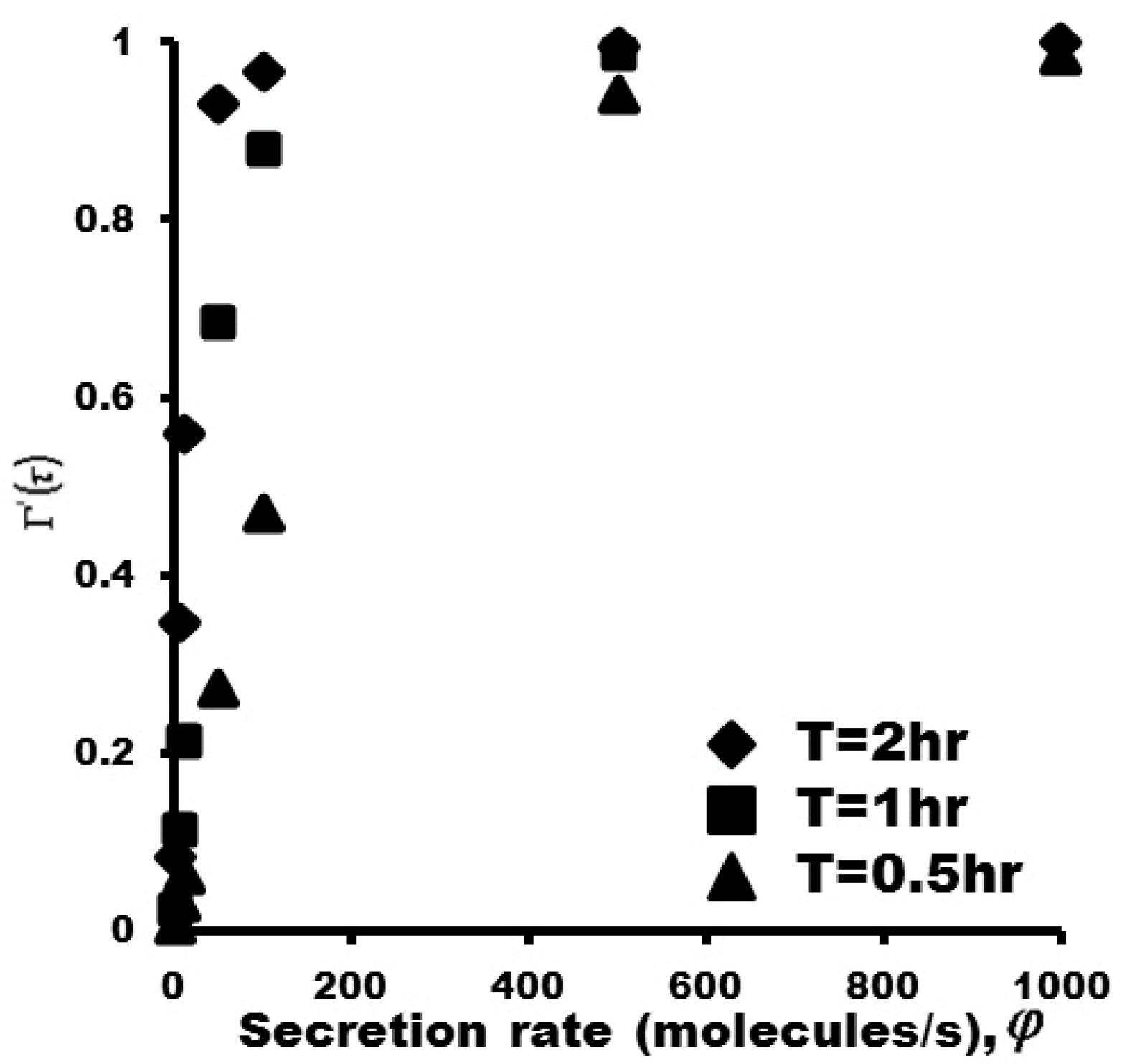
4. Conclusions
Supplementary Files
Supplementary File 1Acknowledgments
Conflicts of Interest
References
- Harari, A.; Vallelian, F.; Meylan, P.R.; Pantaleo, G. Functional heterogeneity of memory CD4 T cell responses in different conditions of antigen exposure and persistence. J. Immunol. 2005, 174, 1037–1045. [Google Scholar] [CrossRef] [PubMed]
- Kindt, T.J.; Goldsby, R.A.; Osborne, B.A. Immunology; W.H. Freeman: New York, NY, USA, 2007. [Google Scholar]
- Stanimirova, R.D.; Marinova, K.G.; Danov, K.D.; Kralchevsky, P.A.; Basheva, E.S.; Stoyanov, S.D.; Pelan, E.G. Competitive Adsorption of the Protein Hydrophobin and an Ionic Surfactant: Parallel vs Sequential Adsorption and Dilatational Rheology. Colloid Surf. A 2014, 457, 307–317. [Google Scholar] [CrossRef]
- Turcanu, V.; Williams, N.A. Cell identification and isolation on the basis of cytokine secretion: A novel tool for investigating immune responses. Nat. Med. 2001, 7, 373–376. [Google Scholar] [CrossRef] [PubMed]
- Bevan, M.J. Helping the CD8(+) T-cell response. Nat. Rev. Immunol. 2004, 4, 595–602. [Google Scholar] [CrossRef] [PubMed]
- Darrah, P.A.; Patel, D.T.; de Luca, P.M.; Lindsay, R.W.; Davey, D.F.; Flynn, B.J.; Hoff, S.T.; Andersen, P.; Reed, S.G.; Morris, S.L.; et al. Multifunctional TH1 cells define a correlate of vaccine-mediated protection against Leishmania major. Nat. Med. 2007, 13, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Kannanganat, S.; Ibegbu, C.; Chennareddi, L.; Robinson, H.L.; Amara, R.R. Multiple-cytokine-producing antiviral CD4 T cells are functionally superior to single-cytokine-producing cells. J. Virol. 2007, 81, 8468–8476. [Google Scholar] [CrossRef] [PubMed]
- Román, E.; Miller, E.; Harmsen, A.; Wiley, J.; von Andrian, U.H.; Huston, G.; Swain, S.L. CD4 effector T cell subsets in the response to influenza: Heterogeneity, migration, and function. J. Exp. Med. 2002, 196, 957–968. [Google Scholar] [CrossRef] [PubMed]
- Duvall, M.G.; Precopio, M.L.; Ambrozak, D.A.; Jaye, A.; McMichael, A.J.; Whittle, H.C.; Roederer, M.; Rowland-Jones, S.L.; Koup, R.A. Polyfunctional T cell responses are a hallmark of HIV-2 infection. Eur. J. Immunol. 2008, 38, 350–363. [Google Scholar] [CrossRef] [PubMed]
- Bradshaw, E.M.; Kent, S.C.; Tripuraneni, V.; Orban, T.; Ploegh, H.L.; Hafler, D.A.; Love, J.C. Concurrent detection of secreted products from human lymphocytes by microengraving: Cytokines and antigen-reactive antibodies. Clin. Immunol. 2008, 129, 10–18. [Google Scholar] [CrossRef] [PubMed]
- Love, J.C.; Ronan, J.L.; Grotenbreg, G.M.; van der Veen, A.G.; Ploegh, H.L. A microengraving method for rapid selection of single cells producing antigen-specific antibodies. Nat. Biotechnol. 2006, 24, 703–707. [Google Scholar] [CrossRef] [PubMed]
- Story, C.M.; Papa, E.; Hu, C.C.; Ronan, J.L.; Herlihy, K.; Ploegh, H.L.; Love, J.C. Profiling antibody responses by multiparametric analysis of primary B cells. Proc. Natl. Acad. Sci. USA 2008, 105, 17902–17907. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Han, Q.; Bradshaw, E.M.; Kent, S.C.; Raddassi, K.; Nilsson, B.; Nepom, G.T.; Hafler, D.A.; Love, J.C. On-Chip Activation and Subsequent Detection of Individual Antigen-Specific T Cells. Anal. Chem. 2010, 82, 473–477. [Google Scholar] [CrossRef] [PubMed]
- Ogunniyi, A.O.; Story, C.M.; Papa, E.; Guillen, E.; Love, J.C. Screening individual hybridomas by microengraving to discover monoclonal antibodies. Nat. Protoc. 2009, 4, 767–782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jin, A.; Ozawa, T.; Tajiri, K.; Obata, T.; Kondo, S.; Kinoshita, K.; Kadowaki, S.; Takahashi, K.; Sugiyama, T.; Kishi, H.; et al. A rapid and efficient single-cell manipulation method for screening antigen-specific antibody-secreting cells from human peripheral blood. Nat. Med. 2009, 15, 1088–1092. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Couzis, A.; Somasundaran, P.; Maldarelli, C. A transport model for the adsorption of surfactant from micelle solutions onto a clean air/water interface in the limit of rapid aggregate disassembly relative to diffusion and supporting dynamic tension experiments. Colloid Surf. A Physicochem. Eng. Aspects 2006, 282, 162–182. [Google Scholar] [CrossRef]
- Song, Q.; Yuan, M. Visualizing an adsorption model for surfactant transport from micellar solutions to a clean air/water interface by fluorescence microscope. J. Colloid Interface Sci. 2011, 357, 179–188. [Google Scholar] [CrossRef] [PubMed]
- Pan, R.; Green, J.; Maldarelli, C. Theory and Experiment on the Measurement of Kinetic Rate Constants for Surfactant Exchange at an Air/Water Interface. J. Colloid Interface Sci. 1998, 205, 213–230. [Google Scholar] [CrossRef] [PubMed]
- Eastoe, J.; Dalton, J.S. Dynamic surface tension and adsorption mechanisms of surfactants at the air-water interface. Adv. Colloid Interface Sci. 2000, 85, 103–144. [Google Scholar] [CrossRef]
- Chang, C.-H.; Franses, E.I. Adsorption dynamics of surfactants at the air/water interface: a critical review of mathematical models, data, and mechanisms. Colloid Surface A Physicochem. Eng. Aspects 1995, 100, 1–45. [Google Scholar] [CrossRef]
- Frykman, S.; Srienc, F. Quantitating secretion rates of individual cells: design of secretion assays. Biotechnol. Bioeng. 1998, 59, 214–226. [Google Scholar] [CrossRef]
- Ferri, J.K.; Stebe, K.J. Which surfactants reduce surface tension faster? A scaling argument for diffusion-controlled adsorption. Adv. Colloid Interface Sci. 2000, 85, 61–97. [Google Scholar] [CrossRef]
- Lionello, A.; Josserand, J.; Jensen, H.; Girault, H.H. Protein adsorption in static microsystems: Effect of the surface to volume ratio. Lab Chip 2005, 5, 254–260. [Google Scholar] [CrossRef] [PubMed]
- Charlet, M.; Kromenaker, S.J.; Srienc, F. Surface IgG content of murine hybridomas: Direct evidence for variation of antibody secretion rates during the cell cycle. Biotechnol. Bioeng. 1995, 47, 535–540. [Google Scholar] [CrossRef] [PubMed]
- Henn, A.D.; Rebhahn, J.; Brown, M.A.; Murphy, A.J.; Coca, M.N.; Hyrien, O.; Pellegrin, T.; Mosmann, T.; Zand, M.S. Modulation of single-cell IgG secretion frequency and rates in human memory B cells by CpG DNA, CD40L, IL-21, and cell division. J. Immunol. 2009, 183, 3177–3187. [Google Scholar] [CrossRef] [PubMed]
- Day, Y.S.; Baird, C.L.; Rich, R.L.; Myszka, D.G. Direct comparison of binding equilibrium, thermodynamic, and rate constants determined by surface- and solution-based biophysical methods. Protein Sci. 2002, 11, 1017–1025. [Google Scholar] [CrossRef] [PubMed]
- Foote, J.; Eisen, H.N. Kinetic and affinity limits on antibodies produced during immune responses. Proc. Natl. Acad. Sci. USA 1995, 92, 1254–1256. [Google Scholar] [CrossRef] [PubMed]
- Cho, D.; Narsimhan, G.; Franses, E.I. Adsorption Dynamics of Native and Pentylated Bovine Serum Albumin at Air-Water Interfaces: Surface Concentration/ Surface Pressure Measurements. J. Colloid Interface Sci. 1997, 191, 312–325. [Google Scholar] [CrossRef] [PubMed]
- Um, S.U.; Poptoshev, E.; Pugh, R.J. Aqueous Solutions of Ethyl (Hydroxyethyl) Cellulose and Hydrophobic Modified Ethyl (Hydroxyethyl) Cellulose Polymer: Dynamic Surface Tension Measurements. J. Colloid Interface Sci. 1997, 193, 41–49. [Google Scholar] [CrossRef] [PubMed]
- Ybert, C.; di Meglio, J.M. Study of protein adsorption by dynamic surface tension measurements: Diffusive regime. Langmuir 1998, 14, 471–475. [Google Scholar] [CrossRef]
- Zhmud, B.V.; Poptoshev, E.; Pugh, R.J. Role of Hydration and Conformational Changes in Adsorption Dynamics of Ethyl(Hydroxyethyl)cellulose at the Air/Solution Interface. Langmuir 1998, 14, 3620–3624. [Google Scholar] [CrossRef]
- Torres, A.J.; Hill, A.S.; Love, J.C. Nanowell-based immunoassays for measuring single-cell secretion: characterization of transport and surface binding. Anal. Chem. 2014, 86, 11562–11569. [Google Scholar] [CrossRef] [PubMed]
- Han, Q.; Bradshaw, E.M.; Nilsson, B.; Hafler, D.A.; Love, J.C. Multidimensional analysis of the frequencies and rates of cytokine secretion from single cells by quantitative microengraving. Lab Chip 2010, 10, 1391–1400. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, Q. Protein Adsorption in Microengraving Immunoassays. Sensors 2015, 15, 26236-26250. https://doi.org/10.3390/s151026236
Song Q. Protein Adsorption in Microengraving Immunoassays. Sensors. 2015; 15(10):26236-26250. https://doi.org/10.3390/s151026236
Chicago/Turabian StyleSong, Qing. 2015. "Protein Adsorption in Microengraving Immunoassays" Sensors 15, no. 10: 26236-26250. https://doi.org/10.3390/s151026236