Sensor Saturation Compensated Smoothing Algorithm for Inertial Sensor Based Motion Tracking
Abstract
: In this paper, a smoothing algorithm for compensating inertial sensor saturation is proposed. The sensor saturation happens when a sensor measures a value that is larger than its dynamic range. This can lead to a considerable accumulated error. To compensate the lost information in saturated sensor data, we propose a smoothing algorithm in which the saturation compensation is formulated as an optimization problem. Based on a standard smoothing algorithm with zero velocity intervals, two saturation estimation methods were proposed. Simulation and experiments prove that the proposed methods are effective in compensating the sensor saturation.1. Introduction
In motion tracking, there are many ways to estimate the trajectory of a moving object. Moving objects can be tracked accurately by using visual devices such as camera systems [1,2]. In [1], with 40 landmarks attached on the body, Hong et al. used the Eagle Digital motion capture system with seven cameras to analyze 14 angles and one ratio of gait features. In [2], Lee and Grimson investigated person identification and gender classification based on moments computed from the silhouette of walking people. However, these camera systems are limited in their setup ranges and sometimes have high implementation costs. Moreover, the angle views of the cameras are also limited and they are easily affected by illumination. Due to these reasons, for long distance or outdoor measurements, motion tracking based on camera systems seems to be a difficult task.
To avoid the mentioned disadvantages, inertial measurement units (IMU) can be used instead as wearable devices. IMUs are widely used due to their small size and low cost. With the development of the technology, IMUs are now becoming more accurate. In [3], Tadano et al. proposed a method using quaternion calculations from seven sensor units consisting of a tri-axial acceleration and gyro sensors. The quaternions, which are computed from the sensors attached on limbs and waist, are used in a gait wire frame model to generate the gait animation. To increase the accuracy, the IMUs are used with other aiding devices such as cameras in [4,5] or force sensors in [6].
However, IMUs still have their own limitations such as susceptibility to noise and limited dynamic range. The accuracy of inertial sensor-based estimation can be improved by using zero velocity updates as in [7], or taking advantage of the relative position and attitude of multiple sensors [8,9]. In [7], a robot arm control with an automatic calibration function based on inertial sensors is proposed. The authors state that the drift of the sensors is clearly removed by applying zero velocity updates. In [8], Helten et al. introduce another way which takes into account the relative position and attitude of multiple sensors to improve the accuracy of human motion estimation. Using the same method, Tao et al. [9] estimate limb movement. They also use the limb biomechanical model characteristics to provide constraints for sensors' relations. However, the other drawback of the inertial sensor, the saturation, has not been considered. Saturation is a state in which the signal that needs to be measured is larger than the dynamic range of the sensor. When that happens, the output of the sensor becomes the limiting value of the sensor range. This induces a considerable error between the true and estimated values during motion tracking. In this paper, we propose two methods for estimating the sensor saturation. Assuming that the motion is between not moving intervals (called zero velocity intervals), we formulate a saturation estimation problem as an optimization problem by modifying a smoother used in [10,11]. In the proposed methods, some state constraints mentioned in [12] could be added to increase the accuracy of the algorithm.
The paper is organized in five main sections and a conclusion. Section 2 points out the problem formulation. In Section 3, a standard smoothing algorithm with zero velocity intervals is described in detail. Sections 4 and 5 propose some methods for sensor saturation estimation. Some experiments to verify the proposed methods are given in Section 6. The last section concludes the paper.
2. Problem Formulation
We consider a moving object case where an IMU is attached on the object. There are two coordinate systems in this paper: the navigation coordinate frame and the body coordinate frame. The z axis of the navigation coordinate frame coincides with the local vertical. The choice of x axis is arbitrary. The body coordinate frame is defined as a frame with three axes coinciding with the three axes of the inertial measurement unit. The subscripts b (body) and n (navigation) are used to emphasize that a vector or matrix belongs to the body or navigation coordinate frame, respectively.
Our goal is to estimate attitude (expressed using the quaternion), position and velocity of the object from the sensor data. Let q=[q0 q1 q2 q3]∈R4 be a quaternion representing the rotation relationship between the navigation coordinate frame and the body coordinate frame. Let C(q) ∈ R3×3 be the rotation matrix corresponding to the quaternion q [13], and r ∈ R3 and v ∈ R3 be the position and velocity of the object, respectively. We have the following basic equations [14]:
The inertial measurement unit used in this paper consists of three axis gyroscopes and accelerometers. Let yg ∈ R3 be the gyroscope output and ya ∈ R3 be the accelerometer output. They satisfy the following relationship [15]:
In summary, our goal is to estimate the quaternion, velocity and position of a moving object using the accelerometer and gyroscope data where there could be sensor saturation. Since a smoother is used instead of a filter, we note that the proposed method is offline analysis of attitude and position.
3. Standard Smoothing Algorithm with Zero Velocity Intervals
In this section, a standard smoothing algorithm is formulated in the quadratic optimization problem. A general method of formulating the smoothing problem in the optimization problem is given in [10]. In this section, we apply the result in [10] to an attitude and position estimation problem, where there are zero velocity intervals. Sensor saturation compensation is not considered in this section and will be discussed in Section 4.
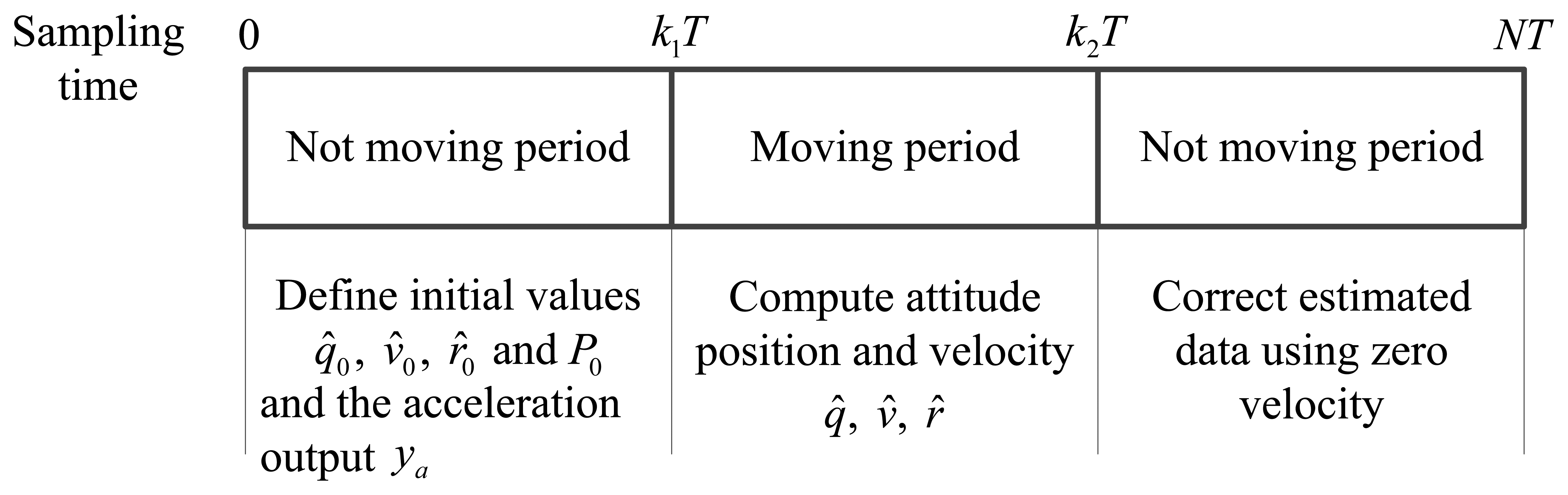
We assume that the motion is a short movement consisting of a moving interval and two not moving intervals (see Figure 1). This type of movement can be found in walking [4,5], golf swing [17] and so on. The sensor data are sampled with the sampling period T. It is assumed that there are total N sampling sensor data and the moving interval starts at k1T and stop at k2T (k1 < k2 < N). The rest are the zero velocity intervals. We use the subscript k to describe a variable is expressed in the discrete time k. For example, a gyroscope output data at time k is denoted by yg,k.
Using the gyroscope output yg in Equation (1), the q, v and r can be estimated by the following equation (“∧” denotes for estimation):
The initial values of position r̂0 and velocity v̂0 are assumed to be zero due to the fact that the object is not moving at the not moving period and the origin of the navigation coordinate frame coincides with the starting point of the object. The initial quaternion q̂0 is obtained from the accelerometer data using the following (note that ab=0 during the zero velocity intervals):
The heading in q̂0 is not determined and can be chosen arbitrarily. Since the noise terms are included in yg and ya in Equation (3), q̂, v̂ and r̂ are different from the true q, v and r. The error in q̂, v̂ and r̂ are estimated using a smoothing algorithm. Thus a smoothing algorithm is not used for directly estimating q, v and r but for estimating errors in q̂, v̂ and r̂. Once the errors are estimated, we can update q̂, v̂ and r̂ to obtain more accurate estimates. A multiplicative error is used for the error in q̂ [18]. A small error in q̂ is denoted by qe. qe is assumed to satisfy the following:
For the error in v̄ and r̄, an additive error model is used. We use symbols ve and re to denote the velocity error and position error, respectively:
The estimation error in q̄, v̄ and r̄ can be expressed using the following state:
This x(t) is estimated using a smoother. To do that, we derive a differential equation for x(t). From the assumption that q̄e and ω−yg is small, we obtain the follow (see [19] for the derivation):
Since the sensor sampling period is T, Equation (8) is discretized with the sampling period T [20]:
Since no external sensors other than the inertial sensor are used, there is no physical measurement during the motion. However, the fact that the velocity is zero during the not moving period can be used as a virtual measurement. In motion analysis, it is assumed that the object is not moving when the gyroscope and the variation of the accelerometer are smaller than threshold values for some specified time. Thus there will be a chance that a moving interval is detected as a zero velocity interval. To reflect this fact, a small noise nv,k is added in the following equation:
The noise nv,k at time k is modeled as a Gaussian white noise with the covariance . Equation 10 can be rewritten in form of following expression in discrete time at time k:
We introduce a set Zm which consist of the discrete time indices belonging to the zero velocity intervals. That is, if k∈Zm, then we can use the Equation (11).
A smoother problem to estimate xk can be formulated as the following optimization problem [10,11]:
Find xk and wk for 0≤k≤N that minimize:
By inserting the constraint xk+1=Ad,kxk+wk into Equation (12), we can remove the variable wk from the optimization problem:
Let the optimization variable x̄ be defined by , then the matrix form of the optimization will be:
Let the minimum solution to the problem. Equation (14) be defined by J*. Note that J* depends on yg,k, ya,k(0≤k≤N), q̂0, r̂0, v̂0 and P0. For later use, we denote J* by a function f as follows:
In Equation (14), constraints can be easily added to improve the accuracy. For example, in gait analysis, while walking on a plane that assumed to be parallel with the xy plane of the local navigation coordinate frame, we can make use of zero z axis position as following:
4. Sensor Saturation Estimation
The sensor saturation occurs when the measured values are over the sensors' dynamic ranges (Figure 2). While it is difficult to know sensor noise values (ng and na in Equation (7)), it is not difficult to know when the sensor saturation occurs.
Each sensor has its own range of measurement. When the measured values are larger than the measurement limit, the saturation happens. Even if the saturation happens in a short time, it could lead to a large accumulated error since the lost information is in a large magnitude data area. The data loss due to the saturation has a considerable influence to the result, especially when the integration is used in data processing.
The saturation can be avoided by using large dynamic range sensors. Usually, large measuring range (with the same sensor resolution) sensors tend to be expensive. Instead of using an expensive large range sensor, we can use a low cost one with smaller measuring limit along with applying a saturation compensation algorithm.
The saturation can happen in gyroscopes and accelerometers in three axes. Symbols yg,x,k,yg,y,k, yg,z,k are used to denote three elements in yg,k∈R3. Similarly, ya,x,k,ya,y,k and ya,z,k are used for ya,k∈R3. We use the fact that the value of the sensor output is smaller than the saturation value outside the saturation interval. In the saturation interval, we assume that the sensor output is equal to the saturation value. Let yg,sat be the saturation value of a gyroscope and Sg,x be the set of gyroscope x saturation inertial indexes:
Similarly, we can define Sg,y, Sg,z, ya,sat (saturation value of an accelerometer), Sa,x, Sa,y and Sa,z. Denote δg,x,k, δg,y,k, δg,z,k, δa,x,k, δa,y,k, δa,z,k, the compensation values of gyroscopes and accelerations in x,y,z axes at the time k, respectively. The compensated sensor value (ȳg,k and ȳa,k) is the sum of sensor output value and compensation value. For example, the compensated x axis gyroscope value is given by:
Let δ be set of δg,x,k, δg,y,k, δg,z,k, δa,x,k, δa,y,k and δa,z,k variables. For example, if Sg,x={5,6,7}, Sa,y={8,9,10}, and Sg,y= Sg,z= Sa,x= Sa,z=⊘ then δ is given by:
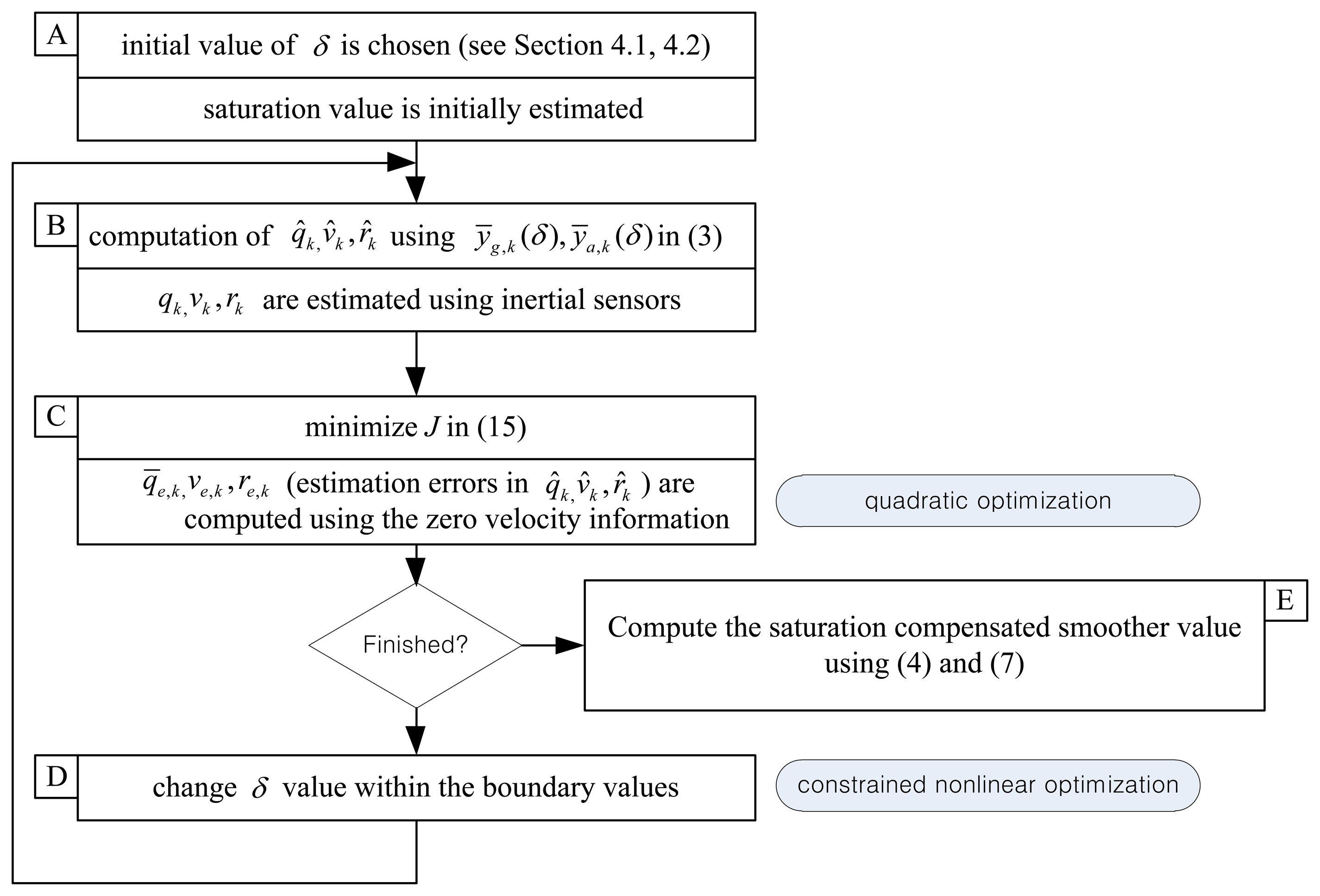
Now the standard smoother algorithm in Section 3 is modified using ȳg,k and ȳa,k. The flowchart of the algorithm is given in Figure 3. The first step (step A in Figure 3) of the algorithm is the initial estimation of, δ which is explained in Sections 4.1 and 4.2. Given δ values, the standard smoother algorithm (steps B and C) is applied to compute the smoother. This standard algorithm (given in Section 3) can be formulated as the quadratic optimization algorithm. How good the computed smoother is can be evaluated using the computed J value in Equation (15). This process (steps B and C) is repeated by changing δ values. The algorithm finishes if the minimum value of J is found. We note that δ optimization can be formulated as a constrained nonlinear optimization problem. Once the minimization process is done, we can compute the saturation compensated smoother values (step E).
Consider the following function (from Equation (15)):
Assuming q̂0, r̂0, v̂0,P0,yg,k and ya,k are constant, the function f in Equation (18) depends on δ. In this section, f is minimized with respect to δ. Two different methods are proposed. The first method directly minimize δ with respect to all possible combination of δ. The second method uses the geometric structure of the sensor saturation.
4.1. Method 1: Direct Estimation of δ
In the first method, the following optimization problem is solved:
In Equation (20), “≤” and “≥” represent element-wise inequalities and δb is a set of bounding positive values of elements in δ. Choice of δb depends on applications. For example, in knee gyroscope data, the maximum angular velocity of a human knee varies from 213 to 1,087°/s [22]; in gait acceleration, the maximum foot acceleration is around 11.82 m/s2 for walking case [23]. Therefore, the gyroscope data upper bound can be chosen as δb = [1,087 − yg,sat 11.82 − ya,sat]T. From Equations (16) and (17), it is easily to be seen that when yg,ya≥0, we have δ ≥0 because gyroscope compensated values (ȳg, ȳa) are larger than saturation value (yg,sat,ya,sat). The initial value of δ can be chosen as a set of 0 and varies in a range which satisfies the condition in Equation (20). With each set of δ, one value of x̄ is obtained. The minimum value of δ which makes x̄ minimizes the quadratic problem (14) is chosen.
4.2. Method 2: Estimation of δ Using Geometric Form
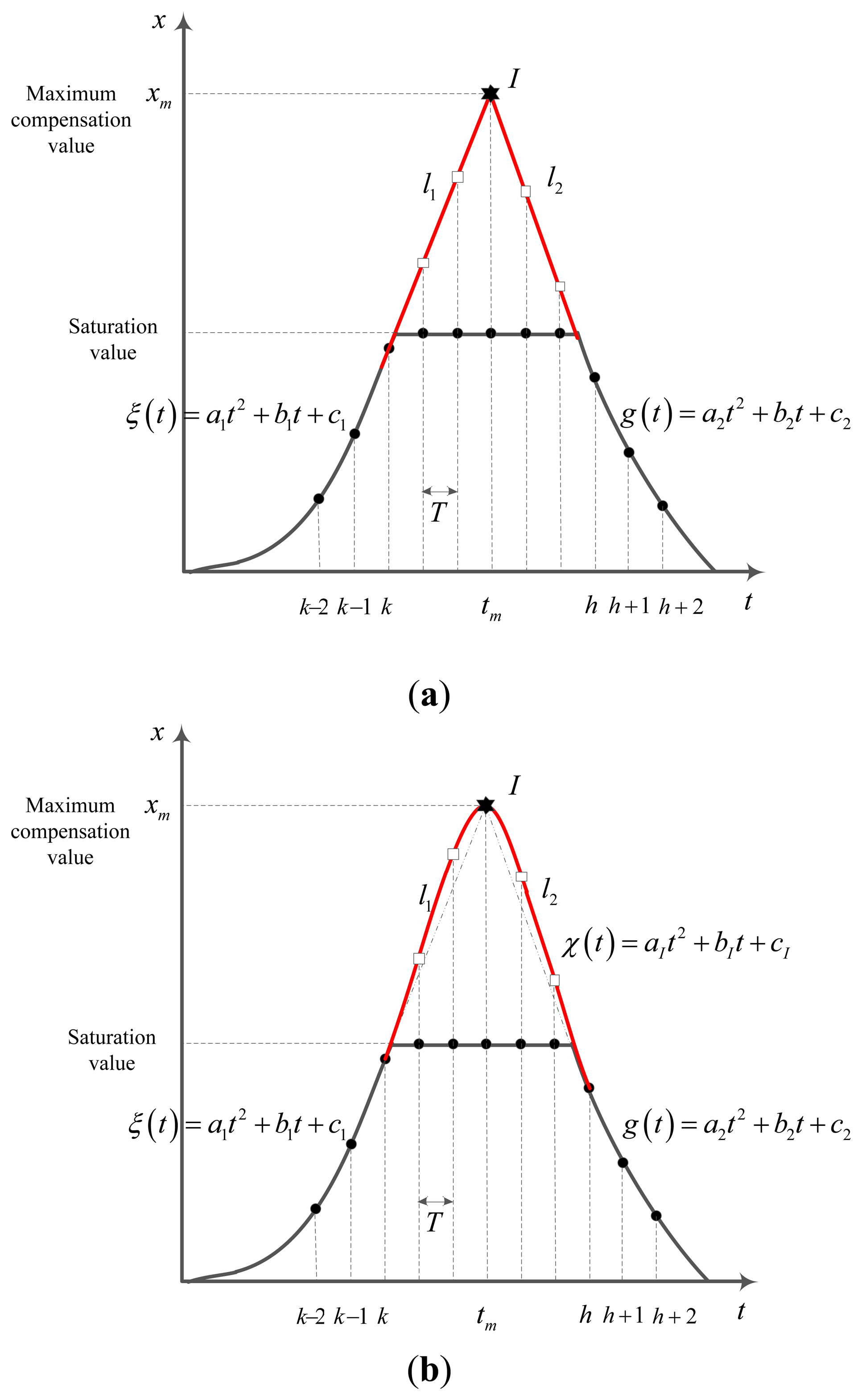
In this method, the saturated sensor data region is approximated by a triangle (see Figure 4a) and quadratic function (see Figure 4b). Using three data before the saturation interval (xk−2, xk−1,xk in Figure 4a), we can obtain a quadratic function. In the next step, a line l1 starting from xk with the slope ξ'(k) is generated. With the same procedure (quadratic function g(t) for xh,xh+1,xh+2), we generate a line l2. l1 and l2 are the reconstruction part of sensor saturation. The intersection point of l1 and l2 (at the time tm) is the maximum value (xm) for compensation. Now consider l1 is created based on (xk,k) and (xm,tm) points, l2 is created based on (xh,h) and (xm,tm) points. Changing the height of the intersection from saturation value to maximum compensation value xm we can generate several sets of basic lines l1,l2 which contain compensation values. The intersection point is defined as following:
The other compensation value is defined by:
Using this method, sets of sensor's compensation values δ can be generated by changing the intersection point's value from saturation value to maximum compensation value. In this case, δ only depends on intersection point. Denote I(xI,tI) the intersection point. Once I is created, the rest compensation data will be obtained based on l1 and l2 lines using Equation (22). The optimization problem (19) will subject to δ value which relates to the intersection point.
With the same idea, a quadratic approximation can be used to generate the lost information (see Figure 3b. Firstly the maximum compensation value can be generated using the same procedure in triangle approximation process. After this step, a quadratic function χ(t) is formed up based on (xk,tk),(xh,th) and (xm,tm) points. In saturation parts, the compensation value at time tk is χ(tk).
5. Sensor Saturation Compensation Algorithm with Multiple Zero Velocity Intervals
Section 4 introduced two methods to compensate sensor saturation in a standard movement situation which contains two zero velocity intervals at the beginning and ending of a moving interval. In this section, we apply the Section 4 methods to multiple zero velocity interval movements. A movement with multiple zero velocity intervals is displayed in Figure 5. In this movement, moving intervals are interposed by zero velocity intervals. An example of this movement can be found in gait analysis in [4,5]. In the characteristic human gait, one foot is assumed to be not moving when the the center of mass is put on the corresponding leg to move the other. Therefore, during the walking process, there are zero velocity intervals separated by moving intervals for each foot.
We divide the movement into segments based on zero velocity intervals so that between two zero velocity intervals there is data from one moving period (see Figure 5). If there are saturations in the movement, we can apply the compensation methods in Section 4 to each segment. The information of the last sampling in the prior segment will be used as the initial value for the following one. The initial error covariance for each segment can be estimated using a Kalman filter with a zero velocity measurement update for previous segment. Note that for the first segment the position and velocity errors are assumed to be zero due to the fact that the initial body coordinate frame coincides with the navigation coordinate frame. The initial covariance of the first segment is also assumed to be small. Repeating the smoothening processes until the last segment, the whole smoothed data is obtained.
6. Simulation and Experiments
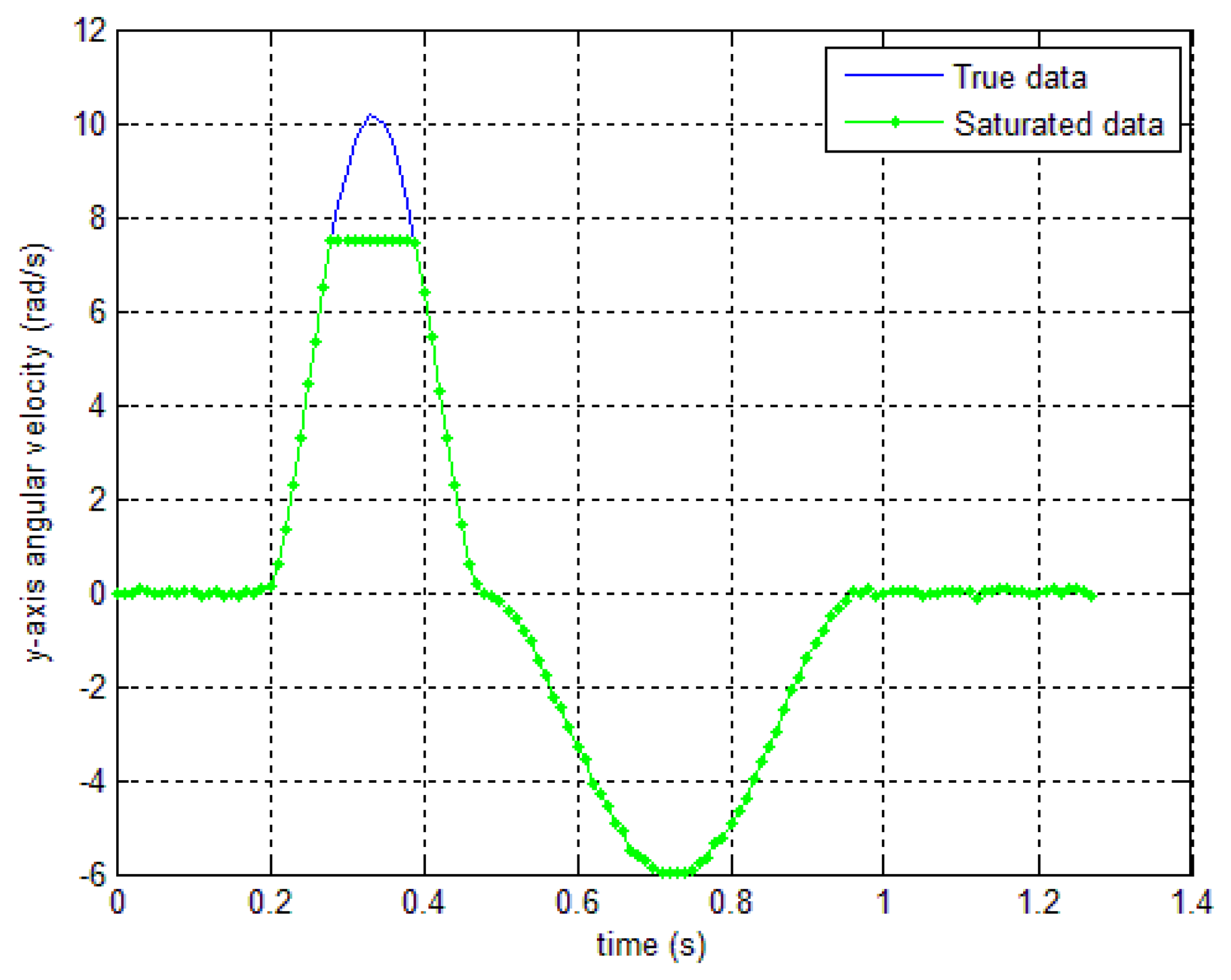
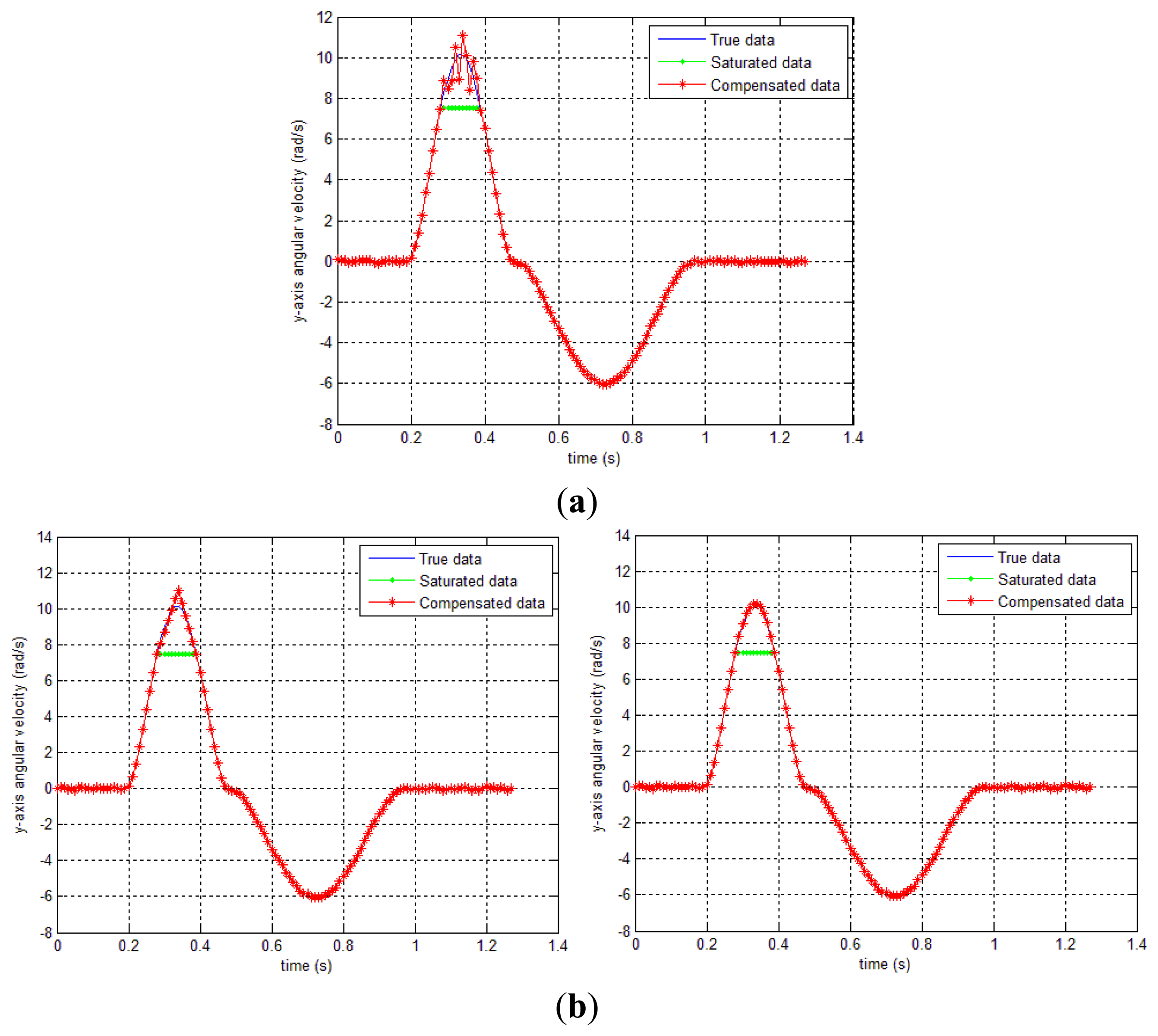
In this section, one simulation result and two experimental results are given to verify the proposed algorithm. First, a simulation is done to verify the proposed method. The sensor is assumed to be located at the end of a bar, which is rotated along the body y axis. There is a sensor's saturation in the gyroscope y axis data as in Figure 6. The saturated data (green “—” line) is obtained with yg,y,sat=7.5. This saturated data is used as an input data for the compensation algorithms in Section 4.
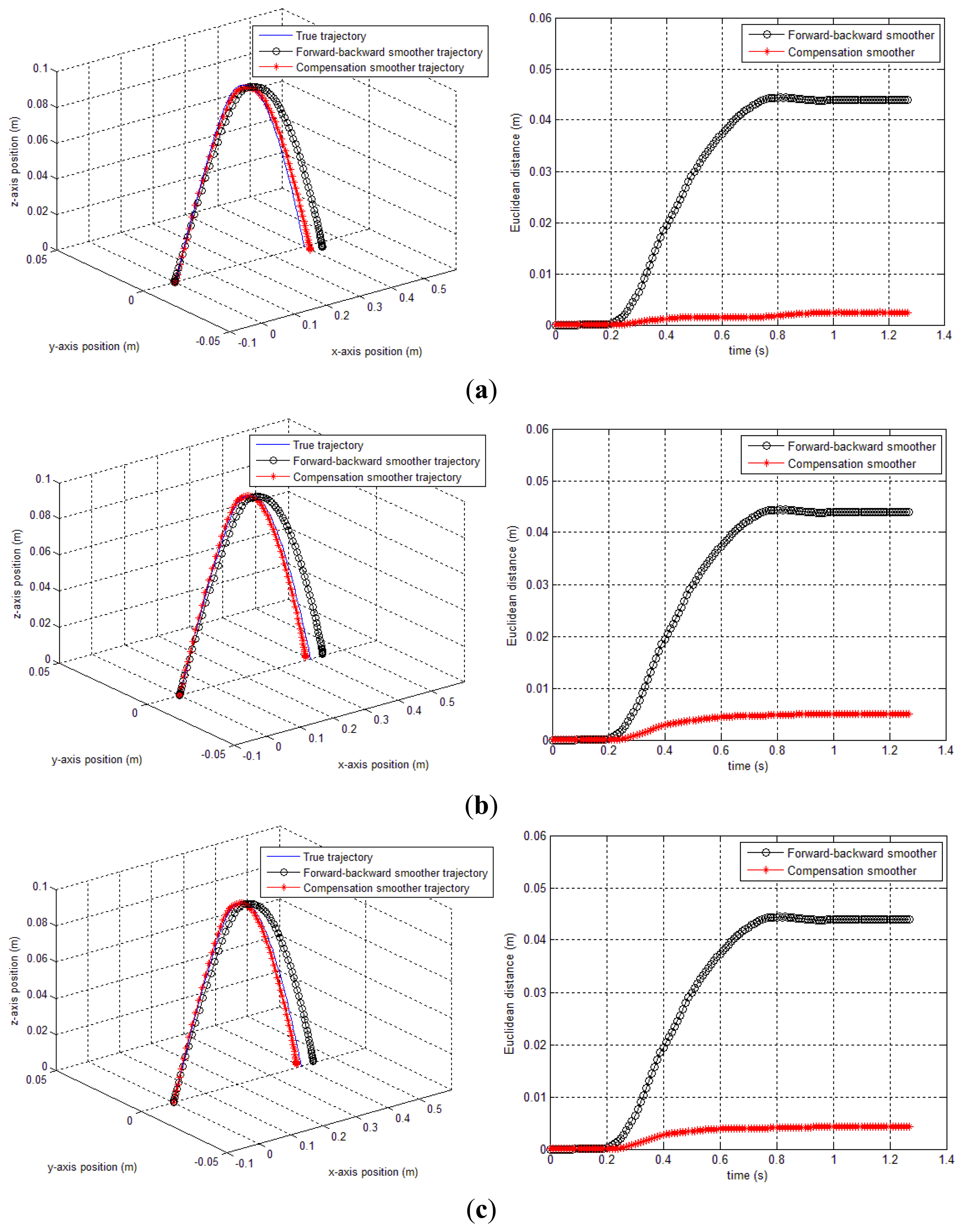
In this simulation, δ only contains y axis compensation (δg,y,k). The smoothing results (forward-backward smoother [20] and the proposed methods) are given in Figure 7 and Table 1. In case of method 1, δb is chosen as 5, so that the performance index J is minimized subject to 0≤δ≤5. Similarly, method 2 (both triangle and quadratic approximation) is applied. In Table 1, we can see that both method 1 and 2 produce significant improvements over the conventional smoothing (forward-backward smoother) result. Among the proposed methods, method 1 gives the best result and the second best is method 2 (quadratic approximation). We note that the method 1 requires more computation than method 2 since it needs more optimization variables. As for method 2, it is not conclusive whether quadratic approximation is better than triangle approximation since triangle approximation sometimes gives better results as seen in our later experiment (see Table 2).
In Figure 8, the gyroscope sensor saturation compensation results by the proposed methods are given. In all three cases, it can be seen that the sensor saturation is well estimated.
In Figure 7, the gyroscope sensor saturation compensation results by the proposed methods are given. In all three cases, it can be seen that the sensor saturation is well estimated.
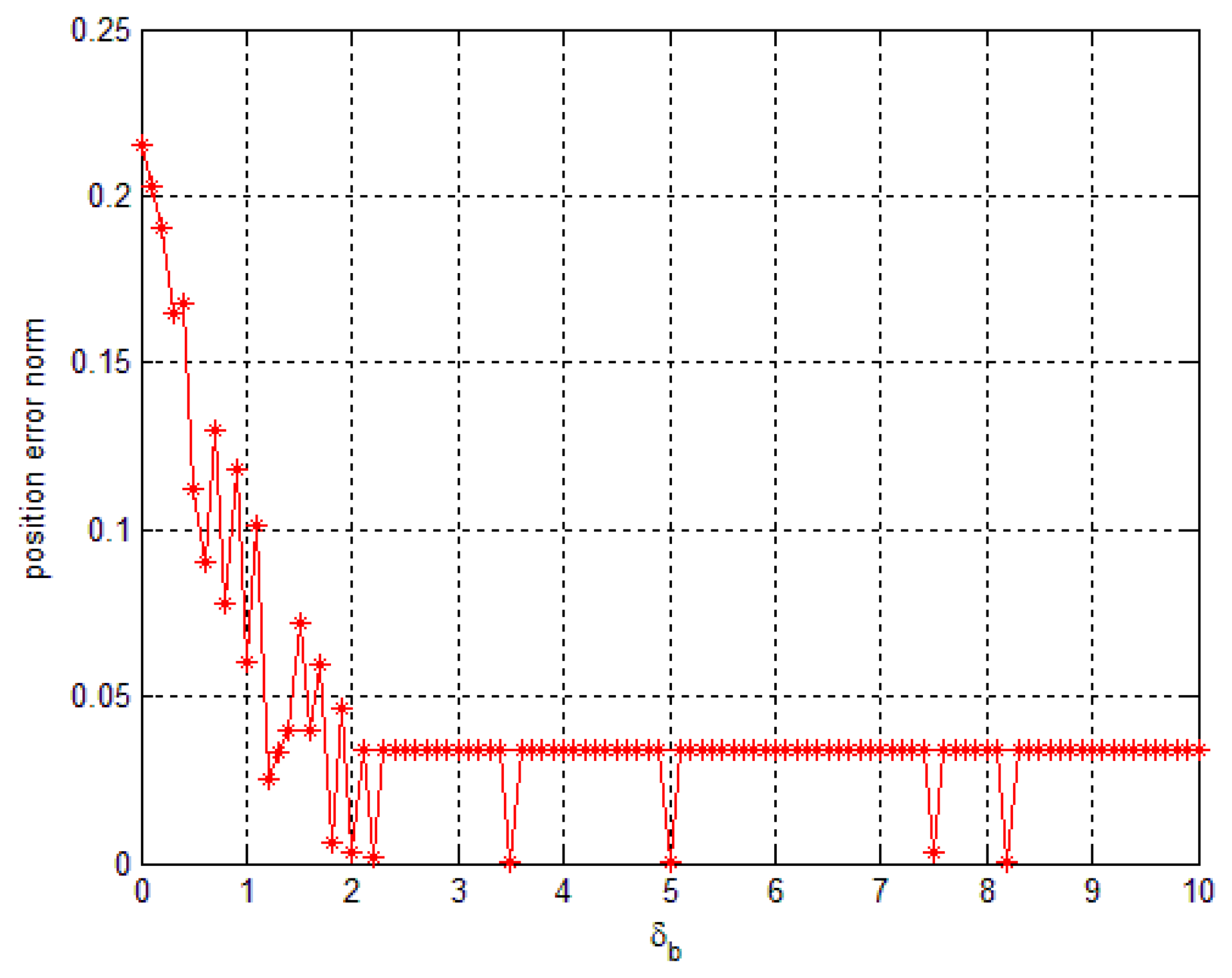
In order to verify the robustness of the proposed algorithms to the saturation, a simulation is done by checking the position norm errors while yg,y,sat value is changed. For example, if we set yg,y,sat=12 in Figure 6, there is no saturation in the sensor. On other hand, if we decrease yg,y,sat value, the sensor saturation increases. With the method 1, when the δb is fixed and the saturation value is changed, the accuracy of the proposed smoother may be affected (if the δb is chosen not large enough). As can be seen from Figure 9 where the δb is chosen as 2.5, the accuracy will decrease when the compensation value that is used to compensate the saturated data is larger than. δb However, this effect can be avoided since the saturation value is known for each sensor. Therefore, we can choose δb as a large number compared with the sensor's saturation value.
Sections 4.1 and 4.2 showed that the accuracy of the method 2 only depends on the saturation value while the accuracy of the method 1 is affected by the saturation value and the. δb Figure 10 illustrates that the saturation is well compensated by method 2, even when the saturation value is changing. In general, compared with a forward-backward smoother, our proposed compensation smoother has better performance.
As mentioned above, how to choose δb may affect the accuracy. In some applications, the δb is known from doing statistical experiments. In the case where δb is unknown, we can choose an arbitrarily large value. This does not affect the result as shown in Figure 11. In Figure 11, when δb is chosen smaller than the compensation value that is used to compensate the saturated data, the error could be large. If we increase, δb the error decreases since a larger saturation can be compensated. However, it could lead to more computations for solving the optimization Equation (19).
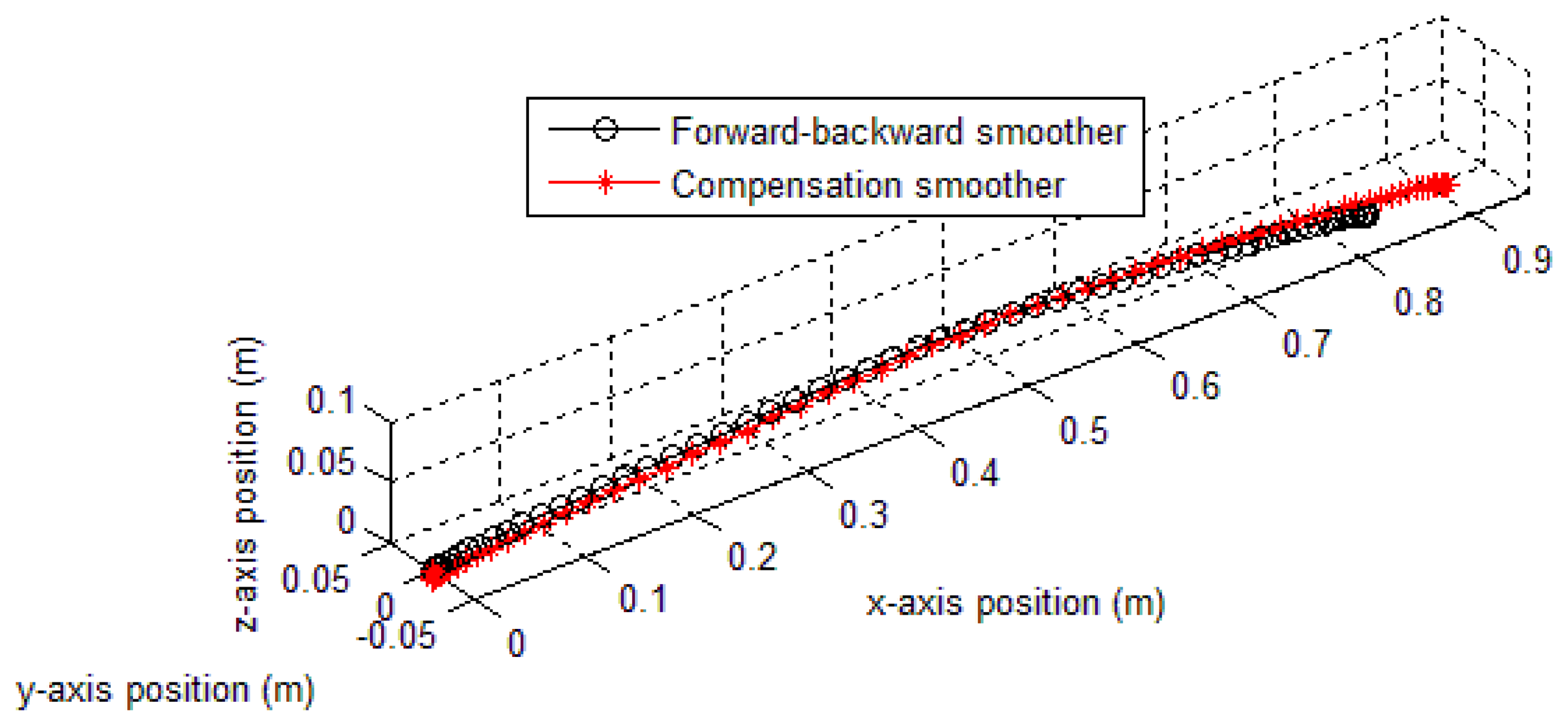
In the first experiment, an object, which is attached with an IMU on the top, moved in a straight line of 0.95 m so that the x axis of the IMU coincides with direction of movement. In this case, there exists saturation in the sensor's accelerometer in the x axis (ya,x). The trajectory of the object is estimated by the forward-backward smoother and our proposed compensation smoother using two methods. Figure 12 shows that the saturated ya,x,k data was compensated using the proposed compensation smoothers.
The estimated position errors are given in Figure 13 (method 1 only, since the results of method 2 are similar) and Table 2. As can be seen from Figure 13, the proposed compensation smoother using method 1 gives a closer result to the true position (0.9121 m, equivalent to 4% error) than the forward-backward smoother (0.8404 m, equivalent to 11.54% error). The proposed compensation smoother using method 2 also gives a good result of 0.9084 m (4.39% error) and 0.8976 m (5.52% error) for triangle and quadratic approximations, respectively.
Another experiment has been done to verify the compensation feasibility of the proposed algorithm. In this experiment, an IMU is attached at the tip of a digitizer (see Figure 14). The tip was moved in a curved line. The position data of the tip was recorded by the digitizer while the trajectory of the IMU is estimated by the proposed compensation and the forward-backward smoothers, respectively. The movement was made so that there is saturation in the yg,z,k data. The estimated trajectories are compared with the true trajectory of the digitizer in Figure 15 (in millimeters). The distance between the start and stop point is used as an evaluation criterion. Based on this criterion, a table of distance errors of the estimated positions and the digitizer's data is formed, as shown in Table 3. Table 3 shows that method 1 gives a best accuracy (7.9 mm error) compared with other estimations. The forward-backward smoother has a worst estimation with a 50.4 mm error result. Moreover, the two approximation methods in method 2 provide similar results (11.8 and 10.3 mm errors).
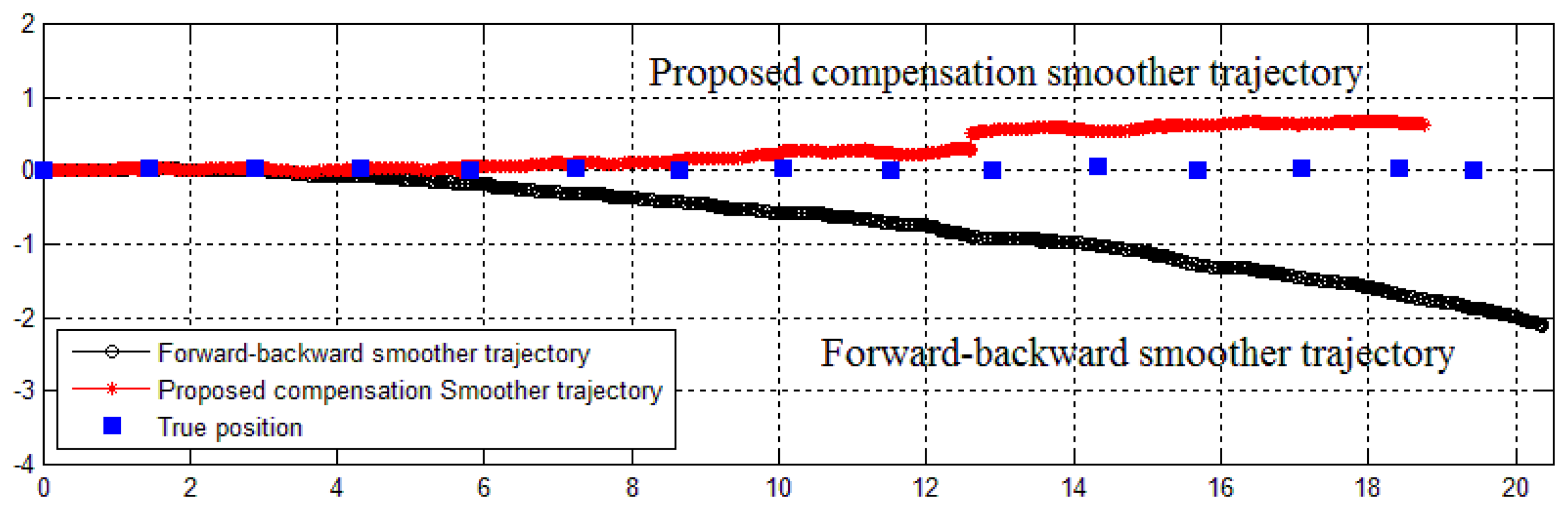
In the last experiment, we verify the compensation smoother application in multiple zero velocity intervals movement (in Section 5). In this experiment, an IMU is attached on a human foot. The volunteer was asked to walk along a straight corridor. A pen is also attached on the volunteer's shoe to mark the steps' positions on the floor. The obtained data from IMU is used to estimate the trajectory of the foot. A comparison of proposed and forward-backward smoothers trajectories is given in Figure 16. The result shows that the last position error of proposed smoother trajectory is 0.9042 m, while it is 2.3128 m for the forward-backward smoother trajectory.
7. Conclusions
This paper has proposed some approaches to compensate for sensor saturation. Saturation is a common problem with IMU sensors in tracking a moving object. The lost data in the saturated parts could be important due to the accumulated errors. In the paper, the authors used a standard smoothing algorithm with zero velocity intervals to compensate sensor saturation. The considered motion includes a moving interval between two zero velocity intervals. Two methods were proposed. The first method directly estimates the saturation compensation while the second one uses a geometric form to estimate the saturation. The proposed smoothing algorithm can be applied in some motions which contain many moving intervals separated by zero velocity intervals. In this case, the motion is divided into segments based on zero-velocity intervals so that between two zero velocity intervals there is one moving interval. The saturation estimation algorithm is applied in each segment from the first to the last one. To verify the feasibility of the two methods, some experiments have been done. The experiments showed that the proposed smoothing algorithm can compensate the sensor saturation and provides a smaller error than a conventional smoother (forward-backward filter). In practical applications, the sensor saturation compensation methods proposed in this paper can be used to improve the accuracy of small dynamic range sensors instead of using a large dynamic range one which usually tends to be more expensive.
Acknowledgments
This work was supported by 2013 Research Funds of Hyundai Heavy Industries for University of Ulsan.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hong, J. Gait Analysis and Identification. Proceedings of the 18th International Conference on Automation & Computing, Loughborough University, Leicestershire, UK, 8 September 2012; pp. 1–6.
- Lee, L.; Grimson, W.E.L. Gait Analysis for Recognition and Classification. Proceedings of the Fifth IEEE International Conference on Automatic Face and Gesture Recognition, Washington, DC, USA, 20–21 May 2002; pp. 148–155.
- Tadano, S.; Takeda, R.; Miyagawa, H. Three Dimensional Gait Analysis Using Wearable Acceleration and Gyro Sensors Based on Quaternion Calculations. Sensors 2013, 13, 9321–9343. [Google Scholar]
- Do, T.N.; Suh, Y.S. Gait Analysis Using Floor Marker and Inertial Sensors. Sensors 2012, 12, 1594–1611. [Google Scholar]
- Tran, N.H.; Suh, Y.S. Inertial Sensor-Based Two Feet Motion Tracking for Gait Analysis. Sensors 2013, 13, 5614–5629. [Google Scholar]
- Tao, W.; Liu, T.; Zheng, R.; Feng, H. Gait Analysis Using Wearable Sensors. Sensors 2012, 12, 2255–2283. [Google Scholar]
- Hoffmann, J.; Bruggemann, B.; Kruger, B. Auto Calibration of a Motion Capture System Based on Inertial Sensors for Tele-manipulation. Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Funchal, Madeira, Portugal, 15–18 June 2010.
- Helten, T.; Muller, M.; Tautges, J.; Weber, A.; Seidel, H.P. Towards Cross-modal Comparison of Human Motion Data. Proceedings of the 33rd Annual Symposium of the German Association for Pattern Recognition (DAGM), Frankfurt/Main, Germany, 31 August–2 September 2011; pp. 61–70.
- Tao, G.; Huang, Z.; Sun, Y.; Yao, S.; Wu, J. Biomechanical Model-based Multi-sensor Motion Estimation. Sens. Appl. Symp. (SAS) 2013, 23, 19–21. [Google Scholar]
- Psiaki, M.L. Backward-Smoothing Extended Kalman Filter. J. Guid. Control Dyn. 2005, 28, 885–894. [Google Scholar]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation; John Wiley & Sons: New York, NY, USA, 2001. [Google Scholar]
- Simon, D. Kalman Filtering with State Constraints: A Survey of Linear and Nonlinear Algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar]
- Kuipers, J.B. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Collinson, R.P. Introduction to Avionics Systems, 2nd ed.; Springer: New York, NY, USA, 2003. [Google Scholar]
- Luinge, H.J.; Veltink, P.H. Measuring Orientation of Human Body Segments Using Miniature Gyroscopes and Accelerometers. Med. Biol. Eng. Comput. 2005, 43, 273–282. [Google Scholar]
- Aggarwal, P.; Syed, Z.; Niu, X.; El-Sheimy, N. A Standard Testing and Calibration Procedure for Low Cost MEMS Inertial Sensors and Units. J. Navig. 2008, 61, 323–336. [Google Scholar]
- Nam, C.N.K.; Kang, H.J.; Suh, Y.S. Golf Swing Motion Tracking Using Inertial Sensors and a Stereo Camera. IEEE Trans. Instrum. Meas. 2013, 63, 943–952. [Google Scholar]
- Creamer, G. Spacecraft Attitude Determination Using Gyros and Quaternions Measurements. J. Austronautical Sci. 1996, 44, 357–371. [Google Scholar]
- Suh, Y.S. Orientation Estimation Using a Quaternion-Based Indirect Kalman Filter with Adaptive Estimation of External Acceleration. IEEE Trans. Instrum. Meas. 2010, 59, 3296–3305. [Google Scholar]
- Brown, R.G.; Hwang, P.Y.C. Introduction to Random Signals and Applied Kalman Filtering; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bober, T.; Putnam, C.A.; Woodworth, G.G. Factors Influencing the Angular Velocity of a Human Limb Segment. J. Biomech. 1987, 20, 511–521. [Google Scholar]
- More Acceleration Perturbations of Daily Living. Available online: http://hypertextbook.com/facts/2006/accelerometer.shtml (accessed on 17 April 2014).







| Estimation Method | Last Position Error | Position Error Norm |
|---|---|---|
| Forward-backward smoother | 0.0458 | 0.1544 |
| Proposed smoother (method 1) | 0.0032 | 0.0009 |
| Proposed smoother (method 2: triangle approximation) | 0.0045 | 0.0019 |
| Proposed smoother (method 2: quadratic approximation) | 0.0036 | 0.0014 |
| Estimation Method | Last Position Error |
|---|---|
| Forward-backward smoother | 0.1096 |
| Proposed smoother (method 1) | 0.0379 |
| Proposed smoother (method 2: triangle approximation) | 0.0416 |
| Proposed smoother (method 2: quadratic approximation) | 0.0524 |
| Estimation Method | Distance Error |
|---|---|
| Forward-backward smoother | 50.4 |
| Proposed smoother (method 1) | 7.9 |
| Proposed smoother (method 2: triangle approximation) | 11.8 |
| Proposed smoother (method 2: quadratic approximation) | 10.3 |
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Dang, Q.K.; Suh, Y.S. Sensor Saturation Compensated Smoothing Algorithm for Inertial Sensor Based Motion Tracking. Sensors 2014, 14, 8167-8188. https://doi.org/10.3390/s140508167
Dang QK, Suh YS. Sensor Saturation Compensated Smoothing Algorithm for Inertial Sensor Based Motion Tracking. Sensors. 2014; 14(5):8167-8188. https://doi.org/10.3390/s140508167
Chicago/Turabian StyleDang, Quoc Khanh, and Young Soo Suh. 2014. "Sensor Saturation Compensated Smoothing Algorithm for Inertial Sensor Based Motion Tracking" Sensors 14, no. 5: 8167-8188. https://doi.org/10.3390/s140508167






