Determination of External Forces in Alpine Skiing Using a Differential Global Navigation Satellite System
Abstract
: In alpine ski racing the relationships between skier kinetics and kinematics and their effect on performance and injury-related aspects are not well understood. There is currently no validated system to determine all external forces simultaneously acting on skiers, particularly under race conditions and throughout entire races. To address the problem, this study proposes and assesses a method for determining skier kinetics with a single lightweight differential global navigation satellite system (dGNSS). The dGNSS kinetic method was compared to a reference system for six skiers and two turns each. The pattern differences obtained between the measurement systems (offset ± SD) were −26 ± 152 N for the ground reaction force, 1 ± 96 N for ski friction and −6 ± 6 N for the air drag force. The differences between turn means were small. The error pattern within the dGNSS kinetic method was highly repeatable and precision was therefore good (SD within system: 63 N ground reaction force, 42 N friction force and 7 N air drag force) allowing instantaneous relative comparisons and identification of discriminative meaningful changes. The method is therefore highly valid in assessing relative differences between skiers in the same turn, as well as turn means between different turns. The system is suitable to measure large capture volumes under race conditions.1. Introduction
Alpine ski racing is a highly dynamic sport. Skiers move at high speed across large areas, adjusting their momentum at relatively high rates [1–4]. Differential global navigation satellite system technology (dGNSS), an efficient method to capture skier trajectories, has been applied by several researchers to investigate performance-related issues [5–8]. To understand the underlying mechanisms governing skiers' momentum (i.e., the direction of the trajectory and the speed along the trajectory) the external forces acting on the skiers (air drag, gravity and ground reaction forces) have to be determined [2,3,9,10]. So far, video-based 3D kinematic systems have been applied to compute the external forces [1,11–14]. This methodology allows accurate reconstruction of the air drag [15] and the resultant force acting on the center of mass. However, video-based 3D kinematic systems are limited in capture volume and need extensive processing time, which is unfortunate since the number of conditions to be investigated in alpine skiing is large [16]. Therefore, combinations of non-differential GNSS and inertial measurement data [17,18] as well as dGNSS [9] have been applied to reconstruct skier center of mass (CoM) position, velocity and acceleration (CoMPVA) as well as segment kinematics in racing situations more efficiently. However, none of these wearable system-based methods has been validated against a reference system which has been proven valid and has been extensively used. The current wearable systems might further be optimized with respect to robustness for applications in obstructed terrain and under racing conditions (factors can include GNSS signal obstruction by the skier's own body, geodetic methodology and measurement frequency). Therefore, the aim of the current study was to propose a non-invasive and robust dGNSS based method to determine the forces acting on the CoM in demanding alpine ski racing settings and to validate the method with a video and body segment parameter-based 3D kinematic system as suggested [9].
2. Methods
2.1. Data Acquisition
A giant slalom course was set with a 27 m gate distance and an offset of 8 m on a 26° incline, water-injected slope (Figure 1). The snow surface was captured by terrestrial surveillance with a tachymeter (Leica TPS 1200, Leica Geosystems AG, Heerbrugg, Switzerland). The surveyed points (on average 12 points per m2) were (a) triangulated using the method of Delaunay [19] and (b) gridded (grid spacing of 0.3 m) and smoothed with a bi-cubic spline function [20,21]. The analysis was based on data from turn eight of the course, allowing the skiers to pick up race- like speed before entering the analysis section. The analyzed section was short (one turn) due to the limitations in capture volume and the extensive processing time of the reference system. Analysis and turn start and end were defined as the point where the CoM and the mean ski trajectory crossed each other in the horizontal plane [22]. The entire turn including the straight phase at turn initiation and completion was named turn cycle. The phase in the turn where the turn radius of the reference trajectory was below 30 m was named turning phase [3]. Six male racers ranging from European Cup to former World Cup level volunteered to participate. Two runs per skier were selected for analysis and thus in total 12 runs were monitored. The current study was approved by the Ethics Committee of the Department of Sport Science and Kinesiology at the University of Salzburg.
2.2. dGNSS Based Method
GNSS is the umbrella term for global navigation satellite systems, while the more widely used term GPS is the name of the American global navigation satellite system. The current study makes use of both the Russian (GLONASS) and the American (GPS) system. We therefore use GNSS as the collective term for both.
2.2.1. Computation of the Center of Mass
The skiers' head trajectories were captured using a dGNSS system consisting of a G5Ant-2AT1 antenna (160 g, Antcom, Torrence, CA, USA) mounted on the helmet (Figure 2) and an Alpha-G3T receiver (430 g, Javad, San Jose, CA, USA) carried in a small cushioned backpack. Dual frequency (L1 and L2) data of the GPS and the GLONASS satellite systems were logged at 50 Hz. Short baseline differential dGNSS solution computation was enabled by using two base stations at the start of the course. The ambiguities of the differential geodetic position solution could be solved for all trials using the kinematic KAR algorithm of the GrafNav (Waypoint, NovAtel Inc., Calgary, AB, Canada) post-processing software.
Typical errors for dGNSS systems are 10 mm ± 1 ppm in horizontal and 20 mm ± 1 ppm in vertical direction [9]. The dGNSS head trajectory (PdGNSS) was filtered with a cubic spline function weighting each 3D position with its accuracy estimate from the differential position solution [5]. The tolerance factor (lambda) was 0.5 for the horizontal and 0.7 for the vertical component. For the approximation of the CoM based on the trajectory of the dGNSS antenna, the biomechanical phenomenon that skiers incline laterally in order to balance the radial force during the turn was used. The skier's inclination was modeled by an inverted pendulum [9,23] which was attached to the dGNSS antenna. The neutral position of the pendulum was given by the normal projection of the dGNSS antenna onto the snow surface. The pendulum was in neutral position during straight skiing, when the radial acceleration was zero. During turning the pendulum was deflected from its neutral position. The deflection representing the skier's lateral tilt was calculated as a linear combination of the gravitational and the dGNSS antenna radial acceleration. The intersection of the pendulum vector with the snow surface yielded the ski position (PSKI). Finally, the approximation of the CoM (CoMdGNSS) was modeled at 53% of the pendulum length measured from the dGNSS antenna (Figure 2). The computation of the CoMdGNSS at 53% of the pendulum length was determined on a full body segment kinematic dataset [2]. CoMdGNSS was low-pass filtered (second-order Butterworth filter; cut-off frequency of 4 Hz). Instantaneous CoM velocity (vdGNSS) and acceleration (adGNSS) were computed as the first and second time derivatives using the finite central difference formulae [24]. The pendulum model was described in detail in [25].
2.2.2. Computation of the External Forces
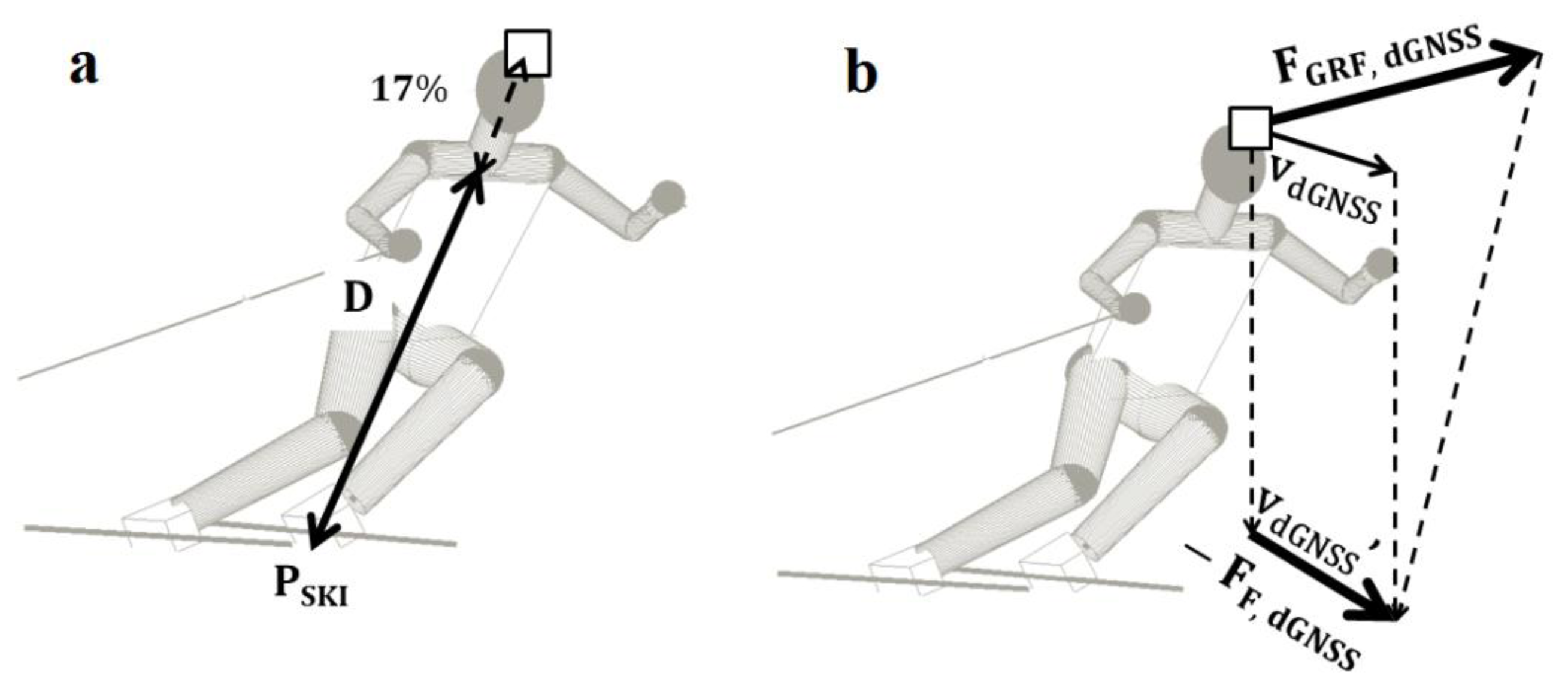
The resultant force (FRES,dGNSS) and the gravitational force (FG) were calculated using the skier's mass (including equipment) and the CoMdGNSS acceleration and gravitational acceleration respectively. The air drag force (FD,dGNSS) was computed according to Equation (1), where ρ is the air density. Air density was calculated from temperature and air pressure measurements taken at a meteorological station mounted along the slope. The effect of air humidity was neglected [26]. The line of action of the drag force was assumed to be opposite to vdGNSS. The ambient wind velocity field (vWIND) was based on two meteorological stations positioned on the top and the bottom part of the slope respectively. Wind speed was lower than 0.6 m/s during the measurement and at about right angles to the main course direction. The drag area (CDA)BARELLE was computed by adapting the model of Barelle (2004) [27], where the drag area was expressed as a function of reduced body extension (D) and arm position. For this study the arms were omitted from the model, and only the body extension was considered. Barelle [27] computed D (the distance between neck and feet) as the projections of the segment lengths L1 (leg), L2 (thigh) and L3 (chest) into the frontal plane using the angles θ1, θ2 and θ3 (Equation (2)). In the dGNSS method dataset D was computed along the vector between the feet position (PSKI) and the dGNSS antenna position (PGNSS) as shown in Figure 3a. The length of D was determined by the reduction of the distance between PSKI and PGNSS by 17% to accommodate for the distance between PGNSS and the neck in order to follow the definition of Barelle [27]. Drag area was computed according to Equation (3):
The ground reaction force (FGRF,dGNSS) was calculated according to Equation (4) and therefore includes all components of the ground reaction force:
The ski friction force (FF,dGNSS) is the component of FGRF,dGNSS in the tangent direction to the direction of motion. FF,dGNSS therefore measures the braking effect of the entire ski manipulation (loading, angulation, angle of attack, etc.) and interaction with the snow on the CoMdGNSS in the global spatial reference frame and might thus be relevant for performance related analysis. The direction of FF,dGNSS was defined as the vertical projection along the gravitational vector of vdGNSS onto snow surface (vdGNSS'). The negative component of FF,dGNSS (−FF,dGNSS) was computed by projecting FGRF,dGNSS normal onto vdGNSS'. FF,dGNSS was finally determined as the inverse of (−FF,dGNSS) [2]. The construction of (−FF,dGNSS) is illustrated in Figure 3b.
2.3. Reference System
2.3.1. Computation of the Center of Mass
The reference force method was derived from video-based 3D kinematic data. Skiers' segment kinematics were captured using six panned, tilted and zoomed HDV cameras (PMW-EX3, Sony, Tokyo, Japan) positioned around the capture volume. The capture frequency of the reference system was 50 Hz and was time-synchronized electronically with the dGNSS system. A standard video-based 3D kinematic system was used as the reference system [28]. Twenty-two joint centers and landmarks on the skier's body (head, neck, right and left (r/L) shoulder, (r/L) elbow, (r/L) hand, (r/L), stick's tail, (r/L) hip, (r/L) knee, (r/L) ankle, (r/L) ski's tip and tail) were reconstructed in 3D using a DLT-based panning algorithm developed by Drenk [29]. CoM position was computed using the Zatsiorsky body segment parameter model [30] with de Leva adjustments [31]. Instantaneous CoM velocity (vCoM) and acceleration (aCoM) were calculated similarly to the dGNSS method.
2.3.2. Computation of the External Forces
The resultant force (FRES,REF) and the gravitational force (FG) were calculated using the skier's mass (including equipment) and the (aCoM) acceleration and gravitational acceleration respectively. The air drag force (FD,REF) was computed according to Equation (5). The drag area ((CDA)MEYER) was computed by applying the “GM1” model of Meyer et al.[15] to the video-based segment kinematics method (Equation (6)), where UpH is the body length, AF is the frontal area, and H and W are the skier's instantaneous height and width. The frontal area was calculated using the orthonormal projection of the skier's silhouette on the plane normal to vCOM. The silhouette was generated by attaching geometric bodies to the reconstructed body landmarks and line segments. The frontal area (AF) was technically determined by counting the pixels within the skier's silhouette [2,17,32]. H and W were computed from segment kinematics in the frontal plane. The air drag model was found valid with respect to wind tunnel testing. (R2 = 0.972, p < 0.001, SD of the dragarea = 0.016) with wind-tunnel tests [15]. The ground reaction force (FGRF,REF) was calculated according to Equation (7). FGRF,REF was decomposed into the component parallel to the direction of motion (FF,REF) with the same method as in the dGNSS method, but using vCoM instead of vdGNSS.
2.4. Comparison of the dGNSS Based Method and the Reference System
For comparison of the dGNSS based method and the reference system, each trial was time-normalized. The dGNSS-based method was then compared with the reference system for the vector amplitude of the ground reaction force (FGRF = FGRF,REF − FGRF,dGNSS), the ski friction (FF = FF,REF − FF,dGNSS), the air drag force (FD = FD,REF − FD,dGNSS) and the resultant force (FRES = FRES,REF − FRES,dGNSS). The vectorial differences between the dGNSS-based method and the reference system were calculated for each time point of each trial. For each trial the offsets of these vectorial differences were calculated. Thereafter the offsets were averaged over the twelve trials and named average vectorial difference offset (AVD-Offset). In order to obtain a precision measure for between-measurement system comparisons (dGNSS and reference system) the standard deviation (precision, SD) of the vectorial differences was calculated for the entire turn cycle for each trial separately and then averaged across the twelve trials. This precision measure was named average vectorial difference between SD (AVD-Offset-Between-SD). To assess the precision of the dGNSS method for relative comparisons between skiers and/or different turns (within-measurement system precision) the SD of the twelve trials was calculated at each time point across the turn cycle (instantaneous AVD-Within-SD) and then averaged for all time points across the turn cycle. This precision measurement was called the average vectorial difference within SD (AVD-Within-SD). The described SD and offset procedures were performed for: (a) the entire turn cycle and (b) the turning phase, the section of the turn where the turn radius of the reference system was below 30 m [28] except for AVD-Within-SD. The average vectorial difference offsets and SD's were also expressed in relation to the respective turn mean forces in order to put the measurement errors into perspective with the size of the forces. These differences were expressed in percentage and computed as division of the vectorial difference offset or SD and the turn mean force of the reference system. Mean force and maximal force were extracted for each trial and averaged across the twelve trials with both the dGNSS method and the reference system for each force. The differences between the dGNSS and the reference system of the turn cycle mean and turn cycle maxima computation were assessed by calculation of the mean error and the SD between the methods. The normality of the data was verified prior to applying parametric statistics using the Lilliefors test (p < 0.05).
3. Results and Discussion
3.1. Results
Using the method described previously the force differences were monitored for twelve trials. Table 1 shows the results of the assessment. The average vectorial difference offset obtained from the dGNSS and the reference system was largest for FGRF but substantially smaller for FF and FD.
The average vectorial difference offset for FGRF and FD was smaller for the turning phase when the turn radius was below 30 m than for the entire turn cycle both in absolute values and relative to the size of the respective turn cycle mean and turning phase mean forces. The average vectorial difference offset of FF was larger for the turning phase than the turn cycle.
The precision offsets for comparison within the dGNSS system (AVD-Within-SD) for FGRF and FF were less than half of the precision offsets between the dGNSS and the reference system (AVA-Between-SD) while this was nearly unchanged for FD. During the turning phase when the turn radius was below 30 m the AVA-Between-SD was reduced in both absolute and relative terms compared to the entire turn cycle for FGRF and FF but not for FD.
Comparing the typical features of turn cycles, the differences in the turn mean were substantially smaller than the AVD-Within-SD and AVD-Between-SD for all forces. The maximum values were underestimated for all forces with the largest error for FGRF.
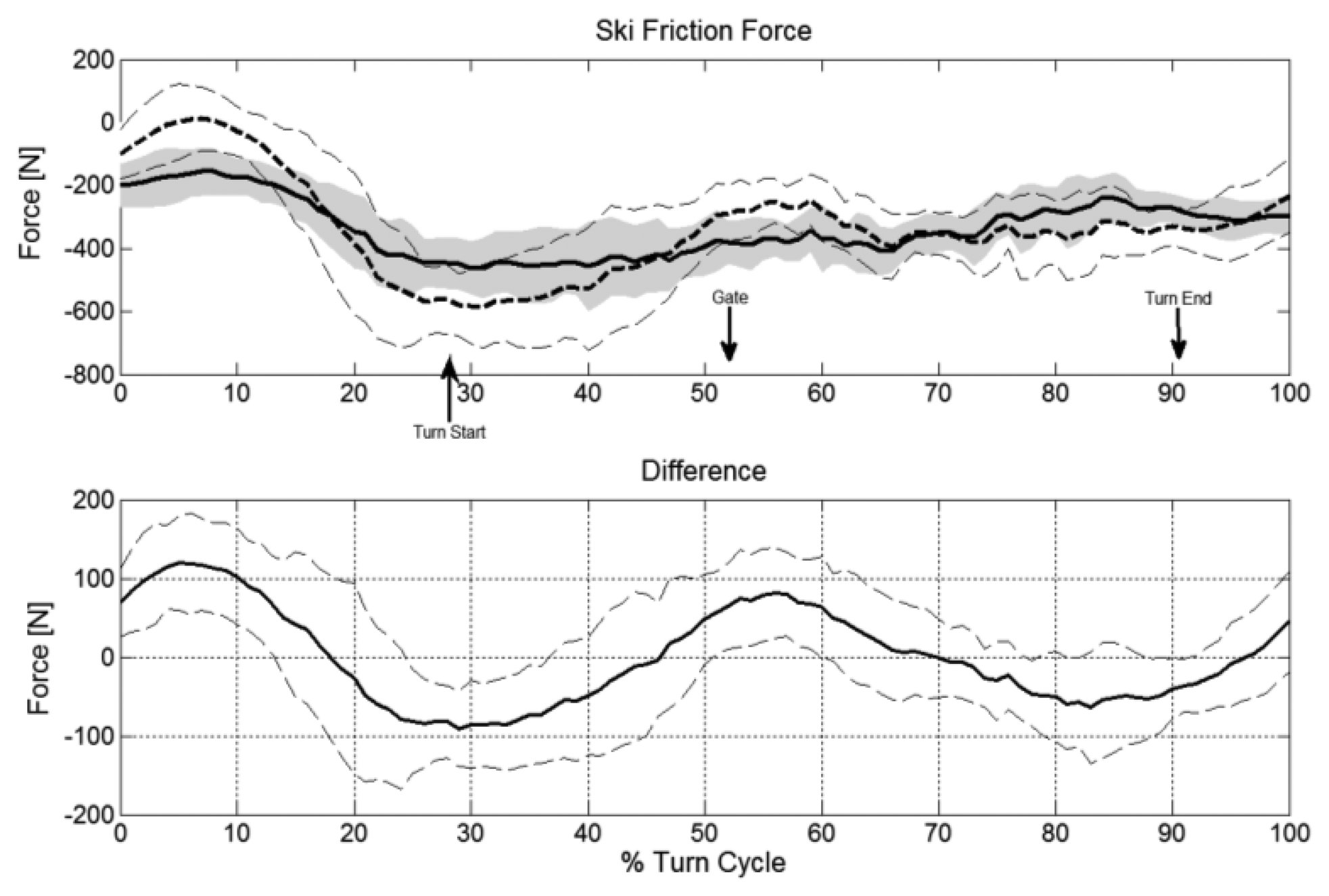
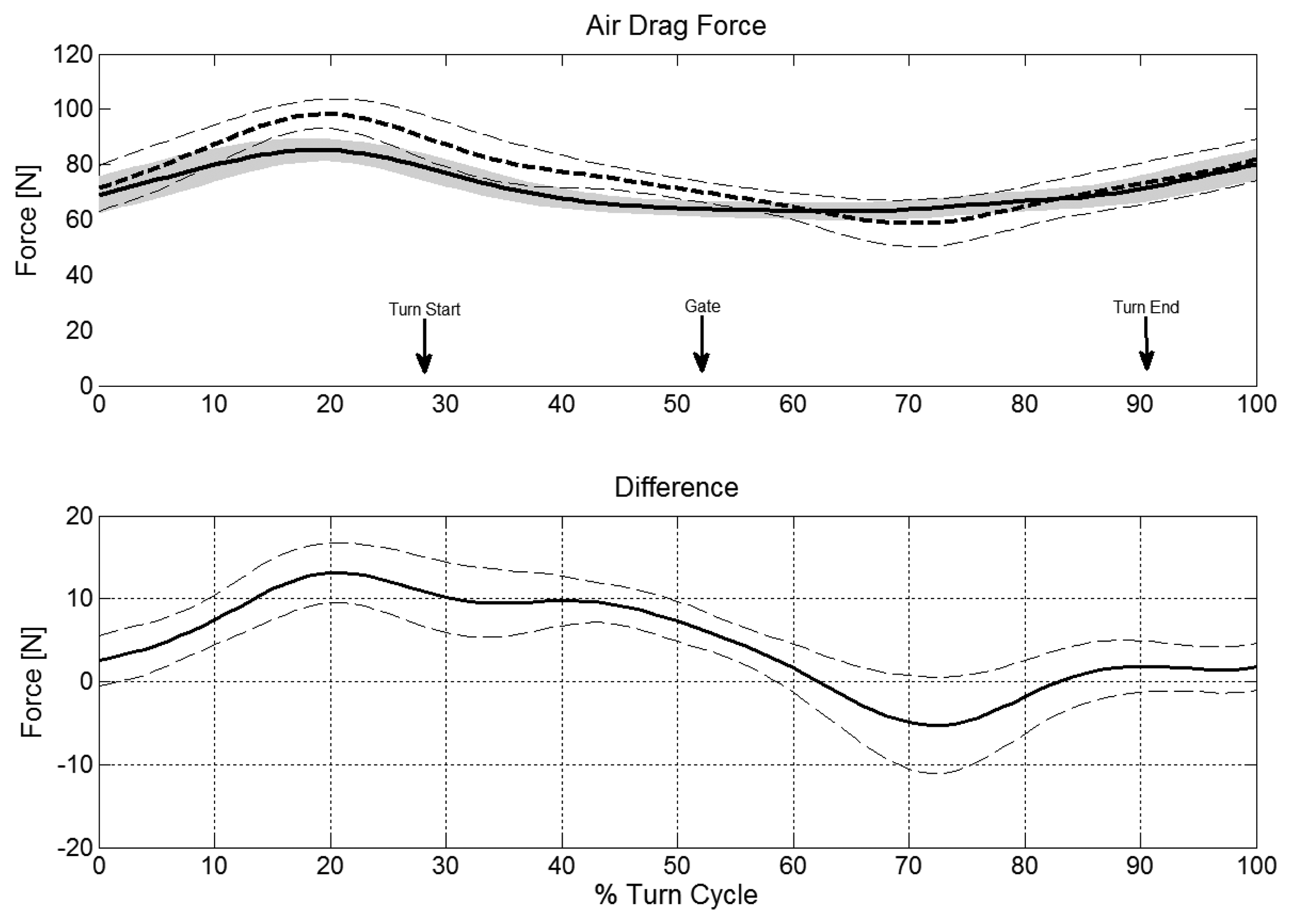
The upper parts of Figure 4, Figure 5 and Figure 6 illustrate FGRF, FF and FD obtained from the reference and the dGNSS method in time-normalized format across the examined turn cycle. The lower parts of Figure 4, Figure 5 and Figure 6 show the progression of the vectorial difference and its AVD-Within-SD for FGRF, FF and FF graphically. All three forces have a variability of the offset. The largest offsets occur in the initiation and completion phase for FGRF and in the initiation phase for FD.
3.2. Discussion
The current study proposed a new approach for the reconstruction of the external forces acting on alpine skiers using a dGNSS-based method. Compared to previous dGNSS-based force modeling [9] the dGNSS antenna was mounted on the helmet instead of the back. The dGNSS method was compared to a kinetic reference system constructed from a video-based 3D kinematic segment model, allowing precise reconstruction of center of mass and air drag. Among the field methods applied to determine air drag in alpine skiing [2,9,14,15,17,27], [15] was chosen as the reference system, since this model most probably accounts best for the different body positions, speed and clothing in giant slalom skiing. The reference system allowed a precise reconstruction of the CoM (mean error 23 mm, SD 10 mm) and thus the resultant force acting on the CoM [33].
A repeatable instantaneous vectorial difference pattern was observed between the dGNSS method and reference system for FGRF, FF and FD (Figure 4, Figure 5 and Figure 6). These patterns oscillated above and below zero and therefore the instantaneous AVD-offsets and the turn mean error compensate across the entire turn cycle and thus differ little from the reference values. Similarly the instantaneous average vectorial difference of FF followed a harmonic pattern around zero (Figure 5) and was approximately compensated in the phase before and after gate passage. Therefore, the offsets of the section before gate passage (−2 N) and after gate passage (5 N) were also small. These findings suggest that comparisons of turn means (typical features of the turn cycle as given in Table (1) between skiers or between different turns are valid as long as they are larger than these precision (SD) boundaries of the method.
The AVD-Offset-Between-SDs represent the precision of the dGNSS method with respect to the reference system in predicting the absolute values of the forces at random time points in the turn cycle. These were relatively large for FGRF and FF but were reduced both in absolute values and relative to the acting forces in the turning phase, when the turn radius was below 30 m.
Because the instantaneous vectorial difference patterns were repeatable for the twelve trials, the AVD-Within-SDs were relatively small: smaller than the AVD-Offset-Between-SDs for FGRF and FF but about equal for FD. The AVD-Offset-SDs describe the precision within the dGNSS method and therefore apply for relative comparisons between skiers or turns when both components are determined with the dGNSS method. In a study investigating slalom skiing [2] it was found that the ground reaction force was 253 N higher at gate passage on a course with a 10 m gate distance compared to a course with a 13 m gate distance. The AVD-Within-SD of the dGNSS method for FGRF was 63 N and thus the dGNSS method is valid to identify such discriminative meaningful changes for the ground reaction force. Similarly the air drag was increased, at 15 N at gate passage in the 13 m course [2], while the AVD-Within-SD for FD was 7 N. As long as the AVD-Within-SD's are smaller than the differences to be investigated, the method is valid for identifying discriminative meaningful changes at random instances in a turn cycle.
The dGNSS method underestimated the turn cycle maxima of all three forces. However, the offset and SD were acceptable with respect to the size of the maximal ground reaction forces [34,35]. Air drag might be maximal in the initiation phase of the turn (Figure 6), when skiers are in a relatively extended body position [2,36]. It is likely that skiers had their arms abducted in that phase of the turn cycle and that these contributed to FD. The underestimation of both maximum and AVD-offset in that phase of the turn may thus partly be caused by the lack of inclusion of the arms in the dGNSS method.
The AVD-offset of FGRF might be caused by the offset in the resultant force, since the offset of the resultant force follows a similar pattern (see results of FRES in the electronic supplementary information) and is substantially larger than the offset of the air drag force. Consequently, the offsets in the first and the last phase of the turn of FGRF might be caused by deficient CoM reconstruction in the dGNSS method. Thus the offset and precision values presented in this study may be valid for the applied dGNSS method and CoM modelling, but may be different for other methods.
3.3. Limitations
The attachment of the measurement device on the head leads to exclusion of the high frequency ground reaction force components. The skier's body acts as a damper [34] and the measurement frequency of the GNSS of 50 Hz is too low to capture the remaining high frequency components transmitted to the head. The same phenomenon is present for the reference system applied in this study. A previous study [11] showed that CoMs reconstructed from video-based 3D kinematic motion capture systems lack the high frequency components due to damping by the lower extremities and the low capture frequency. However, the overall course of the ground reaction force was well reconstructed. Therefore, our reference system seems valid to assess the low frequency component of the ground reaction force. For the assessment of high frequency components or left and right leg ground reaction force information, other types of measurement systems should be applied, such as pressure insoles [11,37–40], force plates [11,37,41–44] or accelerometers [45]. The air drag force model might be improved by adding a model for the arms.
4. Conclusions
This study introduced a dGNSS-based method for the simultaneous determination of all external forces in competitive alpine skiing. The method was found to be technically valid for comparing turn mean forces and allowed instantaneous relative comparisons between skiers with respect to the precision boundaries of 63 N for the ground reaction force, 42 N for the ski friction force and 7 N for the air drag force. Due to its technical validity, its small equipment size/weight and geodetic GNSS measurement robustness the system was found suitable to simultaneously capture CoMPVA[46] and the forces acting on the CoM under racing conditions across large capture volumes. The proposed method might therefore be applied to efficiently investigate competitive alpine skiing and bring better insight to performance and injury-related aspects. The methods strength with respect to performance might be that the ski friction force is expressed in direction of travel and is therefore directly linked to speed regulation. The methods advantage with respect to injury prevention might be that skier loading (ground reaction force) can be determined at the same time as other injury risk factors such as speed are captured with one device.
Acknowledgments
The authors thank Jan Cabri, Geo Boffi and Philip Crivelli for their contribution to this study. This study was partly supported by the International Skiing Federation (FIS).
Conflict of Interest
The authors declare no conflict of interest.
References
- Schiestl, M.; Kaps, P.; Mossner, M.; Nachbauer, W. Calculation of Friction and Reaction Forces during an Alpine World Cup Downhill Race. In The Engineering of Sport, 6th ed.; Moritz, E.F., Haake, S., Eds.; Springer: New York, NY, USA, 2006; Volume 1, pp. 269–274. [Google Scholar]
- Reid, R. A Kinematic and Kinetic Study of Alpine Skiing Technique in Slalom. Ph.D. Thesis, Norwegian School of Sport Sciences, Oslo, Norway, 1 January 2010. [Google Scholar]
- Spörri, J.; Kröll, J.; Schwameder, H.; Müller, E. Turn characteristics of a top world class athlete in giant slalom: A case study assessing current performance prediction concepts. Int. J. Sports Sci. Coach 2012, 7, 647–659. [Google Scholar]
- Supej, M.; Kipp, R.; Holmberg, H.C. Mechanical parameters as predictors of performance in alpine World Cup slalom racing. Scand. J. Med. Sci. Sports 2011, 21, 72–81. [Google Scholar]
- Skaloud, J.; Limpach, P. Synergy of CP-DGPS, Accelerometry and Magnetic Sensors for Precise Trajectography in Ski Racing. Proceedings of the Conference of the ION GPS/GNSS, Portland, OR, USA, 9–12 September 2003.
- Supej, M.; Holmberg, H.C. A new time measurement method using a high-end global navigation satellite system to analyze alpine skiing. Res. Q. Exerc. Sport 2011, 82, 400–411. [Google Scholar]
- Supej, M. 3D measurements of alpine skiing with an inertial sensor motion capture suit and GNSS RTK system. J. Sports Sci. 2010, 28, 759–769. [Google Scholar]
- Gilgien, M.; Singer, J.; Rhyner, H. Comparison of Two Methods to Assess the Choice of Skier Trajectories through Banked Turns in Ski Cross. Proceedings of the 5th International Congress on Science and Skiing, St. Christoph, Austria, 14–19 October 2010.
- Supej, M.; Saetran, L.; Oggiano, L.; Ettema, G.; Saarabon, N.; Nemec, B.; Holmberg, H.C. Aerodynamic drag is not the major determinant of performance during giant slalom skiing at the elite level. Scand. J. Med. Sci. Sports 2013, 23, e38–e47. [Google Scholar]
- Federolf, P. Quantifying instantaneous performance in alpine ski racing. J. Sports Sci. 2012, 30, 1063–1068. [Google Scholar]
- Lüthi, A.; Federolf, P.; Fauve, M.; Oberhofer, K.; Rhyner, H.; Amman, W.; Stricker, G.; Schiefermüller, C.; Eitzlmair, E.; Schwameder, H.; et al. Determination of Forces in Carving Using Three Independent Methods. Proceedings of the 3rd International Congress on Science and Skiing, St. Cloud State University, Aspen, CO, USA, 28 March 2004.
- Schiestl, M.; Kaps, P.; Mossner, M.; Nachbauer, W. Snow Friction and Drag during the Downhill Race in Kitzbuhel. Proceedings of the Program and Abstracts, Mountain and Sport: Updating Study and Research from Laboratory to Field, Rovereto, Italy, 11–12 November 2005.
- Reid, R.; Gilgien, M.; Haugen, P.; Kipp, R.; Smith, G. Force and Energy Characteristics in Competitive Slalom. Proceedings of the 5th International Congress on Science and Skiing, St.Christoph, Austria, 14–19 October 2010; Müller, E., Lindinger, S., Stoggl, T., Eds.; Meyer Sport: Aachen, Germany.
- Gilgien, M.; Reid, R.; Haugen, P.; Kipp, R.; Smith, G. External Forces Acting in Direction of Travel and Their Relation to Energy Dissipation in Slalom. Proceedings of the 14th Annual Congress of the European College of Sport Science, Oslo, Norway, 13 July 2009.
- Meyer, F.; Le Pelley, D.; Borrani, F. Aerodynamic drag modeling of alpine skiers performing giant slalom turns. Med. Sci. Sports Exerc. 2011, 44, 1109–1115. [Google Scholar]
- Madura, JM.; Lufkin, T.; Brown, C. Calculated Descent Times for Different Radii in Ski Racing. Proceedings of 5th International Congress on Science and Skiing, St. Christoph, Austria, 14–19 October 2010.
- Brodie, M.; Walmsley, A.; Page, W. Fusion motion capture: A prototype system using IMUs and GPS for the biomechanical analysis of alpine ski racing. Sports Tech. 2008, 1, 17–28. [Google Scholar]
- Huber, A.; Spitzenpfeil, P.; Waibel, K.; Debus, D.; Fozzy, M.E. CRIPS-Crash Recognition and Injury Prevention in Alpine Ski Racing. Proceedings of the 5th International Congress on Science and Skiing, St. Christoph, Austria, 14–19 October 2010.
- De Berg, M.; Otfried, C.; van Kreveld, M.; Overmars, M. Computational Geometry: Algorithms and Applications, 3rd ed.; Springer-Verlag: Berlin, Germany, 2008. [Google Scholar]
- Gilgien, M.; Reid, R.; Haugen, P.; Smith, G. Digital Terrain Modelling of Snow Surfaces for Use in Biomechanical Investigations in Snow Sports. Proceedings of the 13th Annual Congress of the European College of Sport Science, Lisboa, Portugal, 9–12 July 2008.
- Hugentobler, M. Terrain Modelling with Triangle Based Free-Form Surfaces. Ph.D. Thesis, ETH Zurich, Zurich, Switzerland, 2004. [Google Scholar]
- Supej, M.; Kugovnik, O.; Nemec, B. Kinematic determination of the beginning of a ski turn. Kinesiol. Slov. 2003, 9, 11–17. [Google Scholar]
- Morawski, J.M. Control systems approach to a ski-turn analysis. J. Biomech. 1973, 6, 267–279. [Google Scholar]
- Gilat, A.; Subramaniam, V. Numerical Methods for Engineers and Scientists, 2nd ed.; Wiley & Sons Inc.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Gilgien, M.; Spörri, J.; Kröll, J.; Chardonnens, J.; Cabri, J.; Müller, E. Speed as an Injury Risk Factor in Competitive Alpine Ski Racing Depends on Events. Proceedings of the 17th Annual Congress of the European College of Sport Science, Bruges, Belgium, 4–7 July 2012.
- Van Ingen, S.G.J. The influence of air friction in speed skating. J. Biomech. 1982, 15, 449–458. [Google Scholar]
- Barelle, C.; Ruby, A.; Tavernier, M. Experimental model of the aerodynamic drag coefficient in alpine skiing. J. Appl. Biomech. 2004, 20, 167–176. [Google Scholar]
- Spörri, J.; Kröll, J.; Schwameder, H.; Schiefermuller, C.; Müller, E. Course setting and selected biomechanical variables related to injury risk in alpine ski racing: An explorative case study. Br. J. Sports Med. 2012, 46, 1072–1077. [Google Scholar]
- Drenk, V. Bildmeßverfahren für schwenk und neigbare sowie in der Brennweite variierbare Kameras; Institut für Angewandte Trainingswissenschaft, Bundesinstitut für Sportwissenschaft: Köln, Germany, 1994; pp. 130–142. [Google Scholar]
- Zatsiorsky, V.M. Kinetics of Human Motion, 1st ed.; Human Kinetics Inc.: Champaign, IL, USA, 2002. [Google Scholar]
- De Leva, P. Adjustments to Zatsiorsky-Seluyanov's segment inertia parameters. J. Biomech. 1996, 29, 1223–1230. [Google Scholar]
- Gilgien, M. External Forces Acting in Direction of Travel and Their Relation to Energy Dissipation in Slalom. M.Sc. Thesis, Norwegian School of Sport Sciences, Oslo, Norway, 1 November 2010. [Google Scholar]
- Klous, M.; Müller, E.; Schwameder, H. Collecting kinematic data on a ski/snowboard track with panning, tilting, and zooming cameras: Is there sufficient accuracy for a biomechanical analysis? J. Sports Sci. 2010, 28, 1345–1353. [Google Scholar]
- Babiel, S.; Hartmann, S.; Spitzenpfeil, P.; Mester, J. Ground Reaction Forces in Alpine Skiing, Cross-Country Skiing and Ski Jumping. In Science and Skiing III; Müller, E., Bacharach, D., Klika, R., Schwameder, H., Lindinger, S., Eds.; E&FN Spon: London, UK, 1997; pp. 200–207. [Google Scholar]
- Federolf, P.; Fauve, M.; Luthi, A.; Rhyner, H.; Ammann, W.; Dual, J. Finite Element Simulation of a Carving Alpine Ski. Proceedings of the 3rd International Congress on Science and Skiing, Saint Cloud, MN, USA, 28 March 2004.
- Müller, E.; Schwameder, H. Biomechanical aspects of new techniques in alpine skiing and ski-jumping. J. Sport Sci. 2003, 21, 679–692. [Google Scholar]
- Nakazato, K.; Scheiber, P.; Müller, E. A comparison of ground reaction forces determined by portable force-plate and pressure-insole systems in alpine skiing. J. Sports Sci. Med. 2011, 10, 754–762. [Google Scholar]
- Holden, M.; Parker, R.; Walsh, A. Dynamic Force Measurement Technique to Evaluate Skier Performance. Proceedings of the 3rd International Congress on Science and Skiing, Saint Cloud, MN, USA, 28 March 2004.
- Kruger, A.; Edelmann-Nusser, J. Biomechanical analysis in freestyle snowboarding: Application of a full-body inertial measurement system and a bilateral insole measurement system. Sports Technol. 2009, 2, 17–23. [Google Scholar]
- Klous, M.; Müller, E.; Schwameder, H. Knee Joint Loading an Alpine Skiing: A Comparison between Carved and Skidded Turns. Proceedings of the 13th Annual Congress of the European College of Sport Science, Lisboa, Portugal, 9–12 July 2008.
- Niessen, M.; Müller, E.; Wimmer, M.A.; Schwameder, H.; Riepler, B. Force and Moment Measurements during Alpine Skiing Depending on Height Position. Proceedings of the 16th International Symposium on Biomechanics in Sports, Konstanz, Germany, 21–25 July 1998.
- Wunderly, G.S.; Hull, M.L.; Maxwell, S. A second generation microcomputer controlled binding system for alpine skiing research. J. Biomech. 1988, 21, 299–318. [Google Scholar]
- Wunderly, G.S.; Hull, M.L. A biomechanical approach to alpine ski binding design. Int. J. Sport Biomech. 1989, 5, 308–323. [Google Scholar]
- Federolf, P.; Scheiber, P.; Rauscher, E.; Schwameder, H.; Luthi, A.; Rhyner, H.U.; Müller, E. Impact of skier actions on the gliding times in alpine skiing. Scand. J. Med. Sci. Sports 2008, 18, 790–797. [Google Scholar]
- Chardonnens, J.; Favre, J.; Gremion, G.; Aminian, K. Knee Joint Kinematics Measurement in Alpine Skiing Based on Inertial Sensors. Proceedings of the 5th International Congress on Science and Skiing, St. Christoph, Austria, 14–19 October 2010.
- Gilgien, M. GNSS-Anwendungen im Schneesport-Leistungsoptimierung und Verletzungs-Prophylaxe. In AHORN, Der Alpenraum und seine Herausforderungen im Bereich Orientierung, Navigation und Informationsaustausch; Schweizerisches Institut für Navigation (ION-CH): Davos, Switzerland, 2012. [Google Scholar]



| Differences | FGRF | FF | FD | |
|---|---|---|---|---|
| Average Vectorial Difference (AVD) for Turn Cycle | Offset [N] | −25.8 | 1.3 | −6.4 |
| Offset [% ] | −1.9 | 0.3 | −8.9 | |
| Offset-between SD [N] | 151.7 | 96.2 | 6.1 | |
| Offset-between SD [% ] | 11 | 26.3 | 8.5 | |
| Within SD [N] | 63.2 | 41.5 | 7.0 | |
| Within SD [% ] | 4.6 | 11.4 | 9.8 | |
| Average Vectorial Difference (AVD) for Turning Phase (R < 30 m) | Offset [N] | 7.7 | −16.6 | 3.1 |
| Offset [% ] | 0.5 | −3.8 | 4.8 | |
| Offset-between SD [N] | 124.2 | 81.3 | 5.8 | |
| Offset-between SD [% ] | 7.5 | 18.5 | 9.1 | |
| Typical Turn Cycle Feature | Mean [N] | −22.2 | 1.1 | −4.4 |
| SD of Mean [N] | 24 | 6.8 | 2.9 | |
| Maxima [N] | −71.7 | −23.2 | −18.7 | |
| SD of Maxima [N] | 63.1 | 76.2 | 5.8 | |
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/Licenses/by/3.0/).
Share and Cite
Gilgien, M.; Spörri, J.; Chardonnens, J.; Kröll, J.; Müller, E. Determination of External Forces in Alpine Skiing Using a Differential Global Navigation Satellite System. Sensors 2013, 13, 9821-9835. https://doi.org/10.3390/s130809821
Gilgien M, Spörri J, Chardonnens J, Kröll J, Müller E. Determination of External Forces in Alpine Skiing Using a Differential Global Navigation Satellite System. Sensors. 2013; 13(8):9821-9835. https://doi.org/10.3390/s130809821
Chicago/Turabian StyleGilgien, Matthias, Jörg Spörri, Julien Chardonnens, Josef Kröll, and Erich Müller. 2013. "Determination of External Forces in Alpine Skiing Using a Differential Global Navigation Satellite System" Sensors 13, no. 8: 9821-9835. https://doi.org/10.3390/s130809821






